Probability of a Disease Outbreak in Stochastic Multipatch Epidemic Models

Abstract

Environmental heterogeneity, spatial connectivity, and movement of individuals play important roles in the spread of infectious diseases. To account for environmental differences that impact disease transmission, the spatial region is divided into patches according to risk of infection. A system of ordinary differential equations modeling spatial spread of disease among multiple patches is used to formulate two new stochastic models, a continuous-time Markov chain, and a system of stochastic differential equations. An estimate for the probability of disease extinction is computed by approximating the Markov chain model with a multitype branching process. Numerical examples illustrate some differences between the stochastic models and the deterministic model, important for prevention of disease outbreaks that depend on the location of infectious individuals, the risk of infection, and the movement of individuals.

1 Introduction

With the expansion of global and regional transportation networks, infectious diseases in humans or domestic and wild animals, such as influenza, tuberculosis, SARS, malaria, cholera, and foot-and-mouth disease can be more easily transmitted from region to region (Tatem et al. 2006). Factors such as spatial connectivity, environmental conditions, and the large-scale movement of individuals can significantly affect the likelihood that a disease will persist in a given region. For instance, disease may be absent from rural areas unless infectious individuals from urban centers travel to these more remote regions. Alternatively, the reverse may be the case where the disease is present in rural areas and is spread to urban areas (Scoglio et al. 2010). Similarly, the spread of disease can occur at an accelerated rate in social or environmental “hotspots” such as airports, schools, or common water sources (Arino et al. 2012; Benavides et al. 2012; Khan et al. 2009). Thus, it is important to account for factors such as large-scale movements and environmental heterogeneity in epidemic models.

Most studies regarding the role of movement on disease dynamics have emphasized either a deterministic metapopulation approach (e.g., Allen et al. 2007; Arino and van den Driessche 2003; Arino et al. 2005, 2007; Brauer and van den Driessche 2001; McCormack and Allen 2007; Salmani and van den Driessche 2006; Wang and Mulone 2003; Wang and Zhao 2004) or a stochastic multi-group approach (e.g., Ball 1983, 1991; Ball and Clancy 1993, 1995; Clancy 1994, 1996; Keeling et al. 2001; Neal 2012). Additional epidemic models which include movement of hosts have been developed for particular diseases such as influenza (Hsieh et al. 2007; Rvachev and Longini 1985), tuberculosis (Castillo-Chavez et al. 1998), foot-and-mouth disease (Keeling et al. 2001), and malaria (Gao and Ruan 2012). Many of these models subdivide a spatial region into multiple regions or patches to account for differences in the risk for infection.

In the deterministic setting, patch dynamics are frequently modeled by a system of ordinary differential equations (ODEs) such as Susceptible–Infectious–Recovered (SIR). Often the deterministic models concentrate on asymptotic dynamics of the disease-free or endemic equilibria (e.g., Allen et al. 2007; Arino and van den Driessche 2003; Arino et al. 2005; Brauer and van den Driessche 2001; McCormack and Allen 2007; Wang and Mulone 2003; Wang and Zhao 2004). Model behavior with host movement can become quite complicated after an outbreak has occurred. For example, in an SEIRS model (E=exposed) with constant immigration and death rates, it is shown that as travel rates increase, a stable endemic state may switch to a stable disease-free equilibrium (Salmani and van den Driessche 2006). In another deterministic Susceptible–Infectious–Susceptible (SIS) model with a constant population size, if infectious individuals move between the patches and the rate of susceptible movement approaches zero, contrary to what is expected, eventually the disease is eliminated from the population (Allen et al. 2007). Deterministic models have examined the impact of movement restrictions on disease control. Conducting border checks, restricting movement of infectious individuals and restricting movement to and from high-risk patches where disease is more prevalent results in an effective control (Arino et al. 2007). In the case of influenza, Hsieh et al. (2007) also showed that restricting movement of infectious individuals from low- to high-risk patches is an effective control measure. However, banning all travel of infectious individuals from high- to low-risk patches could result in the low-risk patch becoming disease-free, while the high-risk patch has an even higher disease prevalence (Hsieh et al. 2007). Similarly, Ruan et al. (2006) showed that the spread of SARS can be contained by implementing border screening for infectious individuals. But screening at the borders may only be effective in identifying individuals exhibiting symptoms and movement of exposed individuals may contribute to the spread of disease (Gao and Ruan 2012).

In the stochastic setting, models generally take the form of a continuous-time Markov chain (CTMC) model with movement modeled either by a contact distribution or by transition rates between groups (Ball 1983, 1991; Ball and Clancy 1993, 1995; Clancy 1994, 1996; Neal 2012). In some cases, the general stochastic process can be approximated by a branching process or by an underlying ODE model when the population size is large (Ball 1991; Clancy 1994, 1996). In these cases, a stochastic threshold for disease extinction is obtained but the probability of disease extinction is generally not calculated. The stochastic models have also shown that the total size of the epidemic depends on the speed of movement and total size increases with movement of infectious individuals (e.g., Clancy 1994). Previous studies focused on deterministic models in which the probability of disease extinction cannot be determined, or on stochastic models in which the probability of disease extinction was not calculated.

Our goals in this investigation are to extend some of the work on deterministic multipatch models to closely related stochastic multipatch models to account for the variability in the transmission, recovery, and movement behavior at the initiation of an outbreak. Our approach differs from other stochastic multigroup models in that we begin from the deterministic setting and formulate stochastic multipatch models based on the assumptions of the ODE model. The stochastic multipatch models provide additional information about disease dynamics at the initiation of an outbreak and during an outbreak that cannot be obtained from the deterministic models. The stochastic models applied in this investigation are continuous-time Markov chains (CTMCs) and stochastic differential equations (SDEs). A multitype branching process approximation of the nonlinear CTMC model is used to estimate the probability of disease extinction. We investigate the risk of infection in a patch and the location of an outbreak on the probability of disease extinction. Our stochastic results illustrate that the location of the initial infectious individuals, whether in a high-risk or low-risk area, has a significant impact on the probability of an outbreak. Our stochastic results confirm that at the initiation of an outbreak, directing the movement of infectious individuals into low-risk areas is an effective disease control strategy, while directing the movement of susceptible individuals does not impact the probability of disease extinction.

In the next section, a multipatch ODE model is introduced and the dynamics with respect to disease extinction are summarized. In Sect. 3, a multipatch CTMC model is formulated and an approximating branching process is defined. In Sect. 4, a multipatch SDE model is derived from the CTMC model. Finally, in Sect. 5, numerical examples are presented for the ODE, CTMC, and SDE models as well as estimates for the probability of disease extinction. The last section summarizes our findings on the impact of environmental heterogeneity, spatial connectivity, and movement to disease outbreaks and discusses their implications for disease control.

2 ODE Model

Consider a multipatch SIS model with movement of both susceptible and infectious individuals between patches. Let n be the total number of patches, Ω={1,2,…,n}, and S _j (t) and I _j (t) denote the number of susceptible and infectious individuals in patch j at time t, respectively. Denote the total population size in patch j by N _j (t)=S _j (t)+I _j (t). The model takes the form

(1)

(2)

where S _j (0)>0 and I _j (0)≥0 for all j∈Ω, with standard incidence rate β _j S _j I _j /N _j . The parameters $d_{kj}^{s}\geq0$ and $d_{kj}^{i}\geq0$ represent the rate of movement (dispersal) from patch k to patch j by susceptible and infectious individuals, respectively. The parameters β _j >0, γ _j >0, and α _j ≥0 represent the rates of infection, recovery, and disease-related death in patch j, respectively. This model is similar to the multipatch SIS model of Allen et al. (2007) with the exception that there are disease-related deaths. Solutions to (1)–(2) are nonnegative for t∈[0,∞).

The only demographic processes in this model are disease-related deaths (i.e., no births or other recruitment). Thus, N(t)≤N(0) for t∈[0,∞) and solutions to (1)–(2) are bounded. Summing the equations for $\dot{S}_{j}$ and $\dot{I}_{j}$ in (1)–(2), it follows that for each j∈Ω,

$$ \dot{N}_j=-\alpha_jI_j+\sum _{k\in\varOmega }\bigl(d_{kj}^sS_k-d_{jk}^sS_j+d_{kj}^iI_k-d_{jk}^iI_j \bigr). $$

(3)

Let N denote the total population size in all patches, N=∑ _j∈Ω N _j . It follows from Eq. (3) that

$$ \dot{N}=-\sum_{j\in\varOmega}\alpha_jI_j. $$

(4)

If there are no disease-related deaths, α _j =0 for each j∈Ω, then N(t)≡N(0) is constant.

To characterize the dynamics of model (1)–(2), it is useful to introduce some notation involving the parameters $d_{kj}^{s}$ and $d_{kj}^{i}$. Define the dispersal matrices for susceptible and infectious individuals as

$$ D_s=\bigl[d_{kj}^s\bigr] \quad \mbox{and} \quad D_i=\bigl[d_{kj}^i \bigr]. $$

(5)

In the case of two patches,

For each patch j∈Ω, define the patch reproduction number as

$$ \mathcal{R}_{0j}=\frac{\beta_j}{\gamma_j+\alpha_j}. $$

(6)

If $\mathcal{R}_{0j}>1$, then patch j is said to be a high-risk patch. Otherwise, it is called a low-risk patch (Allen et al. 2007). Whether a patch is high- or low-risk depends on many factors that affect transmission β _j , recovery γ _j , and mortality α _j . These factors may be environmental (water-borne diseases such as cholera) or host-dependent (differences in contacts or susceptibility among hosts).

The following theorem summarizes the dynamics of the SIS epidemic model in each patch when there is no movement. All proofs are given in the Appendix.

Theorem 2.1

Assume the dispersal matrices D _s =D _i =O (zero matrices). For the multipatch epidemic model (1)–(2), the patch reproduction numbers determine the long-term behavior in each patch.

• (i) If $\mathcal{R}_{0j}>1$, then

  $$\lim_{t\rightarrow\infty}\bigl(S_j(t),I_j(t)\bigr)= \left \{ \begin{array}{l@{\quad}l} \bigl(\frac{N_j(0)}{\mathcal{R}_{0j}}, (1-\frac{1}{\mathcal {R}_{0j}} )N_j(0) \bigr), & \alpha_j=0,\\[5pt] (0,0), & \alpha_j>0. \end{array} \right . $$

• (ii) If $\mathcal{R}_{0j}\leq1$, then

  $$\lim_{t\rightarrow\infty}\bigl(S_j(t),I_j(t)\bigr)= \left \{ \begin{array}{l@{\quad}l} (N_j(0),0), & \alpha_j=0,\\[5pt] (C_j,0), & \alpha_j>0, \end{array} \right . $$

  for some C _j where 0≤C _j <N _j (0).

With no disease-related deaths, the population size remains constant, so that if $\mathcal{R}_{0j}>1$, the disease becomes endemic, but with disease-related deaths, if $\mathcal{R}_{0j}>1$, first an outbreak occurs followed by complete population extinction.

To define the basic reproduction number for model (1)–(2), we linearize (2) about I _j (0)≈0 and S _j (0)≈N _j (0). In particular,

$$ \dot{I}_j\approx \biggl[\beta_j- \gamma_j-\alpha_j-\sum_{k\in\varOmega }d^i_{jk} \biggr] I_j+\sum_{k\in\varOmega} d^i_{kj}I_k $$

(7)

for j∈Ω. Following van den Driessche and Watmough (2002), let

(8)

(9)

The basic reproduction number is the spectral radius of FV ⁻¹,

$$ \mathcal{R}_0=\rho\bigl(FV^{-1}\bigr). $$

(10)

The eigenvalues of the linearized system (7), written as $\dot{I}=(F-V)I$, have negative real part if and only if the spectral radius of FV ⁻¹ is less than one. The entries of F and V and, therefore, the value of $\mathcal{R}_{0}$, do not depend on the movement of susceptible individuals (Allen et al. 2007).

If individuals move between the patches (D _s and D _i nonzero), the following theorem shows that there is global disease extinction if $\mathcal{R}_{0}<1$, regardless of the initial population size in each patch.

Theorem 2.2

For the multipatch SIS epidemic model (1)–(2),

• (i) if $\mathcal{R}_{0}<1$, then lim _t→∞ I _j (t)=0 for all patches j∈Ω, and

• (ii) if $\mathcal{R}_{0j}<1$ for a given patch j∈Ω and $d_{jk}^{i}=d_{kj}^{i}=0$ for k≠j, then lim _t→∞ I _j (t)=0.

The disease-free equilibrium becomes unstable when $\mathcal{R}_{0}>1$ in the ODE model and generally a major outbreak occurs. For a small number of infectious individuals, this is not necessarily the case for the corresponding Markov chain (MC) model.

3 Markov Chain Models

3.1 CTMC Model

For a small number of infectious individuals, the predictions of the ODE model do not necessarily agree with the MC model. If $\mathcal{R}_{0}>1$, there is a possibility in the MC model that infectious individuals die or recover before an outbreak occurs. In this case, a MC model with a discrete number of individuals is more realistic than an ODE model.

To formulate a continuous-time Markov chain (CTMC) model, let

$$\vec{X}(t)=\bigl(S_1(t),I_1(t),\ldots,S_n(t),I_n(t) \bigr) $$

denote a discrete-valued random vector where S _j (t),I _j (t)∈{0,1,…,N(0)} for j∈Ω. For simplicity, the same notation is used for the discrete random variables and parameters as for the deterministic model (see Eqs. (1) and (2)). The state transitions and rates for the CTMC model are given in Table 1. Because of the Markov assumption, the time between events is exponentially distributed with parameter

$$ \omega(\vec{X})=\sum_{j\in\varOmega} \biggl[ \beta_j\dfrac {S_j}{N_j}I_j+\gamma_jI_j+ \alpha_jI_j+\sum_{k\in\varOmega\backslash\{j\} } \bigl(d_{jk}^sS_j+d_{jk}^i I_j\bigr) \biggr]. $$

(11)

Table 1 State transitions and rates for the multipatch CTMC model. The expression rΔt+o(Δt) is the infinitesimal transition probability for the change $\Delta\vec{X}(t)=\vec{X}(t+\Delta t)-\allowbreak \vec{X}(t)$, S _j ≡S _j (t), and I _j ≡I _j (t)

To derive a relationship between model parameters and the probability of disease extinction, we apply the powerful theory of multitype branching processes to approximate the nonlinear CTMC model near the disease-free equilibrium. A multitype branching process assumes the transition rates are linear. In particular, in Table 1, the transition rate for the infection process near the disease-free state is β _j I _j .

3.2 Branching Process Approximation

The dynamics of the nonlinear CTMC model can be approximated near the disease-free equilibrium by a multitype (Galton–Watson) branching process (Dorman et al. 2004; Harris 1963; Pénnison 2010). The branching process is applied only to the infectious individuals and the susceptible individuals are assumed to be at the disease-free state. In particular, assume that infectious individuals of type j, I _j , give “birth” to infectious individuals of type k, I _k , and that the number of offspring produced by a type j individual does not depend on the number of offspring produced by other individuals of type j or k≠j. Moreover, assume that the initial population in each patch is sufficiently large, S _j (0)≈N _j (0). Because the multitype branching process is linear near the disease-free state, time-homogeneous, and births and deaths are independent, we can define offspring probability generating functions (pgfs) for the birth and death of the infectious individuals, which in turn can be used to calculate the probability of disease extinction.

We define additional discrete random variables for the number of infected offspring in patch k that arise from an infectious individual in patch j. Let Y _kj denote these offspring random variables. The offspring pgf for I _j defines probabilities associated with “birth” of infectious individuals in patch k or “death” of the infectious individual I _j , given that the process starts with only one infectious individual of type j, I _j =1, and I _k =0 for k≠j,

$$f_j(x_1,\ldots,x_n)=\sum _{\ell_n=0}^{\infty}\cdots\sum_{\ell _1=0}^{\infty}P_j( \ell_1,\ldots,\ell_n)x_1^{\ell_1} \cdots x_n^{\ell_n}, $$

where

$$P_j(\ell_1,\ldots,\ell_n)=\mbox{Prob} \{Y_{1j}=\ell_1,\ldots,Y_{nj}=\ell _n\} $$

(see, e.g., Athreya and Ney 1972; Dorman et al. 2004; Harris 1963; Karlin and Taylor 1975; Pénnison 2010). The offspring pgf for I _j is used to calculate the expected number of offspring produced by an infectious individual of type j and the probability of disease extinction of type j.

The rates in Table 1 with the additional assumption that the infection rate is β _j I _j at the disease-free equilibrium are used to define the offspring pgf for I _j :

$$ f_j(x_1,\ldots,x_n)=\frac{\beta_jx_j^2+\gamma_j+\alpha_j+ \sum_{k\in\varOmega\backslash\{j\}}d_{jk}^ix_k}{\beta_j+\gamma_j+\alpha _j+\sum_{k\in\varOmega\backslash\{j\}}d_{jk}^i} $$

(12)

(Allen and Lahodny 2012; Dorman et al. 2004). The term $\beta_{j}/(\beta_{j}+\gamma_{j}+\alpha_{j}+\sum_{k\in\varOmega\backslash \{j\}}d_{jk}^{i})$ represents the probability that a susceptible individual in patch j becomes infectious and the infectious individual causing the infection does not die which results in two infectious individuals in patch j (Y _jj =2 and Y _ij =0 for i≠j). The term $(\gamma_{j}+\alpha_{j})/(\beta_{j}+\gamma_{j}+\alpha _{j}+\sum_{k\in\varOmega\backslash\{j\}}d_{jk}^{i})=P_{j}(0,\ldots,0)$ represents the probability that an infectious individual in patch j is lost due to recovery or death resulting in zero infectious individuals (Y _ij =0 for all i). The term $d_{jk}^{i}/(\beta_{j}+\gamma _{j}+\alpha_{j}+\sum_{k\in\varOmega\backslash\{j\}}d_{jk}^{i})$ represents the probability of an infectious individual moving from patch j to k resulting in one infectious individual in patch k and zero infectious individuals in patch j (Y _kj =1 and Y _ij =0 for i≠k). The offspring pgfs do not depend on the movement of susceptible individuals, only the facts that S _j (0)≈N _j (0) is large, the births and deaths are independent of each other, and the process is time-homogeneous.

The expectation matrix M=[m _kj ] of the offspring pgfs is a nonnegative n×n matrix whose entry m _kj gives the expected number of infectious offspring in patch k produced by an infectious individual in patch j. That is,

$$ m_{kj}=\frac{\partial f_j}{\partial x_k}\bigg \vert _{\vec{x}=\vec{1}}. $$

(13)

In particular, for the multipatch SIS model,

$$ m_{kj}= \left\{ \begin{array}{l@{\quad}l} \frac{2\beta_j}{\beta_j+\gamma_j+\alpha_j+\sum_{k\in\varOmega \backslash\{j\}}d_{jk}^i}, & k=j,\\[9pt] \frac{d_{jk}^i}{\beta_j+\gamma_j+\alpha_j+\sum_{k\in\varOmega \backslash\{j\}}d_{jk}^i}, & k\neq j. \end{array} \right . $$

(14)

Explicitly, the expectation matrix has the form

where $A_{j}=\beta_{j}+\gamma_{j}+\alpha_{j}+\sum_{k\in\varOmega\backslash\{j\} }d_{jk}^{i}$ for j∈Ω. If the patches are connected by movement of infectious individuals, then M is irreducible.

Let

$$ W=\mbox{diag} \biggl[\beta_j+\gamma_j+ \alpha_j+\sum_{k\in\varOmega\backslash \{j\}}d_{jk}^i \biggr], $$

(15)

an n×n diagonal matrix. The jth diagonal entry in W is the parameter in an exponential distribution for the time between events for one infectious individual of type j (Eq. (11) with only terms affecting I _j ). It can be easily verified that

$$ [M-{\rm{\bf I}}]W=F-V=\bigl[FV^{-1}-{\rm{\bf I}} \bigr]V, $$

(16)

where ${\rm{\bf I}}$ is the n×n identity matrix and matrices F and V are defined as in (8) and (9), respectively (see Allen and van den Driessche 2013). The important identity defined in (16) relates the linear branching process approximation of the CTMC model to the linearization of the ODE model near the disease-free equilibrium. Applying the theory of branching processes, it follows that the continuous-time multitype branching process is subcritical, critical, or supercritical if the spectral abscissa (the maximum real part of any eigenvalue) of $[M-{\rm{\bf I}}] W$ is less than, equal to, or greater than zero, respectively (Athreya and Ney 1972; Dorman et al. 2004; Harris 1963; Karlin and Taylor 1975; Pénnison 2010). It has been verified that the identity (16) leads to the following relationship provided M is irreducible and V is a nonsingular M matrix (Allen and van den Driessche 2013; van den Driessche and Watmough 2002):

$$ \mathcal{R}_0<1\ (=1,>1)\quad {\rm if \ and \ only\ if }\ \rho(M)<1\ (=1,>1). $$

(17)

For the subcritical and critical cases, $\mathcal{R}_{0}\leq1$ and ρ(M)≤1, the probability of ultimate extinction is one

$$ \lim_{t\rightarrow\infty}\mbox{Prob}\bigl\{\vec{I}(t)=\vec{0}\bigr\}=1. $$

(18)

For the supercritical case, $\mathcal{R}_{0}>1$ and ρ(M)>1, if M is irreducible and the f _j are nonsingular (f _j ≠∑a _i x _i ), then

$$ \mathbb{P}_0=\lim_{t\rightarrow\infty}\mbox{Prob}\bigl\{ \vec{I}(t)=\vec{0}\bigr\} =q_1^{i_1}q_2^{i_2} \cdots q_n^{i_n}, $$

(19)

where i _j =I _j (0) and q _j is the unique fixed point lying in (0,1) of the pgf, f _j (q ₁,…,q _n )=q _j , for j∈Ω (Athreya and Ney 1972; Harris 1963; Pénnison 2010). The value of q _j is the probability of disease extinction for patch j. In the supercritical case, the probability of an outbreak is approximately

$$ 1-q_1^{i_1}\cdots q_n^{i_n}. $$

(20)

Although the preceding result is a limiting result, the split between persistence and extinction in the branching process occurs rapidly. That is, either sample paths grow without bound or approach zero. Of course, in the nonlinear CTMC model, the infectious variables are bounded but when $\mathcal{R}_{0}>1$, the linear branching process in this supercritical case is a good approximation to the nonlinear CTMC model near the disease-free equilibrium when the susceptible population size is large. The birth and death process of infectious individuals either results in a sufficient number of births to cause an outbreak or results in death of infectious individuals and disease extinction.

We cannot obtain simple analytical expressions for the extinction probabilities q _j of the branching process approximation of the multipatch model, except in some special cases. For example, a single isolated patch j with no movement into or out of patch j and $\mathcal{R}_{0j}>1$ has a pgf of the form

$$f_j(x_j)=\dfrac{\beta_j x_j^2+\alpha_j+\gamma_j}{\beta_j+\alpha_j+\gamma_j}. $$

In this case, it can be easily shown that the probability of extinction is $q_{j}=1/\mathcal{R}_{0j}$. This classic result is due to Whittle (1955) who applied this result to an SIR epidemic model. For n connected patches, we compute the extinction probability q _j numerically in Sect. 5 and check whether this estimate for disease extinction agrees with simulations of the CTMC model.

4 SDE Model

After an outbreak has occurred, the population size and the number of infectious individuals are large. When the values of the state variables are large, simulation of the discrete-valued Markov chain process becomes computationally intensive. In this case, a system of stochastic differential equations (SDEs), with continuous-valued random variables, is often used to approximate the discrete-valued process. Therefore, to assess the variability, the role of demographic stochasticity, after an outbreak has occurred, we apply a system of SDEs.

A system of Itô SDEs with continuous-valued random variables is derived by applying the transition rates in Table 1 and letting the time step Δt approach zero (Allen 2007; Allen 2010; Allen and Allen 2008). The resulting SDE model is often referred to as the diffusion approximation by Kurtz (1978) or the chemical Langevin equation by Gillespie (2000). The random vector $\vec{X}(t)=(S_{1}(t),I_{1}(t),\ldots,S_{n}(t),I_{n}(t))^{T}$ is a vector of continuous random variables with state space S _j (t),I _j (t)∈[0,N(0)], j∈Ω, t∈[0,∞), where N(0) is the initial total population size. Again, for simplicity, we use the same notation for the susceptible and infectious random variables in the SDE model that were used for the ODE and CTMC models.

Given the transitions and rates in Table 1, the corresponding SDE model has the form

$$ d\vec{X}(t)=\vec{f}\bigl(\vec{X}(t)\bigr)dt+G\bigl(\vec{X}(t)\bigr)d\vec{W}(t). $$

(21)

To order Δt, $\vec{f}(\vec{X}(t))\Delta t=\mathbb{E}(\Delta\vec {X}(t))$, where $\vec{f}$ is the drift vector and $GG^{T}\Delta t=\varSigma \Delta t=\mathbb{E}(\Delta\vec{X}(t)(\Delta\vec{X}(t))^{T})$, where matrix $G(\vec{X}(t))$ is a diffusion matrix. Vector $\vec{W}(t)$ consists of m independent Wiener processes,

$$\vec{W}(t)=\bigl(W_1(t),\ldots,W_m(t) \bigr)^T, $$

where m is the total number of events of the process. A more detailed discussion of Wiener processes and SDEs can be found in Allen (2007), Allen (2010), Øksendal (2003).

The drift vector for the two-patch SIS model has the same form as the ODE model

The diffusion matrix is a 4×10 matrix given by

where

The ten column entries in matrix G account for the ten different events outlined in Table 1. For two patches, infection, recovery, or death in each patch represent 6 events and dispersal of either susceptible or infectious individuals from patch 1 to 2 or 2 to 1 represent for 4 additional events. The explicit form of the system of Itô SDEs for two patches is

If we assume that S _j ≈N _j = constant, then applying properties of the Wiener process, it follows that the differential equations for the expectations of the infectious classes are linear. In this case, the differential equations for the expectations agree with the linearized ODE model, Eq. (7):

$$ \dfrac{d\mathbb{E}(I_j)}{dt}\approx \biggl[\beta_j- \gamma_j-\alpha_j-\sum_{k\in\varOmega} d_{jk}^i \biggr]\mathbb{E}(I_j)+\sum _{k\in\varOmega}d_{kj}^i \mathbb{E}(I_k). $$

(22)

In general, the expectations for the infectious classes in the SDE model are nonlinear; the expectation of I _j in (22) should have the term $\beta_{j}\mathbb{E}(S_{j}I_{j}/N_{j})$. Moment closure methods and application of Itô’s formula can be used to write a closed system of differential equations for the expectations of the nonlinear SDEs. We do not apply these methods, instead we numerically solve the system of SDEs using the Euler–Maruyama numerical method, and compare the simulation results of the CTMC model with the SDE model when the probability of disease extinction is small.

5 Comparison of Stochastic and Deterministic Models

The dynamics of the multi-patch ODE, CTMC, and SDE models are illustrated in several numerical examples. In the first two sets of examples, we consider two- and three-patch SIS models without disease-related mortality. We apply branching process theory to derive the probability of disease extinction and illustrate the significance of the location of the outbreak, risk of infection, and movement rates on disease extinction. In the third set of examples, we include disease-related mortality and illustrate finite-time population extinction in the CTMC and SDE models and their close agreement when there is an outbreak.

5.1 Outbreak Location and Risk of Infection

5.1.1 Two-Patch CTMC Model

Consider a two-patch SIS model without disease-related mortality. The total population size is constant, N(0)=N. Movement of susceptible individuals between the two patches leads to a unique disease-free equilibrium for the ODE model given by

$$ (\bar{S_1},0,\bar{S_2},0)= \biggl(\frac {d_{21}^sN}{d_{12}^s+d_{21}^s},0, \frac {d_{12}^sN}{d_{12}^s+d_{21}^s},0 \biggr). $$

(23)

The next-generation matrix is

$$FV^{-1}=\frac{1}{\gamma_1\gamma_2+\gamma_1d_{21}^i+\gamma_2d_{12}^i} \begin{bmatrix} \beta_1(\gamma_2+d_{21}^i) & \beta_1d_{21}^i\\ \beta_2d_{12}^i & \beta_2(\gamma_1+d_{12}^i) \end{bmatrix} $$

and the basic reproduction number $\mathcal{R}_{0}$ can be explicitly calculated as

$$ \frac{\beta_1(\gamma_2+d_{21}^i)+\beta_2(\gamma_1+d_{12}^i)+\sqrt{[\beta _1(\gamma_2+d_{21}^i)-\beta_2(\gamma_1+d_{12}^i)]^2+4\beta_1\beta _2d_{12}^id_{21}^i}}{2(\gamma_1\gamma_2+\gamma_1d_{21}^i+\gamma_2d_{12}^i)}. $$

If $\mathcal{R}_{0}<1$, solutions of the ODE model approach the stable disease-free equilibrium, and in the CTMC model the number of infectious individuals hits zero in finite time. In particular, if all patches are low-risk, $\mathcal{R}_{0j}<1$, then $\mathcal{R}_{0}<1$. However, in a spatially heterogeneous environment, if there is a mixture of low- and high-risk patches and $\mathcal{R}_{0}>1$, then the two models differ. The solution of the ODE model approaches an endemic equilibrium with persistence of the infection while in the CTMC model, there are two outcomes. Either there is disease extinction with only a few infectious cases or the infection persists for a long time, similar to the ODE model. To predict the probability of disease extinction, we apply the branching process approximation near the disease-free equilibrium.

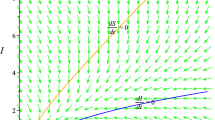
Consider the case where individuals move between a high-risk patch 1 and a low-risk patch 2 as described by the parameter values β ₁=0.5, γ ₁=0.1, β ₂=0.2, γ ₂=0.4, $d_{jk}^{s}=d_{jk}^{i}=0.1$ for j,k=1,2, and N=400. For these parameter values, the patch reproduction numbers are $\mathcal{R}_{01}=5$, $\mathcal{R}_{02}=0.5$, the basic reproduction number is $\mathcal {R}_{0}=2.83$, and the spectral radius of the expectation matrix is ρ(M)=1.45. For this case, the ODE solution and one sample path of the CTMC model illustrating an outbreak are graphed in Fig. 1 with I ₁(0)=1 and I ₂(0)=0. A high prevalence of infection can be seen in the high-risk patch as compared to the low-risk patch.

Fig. 1

Comparison of the ODE solution and one sample path of the CTMC model for two patches with no disease-related mortality illustrating an outbreak and disease persistence in both patches with a higher prevalence of infection in the high-risk patch. Parameter values are β ₁=0.5, γ ₁=0.1, β ₂=0.2, γ ₂=0.4, and $d_{jk}^{s}=d_{jk}^{i}=0.1$, j,k=1,2, with initial conditions S ₁(0)=199, I ₁(0)=2, S ₂(0)=200, and I ₂(0)=0. The patch reproduction numbers are $\mathcal{R}_{01}=5$ and $\mathcal{R}_{02}=0.5$ and basic reproduction number is $\mathcal{R}_{0}=2.83$. Probability of disease extinction is $\mathbb{P}_{0}=0.116$ (see Table 2). The locally stable endemic equilibrium for the ODE model is $(\hat{S}_{1},\hat{I}_{1},\hat{S}_{2},\hat{I}_{2})\approx(68,132,161,39)$

The probability of disease extinction, $\mathbb{P}_{0}$, is computed from the branching process approximation and summarized in Table 2. The value of $\mathbb{P}_{0}$ is a good estimate of the probability of disease extinction for the nonlinear CTMC model, as computed from the proportion of sample paths (out of 10,000) for which the sum I ₁(t)+I ₂(t) hits zero prior to time t=150. In fact, there is a significantly higher probability of disease extinction if infectious individuals are introduced into the low-risk patch versus the high-risk patch. There are also differences in $\mathbb{P}_{0}$ that depend on the rate of movement between the two patches. If movement of infectious individuals is increased in the direction of the high-risk patch, the probability of disease extinction decreases (Table 2 case (b)), but if movement is increased in the direction of the low-risk patch, then the probability of disease extinction increases (Table 2 case (c)). As noted earlier, the probability of disease extinction does not depend on the movement rate of the susceptible individuals and may not depend on whether the susceptible population is at the disease-free equilibrium (Table 2 cases (b) and (c)). These results show for the multipatch SIS model that directing movement of susceptible individuals is not an effective control strategy while directing the movement of infectious individuals toward the low-risk patch can significantly lower the probability of an outbreak (Table 2).

Table 2 Probability of disease extinction $\mathbb{P}_{0}$ calculated from the branching process and numerical approximation (approx.) based on 10,000 sample paths of the two-patch CTMC model with no disease-related mortality. Patch 1 is high-risk and patch 2 is low-risk. Parameter values are β ₁=0.5, γ ₁=0.1, β ₂=0.2, γ ₂=0.4, and $d_{jk}^{s}=0.1$, j,k=1,2 (except results given in parentheses for cases (b) and (c)) with initial conditions I _j (0)=i _j and S _j (0)=200−i _j , j=1,2. The patch reproduction numbers are $\mathcal{R}_{01}=5$ and $\mathcal{R}_{02}=0.5$ and the basic reproduction number in (a) $\mathcal{R}_{0}=2.83$, (b) $\mathcal {R}_{0}=4.21$, and (c) $\mathcal{R}_{0}=1.85$

Suppose movement rates for infectious individuals between the two patches are equal, that is, $d^{i}_{jk}=d$. If we let d→∞, the two patches become homogeneously mixed, the basic reproduction number approaches a limiting value (Allen et al. 2007):

$$\lim_{d\rightarrow\infty} \mathcal{R}_0(d)=\dfrac{\beta_1+\beta _2}{\gamma_1+\gamma_2}, $$

and the extinction probabilities q ₁ and q ₂ converge to a single value: lim _d→∞[q ₁(d)−q ₂(d)]=0. In Fig. 2, the values of $\mathcal{R}_{0}$, q ₁, and q ₂ are plotted as functions of d. The limiting values for this example are $\mathcal{R}_{0}(\infty)=1.4$ and q _i (∞)=1/1.4 which agree with the classic result of Whittle for a single-patch SIR model (Whittle 1955).

Fig. 2

Illustration of the limiting behavior of the basic reproduction number, $\mathcal{R}_{0}$, and extinction probabilities, q ₁ and q ₂, for two patches as a function of movement, d, and no disease-related mortality. Parameter values are β ₁=0.5, γ ₁=0.1, β ₂=0.2, and γ ₂=0.4 with $d_{jk}^{i}=d$ for j,k=1,2. The limiting values of $\mathcal{R}_{0}(d)$ and q _i (d) as d→∞ are $\mathcal{R}_{0}(\infty)=1.4$ and $q_{i}(\infty)=1/\mathcal {R}_{0}(\infty)=1/1.4$, i=1,2

5.1.2 Three-Patch CTMC Model

Next, consider a three-patch model without disease-related mortality and suppose that the patches are arranged in a strip so that there is no direct movement between patches one and three. Suppose patch 1 is high-risk and patches 2 and 3 are low-risk as described by the parameter values β ₁=0.5, γ ₁=0.1, β ₂=0.2, γ ₂=0.4, β ₃=0.1, γ ₃=0.4, $d_{jk}^{s}=d_{jk}^{i}=0.1$ for j,k≠(1,3),(3,1), $d_{jk}^{s}=d_{jk}^{i}=0$ for j,k=(1,3),(3,1), and N=450. For these parameter values, $\mathcal{R}_{01}=5$, $\mathcal {R}_{02}=0.5$, $\mathcal{R}_{03}=0.25$, $\mathcal{R}_{0}=2.77$, and ρ(M)=1.43.

The solution of the ODE model and one sample path of the CTMC model for which an outbreak occurs are graphed in Fig. 3. The solutions show a higher prevalence of infection in high-risk patch 1.

Fig. 3

Comparison of the three-patch ODE solution and one sample path of the CTMC model with no disease-related mortality illustrating an outbreak and disease persistence in each patch with the highest prevalence of infection in the high-risk patch 1. Parameter values are β ₁=0.5, γ ₁=0.1, β ₂=0.2, γ ₂=0.4, β ₃=0.1, γ ₃=0.4, and $d_{jk}^{s}=d_{jk}^{i}=0.1$ for j,k≠(1,3),(3,1), and $d_{jk}^{s}=d_{jk}^{s}=0$, j,k=(1,3),(3,1) with initial conditions S ₁(0)=149, I ₁(0)=1, S ₂(0)=150, I ₂(0)=0, S ₃(0)=150, and I ₃(0)=0. The patch reproduction numbers are $\mathcal{R}_{01}=5$, $\mathcal{R}_{02}=0.5$, and $\mathcal{R}_{03}=0.25$ and basic reproduction number is $\mathcal {R}_{0}=2.77$. Probability of disease extinction is $\mathbb{P}_{0}=0.351$ (see Table 3). The locally stable endemic equilibrium is $(\bar{S}_{1},\bar{I}_{1},\bar {S}_{2},\bar{I}_{2},\bar{S}_{3},\bar{I}_{3}) \approx(53,97,126,24,144,6)$

The results in Table 3 illustrate how disease extinction is determined by the location of an outbreak, risk of infection, and dispersal of infectives. The probability of disease extinction is significantly higher if initially infectious individuals are located in a low-risk patch and if dispersal is greater out of high-risk and into low-risk patches than the reverse direction (Table 3 cases (b) and (c)). Other numerical examples were simulated with a mixture of high- and low-risk patches with different spatial connectivities that gave similar results with respect to risk of infection and location of outbreak.

Table 3 Comparison of the probability of disease extinction $\mathbb {P}_{0}$ computed from the branching process and numerical approximation (approx.) based on 10,000 sample paths of the three-patch CTMC model with no disease-related mortality. Patch 1 is high-risk and patches 2 and 3 are low-risk. Parameter values are β ₁=0.5, γ ₁=0.1, β ₂=0.2, γ ₂=0.4, β ₃=0.1, γ ₃=0.4, $d_{jk}^{s}=0.1$, j,k≠(1,3),(3,1) (except results given in parentheses for case (b)), and $d_{jk}^{i}=d_{jk}^{s}=0$, j,k=(1,3),(3,1) with initial conditions I _j (0)=i _j and S _j (0)=150−i _j , j=1,2,3. The patch reproduction numbers are $\mathcal{R}_{01}=5$, $\mathcal{R}_{02}=0.5$, and $\mathcal{R}_{03}=0.25$ and basic reproduction number in (a) $\mathcal{R}_{0}=2.77$ and (b) $\mathcal {R}_{0}=1.81$

5.2 Finite-Time Extinction

It is well known that stochastic models exhibit finite-time extinction while this is not the case for deterministic models, where the number of infectious individuals asymptotically approaches zero (Mollison 1991). These differences are illustrated in the next set of examples for multipatch models with disease-related mortality.

Consider a two-patch model with a relatively high rate of disease-related mortality compared to the rate of recovery. Suppose that patch 1 is high-risk and patch 2 is low-risk as described by the parameter values β ₁=1.8, γ ₁=0.1, β ₂=0.3, γ ₂=0.4, α ₁=α ₂=0.5, $d_{jk}^{s}=d_{jk}^{i}=0.1$ for j,k=1,2, and initial population size N(0)=400. Then the basic reproduction numbers are $\mathcal{R}_{01}=3$, $\mathcal{R}_{02}=0.33$, and $\mathcal{R}_{0}=2.61$, while ρ(M)=1.44.

In this example, solutions of the ODE model illustrate an outbreak in the high-risk patch prior to global population extinction as t→∞ in both patches. Sample paths for the CTMC model either predict rapid disease extinction or disease extinction after an outbreak with finite extinction time. The solution of the ODE model and one sample path of the CTMC model are graphed in Figs. 4 and 5 with infectious individuals introduced into either the low-risk patch, I ₂(0)=5 ($\mathbb{P}_{0}=0.640$) or high-risk patch, I ₁(0)=5 ($\mathbb{P}_{0}=0.008$). The probability distributions for the finite extinction time, T, and the final population size (S ₁+S ₂) at the time of disease extinction are graphed in Figs. 4 and 5. Sample paths of the SDE model yield similar predictions to the CTMC model when probability of extinction is small (compare Figs. 5 and 6).

Fig. 4

Comparison of the two-patch ODE solution and one sample path of the CTMC model with mortality and the approximate probability distribution for the population size (S ₁(T)+S ₂(T)) and time of disease extinction T for the CTMC model when infectious individuals are introduced into the low-risk patch 2. Probability of disease extinction is $\mathbb{P}_{0}=0.640$ (see Table 4). Initial conditions are S ₁(0)=200, I ₁(0)=0, S ₂(0)=195, and I ₂(0)=5. Parameter values are β ₁=1.8, γ ₁=0.1, β ₂=0.3, γ ₂=0.4, α ₁=α ₂=0.5, $d_{jk}^{s}=d_{jk}^{i}=0.1$, j,k=1,2. The patch reproduction numbers are $\mathcal{R}_{01}=3$ and $\mathcal {R}_{02}=0.33$ and the basic reproduction number is $\mathcal{R}_{0}=2.61$. Mean values of S ₁ and S ₂ at the time of disease extinction T are $\bar{S}_{1}(T)=127$ and $\bar{S}_{2}(T)=130$ with mean disease extinction time $\bar{T}=15.5$. Calculations are based on 10,000 sample paths

Fig. 5

Comparison of the two-patch ODE solution and one sample path of the CTMC model with mortality and the approximate probability distributions for the population size (S ₁(T)+S ₂(T)) and for the time of disease extinction T of the CTMC model when infectious individuals are introduced into the high-risk patch 1. Probability of disease extinction is small, $\mathbb{P}_{0}=0.008$. Initial conditions are S ₁(0)=195, I ₁(0)=5, S ₂(0)=200, and I ₂(0)=0. Parameter values are the same as in Fig. 4. Mean values of S ₁ and S ₂ at the time of disease extinction T are $\bar{S}_{1}(T)=5.84$ and $\bar{S}_{2}(T)=17.4$ with mean disease extinction time $\bar{T}=34.9$. Calculations are based on 10,000 sample paths

Fig. 6

Comparison of the two-patch ODE solution and one sample path of the SDE model with mortality and the approximate probability distributions for the population size (S ₁(T)+S ₂(T)) and for the time of disease extinction T of the SDE model when infectious individuals are introduced into the high-risk patch 1. The SDE and CTMC models yield similar results when the probability of disease extinction is small (see Fig. 5). Parameter values and initial conditions are the same as in Fig. 5. Mean values of S ₁ and S ₂ at the time of disease extinction T are $\bar{S}_{1}(T)=5.79$ and $\bar{S}_{2}(T)=13.6$ with mean disease extinction time $\bar{T}=37.9$. The proportion of sample paths of the SDE model with disease extinction is 0.009. Calculations are based on 10,000 sample paths

As in the preceding section, we compute the probability of disease extinction $\mathbb{P}_{0}$ and compare the results with the CTMC model. The results, summarized in Table 4, show similar trends as in Tables 2 and 3 with $\mathbb{P}_{0}$ greatest when infection is initiated in the low-risk patch and spatial connectivity to the high-risk patch is low. Neither movement of susceptible individuals nor the arrangement of susceptible populations in the patches impact the probability of disease extinction, provided the outbreak size is sufficiently large. With an initial population size in each patch of 200 or 400, the outbreak size is of sufficient magnitude so that there is good agreement between $\mathbb{P}_{0}$ and the proportion of sample paths hitting zero in the CTMC model (sum I ₁(t)+I ₂(t) hits zero before reaching outbreak size 25); see Table 4.

Table 4 Comparison of the probability of disease extinction $\mathbb {P}_{0}$ computed from the branching process and numerical approximation (approx.) based on 10,000 sample paths of the two-patch CTMC model with disease-related mortality. Patch 1 is high-risk and patch 2 is low-risk. Parameter values are β ₁=1.8, γ ₁=0.1, β ₂=0.3, γ ₂=0.4, α ₁=α ₂=0.5, and $d_{jk}^{s}=0.1$, j,k=1,2 (except results given in parentheses for cases (b) and (c)) with initial conditions I _j (0)=i _j and $S_{j}(0)=\bar{N}-i_{j}$, j=1,2. The patch reproduction numbers are $\mathcal{R}_{01}=3$ and $\mathcal {R}_{02}=0.33$ and the basic reproduction number in (a) $\mathcal {R}_{0}=2.61$, (b) $\mathcal{R}_{0}=2.87$, and (c) $\mathcal{R}_{0}=1.84$

6 Discussion

Spatial heterogeneity, infection risk, and movement of individuals impact the spread of disease. We investigate these three factors by constructing stochastic models, CTMC and SDE spatially explicit patch models that are closely related to ODE multipatch models. In addition, we use a multitype branching process approximation of the nonlinear CTMC model near the disease-free equilibrium to predict the probability of disease extinction. The relations (17) between the basic reproduction number $\mathcal{R}_{0}$ from the linearized ODE model and the spectral radius of the expectation matrix ρ(M) from the branching process approximation are crucial for prediction of an outbreak (Allen and van den Driessche 2013).

Our analytical and numerical results confirm the importance of the location of the initial outbreak to disease spread, high-risk versus low-risk patches (Tables 2, 3, and 4 and Figs. 4 and 5). A high rate of transmission, large β _j , may result in a high-risk area due to an environment that has greater susceptibility among hosts or an environment where there are frequent contacts between hosts. Also, abiotic environmental factors such as land-use, temperature, or water availability have a large impact on vector-transmitted or water-borne infectious diseases such as dengue, malaria, or cholera. Heterogeneity in transmission was a major factor in the spread of the 2001 UK foot-and-mouth epizootic: heterogeneity due to spatial aggregation of farms, farm sizes, and susceptibility of host species (Keeling et al. 2001).

Our results also confirm for the multipatch SIS model that to increase the probability of disease extinction, movement restrictions should be imposed into high-risk areas and directed toward low-risk areas, with strategies that focus primarily on the infectious individuals. Careful border screening of exposed and infectious individuals can be an effective method for prevention of disease spread such as in the case of the 2002–2003 SARS epidemic (Ruan et al. 2006). Susceptible movement is not important at the initiation of an outbreak because the susceptible population is assumed to be large but after the outbreak has commenced, susceptible movement should be considered in controlling disease spread. In addition, the high mortality associated with foot-and-mouth disease and SARS emphasizes the need for rapid and effective control measures. If effective control measures are not implemented quickly, then high mortality rates may result in a drastic population reduction, as demonstrated in the 2001 foot-and-mouth outbreak (also see Figs. 5 and 6).

Although this investigation concentrated on the multipatch SIS model, the stochastic models and methods discussed here apply to other more complex epidemic settings, including multipatch models with births and deaths, vector-host models, and stage-structured models (e.g., Allen and Lahodny 2012; Allen and van den Driessche 2013; Griffiths and Greenhalgh 2011; Lahodny 2012). The stochastic probability of disease extinction can be used in conjunction with data to obtain a quantitative measure to assess various control strategies.

Appendix

Proof of Theorem 2.1

For fixed j∈Ω, let i _j =I _j /N _j . For simplicity, we omit the subscript j and write i=I/N and $\mathcal{R}_{0}=\beta/(\gamma+\alpha )$. Now

$$ \frac{di}{dt}=i\bigl[\beta-\gamma-\alpha-(\beta-\alpha)i\bigr], $$

(24)

and

$$ \frac{dN}{dt}=-\alpha iN. $$

(25)

The differential equation (24) is a type of logistic growth equation, which can be expressed as

$$ \frac{di}{dt}=i(a-bi), $$

(26)

where a=β−γ−α and b=β−α.

If $\mathcal{R}_{0}>1$ and α=0, then N=N(0) is a constant and a,b>0. It follows from (26) that

$$\lim_{t\rightarrow\infty}i(t)=1-\frac{1}{\mathcal{R}_0}. $$

Since N is a constant, the result in part (i) follows.

If $\mathcal{R}_{0}>1$ and α>0, then a,b>0. It follows from (26) that

$$\lim_{t\rightarrow\infty}i(t)=1-\frac{\gamma}{\beta-\alpha}>0. $$

Thus, i(t) is bounded below by a positive constant for sufficiently large t. It follows from (25) that

$$\lim_{t\rightarrow\infty}N(t)=0. $$

Thus, I(t)→0 and S(t)→0 as t→∞.

If $\mathcal{R}_{0}\leq1$ and α=0, then N=N(0) is a constant and a≤0. It follows from (26) that

$$\lim_{t\rightarrow\infty}i(t)=0. $$

The result in part (ii) follows.

If $\mathcal{R}_{0}\leq1$ and α>0, it follows from (26) that

$$\lim_{t\rightarrow\infty}i(t)=0. $$

So I(t)→0 as t→∞. Since N(t) is decreasing, S(t)→C for some 0≤C<N(0). □

Proof of Theorem 2.2

To verify part (i), suppose $\mathcal{R}_{0}<1$. For each j∈Ω,

$$ \dot{I_j}\leq \biggl(\beta_j-\gamma_j- \alpha_j-\sum_{k\in\varOmega }d_{jk}^i \biggr)I_j+\sum_{k\in\varOmega}d_{kj}^iI_k. $$

(27)

Then I=(I ₁,…,I _n )^T satisfies

$$ \dot{I}\leq(F-V)I, $$

(28)

where F and V are defined by (8) and (9). Consider the initial-value problem

The solution to this differential equation is X(t)=e ^(F−V)t I(0). Since $\mathcal{R}_{0}<1$, the eigenvalues of F−V have negative real part and since F−V has nonnegative off-diagonal elements, the solution X(t) can be compared with the solution of (28), I(t) (Lakshmikantham and Leela 1969). By the comparison principle, since X(t)→0 as t→∞, I(t)→0 as t→∞ (Lakshmikantham and Leela 1969).

To verify part (ii), fix j∈Ω and suppose that $\mathcal {R}_{0j}<1$ and $d_{jk}^{i}=d_{kj}^{i}=0$ for k≠j. Then

$$ \dot{I}_j=I_j \biggl[\beta_j- \gamma_j-\alpha_j-\frac{\beta _j}{N_j}I_j \biggr]\leq I_j [\beta_j-\gamma_j- \alpha_j ]. $$

Similar to part (i), by the comparison principle, 0≤I _j (t)≤X(t), where $\dot{X}=X [\beta_{j}-\gamma_{j}-\alpha_{j} ]$ and X(0)=I _j (0). Since β _j <γ _j +α _j , lim _t→∞ X(t)=0 implies lim _t→∞ I _j (t)=0. □