Analysis of a mosquito-borne disease transmission model with vector stages and nonlinear forces of infection

Abstract

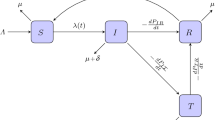
We study a mosquito-borne epidemic model where the vector population is distinct in aquatic and adult stages and a saturating effect of disease transmission is assumed to occur when the population of infectious carriers becomes large enough. A qualitative analysis, including centre manifold analysis, has been performed to determine the existence of stability–instability thresholds.

Appendix: Proof of Routh–Hurwitz conditions in Theorem 4

Consider the cubic polynomial $P( \lambda ) = \lambda ^3 + a_2 \lambda ^2 +a_1 \lambda + a_0$ in (20), where the coefficients are given in (21). We first show that $a_0$ is positive.

Recall that

$$\begin{aligned} a_0= & {} \mu _1\mu _H(\sigma +\mu _H)+\beta _2\mu _1(\sigma +\mu _H)\,g_2(M_I^*)+\beta _1\mu _H(\sigma +\mu _H)\,g_1(I^*)\\&+ \sigma \beta _1\beta _2\,g_1(I^*)g_2(M_I^*)\nonumber \\&+ \mu _H\left[ \beta _1\beta _2\,g_1(I^*)g_2(M_I^*)-\frac{\beta _1\beta _2H^*M_S^*}{(\alpha _1I^*+1)^2(\alpha _2M_I^*+1)^2}\right] . \end{aligned}$$

Substituting $H^{*}$ given in (19), we have that

$$\begin{aligned} \frac{\beta _1 \beta _2 H^{*} M_S^{*}}{( \alpha _1 I^{*}+1 )^{2} ( \alpha _2 M_I^{*} +1 )^{2}} \!=\! \frac{\beta _1 (\sigma + \mu _H) M_S^{*}\,g_1(I^{*})}{ M_I^{*}( \alpha _1 I^{*}+1 ) ( \alpha _2 M_I^{*} +1 )} \!=\! \frac{\mu _1(\sigma + \mu _H)}{(\alpha _1 I^{*}+1)(\alpha _2 M_I^{*} +1)},\nonumber \\ \end{aligned}$$

(24)

where the last equality follows from (18). In view of (24), we get

$$\begin{aligned} a_0= & {} ( \sigma + \mu _H ) \left[ \mu _1 \mu _H \left( 1- \frac{1}{( \alpha _1 I^{*}+1 ) ( \alpha _2 M_I^{*} +1 ) } \right) \right. \nonumber \\&\left. + \mu _1\beta _2\,g_2(M_I^*)+\mu _H\beta _1\,g_1(I^{*})\right] \nonumber \\&+ \beta _1\beta _2( \sigma + \mu _H )\, g_1(I^*)g_2(M_I^*), \end{aligned}$$

(25)

which is positive.

Similarly, using (24) for $a_1$, it follows

$$\begin{aligned} a_1= & {} \mu _1 \mu _H + ( \sigma + \mu _H )\mu _1 \left( 1- \frac{ 1}{( \alpha _1 I^{*}+1 ) ( \alpha _2 M_I^{*} +1 ) } \right) + \mu _H ( \sigma + \mu _H )\nonumber \\&+ \, \beta _2( \sigma + \mu _1 + \mu _H )\,g_2(M_I^*) + \beta _1 ( \sigma + 2 \mu _H ) \, g_1(I^*) + \beta _1\beta _2 g_1(I^*)g_2(M_I^*),\nonumber \\ \end{aligned}$$

(26)

so that $a_1$ is positive.

Finally, from (25), (26) and $a_2$ in (21) it is easy to show that $a_2a_1-a_0>0$, so that all the Routh–Hurwitz conditions in Theorem 4 are verified.