Porous MHD convection: stabilizing effect of magnetic field and bifurcation analysis

Abstract

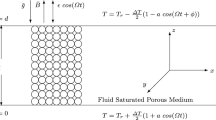
MHD convection in a horizontal porous-layer filled by a plasma, imbedded in a transverse magnetic field and heated from below, is investigated. The critical Rayleigh number is found and, in simple algebraic closed forms, conditions necessary and sufficient for the onset of steady and oscillatory convection are obtained. It is shown that the stabilizing effect of the magnetic field grows with $Q^2$, Q being the Chandrasekhar number. The linearization principle (Rionero, Rend Lincei Mat Appl 25:368, 2014): “Decay of linear energy for any initial data implies decay of nonlinear energy at any instant” continues to hold also in the case at stake and allows to recover for the global nonlinear stability the conditions of linear stability.

Appendix: Proof of Theorem 7

Setting

$$\begin{aligned} P^*_q=\displaystyle \sum _{n=1}^q\pi ^*_n\,,\qquad {\mathbf U}^*_q=\displaystyle \sum _{n=1}^q{{\mathbf {u}}}^*_n, \qquad {\mathbf H}^*_q=\displaystyle \sum _{n=1}^q{\mathbf h}^*_n,\qquad \varTheta ^*_q=\displaystyle \sum _{n=1}^q\theta ^*_n \end{aligned}$$

(114)

one obtains that the following initial boundary value problem holds

$$\begin{aligned}&\left\{ \begin{array}{l} {{\mathbf {U}}}^*_q=-\nabla P^*_q+{\tilde{Q}}\displaystyle {\frac{\partial {{\mathbf {H}}}^*_q}{\partial z}}+{P}^{*}_m({{\mathbf {h}}}\cdot \nabla ){{\mathbf {H}}}^*_q+R\varTheta ^*_q{\mathbf k}\\ \\ {\tilde{P}}_m\displaystyle {\frac{\partial {{\mathbf {H}}}^*_q}{\partial t}}=\varDelta {{\mathbf {H}}}^*_q+{\tilde{Q}}\displaystyle {\frac{\partial {\mathbf U}^*_q}{\partial z}}-{P}^{*}_m({{\mathbf {u}}}\cdot \nabla {\mathbf H}^*_q-{{\mathbf {h}}}\cdot \nabla {{\mathbf {U}}}^*_q) \\ \\ \displaystyle {\frac{\partial \varTheta ^*_q}{\partial t}}=RW^*_q-{\mathbf u}\cdot \nabla \varTheta ^*_q \\ \\ \nabla \cdot {{\mathbf {U}}}^*_q=0 \,, \qquad \nabla \cdot {\mathbf H}^*_q=0\end{array}\right. \end{aligned}$$

(115)

$$\begin{aligned}&{\left\{ \begin{array}{ll} ({{\mathbf {U}}}^*_q)_{t=0}=\displaystyle \sum _{n=1}^q{\mathbf u}^{(0)}_n,\,\,\, (\varTheta ^*_q)_{t=0}=\displaystyle \sum _{n=1}^q \theta ^{(0)}_n,\,\,\, ({\mathbf H}^*_q)_{t=0}=\displaystyle \sum _{n=1}^q{{\mathbf {h}}}^{(0)}_n,\\ \\ {{\mathbf {U}}}^*_q\cdot {{\mathbf {k}}}={{\mathbf {H}}}^*_q\cdot {\mathbf i}={{\mathbf {H}}}^*_q\cdot {{\mathbf {j}}}=\displaystyle {\frac{\partial ({\mathbf H}^*_q\cdot {{\mathbf {k}}})}{\partial z}}=0,\,\,\,z=0,1\,. \end{array}\right. } \end{aligned}$$

(116)

Setting

$$\begin{aligned} \bar{{\mathbf {U}}}_n= & {} \left\{ \begin{array}{ll} {{\mathbf {u}}}_n-{{\mathbf {u}}}^*_n, &{}\quad \text{ for } n=1,2,\ldots ,q,\\ \\ {{\mathbf {u}}}_n,&{}\quad \text{ for } n>q, \end{array}\right. ,\,\, \bar{\mathbf U}=\displaystyle \sum _{n=1}^\infty \bar{{\mathbf {U}}}_n \end{aligned}$$

(117)

$$\begin{aligned} {\bar{\varTheta }}_n= & {} \left\{ \begin{array}{ll} \varTheta _n-\varTheta ^*_n, &{}\quad \text{ for } n=1,2,\ldots ,q,\\ \\ \varTheta _n,&{}\quad \text{ for } n>q, \end{array}\right. ,\,\, {\bar{\varTheta }}=\displaystyle \sum _{n=1}^\infty {\bar{\varTheta }}_n \end{aligned}$$

(118)

$$\begin{aligned} \bar{{\mathbf {H}}}_n= & {} \left\{ \begin{array}{ll} {{\mathbf {h}}}_n-{{\mathbf {h}}}^*_n, &{}\quad \text{ for } n=1,2,\ldots ,q,\\ \\ {{\mathbf {h}}}_n,&{}\quad \text{ for } n>q, \end{array}\right. ,\,\, \bar{\mathbf H}=\displaystyle \sum _{n=1}^\infty \bar{{\mathbf {H}}}_n \end{aligned}$$

(119)

$$\begin{aligned} \bar{P}_n= & {} \left\{ \begin{array}{ll} \pi _n-\pi ^*_n, &{}\quad \text{ for } n=1,2,\ldots ,q,\\ \\ \pi _n,&{}\quad \text{ for } n>q, \end{array}\right. ,\,\, \bar{P}=\displaystyle \sum _{n=1}^\infty \bar{P}_n \end{aligned}$$

(120)

by virtue of (100)–(101) and (117)–(120) one obtains

$$\begin{aligned}&\left\{ \begin{array}{l}\bar{{\mathbf {U}}}=-\nabla \bar{P}+{\tilde{Q}}\displaystyle {\frac{\partial \bar{{\mathbf {H}}}}{\partial z}}+{P}^{*}_m({{\mathbf {h}}}\cdot \nabla )\bar{{\mathbf {H}}}+R{\bar{\varTheta }}{{\mathbf {k}}}\\ \\ {\tilde{P}}_m\displaystyle {\frac{\partial \bar{{\mathbf {H}}}}{\partial t}}=\varDelta \bar{{\mathbf {H}}}+{\tilde{Q}}\displaystyle {\frac{\partial \bar{\mathbf U}}{\partial z}}-{P}^{*}_m({{\mathbf {u}}}\cdot \nabla \bar{\mathbf H}-{{\mathbf {h}}}\cdot \nabla \bar{{\mathbf {U}}}) \\ \\ \displaystyle {\frac{\partial {\bar{\varTheta }}}{\partial t}}=R\bar{W}-{\mathbf u}\cdot \nabla {\bar{\varTheta }} \\ \\ \nabla \cdot \bar{{\mathbf {U}}}=0 \,, \qquad \nabla \cdot \bar{{\mathbf {H}}}=0\end{array}\right. \end{aligned}$$

(121)

$$\begin{aligned}&{\left\{ \begin{array}{ll} (\bar{{\mathbf {U}}})_{t=0}=\displaystyle \sum _{n=1}^q{{\mathbf {u}}}^{(0)}_n,\,\,\, ({\bar{\varTheta }})_{t=0}=\displaystyle \sum _{n=1}^q \theta ^{(0)}_n,\,\,\, (\bar{{\mathbf {H}}})_{t=0}=\displaystyle \sum _{n=1}^q{{\mathbf {h}}}^{(0)}_n,\\ \\ \bar{{\mathbf {U}}}\cdot {{\mathbf {k}}}=\bar{{\mathbf {H}}}\cdot {\mathbf i}=\bar{{\mathbf {H}}}\cdot {{\mathbf {j}}}=\displaystyle {\frac{\partial (\bar{\mathbf H}\cdot {{\mathbf {k}}})}{\partial z}}=0,\,\,\,z=0,1 \,. \end{array}\right. } \end{aligned}$$

(122)

Since

$$\begin{aligned} \displaystyle \lim _{q\rightarrow \infty }\displaystyle \sum _{n=q+1}^\infty \bar{\mathbf u}^{(0)}_n=\displaystyle \lim _{q\rightarrow \infty }\displaystyle \sum _{n=q+1}^\infty {\bar{\theta }}^{(0)}_n=\displaystyle \lim _{q\rightarrow \infty }\displaystyle \sum _{n=q+1}^\infty \bar{\mathbf h}^{(0)}_n=0 \end{aligned}$$

(123)

and (120) under zero initial boundary conditions admits only the null solution, it follows that

$$\begin{aligned} \displaystyle \lim _{q\rightarrow \infty }({{\mathbf {u}}}-\bar{\mathbf U}_q)=\displaystyle \lim _{q\rightarrow \infty }(\theta -{\bar{\varTheta }}_q)=\displaystyle \lim _{q\rightarrow \infty }({{\mathbf {H}}}-\bar{\mathbf H}_q)=0 \end{aligned}$$

(124)

and the theorem is proved.