Skip to main content
SpringerLink
Log in

Isogeometric Analysis for Topology Optimization with a Phase Field Model

  • Published:
Archives of Computational Methods in Engineering Aims and scope Submit manuscript

Abstract

We consider a phase field model for the formulation and solution of topology optimization problems in the minimum compliance case. In this model, the optimal topology is obtained as the steady state of the phase transition described by the generalized Cahn–Hilliard equation which naturally embeds the volume constraint on the amount of material available for distribution in the design domain. We reformulate the model as a coupled system and we highlight the dependency of the optimal topologies on dimensionless parameters. We consider Isogeometric Analysis for the spatial approximation which facilitates encapsulating the exactness of the representation of the design domain in the topology optimization and is particularly suitable for the analysis of phase field problems. We demonstrate the validity of the approach and numerical approximation by solving two and three-dimensional topology optimization problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32

Similar content being viewed by others

Notes

  1. In the standard definition of topology optimization problems in the minimum compliance case, the area/volume constraint is an inequality one, ∫ Ω χ mat   dΩ≤V mat ; see e.g. [13]. However, typically, the optimal design \(\varOmega _{mat}^{*}\) is such that \({V_{mat}^{*}:=\int_{\varOmega} \chi_{mat}^{*} \, d\varOmega\equiv V_{mat}}\) in order to maximize the stiffness of the structure.

  2. For the pure material-void (0–1) designs of Sect. 2.1, the total variation TV mat is defined as \(\mathit{TV}_{mat} = \mathit{TV}(\chi_{mat}) := \sup_{\mathbf{g} \in[C^{1}_{0}(\varOmega )]^{d}, \ \|\mathbf{g}\|_{L^{\infty} \leq1} } \int_{\varOmega} \chi _{mat} \nabla\cdot\mathbf{g} \, d\varOmega\), where \([C^{1}_{0}(\varOmega )]^{d}\) is the vector space of C 1-continuous functions with compact support over Ω. In this case, TV mat coincides with the perimeter of Ω mat .

  3. Other possibilities are the introduction of an augmented Lagrangian functional or the postprocessing filtering of the numerical solution.

  4. Eventually, the constant E 0 could be included among the parameters \(\boldsymbol{\mu}\in\mathcal{D}\); however, the parametric dependence of the penalized objective functional J(ρ;μ) (31) would still be completely represented by only two parameters by means of suitable scalings.

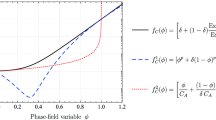
  5. This choice allows a proper balance between the strain energy function ψ E and the bulk and interface energies ψ B and ψ I through all the continuation levels.

  6. The same criterion for the selection of the optimal topological design can be eventually applied in the multiphase approach of Sect. 2.3. However, in this case, the effectivity of the procedure and the selected optimal topology are largely sensitive to the optimization technique used.

  7. When the norm of the residual associated to the solution of the linear system is below the 10−5 threshold, we progressively increase the tolerance on the relative residual. This situation occurs for “large” Δt, which in turn occurs in proximity of the steady state solution, i.e. when the solution of the problem at the previous time step yields a very small residual in the linear system at the current time step. In this case, a fixed tolerance on the relative residual would be too restrictive and would lead to an unnecessary large number of GMRES iterations.

  8. Divergence issues are revealed in the current numerical setting by increasing values in time of the Liapunov objective functional J or by the recursive selection of excessively small values of the adaptive time step Δt n .

  9. In the framework of Isogeometric analysis, we impose the displacement constraints on the degrees of freedom corresponding to the control points on the Dirichlet boundary segments Γ D .

References

  1. Aage N, Poulsen TH, Gersborg-Hansen A, Sigmund O (2008) Topology optimization of large scale Stokes flow problems. Struct Multidiscip Optim 35:175–180

    MathSciNet  Google Scholar 

  2. Adams RA (1975) Sobolev spaces. Academic Press, New York

    MATH  Google Scholar 

  3. Allaire G, Jouve F, Maillot H (2004) Topology optimization for minimum stress design with the homogenization method. Struct Multidiscip Optim 28:87–98

    MathSciNet  MATH  Google Scholar 

  4. Allaire G, Jouve F, Toader A (2004) Structural optimization using sensitivity analysis and level set-method. J Comput Phys 194:363–393

    MathSciNet  MATH  Google Scholar 

  5. Allaire G, de Gournay F, Jouve F, Toader AM (2005) Structural optimization using topological and shape sensitivity via a level set method. Control Cybern 34:59–81

    MATH  Google Scholar 

  6. Allen SM, Cahn JW (1979) A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall 27:1085–1095

    Google Scholar 

  7. Ambrosio L, Buttazzo G (1993) An optimal design problem with perimeter penalization. Calc Var Partial Differ Equ 1:55–69

    MathSciNet  MATH  Google Scholar 

  8. Bazilevs Y, Calo VM, Cottrell JA, Hughes TJR, Reali A, Scovazzi G (2007) Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Comput Methods Appl Mech Eng 197:173–201

    MathSciNet  MATH  Google Scholar 

  9. Bendsøe MP (1983) On obtaining a solution to optimization problems for solid, elastic plates by restriction of the design space. J Struct Mech 11:501–521

    Google Scholar 

  10. Bendsøe MP, Haber RB (1993) The michell layout problem as a low volume fraction limit of the perforated plate topology optimization problem: an asymptotic study. Struct Optim 6:263–267

    Google Scholar 

  11. Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Engrg 71:197–224

    MathSciNet  Google Scholar 

  12. Bendsøe MP, Sigmund O (1999) Material interpolations schemes in topology optimization. Arch Appl Mech 69:635–654

    Google Scholar 

  13. Bendsøe MP, Sigmund O (2003) Topology optimization: theory, methods and applications. Springer, Berlin

    Google Scholar 

  14. Bischoff M, Wall WA, Bletzinger KU, Ramm E (2004) Models and finite elements for thin-walled structures. In: Stein E, de Borst R, Hughes TJR (eds) Encyclopedia of computational mechanics. Solids struct coupled prob 3, vol 2. Wiley, New York, pp 59–137

    Google Scholar 

  15. Bletzinger KU, Maute K (1997) Towards generalized shape and topology optimization. Eng Optim 29:201–216

    Google Scholar 

  16. Bletzinger KU, Ramm E (1993) Form finding of shells by structural optimization. Eng Comput 9:27–35

    Google Scholar 

  17. Bletzinger KU, Reitnger R, Kimmich S, Ramm E (1993) Shape optimization with program CARAT. In: Hörnlein H, Schittkowski K (eds) Software systems for structural optimization. Internat ser numer math, vol 110. Birkhäuser, Basel, pp 97–124

    Google Scholar 

  18. Borden MJ, Scott MA, Evans JA, Hughes TJR (2011) Isogeometric finite element data structures based on Bézier extraction of NURBS. Int J Numer Methods Eng 87:15–47

    MathSciNet  MATH  Google Scholar 

  19. Borden MJ, Verhoosel CV, Scott MA, Hughes TJR, Landis CM (2012) A phase–field description of dynamic brittle fracture. Comput Methods Appl Mech Eng 217–220:77–95

    Google Scholar 

  20. Bourdin B (2011) Filters in topology optimization. Int J Numer Methods Eng 50:2143–2158

    MathSciNet  Google Scholar 

  21. Bourdin B, Chambolle S (2003) Design-dependent loads in topology optimization. Control Optim Calc Var 9:19–48

    MathSciNet  MATH  Google Scholar 

  22. Bourdin B, Chambolle S (2006) The phase field method in optimal design. In: Bendsøe MP, Olhoff N, Sigmund O (eds) IUTAM symposium on topological design optimization of structures. Solid mech appl, vol 137. Springer, Dordrecht, pp 207–215

    Google Scholar 

  23. Brezzi F, Fortin M (1991) Mixed and hybrid finite element methods. Springer, New York

    MATH  Google Scholar 

  24. Burger M, Stainko R (2006) Phase-field relaxation of topology optimization with local stress constraints. SIAM J Control Optim 45:1447–1466

    MathSciNet  MATH  Google Scholar 

  25. Caffarelli LA, Muler NE (1993) An L ∞ bound for solutions of the Cahn–Hilliard equation. Arch Ration Mech Anal 133:129–144

    MathSciNet  Google Scholar 

  26. Cahn JW (1961) On spinodal decomposition. Acta Metall 9:795–801

    Google Scholar 

  27. Cahn JW, Hilliard JE (1958) Free energy of a non-uniform system. I. Interfacial free energy. J Chem Phys 28:258–267

    Google Scholar 

  28. Cahn JW, Hilliard JE (1959) Free energy of a non-uniform system. III. Nucleation in a two-component incompressible fluid. J Chem Phys 31:688–699

    Google Scholar 

  29. Carter W, Taylor J, Cahn J (1997) Variational methods for microstructural-evolution theories. J Min Metals Mater Soc 49:30–36

    Google Scholar 

  30. Cho S, Ha SH (2008) Isogeometric shape design optimization: exact geometry and enhanced sensitivity. Struct Multidiscip Optim 38:53–70

    MathSciNet  Google Scholar 

  31. Choi JS, Yamada T, Izui K, Nishiwaki S, Yoo J (2011) Topology optimization using a reaction–diffusion equation. Comput Methods Appl Mech Eng 200:2407–2420

    MathSciNet  MATH  Google Scholar 

  32. Chung J, Hulbert GM (1993) A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized α-method. J Appl Mech 60:371–375

    MathSciNet  MATH  Google Scholar 

  33. Ciarlet P (1978) The finite element method for elliptic problems. North-Holland, Amsterdam

    MATH  Google Scholar 

  34. Cottrell JA, Hughes TJR, Reali A (2007) Studies of refinement and continuity in isogeometric structural analysis. Comput Methods Appl Mech Eng 196:4160–4183

    MathSciNet  MATH  Google Scholar 

  35. Cottrell JA, Hughes TJR, Bazilevs Y (2009) Isogeometric analysis; towards integration of CAD and FEA. Wiley, New York

    Google Scholar 

  36. Dal Maso G (1993) An introduction to Γ-convergence. Birkhäuser, Boston

    Google Scholar 

  37. de Gournay F, Allaire G, Jouve F (2008) Shape and topology optimization of the robust compliance via the level set method. Control Optim Calc Var 14:43–70

    MATH  Google Scholar 

  38. Duysinx P, Bendsøe MP (1998) Topology optimization of continuum structures with local stress constraints. Int J Numer Methods Eng 43:1453–1478

    MATH  Google Scholar 

  39. Elliott CM (1989) The Cahn–Hilliard model for the kinetics of phase separation. In: Rodrigues JF (ed) Mathematical models for phase change problems. Internat ser numer math, vol 88. Birkhäuser, Basel, pp 35–73

    Google Scholar 

  40. Elliott CM, Garcke H (1996) On the Cahn–Hilliard equation with degenerate mobility. SIAM J Math Anal 27:404–423

    MathSciNet  MATH  Google Scholar 

  41. Evans JA, Bazilevs Y, Babus̆ka I, Hughes TJR (2009) n-widths, supinfs, and optimality ratios for the k-version of the isogeometric finite element method. Comput Methods Appl Mech Eng 198:1726–1741

    MathSciNet  MATH  Google Scholar 

  42. Fife PC (2000) Models for phase separation and their mathematics. Electron J Differ Equ 48:1–26

    MathSciNet  Google Scholar 

  43. Frieboes HB, Lowengrub JS, Wise S, Zheng X, Macklin P, Bearer EL, Cristini V (2007) Computer simulation of glioma growth and morphology. NeuroImage 37:59–70

    Google Scholar 

  44. Gain AL, Paulino GH (2012) Phase-field based topology optimization with polygonal elements: a finite volume approach for the evolution equation. J Struct Multidiscip Optim. doi:10.1007/s00158-012-0781-9

    Google Scholar 

  45. Garcke H (2005) On a Cahn–Hilliard model for phase separation with elastic misfit. Ann Inst Henri Poincaré 22:165–185

    MathSciNet  MATH  Google Scholar 

  46. Garcke H, Weikard U (2005) Numerical approximation of the Cahn–Larché equation. Numer Math 100:639–662

    MathSciNet  MATH  Google Scholar 

  47. Gee MW, Siefert CM, Hu JJ, Tuminaro RS, Sala MG (2006) ML 5.0 smoothed aggregation user’s guide. Sandia National Laboratories. SAND2006–2649

  48. Gersborg-Hansen A, Bendsøe MP, Sigmund O (2006) Topology optimization of heat conduction problems using the finite volume method. Struct Multidisc Optim 31:251–259

    Google Scholar 

  49. Gomez H, Hughes TJR (2011) Provably unconditionally stable, second-order time accurate, mixed variational methods for phase-field models. J Comput Phys 230:5310–5327

    MathSciNet  MATH  Google Scholar 

  50. Gomez H, Calo VM, Bazilevs Y, Hughes TJR (2008) Isogeometric analysis of the Cahn–Hilliard phase–field model. Comput Methods Appl Mech Eng 197:4333–4352

    MathSciNet  MATH  Google Scholar 

  51. Gomez H, Hughes TJR, Nogueira X, Calo VM (2010) Isogeometric analysis of the Navier–Stokes–Korteweg equations. Comput Methods Appl Mech Eng 199:1828–1840

    MathSciNet  MATH  Google Scholar 

  52. Guest JK (2009) Topology optimization with multiple phase projection. Comput Methods Appl Mech Eng 199:123–135

    MathSciNet  MATH  Google Scholar 

  53. Ha SH, Choi KK, Cho S (2010) Numerical method for shape optimization using T-spline based isogeometric method. Struct Multidiscip Optim 42:417–428

    Google Scholar 

  54. Haber RB, Jog CS, Bendsøe MP (1996) A new approach to variable–topology shape design using a constraint on the perimeter. Struct Optim 11:1–12

    Google Scholar 

  55. Haftka RT, Grandhi RV (1986) Structural shape optimization—a survey. Comput Methods Appl Mech Eng 57:91–106

    MathSciNet  MATH  Google Scholar 

  56. Heroux M, Bartlett R, Hoekstra VHR, Hu J, Kolda T, Lehoucq R, Long K, Pawlowski R, Phipps E, Salinger A, Thornquist H, Tuminaro R, Willenbring J, Williams A (2003) An overview of trilinos. Sandia National Laboratories. SAND2003–2927

  57. Hughes TJR (2000) The finite element method: linear static and dynamic finite element analysis. Dover Publications, Mineola

    MATH  Google Scholar 

  58. Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194:4135–4195

    MathSciNet  MATH  Google Scholar 

  59. Hughes TJR, Reali A, Sangalli G (2010) Efficient quadrature for NURBS-based isogeometric analysis. Comput Methods Appl Mech Eng 199:301–313

    MathSciNet  MATH  Google Scholar 

  60. Jansen KE, Whiting CH, Hulbert GM (2000) A generalized-α method for integrating the filtered Navier–Stokes equations with a stabilized finite element method. Comput Methods Appl Mech Eng 190:305–319

    MathSciNet  MATH  Google Scholar 

  61. Jensen JS, Sigmund O (2005) Topology optimization of photonic crystal structures: a high-bandwidth low-loss T-junction waveguide. J Opt Soc Am B 22:1191–1198

    Google Scholar 

  62. Jog CS, Haber RB (1996) Stability of finite element models for distributed-parameter optimization and topology design. Comput Methods Appl Mech Eng 130:203–226

    MathSciNet  MATH  Google Scholar 

  63. Kohn RV, Strang G (1986) Optimal design and relaxation of variational problems. II. Commun Pure Appl Math 39:139–182

    MathSciNet  MATH  Google Scholar 

  64. Kumar AV, Parthasarathy A (2011) Topology optimization using B-spline finite elements. Struct Multidiscip Optim 44:471–481

    MathSciNet  Google Scholar 

  65. Larché FC, Cahn JW (1978) Thermochemical equilibrium of multiphase solids under stress. Acta Metall 26:1579–1589

    Google Scholar 

  66. Lee S, Kwak BM, Kim IY (2007) Smooth boundary topology optimization using B-spline and hole generation. Int J CAD/CAM 7

  67. Lipton R (1994) A saddle-point theorem with application to structural optimization. J Optim Theory Appl 81:549–568

    MathSciNet  MATH  Google Scholar 

  68. Maute K (1998) Topologie- und formoptimierung von dünnwandigen tragwerken. PhD Thesis, University of Stuttgart

  69. Maute K, Ramm E (1997) Adaptive topology optimization of shell structures. AIAA J 35:1767–1773

    MATH  Google Scholar 

  70. Michell AGM (1904) The limit of economy of material in frame structures. Philos Mag 8:589–597

    MATH  Google Scholar 

  71. Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field FE implementations. Int J Numer Methods Eng 83:1273–1311

    MathSciNet  MATH  Google Scholar 

  72. Mlejnek H, Schirrmacher R (1993) An engineering approach to optimal material distribution and shape finding. Comput Methods Appl Mech Eng 106:1–26

    MATH  Google Scholar 

  73. Modica L, Mortola S (1977) Un esempio di Γ −-convergenza. Boll Unione Mat Ital, B 5(14):285–299

    MathSciNet  Google Scholar 

  74. Mohammadi B, Pironneau O (2010) Applied shape optimization for fluids. Oxford University Press, Oxford

    Google Scholar 

  75. Nagy AP, Abdalla NM, Gürdal Z (2010) Isogeometric sizing and shape optimisation of beam structures. Comput Methods Appl Mech Eng 199:1216–1230

    MATH  Google Scholar 

  76. Norato JA, Bendsøe MP, Haber RB, Tortorelli DA (2007) A topological derivative method for topology optimization. Struct Multidisc Optim 33:375–386

    Google Scholar 

  77. Oden JT, Hawkins A, Prudhomme S (2010) General diffuse-interface theories and an approach to predictive tumor growth modeling. Math Models Methods Appl Sci 20:477–517

    MathSciNet  MATH  Google Scholar 

  78. Onuki A (1989) Ginzburg–Landau approach to elastic effects in the phase separation of solids. J Phys Soc Jpn 58:965–985

    Google Scholar 

  79. Osher S, Sethian JA (1988) Front propagating with curvature dependent speed: algorithms based on Hamilton–Jacobi formulations. J Comput Phys 78:12–49

    MathSciNet  Google Scholar 

  80. París J, Navarrina F, Colominas I, Casteleiro M (2009) Topology optimization of structures with local and global stress constraints. Struct Multidiscip Optim 39:419–437

    MathSciNet  Google Scholar 

  81. Park KS, Youn SK (2008) Topology optimization of shell structures using adaptive inner-front (AIF) level set method. Struct Multidiscip Optim 36:43–58

    MathSciNet  Google Scholar 

  82. Pedersen NL (2002) Topology optimization of laminated plates with prestress. Comput Struct 80:559–570

    Google Scholar 

  83. Petersson J (1999) Some convergence results in perimeter-controlled topology optimization. Comput Methods Appl Mech Eng 171:123–140

    MathSciNet  MATH  Google Scholar 

  84. Petersson J, Sigmund O (1998) Slope constrained topology optimization. Int J Numer Methods Eng 41:1417–1434

    MathSciNet  MATH  Google Scholar 

  85. Piegl L, Tiller W (1997) The NURBSbBook. Springer, New York

    Google Scholar 

  86. Poulsen TA (2003) A new scheme for imposing a minimum length scale on topology optimization. Int J Numer Methods Eng 57:741–760

    MathSciNet  MATH  Google Scholar 

  87. Quarteroni A, Valli A (1994) Numerical approximation of partial differential equations. Springer, Berlin

    MATH  Google Scholar 

  88. Quarteroni A, Sacco R, Saleri F (2007) Numerical mathematics. Springer, Berlin

    MATH  Google Scholar 

  89. Ramm E, Maute K, Schwarz S (1998) Adaptive topology and shape optimization. In: Idelsohn S, Oñate E, Dvorkin E (eds) Computational mechanics, new trends and applications. CIMNE, Barcelona

    Google Scholar 

  90. Rozvany GIN (2001) Aims, scope, methods, history and unified terminology of computer aided topology optimization in structural mechanics. Struct Multidiscip Optim 21:90–108

    Google Scholar 

  91. Rozvany GIN, Birker T (1994) On singular topologies in exact layout optimization. Struct Optim 8:228–235

    Google Scholar 

  92. Rybka P, Hoffmann KH (1999) Convergence of solutions to Cahn–Hilliard equation. Commun Partial Differ Equ 24:1055–1077

    MathSciNet  MATH  Google Scholar 

  93. Schwarz S, Maute K, Ramm E (2001) Topology and shape optimization for elastoplastic structural response. Comput Methods Appl Mech Eng 190:2135–2155

    MATH  Google Scholar 

  94. Sederberg TW, Zhengs JM, Bakenov JM, Nasri A (2003) T-splines and T-NURCCSs. ACM Trans Graph 22:477–484

    Google Scholar 

  95. Seo YD, Kim HJ, Youn SK (2010) Isogeometric topology optimization using trimmed spline surfaces. Comput Methods Appl Mech Eng 199:3270–3296

    MathSciNet  MATH  Google Scholar 

  96. Seo YD, Kim HJ, Youn SK (2010) Shape optimization and its extension to topological design based on isogeometric analysis. Int J Solids Struct 47:1618–1640

    MATH  Google Scholar 

  97. Sigmund O (1997) On the design of compliant mechanisms using topology optimization. Mech Struct Mach 25:493–524

    Google Scholar 

  98. Sigmund O (2001) Design of multiphysics actuators using topology optimization—part I: one-material structures. Comput Methods Appl Mech Eng 190:6577–6604

    MATH  Google Scholar 

  99. Sigmund O (2004) Morphology-based black and white filters for topology optimization. Struct Multidiscip Optim 61:238–254

    MathSciNet  Google Scholar 

  100. Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Optim 16:68–75

    Google Scholar 

  101. Sokolowski J, Zolésio JP (2003) Introduction to shape optimization: shape sensitivity analysis. Springer, Berlin

    Google Scholar 

  102. Spatschek R, Müller-Gugenberger C, Brener E, Nestler B (2007) Phase field modeling of fracture and stress-induced phase transitions. Phys Rev E 75:066111

    MathSciNet  Google Scholar 

  103. Stolpe M, Svanberg K (2001) On the trajectories of penalization methods for topology optimization. Struct Multidiscip Optim 21:128–139

    Google Scholar 

  104. Stolpe M, Svanberg K (2003) Modeling topology optimization problems as linear mixed 0–1 programs. Int J Numer Methods Eng 57:723–739

    MathSciNet  MATH  Google Scholar 

  105. Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24:359–373

    MathSciNet  MATH  Google Scholar 

  106. Svanberg K (2002) A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J Optim 12:555–573

    MathSciNet  MATH  Google Scholar 

  107. Takezawa A, Nishiwaki S, Kitamura M (2010) Shape and topology optimization based on the phase field method and sensitivity analysis. J Comput Phys 229:2697–2718

    MathSciNet  MATH  Google Scholar 

  108. van der Zee KG, Oden JT, Prudhomme S, Hawkins AJ (2011) Goal-oriented error estimation for Cahn–Hilliard models of binary phase transition. Numer Methods Partial Differ Equ 27:160–196

    MATH  Google Scholar 

  109. Vese LA, Chan TF (2002) A multiphase level set framework for image segmentation using the Mumford and Shah model. Int J Comput Vis 50:271–293

    MATH  Google Scholar 

  110. Wall WA, Frenzel MA, Cyron C (2008) Isogeometric structural shape optimization. Comput Methods Appl Mech Eng 197:2976–2988

    MathSciNet  MATH  Google Scholar 

  111. Wang MY, Zhou S (2004) Phase field: a variational method for structural topology optimization. Comput Model Eng Sci 6:227–246

    Google Scholar 

  112. Wang D, Zhang WH, Jiang JS (2002) Combined shape and sizing optimization of truss structures. Comput Mech 29:307–312

    MATH  Google Scholar 

  113. Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192:227–246

    MATH  Google Scholar 

  114. Weiss D (2010) Feature-based spline optimization in CAD; a step towards geometry-based structure creation. Struct Multidiscip Optim 42:619–631

    Google Scholar 

  115. Wu W, Yang DZ, Huang YY, Qi M, Wang WQ (2008) Topology optimization of a novel stent platform with drug reservoirs. Med Eng Phys 30:1177–1185

    Google Scholar 

  116. Xie YM, Steven GP (1997) Evolutionary structural optimization. Springer, London

    MATH  Google Scholar 

  117. Yamada T, Izui K, Nishiwaki S, Takezawa A (2010) A topology optimization method based on the level set method incorporating a fictitious interface energy. Comput Methods Appl Mech Eng 199:2876–2891

    MathSciNet  MATH  Google Scholar 

  118. Young V, Querin OM, Steven GP, Xie YM (1999) 3D and multiple load case bi-directional evolutionary optimization (BESO). Struct Optim 18:183–192

    Google Scholar 

  119. Zhou S, Wang MY (2006) 3D Multi-material structural topology optimization with the generalized Cahn–Hilliard equations. Comput Model Eng Sci 16:69–82

    Google Scholar 

  120. Zhou S, Wang MY (2007) Multimaterial structural topology optimization with a generalized Cahn–Hilliard model of multiphase transition. Struct Multidiscip Optim 33:89–111

    MathSciNet  Google Scholar 

Download references

Acknowledgements

L. Dedè and T.J.R. Hughes were partially supported by the Office of Naval Research under contract number N00014-08-0992. M.J. Borden and T.J.R. Hughes were partially supported by the Army Research Office under contract number W911NF-10-1-0216. M.J. Borden was partially supported by Sandia National Laboratories; Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000.

The authors also acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported within this paper (URL: http://www.tacc.utexas.edu).

The authors acknowledge Prof. R.B. Haber, University of Illinois at Urbana–Champaign, for fruitful discussions and advice.

Author information

Author notes

  1. Luca Dedè

    Present address: SB–MATHICSE–CMCS, École Polytechnique Fédérale de Lausanne, Station 8, 1015, Lausanne, Switzerland

Authors and Affiliations

  1. Institute for Computational Engineering and Sciences, The University of Texas at Austin, 1 University Station C0200, Austin, TX, 78712, USA

    Luca Dedè, Micheal J. Borden & Thomas J. R. Hughes

Authors
  1. Luca Dedè
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Micheal J. Borden
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thomas J. R. Hughes
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Luca Dedè.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dedè, L., Borden, M.J. & Hughes, T.J.R. Isogeometric Analysis for Topology Optimization with a Phase Field Model. Arch Computat Methods Eng 19, 427–465 (2012). https://doi.org/10.1007/s11831-012-9075-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11831-012-9075-z

Keywords

Search

Navigation