Merits and Limitations of Mathematical Modeling and Computational Simulations in Mitigation of COVID-19 Pandemic: A Comprehensive Review

Abstract

Mathematical models have assisted in describing the transmission and propagation dynamics of various viral diseases like MERS, measles, SARS, and Influenza; while the advanced computational technique is utilized in the epidemiology of viral diseases to examine and estimate the influences of interventions and vaccinations. In March 2020, the World Health Organization (WHO) has declared the COVID-19 as a global pandemic and the rate of morbidity and mortality triggers unprecedented public health crises throughout the world. The mathematical models can assist in improving the interventions, key transmission parameters, public health agencies, and countermeasures to mitigate this pandemic. Besides, the mathematical models were also used to examine the characteristics of epidemiological and the understanding of the complex transmission mechanism. Our literature study found that there were still some challenges in mathematical modeling for the case of ecology, genetics, microbiology, and pathology pose; also, some aspects like political and societal issues and cultural and ethical standards are hard to be characterized. Here, the recent mathematical models about COVID-19 and their prominent features, applications, limitations, and future perspective are discussed and reviewed. This review can assist in further improvement of mathematical models that will consider the current challenges of viral diseases.

1 Introduction

The new pandemic also known as coronavirus disease (COVID-19), is an infectious disease caused by the contagious virus, severe acute respiratory syndrome (SARS-CoV-2). It has risked the well-being of people and caused major global economic losses [1,2,3,4,5]. COVID-19 pace prevention and global initiatives cannot be well understood by biological and health-care instruments alone, since it is a complex pandemic and the developments in therapies and medical services require certain mathematical tools. Thus, the mathematical models are indispensable for the estimation of main transmission parameters and countermeasures to mitigate this pandemic [6,7,8,9,10].

Many new mathematical models have been used to understand and estimate the dynamics of the COVID-19. It is very important for monitoring and planning by public health organizations. As there is no well-defined vaccine and appropriate treatment drugs, more accurate mathematical models are needed to fine-tune quarantine policies and other government acts such as lockdown, media attention for social isolation and better public health, etc., for the management of illness. Further, stochastic and heterogeneous contacts between individuals should be considered in the established model [11,12,13,14,15,16,17,18]. Recently, Yang et al. [1] released a mathematical model to evaluate the production of COVID-19 in China. The severity and timing of the epidemic peak and the final epidemic factor were expected by various intervention strategies focused on an updated compartmental susceptible-exposure-infectious-recovered (SEIR) system. This is a typical example of the study of transmission and distribution of COVID-19 through the use of mathematical modeling techniques. Therefore, an accurate understanding of the disease's dynamics is important for reducing social infection as infectious diseases add to the broad challenge facing citizens and the country's economy. Another problem is the implementation of a suitable strategy against the transport of diseases. One of the main tools to deal with these challenges is the mathematical modeling technique [18,19,20,21,22,23,24,25].

To estimate better results of the pervasiveness of contagious diseases, several mathematical models have been introduced and these models are based on differential equations. Recently, researchers showed that the fractional differential formulations are useful to estimate a more precisely model global dynamics and can be applied in different domains such as engineering, biology, physics, economics, finance, epidemiology, and theory of control [26,27,28,29,30,31,32]. By using these mathematical models, the rate of change in COVID-19 can be understood and how the disease can affect persons at risk and in under-quarantine. Therefore, recent research is the focus on developing a biological model for infectious diseases using mathematical formulations [33,34,35,36,37,38]. This review work aims to present a constructive discussion about various mathematical models and their merits and limitations; so, researchers can concentrate on appropriate models that can be utilized for the COVID-19 prediction.

1.1 Organization

To ease the flow of paper, the paper begins with a comprehensive abstract. Sect. 1: introduction describes the overall situations and preliminary definitions related to Covid-19. In Sect. 2 the role of different mathematical models in understanding the rise, spread, and forecasting of COVID-19 is reviewed in detail based on the models briefed. Section 3 is dedicated to mathematicalling modelling of COVID-19 simulating the role of aerosols in its transmission. Section 4 discusses the merits of various mathematical modeling bases on the review outcome of Sect. 2. Limitations and future directions are discussed in Sect. 5. Section 6 contains brief discussions of reviewed models and their limitations in general, concluding remarks with usual assumptions made by the researchers. It is strongly believed that the outcomes of this article can assist in the further improvement of mathematical models that will consider the current challenges of viral diseases.

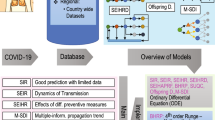
2 Review of COVID-19 Mathematical Modelling

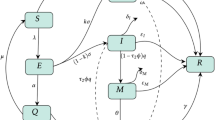
Many people around the world have been hampered by the epidemic of the COVID-19 virus that was originally identified in China. Mathematical models can be very productive in order to better understand and forecast the propagation dynamics of this epidemic [39,40,41,42,43]. Numerous mathematical models varying largely for prediction/forecasting of this disease, role of quarantine, deaths, registered cases, etc. are modeled at different levels. The summary of the models used by researchers is briefed in Table 1 with references. In Table 2 an overview of COVID-19 mathematical models highlighting the study type, model related, advantages and disadvantages are summarized. In this review article, the role of mathematical models in understanding the rise, spread, and forecasting of COVID-19 is provided in detail based on the models briefed. Most of the mathematical modeling of the disease reported is pertinent to the compartmental model. An idea of compartmental models along with intra movements is shown in Fig. 1. The transmission structure of COVID-19 and the spread of infection from a single person is shown in Figs. 1 and 2 respectively for the sake of demonstration.

Table 1 Different mathematical models adopted for modelling of COVID-19

Table 2 COVID-19 mathematical modelling—an overview with topology

Fig. 1

COVID-19 Transmission structure model [73]

Fig. 2

Spred of infection with intial infection by person A [105]

The following assumptions are usually accompanied with different mathematical models and are summarized as follows: (a) the rates of viral mutation in various countries are similar; (b) persons recuperated will achieve permanent immunity to COVID-19; (c) the consequences (also spatial data structures) of climate change will be overlooked in the short-term forecasts; (d) travel behavior of the people was not influenced by the disease; (e) during the incubation period, infected individuals could not infect others; (f) the pandemic does not have strong seasonality in its transmission; (g) even distribution of population in the region of study.

The present contributions in the epidemiological modeling of Covid-19 comprise various types of models: statistical models, mathematical models, network-based models, and phenomenological models. SIR compartmental models are most popular in modeling epidemic dynamics because of its conceptual and mathematical simplicity. Only very few models are based on two-dimensional or three dimensional partial differential equations. Viguerie et al. [107] presented an early version of a SEIRD (Susceptible–Exposed–Infected–Recovered–Deceased) mathematical model based on partial differential equations coupled with a heterogeneous diffusion model. It described the spatiotemporal spread of the COVID-19 pandemic, and aims to capture dynamics also based on human habits and geographical features. Ahmed [108] tried to design the shape of corona virus (COVID-19) using the partial differential equation and found that the PDE method can produce smooth parametric surface representations of any given shapes of viruses having complex geometries.

Liu et al. [126] developed two mathematical models SEIRU and SEIRU δ that incorporate the different phases (referring to Fig. 3) of COVID-19 epidemic infection in China. Proper care was taken to consider the major epidemiological parameters like transmission rate, basic reproductive number, and daily reported cases. The results stress the importance of (1) implementing governmental restrictions to mitigate the brutality of the epidemic, (2) both reported and unreported cases in interpreting the number of reported cases, and (3) asymptomatic infectious cases in the transmission of disease.

Fig. 3

Important phases of COVID-19 transmission: Exposed or latency period is the phase in which an infected person without symptoms causes transmission. The incubation period is the phase before the symptomatic period. The transmissibility period overlaps both symptomatic and asymptomatic periods [126]

Using a mathematical model, the dynamic analysis of health care capacity for COVID-19 was investigated by Cakan [65]. The authors examined the effect of health care efficiency for the case of local and global stability, while some numerical simulations were performed to help the model. It was shown that the model was dependent upon β (effective contact rate); if β is not small, the increase in infectious individuals is unavoidable. If β even increases by 0.17 × 10⁻⁸, the health care capacity will exceed (refer to Fig. 4). The compartment model behaviors based on the proposed model can be seen in Fig. 5. In another study, Almeshal et al. [71] forecasted COVID-19 spreading by logistic regression and compartment modeling. Stochastic and deterministic modeling was used for calculating the size of the spread in Kuwait. In Fig. 6, the effect of variation of reproduction number on spread control and its infection height are shown as obtained from their developed model using the Eq. (1). The rise in the number of reproductions will prolong the expected ending period by around 7 weeks and an approximately 29.57% increase in the outbreak rate. This rise may be since people are repatriating with significantly higher numbers from epicenters and asymptomatic, resulting in transmit the disease to the susceptible individual. Equation (1) can be expressed as follows [71]:

$$R_{o} = \frac{\beta }{\gamma }$$

(1)

here, β and γ are the infection rate and the recovery rate and the proportion of the population infected every day, respectively. This model is based on SIR (Susceptible–Infected–Recovered (SIR) where the compartments are S, I, and R. These are 1) population at risk of infection 2) infected population 3) recovered population, respectively.

Fig. 4

I function variation with t (time) [65]

Fig. 5

The proposed models evolving in all compartments [65]

Fig. 6

Infection rates predicted for R_o (reproduction number) = 2.2 and R_o = 2.3 [71]

Ribeiro et al. [86] used stacking-ensemble learning, CUBIST (cubist regression), RIDGE (ridge regression), ARIMA (autoregressive integrated moving average), SVR (support vector regression), and RF (random forest) to evaluate the task of COIVD-19 cases prediction in Brazil. The developed framework and the mathematical training model implemented are shown in Fig. 7 and Eq. (2), respectively. The efficacy of the models was assessed based on the index of change, mean absolute error, and the criterion of absolute percentage error with a symmetric scale. In most cases, learning from SVR and stacking-ensemble achieves greater efficiency concerning adopted parameters than comparative models. The mathematical training model is expressed as follows:

$$y_{{\left( {t + 1} \right)}} = f\left\{ {y_{t} , \ldots ,y_{{t + 1 - n_{y} }} } \right\} + \in \quad \in \sim \,N\left( {{\mathbf{0}},\sigma^{2} } \right)$$

(2)

where y_(t+1) is one-day prediction, n_y= 5 past cases. ∈ and σ² are the random error and constant variance, respectively. Li et al. [89] examined the COVID-19 modeling data and it was found a fairly small error between both the model developed and the official data curve. Around the same period, the epidemic situation is based on forwarding prediction and backward observation; these relevant analyzes helped applicable countries to make policy choices. The model was developed by analyzing the existing Hubei epidemic data, and after that, the simulation was performed. Li et al. [89] analyzed the key factors influencing the spread of COVID-19 such as the number of simple regenerations, the time of incubation, and the total number of cure days. The authors forecasted the transformation of current epidemic data and showed a significant impact on the epidemic if controls were imposed. Furthermore, according to current data abroad, making ambitious estimates of the disease development patterns in South Korea, Italy, and Iran, pointing out potential outbreaks and the associated control time, and tracking countries' initial transmission dates.

Fig. 7

A framework to forecast COVID-19 [86]

Kyrychko et al. [51] developed a SEIR-type mathematical model of COVID-19 dynamics to estimate the number of cases and deaths in Ukraine. It was estimated that restricting mixing among children and youngsters has a larger impact on reducing the number of cases because of larger mixing rates in these age groups while shielding over-60s might have a smaller effect on reducing the number of cases, but might significant reduction in the number of deaths. Also, the results recommend that dropping work contacts is more efficient at reducing the disease issue than reducing school contacts or implementing shielding for people over 60 age. Badr et al. [103] used daily mobility data (Jan 1 to April 20, 2020) to capture real-time trends in movement patterns for each US province by fitting a statistical model. The mobility patterns were strongly correlated with decreased COVID-19 case growth rates for the most affected provinces in the USA and dropped by 35–63% relative to the normal conditions. The findings also strongly support that social distancing played a crucial role in the reduction of case growth rates in the USA.

Nicholas et al. [104] developed a mathematical model of SARS-CoV-2 transmission based on infectiousness and PCR test sensitivity over time since infection. The authors confirmed that all individuals with symptoms of COVID-19 self-isolated and self-isolation were 100% effective in reducing ahead transmission, while self-isolation of symptomatic individuals would result in a reduction in R of 47% (95% uncertainty interval). Weekly screening of health-care workers and other high-risk groups by use of PCR testing was predicted to decrease their influence on SARS-CoV-2 transmission by 23% (95% UI). Adam et al. [82] studied early dynamics of transmission and control of COVID-19 by combining a stochastic transmission model with data on cases of COVID-19 in Wuhan and international cases over the time during January 2020 and February 2020. It was reported that the median daily reproduction number in Wuhan decayed from 2·35 to 1.05 (95% CI 1·15–4·77) for the case of one-week travel restrictions.

Hernandez-Vargas [47] reviewed in-host mathematical modeling of COVID-19 in humans. The within-host model based on the target cell limited formulation generative number for SARS-CoV-2 was consistent with the wide values of human influenza infection. The immune cell response suggested a slow immune response peaking between 5 and 10 days post-onset of symptoms. The eclipse phase model simulations predict that SARS-CoV-2 may repeat very slowly in the first days after infection, and viral load could be below exposure levels through the first 4 days post-infection.

Many people around the world have been hampered by the epidemic of the COVID-19 virus that was originally identified in China. Mathematical models can be very productive in order to better understand and forecast the propagation dynamics of this epidemic. The fractional-order is linked to the memory effects and hence appears to be most efficient in modeling infectious diseases. Inspired by this, Karthikeyan et al. [80] developed a model for the transmission of COVID-19. It is a fractional-order infected person, symptomless affected, symptomatic infected, regained, and deceased (SEIRD) model. They also compared this model to the traditional one to determine various variables, by utilizing the actual data from Italy, published by the WHO. They found that the fractional-order model is better than the traditional one as it has a low RMSE value.

Liang [44] reported the laws for the transmission of 3 types of pneumonia: SARS, MERS, and COVID-19. He also compared the transmission features of the current COVID-19 with that of SARS and MERS. He developed growth models of transmission by analyzing the rate of growth and continuous suppression of the antiviral disease. The variables required for this growth model are acquired using non-linear fitting. They found that the rate of increase of COVID-19 is almost double that of SARS and MERS with the doubling period of 2 to 3 days, indicating that without human involvement, the percentage of patients with COVID-19 will double in 2 or 3 days.

A massive worldwide crisis is caused by the ongoing COVID-19, with numerous confirmed cases and death rates. Probabilistic statistical methods can help to explain both coronavirus disease administration and monitoring in the absence of any active therapeutics or medicines and with an uncertain epidemiological lifespan. So Piu et al [45] in their report, using epidemic details of up to April 30, 2020, presented a compartmental statistical model to forecast and monitor the dynamic behavior of the COVID-19 pandemic in India. They calculated simple reproduction number R 0, to study simulations and forecasts. For both infection-free and endemic equilibrium points, they conducted the stability investigations w.r.t R 0. In addition, they demonstrated the disease persistence criterion for R 0 > 1.

Kiesha et al. [56] used artificial site communication trends in Wuhan and applied these in the case of school closures, expanded workplace shutdowns, and a decrease in mixing in the general population to investigate how shifts in population mixing have influenced outbreak progress in Wuhan. They simulated the existing path of an outbreak in Wuhan using these datasets and the recent predictions of the epidemiological variables of the Wuhan outbreak and used the SEIR model for various spatial distancing steps. They found that if the phased return to work was during April, physical distancing measures were most effective as this reduced the median number of infections.

The age distribution of novel coronavirus (COVID-19) fatalities across Spain and Japan indicates just a minimal difference, even though the death rate per country indicates a wide variation. So to know the determining factor for this situation, Ryosuke et al. [54] built a mathematical model to explain the propagation dynamics and historical background of 20 COVID-19 and examined the data of fatal incidents of COVID-19 in Spain, and Japan. The parameter representing the age-dependence of vulnerability was calculated by fitting the model with the data published, taking into account the impact of the shift in contact trends during the occurrence of COVID-19 and the fraction of symptomatic infections with COVID-19. They found that if the mortality rate or fraction of symptomatic outbreaks among all cases of COVID-19 does not rely on age, then absurdly variable age-related susceptibility to COVID-19 infections between Japan, and Spain are necessary to justify the similar age-related mortality distribution but varying basic replication numbers (R0).

The mathematical model developed by Veera Krishna [55] was to know the spread and control of COVID 19. He developed the modeling for vulnerable, uncovered, and transmittable inhabitants and isolated inhabitants. They calculated the reproduction number and their results shown the additional diagnostic holders than the actual authenticated holders and proposed a study of the impact of the recognition of cases to identify the magnitude of the epidemic. The mathematical model given in [49] describes how fast COVID 19 spreads through contact and how fast new infections spread the disease. They consider the susceptible, exposed, infected, and isolated people for their modeling. They concluded that for a low contact rate if the reproductive number is less than one, the COVID 19 disease may be controlled.

The mathematical model proposed in [42] describes the time evolution of COVID 19 in Brazil. Their mathematical model describes daily growth and daily change in different cities of Brazil. The model predicted the confirmed cases in July, August. They have not described the effect of factors like social distancing and re-opening of essential services on growth rate as the model depends on the exponential decay curve. SEIR model is used for COVID 19 with the help of the particle swarm optimization to show the evolution of COVID 19 in Hubei province. There is a difference between the estimated value of recovered and hospitalized people by their model and actual data due to small real data consideration into their model [53].

A mathematical model is developed for the understanding of COVID 19 in Nigeria [46] to understand its dynamics. They considered both symptomatic and asymptomatic infected people for mathematical modeling by taking the fraction of people who use facemask into account. Their results show that the disease will be ceased if 55% of the population follows social distancing and face mask usage.

Yousaf et al. [85] performed an analysis based on data collected by the NIH (National Institute of Health)-Islamabad and described a prediction of reported COVID-19 cases and the number of fatalities and recovery rates in Pakistan using the ARIMA (Auto-Regressive Integrated Moving Average Model). The fitted prediction model showed high exponential growth in actual cases, deaths, and recoveries. Based on their forecasting model, the number of reported cases may significantly raise by 2.7 times, 95% forecast interval for the number of cases at the end of May 2020 = (5681–33,079). There might be up to 500 deaths, 95% forecast interval = (168–885) and the number of recoveries may be eight times higher, 95% forecast interval = (2391–16,126). Salgotra et al. [100] used the Genetic Programming (GP) as a predictive model for confirmed cases and death cases along with all three of its most affected states, namely Delhi, Gujarat, and Maharashtra and also India as a whole. The proposed algorithm was described by using the explicit formulation, and it studied the inadequacy of prediction variables. Statistical parameters and metrics were used for the evaluation and validation of the model. The proposed model showed an accurate estimation for COVID-19 cases in India in time series. The pseudo-code for time-series prediction model Algorithm 1 for the confirmed cases (CC) of COVID-19 in India is referred to in Fig. 8.

Fig. 8

Algorithm 1 of the time-series prediction model for the confirmed cases (CC) in India [100]

Wu et al. [69] developed a transmission dynamics model for COIVD-19 and showed that there was a limit to reducing the transmission contact rate. It was estimated that the probability of transmission per contact (β) was virtually unchanged since 26 February, indicating a lack of improvement in personal protection in Ontario. Refers to Fig. 6a, b, the reported cumulative cases and the infected population decreased significantly at peak time as β decreased. The epidemics may be peaked around April 2 if the risk of transmission had decreased by 70%. Similarly, the total confirmed cases and a peak value of the infected population can be decreased by increasing the quarantine rate (q) and, most significantly, the diagnosis rate (δ_I) as shown in Fig. 9d, e and g, h, respectively.

Fig. 9

a, b Effect of the probability of transmission (β), d, e quarantine rate (q), and g, h diagnosis rate (δ_I) of COVID-19 pandemic of Ontario [69]

Higazy [127] formulated the COVID-19 pandemic model by fractional-order model SIDARTHE which had not previously appeared in the literature. The presence of a stable solution of the COVID-19 SIDARTHE fractional-order model was demonstrated and the necessary fractional-order conditions of the four control strategies were created. The responsiveness of the model to fractional order and the parameters of the infection rate were also shown. All studies were simulated numerically using MATLAB increasing the differential equation solver for fractional order. Roda et al. [63] discussed why it was difficult to properly model to predict the COVID-19 pandemic. The authors showed that the main reason for wide variations was the non-identifiability in model calibrations using confirmed case data. Using AIC (Akaike Information Criterion) for model selection, a model with SIR performs much smarter than a model with SEIR in portraying the data stored in the confirmed data. After the City's lockdown and quarantine on January 23, prediction performance for the COVID-19 outbreak in Wuhan, it was found that the effects of the city's strict quarantine indicators on the time course of the epidemic, and simulation the possibility of a second outbreak after the city's return to work. For the SIR and SIER models, the transfer diagrams were shown in Fig. 10. The model equations are also reported by the Eq. (3); where ρI, ρ, β, 1/τ and I₀ are the normal distribution, diagnosis rate, the transmission rate, variance, the initial population size for I compartment on 21^st January at t = 0.

$$\begin{aligned} & S^{\prime} = - \beta IS \\ & I^{\prime} = \beta IS - \left( {\rho + \mu } \right)I \\ & R^{\prime} = \rho I - dR \\ & \, \\ & S^{\prime} = - \beta IS \\ & E^{\prime} = \beta IS - \varepsilon E \\ & I^{\prime} = \varepsilon E - \left( {\rho + \mu } \right)I \\ & R^{\prime} = \rho I - dR \\ \end{aligned}$$

(3)

Fig. 10

Model SIR and SIER transfer diagram [63]

Eikenberry et al. [58] analyzed the role of face masks in the prevention of COVID-19 and established a compartmental model for the overall, asymptomatic public to assess the community-wide impact of mask use, a portion of which could be asymptomatically infectious. Based on data on COVID-19 dynamics in New York and Washington, simulation results indicated that broad implementation of even largely ineffective face masks can significantly reduce COVID-19 community transmission and minimize death and hospitalization. The peak hospitalization and mortality rate from the developed model are presented in Fig. 11.

Fig. 11

Simulated epidemics, cumulative mortality and relative peak hospitalizations [58]

Pathan et al. [128] investigated the rate of mutation of the entire genomic sequence gathered from different countries’ patient dataset using recurrent NN (neural network). The dataset gathered was indeed processed separately to determine the nucleotide mutation and codon mutation. The determined mutation rate was categorized for four different regions, based on the size of the dataset: China, Australia, the USA, and the remaining world. Huge amounts of Thymine (T) and Adenine (A) are mutated to other nucleotides for all regions, but codons were not frequently mutating like nucleotides. The training and testing results of the mutation rate from the model were successful with the proposed neural network model as presented in Fig. 12.

Fig. 12

Mutation rate (nucleotide) forecasting [128]

Chimmula and Zhang [98] assessed the main elements of the current COVID-19 eruption in Canada and the whole world to forecast the patterns and potential stoppage time. The authors described the LSTM (Long Short-Term Memory) networks and a deep learning method for forecasting future COVID-19 cases. Depending on the outcomes of the LSTM network, it was estimated the outbreak could end around June 2020. Scheiner et al. [62] investigated the importance of the death kinetics law and a core component of the SEIR models. The latter approach was contrasted with an alternative approach called the infection-to-death law. To this end, it was tested how well these two mathematical formulations reflect the country-specific data on reported deaths in publicly accessible countries through ranges of 57 countries. The variables of model governance, namely the death transfer coefficient of the model kinetics of death, the obvious fatality to case fraction, and the typical fatal infection to death regulation period were time-invariant. A transmission network model that captured the contact heterogeneity among individuals was developed in which each node represented an individual and the edges represented mingling between individuals through which the disease was transmitted. The developed model was well fitted to the reported data for the COVID-19 epidemic in Wuhan (China), Toronto (Canada), and the Italian Republic using a Markov Chain Monte Carlo (MCMC) optimization algorithm. The model emphasized that the role of containment strategies, personal protection, and social distancing in mitigation of COVID-19 transmission [81, 129].

Mandal et al. [76] formulated a mathematical model introducing a quarantine class and governmental intervention measures to mitigate disease transmission to forecast a short-term trend of COVID-19 for the three highly affected states, Maharashtra, Delhi, and Tamil Nadu, in India; and it suggested that the first two states need further monitoring of control measures to reduce the contact of exposed and susceptible humans. The simulation of the developed mathematical model suggested that both quarantine and governmental intervention strategies like lockdown, media coverage on social distancing, and public hygiene can play an important role in diminishing COVID-19 transmission; while a success rate is highly dependent on the proper implementation of the process. An appropriately formulated mathematical model was developed by Okuonghae et al. [68] to study the influence of various non-pharmaceutical control measures like social distancing, use of face mask and case detection (via contact tracing and subsequent testing) to mitigate the COVID-19 in Lagos, Nigeria. The model results showed that if at least 55% of the population complied with the social distancing regulation with about 55% of the population effectively making use of face masks while in public, the disease will eventually die out in the population. The same applies to the increased case detection rate. The results demand the critical attention of policymakers in strict enforcement of control measures and the medical authority to identify new cases.

The mathematical model similar to the SIRS model was developed by Kassa et al. [70] with or without backward bifurcation and was based on reproduction number, which equals or less than unity for the presence or absence of reinfection. The model was well validated by using available data and the same was used to enforce different mitigation strategies like isolation of at least 30% of the asymptomatic infectious group and provide medical attention for at least 50% of symptomatic patients. The asymptomatic infectious group played a major role in the re-emergence of the disease in the future. Ivorra et al. [83] proposed a new θ-SEIHRD model namely that of infection and the different health and infection conditions of hospitalized people and takes into account the known special characteristics of that disease. It required in particular a novel approach to the fraction of cases found relative to the true total cases infected, allowing the value of this ratio to be analyzed concerning the impact of COVID-19. The model was able to determine hospital bed needs. The data that authorities report on this pandemic were sufficiently complicated to capture important results, but still simpler enough to allow a fair determination of its parameters. In Fig. 13, the evolution of cases in china is depicted available from data and also from the model.

Fig. 13

Several deaths from a.r.c. (adjusted reported cases) and from the developed model (EXP) [83]

Sahin and Sahin [83] predicted the number of actual COVID-19 cases in Italy and the USA The prevision was contrasted in this analysis with the nonlinear fractional model Bernoulli (FANGBM(1,1)) and gray model (GM(1,1), the nonlinear gray model Bernoulli (NGBM(1,1)). There were total handlings of the number of COVID-19 cases in these countries. Models prediction results were calculated in the average absolute percent error (MAPE), R², root average square error (RMSE) estimate values. The FANGBM (1,1) offered the lowest MAPE and RMSE values and the highest R² for these countries with the highest prediction results. Currie et al. [95] described the complexities of the COVID-19 pandemic and explore how simulation modeling will assist decision-makers to make the most informed decisions. The investigation was like a call to arms and policy-makers as a guideline on how the simulation community can provide help. The number and scale of decisions described here indicate that there may be not enough modelers to thoroughly and efficiently address all of these questions, and it needed to choose what we are doing carefully and share results and models quickly across our international networks to optimize the value of modeling simulations to reduce the impact of COVID-19.

Chakraborty and Ghosh [95] carried mathematical modeling for producing short-term (real-time) forecasts of potential COVID-19 events, for multiple countries risk assessment (in case of fatality rates) of the current COVID-19 by defining several significant population characteristics for countries along with other disease characteristics for some of the deeply affected countries. To address the first question, the authors have previously developed a hybrid approach based on the auto-represented integrated moving average model and the Wavelet model, which can generate a short (ten days ahead) forecast for Canada, France, India, and South Korea for the number of cases conducted daily. The ARIMA model can be expressed by Eq. (4) used to forecast the cases on a real-time basis. The real-time forecast for South-Korea based on the developed model is presented in Fig. 14.

$$\begin{aligned} y_{t} & = \theta_{0} + \phi_{1} y_{t - 1} + \phi_{2} y_{t - 2} + \cdots + \phi_{p} y_{t - p} \\ & \quad + \varepsilon_{t} - \theta_{1} \varepsilon_{t - 1} - \theta_{2} \varepsilon_{t - 2} - \cdots - \theta_{q} \varepsilon_{t - q} \\ \end{aligned}$$

(4)

Fig. 14

Forecast of COVID-19 cases for 10 days [95]

Zhang et al. [130] analyzed the regularly accessible new case data from the COVID-19 outbreak in six Western countries of Group of Seven (i.e., France, Canada, United Kingdom, Germany, Italy, and the USA) using a segmented Poisson model. The authors have taken into account the measures by the government concerning COVID 19 (stay-at-home meetings, lock-ups, quarantine, and social distancing). This methodology enabled us to estimate the turning point (at the regular peak of new cases), the timeframe (duration of the outbreak), and the assault rate (percentage of the total population infected during the outbreak) for these countries (referring to Fig. 15). The maximum value of the daily confirmed cases was given by Eq. (5) as follows:

$${\text{max}}\,Y\, = \,\alpha_{2} \left( {\frac{{\beta_{2} }}{{\gamma_{2} }}} \right)^{{\beta_{2} }} e^{{ - \beta_{2} }} \quad {\text{Occuring}}\,{\text{at}}\quad t = \left( {\frac{{\beta_{2} }}{{\gamma_{2} }}} \right)\, = :\,t_{peak}$$

(5)

where α, β, and γ were estimated first, then t_peak peak time was calculated to predict the further spread of the outbreak.

Fig. 15

Model prediction and data obtained having good fitness. Green dash lines represent forecasting [130]

Given the potential transfer of COVID-19 from dead bodies to human beings and the lock-down effect, a mathematical model has been suggested by Atangana [64]. Three incidents have been considered. The first case indicated the body was passed from dead to living (medical professionals performing postmortem treatments and direct communications during funeral ceremonies). This case does not have balancing points, except for disease-free control, a strong sign that corpses due to corona-19 must be handled carefully. In the second example, the transfer rate from dead bodies has been reduced. There was a balance in this situation, as the number of deaths, carriers, and infected persons increased exponentially to a certain degree of stability. In the last case, Atangana [64] used the next-generation matrix to provide a lock-down and social distancing effect. It was found that they hit a zero-output number with a very fast degradation of the number of deaths, contaminated and transported. This is a strong indication that the danger of COVID-19 could be minimized within several months if lock-down guidelines were to be followed. While the proposed mathematical model agreed with the lock-down performance and it is necessary to note the harmful effects of insufficient testing.

Sun and Wang [66] compiled data and trained an ODE (ordinary differential equation) model to fit in the epidemic data from 23rd January to 25th March of Heilongjiang province. To describe the effect, they extended the simulation by using this trained model. The newly reported COVID-19 infections in Heilongjiang province were carried out by an imported ‘escaper’. The Stochastic simulations showed further that substantially that local contacts among imported ‘escapers’ contributed much to the COVID-19 local outbreak, their epidemiologic related cases, and susceptible populations. The ODE used for model development was implemented as follows:

$$\begin{aligned} & dS{/}dt = \lambda C - \beta_{1} SC - \beta_{2} SA + \varepsilon A - \beta_{3} SI \\ & dC{/}dt = \beta_{1} SC + \beta_{2} SA - v_{1} C - v_{2} C - \lambda C + \beta_{3} SI \\ & dI{/}dt = v_{2} C + v_{3} A - \mu IK^{n} /K^{n} + C^{n} + I^{n} \\ & dR{/}dt = \mu IK^{n} /K^{n} + C^{n} + I^{n} \\ & dA{/}dt = v_{1} C - \varepsilon A - v_{3} A \\ \end{aligned}$$

(6)

where λ defines the quarantine discharge rate. The average contact rate between S and C, A, and I is defined by the β_i (i = 1…3). The average contact rate between sensitivity and near contacts is approximately β₁. β₂ describes the average rate of touch among susceptible and asymptomatic patients. β₃ refers to the normal interaction between vulnerable and contaminated populations. β denotes an asymptomatic self-recovery rate as all asymptotical patients may recover untreated. ν₁ & ν₂ is the rate of transition from closer to asymptomatic contacts and diagnosed contacts. ν₃ is the transition to diagnosed cases from asymptomatic. μ is the average recovery (maximum) rate [66].

Soukhovolsky et al. [72] developed a simple phase transition mathematical model with an autoregressive distributed lag based on the data from the World Health Organization and Johns Hopkins University between 01.01.2020 and 04.17.2020. This model was able to make an accurate prediction of the COVID-19 dynamics in 10 days with an exponential feature and predict the effect of the government/health strategies. The developed model by Alkahtani et al. [94] was based on Lagrange polynomial and use the concept of a fractional differential operator. It helped in implementing strategies during the COVID-19 intervention in Italy. The model has 8 components leading to a system of 8 ordinary differential equations and used the concept of the next-generation matrix to derive the reproductive number. Numerical simulations were presented for different values of fractional orders with a detailed overview of the stability of equilibrium points. Singhal et al. [106] established two separate modeling models for monitoring the trend for a variety of cases and also foreseeing cases in the next few days to prepare for this epidemic. One was a mathematical concept that considers different parameters related to virus propagation, while the second was a non-parametric model that was adapted to the available data using the Fourier decomposition method (FDM). The study was conducted for different nations, but comprehensive findings were available for Italy, India, and the USA. The turnaround dates were calculated for the pattern in affected individuals. The developed model fitness for the selected countries is displayed in Fig. 16.

Fig. 16

Model fitness for different countries to active cases [106]

Rodriguez et al. [131] carried the modeling of and prediction of Mexican COVID-19 infections, using only reported cases given in the regular technical report COVID-19 MEXICO, by mathematical and computational models. Mathematical models: Gompertz and logistic, as well as the statistical model, have been used to model the number of instances of COVID-19. The results indicated a great match between the data observed and the Gompertz, Artificial, and Logistic Networks model. The Gompertz, Logistic, and reverse ANN models were then used to estimate the total number of COVID-19 infected before the end of the epidemic. Zhang et al. [67] studied the suitability of fractional-derivative equations (FDEs) for modeling the dynamics and mitigation of the COVID-19 pandemic for the first time in the literature. The model was based on the Susceptible, Exposed, Infectious, and Recovered (SEIR) with a time-dependent feature and was validated promptly. It was used to predict the evolution of the COVID-19 pandemic for three months in China. The simulation results showed significant spatiotemporal variations in the recovery rate and the number of deaths follows the above said temporal FDEs. The developed model was used successfully in the USA, Italy, Japan, and South Korea. Evaluation of non-pharmaceutical strategies to mitigate the COVID-19 epidemic was additionally carried out by a time FDE model based on the random walk particle tracking scheme, which was analogous to a mixing-limited bimolecular reaction model. The model declared that strict social distancing is more effective than self-quarantine as not all infected people can be diagnosed and immediately quarantined.

Ndaïrou et al. [61] have suggested a mathematical compartmental model for the propagation of the disease COVID-19 that focuses on super disseminators’ transmissibility. They measured the fundamental threshold for reproductive numbers, analyze the local stability of the disease-free balance regarding the basic reproductive number, and analyze how sensitive a model is when it comes to changing its parameters. Number simulations indicated the suitability for an outbreak in Wuhan, China of the proposed COVID-19 model. Lalmuanawma et al. [101] comprehensively reviewed the importance and consequent use of artificial intelligence (AI) and machine learning (ML) in screening, predicting, forecasting, contact tracing, and drug development for the COVD-19 pandemic. Khoshnaw et al. [96] developed an updated model by reviewing the existing models. The update included a system of differential equations with transmission parameters. Some key computational simulations and sensitivity analysis were investigated by using three different techniques: non-normalizations, half normalizations, and full normalizations. The transition rates between asymptomatic infected with both reported and unreported symptomatic infected individuals were very sensitive parameters concerning model variables in spreading this disease.

Arino et al. [132] developed an epidemic model, SL1L2I1I2A1A2R, that incorporates an Erlang distribution of times of sojourn in incubating, symptomatically, and asymptomatically infectious compartments that are important in the context of the current COVID-19 pandemic. Li et al. [59] developed a mathematical model to answer those who complain of symptoms of influenza similarity (ILI), who may be at risk for COVID-19 contraction or other emerging or re-emerging respiratory infectious substances, which were to use kits to detect serious lack of testing tools. In the case of an outbreak with the influenza season, the model was applied to determine the effect of mass influenza vaccination on the spread of COVID-19 and other respiratory pathogens. Figure 17 shows an example used in the study to show the dynamics of the infection of COVID-19. Intensive contact tracing followed by quarantine and isolation interventions is indicated. Complete suspected cases of quarantine with symptoms of exposed quarantine (E_f), clinical fever (S_f), and contaminated quarantine (I_q) were recorded.

Fig. 17

Modelling of COVID-19 dynamics [59]

Zhao and Chen [75] defined the dynamics of COVID-19 and specifically parameterize the intervention impacts of control steps, which are more fitting for analytics than other current epidemic modes, and established a prone, unquarantined, quarantined infected, Conferred infected model (SUQC). The SUQC model was used to evaluate the COVID-19 outbreak in Wuhan, Hubei (except for Wuhan), China (except for Hubei), and 4 first-class cities in China with the daily data of reported infections. In Wuhan and Hubei, the model predicted that the end time of the COVID 19 is at around late March, for China, except Hubei, around mid-March, and for the four cities of tier-one before early March 2020. In total 80,511, 49,510 of them from Wuhan, 17,679 from Hubei excl. Wuhan and the rest of 13,322 from other parts of China (excluding Hubei) were reported to be infected in China. Velásquez et al. [97] analyzed historical and expected infection for COVID-19 death based upon the Gaussian reduced-space phase regression, with knowledge collected day by day in 82 days, between 21 January and 12 April 2020, in the sense of chaotic Dynamic Systems. According to the last findings, the mean-field models of COVID-19 can be assumed to be completely used for the outbreak to be quantitatively distributed by outbreaks, fatality, and recovery. It was estimated that about 14 July 2020, the highest in the USA will be 132.074 deaths of approximately 1,157.796 people, as well as 132.800 deaths at the end of epidemics.

Ayinde et al. [91] subjected the combined daily reports of COVID-19 of these three variables into nine single, quadratic, cubic, and quartic statistical models. The best of 36 models was classified and used in modeling and analysis which classified the best. The data collected by the Nigeria Disease Control Center were tracked daily and eventually analyzed for 64 days, two, and three months. The prediction values are troubling, and the authors suggested the Government of Nigeria needs to rapidly review its activities and operations concerning COVID-19 to include some operational & effective mechanisms and measures to avoid these challenges. Abdo et al. [133] performed the analysis and defined the solution to the nonlinear FDEs (fractional differential equation), which describes the deadly and perhaps most parlous virus known as a coronavirus (COVID-19). Applying a fractional AB (Adams Basforth) method, the mathematical model according to 14 nonlinear FDEs was presented and the numerical results were examined. Besides, to achieve more efficient performance, a recently implemented non-local, fractional operator is known as Atangana-Baleanu (AB) was used. To demonstrate the existence, uniqueness, and consistency of the model, the fixed-point theorems of Krasnoselskii and Banach were employed.

Alberti and Faranda [133] concentrated on statistical projections of COVID-19 infections carried out through the integration into real data of asymptotic distributions. By taking as a case-study the epidemic outbreak of COVID-19 infections in the provinces of China and Italy, they found that the forecasts at the earliest stages of the epidemic were marked by significant uncertainties. After the height of the epidemics, those uncertainties decrease dramatically. Differences in the variability of regional standards can be employed to illustrate the delay in the virus spread. The daily infections in three areas of China were shown in Fig. 18 which was used to model the pandemic for real-time forecasting.

Fig. 18

Daily infections in Yunnan, Hubei, and Bejing [133]

In light of recent efforts to develop a global surveillance network for combating pandemics through artificial intelligence, Bekiros and Kouloumpou [77] implemented the new SBDiEM for modeling, prediction, and nowcasting infectious dynamics. This model can be modified for both past and COVID-19 outbreaks. The new approach can have major impacts on national health systems, global stakeholders, and policymakers. Kırbaş et al. [87] confirmed COVID-19 cases of Denmark, Belgium, Germany, France, UK, Finland, Switzerland and Turkey were modeled with Auto-Regressive Integrated Moving Average (ARIMA), Nonlinear Autoregression Neural Network (NARNN), and Long-Short Term Memory (LSTM) approaches. Six model performance metrics were used to select the most accurate model (MSE, PSNR, RMSE, NRMSE, MAPE, and SMAPE). According to the results of the first step of the study, LSTM was found the most accurate model. The results of the second step of the study show that the total cumulative case increase rate was expected to decrease slightly in many countries. The study also revealed that unavailability or limited data makes modeling and prediction more challenging.

Ng et al. [134] modified the SEIRS model with additional exit conditions to extend prediction on the current projections of the pandemic into three possible outcomes; death, recovery, and recovery with a possibility of re-susceptibility. The model also considered specific information such as the aging factor of the population, time delay on the development of the pandemic due to control action measures, as well as re-susceptibility with temporal immune response. The model was verified using two case studies based on real-world data in South Korea and Northern Ireland. Bozkurt et al. [50] studied the knowledge on coronaviruses currently collected and create a model for differential equations with piecemeal constant arguments to address the transmission of bat-borne coronaviruses from and through the natural host to the human host. The Linearized Stability Theorem considers the local stability of the positive balance point of the model. Moreover, by using a proper Lyapunov function, we address global stability. To evaluate the outbreak of early detection, the Allee effect was implemented at times and achieved complex activity stability conditions.

Fanelli and Piazza [135] examined in the time span 22 Jan–15 March 2020, the time dynamics of the outbreak COVID-19 in China, Italy, and France. The first study of simple regular lag-maps points to a certain universality in the spread of the epidemic, which indicates the use of simple mean-field models to capture quantitative images of the spread of the epidemic, especially the heights and times of the peak of infected persons reported. Analysis of the same data on a single susceptible-infected-recovered-death model shows that the kinetically determining the recovery rate appears to be the same regardless of the region, while the infection rates and mortality rates seem more variable. Based on their estimates, they estimated that 2500 ventilating units should be a realistic number for the peak requirement for strategic planning in Italy. Finally, a simulation of the impact on the Italian outbreak of drastic control steps shows that a decrease in infection rate actually causes the epidemic to quench. In order to achieve a significantly declining rate of disease peak and mortality, however, the infection rate must also be substantially and rapidly decreased. Only a collective, albeit painful, initiative by the community as a whole seems to make this possible.

$$\begin{aligned} & P_{1} = \alpha P_{0}^{\beta } \\ & P_{2} = \alpha P_{1}^{\beta } = \alpha^{1 + \beta } P_{0}^{{\beta^{2} }} \cdots \\ & P_{n} = \alpha^{{1 + \beta + \beta^{2} \cdots + \beta^{n - 1} }} P_{0}^{{\beta^{n} }} \\ & 1 + 1 + \beta + \beta^{2} \cdots + \beta^{n - 1} = (1 - \beta^{n} ){/}(1 - \beta ) \\ & P_{n} = \alpha^{{(1 - \beta^{n} ){/}(1 - \beta )}} P_{0}^{{\beta^{n} }} \\ \end{aligned}$$

(7)

Here, population P = (C, R, D), β = 0.912, α = 2.181, C is confirmed cases, R reported death, D is deaths, n is the day. In Fig. 19 the prediction using the developed model is provided.

Fig. 19

Forecasting of COIVD-19 by data fitting [135]

Guliyev et al. [99] used the spatial panel models to investigate the direct and indirect spatial effects on the spreading of the COVID-19 pandemic and its relationship between confirmed cases, deaths thereof, and recovered cases due to treatment are analyzed. The best model, SLX (spatially-lagged X), was determined based on the maximum pseudo-R2, LR-test, LM-test statistics, and minimum AICc (corrected Akaike information criterion) and BIC values (Bayesian information criterion). As per the spatial effects, it is concluded that the rate of deaths and recovered cases has significant positive and negative effects on COVID-19 respectively. Gao et al. [92] reviewed the epidemic prophecy for Wuhan's novel COVID-19 epidemic with the use of Q-Homotopy (Q-HATM) research. To parameterize the model and evaluate the number of unreportable events, we have considered the studies. New research is being performed for unreported cases using the emerging epidemic COVID-19 model. In the context of the Caputo derivative, the serial solution for the considered system exemplifying the coronavirus model is created. The findings obtained are explained utilizing figures showing the behavior. The results show that the method used for nonlinear equations is extremely emphatic and simple to deploy.

Lalwani et al. [78] suggested an Optimum Locking cycle for some particular geographic regions to measure a three-stage susceptible-infected-recovered-dead (3P-SIRD) model that will support the break-up of the transmission chain and will also enable the economy of the country to recover and maintain infrastructure in the battle against COVID-19. The proposed model is new, with parameters such as silent carriers, newly infected individuals, and non-recorded people infected with the deadly virus, the assumed incidence, and the rate of death. These parameters contribute greatly to the description of the model and of critical parameters. The pseudo-code of phase 3 prediction is displayed by Algorithm 3 (referring to Fig. 20). N_S, N_I, N_R, N_S, no. of suspected, infected, recovered, and died people of COVID-19 from beginning to end. T_opt is the optimum period of lockdown, t is the day, and 1, 2, 3 represent phases 1, 2, 3 respectively.

Fig. 20

A pseudo-code for phase 3 prediction Algorithm 3 [78]

Martelloni and Martelloni [79] described a 4-population model: total infected, optimistic currently, recovery, and death. Therefore, in the evaluation of the Sars-Cov-2 outbreak, An alternative approach was suggested to a classic SIRD model. The approach was, however, general to other diseases and thus applicable. It was analyzed the actions of the Swab infection ratio in Italy, Germany, and the USA, and has studied this parameter, we retrieved for these three countries the generalized logistic model previously applied. It was assumed this could be useful for a possible coronaviral outbreak. Pham [136] proposed a specific role model which was calculated the total death toll in the community and especially the cumulative number of deaths caused by the current COVID-19 virus in the USA. The results of the modeling were equated with two associated existing models based on new parameters and many existing framework selection processes. The method presented suits much easier than the two other US-based related models. It was seen that on the last available data point and the next day, errors in the fitted data and expected data points are less than 0.5% and 2% of the total number of deaths in the USA. Singh et al. [84] developed a hybrid approach that required the application of discrete wavelet breakdown to the death data set due to COVID-19, which divided the input data into serial components and then applies to each component sequence the required econometric model for future forecasting of deaths. ARIMA models were popular econometric prediction models that able to generate accurate predictions when applied to decomposed time series wavelets. The data set consisted of daily death cases in most five countries affected by the COVID-19 which have to be checked by the hybrid model and forecast deaths a month beforehand.

Sarkar et al. [60] proposed a model for 17 regions of India as a whole and India that forecasts COVID-19 dynamics. The predicted pandemic life cycle and actual data or historical history to date are shown by a complete scenario, which disclosed the expected inflection point and end-stage of SARS-CoV-2. The proposal model tracked the dynamics of six compartments, namely SS, Asymptomatic (A), RE, I, Isolated Contaminated (Iq), and Quarantined Responsive (Sq), SARIIqSq expressed collectively SARIIqSq. A decrease in the contact rate between uninfected and infected persons will effectively reduce the base reproduction number if the susceptible individual was quarantined. The simulations showed that the removal of an emerging pandemic SARS-CoV-2 was possible through the combination of restrictive social distance and touch tracing. The projections were based on real information with rational assumptions, while the exact path of the outbreak would depend heavily on the implementation of quarantine, isolation, and cautionary measures. The contour plots of COVID-19 for different states of India are shown in Fig. 21 for the sensitive parameter, βs.

Fig. 21

Simple reproductive contour plots R₀ eight provinces of India concerning the possibility of transmission rate βs disease and quarantined rate βs of sensitive persons [60]

3 Mathematical Models that Simulate the Role of Aerosols in Transmission of COVID-19

During the initial spreading period of COVID-19 pandemic, scientists were not sure about the role of aerosols in its transmission. Later, it is identified that the COVID-19 virus could persist in aerosol form and the severity of transmission depends on several factors: infectiousness, dose, and ventilation. Recent studies [137] recognized that aerosols play a major role in spreading of COVID-19 pandemic. Mathematical models are very helpful in understanding the role of aerosols in transmission of this pandemic. Carducci et al. [138] described the state of the art of coronaviruses and airborne transmission with the help of a systematic review using the PRISMA methodology by citing 64 research articles. It is concluded that airborne transmission is possible for severe illness cases without estimating its attributable risk. Nevertheless, it is advised to use masks, keep safe/social distance and air ventilation as a precautionary measure. Comunian et al. [139] published a review article about air pollution and COVID-19 by stressing the role of particulate matter in its spreading.

Girolamo et al. [140] assessed the potential role of atmospheric particulate pollution and airborne transmission in intensifying the first wave pandemic impact of SARS-CoV-2/COVID-19 in Northern Italy. It is found that the number of small potentially infectious particles coalescing on PM2.5 (particulate matter 2.5 micrometers or less in diameter) and PM10 (particulate matter 10 micrometers or less in diameter) particles is estimated to exceed the number of infectious particles needed to activate COVID-19 infection in humans.

Coccia [141] proposed two mechanisms for accelerated diffusion of COVID-19 outbreaks in north Italy with high intensity of population and polluting industrialization by considering air-to-human and human-to-human transmission dynamics. The results reveal that the mechanisms of air-to-human transmission play a critical role rather than human-to-human transmission in spreading of COVID-19. Seminara et al. [142] reviewed about the biological fluid dynamics of airborne COVID-19 infection mechanisms involved in its transmission. The mechanics of the complex two-phase flow processes caused due to the sneezing or speaking or coughing of an infected individual and the airborne particles’ dispersal into the environment is well figured out. This study also evaluated the contrasting effects of natural or forced ventilation of environments on the transmission of contagion of Covid-19.

Khalid et al. [143] explained the disease spread mechanism via aerosols in the atmosphere with the help of molecular communication and is much relevant in context of Coronavirus disease breakout. They presented a complete system model and derive an end-to-end mathematical model for the transmission channel under certain constraints and boundary conditions. Significant numerical results are generated to observe the impact of parameters that affect the performance and justify the feasibility of the proposed setup in related applications. Mittal et al. [144] framed a mathematical model for estimating risk of airborne transmission of COVID-19 to assess the protection afforded by the use of face mask made from a variety of fabrics and proper social distancing. Wang et al. [145] studied about the airborne particulate matter, population mobility and COVID-19 in different cities of China. The study is based on Generalized additive models (GAM) with a quasi-Poisson distribution and identified that the aforementioned factors are highly associated with an increased risk of COVID-19 transmission.

Ronchi et al. [146] explored that how microscopic crowd modelling can be used to assess occupant exposure in confined spaces and the results allowed policy makers to perform informed decisions concerning building usage during a pandemic. Similar work was also reported by Jankovic [147]. Villafruela et al. [148] carried out a CFD analysis of the human exhalation flow using different boundary conditions, ventilation strategies, and environmental conditions. The results confirmed the use of CFD analysis as a powerful tool to predict the contaminant distribution exhaled by a human. Vuorinen et al. [149] Modelled the transport of aerosol and virus exposure with Monte-Carlo simulations in relation to SARS-CoV-2 transmission by inhalation indoors and offered clear quantitative awareness to the exposure time in varied public indoor environments.

The abovementioned studies indicate that aerosol-based transmission of COVID-19 pandemic happens due to prolonged exposure in confined buildings having poor ventilation even though with the distance greater than 1.5 m. if the distance is within 1.5 m, there is high chance of droplet-based transmission. The following preventive measures may be strictly imposed [142,143,144,145,146,147,148,149] to prevent the aerosol-based transmission of COVID-19 pandemic: physical distancing, hand sanitizing, proper mask wearing, sufficient systematic ventilation of indoor environments or suitably filtered (HEPA filter) air, avoiding overcrowding in confined spaces or reduce the duration of the stay, curtail high-emission activities, and last but not least, the strong awareness of aerosol-based transmission of COVID-19 pandemic among the public.

4 Merits of Mathematical Modelling

Based on the literature study, it is understood that the following are the significant merits of mathematical modeling:

• 1. In fact, with the aid of these mathematical models, different countries could do all the preparations in advance to prevent the widespread epidemic with proper planning and mobilizing huge resources. Besides, it was also possible to devise effective strategies to meet the unexpected demands of the health care system.

• 2. It helps the authority to understand the effectiveness of lockdown and to decide when to impose sharp/partial/lenient lockdown depending on the reproduction ratio and incubation ratio of the virus.

• 3. These are indispensable tools for the estimation of main transmission parameters and countermeasures to mitigate this pandemic. It is understood that these mathematical models are key tools in public health management programs even though there is preeminent uncertainty in every model.

• 4. It assists to understand the epidemic’s dynamics clearly and helps in the forecasting of its propagation.

• 5. It helps to formulate a long-term rational strategy to nip the pandemic in the bud by considering social distancing for its prevention, but necessitating social interaction for the economic sustenance of the society. Mathematical models steer between these conflicting objectives.

The authors strongly believe that this review paper can assist in the further improvement of mathematical models that will consider the current challenges of viral diseases.

5 Limitations and Future Directions

The literature reveals the following major limitations:

• 1. Information from the results or predictions of mathematical modeling is helpful to the decision-makers and authorities only if the impact of the underlying assumptions is well understood.

• 2. The huge volume and speed of published COVID-19 literature mean that research results and guidelines are continually changing with the advent of new data.

• 3. The reported treatment results up to date were focused solely on observation or limited clinical studies in which the risk of bias or imprecision about the degree of the treatment-effect has increased (one with more than 250 patients).

• 4. Only analyzed adult patients and the results do not extend to pediatric populations.

• 5. The research articles were restricted to publications or translations in English so that there could be a lack of sufficient foreign knowledge. These all research integrated models of numerical simulation with mathematical methods, data validation, and certain descriptive statistics.

• 6. To simplify both mathematical modeling and data fitting, transmission rates are invariably fixed as constants. Actually, the transmission rates definitely vary with the epidemiological and socioeconomic status and may also be wedged by the outbreak control.

• 7. As Nobel Laureate Robert Solow clarified, mathematical modeling can be made successful and useful by making it simple, doing it right, and making it plausible.

No doubt, their observations have presented a wide range of COVID-19 related epidemiological characteristics and have strengthened our comprehension of the complicated propagation of SARS-CoV-2. But on the other hand, the present modeling work has the abovementioned limitations.

Finally, we propose new directions for further study epically as mathematical predictions in combating the epidemics are yet to reach its perfection and are summarized as follows:

• 1. The asymptomatic human transmissibility is not yet modeled.

• 2. A comparison between findings to other models was not carried out by the researchers as a general practice.

• 3. Age, gender, and subpopulations, and other demographic factors were not considered by the mathematicians for modeling the pandemic.

• 4. Implementation of preventative measures for this outbreak and potential viruses of COVID-19 are not considered.

• 5. Prediction/forecasting based on numerous mathematical models vary greatly such as epidemic nature of the disease, role of quarantine, deaths, registered cases, etc. as these are modeled at different levels of infection.

• 6. Some mathematical models utilize fuzzy differential equations to incorporate some incorrect data in the model. Instead, the infectious viral load in the model might be adopted.

The current emergency needs a better model with high-end accuracy of testing and forecasting of the SARS-CoV-2, which can be correlated with another type of disease by analyzing suspects’ and infected patients’ clinical, mammographic and demographic information. Many of the models are not used enough to illustrate their true functionality but are still in a position to counter the pandemic.

One encouraging guideline for advancing mathematical modeling is to link models with data-driven techniques especially machine learning. The use of broad data sets currently available, including disease, genetic, demographic, geospace, and mobility data, which usually goes beyond the applicability of a traditional mathematical model, will support and enhance mathematical disease models and other artificial intelligence technologies. Mathematical modeling can provide a validating way of validating machine learning predictions and guiding the development of more powerful and robust machine learning as well as data analysis algorithms. This would help each other improve and advance all these various quantitative methods, and their convergence could potentially lead to substantial progress on the COVID-19 study and even beyond.

6 Conclusions

To conclude, mathematical models of infectious disease dynamics have a long history and they continue to mature with ongoing advances in computational tools and ease of access to disease incidence data. They provide an important tool for understanding disease dynamics, evaluating potential control strategies, and predicting future outbreaks. Besides, they can be effectively used during an ongoing outbreak.

The available mathematical models allow us to investigate various investigations and their relative impacts on “flattening the curve” of the COVID-19 pandemic in the world. These models could give us qualitative warnings about the possible dangers of lifting interventions too early or keeping them on for a long duration and risking a second wave of infections afterward. It can also show us to what extent the health systems will be burdened by such measures.

Mathematical models, in general, run on assumptions and those assumptions change as new data becomes available. Since COVID-19 is still a new virus, much important information is still unknown to us and makes the simulation more challenging. As models mature over time with the emergence of new data, their projections will also keep changing and maturing accordingly with every addition of new evidence. Hence, these models become more complex and move a step closer to simulating reality, but we are still far from that with Covid-19.

These mathematical models try to predict the future of outbreaks or epidemics, but these predictions are based on assumptions that need to be taken into considerations and should be compared across multiple equally plausible scenarios. Remember that the mathematical models are not magical crystal balls that can predict future numbers. They are just one of many tools that can be used by decision-makers, all of which rely on the collection and analysis of high-quality epidemiological data. These predictions can be well-matched with weather forecasts which simulate a projection based on past experience and present determinants.

Nowadays, WHO is working with the international network of universities, agencies, and institutes in different countries to develop mathematical models and discuss their adaptations for the particular region and its countries. WHO’s collaboration with the COVID -19 International Modelling Consortium (CoMo) of the University of Oxford in the UK supports countries in their use of mathematical models and helps them understand their benefits and limitations. Mathematical models remind us that the decision-making should rely mainly on the collection and interpretation of high-quality epidemiological data. Mathematical models can guide decisions, but not dictate them.

The COVID-19 pandemic constitutes this generation’s biggest worldwide public health epidemic since the 1918 pandemic. To explore new COVID-19 treatments, the pace and amount of clinical trials underway highlight the need and willingness to deliver high-quality evidence even during a pandemic. To date, no successful treatments have been obtained. In this review, an attempt has been made to comprehensively present the results of mathematical modeling adopted for various scenarios of the COVID-19 pandemic. The following points are summarized:

• In forecasting both reported cases and deaths due to COIVD-19, the mathematical models proposed by researchers showed an accurate prediction for specific regions of a country, different countries, and the entire population.

• Few mathematical models also meet all external validity criteria and can be used to forecast future events. The variables in forecasts of all models played an important role and the other models have only one or two separate variables in predictions.

• The models were less vulnerable to variables. Besides, the test results suggested that, rather than just simple assumptions, the models were highly accurate, since it was based on experimental evidence, such as traditional ones.

• The predictions from the mathematical model findings detail the analysis and simulation of the possibility of a second outbreak after a return to work in the city by the strict quarantine measures taken in different regions in the course of the epidemic.

• The data-driven mathematical modeling showed a comparatively in-depth idea of the pandemic in different regions of the world.

• The prediction by a few models showed more oscillating activity over the next ten days and represented the effect of the wide range of governmental initiatives to contain the epidemic.

• For the study of COVID-19 datasets, many simplifying assumptions were made by the researchers. Two methods to tackle two intertwined problems on COVID-19 were proposed in this regard. Our reviews suggested a hybrid approach that incorporates ARIMA and WBF models as the first issue with short-term forecasts for COVID-19 outbreaks.