Theory for electrochemical impedance spectroscopy of heterogeneous electrode with distributed capacitance and charge transfer resistance

Abstract

Abstract

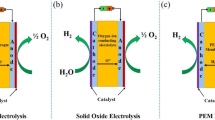
Randles-Ershler admittance model is extensively used in the modeling of batteries, fuel cells, sensors etc. It is also used in understanding response of the fundamental systems with coupled processes like charge transfer, diffusion, electric double layer charging and uncompensated solution resistance. We generalize phenomenological theory for the Randles-Ershler admittance at the electrode with double layer capacitance and charge transfer heterogeneity, viz., non-uniform double layer capacitance and charge transfer resistance ($c_d$ and $R_{CT}$). Electrode heterogeneity is modeled through distribution functions of $R_{CT}$ and $c_d$, viz., log-normal distribution function. High frequency region captures influence of electric double layer while intermediate frequency region captures influence from the charge transfer resistance of heterogeneous electrode. A heterogeneous electrode with mean charge transfer resistance $\overline{R_{CT}}$ shows faster charge transfer kinetics over a electrode with uniform charge transfer resistance ($\overline{R_{CT}}$). It is also observed that a heterogeneous electrode having high mean with large variance in the $R_{CT}$ and $c_d$ can behave same as an electrode having low mean with small variance in the $R_{CT}$ and $c_d$. The origin of coupling of uncompensated solution resistance (between working and reference electrode) with the charge transfer kinetics is explained. Finally, our model provides a simple route to understand the effect of spatial heterogeneity.

Graphical Abstract

SYNOPSIS An electrochemical system consisting of heterogeneous working electrode (non-uniform charge transfer (CT) resistance ($R_{CT}^{(i)}$) and electric double layer capacitance ($c_{d}^{(i)}$)) and ohmic losses ($R_\Omega$) between working and reference electrode. The analysis suggests that electrode with heterogeneity results in faster CT kinetics as compared to CT kinetics over homogeneous electrode.

Appendix

1.1 A. Derivation of surface boundary constraint

The local current density due to diffusional current at an arbitrary position on the electrode surface $(x, y, z=0)$, is given by

$$\begin{aligned} i_f ( \vec {r}_{||}, t) = n F D_O \partial _{z} \delta C_{O}(\vec {r}_{||}, t) \end{aligned}$$

(A.1)

where $D_{O}$ is diffusion coefficient of the oxidized species and $\partial _z = \partial /\partial z$.

Surface boundary condition is derived using the Butler-Volmer equation:

$$\begin{aligned} \frac{i_f(\vec {r}_{||}, t)}{i_0}= & {} \frac{C_O (\vec {r}_{||}, t)}{C_O^0}\mathrm{e}^{\alpha n f \eta (t) } \nonumber \\&- \frac{C_R (\vec {r}_{||}, t)}{C_R^0}\mathrm{e}^{-(1-\alpha ) n f \eta (t)} \end{aligned}$$

(A.2)

where $i_f(\vec {r}_{||}, t)$ is the faradaic current density. For the moderately supporting systems and correcting for double layer, above equation can be rewritten as

$$\begin{aligned} \frac{i(\vec {r}_{||}, t)}{i_0}= & {} \frac{C_O (\vec {r}_{||}, t)}{C_O^0}\mathrm{e}^{\alpha n f \left( \eta (t) -i(\vec {r}_{||}, t)\,R_\Omega \right) } \nonumber \\&- \frac{C_R (\vec {r}_{||}, t)}{C_R^0}\mathrm{e}^{-(1-\alpha ) n f \left( \eta (t) -i(\vec {r}_{||}, t)\,R_\Omega \right) } \nonumber \\&- \frac{c_d}{i_0}\frac{d\eta }{dt} \end{aligned}$$

(A.3)

where $i(\vec {r}_{||}, t) = i_f(\vec {r}_{||}, t) - c_d \frac{d\eta (t)}{dt}$ is the combination of both faradaic and non-faradaic component of current density.[62] Replacing $C_m (\vec {r}_{||}, t)$ by $\delta C_m (\vec {r}_{||}, t) + C_m^0$, where m = O $\mathrm{or}$ R

$$\begin{aligned} \frac{i (\vec {r}_{||}, t)}{i_0}= & {} \frac{\delta C_O (\vec {r}_{||}, t)}{C_O^0}\mathrm{e}^{\alpha n f \left( \eta (t) -i(\vec {r}_{||}, t)\,R_\Omega \right) }\nonumber \\&+\mathrm{e}^{\alpha n f \left( \eta (t) -i(\vec {r}_{||}, t)\,R_\Omega \right) } \nonumber \\&- \frac{\delta C_R (\vec {r}_{||}, t)}{C_R^0}\mathrm{e}^{-(1-\alpha ) n f \left( \eta (t) -i(\vec {r}_{||}, t)\,R_\Omega \right) } \nonumber \\&- \mathrm{e}^{-(1-\alpha ) n f \left( \eta (t) -i(\vec {r}_{||}, t)\,R_\Omega \right) } - \frac{c_d}{i_0}\frac{d\eta }{dt} \end{aligned}$$

(A.4)

For the small external perturbation potential and therefore, small output current density, we can linearize the Butler-Volmer equation,

$$\begin{aligned} \frac{i(\vec {r}_{||}, t)}{i_0}= & {} \frac{\delta C_O (\vec {r}_{||}, t)}{C_O^0} \left( 1+\alpha n f \eta (t) - \alpha nf i(\vec {r}_{||}, t)\,R_\Omega \right) \nonumber \\&+ \left( 1+\alpha n f \eta (t) - \alpha nf i(\vec {r}_{||}, t)\,R_\Omega \right) \nonumber \\&- \frac{\delta C_R (\vec {r}_{||}, t)}{C_R^0}\left( 1-nf\eta (t) + \alpha n f \eta (t)\right. \nonumber \\&\left. + nf i(\vec {r}_{||}, t)\,R_\Omega - \alpha nf i(\vec {r}_{||}, t)\,R_\Omega \right) \nonumber \\&- \left( 1-nf\eta (t) + \alpha n f \eta (t) + nf i(\vec {r}_{||}, t)\,R_\Omega \right. \nonumber \\&\left. - \alpha nf i(\vec {r}_{||}, t)\,R_\Omega \right) - \frac{c_d}{i_0}\frac{d\eta }{dt} \end{aligned}$$

(A.5)

Neglecting higher order terms,

$$\begin{aligned} \frac{i (\vec {r}_{||}, t)}{i_0}= & {} \frac{\delta C_O (\vec {r}_{||}, t)}{C_O^0} - \frac{\delta C_R (\vec {r}_{||}, t)}{C_R^0} + nf\eta (t)\nonumber \\&- nf i (\vec {r}_{||}, t)\,R_\Omega - \frac{c_d}{i_0}\frac{d\eta }{dt} \end{aligned}$$

(A.6)

Using the flux-balance condition and assuming that the ions have same diffusion coefficient ($D_{O} = D_{R} = D$), we have concentration constrains on the oxidized and reduced species as [57] $\delta C_{O} (\vec {r}_{||}, t) + \delta C_{R} (\vec {r}_{||}, t) = 0$. It is assumed that the concentration $\delta C_O(\vec {r}_{||},t)$ has oscillatory time dependence $\mathrm{e}^{j \omega t} \delta C_O(\vec {r}_{||})$ (behaves like the applied potential). For a small sinusoidal applied interfacial potential $\eta (t) = \eta _{0}\, \exp (j \omega t)$, using $i_0 = RT/(nF R_{CT})$ and $i_f(\vec {r}_{||}, t)$ from equation A.1 in the equation A.6,

$$\begin{aligned}&\frac{n F D_O \partial _{z} \delta C_{O}(\vec {r}_{||})\mathrm{e}^{j \omega t} -j \omega c_d \eta _0 e^{j \omega t}}{RT/(nF R_{CT})}\nonumber \\&\quad = \frac{\delta C_O (\vec {r}_{||})\mathrm{e}^{j \omega t}}{C_O^0} + \frac{\delta C_O (\vec {r}_{||})\mathrm{e}^{j \omega t}}{C_R^0}\nonumber \\&\qquad + nf \Big [ \eta _0 \mathrm{e}^{j \omega t} - R_\Omega (nfD\partial _z \delta C_O (\vec {r}_{||},t)\nonumber \\&\quad - c_d \eta _0 j\omega \mathrm{e}^{j \omega t})\Big ]\nonumber \\&\qquad - nf c_d R_{CT} j \omega \eta _0 \mathrm{e}^{j \omega t} \end{aligned}$$

(A.7)

On rearranging the terms, we get

$$\begin{aligned}&\frac{n^2 F^2}{RT} D (R_{CT}+R_\Omega ) \partial _z \delta C_O(\vec {r}_{||}) \nonumber \\&\quad = \delta C_O (\vec {r}_{||}) \left( \frac{1}{C_O^0} + \frac{1}{C_R^0} \right) \nonumber \\&\qquad +nf\eta _0 \mathrm{e}^{j \omega t} \left( 1+ j \omega c_{d} \left( R_\Omega + R_{CT}\right) \right) \nonumber \\&\qquad - nf c_d R_{CT} j \omega \eta _0 \mathrm{e}^{j \omega t} \end{aligned}$$

(A.8)

$R_{CT}+R_\Omega$ can be written as $R_{C\Omega }$ and $n^2 F^2/RT (1/C_O^0+1/C_R^0)$ as $\Gamma$, hence the above equation can be rewritten as

$$\begin{aligned} L_{C\Omega }\;\partial _z \delta C_{O} (\vec {r}_{||})-\delta C_{O} (\vec {r}_{||}) \big |_{z=0} = \left( 1 + j\omega \, \tau _{dl} \right) \left( \frac{\Gamma \;\eta _{0}}{n F } \right) \end{aligned}$$

(A.9)

where double layer relaxation time is $\tau _{dl}=R_{\Omega }c_{d}$. $L_{C\Omega }$ is phenomenological kinetics-ohmic length is defined as

$$\begin{aligned}&L_{C\Omega } = L_{CT}+L_{\Omega } \nonumber \\&L_{CT} = \Gamma \, D\, R_{CT} \nonumber \\&L_{\Omega } = \Gamma \, D\, R_{\Omega } \end{aligned}$$

(A.10)

1.2 B. Small ${\varvec{R}}_{{\varvec{CT}}}$ and ${\varvec{c}}_{{\varvec{d}}}$ fluctuation approximation

Replacing local $R_{CT}$ in equation 5 by $\overline{R_{CT}} + \delta R_{CT}$ and $c_d$ by $\overline{c_{d}} + \delta c_{d}$, it becomes

$$\begin{aligned} Y_{R}(\omega )= & {} \left( \frac{A_{0}}{y_W(\omega )^{-1}+ \overline{R_{CT}} + \delta R_{CT} + R_\Omega } \right) \nonumber \\&\Big (1+j \omega R_\Omega (\overline{c_d} + \delta c_d)\Big ) \end{aligned}$$

(B.1)

above equation can be written as,

$$\begin{aligned} Y_{R}(\omega )= & {} \frac{A_{0} }{y_W^{-1}(\omega ) + \overline{R_{C\Omega }} + \delta R_{CT}}\nonumber \\&\Big (1+ \overline{c_d} \,j \omega R_{\Omega } + j \omega \delta c_d R_{\Omega } \Big ) \end{aligned}$$

(B.2)

where $\overline{R_{C\Omega }} = \overline{R_{CT}} + R_\Omega$. On rearranging the terms, we get

$$\begin{aligned} Y_{R}(\omega )= & {} \frac{A_{0} \Big (1+ j \omega \,c_d \overline{R_{C\Omega }} \Big ) }{\Big (y_W^{-1}(\omega ) + \overline{R_{C\Omega }}\Big )\bigg (1 + \frac{\delta R_{CT}}{y_W^{-1}(\omega ) + \overline{R_{C\Omega }}}\bigg )}\nonumber \\&\bigg (1+\frac{ j \omega \delta c_d R_{\Omega } }{1+ j \omega \, \overline{c_d} R_{\Omega }}\bigg ) \end{aligned}$$

(B.3)

On expanding and ensemble averaging admittance responses over surface heterogeneity, fluctuations in charge transfer resistance and electric double layer capacitance (are dependent on each other) at the electrode surface, the classical Randles-Ershler admittance for small heterogeneity can be written as

$$\begin{aligned} \overline{Y_{R}}(\omega )= & {} \overline{Y_{R}^0}(\omega ) \Bigg [ 1+ \frac{ \overline{\delta R_{CT}^2}}{\big (y_W^{-1}(\omega ) + \overline{R_{C\Omega }}\big )^2} \nonumber \\&- \bigg ( \frac{j \omega R_{\Omega }\overline{\delta R_{CT} \, \delta c_{d}}}{\big (y_W^{-1}(\omega ) + \overline{R_{C\Omega }}\big )\big (1+ j \omega \,\overline{c_d} R_{\Omega }\big )} \bigg ) \Bigg ] \end{aligned}$$

(B.4)