Electro-Magnetohydrodynamic Oscillatory Flow of a Dielectric Fluid Through a Porous Medium with Heat Transfer: Brinkman Model

Abstract

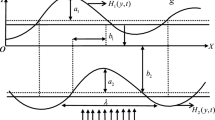
The objective of the present study is to investigate the effect of electro-magnetic field and heat transfer on the oscillatory flow of a dielectric fluid through a Darcy’s Brinkman model in a symmetric flexible sinusoidal wavy channel. The equations which govern the Electro-Magneto hydro dynamic of oscillatory flow for a dielectric fluid are made non-dimensional and coordinate transformation is employed to convert the irregular boundary to a regular boundary. The obtained system of equations is solved analytically by using the regular perturbation method with a small amplitude ratio. Approximate solution for the mean axial velocity, the mean electric potential, the mean temperature, and the mean pressure gradient is obtained. Further, the effect of pertinent parameters is demonstrated and discussed. The phenomena of reflux (the mean flow reversal) are discussed. It is found that the critical reflux pressure is greater for a fluid without an electric field. Also, the increase of magnetic field decreases the flow rate which is helpful to control the blood flow during the surgeries.

Appendix

$$\begin{array}{@{}rcl@{}} && h = 1+L_{2}, \\ && c_{1}=\frac{\text{csch}\left( \sqrt{e\tau} \right)\left( g^{\prime}(-1)-g^{\prime}(1)\right)}{2\sqrt{e\tau}},\\ && c_{2}=-\frac{g(-1)-g(1)+g^{\prime}(-1)+g^{\prime}(1)}{2\sqrt{e\tau}\coth(\sqrt{e\tau})-2\sinh(\sqrt{e\tau})},\\ && c_{3}=\frac{\sqrt{e\tau}\coth(\sqrt{e\tau})(g(-1)-g(1))+\sinh(\sqrt{e\tau})g^{\prime}(-1) +g^{\prime}(1)}{2\sqrt{e\tau}\coth(\sqrt{e\tau})-2\sinh(\sqrt{e\tau})}, \\ && c_{4}=\frac{-\sqrt{e\tau}(g(-1)+g(1))+\coth(\sqrt{e\tau})\left( -g^{\prime}(-1)+g^{\prime}(1)\right)}{2\sqrt{e\tau} }, \\ && c_{5}=\frac{4 i a_{1} L_{2}{~}^{3} \left( 45 \sqrt{e\tau} \cosh \left( \sqrt{e\tau}\right)+(-45+(-15+e\tau )e \tau ) \sinh \left( \sqrt{e\tau} \right)\right)}{45 \left( 1+L_{2}\right){~}^{3} (e\tau )^{2} \ln \left( 1 + 2 L_{2}\right) \left( \sqrt{e\tau} \cosh \left( \sqrt{e\tau} \right)- \sinh \left( \sqrt{e\tau} \right)\right)}, \\ && c_{6}=\frac{i a_{1} L_{2}}{360 \left( 1+L_{2}\right){~}^{4} (e\tau )^{5/2} \left( \sqrt{e\tau} \cosh \left( \sqrt{e\tau} \right)- \sinh \left( \sqrt{e\tau} \right)\right)}(360 \left( e\tau + 4 L_{2} e\tau + 6 L_{2}{~}^{2} (1+e\tau )\right)\cosh(\sqrt{e\tau} )+\sqrt{e\tau} \\ && \left( -720 L_{2} \left( 1 + 4 L_{2}\right)-30 \left( 6+L_{2}\left( 20 + 23 L_{2}\right)\right) e\tau +\left( 15 + 46 L_{2} \left( 1+L_{2}\right)\right) (e\tau )^{2}\right)\text{} \sinh \left( \sqrt{e\tau} \right)), \\ \end{array} $$

$$\begin{array}{@{}rcl@{}} && c_{7}=\frac{\text{Sech}(\sqrt{e\tau})(\tau(2D-k(-1)-k(1))+ 4 e c_{20})}{2e\tau}, \\ && c_{8}= 1/2\text{csch}(\sqrt{e\tau})(k(-1)-k(1)), \\ && c_{9}=\frac{1}{2} (n(-1)-n(1)), \\ && c_{10}=\frac{1}{2} (-n(-1)-n(1)), \\ && c_{11}=\frac{L_{2} \left( a (2{} -2 L_{2} (2 (L_{2}-2) L_{2}+ 3)){}-(1{}-2 L_{2})^{2} (w(-1){}-w(1))\right)}{(1-2 L)^{2} \log (1-2 L_{2})}, \\ && c_{12}=\frac{1}{2} a (L_{2}-2)-w(1). \end{array} $$