Graph-regularized multi-view semantic subspace learning

Abstract

Many real-world datasets are represented by multiple features or modalities which often provide compatible and complementary information to each other. In order to obtain a good data representation that synthesizes multiple features, researchers have proposed different multi-view subspace learning algorithms. Although label information has been exploited for guiding multi-view subspace learning, previous approaches did not well capture the underlying semantic structure in data. In this paper, we propose a new multi-view subspace learning algorithm called multi-view semantic learning (MvSL). MvSL learns a nonnegative latent space and tries to capture the semantic structure of data by a novel graph embedding framework, where an affinity graph characterizing intra-class compactness and a penalty graph characterizing inter-class separability are generally defined. The intuition is to let intra-class items be near each other while keeping inter-class items away from each other in the learned common subspace across multiple views. We explore three specific definitions of the graphs and compare them analytically and empirically. To properly assess nearest neighbors in the multi-view context, we develop a multiple kernel learning method for obtaining an optimal kernel combination from multiple features. In addition, we encourage each latent dimension to be associated with a subset of views via sparseness constraints. In this way, MvSL is able to capture flexible conceptual patterns hidden in multi-view features. Experiments on three real-world datasets demonstrate the effectiveness of MvSL.

1 Introduction

In many real-world data analytic problems, instances (items) are often described with multiple modalities or views. It becomes natural to integrate multi-view information to obtain a more robust representation, rather than relying on a single view. A good integration of multi-view features can lead to a more comprehensive description of the data items, which could improve performance of many related applications.

An active area of multi-view learning is multi-view latent subspace learning, which aims to obtain a compact latent representation by taking advantage of inherent structures and relations across multiple views. A pioneering technique in this area is canonical correlation analysis (CCA) [1], which tries to learn the joint projections of two views so that the correlation between them is maximized. Recently, a lot of techniques have been applied to multi-view subspace learning, such as matrix factorization [2,3,4,5], graphical models [6, 7], Gaussian processes [8, 9] and spectral embedding [10], low rank representation [11], sparse coding [12].

Among the many techniques, matrix factorization methods have received more and more attention as fundamental tools for latent representation (subspace) learning. A useful representation acquired by matrix factorization typically makes latent structures in the data explicit (through the basis vectors), and usually reduces the dimensionality of input views, so that further analysis can be effectively and efficiently carried out (with encoding vectors). Among different matrix factorization methods, nonnegative matrix factorization (NMF) [13] is an attractive one due to its theoretical interpretation and desired performance. NMF aims to find two nonnegative matrices, a basis matrix and an encoding matrix, whose product provides a good approximation to the original matrix. It tries to formulate a feasible model for learning object parts, which is closely relevant to human perception mechanism. Recently, variants of NMF have been proposed for multi-view subspace learning [4, 5, 14].

Labeled data has been incorporated into multi-view representation learning. In terms of the style of incorporating label information, existing supervised or semi-supervised multi-view representation learning methods can be divided into three categories: (1) large-margin based methods [6, 9, 15]. This kind of methods uses the large-margin principle to maximize the margin between instances of different classes, but ignores the intra-class semantic structures. (2) Fisher discriminant analysis based methods [16,17,18,19]. Fisher’s discriminant analysis is widely used in feature learning, which employs the famous Fisher criterion to minimize the within-class scatter while maximize the between-class scatter. However, Fisher’s discriminant analysis based methods are optimal only in cases where the data of each class follows Gaussian distribution. In reality, this assumption is too restrictive since real world datasets often exhibit complex non-Gaussian distributions [20, 21]. (3) Methods that reconstruct the label indicator matrix through multiplying the encoding matrix by a weight matrix [14, 22]. These methods intrinsically impose implicit relationship constraints on encodings of labeled items. Nevertheless, such indirect constraints could be insufficient for capturing the semantic relationships between data items.

In this paper, we propose a new multi-view subspace learning algorithm called multi-view semantic learning (MvSL), to better capture the semantic structure of multi-view data. MvSL is a nonnegative factorization method which jointly factorizes data matrices of different views. In MvSL, each view is factorized into a basis matrix and a common encoding matrix which is shared by multiple views. We regularize the encoding matrix by a general graph embedding framework: we construct an affinity graph characterizing the intra-class compactness and a penalty graph characterizing the inter-class separability. The general idea is to let intra-class items be near each other while keeping inter-class items away from each other in the learned common subspace across multiple views.

It is worthy to highlight several aspects of the new method here:

• 1. We investigate three specific definitions of the graphs. The first one, simple graph embedding (SGE), simply assigns equal affinity/penalty weights to each pair of intra-class/inter-class items. The second one, dubbed as local discriminant graph embedding (LDGE), only imposes affinity constraints in local neighborhood of a class and penalizes nearest inter-class items. In contrast with the Fisher criterion, LDGE does not make Gaussian assumption for data and could better capture the complex distribution of real-world data [21]. We further add manifold information in the affinity graph of LDGE to derive the third definition: transductive graph embedding (TGE). A sub-challenge in LDGE and TGE is how to identify nearest neighbors in the multi-view context. To this end, we develop a new multiple kernel learning algorithm to find the optimal kernel combination for multi-view features. The algorithm tries to let the kernel combination optimally preserve the semantic relations among labeled items.

• 2. Features coming from the same view are likely to have the same sparsity pattern in their low-dimensional representation [23, 24]. In order to promote group sparsity in the basic matrix, we propose to incorporate a $\ell _{1,2}$ norm regularizer on the basis matrices to encourage basis matrix to be column-sparseness [2]. Since $\ell _{1,2}$ norm regularizer encourages the sum of each column’s $\ell _{2}$ norm to be minimized, some columns of matrix will be zero-valued. In this way, each latent dimension has the flexibility to be only associated with a subset of each views, thus enhancing the expressive power of the model and avoiding the high computational burden.

• 3. To solve MvSL, we develop a block coordinate descent [25] optimization algorithm.

For empirical evaluation, three real-world multi-view datasets are employed. The encouraging results of MvSL are achieved in comparison with the state-of-the-art algorithms.

2 Related work

In this section, we will briefly review research fields that are directly related to our work, namely, label exploitation in multi-view subspace learning, nonnegative matrix factorization and graph embedding.

2.1 Label exploitation in multi-view subspace learning

General speaking, multi-view subspace learning methods could be divided into two categories: methods that do not use label information (i.e. unsupervised) and those using label information (semi-supervised or supervised). Unsupervised multi-view subspace learning methods, such as CCA [1], co-training [26] and their variants [27,28,29,30], only use the multiple features information of the data items for learning. Due to ignoring the label information, the performance of unsupervised multi-view subspace learning has much room to promote. In order to utilize the label information, (semi-) supervised multi-view subspace learning algorithms were developed. According to different ways to use label information, these algorithms could be divided into three categories: (1) algorithms exploiting the large-margin principle, (2) algorithms that make use of Fisher’s discriminant analysis technique, and (3) algorithms that reconstruct the label indicator matrix.

The large-margin principle is successfully used in SVM. In multi-view case, Chen et al. [6, 15] integrate the large-margin idea into Markov network for multiple features, which jointly maximizes data likelihood and minimizes a prediction loss on the labeled data. Xu et al. [9] propose a large-margin Gaussian process approach for discovering discriminative latent subspace shared by multi-view data. However, the latent spaces learned by this kind of methods ignore the intra-class semantic structures of the data.

Fisher’s discriminant analysis has been employed in multi-view subspace learning. In [16], Diethe et al. propose two view Fisher’s discriminant analysis which tries to capture the correlation between two views in an CCA style. They then extend it to the multi-view setting by convex formulation and also propose a sparse version [18]. Chen and Sun propose a different multi-view Fisher’s discriminant analysis which minimizes the prediction error of each view’s output and takes fisher terms as constraints [17]. They also design a new solution for the multi-class case by using hierarchical clustering. Rather than learning a discriminative score, Kan et al. aim to learn a common subspace shared by multiple views in which within-class/between-class variations are minimized/maximized (i.e. the Fisher criterion) [19]. However, the Fisher criterion is optimal only in cases where the data of each class is approximately distributed as Gaussian. This assumption is too restricted since data often exhibit complex non-Gaussian distributions [20, 21].

The third category is to reconstruct the label indicator matrix through multiplying the encoding matrix by a weight matrix [14, 22]. Each column of the label indicator matrix stores the 1-of-C coding for an item’s label information (C denotes the number of classes). The weight matrix acts as a set of C linear regression models in the learned subspace (i.e. the encoding matrix) for label prediction. A regression model forces items with the corresponding label to reside on its positive hyperplane while letting other-class items reside on the negative hyperplane, where “positive/negative” means the regression output equals 1/0. This can be viewed as imposing implicit relationship constraints on encodings of labeled items. However, this scheme cannot well capture the semantic relationships between data items. For example, two items with the same label could be far away from each other in the learned subspace as long as they both reside on the positive hyperplane of the class.

To sum up, there is still lack of effective methods for learning a common latent subspace which well captures the semantic structures in multi-view data. Our MvSL is different from the above works in that we devise a general graph embedding framework to address this problem. The framework imposes direct relationship constraints on (labeled) data items in the target subspace and we explore graph definitions which can characterize non-Gaussian distributions in real world data.

2.2 NMF and multi-view extensions

NMF is an effective subspace learning method to capture the underlying structure of the data in the parts-based low dimensional representation space. It accords with the cognitive process of human brain from the psychological and physiological studies [13, 31, 32]. Here we briefly review NMF. In this paper, vectors and matrices are denoted by lowercase boldface letters and uppercase boldface letters respectively. For a matrix ${\mathbf {X}}$, we denote its (i, j)-th element by $X_{ij}$. The i-th element of a vector ${\mathbf {b}}$ is denoted by $b_{i}$. Given an input nonnegative data matrix ${\mathbf {X}}\in {\mathbb{R}}^{M\times N}_{+}$ where each column represents a data item and each row represents a feature. NMF aims to find two nonnegative matrices ${\mathbf {U}} \in {\mathbb{R}}^{M\times K}_{+}$ and ${\mathbf {V}} \in {\mathbb{R}}^{K\times N}_{+}$ whose product can well approximate the original data matrix:

$$\begin{aligned} {\mathbf {X}} \approx {\mathbf {U}} {\mathbf {V}}. \end{aligned}$$

$K < \min (M,N)$ denotes the desired reduced dimensionality, and to facilitate discussion, we call ${\mathbf {U}}$ the basis matrix and ${\mathbf {V}}$ the encoding matrix.

It is known that the objective function above is not convex in ${\mathbf {U}}$ and ${\mathbf {V}}$ together, so it is unrealistic to expect an algorithm to find the global minimum. Lee and Seung [13] presented multiplicative update rules to find the locally optimal solution as follows:

$$\begin{aligned} U_{ik}^{t+1} = U_{ik}^t \frac{({\mathbf {X}}({\mathbf {V}}^t)^T)_{ik}}{({\mathbf {U}}^t {\mathbf {V}}^t ({\mathbf {V}}^t)^T)_{ik}} \\ V_{kj}^{t+1} = V_{kj}^t \frac{(({\mathbf {U}}^{t+1})^T {\mathbf {X}})_{kj}}{(({\mathbf {U}}^{t+1})^T {\mathbf {U}}^{t+1} {\mathbf {V}}^t)_{kj}}. \end{aligned}$$

In recent years, many variants of the basic NMF model have been proposed. In the multi-view context, researchers have extended NMF to better leverage multi-view information. Liu et al. develop a multi-view NMF method named multiNMF for data clustering [5], where a unified encoding matrix is learned across different views. Kalayeh et al. propose an approach based on multi-view NMF for image annotation [4]. It treats tags and visual features of images as different views. Given an image i to be annotated, it first finds k nearest neighbors of i from images with tags, by averaging distances calculated by multiple visual features. Then it adopts a similar scheme as MultiNMF to factorize these nearest neighbors and uses the learned basis vectors to generate encoding for i. Based on the encoding, i’s tag vector is predicted. In [33], the graph regularized NMF (GNMF) [20] is extended to the multi-view setting. Although this work considers using graphs to regularize the learned encoding space, it only constrains affinity relationships and does not incorporate label information to learn semantic structures. Some semi-supervised multi-view NMF methods have been proposed [14, 22, 34]. However, [14] and [22] are based on label indicator matrix reconstruction, while [34] adopts simple graph definitions similar to our SGE. None of these works develop a complete graph embedding framework in the multi-view NMF context for capturing semantic relationships between items.

2.3 Graph embedding

Yan et al. formulate popular dimensionality reduction methods in a general graph embedding framework [21]. After that, the idea of graph embedding has been widely applied. For example, a number of works [20, 35, 36] have exploited graph embedding as regularization of NMF. Shi et al. [37] propose an adaptive graph embedding method which customizes the neighborhood size of each item when constructing graphs. Nevertheless, these works only consider single-view data. When multiple features exist, it is not known how to well assess nearest neighbors, which is a key component for graph embedding. Although [38] proposes a graph embedding approach for multi-view face recognition, it learns a graph embedding model for each view separately. This would easily amplify the inconsistency between different views. Moreover, it only gives a solution for two views and generalization to multiple views is not a trivial task. Our work is different from the above ones in that we design a general graph embedding framework for learning a unified semantic subspace from partially labeled multi-view data, with a multiple kernel learning solution for nearest neighbor assessment.

Fig. 1

An illustration of the work flow of the proposed approach. Fully White color in the matrices means value 0

3 Multi-view semantic learning

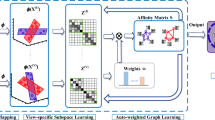
In this section, we present the multi-view semantic learning (MvSL) algorithm for latent representation learning from partially labeled multi-view data. As illustrated in Fig. 1, we first obtain various features to construct the set of data matrices $\{{\mathbf {X}}^{(v)}\}_{v=1}^H$ where ${\mathbf {X}}^{(v)} \in {\mathbb{R}}_+^{M_v \times N}$, $M_v$ denotes the dimensionality of view v, H denotes the number of views and N is the total number of items. The data matrices are then factorized into basis matrices $\{{\mathbf {U}}^{(v)}\}_{v=1}^H$ and the low-dimensional consensus encoding matrix ${\mathbf {V}}$. We regularize ${\mathbf {V}}$ by an affinity graph $G^a$ and a penalty graph $G^p$. Nodes in the dotted circles are labeled. The edges in $G^a$/$G^p$ mean pairwise affinity/separation constraints (dotted edges connect nodes in local neighborhoods). The graph embedding framework is general and various graph definitions can be adopted. Figure 1 shows an instantiation of Transductive Graph Embedding which will be presented in Sect. 4. Note that in Fig. 1 fully white elements in the matrices mean their values are 0. By imposing a structured sparseness constraint on each basis matrix ${\mathbf {U}}^v$, some basis vectors could be zeroed-out so that a latent dimension in the encoding space can be associated with just a few views. This is flexible and enhances the expressive power of the model. For example, in Fig. 1, the second column of ${\mathbf {U}}^{(1)}$ and the third column of ${\mathbf {U}}^{(2)}$ are zero columns, which means the second latent dimension is not associated with view 1 and the third is independent of view 2. Next, we discuss the design of each component of MvSL, and formulate the whole optimization problem in the end.

3.1 Multi-view NMF

The consensus principle is the fundamental principle in multi-view learning [39,40,41]. MvSL jointly factorizes $\{{\mathbf {X}}^{(v)}\}_{v=1}^H$ into different basis matrices $\{{\mathbf {U}}^{(v)}\}_{v=1}^H$ and a consensus encoding matrix $\mathbf V$ [2, 4, 5]:

$$\begin{aligned}&\min _{\{{\mathbf {U}}^{(v)}\}_{v=1}^H,{\mathbf {V}}} \quad \frac{1}{2} \sum _{v=1}^H \Vert {\mathbf {X}}^{(v)}-{\mathbf {U}}^{(v)} {\mathbf {V}}\Vert _F^2 \nonumber \\&{\text{s.t.}} \quad U_{ik}^{(v)} \ge 0, V_{kj} \ge 0, \quad \forall i, j, k, v. \end{aligned}$$

(1)

In this way, each item is forced to have the same encoding under different views and the basis matrices of different views are coupled together through ${\mathbf {V}}$. However, the standard unsupervised NMF fails to guarantee that the learned latent space captures the semantic structures of the data. In what follows, we present the graph embedding regularization on the encoding matrix ${\mathbf {V}}$.

3.2 Graph embedding framework

The graph embedding framework defines two graphs for regularization. The affinity graph $G^{a}=\{ {\mathbf {V}}, {\mathbf {W}}^{a} \}$ is an undirected weighted graph with item set ${\mathbf {V}}$ as its vertex set, and ${\mathbf {W}}^{a} \in {\mathbb{R}}^{N\times N}$ as its weighted adjacency matrix which characterizes the intra-class compactness. The penalty graph $G^{p}= \{{\mathbf {V}}, {\mathbf {W}}^{p} \}$ characterizes inter-class separability, where ${\mathbf {W}}^{p}$ denotes the weighted adjacency matrix for penalty relationships. The graph embedding objectives are defined as follows:

$$\begin{aligned}&\min _{{\mathbf {V}}} \frac{1}{2} \sum _{i=1}^{N} \sum _{j=1}^{N} W^a_{ij} \Vert {\mathbf {v}}_i - {\mathbf {v}}_j\Vert _2^2 = \min _{{\mathbf {V}}} \frac{1}{2} tr [ {\mathbf {V}} {\mathbf{L}}^a \left( {\mathbf {V}}\right) ^T ], \end{aligned}$$

(2)

$$\begin{aligned}&\max _{{\mathbf {V}}} \frac{1}{2} \sum _{i=1}^{N} \sum _{j=1}^{N} W^p_{ij} \Vert {\mathbf {v}}_i - {\mathbf {v}}_j\Vert _2^2 = \max _{{\mathbf {V}}} \frac{1}{2} tr [ {\mathbf {V}} {\mathbf {L}}^p \left( {\mathbf {V}}\right) ^T ], \end{aligned}$$

(3)

where $tr(\cdot )$ denotes the trace of a matrix, N is the number of items and ${\mathbf {L}}^a = {\mathbf{D}}^a - {\mathbf {W}}^a$ is the graph Laplacian matrix for $G^a$ with the (i, i)-th element of the diagonal matrix ${\mathbf {D}}^a$ equals $\sum _{j=1}^{N} W_{ij}^a$ (${\mathbf {L}}^p$ is for $G^p$). Generally speaking, Eq.  (2) means items belonging to the same class should be near each other in the learned latent space, while Eq. (3) tries to keep items from different classes as distant as possible. However, only with the nonnegative constraints Eq. (3) would diverge. Note that there is an arbitrary scaling factor in solutions to problem (1): for any invertible $K \times K$ matrix ${\mathbf {Q}}$, we have ${\mathbf {U}}^{(v)}{\mathbf {V}} = ({\mathbf {U}}^{(v)} {\mathbf {Q}})({\mathbf {Q}}^{-1}{\mathbf {V}})$. It means for any solution $\langle \{{\mathbf {U}}^{(v)}\}_{v=1}^H,{\mathbf {V}} \rangle$ of (1), we can always find a proper ${\mathbf {Q}}$ such that $\langle \{{\mathbf {U}}^{(v)}{\mathbf {Q}}\}_{v=1}^H, {\mathbf {Q}}^{-1}{\mathbf {V}} \rangle$ is an equivalent solution and all elements of ${\mathbf {Q}}^{-1}{\mathbf {V}}$ are within [0, 1]. Therefore, without loss of generality, we add the constraints $\{V_{kj} \le 1, \forall k,j\}$ on ${\mathbf {V}}$.

The graph embedding framework can be instantiated by a specification of $G^a$ and $G^p$, or more concretely, ${\mathbf {W}}^{a}$ and ${\mathbf {W}}^{p}$. Any graph definitions which can capture data semantic structures could be used. In Sect. 4, we explore three different specifications and analyze their advantages and drawbacks. We will also present the multiple kernel learning method for nearest neighbor assessment therein.

3.3 Sparseness constraint

Since similarities among data items within a group may share the same sparsity pattern, a structured sparseness regularizer is added to the objective function to encourage some basis column vectors in ${\mathbf {U}}^{(v)}$ to become 0 [42]. This makes view v independent of the latent dimensions which correspond to these zeros-valued basis vectors. By employing $\ell _{1,q}$ norm regularization, the interpretation of latent factors could be improved. In this work, we choose $q=2$. $\ell _{1,2}$ norm of matrix $\mathbf U$ is defined as:

$$\begin{aligned} \Vert {\mathbf {U}}\Vert _{1,2} = \sum _{k=1}^K \Vert {\mathbf {u}}_k\Vert _2, \end{aligned}$$

(4)

3.4 Objective function of MvSL

By synthesizing the above objectives, the optimization problem of MvSL is formulated as:

$$\begin{aligned}&\min _{\{{\mathbf {U}}^{(v)}\}_{v=1}^H,{\mathbf {V}}} \quad \frac{1}{2} \sum _{v=1}^H \Vert {\mathbf {X}}^{(v)}-{\mathbf {U}}^{(v)} {\mathbf {V}}\Vert _F^2 + \alpha \sum _{v=1}^H \Vert {\mathbf {U}}^{(v)}\Vert _{1,2} \nonumber \\&\quad + \frac{\beta }{2} \{ tr [ {\mathbf {V}} {\mathbf {L}}^a {\mathbf {V}}^T ] - tr [ {\mathbf {V}} {\mathbf {L}}^p {\mathbf {V}}^T ] \} \nonumber \\&{\text{s.t.}} \quad U_{ik}^{(v)} \ge 0, 1 \ge V_{kj} \ge 0, \quad \forall i, j, k, v. \end{aligned}$$

(5)

4 Graph embedding for multi-view semantic learning

We discuss three instantiations of the graph embedding framework for capturing the semantic structures of multi-view data, namely, Simple graph embedding (SGE), local discriminant graph embedding (LDGE) and transductive graph embedding (TGE). The former two construct the affinity graph and the penalty graph in labeled items while TGE also takes unlabeled data into regularization.

4.1 Simple graph embedding

We first present a simple instantiation called SGE which treats all the labeled items equally. Since we only consider labeled items in SGE and LDGE, some additional notations are defined as follows. Let ${\mathbf {V}}^{l} \in {\mathbb{R}}^{K\times N^l}$, the first $N^{l}$ columns of ${\mathbf {V}}$, be the latent representation of the $N^{l}$ labeled items and ${\mathbf {V}}^{u} \in {\mathbb{R}}^{K\times N^u}$ be the latent representation of the remaining $N^{u}$ unlabeled items (i.e. ${\mathbf {V}} = [\mathbf {V}^l {\mathbf {V}}^u]$ and $N^l+N^u=N$). We denote the affinity graph and the penalty graph as $G^{al}$ and $G^{pl}$, respectively, where $G^{al}=\{ {\mathbf {V}}^l, {\mathbf {W}}^{al} \}$ and $G^{pl}= \{{\mathbf {V}}^l, {\mathbf {W}}^{pl} \}$. The $N^l\times N^l$ weighted adjacency matrices ${\mathbf {W}}^{al}$ and ${\mathbf {W}}^{pl}$ are defined as

$$ W_{ij}^{al} = \left\{ \begin{array}{ll} \frac{1}{N^l_{y_i}} - \frac{1}{N^l}, & {\text{if}} \ y_i=y_j\\ 0, & {\text{otherwise}} \end{array} \right. , $$

(6)

$$ W_{ij}^{pl} = \left\{ \begin{array}{ll} \frac{1}{N^l}, & {\text{if}} \ y_i \ne y_j\\ 0, & {\text{otherwise}} \end{array} \right. , $$

(7)

where $y_i$ denotes the label of item i, $N^l_{y_i}$ is the total number of items with label $y_i$. SGE imposes affinity/separation constraints on all pairs of intra-/inter-class items, so the affinity/separation weights are normalized to balance the influence of different classes and the influence of affinity/separation constraints. Apparently, SGE is a coarse definition and items coming from the same and different class are equally valued in the affinity graph and the penalty graph, respectively. In the next, we will present two fine instantiations of graph embedding which characterize semantic structures in local neighborhoods.

4.2 Local discriminant graph embedding

The idea of local discriminant embedding has been well exploited and shown to achieve good data representation [21, 43, 44]. For LDGE, the entries in the weighted adjacency matrices ${\mathbf {W}}^{al}$ and ${\mathbf {W}}^{pl}$ are defined as [21]

$$ W_{ij}^{al}= \left\{ \begin{array}{ll} 1, & {\text{if}} \, {i} \in N_{ka}^+ (j) \; or \; j \in N_{ka}^+ (i)\\ 0, & {\text{otherwise}} \end{array} \right. , $$

(8)

$$ W_{ij}^{pl}= \left\{ \begin{array}{ll} 1, & {\text{if}} \ (i,j) \in N_{kp} (y_i) \; or \; (j,i) \in N_{kp} (y_j)\\ 0, & {\text{otherwise}} \end{array} \right. , $$

(9)

where $N_{ka}^+ (i)$ indicates the index set of the ka nearest neighbors of item i in the same class, and $N_{kp} (y)$ is a set of item pairs that are the kp nearest pairs among the set $\{(i,j), i \in \pi _y, j \notin \pi _y \}$ where $\pi _y$ is the set of items with class label y.

In LDGE, the affinity graph describes local affinity structure around each item and each item is connected to its $N_{ka}$ nearest neighbors of the same class. The penalty graph describes the unfavored similarities relationship of inter-class marginal items and the marginal item pairs of different classes are connected.

Using the above two instantiations of graph embedding, the supervised graph-preserving criteria can be written as follows:

$$\begin{aligned}&\min _{{\mathbf {V}}^l} \frac{1}{2} \sum _{i=1}^{N^l} \sum _{j=1}^{N^l} {\mathbf {W}}^{al}_{ij} \Vert {\mathbf {v}}_i^l - {\mathbf {v}}_j^l\Vert _2^2 = \min _{{\mathbf {V}}^l} \frac{1}{2} tr [ {\mathbf {V}}^l {\mathbf {L}}^a ( {\mathbf {V}}^l ) ^T ], \end{aligned}$$

(10)

$$\begin{aligned}&\max _{{\mathbf {V}}^l} \frac{1}{2} \sum _{i=1}^{N^l} \sum _{j=1}^{N^l} {\mathbf {W}}^{pl}_{ij} \Vert {\mathbf {v}}_i^l - {\mathbf {v}}_j^l\Vert _2^2 = \max _{{\mathbf {V}}^l} \frac{1}{2} tr [ {\mathbf {V}}^l {\mathbf {L}}^p ( {\mathbf {V}}^l) ^T ]. \end{aligned}$$

(11)

4.3 Transductive graph embedding

LDGE only uses label information to capture the local semantic structure for the data but ignores the large amount of unlabel items. The local geometric information in unlabeled data has been shown to be useful for data representation learning [20]. Therefore, in TGE we use both labeled items ${\mathbf {V}}^{l} \in {\mathbb{R}}^{K\times N^l}$ and unlabeled items ${\mathbf {V}}^{u} \in {\mathbb{R}}^{K\times N^u}$ to define the weighted adjacency matrices ${\mathbf {W}}^{a}$ and ${\mathbf {W}}^{p}$ as follow [45]

$$ W_{ij}^a = \left\{ \begin{array}{ll} \sigma , & {\text{if}} \ i \in N_{ka}^+ (j) \; or \; j \in N_{ka}^+ (i)\\ 1, & {\text{if}} \ (i\; or\; j \in {\mathbf {V}}^{u})\;and\; (i \in N_{ka} (j) \; or \; j \in N_{ka} (i))\\ 0, & {\text{otherwise}} \end{array} \right., $$

(12)

$$ {W}_{ij}^p= \left\{ \begin{array}{ll} \sigma , & {\text{if}} \ (i,j) \in N_{kp} (y_i) \; or \; (j,i) \in N_{kp} (y_j)\\ 0, & {\text{otherwise}} \end{array} \right. , $$

(13)

where $\sigma$ is a real weight which is greater than 1, and $N_{ka} (i)$ denotes the index set of the ka nearest neighbors of item i. TGE simultaneously utilizes the partial label information and manifold learning theory to construct the affinity graph. The combination of local semantic structures and local geometric structures could lead to a better data representation.

4.3.1 Comparison of SGE, LDGE and TGE

It is well accepted that data itmes from the same class may have intra-class diversity and those from different classes may share inter-class similarity. SGE ignores intra-class diversity and inter-class similarity in that it imposes the same affinity/penalty constraints on every intra-class pairs and inter-class pairs, respectively. Squeezing intra-class variance may trouble the encoding learning since our projective function (defined implicity by the basis matrix) has limited expressiveness power. Imposing the same penalty on all pairs of items between two classes could make the objective function insensitive to important pairs on the margin between the two classes. However, the merit of SGE is that it is simple and efficient, i.e. no nearest neighbor computation. In comparison with SGE, LDGE only require item pairs in local neighborhoods to be regularized, thus avoiding the issues mentioned above. On the basis of LDGE, TGE further takes full advantage of the whole dataset with manifold constraints. While SGE and LDGE only exploit labeled data, TGE also incorporates unlabeled data by adding affinity constraints in local neighborhoods of all the data items. In this way, the semantic information can be transferred from labeled data to unlabeled data so that a better semantic representation could be learned. Nevertheless, both LDGE and TGE need nearest neighbor finding (in the labeled data and the whole dataset respectively). Their time costs are much higher than that of SGE. Hereafter, we refer to MvSL with the three graph embedding instantiations, SGE, LDGE and TGE, as MvSL-S, MvSL-L and MvSL-T, respectively.

The remaining question is how to estimate nearest neighbors, which is a routine function for constructing $G^a$ and $G^p$ in LDGE and TGE. Since real-life datasets are diverse and noisy, single-view features may not be sufficient to characterize the affinity relations among items. Hence, in the next subsection we propose to use multiple features for assessing the similarity between data items.

4.4 Multiple kernel learning

We develop a novel multiple kernel learning (MKL) [46, 47] method for estimating nearest neighbors, where each kernel function corresponds to a view. A kernel function measures the similarity between items in terms of one view. We use ${\mathbf {K}}_v(i,j)$ to denote the kernel value between items i and j in terms of view v. To make all kernel functions comparable, we normalize each kernel function into [0, 1] as follows:

$$\begin{aligned} {\mathbf {K}}_v(i,j) \leftarrow \frac{{\mathbf {K}}_v(i,j)}{\sqrt{{\mathbf {K}}_v(i,i) {\mathbf {K}}_v(j,j)}}. \end{aligned}$$

(14)

To obtain a comprehensive kernel function, we linearly combine multiple kernels as follow:

$$\begin{aligned} {\mathbf {K}}(i,j,\pmb {\eta }) = \sum _{v=1}^{H}\eta _v {\mathbf {K}}_v(i,j), \quad \sum _{v=1}^{H} \eta _v = 1, \eta _v \ge 0, \end{aligned}$$

(15)

where $\pmb {\eta } = [\eta _1,\ldots ,\eta _H]^T$ is the weight vector to be learned. This combined kernel function can lead to better estimation of similarity among items than any single kernel. For example, only relying on color information could not handel images of concept “zebra” well since the background may change arbitrarily, while adding texture information can better characterize zebra images.

Then we need to design the criterion for learning $\pmb {\eta }$. Since our goal is to model the semantic relations among items, the learned kernel function should be accommodated to the semantic structure among classes. We define an ideal kernel to encode the semantic structure:

$$\begin{aligned} {\mathbf{K}}_{ideal}( i, j) =\left\{ \begin{array}{ll} 1, &{} {\text{if}} \ y_i = y_j\\ 0, &{} {\text{otherwise}} \end{array} \right. , \end{aligned}$$

(16)

where $y_i$ denotes the label of item i. For each pair of items, we require its combined kernel function value to conform to the corresponding ideal kernel value. This leads to the following least square loss

$$\begin{aligned} l(i,j,\pmb {\eta }) = ( {\mathbf {K}}(i,j,\pmb {\eta }) - {\mathbf {K}}_{ideal}( i, j))^2 \end{aligned}$$

(17)

Summing $l(i,j,\pmb {\eta })$ over all pairs of labeled items, we could get the optimization objective. However, in reality we would get imbalanced classes: the numbers of labeled items for different classes can be quite different. The item pairs contributed by classes with much larger number of items will dominate the overall loss. In order to tackle this issue, we normalize the contribution of each pair of classes (including same-class pairs) by its number of item pairs. This is equivalent to multiplying each $l(i,j,\pmb {\eta })$ by a weight $t_{ij}$ which is defined as follows

$$\begin{aligned} {\mathbf{ t}}_{ij} =\left\{ \begin{array}{ll} \frac{1}{n_i^2}, & {\text{if}} \ y_i = y_j\\ \frac{1}{2 n_i n_j}, & {\text{otherwise}} \end{array} \right. , \end{aligned}$$

(18)

where $n_i$ denotes the number of items belonging to the class with label $y_i$. Therefore, the overall loss becomes $\sum _{i,j} t_{ij} l(i,j,\pmb {\eta })$. To prevent overfitting, a $L_2$ regularization term is added for $\pmb {\eta }$. The final optimization problem is formulated as

$$\begin{aligned}&\min _{\pmb {\eta }}\quad \sum _{i,j=1}^{N^l} t_{ij} l(i,j,\pmb {\eta }) + \lambda \Vert \pmb {\eta }\Vert ^2_2 \nonumber \\&s.t. \sum _{v=1}^{H} \eta _v = 1, \eta _v \ge 0 \end{aligned}$$

(19)

where $\lambda$ is a regularization tradeoff parameter. The optimization problem of (19) is a classical quadratic programming problem which can be solved efficiently using any convex programming software. When $\pmb {\eta }$ is obtained, we could assess the similarity relationship between labeled items in terms of multi-view features according to (15). Then, according to Eqs. (12) and (13) we can construct the weighted adjacency matrix $\mathbf W^a$ and $\mathbf W^p$, respectively.

5 Optimization

In this section, we will discuss how to optimize (5). When $\mathbf V$ is fixed, (5) is convex in $\{{\mathbf {U}}^{(v)}\}_{v=1}^H$, and vice versa. Thus, we adopt a block coordinate descent method [25] which optimizes one block of variables while fixing the other block, as shown in Algorithm 1. For the convenience of description, we define

$$\begin{aligned}&\mathcal {O}\{(\mathbf U^{(1)},\ldots ,\mathbf U^{(H)}, {\mathbf{V}}) \} \nonumber \\&\quad = \frac{1}{2} \sum _{v=1}^H \Vert {\mathbf {X}}^{(v)}-{\mathbf {U}}^{(v)} {\mathbf {V}}\Vert _F^2 + \alpha \sum _{v=1}^H \Vert {\mathbf {U}}^{(v)}\Vert _{1,2} \nonumber \\&\qquad +\frac{\beta }{2} \{tr [ {\mathbf {V}} {\mathbf{L}}^a ({\mathbf {V}})^T ] - tr [ {\mathbf {V}} {\mathbf {L}}^p ({\mathbf {V}})^T ] \} \end{aligned}$$

(20)

5.1 Optimizing $\{{\mathbf {U}}^{(v)}\}_{v=1}^H$

When ${\mathbf {V}}$ is fixed, $\mathbf U^{(1)},\ldots ,\mathbf U^{(H)}$ are independent with one another. Since the way of optimization is the same, we concentrate on an arbitrary view and use ${\mathbf {X}}$ and ${\mathbf {U}}$ to denote the data matrix and the basis matrix for the view respectively. The optimization problem involving ${\mathbf {U}}$ can be formulated as

$$\begin{aligned}&\min _{{\mathbf {U}}} \quad \phi ({\mathbf {U}}): = \frac{1}{2} \Vert {\mathbf {X}} - {\mathbf {U}} {\mathbf {V}}\Vert _F^2 + \alpha \Vert {\mathbf {U}}\Vert _{1,2} \nonumber \\&{\text{s.t.}} \quad U_{ik} \ge 0, \quad \forall i, k. \end{aligned}$$

(21)

Two parts of $\phi ({\mathbf {U}})$ are both convex functions. The first part of $\phi (\mathbf {U})$ is differentiable and its gradient is Lipschitz continuous. Hence, we propose an optimization algorithm based on the composite gradient mapping technique proposed for solving composite objective functions [48]. The core idea is to minimize the auxiliary function and adjust the candidate of the Lipschitz constant of the first part of $\phi (\mathbf {U})$ iteratively. In this way, we could decrease the objective function effectively. Suppose $f(\mathbf {U}) = \frac{1}{2} \Vert {\mathbf {X}} - {\mathbf {U}} {\mathbf {V}}\Vert _F^2$ and $\mathbf {U}^t$ be the value of $\mathbf {U}$ in the t-th iteration. In our work, the auxiliary function of (21) is formulated as

$$\begin{aligned} m_L(\mathbf {U}^t; {\mathbf {U}})&= f(\mathbf {U}^t) + tr\left[ \nabla f(\mathbf {U}^t)^T (\mathbf {U} - {\mathbf {U}}^t) \right] \nonumber \\&\quad + \frac{L}{2} \Vert {\mathbf {U}} - {\mathbf {U}}^t\Vert _F^2 + \alpha \Vert {\mathbf {U}}\Vert _{1,2}, \end{aligned}$$

(22)

where L is the Lipschitz constant to be estimated, $L_f$, of $f(\cdot )$, and $\nabla f(\mathbf {U}^t)$ is the gradient of $f(\cdot )$ at $\mathbf {U}^t$:

$$\begin{aligned} \nabla f(\mathbf {U}^t) = {\mathbf {U}}^t {\mathbf {V}} {\mathbf {V}}^T - {\mathbf {X}}\mathbf {V}^T. \end{aligned}$$

(23)

We could find the candidate for $\mathbf {U}^{t+1}$ which is denoted as $T_L(\mathbf {U}^t)$ by minimizing $m_L(\mathbf {U}^t; {\mathbf {U}})$ with the nonnegative constraints:

$$\begin{aligned} T_L(\mathbf {U}^t) = \arg \min _{U_{ik} \ge 0, \forall i, k} m_L(\mathbf {U}^t; {\mathbf {U}}) \end{aligned}$$

(24)

We develop a linear time solver for (24). At first, we rewrite $m_L(\mathbf {U}^t; {\mathbf {U}})$ as follows:

$$\begin{aligned}&m_L(\mathbf {U}^t; {\mathbf {U}}) \\&\quad = \frac{L}{2} \Vert {\mathbf {U}}-\mathbf {U}^t\Vert _F^2 + tr\left[ \nabla f(\mathbf {U}^t)^T {\mathbf {Y}} \right] + \alpha \Vert {\mathbf {U}}\Vert _{1,2} + f(\mathbf {U}^t) \\&\quad = \frac{L}{2} \left\{ \Vert {\mathbf {U}}-\mathbf {U}^t\Vert _F^2 + \frac{2}{L} tr\left[ \nabla f(\mathbf {U}^t)^T {\mathbf {Y}} \right] + \frac{1}{L^2} \Vert \nabla f(\mathbf {U}^t) \Vert _F^2 \right\} \\&\qquad + \ \alpha \Vert {\mathbf {U}}\Vert _{1,2} + f(\mathbf {U}^t) - \frac{1}{2L} \Vert \nabla f(\mathbf {U}^t) \Vert _F^2 \\&\qquad = \frac{L}{2} \Vert {\mathbf {U}}-\mathbf {U}^t + \frac{1}{L} \nabla f(\mathbf {U}^t) \Vert _F^2 + \alpha \Vert {\mathbf {U}}\Vert _{1,2} + const. \end{aligned}$$

The optimization problem (24) becomes

$$\begin{aligned}&\min _{\mathbf {U}}\quad \frac{L}{2} \Vert {\mathbf {U}}-\mathbf {U}^t + \frac{1}{L} \nabla f(\mathbf {U}^t) \Vert _F^2 + \alpha \Vert {\mathbf {U}}\Vert _{1,2} \nonumber \\&{\text{s.t.}} \quad U_{ik} \ge 0, \quad \forall i, k. \end{aligned}$$

(25)

It is easy to see that (25) can be transformed as independent optimization subproblem for different columns of $\mathbf {U}$. Let $\mathbf {u}$ be an arbitrary column of $\mathbf {U}$ and $\mathbf {b}$ be the column of $( {\mathbf {U}}^t - \frac{1}{L}\nabla f(\mathbf {U}^t) )$ at the same index. The subproblem for this column can be written as

$$\begin{aligned}&\min _{\mathbf {u}} \quad \frac{1}{2} \Vert {\mathbf {U}} - {\mathbf {b}} \Vert _2^2 + \frac{\alpha }{L} \Vert {\mathbf {U}}\Vert _{2} \nonumber \\&{\text{s.t.}} \quad u_{i} \ge 0, \;\; \forall i. \end{aligned}$$

(26)

This problem is proved [49] that it can be handled without the nonnegativity constraints. Let $[\cdot ]_+$ denote the element-wise projection operator to nonnegative numbers. So (26) can be transformed into

$$\begin{aligned} \min _{\mathbf {u}} \;\; \frac{1}{2} \Vert {\mathbf {U}} - [{\mathbf {b}}]_+ \Vert _2^2 + \frac{\alpha }{L} \Vert {\mathbf {U}}\Vert _{2}. \end{aligned}$$

(27)

This transformation is important since (27) can be solved via Fenchel duality [50, 51] as follows.

Define $\mathbf {a}$ as the dual variable. We have:

$$\begin{aligned}& \min _{\mathbf {u}} \left[ \frac{1}{2} \Vert {\mathbf {U}} - [{\mathbf {b}}]_+ \Vert _2^2 + \frac{\alpha }{L} \Vert {\mathbf {U}}\Vert _{2} \right] \\& \quad = \min _{\mathbf {u}} \max _{\mathbf {a}} \left[ {\mathbf {a}}^T ([{\mathbf {b}}]_+- {\mathbf {U}}) - \frac{1}{2} \Vert {\mathbf {a}}\Vert _2^2 + \frac{\alpha }{L} \Vert {\mathbf {U}}\Vert _{2} \right] \\& \quad = \max _{\mathbf {a}} \min _{\mathbf {u}} \left[ -\mathbf {a}^T {\mathbf {U}} + \frac{\alpha }{L} \Vert {\mathbf {U}}\Vert _{2} + {\mathbf {a}}^T [{\mathbf {b}}]_+ - \frac{1}{2} \Vert {\mathbf {a}}\Vert _2^2 \right] \\& \quad = \max _{\mathbf {a}} \left[ {\mathbf {a}}^T [{\mathbf {b}}]_+- \frac{1}{2} \Vert {\mathbf {a}}\Vert _2^2 \;\; s.t. \Vert {\mathbf {a}}\Vert _2 \le \frac{\alpha }{L} \right] , \end{aligned}$$

which is equivalent to the following problem

$$\begin{aligned} \min _{\mathbf {a}} \frac{1}{2} \Vert {\mathbf {a}} - [{\mathbf {b}}]_+\Vert _2^2 \;\; s.t. \Vert {\mathbf {a}}\Vert _2 \le \frac{\alpha }{L}. \end{aligned}$$

(28)

Moreover, $\mathbf {a}$ satisfies the relation ${\mathbf {a}} = [{\mathbf {b}}]_+- {\mathbf {U}}$. Thus, by solving (28) we can easily obtain a solution for (27). Apparently (28) can be solved simply by normalization.

5.2 Optimizing $\mathbf V$

When $\{\mathbf {U}^{(v)}\}_{v=1}^H$ are fixed, the subproblem for $\mathbf {V}$ can be written as

$$\begin{aligned}&\min _{\mathbf {V}} \quad \psi (\mathbf {V}) := \bigg ( \frac{1}{2} \sum _{v=1}^H \Vert {\mathbf {X}}^{(v)}-\mathbf {U}^{(v)} {\mathbf {V}}\Vert _F^2 \nonumber \\&\quad + \frac{\beta }{2} \{ tr [ {\mathbf {V}} {\mathbf{L}}^a {\mathbf {V}}^T ] - tr [ {\mathbf {V}} {\mathbf{L}}^p {\mathbf {V}}^T ] \} \bigg ) \nonumber \\&{\text{s.t.}} \quad 1 \ge V_{kj} \ge 0, \;\; \forall j, k. \end{aligned}$$

(29)

(29) is a bounded non-negative quadratic programming problem for $\mathbf {V}$. Sha et al. [52] developed a general multiplicative optimization scheme for this type of problems. Inspired by [52], we propose a multiplicative update algorithm for optimizing $\mathbf {V}$.

At first, we rewrite the first term of $\psi (\mathbf {V})$ as:

$$\begin{aligned}&\frac{1}{2} \sum _{v=1}^H \Vert {\mathbf {X}}^{(v)}-\mathbf {U}^{(v)} {\mathbf {V}}\Vert _F^2 \\&\quad = \frac{1}{2} \sum _{v=1}^H tr[\mathbf {V}^T (\mathbf {U}^{(v)})^T {\mathbf {U}}^{(v)} {\mathbf {V}}] \\&\qquad - 2 tr[\mathbf {V}^T (\mathbf {U}^{(v)})^T {\mathbf {X}}^{(v)}] + const. \end{aligned}$$

For convenience, let $\mathbf {P} = \sum _{v=1}^H (\mathbf {U}^{(v)})^T {\mathbf {U}}^{(v)}$ and $\mathbf {Q} = \sum _{v=1}^H (\mathbf {U}^{(v)})^T {\mathbf {X}}^{(v)}$. Equation (29) can be transformed into

$$\begin{aligned}&\min _{\mathbf {V}} \quad \frac{1}{2} tr[\mathbf {V}^T {\mathbf {P}} {\mathbf {V}}] - tr[\mathbf {V}^T {\mathbf {Q}}] \nonumber \\&\quad + \frac{\beta }{2} \{tr [ {\mathbf {V}} {\mathbf{L}}^a {\mathbf {V}}^T ] - tr [ {\mathbf {V}} {\mathbf{L}}^p {\mathbf {V}}^T ] \} \nonumber \\&{\text{s.t.}} 1 \ge V_{kj} \ge 0, \quad \forall j, k. \end{aligned}$$

(30)

The second term is linear term for $\mathbf V$. We only need to focus on the quadratic terms which can be represented as follows

$$\begin{aligned}&\frac{1}{2} tr[\mathbf {V}^T {\mathbf {P}} {\mathbf {V}}] = \frac{1}{2} \sum _{j=1}^{N} {\mathbf {v}_j}^T {\mathbf {P}} {\mathbf {V}}_j, \end{aligned}$$

(31)

$$\begin{aligned}&\frac{\beta }{2} \{tr [ {\mathbf {V}} {\mathbf{L}}^a {\mathbf {V}}^T ] - tr [ {\mathbf {V}} {\mathbf{L}}^p {\mathbf {V}}^T ] \} \nonumber \\&\quad = \frac{\beta }{2} \sum _{k=1}^K \{ {\bar{\mathbf {v}}_k}^T (\mathbf {D}^a + {\mathbf {W}}^p) \bar{\mathbf {v}}_k - {\bar{\mathbf {v}}_k}^T (\mathbf {D}^p + {\mathbf {W}}^a) \bar{\mathbf {v}}_k \} , \end{aligned}$$

(32)

where $\mathbf {v}_j$ and $\bar{\mathbf {v}}_k$ represent the j-th column vector and k-th row vector of $\mathbf {V}$, respectively. Each summand in Eqs. (31) and (32) is a quadratic function of a vector variable. Therefore, we can obtain upper bounds for these summands:

$$\begin{aligned}&(\mathbf {v}_j)^T {\mathbf {P}} {\mathbf {V}}_j \le \sum _{k=1}^K \frac{(\mathbf {P} {\mathbf {V}}_j^{t})_k}{V_{kj}^{t}} (V_{kj})^2,\\&(\bar{\mathbf {v}}_k)^T (\mathbf {D}^a + {\mathbf {W}}^p) \bar{\mathbf {v}}_k \le \sum _{j=1}^{N} \frac{((\mathbf {D}^a + {\mathbf {W}}^p) \bar{\mathbf {v}}_k^{t})_j}{V_{kj}^{t}} (V_{kj})^2,\\&-(\bar{\mathbf {v}}_k)^T (\mathbf {D}^p + {\mathbf {W}}^a) \bar{\mathbf {v}}_k \\&\quad \le - \sum _{i,j} (\mathbf {D}^p + {\mathbf {W}}^a)_{ij} V_{ki}^{t} V_{kj}^{t} \left( 1 + \log \frac{V_{ki} V_{kj}}{V_{ki}^{t} V_{kj}^{t}} \right) , \end{aligned}$$

where we let $\mathbf {V}^{t}$ denote the value of $\mathbf {V}$ in the t-th iteration of the update algorithm and $\mathbf {v}_j^{t}$, $\bar{\mathbf {v}}_k^{t}$ represent its j-th column vector and k-th row vector, respectively. Gathering the bounds for all the summands, we have the auxiliary function for $\mathcal {O}(\mathbf {V})$:

$$\begin{aligned}&\mathcal {G}(\mathbf {V}^{t}; {\mathbf {V}}) \nonumber \\&\quad = \frac{1}{2} \sum _{j=1}^{N} \sum _{k=1}^K \frac{(\mathbf {P} {\mathbf {V}}_j^{t})_k + \beta ((\mathbf {D}^a + {\mathbf {W}}^p) \bar{\mathbf {v}}_k^{t})_j}{V_{kj}^{t}} (V_{kj})^2 \nonumber \\&\qquad -\frac{\beta }{2} \sum _{k=1}^K \sum _{i,j} (\mathbf {D}^p + {\mathbf {W}}^a)_{ij} V_{ki}^{t} V_{kj}^{t} \left( 1 + \log \frac{V_{ki} V_{kj}}{V_{ki}^{t} V_{kj}^{t}} \right) \nonumber \\&\qquad - \sum _{j=1}^{N} \sum _{k=1}^K Q_{kj} V_{kj}. \end{aligned}$$

(33)

The estimate of $\mathbf {V}$ in the $(t+1)$-th iteration is then computed as

$$\begin{aligned} {\mathbf {V}}^{t+1} = \arg \min _{\mathbf {V}} {\mathcal {G}}(\mathbf {V}^{t}; {\mathbf {V}}). \end{aligned}$$

(34)

Differentiating $\mathcal {G}(\mathbf {V}^{t}; {\mathbf {V}})$ with respect to each $V_{kj}$, we have

$$\begin{aligned}&\frac{\partial {\mathcal {G}}(\mathbf {V}^{t}; {\mathbf {V}})}{\partial V_{kj}} \\&\quad = \frac{(\mathbf {P} {\mathbf {V}}_j^{t})_k + \beta ((\mathbf {D}^a + {\mathbf {W}}^p) \bar{\mathbf {v}}_k^{t})_j}{V_{kj}^{t}} V_{kj}\\&\qquad - \frac{\beta ((\mathbf {D}^p+\mathbf {W}^a)\bar{\mathbf {v}}^{t}_k)_j}{V_{kj}} V_{kj}^{t} - Q_{kj} \end{aligned}$$

Setting $\partial {\mathcal {G}}(\mathbf {V}^{t}; {\mathbf {V}}) / \partial V_{kj} = 0$, we get the update rule for $\mathbf {V}$

$$\begin{aligned} V^{t+1}_{kj}= \min \left\{ 1, V^{t}_{kj} \frac{-B_{kj} + \sqrt{B_{kj}^2 + 4 A_{kj} C_{kj} } }{2 A_{kj}} \right\} , \end{aligned}$$

(35)

$$\begin{aligned} A_{kj}= (\mathbf {P}\mathbf {v}^{t}_j)_k + \beta ((\mathbf {D}^a+\mathbf {W}^p)\bar{\mathbf {v}}^{t}_k)_j, \end{aligned}$$

(36)

$$\begin{aligned} B_{kj}= - Q_{kj}, \end{aligned}$$

(37)

$$\begin{aligned} C_{kj}= \beta ((\mathbf {D}^p+\mathbf {W}^a)\bar{\mathbf {v}}^{t}_k)_j. \end{aligned}$$

(38)

It is not difficult to find out $\mathcal {O}(\mathbf {V}^{t+1}) \le {\mathcal {G}}(\mathbf {V}^{t}; {\mathbf {V}}^{t+1}) \le {\mathcal {G}}(\mathbf {V}^{t}; {\mathbf {V}}^{t}) = {\mathcal {O}}(\mathbf {V}^{t})$. Therefore, the update rule for $\mathbf {V}$ monotonically decreases Eq. (5).

5.3 Optimizing MvSL-S and MvSL-L

It is obvious that MvSL-S and MvSL-L have the same objective function, which can be formulated as:

$$\begin{aligned}&\min _{\{\mathbf {U}^{(v)}\}_{v=1}^H,\mathbf {V}} \quad \frac{1}{2} \sum _{v=1}^H \Vert {\mathbf {X}}^{(v)}-\mathbf {U}^{(v)} {\mathbf {V}}\Vert _F^2 + \alpha \sum _{v=1}^H \Vert {\mathbf {U}}^{(v)}\Vert _{1,2} \nonumber \\&\quad + \frac{\beta }{2} \{ tr [ {\mathbf {V}}^l {\mathbf{L}}^a (\mathbf {V}^l)^T ] - tr [ {\mathbf {V}}^l {\mathbf{L}}^p (\mathbf {V}^l)^T ] \} \nonumber \\&{\text{s.t.}} \quad U_{ik}^{(v)} \ge 0, 1 \ge V_{kj} \ge 0, \quad \forall i, j, k, v. \end{aligned}$$

(39)

It is easy to see that the update rule of $\mathbf {U}$ in (39) is the same as that in (5) and the update rule of $\mathbf {V}^l$ in (39) is the same as $\mathbf {V}$ in (5). We will optimize $\mathbf {V}^u$ in (39) as follow.

Similarly, the auxiliary function for $\mathcal {O}^u(\mathbf {V}^u)$ can be derived

$$\begin{aligned} {\mathcal {G}}^u(\mathbf {V}^{u,t}; {\mathbf {V}}^u) = \frac{1}{2} \sum _{j=1}^{N^u} \sum _{k=1}^K \frac{(\mathbf {P} {\mathbf {V}}_j^{u,t})_k}{V_{kj}^{u,t}} (V_{kj}^u)^2 - \sum _{j=1}^{N^u} \sum _{k=1}^K Q^u_{kj} V_{kj}^u \end{aligned}$$

(40)

and the update rule can be obtained by setting the partial derivatives to 0:

$$\begin{aligned} V^{u,t+1}_{kj} = \min \left\{ 1, V^{u,t}_{kj} \frac{ Q^u_{kj} - | Q^u_{kj}| }{2 (\mathbf {P}\mathbf {v}^{u,t}_j)_k} \right\} \end{aligned}$$

(41)

5.4 Computational complexity

The major space cost of MvCL is due to the matrices $\{\mathbf {U}^{(v)}\}_{v=1}^H$, $\mathbf {V}$, $\mathbf {W}^a$ and $\mathbf {W}^p$, which is $O(K (\sum _{v=1}^H M_v + N) + 2N^2 )$. Nearest neighbor graph needs $O({N}^2\sum _{v=1}^H{{M}_v)}$ to construct. The time complexity of main algorithm consists of two parts, corresponding to the subproblems for $\{\mathbf {U}^{(v)}\}_{v=1}^H$ and $\mathbf {V}$ respectively. For optimizing each $\mathbf {U}^{(v)}$, we need to run Algorithm 2. The core step is the optimization of (24), which requires solving (26) for each column of $\mathbf {U}^{(v)}$. The cost of solving (26) for a column of $\mathbf {U}^{(v)}$ is $O(M_v)$, so the total cost of solving (24) is $O(M_v K)$. In the outer loop of Algorithm 2 we also need to compute $\nabla f(\mathbf {U})$ ($O(M_v K^2)$ if we pre-compute $\mathbf {V}\mathbf {V}^T$ and $\mathbf {X}^{(v)}\mathbf {V}^T$). Assume we run T iterations of the outer loop of Algorithm 2, and the total number of iterations of the inner loop is upper bounded by $2(T+1)+\log _2\frac{L_f}{L_0}$ [48]. The major cost for optimizing $\mathbf {U}^{(v)}$ is $O(M_v K(2(T+1)+log_2\frac{L_f}{L_0})+T M_vK^2)$. Regarding $\mathbf {V}$, let N be the number of items. In each iteration, we need to compute three matrices for $\mathbf {V}$ (Eqs. (36)–(38)): $\mathbf {A}$ ($O(NK^2+N^2K)$), $\mathbf {B}$ (O(NK)) and $\mathbf {C}$ ($O(N^2K)$). Combining these pieces and the costs of Eqs.(35) together, the major cost for optimizing $\mathbf {V}$ is $O(T'(NK+NK^2+N^2K))$, where $T'$ is the number of iterations. The comparison of time complexity between different algorithms is described in Table  1.

Table 1 Comparison of time complexity

6 Experiment

In this section, we conduct the experiments on two real-world data sets to validate the effectiveness of the proposed algorithm MvSL.

Table 2 Statistics of the datasets

6.1 Data set

We use three real-world datasets to evaluate the proposed factorization method.

The first dataset came from the Reuters Multilingual collection [53]. Totally 111,740 Reuters news documents comprised the test collection, which were written in five different languages (English, French, German, Spanish and Italian). Documents belonging to more than one of the six categories were assigned to the smallest category. Each document was translated into the other four languages and represented as a bag of words using a TFIDF-based weighting scheme. We randomly choosed 1800 documents, with 300 for each category. For each document, we took English, Italian and Spanish translations as the first, second and third views respectively.

The second dataset came from Microsoft Research Asia Internet Multimedia Dataset 2.0 (MSRA-MM 2.0) [54]. MSRA-MM 2.0 consists of 1011738 images that were collected from 1165 query concepts in Microsoft Bing Search. Each concept has approximately 500–1000 images. For each image, its relevance to the corresponding query was labeled with 3 levels: very relevant, relevant and irrelevant. 7 feature types were extracted for each image. We choosed 25 query concepts from the Animal, Object and Scene branches, and then randomly selected 200 images from each concept while removing irrelevant images. We selected 4 type features as 4 different views: 64D HSV color histogram, 144D color correlogram, 75D edge distribution histogram and 128D wavelet texture.

The third dataset was constructed from ImageNet [55], an image dataset organized according to the WordNet hierarchy. Currently, there are more than 100,000 synsets in WordNet are indexed and each synset included more than 500 images on average. We randomly select 50 leaf synsets in the hierarchy as categories and randomly choosed 200 images from each candidate synset. Three different features of this dataset were 64D HSV histogram, 1000D bag of SIFT visual words, and 512D GIST descriptors. The statistics of these datasets are summarized in Table  2.

6.2 Evaluation methodology

To validate the performance of our method, we compare the proposed MvSL with the following baselines:

• NMF [13].

• Feature concatenation (ConcatNMF): This method constructs new data matrix by concatenating the features of all the views and then applies NMF to the new data matrix.

• Multi-view NMF (MultiNMF): MultiNMF [5] is an unsupervised multi-view NMF algorithm.

• Semi-supervised Unified Latent Factor method (SULF): SULF [14] is a semi-supervised multi-view nonnegative factorization method which factorizes partial label information as a constraint on $\mathbf {V}^l$.

• Graph regularized NMF (GNMF): GNMF [20] is a graph regularized version of NMF. We spread it to the multi-view case and constructed the affinity graph for approximating data manifolds with the within-class affinity graph defined in Eq. (8) to make it a semi-supervised method on multi-view data.

• Multi-view NMF with fisher discriminant analysis (MvFisher): MvFisher is a semi-supervised multi-view learning method. Firstly, MvFisher factorized mult-view data by Eq. (1), and then used fisher’s discriminant analysis with partially labeled latent subspace (i.e. $\mathbf {V}^l$).

Since the large-margin based multi-view learning methods ignore the intra-class semantic structures of the data, the latent subspace learned by this kind of methods will acquire inferior representation compared with MvFisher and MvSL. It is to see that the first three are unsupervised methods while the last three are semi-supervised methods.

We evaluated the seven factorization methods by classification and clustering. For three datasets, we varied the percentage of training items from 10 to 50%. We generated five random train-test splits and run each method on each split three times. The averaged performance and standard deviation were reported. In case the method has parameters, we tuned the parameters on a separate random split. The dimensionalities of the latent space were empirically set to 50, 100 and 150, for Reuters, MM2.0 and imageNet respectively.

We exploited the learned latent representations of different methods for classification and clustering. For classification, the training items were imported to a kNN classifier ($k=9$). For clustering, k-means was used as the clustering method. Due to semi-supervised methods exploiting the label information of training data, we just applied clustering on test items for fairness. accuracy and normalized mutual information (NMI) are adppted to evaluate clustering performance, whose definitions are as follows:

$$\begin{aligned} {\rm Accuracy}= \frac{\sum _{i=1}^{n} \delta (s_i,map(r_i))}{n}, \end{aligned}$$

(42)

$$\begin{aligned} {\rm NMI}(C,C^\dag )= \frac{MI(C,C^\dag )}{\max (H(C),H(C^\dag ))}, \end{aligned}$$

(43)

where $\delta (x,y)$ is the indicator function that $\delta (x,y)=1$ if $x=y$ and $\delta (x,y)=0$ otherwise. $map(r_i)$ is the permutation mapping function that maps cluster label $r_i$ to the equivalent cluster label from the data corpus. The best mapping can be obtained by the Kuhn-Munkres algorithm [56]. H(C) and $H(C^\dag )$ denotes the entropy of cluster set C and $C^\dag$ respectively. And $MI(C,C^\dag )$ is the mutual information between C and $C^\dag$:

$$\begin{aligned} MI(C,C^\dag ) = \sum _{c_i \in C, c_j^\dag \in C^\dag } p(c_i,c_j^\dag ) \log _2 \frac{p(c_i,c_j^\dag )}{p(c_i)p(c_j^\dag )}. \end{aligned}$$

(44)

where $p(c_i)$ represents the probability that a randomly selected item from all testing items belongs to cluster $c_i$, and $p(c_i,c_j^\dag )$ stands for the joint probability that any arbitrarily selected item is in $c_i$ and $c_j^\dag$ simultaneously.

Table 3 Classification performance of different factorization methods on the Reuters dataset (accuracy ± std. dev., %)

Table 4 Classification performance of different factorization methods on the MM2.0 dataset (accuracy ± std dev, %)

Table 5 Classification performance of different factorization methods on the imageNet dataset (accuracy ± std dev, %)

6.3 Experiment results

Tables 3,   4 and 5 show the classification performance of different factorization methods on MM2.0, Reuters and imageNet, respectively. As we can see, multi-view learning methods outperform single view learning methods and semi-supervised methods outperform unsupervised methods. On the other hand, directly constrained multi-view learning methods (MvSL) have an advantage over the implicitly constrained ones. The detailed observations are revealed as follows.

• Semi-supervised algorithms are superior to unsupervised algorithms in general, which denoted that using label information could obtain better discriminative structures in the latent spaces.

• Multi-view algorithms are more preferable for multi-view data. This is in accord with the results of previous multi-view learning work.

• MvSL, MvFisher and GNMF show superior performance over SULF. SULF models partial label information as a factorization constraint on $\mathbf V^l ,$ which can be viewed as indirect affinity constraints on encoding of within-class items. On the contrary, the graph embedding terms in MvSL, MvFisher and GNMF impose direct affinity constraints on item encodings and therefore could be favor to learn more explicit semantic structures in the learned latent spaces.

• MvFisher shows superior performance over GNMF. MvFisher takes into account both the variance between the classes and the variance within the classes , but GNMF ignores the variance between the classes. So MvFisher could lead to a better semantic structures in the learned latent spaces.

• MvSL methods outperform other algorithms under all cases. On the one hand, MvSL methods do not need the datasets obey gaussian distribution; on the other hand, MvSL methods utilize the partial label information to construct a graph embedding framework, which encouraged items of the same category to be near with each other and kept items belonging to different categories as distant as possible in the latent subspace. What’s more, MvSL methods allow each latent dimension in the latent subspace to be correlative with a subset of views by imposing $\ell _{1,2}$-norm on each basis $\mathbf U^{(v)}$. Therefore, MvSL methods can learn flexible latent factor sharing among multi-view data.

• The performance of MvSL-T is better than that of MvSL-L and MvSL-S. The reason is that MvSL-T exploits not only label information but also unlabel information via a graph embedding framework. These properties could help MvSL-T to learn a clearer semantic latent space. We performed F-test for 5 $\times$ 2 cross-validation with significance level 0.05. The results indicated that MvSL was significantly superior over all the baselines, MvSL-T was superior than MvSL-L and MvSL-L was superior than MvSL-S.

• The clustering results are shown in Figs.   2 and   3, for Reuters and MM2.0 respectively. The observations were very similar to those for the classification results. According to F-test with significance level 0.05, we found MvSL outperformed the baseline methods under all cases, MvSL-T was superior than MvSL-L and MvSL-L was superior than MvSL-S.

In Table  6, we compare MvSL to related methods with important properties.

Fig. 2

Clustering performance of different methods on Reuters. Error bars represent standard deviations

Fig. 3

Clustering performance of different methods on MM2.0. Error bars represent standard deviations

Table 6 Comparison between MvSL and related works

6.4 Parameter sensitive analysis

There are two essential parameters in new methods. $\beta$ controls the importance of the semi-supervised part of MvSL, while $\alpha$ measures the sparsity degree of the basis matrices. We study their influence on MvSL’s performance by changing one parameter while keeping the other parameter constant.

The results are shown in Figs. 4 and 5 for Reuters and MM2.0 respectively. It is easy to see that the general behavior of the two parameters was the same: when increasing the parameter from 0, the performance curves went up firstly and then went down. This denotes that when assigned appropriate weights, the sparseness and semi-supervised constraints really promote to learn a better latent subspace. On the one hand, the models performance was not very sensitive to the value of $\alpha$. MvSL achieved its best performance when $\alpha$ was in [15, 25] and [10, 20] for Reuters and MM2.0 respectively. On the other hand, $\beta$’s impact in Reuters seemed to be weaker than its impact in image datasets. The reason may be that in Reuters $\alpha$ prevailed the performance boost (as shown in Fig. 4a). Based observations, we set $\alpha =15$, $\beta =0.02$ for other experiments. As to real number $\sigma$ in (12), we found that when $\sigma =2$ experiments have well performance.

As we described, MvSL uses ka nearest neighbor graph and kp nearest neighbor graph to character the intra-class and inter-class relationship, respectively. The affinity graph of MvSL relies on how the assumption that two neighboring items share the same label. Obviously this assumption is more likely to fail as ka increases. The observations of kp was very similar to ka. This is the reason why the performance of MvSL decreases as ka or kp increases, as shown in Fig. 6.

Fig. 4

Influence of different parameter settings on the performance of MvSL in the Reuters dataset: a varying $\alpha$ while setting $\beta =0.02$, b varying $\beta$ while setting $\alpha =15$

Fig. 5

Influence of different parameter settings on the performance of MvSL in the MM2.0 dataset: a varying $\alpha$ while setting $\beta =0.02$, b varying $\beta$ while setting $\alpha =15$

Fig. 6

The performance of MvSL decreases as ka and kp increases: a varying ka while setting $kp=3$, b varying kp while setting $ka=5$

7 Conclusion

In this paper, we have proposed a novel nonnegative latent representation learning algorithm, called Multi-view semantic learning (MvSL), for representation learning with multi-view data. MvSL efficiently learns a latent subspace embedded in multiple views based on non-negative matrix factorization. A graph embedding framework was constructed by both partial label information and unlabel information, which encouraged items came from same category to be near with each other and kept items belonging to various categories as distant as possible. What’s more, a novel multiple kernel learning method effectively estimated the items pair similarity among multi-view data, which further extended graph embedding framework. Another property of MvSL was that it encourages each latent dimension of learned latent subspace only to be associated with a subset of views by imposing $\ell _{1,2}$-norm on each basis $\mathbf U^{(v)}$. Therefore, MvSL is able to learn a more meaningful latent subspace shared across the views. An efficient multiplicative-based iterative algorithm is developed to solve the proposed optimization problem. We used three real-world datasets to evaluate the empirical performance of MvSL. Experimental results indicated that MvSL was effective and outperformed baseline methods.