Introduction

One of the most crucial issues in rock mechanics studies and geomechanical topics in hydrocarbon reservoir engineering is the evaluation of in-situ stresses and factors affecting stress perturbation. These geomechanical topics include hydraulic fracturing, wellbore stability, determination of rock mass permeability and optimum mud weight, prevention of sand production, selection of appropriate strategies for well completion, reservoir production rate, as well as the evaluation of earthquake potential (Zoback 2007; Hudson et al. 1988; Latham et al. 2013; Matsumoto et al. 2015; Zang et al. 2009; Dehghan et al. 2017; Farsimadan et al. 2020). Moreover, it is important to consider the stress conditions for accurate prediction of the mechanical behavior of jointed rock mass (Wu et al. 2019). Many studies have been conducted to measure in-situ stresses and research shows that fractures play an important role in the distribution and perturbation of tectonic stresses (Bruno et al. 1994; Day-Lewis et al. 2010; Rajabi et al. 2017; Schoenball et al. 2017; Hickman et al. 2004; Barton et al. 1994; Sahara et al. 2014; Khodaei et al. 2020).

Bruno et al. (1994) showed significant azimuth changes of maximum horizontal stress in a reservoir with the depth and location of a subsurface structure using field data analytically and finite element modeling. Day-Lewis et al. (2010) investigated the direction of maximum horizontal compressive stress as a function of depth in two research wells near the San Andreas Fault in central and southern California. They found that the stress orientation shows the scale-invariant fluctuations at distances of 10 cm to several kilometers of the fault. The similarity between the scale of stress orientation fluctuations and the magnitude of earthquake frequency with the size of faults showed that these fluctuations are controlled by the stress perturbation that is due to the slip of faults in the crust under critical stress in the proximity of faults. Sahara et al. (2014) performed an analysis on the occurrence of breakout, breakout orientation and fracture characteristics. They observed that breakout orientation in the form of anomalies, centrally occurs adjacent to the fault cores and decreases with distance from the fault core. The pattern of breakout orientation in the proximity of natural fractures shows that the rotation of breakout relative to the direction of mean horizontal stress (Shmin) is strongly influenced by the fracture orientation. Breakouts are also commonly found asymmetrically in zones with high fracture densities. In addition to the principal stresses heterogeneities, breakout heterogeneities are affected by mechanical heterogeneities, such as weak zones with different elastic modulus, rock strength and fracture patterns. Rajabi et al. (2017) performed the first analysis of tectonic stress in Clarence-Moreton Basin in New South Wales area of Australia. Their observations suggested that structures can play an important role in controlling stresses so that stress perturbation as a result of faults and fractures highly influences wellbore stability and permeability of reservoir rock, especially for safe and sustainable extraction of methane gas from gas reservoirs in this region.

Extensive research has been previously done on the generation of discrete fractures networks using stochastic approaches to determine the properties of jointed rock and their geomechanical and hydromechanical behavior (Min et al. 2004; Baghbanan et al. 2007, 2008; Li et al. 2019), as well as geomechanical modeling using finite difference method (Oda et al. 1993; Kobayashi et al. 2001; Rutqvist et al. 2013). Among the most important researches on generating a discrete fracture network using stochastic approaches is the generation of a two-dimensional stochastic fracture pattern using field data in the Sellafield area of the United Kingdom to determine the equivalent permeability tensor of the fractured rock mass by Min et al. (2004). Also, Baghbanan et al. (2007, 2008), generated a discrete fracture network with the assumption that the geometry of the fractures are stochastically distributed in the network; therefore, they could investigate the hydraulic and hydromechanical behaviors that are dependent on the rock mass size and estimate the representative elementary volume.

Concerning geomechanical continuum modeling, Oda et al. (1993) developed an elastic stress/strain relationship using crack tensor method to determine the influence of joints on the elastic behavior of rock mass in a three-dimensional finite element model. Kobayashi et al. (2001) investigated the coupling of mechanical and hydraulic behavior of fractured rock mass during a hypothetical shaft sinking in the Sellafield area of the United Kingdom using a continuum approach (finite element method) and combining the crack tensor theory and the Barton and Bandis model. Rutqvist et al. (2013) investigated the coupling of geomechanical model and fluid flow in the fractured rock using a continuum model and crack tensor approach.

In these studies, the investigation of stress perturbation is based on an approach that utilizes scalar/vector formulations which analyzes the magnitude and orientation of principal stresses, individually. However, in nature, stress is a tensor and its magnitude and orientation must be taken into consideration simultaneously. As far as we are aware, the first use of a tensor-based approach in this matter can be credited to Lei et al. (2018). In this study, by combining numerical and mathematical analysis, local stress variability in fractured rocks was investigated under static stress loading conditions. Moreover, in previous studies, limited research has been done on the effect of different rock and fracture parameters on the stress field perturbation (regarding the geometrical properties of fracture). In this study, four different parameters including rock tensile strength, rock cohesion, fracture normal stiffness and fracture dilation angle were evaluated.

Research methodology

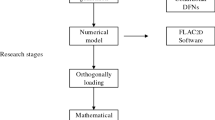
In this section, in order to determine the correlation between the geometric properties of fracture network (including fracture density and fracture length) and stress variability, as well as to investigate the effects of rock and fracture parameters on the distribution of local stress perturbation, a similar approach to the one that was proposed by Lei et al. (2018) was followed. They generated different DFN realizations based on the fracture intensity. Then, they used FEM–DEM approach as the numerical method and tensor-based mathematical formulation to analyze the stress data. Their study aimed to investigate how the intensity and the connectivity of the fracture network would affect the stress variability. Of all the rock and fracture parameters, they studied only the effect of friction coefficient parameter on the stress distribution. In this work, the discrete fracture network was first generated by stochastic realization based on the fracture density. Then, the finite difference method in the continuum approach was utilized as the geomechanical modeling and numerical method. Subsequently, different realizations of the discrete fracture network were subjected to orthogonal tectonic stress loading. Finally, in order to analyze the stress, the correlations between the geometric properties of fracture and stress distribution and the effects of different parameters were evaluated using tensor-based equations. Figure 1 shows the methodologies and analyses used to achieve the goals of this research.

Fig. 1
figure 1

Flowchart of the methodologies and analyses implemented in this study

Full size image

Stochastic approach in the generation of fracture network

In the stochastic approach, fractures are considered as straight lines in two-dimensional model and as planar discs/polygons in three-dimensional model and the geometrical properties, such as location, frequency, length, orientation and fracture aperture are considered as dependent variables on the probability distribution of the outcrop mapping. Orientational data can be processed using Fisher, normal, or even uniform distribution functions (Einstein et al. 1983) and fracture lengths may display negative exponential, lognormal, gamma, or power-law distributions (Davy 1993; Bonnet et al. 2001).

In the present study, the fracture network length was determined using the power-law according to the following equations (Bonnet et al. 2001; Lei et al. 2016):

$$n(l) = \alpha l^{ - a} = \frac{\alpha }{{l^{a} }},l \in [l_{\min } ,l_{\max } ]$$
(1)

whereas in this equation, n(l) is the number of fractures, a is the power-law length exponent, α is the density term, l is the fracture length and lmin and lmax are the smallest and largest fracture lengths.

In theory, in two-dimensional model, a is limited to the interval of [1, ∞), however extensive measurements based on navigation maps show that in natural fracture systems, a generally varies between 1.3 and 3.5 (Bonnet et al. 2001). The density term (i.e., α) is dependent on the total number of fractures in the system and is a function of different fracture orientations (Davy et al. 2010).

The fracture frequency can be described from two aspects of fracture density and fracture intensity and can be determined using the Pij system, where i is the dimension of the sample and j is the dimension of the measurement. In this paper, the fracture density (P20) was determined using a window sampling approach that is defined as the number of fractures per unit area (Zeeb et al. 2013):

$$\begin{gathered} P_{20} = P_{WS} = \frac{N}{A} \hfill \\ A = L^{2} \hfill \\ \end{gathered}$$
(2)

In this equation, N is the number of fractures, A is the surface area and L is the size of the model.

In this study, using open-source software of Alghalandis Discrete Fracture Network Engineering (ADFNE) (Alghalandis 2014, 2016, 2017), a fracture network in the size of 1 m × 1 m was stochastically generated. Determination of the location and orientation of fractures were done using a uniform distribution function and Fisher distribution function completely randomly. The largest and smallest fracture lengths were calculated using the power-law model to be 50 m and 0.02 m, respectively. Considering five different values for the power-law length exponent from 1.5 to 3.5 and 3 fracture densities of 80 m−2, 2 × 80 m−2 and 4 × 80 m−2, a total of 15 different fracture network realizations were generated. Figure 2 illustrates the different realizations of the fracture networks randomly generated at different densities.

Fig. 2
figure 2

Different realizations of the discrete fracture network for (a) fracture density of P20 = 80 m−2, (b) fracture density of P20 = 160 m−2 and (c) fracture density of P20 = 320 m−2

Full size image

Numerical method and geomechanical parameters

In this study, FLAC2D software (Itasca Consulting Group Inc 2017) was employed to determine the stress distribution in response to tectonic stress loading that included three types of orthogonal effective principal tectonic stress loading at stress ratios of SR = 1, SR = 2 and SR = 3 (Fig. 3). The most important advantage of this software is the complete perseverance of not only the fracture dead-ends after meshing but also the backbone of the fracture. Figure 4 shows a comparison of the shape of the fracture network after meshing using finite difference method (FLAC2D software) and solely the backbone.

Fig. 3
figure 3

Types of loading effective tectonic stresses at different ratios

Full size image
Fig. 4
figure 4

Comparison of changes in the fracture network pattern after meshing in FLAC2D software and the backbone

Full size image

For intact rock and fracture shear stress/strain behavior, the Mohr–Coulomb model was used. Characteristics of a limestone sample were considered as rock mechanical properties. Table 1 presents the main parameters of rock and fracture for the geomechanical model. Four parameters including rock cohesion, CR, at values of 15 MPa, 20 MPa and 30 MPa, tensile strength of rock, σtR, at values of 5 MPa, 10 MPa and 20 MPa, normal stiffness, kn, at values of 500 GPa/m, 1000 GPa/m and 2000 GPa/m and fracture dilation angle, ψF, at 0 and 15° were evaluated.

Table 1 Rock and fracture parameters (Figueiredo et al. 2015)
Full size table

Fractures with material fillings can be considered as an equivalent model of solids in which the elastic modulus of fracture is calculated using the following equation:

$$\frac{1}{{E_{F} }} = \frac{1}{{E_{R} }} + \frac{1}{{k_{n} d}}$$
(3)

whereas in this equation, d is the size of the mesh element.

Figueiredo et al. (2015) developed a simple model with a vertical fracture to validate the use of mesh element size and quantity and whether it has the ability to estimate the stress correctly or not. It was found that the difference between the model made with the analytical solution was less than 5% and this model is quite suitable for the calculation of stress distribution and stress concentration around the fracture.

In this paper, the model size is considered to be 1 m × 1 m with 40,000 meshes per square meter (200 × 200 mesh) and with the mesh element length of d = 0.5 cm in accordance with the geometry and model in the study of Figueiredo et al. (2015).

Determination of perturbation and dispersion of stress field using mathematical equations

Stress data analysis was performed using the recent developed tensor-based mathematical formulas (Gao 2017; Gao and Harrison 2016, 2018). Euclidean distance was used for the distribution of local stress perturbation, which represents the distance between the local stress tensor, Si and the mean stress tensor, S̅.

$$d\left( {S_{i} ,\overline{S} } \right) = \left\| {S_{i} - \overline{S}} \right\|_{F}$$
(4)

where \(\left\| . \right\|\) represents the Euclidean norm.

In two-dimensional models of the stress tensor field S, which is comprised of n part of the stress size, the stress tensor of part i is formulated as follows:

$$2D \to S_{i} = \left[ {\begin{array}{*{20}c} {S_{xx,i} } & {S_{xy,i} } \\ {symmetric} & {S_{yy,i} } \\ \end{array} } \right]$$
(5)

The mean stress field is also determined using the following equation:

$$2D \to \overline{S} = \frac{1}{n}\sum\limits_{i = 1}^{n} {S_{i} } = \frac{1}{n}\left[ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {S_{xx,i} } } & {\sum\limits_{i = 1}^{n} {S_{xy,i} } } \\ {symmetric} & {\sum\limits_{i = 1}^{n} {S_{yy,i} } } \\ \end{array} } \right]$$
(6)

Figure 5 shows that the mean stress tensor is equivalent to the far-field stress tensor (different ratios of tectonic stress loading).

Fig. 5
figure 5

Calculated mean stress tensor in the fractured rock model under different tectonic stress conditions

Full size image

Figure 6 illustrates the geometry and meshing of the finite difference model used in the present study in a discrete fracture network sample (a = 1.5 and P20 = 80 m−2) and the way of determination of the local stress tensor at two different positions. Table 2 presents the way of calculation of local stress tensor and d(Si, S̅) for the same fracture sample at the stress ratio SR = 3, (in the main parameters).

$$\overline{S} = \frac{1}{n}\sum\limits_{i = 1}^{n} {S_{i} } = \left[ {\begin{array}{*{20}c} {29.99} & {0.00054} \\ {0.00054} & {10} \\ \end{array} } \right]$$
Fig. 6
figure 6

Geometry and meshing in the finite-difference model and determination of local stress tensor in two different positions

Full size image
Table 2 Method of calculation for local stress tensor and d(S, S̅) for a fracture sample with SR = 3, a = 1.5 and P20 = 80 m−2
Full size table

The effective variance was used to describe the variability and dispersion of the stress field in the fractured rock:

$$V_{e} (S) = \sqrt[{\frac{1}{2}p(p + 1)}]{\left| \Omega \right|}$$
(7)

where \(\left| . \right|\) is the determinant of matrix Ω, p is the stress tensor dimension (here p = 2 for two-dimensional model), s̄ is the mean stress vector and Ω is the covariance matrix of the stress vector.

$$\Omega = {\text{cov}} (s,s) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left[ {(s_{i} - \overline{s}).(s_{i} - \overline{s})^{T} } \right]} ,\overline{s} = \frac{1}{n}\sum\limits_{i = 1}^{n} {s_{i} }$$
(8)

For the Si stress tensor, the form of the distinct components of the si stress vector is as follows:

$$s_{i} = \left[ {\begin{array}{*{20}c} {S_{xx,i} } & {S_{xy,i} } & {S_{yy,i} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {S_{xx,i} } & {S_{yx,i} } & {S_{yy,i} } \\ \end{array} } \right]^{T}$$
(9)

Results and data analysis

The analysis of results obtained regarding the effect of different rock and fracture parameters on 2D fractured rock's mechanical behavior under several different tectonic stress loading conditions is presented. In the next step, following the stochastic generation of the fracture network, which comprised different realizations that were differentiated considering the various distinct lengths and densities of fractures that were considered, the numerical modeling was performed. In this process finite-difference method was employed and three boundary loading conditions of 1) Sxx = 10 MPa, Syy = 10 MPa, 2) Sxx = 20 MPa, Syy = 10 MPa and 3) Sxx = 30 MPa, Syy = 10 MPa were applied orthogonally.

Sequentially, the analysis of stress data was carried out using mathematical formulations to examine the effect of the fracture network's geometric properties and rock and fracture parameters on the distribution of stress. Figures 7, 8, 9 and 10 show the relationship between the fracture density and the power-law length exponent a (fracture length indicator) with the mean local stress perturbation md(S, S̅) and the effective variance Ve (stress distribution scattering indicator) at different values of kn, ψF, CR and σtR, respectively.

Fig. 7
figure 7

Curves of mean stress perturbation (md(S, S̅)) and effective variance (Ve) in terms of power-law length exponent (a) at different values of normal stiffness and fracture density

Full size image
Fig. 8
figure 8

Curves of mean stress perturbation (md(S, S̅)) and effective variance (Ve) in terms of power-law length exponent (a) at different values of angle of dilation and fracture density

Full size image
Fig. 9
figure 9

Curves of mean stress perturbation (md(S, S̅)) and effective variance (Ve) in terms of power-law length exponent (a) at different values of rock cohesion and fracture density

Full size image
Fig. 10
figure 10

Curves of mean stress perturbation (md(S, S̅)) and effective variance (Ve) in terms of power-law length exponent (a) at different values of rock tensile strength and fracture density

Full size image

It is conspicuous that two rock mass parameters, CR and σtR, have minimal effect on the variations of md(S, S̅) and Ve therefore, their influence can be ignored. The fracture normal stiffness, kn, can be defined as the normal spring stiffness of each joint element. It mainly acts as the link between the normal stress on each element to the normal displacement. The data explicitly indicate that the fracture normal stiffness has a significant influence on the stress perturbation distribution, md(S, S̅) and Ve. In general, as kn increases, the values of md(S, S̅) and Ve decrease (the difference in the decrease in Ve values is more significant from kn = 500 GPa/m to kn = 1000 GPa/m than from the kn = 1000 GPa/m to kn = 2000 GPa/m). Also, the difference in Ve values for different ψF is higher at high fracture density (P20 = 320 m−2). In this study, no change in md(S, S̅) and Ve was observed in all fracture network realizations by varying the tensile strength (σtF) from zero to 5 MPa.

Moreover, from these figures and Table 3, it was found that the mean local stress perturbation and effective variance, in the order of highest to lowest, are sensitive to fracture density, fracture length and fracture normal stiffness.

Table 3 Comparison of md(S, S̅) and Ve sensitivity to P20, kn and a
Full size table

Figures 11, 12 and 13 show the distribution of local stress perturbation in fractured rocks at different kn values (as the most important parameter affecting the perturbation and distribution of the local stress) at tectonic stress ratios of 1, 2 and 3, respectively. The stress distribution at the stress ratio of 1 (SR = 1), which is isotropic, is quite uniform, while fluctuations are observed in anisotropic stresses (SR = 2 and SR = 3). With the increase in tectonic stress, local stress perturbations are detected at the tip and intersection of fractures. Generally, in the generated fracture networks, local stress perturbations decreased with the increase in power-law length exponent (a) (decrease in fracture length) and normal stiffness (kn) and it increased with an increase in fracture density (P20).

Fig. 11
figure 11

Distribution of local stress perturbation at stress ratio of 1 at different normal stiffness values for (a) fracture density of P20 = 80 m−2, (b) fracture density of P20 = 160 m−2 and (c) fracture density of P20 = 320 m−2

Full size image
Fig. 12
figure 12

Distribution of local stress perturbation at stress ratio of 2 at different normal stiffness values for (a) fracture density of P20 = 80 m−2, (b) fracture density of P20 = 160 m−2 and (c) fracture density of P20 = 320 m−2

Full size image
Fig. 13
figure 13

Distribution of local stress perturbation at stress ratio of 3 at different normal stiffness values for (a) fracture density of P20 = 80 m−2, (b) fracture density of P20 = 160 m−2 and (c) fracture density of P20 = 320 m−2

Full size image

Conclusion

The geometrical properties of fracture network and different rock and fracture parameters have a significant influence on the behavior of fractured rocks. In this study, these effects on stress distribution in a geological environment were investigated.

  1. 1.

    The fracture network with fracture density of 320 m−2, power length exponent of 1.5, at 30–10 tectonic stress loading and normal stiffness of 500 GPa/m (as the parameter that most critically affects the stress distribution), has the highest local stress perturbation compared to other fracture networks presented in this study.

  2. 2.

    As the stress ratio \({S}_{xx}^{\infty }/{S}_{yy}^{\infty }\) increases, the stress perturbation becomes more noticeable at the tip and intersection of fractures.

  3. 3.

    The mean distribution of local stress perturbation (md(S, S̅)) and effective variance (Ve) have a direct relationship with the increase in stress ratio and fracture density and an inverse relationship with increasing power-law length exponent (fracture length reduction).

  4. 4.

    Investigation of the effect of four different parameters of rock and fracture revealed that kn has a significant effect on stress distribution. The rock parameters, including CR and σtR, have minute effect on the variations of md(S, S̅) and Ve. Generally, with increasing kn, the values of md(S, S̅) and Ve are decreased.

  5. 5.

    To give an instance, in one of the studied cases (P20 = 320 m−2, a = 1.5 and SR = 3), with increasing kn value from 500 to 2000 GPa/m, md(S, S̅) and Ve were decreased from 11.5 to 8.2 MPa (28.69%) and from 30 to 12.1 MPa2 (59.66%), respectively. It can be stated that the difference in the decrease of Ve for kn = 500 GPa/m to kn = 1000 GPa/m is higher than kn = 1000 GPa/m to kn = 2000 GPa/m and the difference in values of Ve for ψF = 0° and ψF = 15° is observed to a certain extent at the highest fracture density studied (P20 = 320 m−2).