Characterising Clifford parallelisms among Clifford-like parallelisms

Abstract

We recall the notions of Clifford and Clifford-like parallelisms in a 3-dimensional projective double space. In a previous paper the authors proved that the linear part of the full automorphism group of a Clifford parallelism is the same for all Clifford-like parallelisms which can be associated to it. In this paper, instead, we study the action of such group on parallel classes thus achieving our main results on characterisation of the Clifford parallelisms among Clifford-like ones.

1 Introduction

It is a widely used strategy in mathematics to define a new structure by modifying a given one. The definition of a Clifford-like parallelism from Blunck et al. (2010) and Havlicek et al. (2019a), which is recalled in Sect. 2, follows these lines. The starting point is a projective double space $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$, that is, a projective space ${\mathbb P}$ together with a left parallelism $\mathrel {\parallel _{\ell }}$ and a right parallelism $\mathrel {\parallel _{r}}$ on its line set such that the so-called double space axiom (DS) is satisfied. The given parallelisms $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$ are called the Clifford parallelisms of $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ in analogy to the classical example arising from the three-dimensional elliptic space over the real numbers. The parallel classes of $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$ are then used to define parallelisms that are Clifford-like w.r.t. $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$. Among them are the initially given parallelisms $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$. We restrict ourselves most of the time to the case when ${\mathbb P}$ is three-dimensional, and we make use of an algebraic description of such a double space in terms of an appropriate four-dimensional algebra H over a commutative field F. Thereby we adopt the notation $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ and we have to distinguish two cases, (A) and (B). In case (A), H is a quaternion skew field with centre F, the left and right parallelisms do not coincide and, in general, there are Clifford-like parallelisms of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ different from $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$. In case (B), H is a commutative extension field of F satisfying some extra property, and ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$ is the only Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$. We include case (B) for the sake of completeness and in order to obtain a unified exposition that covers both cases, even though several of our results are trivial in case (B).

In Sect. 3 we study automorphisms of a Clifford-like parallelism of a projective double space $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ being motivated by the following result: if a projective collineation of ${\mathbb P}(H_F)$ preserves at least one Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$, then all its Clifford-like parallelisms are preserved.¹ This follows from (Havlicek 2019b, Thm. 3.5) in case (A) and holds trivially in case (B). In our algebraic setting these projective collineations are induced by F-linear transformations of H which are described in Sect. 3.1, where we determine all F-semilinear automorphisms of the right parallelism. In preparation for Sect. 4, we exhibit for a quaternion skew field H the orbits of certain points and lines of ${\mathbb P}(H_F)$ under the group of inner automorphisms of H and we determine all $\mathrel {\parallel _{r}}$-classes that are fixed under a left translation of H.

The main results are stated in Sect. 4. In Theorem 4.1, we consider a three-dimensional projective space ${\mathbb P}$ that is made into a double space in two ways. If there exists a parallelism $\parallel$ on ${\mathbb P}$ that is Clifford-like w.r.t. both double space structures then the given double spaces coincide up to a change of the attributes “left” and “right” in one of them. This finding improves (Havlicek et al. 2019a, Thm. 4.15) (see Corollary 4.2) and it simplifies matters considerably. Indeed, when dealing with a Clifford-like parallelism, there is only one corresponding double space structure in the background. In Theorems 4.3, 4.5 and 4.6 we characterise the Clifford parallelisms among the Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ via the existence of automorphisms with specific properties. For example, Theorem 4.3 establishes that a Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ is Clifford precisely when it admits an automorphism that fixes all its parallel classes and acts non-trivially on the point set of the projective space ${\mathbb P}(H_F)$.

Next, let us emphasise that some of our investigations are in continuity with classical results on dilatations in kinematic spaces. For example, in our proof of Theorem 4.3 we could use the fact that the existence of a proper non-trivial dilatation (namely a non-identical collineation with a fixed point and the property that all parallel classes remain invariant) is possible only in the commutative case, i.e. in our case (B) (see Marchi and Perelli Cippo 1980, Teorema 2 or Karzel and Maxson 1984, (II.10)). We decided instead to include a short direct proof in order to keep the paper self-contained. There are also neat connections to the theory of Sperner spaces and (generalised) translation structures; we refer the interested reader to Bader and Lunardon (2011); Seier (1971, 1973) and the many references given there.

Finally, another remark seems appropriate. Any Clifford-like parallelism on the three-dimensional real projective space is Clifford (see Remark 3.6). The Clifford parallelisms on this space are the only topological parallelisms that admit an automorphism group of dimension at least 4; see (Löwen 2019b) and the intimately related articles (Betten and Löwen 2017; Betten and Riesinger 2014; Löwen 2018, 2019a). In contrast to our considerations, in this beautiful result only the “size” of an automorphism group is taken into account and not its action on the parallel classes.

2 Preliminaries on Clifford and Clifford-like parallelisms

A parallelism $\parallel$ on a projective space ${\mathbb P}$ is an equivalence relation on the set ${\mathcal L}$ of lines such that each point of ${\mathbb P}$ is incident with precisely one line from each equivalence class. (If ${\mathbb P}$ is a finite projective space then a parallelism is also called a packing or a resolution.) For each line $M\in {\mathcal L}$ we write ${\mathcal S}(M)$ for the parallel class of M, that is, the equivalence class containing M. This notation arises quite naturally, since any parallel class is in fact a spread (of lines) of ${\mathbb P}$. When considering several parallelisms, we distinguish among the above notions and symbols by adding appropriate attributes, subscripts or superscripts. We refer to Betten et al. (2019), (Hirschfeld 1985, Ch. 17), Johnson (2003, 2010) and (Karzel and Kroll 1988, § 14) for a wealth of results about parallelisms and further references.

Let ${\mathbb P}$ and ${\mathbb P}'$ be projective spaces with parallelisms $\parallel$ and $\parallel '$, respectively and let $\kappa$ be a collineation of ${\mathbb P}$ to ${\mathbb P}'$ such that, for all lines $M,N\in {\mathcal L}$, $M\parallel N$ implies $\kappa (M)\parallel ' \kappa (N)$. Then $\kappa$ takes any $\parallel$-class to a $\parallel '$-class by (Havlicek 2019b, Lemma 2.1). Such a $\kappa$ is frequently called an isomorphism² of $({\mathbb P},\parallel )$ to $({\mathbb P}',\parallel ')$.

Suppose that a projective space ${\mathbb P}$ is endowed with two (not necessarily distinct) parallelisms, a left parallelism $\mathrel {\parallel _{\ell }}$ and a right parallelism $\mathrel {\parallel _{r}}$. Following (Karzel et al. 1973), $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ constitutes a projective double space if the following axiom is satisfied.

• (DS) For all triangles $p_0,p_1,p_2$ in ${\mathbb P}$ there exists a common point of the lines $M_1$ and $M_2$ that are defined as follows. $M_1$ is the line through $p_2$ that is left parallel to the join of $p_0$ and $p_1$, $M_2$ is the line through $p_1$ that is right parallel to the join of $p_0$ and $p_2$.

Given a projective double space $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ each of $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$ is referred to as a Clifford parallelism³ of $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$. More generally, a Clifford-like parallelism of $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ is defined as a parallelism $\parallel$ on ${\mathbb P}$ such that, for all $M,N\in {\mathcal L}$, $M\parallel N$ implies $M\mathrel {\parallel _{\ell }}N$ or $M\mathrel {\parallel _{r}}N$ (see Havlicek et al. 2019a, Def. 3.2). Each parallel class of a Clifford-like parallelism $\parallel$ of $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ is a left or a right parallel class: see (Havlicek et al. 2019a, Thm. 3.1), where this topic appears in the wider context of “blends” of parallelisms. A Clifford-like parallelism of $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ is said to be proper if it does not coincide with one of $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$. In what follows, whenever we say that a parallelism $\parallel$ on a projective space ${\mathbb P}$ is Clifford (respectively Clifford-like) it is intended that ${\mathbb P}$ can be made into a double space $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ such that $\parallel$ is one of its Clifford (respectively Clifford-like) parallelisms.

An algebraic description—up to isomorphism—of all projective double spaces $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$ that contain at least two distinct lines and satisfy the so-called “prism axiom” was given in Karzel et al. (1973). It is based on quaternion skew fields and purely inseparable commutative field extensions of characteristic two. According to (Karzel et al. 1974, Satz 1) and (Kroll 1975, Satz 2), the prism axiom appearing in Karzel et al. (1973) is redundant; see also the surveys in (Karzel and Kroll 1988, § 14) and (Johnson 2003, pp. 112–115). This is why we omit to consider this axiom here. From now on we exhibit exclusively three-dimensional projective double spaces.⁴ We therefore recall only their algebraic description in the next few paragraphs.

We adopt the following settings throughout this article: F denotes a commutative field and H is an F-algebra with unit $1_H$ satisfying one of the following conditions.

• (A) H is a quaternion skew field with centre $F1_H$.

• (B) H is a commutative field with degree $[H \mathbin {:} F1_H]=4$ and such that $h^2\in F1_H$ for all $h\in H$.

In what follows, we identify any $f\in F$ with $f1_H\in H$, whence F turns into a subfield of H. If E is a subfield of H, then H is a left vector space and a right vector space over E. We denote these spaces as ${}_E H$ and $H_E$, respectively. Whenever E is contained in the centre of H, we do not distinguish between $_E H$ and $H_E$. In each of the cases (A) and (B), $H_F$ is an infinite kinematic (or, in a different terminology: quadratic) F-algebra, i.e.,

$$\begin{aligned} h^2\in F + Fh \text{ for } \text{ all } h\in H . \end{aligned}$$

(1)

If (B) applies then the characteristic ${{\,\mathrm{Char}\,}}F$ equals two and H is a purely inseparable extension of F.

All F-linear endomorphisms of $H_F$ constitute the F-algebra ${{\,\mathrm{End}\,}}(H_F)$. The left regular representation $\lambda :H\rightarrow {{\,\mathrm{End}\,}}(H_F)$ sends each $h\in H$ to the mapping $\lambda (h)=:\lambda _h$ given as $\lambda _h(x):=hx$ for all $x\in H$. The image $\lambda (H)$ is an isomorphic copy of the field H within ${{\,\mathrm{End}\,}}(H_F)$. The elements of the multiplicative group⁵$\lambda (H^*)={{\,\mathrm{GL}\,}}(H_H)$ are the left translations. Similarly, the right regular representation $\rho :H\rightarrow {{\,\mathrm{End}\,}}(H_F)$ sends each $h\in H$ to $\rho (h)=:\rho _h$ given as $\rho _h(x):= xh$ for all $x\in H$. In this way we obtain $\rho (H)$ as an antiisomorphic copy of H within ${{\,\mathrm{End}\,}}(H_F)$ and the group of right translations⁶$\rho (H^*)={{\,\mathrm{GL}\,}}({}_HH)$. For all $g,h\in H$, the mappings $\lambda _g$ and $\rho _h$ commute. The multiplicative group $H^*$ admits the representation $\tilde{(\;\,)}:H^*\rightarrow {{\,\mathrm{GL}\,}}(H_F)$ sending each $h\in H^*$ to ${\tilde{h}}:=\lambda _h^{-1}\circ \rho _h$, which is an inner automorphism of the field H. Clearly, in case (B) the group $\widetilde{H^*}$ comprises only the identity ${{\,\mathrm{id}\,}}_H$.

The projective space on the vector space $H_F$, in symbols ${\mathbb P}(H_F)$, is understood to be the set of all subspaces of $H_F$ with incidence being symmetrised inclusion. We adopt the usual geometric terms: Points, lines, and planes of ${\mathbb P}(H_F)$ are the subspaces of $H_F$ with vector dimension one, two, and three, respectively; the set of all lines is written as ${\mathcal L}(H_F)$. The following notions rely on $H_F$ being an F-algebra. In ${\mathbb P}(H_F)$, lines M and N are defined to be left parallel, $M\mathrel {\parallel _{\ell }}N$, if $\lambda _c(M)=N$ for some $c\in H^*$. Similarly, M and N are said to be right parallel, $M\mathrel {\parallel _{r}}N$, if $\rho _c(M)=N$ for some $c\in H^*$. Then $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ is a projective double space. The parallelisms $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$ are distinct in case (A) and identical in case (B).

Remark 2.1

The left and right parallelism w.r.t. $(H,+,\cdot )$ are the same as the right and left parallelism defined by the opposite field of H. So, from a geometric point of view, the choice of the attributes “left” and “right” is immaterial.

The multiplication on the field $(H,+,\cdot )$ may be altered without changing the associated projective double space $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$. Let us choose any $e\in H^*$. Then we can define a multiplication $\cdot ^e$ on H via $x\cdot ^e y := x\cdot e^{-1}\cdot y$ for all $x,y\in H$. This makes $(H,+,\cdot ^e)$ into an F-algebra, which will briefly be written as $H^e$. The left translation $\lambda _e$ (w.r.t. H) is an F-linear isomorphism of H to $H^e$, whence the arbitrarily chosen element $e\in H^*$ turns out to be the unit element of $H^e$. The projective double spaces arising from the F-algebras H and $H^e$ are the same, since $\lambda _{h}=\lambda ^e_{h\cdot e}$ and $\rho _{h}=\rho ^e_{e\cdot h}$ for all $h\in H^*$.

Let us briefly sketch a more conceptual verification of our second observation. The point Fe and the parallelisms $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$ can be used to make the point set ${\mathbb P}(H_F)$ into a two-sided incidence group with unit element Fe (Karzel et al. 1973, §3). (The prism axiom appearing in Karzel et al. (1973) can be avoided (Karzel et al. 1974, Satz 1), (Kroll 1975, Satz 2).) Then, using the group structure on ${\mathbb P}(H_F)$, the F-vector space H can be endowed with a multiplication making it into a field with unit element e (see Ellers and Karzel 1963, Satz 1 and Wähling 1967, Hauptsatz). This field, which coincides with our $H^e$, therefore provides an alternative description of the projective double space $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$.

Remark 2.2

There are various other ways to define a Clifford parallelism on a three-dimensional (necessarily pappian) projective space. We refer to (Betten and Riesinger 2012; Blunck et al. 2010), (Havlicek 1995, p. 46), (Havlicek 1997, Sect. 2), Havlicek (2015, 2016) and the references given there. On that account, it is our aim to make use only of the above algebraic approach.

Let ${\mathcal A}(H_F)\subset {\mathcal L}(H_F)$ denote the star of lines with centre F1. By (1), each line $L\in {\mathcal A}(H_F)$ is readily seen to be a maximal commutative subfield of H and hence an F-subalgebra. Next, we recall an explicit construction that gives all Clifford-like parallelisms of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$. Upon choosing any $\widetilde{H^*}$-invariant subset ${\mathcal F}\subseteq {\mathcal A}(H_F)$, one obtains a partition of ${\mathcal L}(H_F)$ by taking the left parallel classes of all lines in $\mathcal F$ and the right parallel classes of all lines in ${\mathcal A}(H_F)\setminus {\mathcal F}$. This partition determines an equivalence relation, which turns out to be a Clifford-like parallelism $\parallel$ of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$. See (Havlicek et al. 2019a, Thm. 4.10) for a proof in the case when (A) applies; in case (B) the result is trivial due to ${\parallel }={\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$.

Remark 2.3

Let $\parallel$ be any parallelism on ${\mathbb P}(H_F)$ and let ${\mathcal S}(M)$, $M\in {\mathcal L}(H_F)$, be one of its parallel classes. We recall that the kernel of the spread ${\mathcal S}(M)$ consists of all endomorphisms $\varphi$ of the abelian group $(H,+)$ such that $\varphi (N)\subseteq N$ for all $N\in {\mathcal S}(M)$. This kernel, which will be denoted by ${{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}(M)\bigr )$, is a field; see, for example, (Lüneburg 1980, Thm. 1.6). Consequently, if $\varphi \in {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}(M)\bigr )$ and $\varphi \ne 0$, then $\varphi (N)=N$ for all $N\in {\mathcal S}(M)$. The following simple reasoning will repeatedly be used. If $\varphi _1,\varphi _2\in {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}(M)\bigr )$ satisfy $\varphi _1(g)=\varphi _2(g)$ for some $g\in H^*$, then $(\varphi _1-\varphi _2)(g)=0$ forces that $\varphi _1-\varphi _2$ is not injective. Therefore $\varphi _1-\varphi _2$ is the zero endomorphism or, in other words, $\varphi _1=\varphi _2$.

Proposition 2.4

If Clifford parallelisms $\parallel$ and $\parallel '$ on a three-dimensional projective space have two distinct parallel classes in common, then these parallelisms coincide.

Proof

By virtue of the algebraic description of all projective double spaces and by Remark 2.1, we may assume the following. The parallelism $\parallel$ is the right parallelism $\mathrel {\parallel _{r}}$ coming from an F-algebra $(H,+,\cdot )$ subject to (A) or (B). There is a multiplication ${\cdot '}:H\times H\rightarrow H$ making the F-vector space $H_F$ into an F-algebra $(H,+,\cdot ')$ subject to (A) or (B) such that $\parallel '$ coincides with the right parallelism $\mathrel {\parallel _{r}'}$ arising from $(H,+,\cdot ')$. These algebras share a common unit element $1\in H^*$, say.

By our assumption, there are distinct lines $L_1,L_2\in {\mathcal A}(H_F)$ such that ${\mathcal S}_{r}(L_1)={\mathcal S}_{r}'(L_1)$ and ${\mathcal S}_{r}(L_2)={\mathcal S}_{r}'(L_2)$. Choose any $z\in L_{n}$ where $n\in \{1,2\}$. Then $\lambda _z$ and $\lambda _z'$ are both in ${{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(L_{n})\bigr )$. According to Remark 2.3, $\lambda _z(1)=z=\lambda _z'(1)$ implies $\lambda _z=\lambda _z'$. Hence

$$\begin{aligned} z\cdot x = \lambda _z(x)=\lambda _z'(x) = z \cdot ' x \text{ for } \text{ all } x\in H \text{ and } \text{ all } z\in L_1\cup L_2 . \end{aligned}$$

(2)

More generally, the equality in (2) is fulfilled for all $x\in H$ and all z from the subfield of $(H,+,\cdot )$ that is generated by $L_1\cup L_2$. This subfield coincides with $(H,+,\cdot )$, since $L_1$ is a maximal subfield of $(H,+,\cdot )$. All things considered, we obtain $(H,+,\cdot )=(H,+,\cdot ')$ and therefore ${\parallel } = {\mathrel {\parallel _{r}}} = {\mathrel {\parallel _{r}'}} = {\parallel '}$. $\square$

Remark 2.5

Note that the above theorem may alternatively be established by using the one-to-one correspondence between Clifford parallelisms and external planes to the Klein quadric (see Havlicek 2016, Cor. 4.5).

3 Automorphisms, their orbits and actions

This section is devoted to deepen the study of the automorphisms of the Clifford parallelisms of a three-dimensional projective double space $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ as described in Sect. 2. In particular we obtain a description of the orbits of certain points and lines under the action of the group $\widetilde{H^*}$, and we characterise the right parallel classes fixed (as a set) by a given left translation. In order to avoid trivialities, we shall repeatedly confine ourselves to case (A). These findings will lead us in Sect. 4 to the proof of our main results.

3.1 Automorphisms

In this subsection H always denotes an F-algebra subject to (A) or (B). Given any parallelism $\parallel$ on ${\mathbb P}(H_F)$, we are going to use from now on the phrase automorphism of $\parallel$ for any $\beta$ in the general semilinear group $\Gamma \hbox {L} (H_F)$ that acts as a $\parallel$-preserving collineation on ${\mathbb P}(H_F)$. The symbol $\Gamma _\parallel$ denotes the automorphism group of $\parallel$. This terminology is in accordance with the one in Havlicek (2019b).

The Clifford parallelisms of the projective double space $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ give rise to automorphism groups $\Gamma _{\mathrel {\parallel _{\ell }}}=:\Gamma _{\ell }$ and $\Gamma _{\mathrel {\parallel _{r}}}=:\Gamma _{r}$. These groups coincide, that is,

$$\begin{aligned} \Gamma _{\ell }=\Gamma _{r}. \end{aligned}$$

(3)

In case (A), a proof can be derived from (Pianta 1987, p. 166); see (Havlicek 2019b, Sect. 2) for further details. In case (B), equation (3) is trivial. The group $\lambda (H^*)$ of left translations, the group $\rho (H^*)$ of right translations and the group $\widetilde{H^*}$ of inner automorphisms are subgroups of $\Gamma _{\ell }=\Gamma _{r}$.

Lemma 3.1

Let ${\mathcal S}_{r}(M)$ be the right parallel class of a line $M\in {\mathcal L}(H_F)$. The elements of the kernel ${{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(M)\bigr )$ are precisely the mappings $\lambda _g$ with g ranging in the line that contains the point F1 and is right parallel to M. Consequently,

$$\begin{aligned} \lambda (H) = \bigcup _{L\,\in \,{\mathcal A}(H_F)} {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(L)\bigr ) = \bigcup _{M\,\in \,{\mathcal L}(H_F)} {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(M)\bigr ) . \end{aligned}$$

(4)

A similar result holds with the role of “left” and “right” interchanged.

Proof

There is a $d\in H^*$ such that $F1\subseteq \rho _d(M)=Md$. Choose any $g\in Md$. Then, for all $h\in H^*$, $\lambda _g(Mdh)=g(Mdh)=(gMd)h\subseteq Mdh$, whence $\lambda _g\in {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(M)\bigr )$. Conversely, let $\varphi \in {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(M)\bigr )$. Then $\varphi (1)\in Md$ gives $\lambda _{\varphi (1)}\in {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(M)\bigr )$, and $\varphi (1)=\lambda _{\varphi (1)}(1)$ implies $\varphi =\lambda _{\varphi (1)}$ according to Remark 2.3.

Equation (4) is now immediate, since each element of H is contained in at least one line of the star ${\mathcal A}(H_F)$ and each right parallel class contains a line passing through F1. $\square$

Any line $L\in {\mathcal A}(H_F)$ is a commutative quadratic extension field of F contained in H. The above Lemma illustrates the rather obvious result that the restriction to L of the representation $\lambda$ (respectively $\rho$) provides an isomorphism of the field L onto the kernel of the right (respectively left) parallel class of the line L. This proves anew that all left and right parallel classes are regular spreads (see Blunck et al. 2010, 4.8 Cor., Havlicek 2015, Prop. 3.5 or Havlicek 2016, Prop. 4.3). Maybe less obvious is the following conclusion. Any semilinear transformation $\varphi \in \Gamma \hbox {L}(H_F)$ that fixes all lines of one right (respectively left) parallel class is a left (respectively right) translation and therefore in the automorphism group $\Gamma _{\ell }=\Gamma _{r}$.

In the next proposition we describe the automorphism group $\Gamma _{\ell }= \Gamma _{r}$. Alternative proofs, which cover only the case when H is a quaternion skew field, can be retrieved from (Blunck et al. 2018, Sect. 4), (Pianta 1987, Thm. 1) and (Pianta and Zizioli 1990, Prop. 4.1 and 4.2). Below, we follow the exposition in (Havlicek 2019b, Sect. 2).

Proposition 3.2

Let $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ be a projective double space, where H is an F-algebra subject to (A) or (B). The automorphism group of the right parallelism satisfies

$$\begin{aligned} \Gamma _{r}= \lambda (H^*)\rtimes {{\,\mathrm{Aut}\,}}(H/F), \end{aligned}$$

(5)

where ${{\,\mathrm{Aut}\,}}(H/F)$ denotes the group of all automorphisms of the field H that fix F as a set.

Proof

A direct verification shows that the group ${{\,\mathrm{Aut}\,}}(H/F)$ is a subgroup of $\Gamma _{r}$. As we noted at the beginning of this subsection, the same applies for the group $\lambda (H^*)$. For all $\gamma \in \Gamma _{r}$ and all lines $M\in {\mathcal L}(H_F)$, we have

$$\begin{aligned} {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(\gamma (M))\bigr ) =\gamma \circ {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(M)\bigr )\circ \gamma ^{-1} . \end{aligned}$$

(6)

Using (4), this implies that $\lambda (H^*)$ is a normal subgroup of $\Gamma _{r}$.

Let us choose any $\beta \in \Gamma _{r}$. We define $\varphi :=\lambda _{\beta (1)}^{-1}\circ \beta$, whence $\varphi \in \Gamma _{r}$ fixes $1\in H$. In order to verify

$$\begin{aligned} \varphi \circ \lambda _z\circ \varphi ^{-1} = \lambda _{\varphi (z)} \text{ for } \text{ all } z\in H, \end{aligned}$$

(7)

we proceed as follows. There is a line L with $1,z\in L$. Applying (6) to $\gamma :=\varphi$ and $M:=L$ gives that $\varphi \circ \lambda _z\circ \varphi ^{-1}$ as well as $\lambda _{\varphi (z)}$ belongs to ${{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(\varphi (L))\bigr )$. Now $(\varphi \circ \lambda _z\circ \varphi ^{-1})(1)=\lambda _{\varphi (z)}(1)$ together with Remark 2.3 establishes (7). For all $x,y\in H$, we have

$$\begin{aligned} \begin{aligned} \varphi (xy)&= (\varphi \circ \lambda _x\circ \lambda _y)(1)\\&= \bigl ((\varphi \circ \lambda _x\circ \varphi ^{-1}) \circ (\varphi \circ \lambda _y\circ \varphi ^{-1})\bigr )(1)\\&= (\lambda _{\varphi (x)}\circ \lambda _{\varphi (y)})(1)\\&= \varphi (x)\varphi (y)\\ \end{aligned} \end{aligned}$$

so that $\varphi$ is an automorphism of the field H. Furthermore, $\varphi (1)=1$ together with $\varphi$ being F-semilinear implies $\varphi (F)=F$. $\square$

Take notice that F is the centre of the quaternion skew field H in case (A) and so under these circumstances ${{\,\mathrm{Aut}\,}}(H/F)={{\,\mathrm{Aut}\,}}(H)$.

Suppose that $\varphi \in {{\,\mathrm{Aut}\,}}(H/F)$ is F-linear or, equivalently, that $\varphi$ fixes F elementwise. Then $\varphi \in \widetilde{H^*}$ is an inner automorphism of the field H. In case (A), this follows from the theorem of Skolem-Noether (Jacobson 1989, Thm. 4.9). In case (B), any inner automorphism of H is trivial and $\varphi ={{\,\mathrm{id}\,}}_H$, since any $h\in H^*\setminus F^*$ is a double zero of the polynomial $h^2+t^2\in F[t]$, which is the minimal polynomial of h over F. So, by (5), the group of all F-linear automorphisms of $\mathrel {\parallel _{r}}$ can be written in the form

$$\begin{aligned} \Gamma _{r}\cap {{\,\mathrm{GL}\,}}(H_F) = \lambda (H^*) \rtimes \widetilde{H^*} . \end{aligned}$$

(8)

Let $\parallel$ be any Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$. The group appearing in (8) coincides with the group $\Gamma _\parallel \cap {{\,\mathrm{GL}\,}}(H_F)$ comprising all F-linear automorphisms of $\parallel$ (see Havlicek 2019b, Thm. 3.5). The problem to determine the full automorphism group $\Gamma _\parallel$ without extra assumptions on H, F or $\parallel$ seems to be open. Partial solutions can be found (Havlicek 2019b, Sect. 3). The examples in (Havlicek 2019b, Sect. 4) show the existence of proper Clifford-like parallelisms $\parallel$ satisfying $\Gamma _\parallel =\Gamma _{\ell }=\Gamma _{r}$ and also of proper Clifford-like parallelisms $\parallel$ satisfying $\Gamma _\parallel \subset \Gamma _{\ell }=\Gamma _{r}$.

3.2 Orbits under the group of inner automorphisms

In this subsection H denotes an F-algebra subject to (A), that is, a quaternion skew field with centre F. The following outcomes fail in case (B), since there the group of inner automorphisms is trivial.

Recall that, given any $h\in H$, the trace and the norm of h are the elements of F defined, respectively, by ${{\,\mathrm{tr}\,}}(h)=h+{\overline{h}}$ and $N(h)=h{\overline{h}}={\overline{h}}h$, where ${\overline{h}}$ denotes the conjugate of h. The conjugation is an antiautomorphism of H of order 2 that fixes F elementwise. The identity $h^2-{{\,\mathrm{tr}\,}}(h)h+N(h)=0$ holds for any $h\in H$. The norm N is a multiplicative quadratic form and its associated symmetric bilinear form is

$$\begin{aligned} \langle \,\cdot \,,\cdot \,\rangle :H\times H\rightarrow F:(x,y)\mapsto \langle x,y\rangle ={{\,\mathrm{tr}\,}}(x{\overline{y}})=x{\overline{y}}+y{\overline{x}} . \end{aligned}$$

(9)

The form $\langle \,\cdot \,,\cdot \,\rangle$ is non-degenerate and so the mapping sending each subspace X of $H_F$ to its orthogonal subspace $X^\perp$ is a polarity of ${\mathbb P}(H_F)$.

The next result is briefly mentioned in (Blunck et al. 2010, Rem. 4.5) and (Lam 2005, p. 76, Ex. 10) (${{\,\mathrm{Char}\,}}F\ne 2$ only). For the sake of completeness, a proof will be presented below.

Lemma 3.3

Given quaternions $q_1,q_2\in H$ there exists an inner automorphism of H taking $q_1$ to $q_2$ if, and only if, ${{\,\mathrm{tr}\,}}(q_1)={{\,\mathrm{tr}\,}}(q_2)$ and $N(q_1)=N(q_2)$.

Proof

From ${{\,\mathrm{tr}\,}}(q_1)={{\,\mathrm{tr}\,}}(q_2)$ and $N(q_1)=N(q_2)$, the quaternions $q_1,q_2$ are zeros of the polynomial $m(t)=t^2-{{\,\mathrm{tr}\,}}(q_1)t+N(q_1)\in F[t]$. If m(t) is reducible over F, then m(t) has no zeros in H outside F. Thus $q_1\in F$ and $m(t)=(t-q_1)^2$. Now $m(q_2)=0$ yields $q_2=q_1$, whence the identity ${{\,\mathrm{id}\,}}_H$ is a solution. On the other hand, if m(t) is irreducible over F, then ${{\,\mathrm{id}\,}}_F$ can be extended in a unique way to an isomorphism $\gamma$ of the commutative field $F1\oplus Fq_1\subset H$ onto the commutative field $F1\oplus Fq_2\subset H$ such that $\gamma (q_1)=q_2$; see, for example, (Cohn 2003, Prop. 7.2.2). By the theorem of Skolem-Noether (Jacobson 1989, Thm. 4.9), this $\gamma$ extends to an inner automorphism of H.

The proof of the converse is straightforward. $\square$

The above result describes the orbits under the action of the inner automorphism group $\widetilde{H^*}$ on quaternions.⁷ By considering the vector space $H_F$ as an affine space, the orbit of any $q\in H$ is the intersection of the affine quadric $\{x\in H\mid N(x)=N(q)\}$ with the hyperplane $\{x\in H\mid {{\,\mathrm{tr}\,}}(x)={{\,\mathrm{tr}\,}}(q)\}$. Here, however, we aim at providing a description of the orbits of the points of ${\mathbb P}(H_F)$ under the action of $\widetilde{H^*}$. Since the behaviour of the points of the plane $(F1)^\perp =\{x\in H\mid {{\,\mathrm{tr}\,}}(x)=0\}$ is different from that of any other point, these points will be excluded in the next proposition.

Proposition 3.4

Let H be a quaternion skew field with centre F and let Fq, $q\in H^*$, be a point of ${\mathbb P}(H_F)$ such that ${{\,\mathrm{tr}\,}}(q)\ne 0$. Then the following hold.

• (a) The orbit of Fq under the action of the group $\widetilde{H^*}$ of inner automorphisms of H is a quadric of ${\mathbb P}(H_F)$, say ${\mathcal O}_q$, which is given by the quadratic form

  $$\begin{aligned} \omega _q:H\rightarrow F:x\mapsto {{\,\mathrm{tr}\,}}(q)^2\,N(x)- N(q)\,{{\,\mathrm{tr}\,}}(x)^2 . \end{aligned}$$

• (b) If $q\in F^*$, then ${\mathcal O}_q$ consists of a single point.

• (c) If $q\in H^*\setminus F^*$, then ${\mathcal O}_q$ is an elliptic quadric, no line through F1 is tangent to ${\mathcal O}_q$, and the polar form of $\omega _q$ is non-degenerate.

Proof

(a) If Fp is in the $\widetilde{H^*}$-orbit of Fq, then there are $c\in F^*$ and $h\in H^*$ such that $p= c h^{-1}qh$. Consequently, $N(p)=c^2 N(q)$ and ${{\,\mathrm{tr}\,}}(p)=c{{\,\mathrm{tr}\,}}(q)$. This entails $\omega _q(p)=c^2\omega _q(q)=0$.

Conversely, let a point $Fp'$, $p'\in H^*$, be given with $\omega _q(p')=0$. Then $p'\ne 0$ implies $N(p')\ne 0$ and so ${{\,\mathrm{tr}\,}}(p')\ne 0$ follows from $\omega _q(p')=0$. We define

$$\begin{aligned} p:={{\,\mathrm{tr}\,}}(q){{\,\mathrm{tr}\,}}(p')^{-1}p' . \end{aligned}$$

Then ${{\,\mathrm{tr}\,}}(p)={{\,\mathrm{tr}\,}}(q)\ne 0$, and $\omega _q(p)=0$ establishes $N(p)=N(q)$. Now Lemma 3.3 implies the existence of an $h\in H^*$ such that $p=h^{-1}qh$.

(b) The quadric ${\mathcal O}_q$, $q\in F^*$, is the $\widetilde{H^*}$-orbit of F1, whence it consists of this single point only.

(c) The point F1 is not in the $\widetilde{H^*}$-orbit of Fq and so F1 is off the quadric ${\mathcal O}_q$. From $q+{\overline{q}} = {{\,\mathrm{tr}\,}}(q)\in F^*$ and $\omega _q({\overline{q}})=0$, the line joining Fq and F1 meets ${\mathcal O}_q$ residually at $F{\overline{q}}\ne Fq$ and so it is not tangent to ${\mathcal O}_q$. Also, the point Fq is a regular point of ${\mathcal O}_q$. By the transitive action of the group $\widetilde{H^*}$ on the points of ${\mathcal O}_q$, the same applies to all other points of ${\mathcal O}_q$. The quadric ${\mathcal O}_q$ cannot be ruled, because it does not contain any point of the plane $\{x\in H\mid {{\,\mathrm{tr}\,}}(x)=0\}$.

The polar form of $\omega _q$ is

$$\begin{aligned} (x,y)\mapsto {{\,\mathrm{tr}\,}}(q)^2\langle x,y\rangle - 2 N(q){{\,\mathrm{tr}\,}}(x){{\,\mathrm{tr}\,}}(y) = {{\,\mathrm{tr}\,}}(q)^2{{\,\mathrm{tr}\,}}(x{\overline{y}}) -2N(q){{\,\mathrm{tr}\,}}(x){{\,\mathrm{tr}\,}}(y) . \end{aligned}$$

If Char $F\ne 2$ then the polar form of $\omega _q$ is non-degenerate, since otherwise ${\mathcal O}_q$ would contain a singular point. In the case of ${{\,\mathrm{Char}\,}}F=2$ the form $\omega _q$ is non-degenerate, because it merely is a non-zero scalar multiple of the non-degenerate alternating bilinear form $\langle \,\cdot \,,\cdot \,\rangle$ from (9). $\square$

Proposition 3.5

Let H be a quaternion skew field with centre F and, in ${\mathbb P}(H_F)$, let L be a line that passes through the point F1 and is not contained in the plane $(F1)^\perp$. Every plane through an arbitrary line in the $\widetilde{H^*}$-orbit of L contains infinitely many lines of this orbit.

Proof

By virtue of the action of $\widetilde{H^*}$ on $\widetilde{H^*}(L)$, it is enough to show the assertion for an arbitrary plane E passing through L.

On the line L, we can pick one point, say Fq, other than F1 such that ${{\,\mathrm{tr}\,}}(q)\ne 0$. By Proposition 3.4, the orbit of Fq is an elliptic quadric ${\mathcal O}_q$. Furthermore, the line L is a bisecant of this quadric that meets ${\mathcal O}_q$ at Fq and $F{\overline{q}}\ne Fq$. The plane E contains the bisecant L of ${\mathcal O}_q$ and so E cannot be a tangent plane of ${\mathcal O}_q$. This implies that E intersects ${\mathcal O}_q$ along a regular conic. As F is infinite, so is this conic. By joining each of the points of the conic with F1 we get infinitely many lines through F1 in the plane E. All of them are in $\widetilde{H^*}(L)$. $\square$

Remark 3.6

The orbit of any line $L\in {\mathcal A}(H_F)$ under the group $\widetilde{H^*}$ is infinite (Faith 1958, Thm. 3). This result was improved in Wähling (1981) by showing that any such orbit has cardinality |F|. Limited to the case of quaternion skew fields and lines of ${\mathcal A}(H_F)$ that are not in $(F1)^\perp$, the last proposition enriches this result with a geometric insight.

From (Havlicek et al. 2019a, Thm. 4.12), the group $\widetilde{H^*}$ acts transitively on ${\mathcal A}(H_F)$ if, and only if, F is a formally real pythagorean field and H is an “ordinary” quaternion skew field with centre F. Precisely under these circumstances, $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ admits no proper Clifford-like parallelisms.

3.3 Parallel classes fixed by automorphisms

First, let $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ be a projective double space as specified in Sect. 2. Suppose that a left translation $\lambda _g$, $g\in H^*$, acts as a non-identical collineation on ${\mathbb P}(H_F)$. Hence $g\in H^*\setminus F^*$. Any line $M\in {\mathcal L}(H_F)$ is left parallel to its image $\lambda _g(M)$ and so $\lambda _g$ fixes all left parallel classes. As we saw in Lemma 3.1, ${\mathcal S}_{r}(F1\oplus Fg)$ is the only right parallel class that is fixed linewise under $\lambda _g$. If $\lambda _g$ fixes also all lines of a left parallel class, then Lemma 3.1 forces $\lambda _g$ to be a right translation as well, that is, g has to be in the centre of H. In case (A) this gives a contradiction. In case (B), H is a commutative field and so this condition imposes no restriction on g; due to ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$, the given $\lambda _g$ fixes precisely one left parallel class linewise, namely ${\mathcal S}_{\ell }(F1\oplus Fg)$.

For the rest of this subsection we confine ourselves to the case (A).

Proposition 3.7

Let H be a quaternion skew field with centre F and let $g\in H^*\setminus F^*$. In $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$, a right parallel class is invariant under the left translation $\lambda _g$ precisely when it is of the form ${\mathcal S}_{r}(M)$, where M is a line satisfying at least one of the following conditions:

$$\begin{aligned} M= & {} F1\oplus Fg ; \end{aligned}$$

(10)

$$\begin{aligned} F1\subseteq & {} M \subseteq g^{-1}(F1)^\perp . \end{aligned}$$

(11)

Fig. 1

${{\,\mathrm{Char}\,}}F\ne 2$

Proof

(a) Suppose that (10) holds. From Lemma 3.1, all lines of the right parallel class ${\mathcal S}_{r}(M)$ are fixed under $\lambda _g$.

(b) Suppose that a line M satisfies (11). The line $M^\perp$ is left parallel and right parallel to M (see Havlicek et al. 2019a, Cor. 4.4) and it is contained in $(F1)^\perp$. The line gM is also left parallel to M. As $M^\perp$ and gM are incident with the plane $(F1)^\perp$, they share a common point and so they must coincide. Taking into account that $\lambda _g\in \Gamma _{r}$ and $M^\perp \mathrel {\parallel _{r}}M$ we obtain $\lambda _g\bigl ({\mathcal S}_{r}(M)\bigr )={\mathcal S}_{r}(gM)={\mathcal S}_{r}(M^\perp )={\mathcal S}_{r}(M)$, as required.

(c) Conversely, any $\lambda _g$-invariant right parallel class can be written as ${\mathcal S}_{r}(M)$ with $F1\subseteq M$. Then $\lambda _g(M)\mathrel {\parallel _{\ell }}M \mathrel {\parallel _{r}}\lambda _g(M)$. Again from (Havlicek et al. 2019a, Cor. 4.4), there are only two possibilities. First, $\lambda _g(M)=gM=M$, which implies $Fg\subseteq M$ and establishes (10). Second, $\lambda _g(M)=gM=M^\perp$. From $F1\subseteq M$ we obtain $\lambda _g(M) = M^\perp \subseteq (F1)^\perp$. Applying $\lambda _g^{-1}$ results in $M\subseteq g^{-1}(F1)^\perp$, whence (11) holds. $\square$

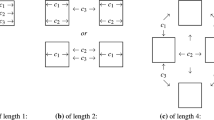
Remark 3.8

Figures 1 and 2 depict the possible cases in Proposition 3.7 under the assumption ${{\,\mathrm{Char}\,}}F\ne 2$ and ${{\,\mathrm{Char}\,}}F = 2$, respectively. In all cases, there are distinct points F1 and Fg as well as distinct planes $(F1)^\perp$ and $g^{-1}(F1)^\perp$. Furthermore, $(F1)^\perp \cap \bigl (g^{-1}(F1)^\perp \bigr ) = (F1\oplus Fg)^\perp$.

The pictures on the left-hand side show the situation when $F1\not \subseteq g^{-1}(F1)^\perp$ or, in other words, when $Fg\not \subseteq (F1)^\perp$, which in turn is equivalent to ${{\,\mathrm{tr}\,}}(g)\ne 0$. Here there are no lines M subject to (11). The pictures on the right-hand side show the opposite situation. Here the set of all lines M that satisfy (11) comprises a pencil of lines. In detail, the circumstances are as follows.

Figure 1, left: the line $F1\oplus Fg$ intersects the plane $(F1)^\perp$ at $F(g-{\overline{g}})$ and the plane $g^{-1}(F1)^\perp$ at $Fg'$, $g':=g^{-1}(g-{\overline{g}})$; the points F1, Fg, $F(g-{\overline{g}})$ and $Fg'$ are mutually distinct; the lines $F1\oplus Fg$ and $(F1\oplus Fg)^\perp$ are skew.

Figure 1, right: $(F1\oplus Fg)\cap (F1)^\perp = Fg$, $(F1\oplus Fg)\cap {g^{-1}(F1)^\perp } = F1$; the lines $F1\oplus Fg$ and $(F1\oplus Fg)^\perp$ are skew.

Fig. 2

${{\,\mathrm{Char}\,}}F= 2$

Figure 2, left: $(F1\oplus Fg) \cap (F1)^\perp = F1$, $(F1\oplus Fg) \cap g^{-1}(F1)^\perp = Fg^{-1}$; the points F1, Fg and $Fg^{-1}$ are mutually distinct; the lines $F1\oplus Fg$ and $(F1\oplus Fg)^\perp$ are skew.

Figure 2, right: the line $F1\oplus Fg$ coincides with $(F1\oplus Fg)^\perp$.

Finally, note that the situations depicted on the right-hand side, namely $Fg\subseteq (F1)^\perp$, comprises precisely the cases when the left translation $\lambda _g$ acts as an involution on the projective space.

4 Main results

The definition of a Clifford-like parallelism in (Havlicek et al. 2019a, Def. 3.2) is essentially based on a given projective double space $({\mathbb P},{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}})$. We are thus led to the problem of whether or not distinct projective double spaces can share a Clifford-like parallelism.

Theorem 4.1

Let $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ be a projective double space, where H is an F-algebra subject to (A) or (B). Furthermore, let $\mathrel {\parallel _{\ell }'}$ and $\mathrel {\parallel _{r}'}$ be parallelisms such that $\bigl ({\mathbb P}(H_F),\mathrel {\parallel _{\ell }'},\mathrel {\parallel _{r}'}\bigr )$ is also a projective double space. Suppose that a parallelism $\parallel$ of ${\mathbb P}(H_F)$ is Clifford-like with respect to both double space structures. Then, possibly up to a change of the attributes “left” and “right” in one of these double spaces, ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{\ell }'}}$ and ${\mathrel {\parallel _{r}}}={\mathrel {\parallel _{r}'}}$.

Proof

First, we consider case (A). We take any line of the star ${\mathcal A}(H_F)$. We noted in Remark 3.6 that the orbit of this line under the group $\widetilde{H^*}$ of all inner automorphisms of H is infinite. Thus there are three mutually distinct lines, say $L_1$, $L_2$ and $L_3$, in this orbit. From (Havlicek et al. 2019a, Thm. 4.10), the $\parallel$-classes of these lines are of the same kind w.r.t. $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$, i.e., we have either ${\mathcal S}(L_{n})={\mathcal S}_{\ell }(L_{n})$ for all $n\in \{1,2,3\}$ or ${\mathcal S}(L_{n})={\mathcal S}_{r}(L_{n})$ for all $n\in \{1,2,3\}$.

Next, we turn to case (B). There exist three mutually distinct lines $L_1, L_2,L_3\in {\mathcal A}(H_F)$. Their $\parallel$-classes are of the same kind w.r.t. $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ due to ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}={\parallel }$.

In both cases, the parallel classes ${\mathcal S}(L_n)$, $n\in \{1,2,3\}$, are mutually distinct. Consequently, among them there are at least two distinct classes of the same kind w.r.t. the double space $({\mathbb P}(H_F),\mathrel {\parallel _{\ell }'},\mathrel {\parallel _{r}'})$. Up to a change of notation, we may assume ${\mathcal S}(L_n)={\mathcal S}_{r}(L_n)={\mathcal S}_{r}'(L_n)$ for $n\in \{1,2\}$. Now Proposition 2.4 shows that the Clifford parallelisms $\mathrel {\parallel _{r}}$ and $\mathrel {\parallel _{r}'}$ coincide. This in turn forces ${\mathrel {\parallel _{\ell }}} = {\mathrel {\parallel _{\ell }'}}$, since the left parallelism is uniquely determined by the right one (see Karzel and Kroll 1988, pp. 75–76 or Herzer 1977, §6). $\square$

Corollary 4.2

Any Clifford-like parallelism $\parallel$ of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ other than $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$ is not Clifford.

Proof

Assume to the contrary that ${\parallel }=:{\mathrel {\parallel _{\ell }'}}$ is Clifford. Then there is a parallelism, say $\mathrel {\parallel _{r}'}$, such that $\bigl ({\mathbb P}(H_F),\mathrel {\parallel _{\ell }'},\mathrel {\parallel _{r}'}\bigr )$ is a projective double space. Applying Theorem 4.1 gives therefore ${\parallel }={\mathrel {\parallel _{\ell }}}$ or ${\parallel }={\mathrel {\parallel _{r}}}$, a contradiction. $\square$

The above corollary, when restricted to case (A), is just a reformulation of (Havlicek et al. 2019a, Thm. 4.15). Therefore, the rather technical proof in Havlicek et al. (2019a), which relies on H being a quaternion skew field, can now be avoided.

Our final results provide the announced characterisations of Clifford parallelisms among Clifford-like parallelisms.

Theorem 4.3

Let $\parallel$ be a Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$, where H is an F-algebra subject to (A) or (B). Then the following assertions are equivalent.

• (a) The parallelism $\parallel$ is Clifford.

• (b) The parallelism $\parallel$ admits an automorphism $\beta \in \Gamma _\parallel$ that stabilises all its parallel classes and acts as a non-identical collineation on the projective space ${\mathbb P}(H_F)$.

Proof

(a) $\Rightarrow$ (b). There exists a $g\in H^*\setminus F^*$. Corollary 4.2 shows that ${\parallel } = {\mathrel {\parallel _{\ell }}}$ or ${\parallel } = {\mathrel {\parallel _{r}}}$. In the first case the left translation $\lambda _g$ has the required properties, in the second case the same applies to the right translation $\rho _g$.

(b) $\Rightarrow$ (a) In case (B), ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$ implies that ${\parallel }={\mathrel {\parallel _{\ell }}}$ is Clifford.

From now on we deal with case (A) only. We select one line $N_1$ through F1 that is not in $(F1)^\perp$. We assume w.l.o.g. that the parallel class ${\mathcal S}(N_1)$ is a left parallel class. (Otherwise, we have to interchange the attributes “left” and “right” in what follows.) Let $g:=\beta (1)$. We consider the left translation $\lambda _g$ and the product

$$\begin{aligned} \alpha :=\lambda _g^{-1}\circ \beta . \end{aligned}$$

(12)

We choose one $N\in \widetilde{H^*}(N_1)$. Then the parallel class ${\mathcal S}(N)$ is a left parallel class. Thus

$$\begin{aligned} N \mathrel {\parallel _{\ell }}\beta (N)\mathrel {\parallel _{\ell }}g^{-1}\beta (N) =\alpha (N). \end{aligned}$$

(13)

Formula (13) and $\alpha (1)=1\in N$ together force $\alpha (N)=N$. By Proposition 3.5, every plane through N contains at least two lines from the orbit $\widetilde{H^*}(N_1)$, and so any such plane is fixed under $\alpha$. The lines and planes through F1 are the “points” and “lines” of a projective plane; “incidence” is given by symmetrised inclusion. Our $\alpha$ acts on this projective plane as a collineation. By the above, all “lines” through the “point” N are fixed under $\alpha$, and so N serves as a “centre” of this collineation. But N may vary in the orbit $\widetilde{H^*}(N_1)$, which comprises more than one line by the theorem of Cartan-Brauer-Hua (Lam 2001, (13.17)). Consequently, this collineation has more than one “centre”, that is, $\alpha$ fixes all lines of the star ${\mathcal A}(H_F)$.

We now consider the action of $\alpha$ on the projective space ${\mathbb P}(H_F)$. Since all lines of ${\mathcal A}(H_F)$ are fixed, $\alpha$ acts as a perspective collineation with centre F1. This implies that $\alpha$ is F-linear. Since $\alpha$ and $\lambda _g^{-1}$ are F-linear, so is $\beta$. From $\beta \in \Gamma _\parallel \cap {{\,\mathrm{GL}\,}}(H_F) = \Gamma _{\ell }\cap {{\,\mathrm{GL}\,}}(H_F)$ (see Havlicek 2019b, Thm. 3.5) and $\lambda _g^{-1}\in \Gamma _{\ell }\cap {{\,\mathrm{GL}\,}}(H_F)$ follows $\alpha \in \Gamma _{\ell }\cap {{\,\mathrm{GL}\,}}(H_F)$. Now pick any line $L\in {\mathcal L}(H_F)$. The left parallel line to L through F1 is fixed under $\alpha \in \Gamma _{\ell }$, whence we have $L\mathrel {\parallel _{\ell }}\alpha (L)$. On the other hand, L is incident with at least one plane through F1. This plane is $\alpha$-invariant. Therefore the left parallel lines L and $\alpha (L)$ are coplanar, which in turn implies $L=\alpha (L)$. So we arrive at $\alpha =c{{\,\mathrm{id}\,}}_H$ for some $c\in F^*$. Now, using $\alpha (1)=1$, we end up with $\alpha ={{\,\mathrm{id}\,}}_H$.

Next, we give an explicit description of $\beta$. By virtue of (12), our assumption that $\beta$ does not fix all lines of ${\mathbb P}(H_F)$, and $\alpha ={{\,\mathrm{id}\,}}_H$, we have

$$\begin{aligned} \beta =\lambda _g \text{ and } g\in H^*\setminus F^*. \end{aligned}$$

Finally, we claim that ${\parallel }={\mathrel {\parallel _{\ell }}}$. Assume to the contrary that ${\parallel }\ne {\mathrel {\parallel _{\ell }}}$. So there is a line $M_1$ with ${\mathcal S}(M_1)={\mathcal S}_{r}(M_1)$ and $F1\subseteq M_1$. Then ${\mathcal S}(M)={\mathcal S}_{r}(M)$ for all lines $M\in \widetilde{H^*}(M_1)$, which forces

$$\begin{aligned} \beta \bigl ({\mathcal S}_{r}(M)\bigr )={\mathcal S}_{r}(M) \text{ for } \text{ all } M\in \widetilde{H^*}(M_1) . \end{aligned}$$

(14)

We now distinguish three cases.

Case (i). Let $F1\not \subseteq g^{-1}(F1)^\perp$. From Proposition 3.7 and (14), any line $M\in \widetilde{H^*}(M_1)$ has to satisfy (10). This implies $\widetilde{H^*}(M_1) = \{F1\oplus Fg\}$ and contradicts the theorem of Cartan-Brauer-Hua (Lam 2001, (13.17)), which says $|\widetilde{H^*}(M_1)|>1$.

Case (ii). Let $F1\subseteq g^{-1}(F1)^\perp$ and $M_1\not \subseteq (F1)^\perp$. We choose any plane E other than $g^{-1}(F1)^\perp$ through the line $M_1$. Let ${\mathcal M}_{E}$ denote the set of all lines that are incident with E and belong to $\widetilde{H^*}(M_1)$. By Proposition 3.5, the set ${\mathcal M}_{E}$ is infinite. From Proposition 3.7 and (14), any line $M\in {\mathcal M}_{E}$ has to satisfy (10) or (11), that is $M=F1\oplus Fg$ or $M=g^{-1}(F1)^\perp \cap E$. This implies $|{\mathcal M}_{E}|\le 2$, an absurdity.

Case (iii). Let $F1\subseteq g^{-1}(F1)^\perp$ and $M_1\subseteq (F1)^\perp$. From Remark 3.8, this applies precisely when

$$\begin{aligned} M_1=F1\oplus Fg=(F1)^\perp \cap \bigl (g^{-1}(F1)^\perp \bigr ) ; \end{aligned}$$

(15)

see the right-hand side of Figure 2. The plane $(F1)^\perp$ is $\widetilde{H^*}$-invariant, whence it contains all lines of $\widetilde{H^*}(M_1)$. From Proposition 3.7 and (14), any line $M\in \widetilde{H^*}(M_1)$ has to satisfy (10) or (11). By virtue of the second equation in (15), this implies $\widetilde{H^*}(M_1) = \{F1\oplus Fg\}$ and, as in Case (i), contradicts the theorem of Cartan-Brauer-Hua. $\square$

Remark 4.4

Note that, as a consequence of the previous theorem, the group of automorphisms that preserve all parallel classes with respect to a given Clifford-like parallelism $\parallel$ of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$ is contained in ${{\,\mathrm{GL}\,}}(H_F)$. Moreover this group is the group of left translations (or right translations respectively) precisely when ${\parallel }={\mathrel {\parallel _{r}}}$ (respectively ${\parallel }={\mathrel {\parallel _{\ell }}}$). If, on the other hand, $\parallel$ is a proper Clifford-like parallelism, then this group is the group of all $\lambda _g$ with $g\in F^*$, thus, from the projective point of view, it comprises only the identity map.

Theorem 4.5

Let $\parallel$ be a Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$, where H is an F-algebra subject to (A) or (B). Then the following assertions are equivalent.

• (a) The parallelism $\parallel$ is Clifford and ${\mathrel {\parallel _{\ell }}}\ne {\mathrel {\parallel _{r}}}$.

• (b) The parallelism $\parallel$ admits an automorphism $\beta \in \Gamma _\parallel$ that stabilises a single parallel class of $\parallel$ and, furthermore, fixes all lines of this particular parallel class.

Proof

(a) $\Rightarrow$ (b). Corollary 4.2 shows that ${\parallel } = {\mathrel {\parallel _{\ell }}}$ or ${\parallel } = {\mathrel {\parallel _{r}}}$. Let, for example, ${\parallel }={\mathrel {\parallel _{r}}}$. We infer from ${\mathrel {\parallel _{\ell }}}\ne {\mathrel {\parallel _{r}}}$ that H is a quaternion skew field. There exists a $g\in H\setminus \bigl (F1 \cup (F1)^\perp \bigr )$; cf. the left-hand sides of Figs. 1 and 2 for illustrations. Then no line $M\in {\mathcal L}(H_F)$ satisfies (11). By Proposition 3.7, $\beta :=\lambda _g$ stabilises a single right parallel class, namely ${\mathcal S}_{r}(F1\oplus Fg)$, and, furthermore, $\beta$ fixes all lines of ${\mathcal S}_{r}(F1\oplus Fg)$.

(b) $\Rightarrow$ (a). The only $\beta$-invariant parallel class can be written in the form ${\mathcal S}(L)$ with $L\in {\mathcal A}(H_F)$. Let us assume that ${\mathcal S}(L)$ is a right parallel class. Since all lines of ${\mathcal S}_{r}(L)$ are fixed under $\beta$, we obtain $\beta \in {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(L)\bigr )^*=\lambda (L^*)$ from Lemma 3.1. Consequently, all left parallel classes are stabilised under $\beta$, whence none of them is a parallel class of $\parallel$. This shows ${\mathrel {\parallel _{\ell }}}\ne {\parallel }={\mathrel {\parallel _{r}}}$. $\square$

Theorem 4.6

Let $\parallel$ be a Clifford-like parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$, where H is an F-algebra subject to (A) or (B). Then the following assertions are equivalent.

• (a) The parallelism $\parallel$ is Clifford and ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$.

• (b) If an automorphism $\beta \in \Gamma _\parallel$ fixes all lines of at least one parallel class of $\parallel$, then all parallel classes of $\parallel$ are stabilised under $\beta$ .

• (c) The parallelism $\parallel$ admits an automorphism $\beta \in \Gamma _\parallel$ that stabilises all its parallel classes, fixes at least one of its parallel classes linewise, and acts as a non-identical collineation on the projective space ${\mathbb P}(H_F)$.

Proof

(a) $\Rightarrow$ (b). We have ${\parallel }={\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$. Let $\beta \in \Gamma _\parallel$ fix all lines of a right⁸ parallel class, which will be written as ${\mathcal S}_{r}(L)$ with $L\in {\mathcal A}(H_F)$. From Lemma 3.1, $\beta \in {{\,\mathrm{K}\,}}\bigl (H,{\mathcal S}_{r}(L)\bigr )^*=\lambda (L^*)$ and so $\beta$ stabilises all left parallel classes or, said differently, all $\parallel$-classes.

(b) $\Rightarrow$ (c). We may assume w.l.o.g. that there exists a line $L\in {\mathcal A}(H_F)$ with the property ${\mathcal S}(L)={\mathcal S}_{r}(L)$. There is a $g\in L^*\setminus F^*$. The left translation $\lambda _g=:\beta$ fixes all lines of ${\mathcal S}(L)={\mathcal S}_{r}(L)$ and acts as a non-identical collineation on ${\mathbb P}(H_F)$. So, by our assumption, $\beta$ stabilises all $\parallel$-classes. Thus $\beta$ meets all the requirements appearing in (c).

(c) $\Rightarrow$ (a). We may assume w.l.o.g. that $\beta$ fixes all lines of a right parallel class, ${\mathcal S}_{r}(L)={\mathcal S}(L)$ with $L\in {\mathcal A}(H_F)$. There are two possibilities.

Case (i): ${\mathrel {\parallel _{\ell }}}\ne {\mathrel {\parallel _{r}}}$. Theorem 4.3 gives that $\parallel$ is a Clifford parallelism of $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$. From (Havlicek et al. 2019a, Cor. 4.3), the parallelisms $\mathrel {\parallel _{\ell }}$ and $\mathrel {\parallel _{r}}$ have no parallel classes in common. Consequently, ${\mathcal S}_{r}(L)$ being one of the $\parallel$-classes yields ${\parallel }={\mathrel {\parallel _{r}}}$. From Lemma 3.1, the given automorphism $\beta$ is a left translation $\lambda _g$ for some $g\in H^*$. Since $\beta$ acts non-identical on ${\mathbb P}(H_F)$, we have $g\in H^*\setminus F^*$. Hence, by Proposition 3.7, at least one right parallel class is not stabilised under $\beta$, a contradiction.

Case  (ii): ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$. Now ${\mathrel {\parallel _{\ell }}}={\mathrel {\parallel _{r}}}$ is the only Clifford-like parallelism of the projective double space $\bigl ({\mathbb P}(H_F),{\mathrel {\parallel _{\ell }}},{\mathrel {\parallel _{r}}}\bigr )$, whence $\parallel$ turns out to be Clifford. $\square$