1 Introduction

The study of complex networks is inspired by empirical analysis of real networks. Indeed, complex networks allow us to understand various real systems, ranging from technological to biological networks [1]. For instance, we need a set of neurons connected by synapses to ensure our ability to read this text; our body is ruled by interactions between thousands of cells; communication infrastructures, such as the Internet, are formed by routers and computer cables and optical fibers; and the society consists of people connected by social relationships such as friendship and familiar or professional collaborations [1,2,3].

These systems are called complex systems because it is not possible to predict their collective behavior from their individual components. But understanding the mathematical description of these systems makes us capable to predict them and possibly control them. These are some of the great scientific challenges of the present time, since they play a key role in our daily life [4]. Examples include the understanding of the spreading viruses throughout transportation networks that allowed the prediction of the H1N1 pandemic [5] in 2009 or the new coronavirus in 2019/2020 [6], and the use of mobile call network to find those responsible for the terrorist attack on a train in Madrid in 2004 [7].

Despite of the differences among complex systems found in nature or society, the structures of these networks are much similar to each other, because they are governed by the same principles. Then, we can use the same set of mathematical and computational tools to explore these systems. In general terms, a network is a system that can be represented as a graph, composed by elements called nodes or vertices and a set of connecting links (edges) that represent the interactions among them [8]. In Fig. 1, we show a classic and famous example of a social network that became known as Zachary’s karate club [9]. In this example, nodes represent people and the links between them represent the interaction among members of the club.

Fig. 1
figure 1

A network representation of social interactions of a group that belongs to the same karate club. This social network was studied by W. W. Zachary [9] from 1971 to 1972 and it captures the links of 34 members who integrated with each other outside the club

Full size image

The advantage of modeling a system as a graph is that problems become simpler and more tractable. For example, we can cite the Konigsberg problem as a first mathematical problem solved using a graph. The mathematician Leonard Euler wanted to solve the following puzzle (see Fig. 2): if you are in the center of the old city called Konigsberg, how can you across all seven bridges crossing only once for each one of them? To solve this problem, a mathematical abstraction is required: a graph. Euler represented each part of the city by nodes that are connected by edges or links (the bridges between them). So, if each node has two or any even number of links, it is possible to enter and leave in this region of the city by different bridges. However, if a node has a odd number of edges, it should be either the starting or the end point of the pathway. Here is the solution of the problem: you never find such path, no matter how smart you are, because all nodes have odd number of links [10].

Fig. 2
figure 2

In the left side: the center of Konigsberg city and the seven bridges connecting one part of the town to another. In the right side: The representation of the problem using a graph. Each node represents one part of the city and the links between them represent the bridges

Full size image

On the one hand, the language for the description of networks is found in mathematical graph theory; on the other hand, the study of very large systems requires a statistical characterization and also high-performance computing tools. For instance, the human brain is estimated to have N ≈ 1011 neurons and the WWW network has about N ≈ 1012 online documents [2]. In face of this context, we introduced basic concepts of network theory and its statistical characterization in the next section. In the third section, we described network models that can be used to study dynamical processes such as epidemic spreading; diffusion of information, gossip, memes in a social network; or diffusion of energy in a power grid network. Finally, in the last section, we summarized our review and showed the interdisciplinary importance of complex networks.

2 Basic Concepts and Statistical Characterization of Networks

From a mathematical point of view, we can represent a network by means of an adjacency matrix A. A graph of N vertices has a N × N adjacency matrix. The edges can be represented by the elements Aij of this matrix such that [8]

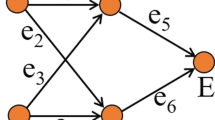
$$ A_{ij} = \left\{\begin{array}{lc} 1, ~~~ \text{if the vertices \textit{i} and \textit{j} are connected}\\ 0, ~~~~~~ \text{otherwise}, \end{array}\right. $$
(1)

for a undirected and unweighted graph, like the one shown in Fig. 1. In this case, the adjacency matrix is symmetric, it means Aij = Aji, while for directed ones (as we showed in Fig. 3), the matrix is not symmetric and the element Aij = 1 indicates that the node i points to the node j, but the reverse is not necessarily true. We can find different examples of directed and undirected graphs in natural or artificial systems. For example, in a ecological web, the directed links indicate which animal is predator of the other, while in a social network, the romantic ties are represented by undirected edges—at least we hope so [4].

Fig. 3
figure 3

A simple example of a directed graph

Full size image

Beyond these examples, we also can find networks for which the links have different weight ωij. The weight can represent the flow of people on a flight in a transportation network or the current flowing through a transmission line in a power grid. In these cases, the elements of the adjacency matrix are better described as Aij = ωij and, generally, 0 ≤ ωij ≤ 1.

A relevant information that can be obtained from the adjacency matrix is the degree ki of a vertex i defined as the number of edges attached to the vertex i, i.e., the number of nearest neighbors of the vertex i. The degree of the vertices can be written by means of the adjacency matrix as [8]

$$ k_{i} = {\sum}_{j=1}^{N} A_{ij}. $$
(2)

In Fig. 4a, we show the Zachary’s karate club network with a scale that differentiates the most connected nodes from the least connected ones. If this measure is used to determine the centrality of an specific node, the most central nodes is the one with more connections. In directed networks, the in-degree and the out-degree are, respectively, defined by

$$ k_{i}^{\text{in}} = {\sum}_{j=1}^{N} A_{ji} ~~~~~~~ \text{and} ~~~~~~~ k_{i}^{\text{out}} = {\sum}_{j=1}^{N} A_{ij}, $$
(3)

that also can be used as a centrality measures. The total number of connections is \(k_{i} = k_{i}^{\text {in}} + k_{i}^{\text {out}}\). A centrality measure [11], as the name implies, assigns a value to the nodes according to a specific concept. There are different types of centrality measures depending on the importance assessed, as we will see throughout this section.

Fig. 4
figure 4

Some most common centrality measures exemplified in the karate club network. We used networkx and matplotlib from python (python.org) to plot the figures. We used the free code available at https://aksakalli.github.io

Full size image

A central issue in the structure of a graph is the connectedness of its vertices, i.e., the possibility of establishing a path between any two nodes [2]. This is important, for instance, when we have a gossip spreading in a social network or a nerve impulse propagating in a neural network [8].

A path \(\mathcal {P}_{ij}\) is defined as an ordered collection of n + 1 vertices connected by n edges in such a way that connect the vertices i and j, as shown in Fig. 5. The concept of path leads us to define the distance between any pair of vertices in the network. The distance between the nodes i and j is defined as the number of edges in the shortest connecting path denoted as ℓij. The average shortest path length is defined as the value of ℓij averaged over all the possible pairs of vertices in the network [12] according to

$$ \langle l \rangle = \frac{1}{N(N-1)} {\sum}_{i \neq j} l_{ij}. $$
(4)
Fig. 5
figure 5

One possible path connecting the node A to the node B in a network is highlighted

Full size image

Typically, the number of neighbors in a complex network at a distance ℓ can be approximated by 〈k〉ℓ, considering that each vertex has degree equal to the average degree of the network 〈k〉 and there is no loop. A loop or a cycle is a closed path \(\mathcal {P}_{ij} (i = j)\) in which all nodes and all edges are distinct [8]. Since the quantity 〈k〉ℓ rapidly grows with ℓ, we can thus roughly estimate 〈ℓ〉 by the condition \(\langle k \rangle ^{\ell } \sim N\), then [2, 12]

$$ \langle \ell \rangle \simeq \frac{\ln N}{\ln \langle k \rangle}. $$
(5)

For a d-dimensional lattice, the number of neighbors at a distance ℓ scales as ℓd implies that \(\langle \ell \rangle \sim N^{1/d}\). So, the growth of 〈ℓ〉 slower than any positive power of N characterizes the network with the small-world property [2]. This scaling behavior is observed in many real-world phenomena, including websites, social networks, food chains, metabolic processing networks, etc [1, 3, 8].

Beyond the small-world characteristic, a network can be also described by the structure of the neighborhood of a vertex. The tendency to form cliques (fully connected sub-graphs) in the neighborhood of a given vertex is observed in many natural networks; for example, a group of people that interact with each other as friends. This property is called clustering and implies that if the vertex i is connected to the node j, and this one is connected to l, there is a high probability that i is also connected to l. The clustering C(i) can be measured as the relative number of connections among the neighbors of i [12]:

$$ C(i) = \frac{n_{i}}{k_{i}(k_{i} - 1)/2}. $$
(6)

Here, ki is the degree of the node i and ni is the total number of edges among its nearest neighbors. The mean clustering coefficient is given by

$$ \langle C \rangle = \frac{1}{N} {\sum}_{i} C(i). $$
(7)

We can also define other measures that can be classified as centrality measures. For example, it is possible to define the importance of a node observing how many times it behaves like a bridge connecting any two vertices of the network along the shortest path between them [13]. Thus, the betweenness of a vertex i,

$$ b(i) = {\sum}_{k \neq i \neq j} \frac{\sigma (k i j)}{\sigma (k j)} $$
(8)

where σ(kj) is the total number of the shortest paths from k and j and σ(kij) is the quantity of such paths that pass through the node i. This centrality measure was also calculated for the nodes that composed the Zachary’s karate club (see Fig. 4b).

The relevance of a node can also be based on the shortest path. From this point of view, the centrality measure, called closeness centrality, is given by the inverse of the average distance of a node to all others [11]

$$ g(i) = \frac{1}{{\sum}_{i \neq j}l_{ij}}. $$
(9)

Consequently, the lower is the distance of a node in relation to the others, the more central (influence) it is considered. In Fig. 4c, this measure is shown for nodes of Zachary’s karate club network.

Another useful measure of the influence of the nodes is the eigenvector centrality [14] that quantifies the importance of a node according to the concept that connections to high-influencer nodes contribute more to the significance of the node in question. Let us assume that the vector x has the centrality score of a node i, so we can write an eigenvalue equation: \(A\vec {x} = \lambda \vec {x}\), where A is the adjacency matrix and λ is an eigenvalue. The Perron-Frobenius theorem [11] ensures that if all components of the eigenvector x are positive, there is only one eigenvalue able to satisfy this equation and it is possible to determine a unique eigencentrality to each node.

To put this measure in more practical terms, we can analyze the PageRank, which is a variation of eigenvector centrality developed by Google. This measurement analyzes the importance of a web page according to the number of pages that link to it [15, 16]. Although this measure was created as a tool to search web site, it has been used to rank nodes of any network, as for example, in Ref. [17], the authors used this measure for ranking researchers in a co-citation network. It also can be used on Twitter to inform users with suggestions of other accounts that they would like to follow [18] or even to rank public streets, trying to predict human movement and traffic flow [19, 20]. We can calculate a pagerank of each node i of a network according to an algorithm that provides the following relation [15]:

$$ PR(i) = \frac{{\sum}_{j \epsilon V_{i}} PR(j)}{N}, $$
(10)

where PR(j) is the pagerank of each neighbor j of the node i. Both measures, eigenvector and pagerank, were also calculated for Zachary’s karate club network as we see in Fig. 4 d and e.

Apart from such properties described above, looking at very large systems as a social network or the World Wide Web, an appropriate description can be done by means of statistical measures as the degree distribution P(k). The degree distribution provides the probability that a vertex chosen at random has k edges [1, 21]. The average degree is an information that can be extracted from P(k) and it is given by the average value of k over the network, it means,

$$ \langle k \rangle = \frac{1}{N} {\sum}_{i=1}^{N} k_{i} = {\sum}_{k} k P(k). $$
(11)

Similarly, it is useful to generalize and calculate the n th moment of the degree distribution [2]

$$ \langle k^{n} \rangle = {\sum}_{k} k^{n} P(k). $$
(12)

We can classify networks according to their degree distribution. The basic classes are homogeneous and heterogeneous networks. The first ones exhibit a fast decaying tail, for example, a Poisson distribution. Here, the average degree value corresponds to the typical value in the system. On the other hand, heterogeneous networks exhibit heavy tail that can be approximated by a power-law decay, \(P(k) \sim k^{-\gamma }\). In this second case, the vertices will often have a small degree, but there is a non-negligible probability of finding nodes with very large degree values; thus, depending on γ, the average degree does not represent any characteristic value of the distribution [2]. The contrast between these types of distributions is illustrated in Fig. 6, where both Poisson and power-law degree distributions with the same average degree value are compared.

Fig. 6
figure 6

Comparison of Poisson and power-law degree distributions in a linear scale (left side) and in a log-log plot (right side) that highlights the heavy tail of the heterogeneous distribution. Full circles represent the Poisson distribution and empty squares represent the power-law one

Full size image

The role of the heterogeneity can be understood by looking at the first two moments of a power-law distribution \(P(k) \sim k^{-\gamma }\). In the thermodynamic limit, \(\langle k^{2} \rangle \rightarrow \infty \), for 2 < γ ≤ 3. This means that the fluctuations around the average degree are unbounded. We observe a scale free network since the absence of any intrinsic scale for the fluctuations implies that the average degree is not a characteristic scale for the system [1, 12]. However, for γ ≥ 3, the second moment remains finite. Indeed, besides the shape of the power-law degree distribution, the exponent γ has profound implications on dynamical processes running on top of heterogeneous substrates.

For example, the susceptible-infected-susceptible (SIS) model [22, 23] is the classical epidemic model widely used to study epidemic dynamics in networks. In this approach, each vertex j of the network can be infected or susceptible. A susceptible node can become infected by its infected neighbors with rate λ and, an infected node can become spontaneously healthy at rate μ [24]. This dynamics exhibits a phase transition between a disease-free state and an active stationary phase where a finite fraction of nodes is infected. These regimes are separated by an epidemic threshold λc [24, 25]. Different mean-field approaches provide different epidemic thresholds. The quenched mean-field (QMF) theory [26] explicitly takes into account the actual connectivity of the network through its adjacency matrix. While in the heterogeneous mean-field (HMF) theory, the density of infected individuals depends only on the vertex degree. Both theories predict a vanishing threshold, in the thermodynamic limit, for random uncorrelated networks with a power-law degree distribution with γ < 3, despite of different scaling for 5/2 < γ < 3. But QMF also predicts a vanishing threshold for γ > 3 while HMF predicts a finite threshold in this range [27]. In fact, Chatterjee and Durrett [28] proved that the SIS model presents a null epidemic threshold, as the system size increases, for uncorrelated random networks with any γ.

However, the dynamics of Kuramoto oscillators on heterogeneous scale-free networks [29] behaves differently. The Kuramoto model is one of the most studied coupled phase oscillator models to describe synchronization processes, observed in many physical, technological, and biological systems [30]. This model also presents a phase transition among a state that the oscillators are moving incoherently, and a state where all oscillators are in phase (synchronization). The HMF and QMF present the same results that those obtained for the SIS model. However, for the Kuramoto model, the HMF theory forecast for the critical coupling Kc is in better agreement with numerical calculations because, for γ > 3, the Kc converges to a constant value in the thermodynamic limit while vanishes for γ < 3.

Other typical feature of networks is the tendency of nodes with a given degree to connect with nodes with similar or dissimilar degree. When high or low degree vertices connect to other vertices with similar degree with higher probability, one says the correlations presented in the network are assortative. Conversely, if nodes of different degree are more likely to attach, the correlations are called disassortative [31].

One way to quantify the degree correlations is in terms of the conditional probability \(P(k^{\prime }|k)\) that a node with degree k is connected with a vertex with degree \(k^{\prime }\) [2]. Since determining \(P(k^{\prime }|k)\) can be a rather complicated task, a simple approach is given by the average degree of the nearest neighbors of a vertex i with degree ki [32],

$$ k_{nn,i} = \frac{1}{k_{i}} {\sum}_{j \in \mathcal{N}(i)} k_{j}, $$
(13)

where the sum runs over by the nearest neighbors of i. Then, the behavior of the degree correlations is obtained by the average degree of the nearest neighbors, knn(k), for vertices of degree k [33]:

$$ k_{nn}(k) = \frac{1}{N_{k}} {\sum}_{i/k_{i} = k} k_{nn,i}, $$
(14)

where Nk is the number of nodes of degree k and the sum runs over all vertices with the same degree k. This quantity is related to the correlations between the degrees of connected nodes because in average it can be expressed as

$$ k_{nn}(k) = {\sum}_{k^{\prime}} k^{\prime}P(k^{\prime}|k). $$
(15)

If degrees of neighboring vertices are uncorrelated, \(P(k^{\prime }|k)\) is just a function of \(k^{\prime }\) and knn(k) is a constant. If knn increases with k, then vertices with high degrees have a larger likelihood of being connected to each other. On the other hand, if knn decreases with k, high degree vertices have larger probabilities of having neighbors with low degrees [2, 33, 34].

3 Networks Classes

In general, a network model produces graphs with properties similar to the real system. However, the advantage of using a model is to reduce the complexity of the real world to a level that one can be treated in a more practical way. Therefore, networks are considered a powerful means of representing patterns of connections between parts of systems such as Internet, power grid, food webs, and social networks [3, 8, 35].

On the one hand, technological networks as Internet are physical infrastructure networks that can be represented by static networks, i.e., the nodes and edges are fixed or change very slowly over time [11]. On the other hand, networks that describe some form of social interaction between people have an intrinsic time-varying nature that should be taken into account. For instance, in a scientific collaboration network, the authors are not in contact with all their collaborators simultaneously during all the time. Indeed, real contact networks are dynamic with connections that appear and disappear with different characteristic time scales [36, 37].

From the viewpoint of dynamical processes, both classes of networks—static and temporal—are important. The first one has been widely studied and it is convenient for analytical tractability, whereas the second one is, in some cases, more realistic. Within these two large classes, there are several sub-classes in which we can distinguish networks according to their degree distribution, elements of connections such as Euclidean distance or other metrics. Network models have been improved because of the need to take into account more and more real characteristics. In this section, we presented the historical evolution from simple models as lattices and homogeneous networks until more refined models with heterogeneous connectivity, temporal feature, or more elaborated types of connection, such as multilayers and metapopulations.

3.1 Regular Lattices

Lattice models are the simplest example of networks. They are used in studies involving cellular automata and agent-based models [38, 39]. In a regular lattice, each site can represent, for example, an individual positioned on a regular grid of points. They are connected only with their nearest neighbors as we can see in the Fig. 7. The regular lattices are homogeneous since all sites have the same number of connections.

Fig. 7
figure 7

Regular lattices of one, two, and three dimensional, respectively

Full size image

They were very used to study dynamical process in general, such as reaction-diffusion process and epidemic dynamics [40, 41] but their simplified topology is unrealistic compared with real systems. The advantage of this kind of network is the convenience of solving analytical problems exactly, as Ising Model [42] and Voter Model [43].

3.2 Random Regular Network

The other simple prototype of a network was investigated by Erdős and Rényi, in 1959 [44]. In its original formulation, a graph is constructed starting from a set of N nodes and all edges among them have the same probability of existing. This generates a homogeneous graph in which the vertices have a number of neighbors that do not differ much from the average degree 〈k〉 (see Fig. 8), with connectivity distribution as a Poisson.

Fig. 8
figure 8

A simple example of a random regular graph

Full size image

3.3 Small-World Networks

Afterwards, in 1998, Watts and Strogatz (WS) proposed a more realistic model inspired by social networks that became known as the small-world model [45]. WS networks are constructed from N vertices initially arranged in one-dimensional lattice with periodic boundary conditions, each vertex has m connections with the nearest neighbors. Vertices are then visited clockwise and for each of them the clockwise edges are rewired with probability p. The rewiring process generates connected networks and conserves the number of edges (〈k〉 = m). However, even at small p, the emergence of shortcuts among distant nodes greatly reduces the average shortest path length (see Fig. 9). This algorithm produces a network with small-world property but it is not capable to generate a heterogeneous degree distribution with a power-law form.

Fig. 9
figure 9

A Watts-Strogatz network with size N = 20 in which as the p value increases, the network becomes more and more random. In the first case, p = 0; in the second graph, p = 0.1; and finally, in the last illustration, p = 1

Full size image

3.4 Growth and Preferential Attachment Networks

3.4.1 Barabasi-Albert Model

Concomitantly, Barabási and Albert [46] proposed a preferential attachment model suited to reproduce the feature of time growth of many real networks. In this model, new vertices are added to the system at every step. Each new vertex is connected to those nodes already present in the network with a probability proportional to their degrees at that time. The properties of growth and preferential attachment are suitable to model realistic networks as the Internet and the World Wide Web [3, 8]. This class of networks provides an example of the emergence of graphs with a power-law degree distribution [\(P(k) \sim k^{-\gamma }\)], with γ = 3 (see Fig. 10) and small-world properties. Despite considering the addition of new nodes, when we deal with a dynamic process in this network, we consider it static since it is grown first and after the dynamics run through the substrate.

Fig. 10
figure 10

An illustration of a small Barabasi-Albert network (left side) and the connectivity distribution of a large (N = 106) BA network (right side). We can note the presence of hubs—nodes with high degree—in the power-law degree distribution. The dashed line is a guide to the eyes with slope \(P(k) \sim k^{-3}\)

Full size image

3.4.2 Fitness Model

The Barabasi-Albert model does not take into account that nodes can have other attributes that make them more attractive to receive new links. Bianconi and Barabasi [47] proposed a model where each individual has a characteristic that determine its ability to make links. The model is similar to the BA network but, besides the degree, the fitness of each node is also involved in the completion for making new connections. The network has the growth property, the same as BA model, but now the nodes are characterized by their fitness parameter η chosen randomly according to an arbitrary distribution ρ(η) and the probability that a new edge will connect to a node i is

$$ {\prod}_{i} = \frac{\eta_{i} k_{i}}{{\sum}_{j} \eta_{j} k_{j}}, $$
(16)

where the sum is over all nodes already present in the network. In the case of a uniform distribution of the parameter fitness in the interval [0, 1], one also obtains a network with a power-law degree distribution \(P(k) \sim k^{-\gamma }\) but with γ ≈ 2.25. It is interesting because a little randomness in fitness leads to a network with a non-trivial power-law degree exponent.

3.4.3 Homophilic Model

In some situations, it can be reasonable to assume that besides degrees and fitness, nodes are more likely to connect with their similar. The impact of homophily has already been studied on social networks [48, 49]. Just think a little to understand that this behavior is really quite predictable. People tend to create ties of friendship with others of similar job, the same religion, or even fans of the same soccer team.

To consider this tendency, de Almeida and collaborators [50] include a homophilic term in the BA model. So, the probability that a node j entering the network will connect to another node i already present in the network is

$$ {\prod}_{i} = \frac{(1 - A_{ij}) k_{i}}{{\sum}_{l} (1 - A_{il}) k_{l}}, $$
(17)

where the parameter Aij = |ηi − ηj| represents the similitude of the nodes i and j, since we named ηi as a intrinsic property (fitness) of each node i. This algorithm also generates a network with a power-law degree distribution but with γ = 2.75.

These models based on growth and preferential attachment have been successful in the area of complex networks because through a simple dynamical principle, a power-law degree distribution and small-world properties are able to emerge from these graphs.

3.5 Uncorrelated Random Networks

In addition to their power-law degree distributions, real networks are also characterized by the presence of degree correlations reflected on their conditional probabilities \(P(k^{\prime }|k)\) (as we saw in Section 2). For uncorrelated networks, \(P(k^{\prime }|k)\) can be estimated as the probability that any edge points to a vertex with degree \(k^{\prime }\), leading to \(P_{unc}(k^{\prime }|k) = k^{\prime }P(k^{\prime })/\langle k \rangle \) [51]. Thus, using (15) the average nearest-neighbor degree becomes

$$ k_{nn}^{unc}(k) = \frac{\langle k^{2} \rangle}{\langle k \rangle^{2}}, $$
(18)

that is independent of the degree k.

Although most real networks show the presence of correlations, uncorrelated random graphs are important from a numerical point of view, since we can test the behavior of dynamical systems whose theoretical solution is available only in the absence of correlations. For this purpose, Catanzaro et al. [34] presented an algorithm to generate uncorrelated random networks with power law degree distributions, called uncorrelated configuration model (UCM). The steps of the algorithm are the following:

  • In a set of N disconnected vertices, each node i is signed with a number ki of stubs, where ki is a random variable with distribution \(P(k) \sim k^{-\gamma }\) under the restrictions k0 ≤ ki ≤ N1/2 and \({\sum }_{i} k_{i}\) even. It means that no vertex can have either a degree smaller than the minimum degree k0 or larger than the cutoff kc = N1/2.

  • The network is constructed by randomly choosing two stubs and connecting them to form edges, avoiding both multiple and self-connections.

It is possible to show that [51], to avoid correlations in the absence of multiples and self-connections, the random network must have a structural cutoff scaling at most as \(k_{c}(N) \sim N^{1/2}\).

In Fig. 11a, we show a power-law degree distribution for the UCM model [34] with different values of the degree exponent γ and we checked the lack of correlations. We can observe in Fig. 11b a flat behavior of knn(k) [see 15 and 18] for all values of γ. In each realization of the degree sequence, one obtains a random maximum degree \(k_{\max \limits }\), with an average \( \langle k_{\max \limits } \rangle = k_{c}\). For γ > 3, both mean and the standard deviation of \(k_{\max \limits }\) scale as \(k_{c} \sim N^{1/\gamma -1}\). As we can see in Fig. 11b, this implies that \(k_{\max \limits }\) has large fluctuations for different network realizations [52]. As said previously, this algorithm is very useful in order to check the accuracy of many analytical solutions of dynamical process on networks.

Fig. 11
figure 11

a Power-law degree distribution \(P(k) \sim k^{-\gamma }\) and b average nearest-neighbor degree for networks generated according to the algorithm proposed by the uncorrelated configuration model, with different values of the degree exponent γ

Full size image

3.6 Networks with Euclidean Distance

Most of scale-free networks does not consider the relevant Euclidean distance between nodes. But real-life systems are, in fact, on top of a geographical space. City streets can be mapped as a square lattice, an ecological network that describes a food chain is embedded in a three-dimensional space, etc. In the next models, the Euclidean metric is taking into account.

3.6.1 Euclidean Distance as a Characteristic for Preferential Attachment

The physical proximity is a great factor in social tie formation even in virtual social networks [53, 54], so we can take the geographical proximity in account using the network model proposed by Soares and collaborators [55]. They consider a square lattice substrate and starting with one node located in some arbitrary origin of the space. The second node is added in the network and it is connected to the first node. Its localization is randomly chosen at a distance r from the first node. This distance r is distributed according to \(P_{G}(r) \propto \frac {1}{r^{2+\alpha _{G}}}\); where αG > 0 represents the growth pattern of the network, because of this, we named it with the sub-index G. The new center of mass (origin) is calculated, considering that each node has mass m = 1. A third node includes obeying the same spatial distribution but it will be connected to node i = 1 or i = 2 according to the probability

$$ P_{A} \propto \frac{k_{i}}{r_{i}^{\alpha_{A}}}, $$
(19)

where αA ≥ 0 characterizes the attachment pattern of the network, therefore, sub-index A. Both processes are repeated until the network completes N nodes. If we take αA = 0, we return to the well-known Barabasi-Albert model. This model maintains the preferential attachment according to the degree of the nodes, but it also uses the geographical distance as a criterion to compete for links, as we can observe in Fig. 12.

Fig. 12
figure 12

An example of a network with size N = 20 generated according to the rules proposed by Soares et. al. [55]. Here αA = αG = 2. Note that the nearest links are more likely but long-range connections can also happen

Full size image

For this network, the degree distribution is given by

$$ P(k)=P(0) e_{q}^{-k/\kappa} $$
(20)

where κ > 0 is the characteristic number of connections, P(0) is a constant to be normalized, q is the entropic index, and eq(x) is the q-exponential defined by

$$ \begin{array}{@{}rcl@{}} {e_{q}^{x}}= \left[1+(1-q)x\right]^{1/(1-q)} & ({e_{1}^{x}}=e^{x}). \end{array} $$
(21)

The parameter αG does not affect the behavior of the connectivity distribution P(k) because it refers just to the distance distribution in relation to the center of mass and does not impact on the preferential attachment rules. But as αA increases, the connectivity distribution changes and a topological phase transition occurs. The network changes from a completely heterogeneous network (αA = 0) to an increasingly homogeneous network as αA becomes bigger [55].

3.6.2 Spatial Waxman Model

In 1988, Waxman [56] proposed a random graph (see Fig. 13) considering that longer links are more expensive or difficult to construct so they should be less likely. His model is a generalization of the Erdos-Renyi graph and it is very realistic when we consider, for example, a power grid or a land transport network. In this model, a pair of nodes i and j is randomly chosen from a set of nodes distributed in a square lattice and they link with each other with a probability that depends on their distance, given by the function

$$ P(d_{ij}) = a\exp(-b d_{ij}), $$
(22)

where a and b are positive parameters that control the geographical constraints which must be estimated depending on the type of network that is modeled. The parameter a is related to short and long edges while the parameter b controls the edge density. Although Waxman model is favorable in considering geographical properties of networks, it does not yield a power-law degree distribution, failing to predict most real systems.

Fig. 13
figure 13

An example of a network with size N = 20 generated according to the Waxman algorithm [56]

Full size image

3.6.3 Scale Free on Lattice

In paper [57], Rozenfeld and colleagues proposed a model that consists in a network with a power-law degree distribution, \(P(k) \sim k^{-\gamma }\), with γ > 2, embedded in a d-dimensional lattice. They consider a d-dimensional regular network with periodic boundary conditions. Each site is randomly chosen and it connects to its nearest neighbors until it reaches k neighbors, previously determine by the power-law degree distribution or until all nodes that are in a pre-established limit radius \(r(k) \sim k^{1/d}\) have been explored.

This method predicts longer-range interaction due to the power-law property of the degree distribution previously imposed, but consider the Euclidean distance as a important factor to make links between nodes.

3.7 Temporal Networks

As shown in the previous sections, the network structure helps us to understand the behavior of dynamical systems. However, in many cases, the edges are not continuously active. For example, in communication networks via email, edges represent sequences of instantaneous contacts [36]. In closed gatherings of individuals such as schools and conferences, the agents are not simultaneously establishing interactions in the system [58, 59]. Similarly to the network topology, the intrinsic time evolution of the network can also affect the system’s dynamics as, for example, disease contagion or information diffusion [60,61,62].

Indeed, this mixing of time scales can induce new phenomenology on the dynamics on temporal networks, in stark contrast with what is observed in static networks. Moreover, the time evolution of temporal network contacts [63,64,65], characterized by long time of inactivity, alternate with periods of intense activity, can induce, for example, a slow dynamical in spreading processes as epidemics, diffusion, or synchronization [66,67,68,69,70].

3.7.1 Activity-Driven Model

One of many examples of temporal networks is the activity-driven network [37]. Indeed, it represents a class of social temporal network models based on the observation that the establishment of social contacts is driven by the activity of individuals, prompting them to interact with their peers at different levels of intensity. Based on the empirical measurement of heterogeneous levels of activity denoted by a, across different datasets, activity strength has been found to be distributed according to a power-law form, \(F(a) \sim a^{-\gamma }\) [37].

The activity-driven network model proposed by Perra et al. [37] is defined as follows: N nodes (individuals) in the network are endowed with an activity ai ∈ [ε,1], extracted randomly from an activity distribution F(a). Every time step Δt = 1/N, an agent i is uniformly chosen at random. With probability ai, the agent becomes active and generates m links that are connected to m other agents, uniformly chosen at random. Those links last for a period of time Δt. Time is updated as t → t + Δt. The topological properties of the integrated network at time t (i.e., the network in which nodes i and j are connected if there has ever been a connection between them at any time \(t^{\prime } \leq t\)) were studied in Ref. [71]. The main result is that the integrated degree distribution at time t, Pt(k), scales in the large t limit as the activity distribution, i.e.,

$$ P_{t}(k) \sim t^{-1} F\left( \frac{k}{t} - \langle {a} \rangle \right), $$
(23)

considering m = 1.

Empirical measurements report activity distributions in real temporal networks exhibiting heavy tails of the form \(F(a) \sim a^{-\gamma }\) [37]. This expression thus relates in a simple way the functional form of the activity distribution and the degree distribution of the integrated network at time t, and allows to explain the power-law form of the latter observed in social networks [72].

3.7.2 Adaptive Networks

In adaptive networks, the connection between nodes and the states of these nodes evolves together in a dependent way [73]. In traditional temporal networks, the connections between nodes evolve independently of the dynamics running on top of this network. However, in adaptive networks, topologies change adaptively with respect to the changes in the states of each individual. An appropriate example is the disease spreading. Let us suppose that the nodes are individuals that can be in two states: infected or susceptible. Infected nodes can become susceptible spontaneously and susceptible ones, if it is in contact with an infected person, can also become infected with a given probability. This is the rule, in a simplified way, of the SIS model [22, 23] as it was explained before in Section 2. However, if this dynamical process is running on top of a adaptive network, susceptible nodes can cut links to infected neighbors with a certain probability, in an attempt to minimize contagion. In other words, the evolution of the disease affects the network topology but the dynamics of the node connections also affects the prevalence of the disease.

Adaptive networks are very useful to model many real systems, including transportation networks, neural networks, biological networks, and social networks[73, 74].

3.8 Metapopulation Model

Metapopulations are characterized as a set of nodes that corresponds to the inter-population level and inside of each node, an intra-population level. Basically, one has a complex network composed by nodes that do not represent individuals but represent a population of them; this means that a metapopulation network is formed by a set of networks characterizing interconnected populations [75, 76]. The inner structured can be a homogeneously mixed of individuals or can constitute by a network of any topology—lattice, scale free, etc. Inside of each population, there are particles or individuals that can be in the states A, B, or C. For example, if we study a rumor propagation, these individuals can be separated in three groups: those who spread the news (or gossip), called spreaders; those who know the information but are not interested in spreading anymore, name stiflers; and finally, there are a group of people who does not yet know the news but is able to receive it (ignorants). Or, if we have an epidemic spreading, these individuals can be infected, susceptible, or recovered, as represented in the Fig. 14.

Fig. 14
figure 14

Illustration of a simple example of a metapopulation network

Full size image

In metapopulation, the dynamic spreading occurs inside of each population but the interaction between one population to another occurs due to the mobility of the individuals that can migrate [77]. This model is widely used because the mobility is a relevant factor in the spread of human diseases [78] such Sars-Cov-2 pandemic [79, 80], and also vector-borne [81,82,83] and livestock diseases [84, 85].

3.9 Multilayer Networks

In most real-world systems, a set of components can link with each other in multiple type of relationships. To model such systems, multilayers appear as a crucial tool, in which multiple systems are included as layers of connectivity. In each layer, we have a set of nodes that can be the same or not in the other layers (see Fig. 15). The dynamic process can spread in different ways horizontally (inside the layer) and vertically (between layers) [86, 87].

Fig. 15
figure 15

An illustration of a multilayer network that was drawn using the package pymnet from python (www.mkivela.com/pymnet)

Full size image

To make clear, let us go to the following example involving vector-borne diseases. There are many infectious diseases that are transmitted from a human to another by a vector. The most well-known vectors are insects for diseases including malaria, dengue fever, or Zika virus [83]. So, we can model this phenomena using a multilayer composed by two layers, one representing the human population and its mobility, and other representing the same for insects. The disease propagation just occurs between layers since one infected human can infect a insect which, in turn, can sting a healthy human and infect him.

Other example is related to social interactions. We can think a multilayer network composed by layers that represent social networking site such as Facebook, Twitter, and Instagram. Each node is an individual that might currently be logged into all social networks or just into Instagram, for example, but not logged in Facebook and Twitter. In addition, the friendships of a particular person on a website may be different from the friendships (followers) that the same person has on other networks.

4 Final Remarks

In this paper, we briefly reviewed complex systems. We introduced this field for a broad audience, on the purpose of summarizing tools and models of complex networks. We synthesized the primary literature on this topic over the years and we provided a comprehensive list of citations for those who desire to learn further.

In addition to the references cited throughout the paper, the reader can also find great material about other traditional complex network measurements in reference [88], an interesting explanation about community structures and algorithms to detect them in graphs can be found in reference [89], a current and complete survey of theory and applications of random walks on networks can be obtained in reference [90], and a suitable and recent investigation showed how transformations between systems can generate complex networks can be found in reference [91] .

We expected that the reader is able to identify scenarios which can use complex networks tools to model real-world systems and to solve feasible problems. In fact, the applicability of this subject is wide-ranging and powerful. Due to its interdisciplinarity, we are capable of investigating many dynamical processes that really affect our daily lives, from biological until technological contexts. From this knowledge, we can make useful predictions involving, for example, epidemic dynamics [6, 79, 80, 92,93,94,95], vector-borne or livestock diseases [40, 41, 82, 84, 85, 96], spreading rumors [97,98,99,100,101], and synchronization [29, 30, 70, 102].

It is important to mention that nowadays the tools of complex networks go beyond such traditional applications mentioned above. In fact, there are many relevant applications involving machine learning [103], semantic representation of language [104, 105], systems biology investigations [106, 107], and public sector as intelligent system and policy networks [108,109,110,111].

In conclusion, we emphasized that there are other methods to quantify the basic structure of networks such as node similarity and network’s community [112,113,114,115]. Such measures are important in a range of practical problems, including the advancements in artificial intelligence and deep learning areas in which approaches related to struc2vec, node2vec, and sim2vec algorithms are used [116, 117]. However, as mentioned before, the aim of this paper is not to provide a detailed analysis about all areas concerning complex networks, but we hope that the overview presented here is enough to supply the necessary background to sharpen the reader’s curiosity to go beyond.