Dynamic response of structure with tuned mass friction damper

Abstract

The effectiveness of tuned mass friction damper (TMFD) in suppressing the dynamic response of the structure is investigated. The TMFD is a damper which consists of a tuned mass damper (TMD) with linear stiffness and pure friction damper and exhibits non-linear behavior. The response of the single-degree-of-freedom (SDOF) structure with TMFD is investigated under harmonic and seismic ground excitations. The governing equations of motion of the system are derived. The response of the system is obtained by solving the equations of motion, numerically using the state-space method. A parametric study is also conducted to investigate the effects of important parameters such as mass ratio, tuning frequency ratio and slip force on the performance of TMFD. The response of system with TMFD is compared with the response of the system without TMFD. It was found that at a given level of excitation, an optimum value of mass ratio, tuning frequency ratio and damper slip force exist at which the peak displacement of primary structure attains its minimum value. It is also observed that, if the slip force of the damper is appropriately selected, the TMFD can be a more effective and potential device to control undesirable response of the system.

Introduction

The tuned mass damper (TMD) is the most popular and widely used device to control vibration in civil and mechanical engineering applications ranging from small rotating machines to tall civil engineering structures. Its basic purpose is to reduce the response of main system by tuning an additional vibrating mass to a frequency close to the resonant frequency of the main system. The vibration of main system causes the TMD to vibrate out of phase with the main system in resonance condition so that the vibrational energy is dissipated through the damping of the TMD. Similar to the TMD, friction damper (FD) were found to be very efficient, not only for rehabilitation and strengthening of existing structures but also for the design of structures to resist excessive vibrations (Colajanni and Papia 1995; Qu et al. 2001; Mualla and Belev 2002; Pasquin et al. 2004). Lee et al. (2008) have shown that the seismic design of the bracing-friction damper system for the retrofitting of a damaged building is very effective for the structural response reduction of the building. The FD dissipates energy through sliding, i.e., due to friction between adjoining surfaces. As the energy dissipation of friction damper depends on the relative displacement within the device and is not sensitive to the relative velocity, it is considered as hysteretic device. When compared to other passive dampers, it has advantages of simple mechanism, economical, less maintenance and powerful energy dissipation ability.

The effectiveness of a TMD and a FD to control structural responses caused by different types of excitations is now well established. The first study of the performance of a system with TMD was published by Ormondroyd and Den Hartog (1928). They had studied the response of an undamped linear SDOF system with undamped TMD and viscously damped TMD, under the sinusoidal excitation. Further, the fundamental theory of tuned vibration absorber has been presented in the classical work presented by Den Hartog (1956). Ormondroyd and Den Hartog (1928) developed the ‘fixed point theory’ for viscously damped TMD. Snowdon (1959) extended this theory to system having complex stiffness. Since the applications of TMD are wide, numerous variations of initial TMD have been conceptualized. However, with the exception of few, they emerge to be bound to the assumption of a linear behavior of the primary and secondary system. On the other hand, in several applications, a non-linear behavior of the primary and secondary system has been bound to take into account; first due to noticeable non-linear behavior of primary as well as secondary system; and second, the non-linear behavior of secondary system results in a better performance of the damping device in terms of construction, installation and maintenance.

Inaudi and Kelly (1995) proposed a TMD with the damping provided by two friction devices acting perpendicular to the direction of motion of TMD. The system was non-linear and showed a level of efficiency comparable to that of viscous damper. Abe (1996) considered a structure with a bi-linear behavior to which a TMD with bi-linear hysteretic damper is attached. Ricciardelli and Vickery (1999) considered a SDOF system to which a TMD with linear stiffness and dry friction damping was attached. The system was analyzed for harmonic excitation, and the design criteria for friction TMD system were proposed. Lee et al. (2005) performed a feasibility study of tunable FD and showed that proper sizing of the mass and the fulfillment of the damper criteria, allows the designer to use the benefit of FD and TMD. Almazan et al. (2007) studied and proposed a bi-directional and homogeneous TMD for passive control of vibrations. TMD with non-linear viscous damping has been studied by Rudinger (2007). Gewei and Basu (2010) analyzed dynamic characteristics of SDOF system with friction-tuned mass damper, using harmonic and static linearization solution. Pisal and Jangid (2015) studies seismic response of multi-story structure with multiple tuned mass friction dampers.

Literature review reveals that exclusive and extensive work have been done in the research areas related to TMD and FD; but the tuned mass friction damper (TMFD) has been explored by very few authors. The present study specifically addresses the working of TMFD. The advantage of TMFD is that it can work as an FD when mass is slipping and as an added mass when the mass is in stick state. In this paper, the performance of a TMFD attached to a damped linear SDOF structure is investigated under seismic and harmonic excitations. The specific objectives of the study are: (1) to formulate the equations of motion and develop solution procedure for the response of SDOF structure with TMFD, under harmonic and seismic excitations, numerically; (2) to investigate the existence of different modes of vibration; (3) to investigate the influence of important parameters such as mass ratio, tuning frequency ratio and damper slip force on the performance of TMFD; (4) to obtain the optimum values of important parameters such as tuning frequency ratio and damper slip force for different mass ratios of TMFD; and (5) to compare the response of SDOF structure attached with TMFD to the response of same structure without TMFD.

Modeling of SDOF structure with TMFD

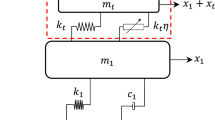
The system arrangement considered for the study consists of two-degree-of-freedom (2-DOF) system as shown in Fig. 1. $m_{\text{p}}$, $k_{\text{p}}$ and $c_{\text{p}}$ represent the mass, linear stiffness and viscous damping of primary structure, respectively.

Fig. 1

SDOF structure with TMFD

The natural frequency of the primary structure can be shown as:

$$\omega_{\text{n}} = \sqrt {k_{\text{p}} /m_{\text{p}} }$$

(1)

The damping ratio and time period of the primary structure can be shown as:

$$\xi_{\text{p}} = c_{\text{p}} /2\sqrt {k_{\text{p}} m_{\text{p}} }$$

(2)

$$T_{n} = 2\pi /\omega_{n}$$

(3)

The secondary system termed as TMFD has a mass $m_{\text{d}}$, linear stiffness $k_{\text{d}}$ and a friction damper with slip force $f_{\text{s}}$. The friction force mobilizing in the damper has ideal Coulomb-friction characteristics as shown in Fig. 2.

Fig. 2

Modeling of force in friction damper

The natural frequency of TMFD can be shown as:

$$\omega_{\text{d}} = \sqrt {k_{\text{d}} /m_{\text{d}} }$$

(4)

The mass ratio and tuning frequency ratio of the two systems are defined as:

$$\mu \, = \,m_{\text{d}} /m_{\text{p}}$$

(5)

$$f\, = \,\omega_{d} /\omega_{n}$$

(6)

where $\mu$ represents the mass ratio; and $f$ represents the tuning frequency ratio.

Governing equations of motion and solution procedure

The governing equations of motion of 2-DOF system, when subjected to dynamic excitations are expressed as:

$$m_{\text{p}} {\ddot{x}}_{\text{p}} + \,c_{\text{p}} \dot{x}_{\text{p}} + k_{\text{p}} x_{\text{p}} \, + k_{\text{d}} (x_{\text{p}} - x_{\text{d}} ) = - m_{\text{p}} {\ddot{x}}_{\text{g}} (t)\, + \,f_{\text{s}} \,\text{sgn} (\dot{x}_{\text{d}} - \dot{x}_{\text{p}} )\;,$$

(7a)

$$m_{\text{d}} {\ddot{x}}_{\text{d}} \, - k_{\text{d}} (x_{\text{p}} - x_{\text{d}} ) = - m_{\text{d}} {\ddot{x}}_{\text{g}} \,(t) - \,f_{\text{s}} \,\text{sgn} (\dot{x}_{\text{d}} - \dot{x}_{\text{p}} )\;,$$

(7b)

where $(x_{\text{d}} - x_{\text{p}} )$ can be termed as stroke or displacement of the damper and ‘sgn’ denotes the signum function.

Equations (7) can be written in matrix form as:

$$M\,{\ddot{X}}(t)\, + C\,\dot{X}(t)\, + \,K\,X(t)\, = \,E\,{\ddot{x}}_{\text{g}} (t) + \,B\,F_{\text{s}} (t)$$

(8)

$$X(t)\; = \left\{ \begin{aligned} x_{\text{p}} (t) \hfill \\ x_{\text{d}} (t) \hfill \\ \end{aligned} \right\}\;,$$

(9)

where $x_{\text{p}} (t)$ and $x_{\text{d}} (t)$ denote the displacement relative to the ground, of the primary and secondary system, respectively; $M$, $C$ and $K$ denote the mass, damping and stiffness matrix of the configured system, respectively; E and B are placement matrices for the excitation force and friction force, respectively; $X(t)$, $\dot{X}(t)$ and ${\ddot{X}}(t)$ are the relative displacement, velocity and acceleration vector of the configured system, respectively; ${\ddot{x}}_{\text{g}} (t)$ denotes the ground acceleration; and $F_{\text{s}} (t)$ denotes the friction force provided by the TMFD. These matrices are expressed as:

$$M\; = \;\left[ {\begin{array}{*{20}c} {m_{\text{p}} } & 0 \\ 0 & {m_{\text{d}} } \\ \end{array} } \right]$$

(10)

$$C\; = \;\left[ {\begin{array}{*{20}c} {c_{\text{p}} } & 0 \\ 0 & 0 \\ \end{array} } \right]\,$$

(11)

$$K\; = \;\left[ {\begin{array}{*{20}c} {k_{\text{p}} + k_{\text{d}} } & { - k_{\text{d}} } \\ { - k_{\text{d}} } & {k_{\text{d}} } \\ \end{array} } \right]\,$$

(12)

$$F_{\text{s}} = f_{\text{s}} \;\text{sgn} \;(\dot{x}_{\text{d}} - \dot{x}_{\text{p}} )$$

(13)

where $\dot{x}_{\text{d}}$ denotes the velocity of TMFD and $\dot{x}_{\text{p}}$ denotes the velocity of the primary structure. The damper forces are calculated using the hysteretic model proposed by Constantinou et al. (1990), using Wen’s equation (Wen 1976), which is expressed as:

$$F_{\text{s}} = f_{\text{s}} \,Z_{\text{h}}$$

(14)

where $f_{\text{s}}$ is the limiting friction force or slip force of the damper and $Z_{\text{h}}$ is the non-dimensional hysteretic component which satisfies the following first-order non-linear differential equation,

$$q_{\text{h}} \;\frac{{{\text{d}}Z_{h} }}{{{\text{d}}t}} = A_{\text{h}} \;{\kern 1pt} (\dot{x}_{\text{d}} - \dot{x}_{\text{p}} ) - \beta_{\text{h}} \;\left| {(\dot{x}_{\text{d}} - \dot{x}_{\text{p}} )} \right|\,Z_{\text{h}} \;\left| {Z_{\text{h}} } \right|^{{n_{\text{h}} - 1}} - \tau_{\text{h}} \;(\dot{x}_{\text{d}} - \dot{x}_{\text{p}} )\;\left| {Z_{\text{h}} } \right|^{{n_{\text{h}} }} \;,$$

(15)

where $q_{\text{h}}$ represents the yield displacement of frictional force loop, and $A_{\text{h}}$, $\beta_{\text{h}}$, $\tau_{\text{h}}$ and $n_{\text{h}}$ are non-dimensional parameters of the hysteretic loop which control the shape of the loop. These parameters are selected in such a way that it provides typical Coulomb-friction damping. The recommended values of these parameters are taken as $q_{\text{h}}$ = 0.0001 m, $A_{\text{h}}$ = 1, $\beta_{\text{h}}$ = 0.5, $\tau_{\text{h}}$ = 0.05, and $n_{\text{h}}$ = 2, (Bhaskararao and Jangid 2006a). The hysteretic displacements component $Z_{\text{h}}$ is bounded by peak values of $\pm 1$ to account for the conditions of sliding and non-sliding phases. The limiting friction force or slip force of the friction damper is expressed in the normalized form by $R_{\text{f}}$, which can be expressed as:

$$R_{\text{f}} \, = \,\frac{{f_{\text{s}} }}{{m_{\text{d}} \cdot g}},$$

(16)

where $\,g$ represents the acceleration due to gravity.

The governing equations of motion shown by Eq. (8) are solved using the state-space method (Hart and Wong 2000; Lu 2004) and re-written as:

$$\dot{Z}(t + 1) = AZ(t + 1) + E{\kern 1pt} {\ddot{x}}_{{{\text{g}}\,}} (t + 1) + BF_{\text{s}} (t + 1)\;,$$

(17)

$$Z(t)\; = \;\left\{ {\begin{array}{*{20}c} {x_{p} {\kern 1pt} (t)} \\ {x_{{d{\kern 1pt} }} (t)} \\ {\dot{x}_{p} {\kern 1pt} (t)} \\ {\dot{x}_{d} (t)} \\ \end{array} } \right\}\;,$$

(18)

where vector $Z(t)$ denotes the state of the structure; $A$ represents the system matrix that is composed of mass, stiffness and damping matrices of the configured system and can be expressed as:

$$A = \left[ \begin{aligned} 0\quad \quad \quad \quad \quad I \hfill \\ M^{ - 1} K\quad M^{ - 1} C \hfill \\ \end{aligned} \right]\;,$$

(19)

where $I$ denotes the identity matrix.

Eq. (17) is further discretized in time domain assuming the excitation and control forces to be constant within any time interval; the solution may be written in an incremental form (Hart and Wong 2000; Lu 2004) as,

$$Z(j + 1) = A_{\text{d}} Z(j) + E_{\text{d}} {\ddot{x}}_{{{\text{g}}\,}} (j) + B_{\text{d}} F_{\text{s}} (j)\;,$$

(20)

where $(j)$ and $(j + 1)$ denote that the variables are evaluated at the $(j)th$ and $(j + 1)th$ time step.

$$B_{\text{d}} \, = \;A^{ - 1} \,(A_{\text{d}} - I)\,B$$

(21a)

$$E_{\text{d}} \, = \;A^{ - 1} \,(A_{\text{d}} - I)\,E$$

(21b)

Also, $A_{\text{d}} = e^{A\Delta t}$ denotes the discrete-time system matrix with $\Delta t$ as the time interval.

Numerical study

For the numerical study, the damping ratio of the SDOF structure is taken as 2 %. The natural frequency of the SDOF structure is considered to be 2 Hz which indicates that the fundamental time period of the structure is 0.5 s. The total mass of primary structure, $m_{\text{p}}$, is taken as 10,000 kg.

Numerical study for harmonic excitation

The response of primary structure with TMFD is investigated under harmonic ground excitation. The harmonic excitation is taken as ${\ddot{x}}{}_{{{\text{g}}{\kern 1pt} }}(t) = {\kern 1pt} {\kern 1pt} 0.1\,g\,\,\sin \;(4\pi {\kern 1pt} t)$. Also, the influence of parameters such as mass ratio $\mu$, tuning frequency ratio $f$ and friction force $f_{\text{s}}$ on the response of the system is investigated by varying mass $m_{\text{d}}$ and natural frequency $\omega_{\text{d}}$ of the TMFD, respectively. The response quantity considered for the study is peak value of displacement amplification factor $R_{\text{d}}$ of the primary structure as the stresses in the structural members are directly proportional to the displacement of the structure. $R_{\text{d}}$ is a dimensionless quantity which can be defined as the ratio of peak displacement response, $x_{\text{p}}$, to the peak static displacement response, $x_{\text{pst}}$, of the primary structure.

The value of the stiffness of the structure is chosen such as to provide fundamental time period of 0.5 s. For the present study, the results are obtained with time interval, $\Delta t = 0.02$. The number of iteration in each time step is taken as 200 to determine the incremental frictional force in the TMFD.

Effect of TMFD and excitation frequency

Figure 3 depicts the comparison of peak displacement amplification factor, $R_{\text{d}}$ of the primary structure with TMFD and without TMFD for different values of $R_{\text{f}}$. To investigate the effect of excitation frequency, the value of $\omega_{\text{n}}$ is kept constant and value of excitation frequency $\omega$ is varied.

Fig. 3

Comparison of peak displacement amplification factor, R _d of structure with and without TMFD

In case of controlled system with a high value of normalized slip force $(R_{\text{f}} \, = \,5)$, the TMFD and primary structure behave as a rigidly connected structure and no relative motion between the damper and primary structure takes place. Thus, TMFD behaves as an additional mass, resulting in a modified SDOF system having response similar to the uncontrolled system but having lower resonant frequency. Similarly, in case of controlled system with a lower value of normalized slip force $({\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{e}} . {\text{g}} .\;{\kern 1pt} R_{\text{f}} \, = \,0.01)$, the two peaks are observed in the response curve of the system. It shows that the system is behaving as a 2-DOF system and relative motion between the two systems occurs. Also, there exists a ranges of excitation frequencies at which the system behaves as a modified SDOF system (i.e., as an additional mass) and its responses are higher than the 2-DOF system, and outside this range, the response of modified SDOF system has response lower than 2-DOF system. Thus, there exists a range of excitation frequencies at which the response can be controlled by modified SDOF system, and outside this range, the response can be controlled by 2-DOF system.

To confirm the periodic behavior of the system with sliding interface under harmonic ground excitation, as reported by many researchers in the past (Westermo and Udwadia 1982; Younis and Tadjbakhsh 1984; Matsui et al. 1991; Iura et al. 1992; Bhaskararao and Jangid 2006b), time variation of velocities of the two system (i.e., $\dot{x}_{p} (t)$ and $\dot{x}_{\text{d}} (t)$) is plotted in Fig. 4, for three different values of normalized damper slip force. The parameters considered for the study are $\mu$ = 0.02, $\xi_{\text{p}}$ = 0.02, ${\omega \mathord{\left/ {\vphantom {\omega {\omega_{\text{n}} }}} \right. \kern-0pt} {\omega_{\text{n}} }}$ = 1 and $f$ = 1. It is observed from the figure that for relatively higher value of $R_{\text{f}}$, both systems vibrate together with same value of $\dot{x}_{\text{p}}$ and $\dot{x}_{\text{d}}$ (i.e., similar response), known as stick mode (ref Fig. 4a), which shows that TMFD is working as an additional mass. However, the value of $R_{\text{f}}$ decreases the response and mode of vibration changes from stick to stick–slip mode (Fig. 4b, c), which shows that TMFD is working as FD. Hence, the system with TMFD subjected to harmonic excitation responds in two different periodic modes, namely stick mode and stick–slip mode, depending on the system parameters and level of excitation. The similar observations are noticed in the hysteretic loop of the system for different values of normalized damper slip force as shown in Fig. 5. In this figure, vertical lines show the stick state of the damper, while the slip state is recognized by horizontal lines. Thus, the system with TMFD responds in two different periodic modes, namely, stick mode and stick–slip mode, depending on the system parameters and level of excitation under harmonic excitation.

Fig. 4

Velocity response of structure with TMFD

Fig. 5

Hysteretic loops for structure with TMFD

Effect of friction force

To investigate the effect of damper slip force, the variation of peak displacement amplification factor, $R_{\text{d}}$ of primary structure is plotted against the normalized damper friction force, $R_{\text{f}}$ in Fig. 6. The value of $R_{\text{f}}$ is varied from 0.01 to 1, for different values of mass ratio and tuning frequency ratio. It is observed from Fig. 6 that peak displacement amplification factor, $R_{\text{d}}$ of the primary structure decreases with increase in the value of $R_{\text{f}}$ for all values of $\mu$ and $f$ up to certain point, and after that, it gradually increases. It shows that there exists an optimum value of slip force for which the $R_{\text{d}}$ of primary structure attains its minimum value implying that at this value, TMFD is very effective in controlling the response of the primary system. It is also observed that as the value of mass ratio and tuning frequency ratio increases, the value of $R_{\text{f}}$ tends to decrease with the higher reduction in the value of $R_{\text{d}}$. Thus, an optimum value of $R_{\text{f}}$ exists, at which the response of the system decreases significantly, and at this value of $R_{\text{f}}$, TMFD is very effective in controlling the response of the primary structure.

Fig. 6

Variation of peak displacement amplification factor, R _d with normalized damper slip force

Effect of tuning frequency ratio

The effect of tuning frequency ratio on the peak displacement amplification factor, $R_{\text{d}}$ of the primary structure is shown in Fig. 7. The response of the primary system is plotted for different values of mass ratio and normalized slip force by varying $f$ from 0.1 to 2. For this purpose, $\omega_{\text{n}}$ is kept constant and $\omega_{\text{d}}$ is varied. It is observed that the peak value of $R_{\text{d}}$ of the primary structure decreases with increase in tuning frequency ratio up to certain value and further increases with increase in tuning frequency ratio. The optimum value of tuning frequency ratio is lying in the range 0.9–1, depending on the mass ratio following the inverse relationship with the mass ratio. It shows that there exists an optimum value of tuning frequency ratio at which system has its minimum response. It is also observed that there is a reduction in the value of $R_{\text{d}}$ with respect to the value of normalized slip force. Thus, at an optimum value of tuning frequency ratio, the response of the primary structure reduces to its maximum value.

Fig. 7

Variation of peak displacement amplification factor, R _d with tuning frequency ratio

Effect of mass ratio

The effect of mass ratio on peak displacement amplification factor, $R_{\text{d}}$ of primary structure is studied in Fig. 8 by plotting the peak value of $R_{\text{d}}$ of primary structure against the mass ratio, $\mu$ for different values of tuning frequency ratio and normalized slip force. It is observed that there is significant reduction in the value of $R_{\text{d}}$ with the increase in the value of mass ratio up to a certain point for all values of slip force $R_{\text{f}}$, and after that, it tends to be a constant value. This indicates that there is no advantage in increasing the mass ratio beyond 10 % and, at maximum up to 15 %. Also, as the value of tuning frequency ratio increases, there is reduction in the value of $R_{\text{d}}$. Hence, at an optimum value of mass ratio, the response of the primary structure reduces significantly.

Fig. 8

Variation of peak displacement amplification factor, R _d with mass ratio

Optimum parameters

It is observed from the numerical study that there exists a range of optimum values of controlling parameters which influences the performance of TMFD. If the optimum values of influencing parameters are chosen appropriately, there is significant reduction in response of the primary structure and the TMFD works effectively. It is also observed that these parameters are inter-related, i.e., the value of one parameter changes with respect to the value of other parameter. Thus, the optimum values of the tuning frequency ratio and normalized slip force are found out for the different values of mass ratio along with the percentage reduction in the value of $R_{\text{d}}$ as mentioned in Table 1. It is observed from the table that as the value of mass ratio increases, the optimum value of tuning frequency ratio decreases and the optimum value of normalized slip force is almost constant. Also, with the proper selection of optimum values of controlling parameters, response can be reduced to 97 %. Thus, by selecting appropriate optimum values of controlling parameters, higher efficiency of TMFD with higher response reduction can be achieved.

Table 1 Optimum parameters of TMFD for harmonic ground excitation

Numerical study for earthquake excitation

In this section, the response of primary structure with TMFD is investigated under earthquake excitations. The earthquake time histories along with their peak ground acceleration (PGA) and components which are used for this study are represented in Table 2. The earthquake ground motions and their corresponding fast Fourier transform (FFT) plots are shown in Figs. 9 and 10, respectively.

Table 2 Details of earthquakes considered for numerical study

Fig. 9

Acceleration time histories of selected earthquake ground motions

Fig. 10

FFT amplitudes of selected earthquakes

The important parameters on which the efficiency of TMFD depends such as mass ratio, tuning frequency ratio and slip force are discussed here. The efficiency of TMFD is investigated by comparing the response of the structure without TMFD (also known as uncontrolled system) to the response of the structure with TMFD (also known as controlled system). For this purpose, the input parameters of the primary structure are kept constant and parameters of the TMFD are varied.

The value of the stiffness of the structure is chosen such that it provides fundamental time periods of 0.25, 0.50 and 1.00 s, respectively. For the present study, the results are obtained with the interval, $\Delta t = 0.02,\,\,0.01$, respectively. The number of iterations in each time step is taken as 50-200 to determine the incremental frictional force of the TMFD.

Effect of mass ratio

The effect of mass ratio on the performance of TMFD is studied by plotting the peak displacement response of the structure against the varying mass ratio in Fig. 11. The time periods of the primary structure considered for the study are 0.25, 0.50 and 1.00 s, respectively, which represents the variation from stiff to flexible structure. It is observed that the peak response of the structure for the considered earthquake excitations reduces with increase in the mass ratio up to a certain point, and after that, it reduces marginally. This indicates that there is no advantage in increasing the mass ratio beyond this point. It is also observed that the optimum value of mass ratio changes with respect to the type of structure. Thus, it is visible from Fig. 11 that at an optimum value of mass ratio, the response of the primary structure reduces significantly.

Fig. 11

Variation of peak displacement with mass ratio a Imperial Valley, 1940, b Landers, 1992; c Kobe, 1995

Effect of tuning frequency ratio

Figure 12 shows the variation of peak displacement response of the primary structure against the tuning frequency ratio,$f$ for different values of the fundamental time period of the primary structure. For this study, the time period of primary structure is kept constant, while the time period of the TMFD is varied in such a way that $f$ varies from 0.1 to 2. It is noted from the figure that there is reduction in peak displacement of the structure when $f$ is in the range of 0.8–1.0. Further, at the tuning frequency ratio which is far from this range, the values of peak responses are higher. This reveals that at an optimum value of tuning frequency ratio, the response of the primary structure reduces to its minimum value.

Fig. 12

Variation of peak displacement with tuning frequency ratio a Imperial Valley, 1940; b Landers, 1992; c Kobe, 1995

Effect of friction force

To investigate the effect of normalized damper friction force, the variation of peak displacement of main structure is plotted with respect to the varying normalized friction force, $R_{\text{f}}$ in Fig. 13. It is observed that the peak displacement response of the structure decreases with increase in friction force of the damper up to a certain point, and after that, it again increases with increase in the value of friction force, $R_{\text{f}}$. It shows that an optimum value of normalized slip force exists at which the system reaches its minimum response. It is also observed that the range of variation of slip force depends on the characteristics of an earthquake. Further, there is more reduction in the peak displacement of the flexible structure as compared to the reduction in peak displacement of stiff structure. This indicates that TMFD is more beneficial in reducing the response of the flexible structure in comparison to the stiff structure. Thus, an optimum value of $R_{\text{f}}$ exists at which the response of the system decreases significantly, and at this value of $R_{\text{f}}$, TMFD is very effective in controlling the response of the primary structure. Also, the range of variation of slip force depends on the characteristics of an earthquake. TMFD is more beneficial in reducing the response of the flexible structure as compared to the stiff structure.

Fig. 13

Variation of peak displacement with R _f a Imperial Valley, 1940; b Landers, 1992; c Kobe, 1995

Optimum parameters

It is observed from the numerical study that there exists a range of optimum values of parameters such as friction force, mass ratio and tuning frequency ratio, which influences the performance of TMFD. If the optimum values of these parameters are selected appropriately, there is significant reduction in response of the primary structure and the TMFD works effectively. It is also observed that the variation in the range of optimum values of controlling parameters of the system depends on the dynamic characteristics of earthquakes. Thus, the optimum values of the tuning frequency ratio and normalized slip force were found out for the different values of mass ratio along with the percentage reduction in the peak value of displacement for considered earthquakes. These parameters are presented in Tables 3, 4 and 5 for Imperial Valley (1940), Landers (1995) and Kobe (1995) earthquakes, respectively. It is observed from these tables that as the value of mass ratio increases, the optimum value of tuning frequency ratio decreases and, on the other hand, the optimum value of $R_{f}$ increases. Further, the optimum values of the parameters mentioned in these tables are used to depict the comparison of displacement time history of primary structure without TMFD and with TMFD for the Imperial Valley (1940), Landers (1992) and Kobe (1995) earthquake, respectively, in Fig. 14. It is observed that the displacement response of the primary structure without TMFD is relatively high. On the other hand, the response of the primary structure with TMFD is significantly less. Thus, TMFD can be a more effective and potential device to control response of the structure, if optimum parameters are appropriately selected.

Table 3 Optimum parameters of TMFD for Imperial Valley (1940) earthquake

Table 4 Optimum parameters of TMFD for Landers (1992) earthquake

Table 5 Optimum parameters of TMFD for Kobe (1995) earthquake

Fig. 14

Comparison of displacement response time history of main structure with and without TMFD

Conclusions

The response of an SDOF structure with TMFD is investigated for harmonic and earthquake excitation. The governing differential equations of motion are solved numerically, using the state-space method, to find out the response of system in different modes of vibration. The parametric study is also conducted to investigate the fundamental characteristics of the TMFD and the effect of important parameters such as mass ratio, tuning frequency ratio and friction force on the efficiency of TMFD. The peak displacement amplification factor and peak displacement response of the main structure are considered to study the performance of TMFD for harmonic and seismic excitation, respectively. On the basis of trends of results obtained, the following conclusions are drawn:

• 1. There exists a range of excitation frequencies at which the response can be controlled by modified SDOF system, and outside this range, the response can be controlled by 2-DOF system.

• 2. The system with TMFD subjected to harmonic or earthquake excitation responds in two different periodic modes, namely, stick mode and stick–slip mode, depending on the system parameters and level of excitation.

• 3. An optimum value of $R_{\text{f}}$ exists, at which the response of the system decreases significantly, and at this value of $R_{\text{f}}$, TMFD is very effective in controlling the response of the primary structure. In case of earthquake excitation, the range of variation of slip force depends on the characteristics of an earthquake. Also, the optimum value of $R_{\text{f}}$ increases with the increase in value of mass ratio.

• 4. At an optimum value of tuning frequency ratio, the response of the primary structure reduces to its minimum value. As the value of mass ratio increases, the optimum value of tuning frequency ratio decreases.

• 5. At an optimum value of mass ratio, the response of the primary structure reduces significantly.

• 6. TMFD is more beneficial in reducing the response of the flexible structure as compared to the stiff structure.

• 7. TMFD can be a more effective and potential device to control the response of the structure, if optimum parameters are appropriately selected.