Instability due to trapped electrons in magnetized multi-ion dusty plasmas

Abstract

An attempt has been made to find out the effects of trapped electrons in dust-ion-acoustic solitary waves in magnetized multi-ion plasmas, as in most space plasmas, the hot electrons follow the trapped/vortex-like distribution. To do so, we have derived modified Zakharov–Kuznetsov equation using reductive perturbation method and its solution. A small-$k$ perturbation technique was employed to find out the instability criterion and growth rate of such a wave.

Introduction

Dust particles are found not only in laboratory plasmas (plasma processing and plasma crystal where low temperature plasmas are used) but also in astrophysical plasma systems (planetary rings, interstellar molecular clouds, protostellar disks, interstellar and circumstellar clouds, asteroid zones, planetary atmospheres, interstellar media, cometary tails, nebulae, Earth’s ionosphere, etc) [1–9]. Therefore the electrostatic modes in dusty plasma have become a field of great interest. These dust grains in plasmas are very small (micron or sub-micron sized) and can have the opposite polarity due to the size effect on secondary emission; the smaller one is positively charged, whereas the larger one is negative charged [10]. The important elementary dust grain charging processes are (1) interaction of dust grains with gaseous plasma particles, (2) interaction of dust grains with energetic particles (electrons and ions) and (3) interaction of dust grains with photons. When dust grains are immersed in a gaseous plasma, the plasma particles are collected by the dust grains which act as probes. The dust grains are, therefore, charged by the collection of the plasma particles flowing onto their surfaces. When energetic plasma particles are incident onto a dust grain surface, they are either backscattered/reflected by the dust grain or they pass through the dust grain material. During their passage they may lose their energy partially or fully. A portion of the lost energy can go into exciting other electrons that in turn may escape from the material. The emitted electrons are known as secondary electrons. These secondary electrons make the grain surface positive. The interaction of photons incident onto the dust grain surface causes photoemission of electrons from the dust grain surface. The dust grains, which emit photoelectrons, may become positively charged. The emitted electrons collide with other dust grains and are captured by some of these grains which may become negatively charged. There are, of course, a number of other dust grain charging mechanisms [11], namely thermionic emission, field emission, radioactivity, impact ionization, etc. These are significant only in some different special circumstances. But both the ion temperature and ion-neutral collisions play important roles in the dust grain charging. With the decrease of ion temperature due to ion-neutral collisions, the magnitude of dust grain charge decreased accordingly. The grain charge in a collisionless regime is estimated to be much higher than that in a collisional regime [12] (Some dusty plasma parameters are shown in Table 1). The existence of positive and negative ion plasma are shown in the experimental investigation of Cooney et al. [13]. The latter may also support the formation of ion acoustic shocks when the ratio of the negative ion to positive ion number density exceeds about 0.9 [14]. It should be noted that collective interactions in positive and negative ion plasmas have potential applications in natural and technological environments like the D-region of the Earth’s ionosphere, the Earth’s mesosphere, the solar photosphere, and the microelectronics plasma processing reactors [15].

Table 1 Dusty plasma parameters [11, 16]

In 2008 Sayed et al. [17] considered non-magnetized dusty plasma mode having positive and negative ions with positive and negative dust and Maxwellian distributed electrons. But the most real plasmas are magnetized, and it can change its characteristics according to the wave direction. Considering this magnetic properties Haider et al. [18] have studied the instability of solitary structure containing positive and negative ions, Mxwellian electrons and positively and negatively charges stationary dust. These modes are only valid if a complete depletion of the background electrons and ions is possible, and both positive and negative dust fluids are cold. In practice, the hot electrons may not follow a Maxwellian distribution due to the formation of phase space holes caused by the trapping of hot electrons in a wave potential. Accordingly, in most space plasmas, the hot electrons are trapped following the vortex-like distribution [19–21]. Rahaman and Manun [22] have explained the effect of trapped electrons in dust-ion-acoustic (DIA) solitary waves (SWs) with arbitrarily charged dust. But they did not consider magnetic field. Later Haider et al. [23] have also studied the propagation of SWs in the presence of magnetized plasma with both positive and negative ions fluid, vortex-like distributed electrons and charge fluctuating stationary dusts. They have derived modified Korteweg-de Vries (mK-dV) equation and its solution. K-dV or mK-dV equation has studied for one dimensional cases. So, a necessary is felt to study the SWs in three dimensionally and its instability criterion as well as its growth rate.

In the present work, the propagation of DIA Solitary structures have been studied in magnetized dusty plasma consisting negatively and positively charged ion fluid, trapped electrons following vortex-like distribution, and arbitrary charged stationary dust where restoring force provided by the plasma thermal pressure of electrons and the inertia is due to the ion mass for instability analysis. Using reductive perturbation method [24] we have derived the modified Zakharov–Kuznetsov (mZK) equation which is also known as mK-dV equation in three dimension and its solution. We have also studied instability criterion and growth rate for such a SWs.

Basic equations

In the present work, collisionless magnetized dusty plasmas have been considered. We assume that (1) the ions (negatively and positively charged) are mobile, (2) the electrons follow the vortex-like distribution, and (3) charge fluctuating stationary dust. We have also consider that there is an external static magnetic field ${\mathbf{B}}_{0}$ acting along the $z$-direction (${\mathbf{B}}_{0}=\hat{k}{ B_0}$), where $\hat{k}$ is the unit vector along the $z$-direction which is very strong that the electrons and dusts are moving along the magnetic field direction very fast, i.e. the response of electrons and dusts look like as that in the unmagnetized plasma. The nonlinear dynamics of the DIA SWs propagating in such a multi-component dusty plasma is governed by

$$\begin{aligned}&\frac{\partial n_{\rm s}}{\partial t}+\nabla \cdot (n_{\rm s} {\mathbf u} _{\rm s})=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial {\mathbf u} _n}{\partial t}+({\mathbf u} _n\cdot \nabla ){\mathbf u} _n=\nabla \psi -\omega _{cn} {\mathbf u} _n\times \hat{k}, \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial {\mathbf u} _p}{\partial t}+({\mathbf u} _p\cdot \nabla ){\mathbf u} _p=-\beta \nabla \psi +\beta \omega _{cn} {\mathbf u} _p\times \hat{k}, \end{aligned}$$

(3)

$$\begin{aligned}&\bigtriangledown ^2\psi =\mu _0n_{\rm e}+n_n-\mu _pn_p-j\mu _{\rm d}, \end{aligned}$$

(4)

where $n_{\rm s}$ ($n_n$/$n_p$) is the ion number density (negative/positive) normalized by its equilibrium value $n_{\rm s0}$, $u_n$ ($u_p$) is the negative (positive) ion fluid speed normalized by $C_n=(k_{\mathrm{B}}T_{\rm e}/m_n)^{1/2}$, with $k_\mathrm{B}$ is the Boltzmann constant, $T_{\rm e}$ is the temperature of electrons and $m_n$ being the rest mass of negative ions. $\psi$ is the DIA wave potential normalized by $k_{\mathrm{B}}T_{\rm e}/e$, with $e$ being the magnitude of the charge of an electron. $\omega _{cn}$ is the negative ion cyclotron frequency $(eB_0/m_{\rm nc})$ normalized by plasma frequency $\omega _{\rm pn}=(4\pi n_{n0}e^2/m_n)^{1/2}$ with $c$ being the speed of light. The time variable $(t)$ is normalized by ${\omega _{pn}}^{-1}$, the space variables are normalized by Debye radius $\lambda _D=(k_{\mathrm{B}}T_{\rm e}/4 \pi n_{n0}e^2)^{1/2}$.

At equilibrium we have

$$\begin{aligned}&n_{p0}+jn_{d0}=n_{\rm e0}+n_{n0}, \end{aligned}$$

where, $jn_{d0}=n_{d+}-n_{d-}$ with $n_{d+}$ being the positive dust number density and $n_{d-}$ being the number density of negative dust. $j=1$ for the condition $n_{d+}>n_{d-}$ and $j=-1$ for the condition $n_{d+}<\,n_{d-}$, i.e. the value of $j$ dependents on net charge of dust grain and $\beta$ is the mass ratio of negative ion to positive ion ($m_n/m_p$). We can also write

$$\begin{aligned}&\mu _0=\mu _p+j\mu _d-1, \end{aligned}$$

(5)

where, $\mu _0 = n_{\rm e0}/n_{n0}$, $\mu _p = n_{p0}/n_{n0}$ and $\mu _d = n_{d0}/n_{n0}$.

To model the electron distribution in presence of trapped particles, we employ a vortex-like electron distribution of Schamel [19], which solves the Vlasov equation and using the similar procedure of Haider et al. [23] one can have the distribution of electron number density as

$$\begin{aligned}&n_{\rm e}=\left[ 1+\psi -\frac{4(1-\sigma )}{3\sqrt{\pi }}\psi ^{3/2} +\frac{1}{2}\psi ^{2}\right] . \end{aligned}$$

(6)

Derivation of mZK equation

To derive a dynamical equation for the nonlinear propagation of the electrostatic waves in a magnetized dusty plasma, under consideration, we use (1)–(4) and (6), and employ the reductive perturbation technique [24]. To do so, introducing the stretched coordinates [25–28]

$$\begin{aligned} \left. \begin{array}{l} X=\epsilon ^{1/4}x,\\ Y=\epsilon ^{1/4}y,\\ Z=\epsilon ^{1/4}(z-V_0t),\\ \tau \,=\epsilon ^{3/4}t,\ \end{array} \right\} \end{aligned}$$

(7)

where $\epsilon$ is a smallness parameter ($0<\epsilon <1$) measuring the weakness of the dispersion and $V_0$ is the Mach number (the phase speed normalized by $C_i$). $n_i$, $u_i$ and $\psi$ can be expand about their equilibrium values in power series of $\epsilon$, viz.,

$$\begin{aligned} \left. \begin{array}{l} n_s\,\,\,\, =1+\epsilon n_s^{(1)}+\epsilon ^{3/2}n_s^{(2)}+ \cdot \cdot \cdot ,\\ \psi \,\,\,\, =\epsilon \psi ^{(1)}+\epsilon ^{3/2}\psi ^{(2)}+\cdot \cdot \cdot ,\\ u_{sx}\,=\epsilon ^{5/2}u_{sx}^{(1)}+\epsilon ^{3/2}u_{sx}^{(2)} +\cdot \cdot \cdot ,\\ u_{sy}\,=\epsilon ^{5/2} u_{sy}^{(1)}+\epsilon ^{3/2}u_{sy}^{(2)}+ \cdot \cdot \cdot ,\\ u_{sz}\,=\epsilon u_{sz}^{(1)}+\epsilon ^{3/2}u_{sz}^{(2)}+ \cdot \cdot \cdot , \end{array} \right\} \end{aligned}$$

(8)

here, $s$ represents the species ($n$ for negative ions and $p$ for positive ions).

Using the stretched coordinates and (8) in (1)–(4) and equating the coefficients of $\epsilon ^{5/4}$ from the continuity and momentum equation, one can obtain the $x$-, $y$- and $z$- components of momentum equations, and first-order continuity equations as

$$\begin{aligned} \left. \begin{array}{l} u_{nx}^{(1)}=-\frac{1}{\omega _{cn}}\frac{\partial \psi ^{(1)}}{\partial Y},u_{ny}^{(1)}=\frac{1}{\omega _{cn}}\frac{\partial \psi ^{(1)}}{\partial X},\\ u_{nz}^{(1)}=-\frac{1}{V_0}\psi ^{(1)}, n_n^{(1)}=-\frac{1}{V_0^2}\psi ^{(1)},\\ u_{px}^{(1)}=-\frac{1}{\omega _{cn}}\frac{\partial \psi ^{(1)}}{\partial Y}, u_{py}^{(1)}=\frac{1}{\omega _{cn}}\frac{\partial \psi ^{(1)}}{\partial X},\\ u_{pz}^{(1)}=\frac{\beta }{V_0}\psi ^{(1)}, n_p^{(1)}=\frac{\beta }{V_0^2}\psi ^{(1)}. \end{array} \right\} \end{aligned}$$

(9)

Equating the coefficients of $\epsilon$ from Poisson’s equation, we get

$$\begin{aligned}&0=\mu _0\psi ^{(1)}+n_n^{(1)}-n_p^{(1)}. \end{aligned}$$

(10)

Using the value of $n_n^{(1)}$ and $n_p^{(1)}$ from (9) and into (10), we get the linear dispersion relation

$$\begin{aligned}&V_0=\sqrt{\frac{1+\beta \mu _p}{\mu _0}} . \end{aligned}$$

(11)

Again, following the same procedure, one can obtain the next higher order continuity equations as

$$\begin{aligned}&\frac{\partial n_s^{(1)}}{\partial \tau }- V_0\frac{\partial n_s^{(2)}}{\partial Z}+\frac{\partial u_{sx}^{(2)}}{\partial X} +\frac{\partial u_{sy}^{(2)}}{\partial Y}+\frac{\partial u_{sz}^{(2)}}{\partial Z}=0, \end{aligned}$$

(12)

here, $s$ represents the species ($n$ for negative ions and $p$ for positive ions).

The $z$-component of momentum equations are

$$\begin{aligned} \left. \begin{array}{l} \frac{\partial u_{nz}^{(1)}}{\partial \tau }- V_0\frac{\partial u_{nz}^{(2)}}{\partial Z}-\frac{\partial \psi ^{(2)}}{\partial Z}=0,\\ \frac{\partial u_{pz}^{(1)}}{\partial \tau }- V_0\frac{\partial u_{pz}^{(2)}}{\partial Z}+\beta \frac{\partial \psi ^{(2)}}{\partial Z}=0. \end{array} \right\} \end{aligned}$$

(13)

To the next higher order of $\epsilon$, i.e. equating the coefficients of $\epsilon ^{3/2}$, we can express Poisson’s equation, and $x$- and $y$- components of the momentum equations for both negative and positive ions as

$$\begin{aligned}&\left( \frac{\partial ^2}{\partial {X}^2}+ \frac{\partial ^2}{\partial {Y}^2}+\frac{\partial ^2}{\partial {Z}^2}\right) \psi ^{(1)} =\mu _0\psi ^{(2)}-\mu _0 \frac{4(1-\sigma )}{3 \sqrt{\pi }} \left[ \psi ^{(1)}\right] ^{3/2}+\,n_n^{(2)}-\mu _pn_p^{(2)}, \end{aligned}$$

(14)

$$\begin{aligned} \left. \begin{array}{l} u_{nx}^{(2)}=-\frac{V_0}{\omega _{cn}^2} \frac{\partial ^2\psi ^{(1)}}{\partial Z\partial X},\quad u_{ny}^{(2)}=-\frac{V_0}{\omega _{cn}^2} \frac{\partial ^2\psi ^{(1)}}{\partial Y\partial Z},\\ u_{px}^{(2)}=\frac{V_0}{\beta \omega _{cn}^2} \frac{\partial ^2\psi ^{(1)}}{\partial Z\partial X},\quad u_{py}^{(2)}=\frac{V_0}{\beta \omega _{cn}^2} \frac{\partial ^2\psi ^{(1)}}{\partial Y\partial Z}. \end{array} \right\} \end{aligned}$$

(15)

Now, using (9)–(15), we can readily obtain

$$\begin{aligned}&\frac{\partial \psi ^{(1)}}{\partial \tau }+AB\sqrt{\psi ^{(1)}}\frac{\partial \psi ^{(1)}}{\partial Z}+\frac{1}{2}A\frac{\partial }{\partial Z}\left[ \frac{\partial ^2}{\partial Z^2}+D\left( \frac{\partial ^2}{\partial X^2}+\frac{\partial ^2}{\partial Y^2}\right) \right] \psi ^{(1)}=0, \end{aligned}$$

(16)

where

$$\begin{aligned} \left. \begin{array}{l} A=\left( \frac{V_0}{\mu _0}\right) ,\\ B=\frac{\mu _0 (1-\sigma )}{\sqrt{\pi }},\\ D=1+\frac{1}{\omega _{cn}^2}+\frac{\mu _p}{\beta \omega _{cn}^2}. \end{array} \right\} \end{aligned}$$

(17)

The Eq. (16) is known as the modified Zakharov–Kuznetsov (mZK) equation.

Fig. 1

(Color online) Variation of the amplitude of solitary wave $\sigma$ and $\mu _d$ for $U=0.1$, $\beta =0.1$, $\mu _p=1.5$ and $\delta =45^\circ$ where upper surface represents the value of $j=1$ and lower surface represent the value of $j=-1$

Fig. 2

(Color online) Variation of the amplitude of solitary wave (dashed curve for $j=1$ and solid curve for $j=-1$) with $\delta$ for $U=0.1$, $\sigma =0.5$, $\mu _p=1.5$ and $\mu _d=0.1$ having the values of $\beta =0.2$ (red), $\beta =0.5$ (blue) and $\beta =0.8$ (black)

Fig. 3

(Color online) Variation of the width of solitary wave (red curve for $j=1$ and blue curve for $j=-1$) with $\delta$ for $U=0.1$, $\beta =0.1$, $\mu _p=1.5$ and $\mu _d=0.1$ having the values of $\omega _{ci}=0.2$ (solid line), $0.4$ (dashed line) and $0.6$ (dotted line)

Fig. 4

(Color online) Variation of the width of solitary wave with $\beta$ and $\mu _p$ for $U=0.1$, $\omega _{ci}=0.5$, $\delta =30^{\circ }$ and $\mu _d=0.1$ where upper surface represents the value of $j=-1$ and lower surface represent the value of $j=1$

Solution of mZK equation

The solution of the mZK equation [29] is given by

$$\begin{aligned}&\psi _0({\cal{Z}})=\psi _m {\mathrm{sech}}^4 ( {\cal{Z}}/\Delta ) , \end{aligned}$$

(18)

where $\psi _m=(15U/8\delta _1)^2$ is the amplitude and $\Delta =\sqrt{16\delta _2/U}$ is the width of the solitary waves with $U$ is soliton speed normalized by the positive ion-acoustic speed $(C_i)$ and

$$\begin{aligned}&\delta _1=A B\cos \delta ,\\&\delta _2=\frac{1}{2}A(\cos ^3\delta +D\sin ^2\delta \cos \delta ). \end{aligned}$$

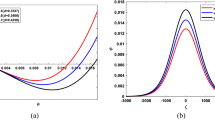
It has been found that the amplitude of the solitary waves is proportional to the soliton speed $U$ and the width is inversely proportional to this soliton speed. That is, the profile of the faster soliton will be taller and narrower then slower one. From (17) we can say that $V_0$, $\mu _0$ and $(1-\sigma )$ are always positive, i.e. $A$ and $B$ are positive. It means that the solitary waves associate with positive potential always. Similar result have found in the work of Rahman and Mamun [22] and Haider et al. [23]. In both the work only positive solitary waves are found. The soliton amplitude increases with increasing temperature ratio of free to trapped electrons for both positive and negative dust grains; but Fig. 1 indicates that amplitude goes higher for increasing the number density of positively charged dust grains whereas the amplitude decreases with increasing the negatively charged dust grain number density. The number density of positive or negative dust grains effect the net charge of the dust grains. As $jn_{d}=n_{d+}-n_{d-},$ the number density of positive dust grains increases in the system it causes the increase the positiveness or decreasing the negativeness of the net charge. Similarly number density of negative dust grains causes the richness of negativity of the net charge. That is the net charge of the dust grains effect the amplitude of the SWs but can’t make it negative. Figure 2 indicates the variation of amplitude of SWs with propagation angle ($\delta$) and mass ratio of negative to positive ions ($\beta$). For both the cases of charge density of dust grains ($j=1$ or $j=-1$) the amplitude increases with propagation angle. It is found that the higher the value of $\beta$, the lower the amplitude. But the variation of width with propagation angle not similar to amplitude. For lower limit of the angle $(0^\circ -50^\circ )$ the width increases with it and decreases for higher limits of the angle $(50^\circ -90^\circ )$ as shown in Fig. 3 for both positively and negatively charged dust grains. It is also clear that an increase of the external magnetic field leads to a decrease in the potential width, i.e., a stronger magnetic field leads to steeper and thus narrower soliton profiles. This can be related to the effects of transverse perturbation. The Larmor radius for the ion motions are smaller at larger gyration frequency and then they contribute less to the nonlinearity of the plasma. Lower nonlinearity leads to lower dispersion which cause the reduction in the soliton width and soliton become more spiky. The width of the SWs is lower for positive dust grains ($j=1$) then negative dust grains ($j=-1$), thus the positive dust grains makes the soliton profile more steeper. From the Fig. 4 we have found that the width of the solitary waves decreases with both $\mu _p$ and $\beta$ but it is higher for $j=-1$ then $j=1$.

Instability

Using the method of small-$k$ perturbation expansion the instability criterion [29–36] of the obliquely propagating solitary waves can be express as $S_i>0$ where

$$\begin{aligned}&S_i=l_\eta ^2\left[ \beta \omega _{cn}^2+(1+\mu _p)\sin ^2\delta \right] +l_\zeta ^2\left[ \beta \omega _{cn}^2 -\frac{9}{7}\left( \beta \omega _{cn}^2 +\beta +\mu _p\right) \tan ^2\delta \right] . \end{aligned}$$

(19)

If this instability criterion $S_i>0$ is satisfied, the growth rate $\Gamma$ of the unstable perturbation of these solitary waves is given by [29–36]

$$\begin{aligned}&\Gamma =\frac{2 U\sqrt{(\beta \omega _{ci}^2+\beta +\mu _p)S_i}}{\sqrt{63} (\beta \omega _{ci}^2+\beta +\mu _p \sin ^2\delta )}. \end{aligned}$$

(20)

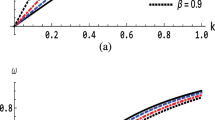
The Eq. (20) represents that the growth rate $\Gamma$ of the unstable perturbation is a linear function of DIA wave speed $U$, but a nonlinear function of propagating angle $\delta$, ion-cyclotron frequency $\omega _{cn}$, negative to positive ion mass ratio $\beta$, ratio of positive ion to negative ion number density $\mu _p$ and direction cosine ($l_\zeta$, and $l_\eta$). The variation of growth rate ($\Gamma$) with nonlinear functions $\delta$, $\omega _{ci}$, $\beta$, $\mu _p$, $l_\zeta$ and $l_\eta$ are shown in Figs. 6, 7 and 8. Earlier, $S_i=0$ plot has been shown in Fig. 5, where the surface indicates that the critical condition of the SWs to be stable or unstable.

Figure 6 indicates the variation of the growth rate with $\delta$ and $\omega _{cn}$ for the value of $U=0.1$, $\mu _p=1.5$, $l_\eta =0.6$, $l_\zeta =0.5$ and $\beta =0.1$. The growth rate varies inversely with both propagating angle and negative ion ciclotron frequency. The growth rate ($\Gamma$) increases with increasing $\mu _p$ but decreases with increasing $\beta$ (Fig. 7). The direction cosines $l_\zeta$ and $l_\eta$ nonlinearly effect the growth rate which is shown in Fig. 8 for $U=0.1$, $l_\eta =0.6$, $l_\zeta =0.5$, $\omega _{cn}=0.5$ and $\delta =10^{\circ }$. $l_\eta$ enhances the growth rate where as $l_\zeta$ does this inversely.

Fig. 5

(Color online) $S_i=0$ curve, showing the variation of $\omega _{cn}$ with $l_\eta$ and $l_\zeta =0.5$ for $\mu _p=1.5$, $\delta =10^{\circ }$ and $\beta =0.1$

Fig. 6

(Color online) Variation of the growth rate ($\Gamma$) with $\delta$ and $\omega _{cn}$ for $U=0.1$, $\mu _p=1.5$, $l_\eta =0.6$, $l_\zeta =0.5$ and $\beta =0.1$

Fig. 7

(Color online) Variation of the growth rate ($\Gamma$) with $\beta$ and $\mu _p$ for $U=0.1$, $l_\eta =0.6$, $l_\zeta =0.5$, $\omega _{cn}=0.5$ and $\delta =10^{\circ }$

Fig. 8

(Color online) Variation of the growth rate ($\Gamma$) with $l_\zeta$ and $l_\eta$ for $U=0.1$, $\beta =0.1$, $\mu _p=1$, $\omega _{cn}=0.5$ and $\delta =10^\circ$

Discussion

The nonlinear propagation of DIA solitary waves in multi component dusty plasma has analyzed where inertia provided by the positive and negative ions and restoring forces are provided by the hot trapped electrons in the presence of external magnetic field using reductive perturbation method. To analyzed this modified ZK equation has been derived as well as its solution. After that, the instability criterion and growth rate has also been studied using small-$k$ perturbation technique. The results can be summarized as follows:

• 1. The trapped electrons are responsible for DA solitary waves which have smaller width, larger amplitude, and higher propagation velocity than that involving Maxwellian electrons, and that they can be represented in the form ${\rm sech}^4({\cal{Z}}/\Delta )$, instead of ${\rm sech}^2({\cal{Z}}/\Delta )$ which is the stationary solution of the standard ZK equation.

• 2. The dynamics of weakly dispersive non-linear DIA waves in the presence of the vortex-like distributed electrons is governed by the mZK equation instead of ZK equation, the stationary solution of which is represented in the form of an inverted secant hyperbolic fourth profile. Thus, the potential polarity of the DIA solitary waves in this system is different from the usual IA, DA or DIA solitary waves.

• 3. The solitary waves may associate with only positive potential.

• 4. The amplitude of SWs for dust grain having positively charged is higher then that for negatively charged but opposite picture is found in the case of width. It means that SWs associated with negative charged dust grain is narrower. It has also been shown that the basic features (height and thickness) of such DIA solitary structures are completely different from those of the usual IA solitary structures.

• 5. The soliton speed $U$ effects the amplitude linearly and the width inversely, the profile of the faster solitary wave will be taller and narrower then slower one.

• 6. The amplitude and width of the solitary wave are significantly modified by the parameter temperature ratio of free and trapped elections.

• 7. The width of the solitary waves decreases with increasing ratio of the positive and negative ion mass, positive ion number density and ion-cyclotron frequency. This indicates that higher the ratio of positive and negative ion mass, positive ion number density and ion-cyclotron frequency narrower the soliton profile. The width of SWs also increases with propagating angle for its lower range, but decreases for its upper range.

• 8. The SWs are more narrower for positively charged dust grain then for negative charged dust.

• 9. The magnitude of the external magnetic field ${\mathbf{B}}_{0}$ has no direct effect on the SW amplitude. However, it does have a direct effect on the width of the SWs and we have found that, as the magnitude of ${\mathbf{B}}_{0}$ increases, the width of the waves decreases, i.e. the magnetic field makes the solitary structures more spiky.

• 10. The parametric regimes for which the solitary waves become stable and unstable are identified. These are ion cyclotron frequency, direction of propagation and direction cosine.

• 11. Direction of propagation, ion cyclotron frequency, direction cosine ($l_\zeta$ and $l_\eta$), ratio of positive and negative mass and positive ion number density are the depending factors which can significantly modify the growth rate ($\Gamma$) of the unstable solitary structures.

It should be noted that the width of the SWs goes zero and amplitude goes to infinity and $\delta \rightarrow 90^\circ$. It means that, for large angles, the assumption that the waves are electrostatic is no longer valid, and we should look for fully electromagnetic structures. Finally, The present work can provide a guideline to explain solitary structure of D-region of the Earth’s ionosphere and mesosphere, solar photosphere and the microelectronics plasma processing reactors, which will be able to detect the DIA solitary structures, and to identify their basic features predicted in this theoretical investigation.