Linear and nonlinear analysis of dust acoustic waves in dissipative space dusty plasmas with trapped ions

Abstract

The propagation of linear and nonlinear dust acoustic waves in a homogeneous unmagnetized, collisionless and dissipative dusty plasma consisted of extremely massive, micron-sized, negative dust grains has been investigated. The Boltzmann distribution is suggested for electrons whereas vortex-like distribution for ions. In the linear analysis, the dispersion relation is obtained, and the dependence of damping rate of the waves on the carrier wave number $k$, the dust kinematic viscosity coefficient $\eta _{d}$ and the ratio of the ions to the electrons temperatures $\sigma _{i}$ is discussed. In the nonlinear analysis, the modified Korteweg–de Vries–Burgers (mKdV–Burgers) equation is derived via the reductive perturbation method. Bifurcation analysis is discussed for non-dissipative system in the absence of Burgers term. In the case of dissipative system, the tangent hyperbolic method is used to solve mKdV–Burgers equation, and yield the shock wave solution. The obtained results may be helpful in better understanding of waves propagation in the astrophysical plasmas as well as in inertial confinement fusion laboratory plasmas.

Introduction

Physics of dusty plasma studies the properties of charged dust in the presence of electrons and ions [31]. These media have been observed in lower and upper mesosphere, planetary magnetosphere, cometary tails, planetary rings, interplanetary spaces, interstellar media, etc. [17, 18, 26, 39]. The importance of studying such task appears also in the laboratory and plasmas technology such as low temperature physics (radio frequency), plasma discharge [5], and fabrication of modern materials such as semi conductors, optical fibres, nanostructural materials, and dusty crystals [6, 45].

Most of space and laboratory dusty plasma environments' dust are negatively charged [26]. However, there are also some space (i.e., upper part of ionosphere or lower part of magnetosphere) and some laboratory environments' dust are positively charged [13, 16, 32]. It has been noticed, theoretically and experimentally, that dust charge dynamics in dusty plasma modifies the existing plasma wave features and introduces different types of new wave modes [3]. For examples, dust ion acoustic (DIA) mode [27, 40], dust acoustic (DA) mode [23, 31], dust-drift mode [42], dust lattice (DL) mode [25] and Shukla–Varma mode [41], etc. Therefore, it is paramount to study linear and nonlinear waves in various configurations of laboratory and space plasma [4, 14, 19, 46]. Nonlinear dust acoustic solitary and shock waves in plasmas have a considerable attention to study the propagation behaviour of the nonlinear waves. Among such theoretical studies on dusty plasma, many authors studied solitary and shock waves in the frame of KdV–Burgers, mKdV–Burgers, KP–Burgers and mKP–Burgers-type equations, which are usually deduced from a dissipative plasma system. The dust fluid dissipation could be caused by dust fluid viscosity, dust–dust collision, dust charge fluctuation, and Landau damping, which would modify the wave structures [15, 21, 28, 47], and shock waves can be excited in the system under appropriate conditions.

Shukla and Mamun [38] derived KdV–Burgers equation by reductive perturbation method and they have analysed the properties of nonlinear waves (solitons and shock waves) for strongly coupled unmagnetized dusty plasmas. Dusty plasma system with an iso-nonthermal ion distribution has been studied by [24], and they have studied the properties of shock waves via the obtained mKdV–Burgers equation that was derived using a set of generalized hydrodynamic equations. Pakzad and Javidan [29] have interpreted the dust acoustic solitary and shock waves in strongly coupled dusty plasmas with nonthermal ions. Recently, [35] have investigated arbitrary amplitude DA waves in a nonextensive dusty plasma, where they have examined the effects of electrons and ions nonextensivity on the DA soliton profile. Shahmansouri and Tribeche [36] have also investigated the properties and formation of DA shock waves in complex plasmas. They have found that the influence of electrons and ions nonextensivity and dust charge fluctuation affect the basic properties of the collisionless DA shock waves drastically.

It is well known that the presence of trapped particles can significantly modify the wave propagation characteristics in collisionless plasmas [33]. In most laboratory dusty plasmas, ions are not always isothermal because they are trapped by the large amplitude DA wave potential. Accordingly, they may follow a vortex-like distribution [34], which affect drastically on the nonlinear propagation mode. Some recent theoretical studies focused on the effects of ion and electron trapping which is common not only in space plasmas but also in laboratory experiments [1, 30, 37]. El-Wakil et al. [11] theoretically investigated higher order contributions to nonlinear DA waves that propagate in a mesospheric dusty plasma with a complete depletion of the background (electrons and ions). Duha et al. [7] studied small amplitude DIA solitary and shock waves due to dust charge fluctuation with trapped electrons by reductive perturbation method. They showed that the effects of vortex-like/trapped electron distribution modify the properties of the DIA solitary and shock waves.

The major topic of this work is to study the linear (dispersion relation) and nonlinear (solitons, monotonic as well as oscillatory shocks) properties of the DA waves in a homogeneous system of an unmagnetized, collisionless and dissipative dusty space plasma. Here, the study is devoted for a plasma system consisting of extremely massive, micron-sized, negative dust grains, electrons that obey a Boltzmann distribution and the trapped ions described by the vortex-like distribution (Sect. 2). The normal mode method is used to investigate the obtained dispersion relation (Sect. 3). The reductive perturbation technique is used to obtain the one-dimensional mKdV–Burgers equation. Moreover, the bifurcation analysis has been illustrated to recognize different classes of admissible solutions (Sect. 4). Finally, some concluding remarks are given in Sect. 5.

Governing equations

Let us consider a homogeneous system of an unmagnetized, collisionless and dissipative dusty plasma. The system consists of extremely massive, micron-sized, negatively dust grains, electrons obey a Boltzmann distribution and ions follow the vortex-like distribution representing the ions trapped in the DA wave potential. The dynamics of the DA waves are governed by the following basic set of equations

$$\begin{aligned} \frac{\partial n_{d}}{\partial t}+\frac{\partial \left( n_{d}u_{d}\right) }{\partial x}= 0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial u_{d}}{\partial t}+u_{d}\frac{\partial u_{d}}{\partial x}+q \frac{\partial \phi }{\partial x}-\eta _{d}\frac{\partial ^{2}u_{d}}{\partial x^{2}}= 0, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial ^{2}\phi }{\partial x^{2}}+qn_{d}-n_{e}+n_{_{i}}= 0. \end{aligned}$$

(3)

In the above equations, $n_{d}$ is the dust grain number density, $u_{d}$ is the dust fluid velocity, $q$ is the number of charges residing on the dust grain surface, $\phi$ is the electrostatic potential and $\eta _{d}$ is the corresponding viscosity coefficient. The density of the Boltzmann distributed electrons, $n_{e}$, is given by

$$\begin{aligned} n_{e}=\mu _{e}\exp \left( \sigma _{i}\phi \right) , \end{aligned}$$

(4)

where $\mu _{e}$ is the initial equilibrium density of electrons and $\sigma _{i}= T_{i} / T_{e}$, with $T_{e}$ is the temperature of electrons and $T_{i}$ is the temperature of ions. The ion density, $n_{_{i}}$, obeys the vortex-like distribution function [34] is given by

$$\begin{aligned} n_{_{i}}=\mu _{i}\left[ \exp \left( -\phi \right) -\frac{4}{3}b(-\phi )^{\frac{3}{2}}\right] , \end{aligned}$$

(5)

where $\mu _{i}$ is the ions initial equilibrium density and $b$ is a constant representing the vortex parameter which depends on the temperature parameters of resonant ions (both free and trapped) and is given by

$$\begin{aligned} b=\frac{1}{\sqrt{\pi }}(1-\beta ), \end{aligned}$$

(6)

where $\beta$ is a trapping parameter that determines the number of the trapped ions, and defined as the ratio of the free-ion temperature to the trapped-ion temperature. The case of $\beta <0$ refers to a vortex-like excavated trapped-ion distribution, and if $\beta =1$ (or $\beta =0$) we have Maxwellian (or flat-topped) ion distribution. This work focus on the case of $\beta <0$.

Linear analysis

To derive a dynamical equation for the dispersion relation of the DA waves from the basic equations (1, 2, 3, 4, 5), we use the normal mode method. With such method, we expand the dependent variables ($n_{d}$, $u_{d}$ and $\phi$) in terms of their equilibrium and perturbed parts as ($n_{d}=1+\tilde{n}_{d}$, $u_{d}=0+\tilde{u}_{d}$ and $\phi =0+\tilde{\phi }$). The perturbed quantities are proportional to $\exp [i(kx-\omega t)]$, and then the basic equations (1, 2, 3, 4, 5) are linearized and the corresponding first-order approximation yield

$$\begin{aligned} \tilde{n}_{d}= \frac{qk^{2}}{\omega ^{2}+i\eta _{d}k^{2}\omega }\tilde{\phi }, \end{aligned}$$

(7)

$$\begin{aligned} \tilde{u}_{d}= \frac{qk}{\omega +i\eta _{d}k^{2}}\tilde{\phi }. \end{aligned}$$

(8)

In connection with Poisson equation (3), the linear dispersion relation follows

$$\begin{aligned} \left( k^{2}+\mu _{i}+\mu _{e}\sigma _{i}\right) \omega ^{2}+i\eta _{d}k^{2}\left( k^{2}+\mu _{i}+\mu _{e}\sigma _{i}\right) \omega -q^{2}k^{2}=0. \end{aligned}$$

(9)

Let us consider

$$\begin{aligned} \omega =\omega _{r}+i\omega _{i}, \end{aligned}$$

(10)

where $\omega _{r}$ and $\omega _{i}$ are the real and imaginary parts of the frequency $\omega$.

By inserting Eq. (10) into Eq. (9), one obtains

$$\begin{aligned}&2\left( k^{2}+\mu _{i}+\mu _{e}\sigma _{i}\right) \omega _{r}\omega _{i}+\eta _{d}k^{2}\left( k^{2}+\mu _{i}+\mu _{e}\sigma _{i}\right) \omega _{r} =0, \end{aligned}$$

(11a)

$$\begin{aligned}&\left( k^{2}+\mu _{i}+\mu _{e}\sigma _{i}\right) \omega _{i}^{2}-\left( k^{2}+\mu _{i}+\mu _{e}\sigma _{i}\right) \omega _{r}^{2}+\eta _{d}k^{2}\left( k^{2}+\mu _{i}+\mu _{e}\sigma _{i}\right) \omega _{i}+q^{2}k^{2}=0. \end{aligned}$$

(11b)

By solving Eq. (11), one gets $\omega _{r}=0$, whereas $\omega _{i}$ is given by

$$\begin{aligned} \omega _{i}=\frac{-k^{2}\eta _{d}}{2}+\frac{\sqrt{-4q^{2}k^{2}+k^{4}\eta _{d}^{2}(k^{2}+\mu _{i}+\mu _{e}\sigma _{i})}}{2\sqrt{k^{2}+\mu _{i}+\mu _{e}\sigma _{i}}}, \end{aligned}$$

(12)

which depends mainly on the plasma parameters $k$, $\eta _{d}$ and $\sigma _{i}$. The behaviour of the damping rate $\omega _{i}$ with such parameters is illustrated as shown in Figs. 1, and 2. From these figures, one can see that, the instability damping rate $\omega _{i}$ decreases by increasing the plasma parameters (carrier wave number $k$, the dust kinematic viscosity coefficient $\eta _{d}$ and the ratio of the ion to the electron temperatures $\sigma _{i}$).

Fig. 1

The variation of $\omega _{i}\, \text { vs. } \,\eta _{d}$ at different values of $\sigma _{i}$ for $\mu _{e}=8$, $\mu _{i}=7$, $k=2,q=1$

Fig. 2

Contour plot of $\omega _{i}\,\text { vs. }\,k$ and $\eta _{d}$ for $\mu _{e}=1.1, \,\mu _{i}=0.1$, $\sigma _{i}=0.2, q=1$

Nonlinear analysis

Derivation of the mKdV–Burgers equation

To extend our analysis, the nonlinear dynamical features of DA waves are treated. This can be done using the standard reductive perturbation method. The reductive perturbation method is mostly applied to small amplitude nonlinear waves [43, 44]. This method rescales both space and time in the governing equations of the system to introduce space and time variables, which are appropriate for the description of long-wavelength phenomena. Accordingly, the independent variables are stretched as

$$\begin{aligned} \tau =\varepsilon ^{\frac{3}{4}}t,\quad \ \xi =\varepsilon ^{\frac{1}{4} }(x-\lambda t), \end{aligned}$$

(13)

where $\varepsilon$ is a small dimensionless expansion parameter measuring the strength of nonlinearity and $\lambda$ is the wave speed. The value of $\eta _{d}$ is assumed to be small, so that we may set its value as $\eta _{d}=\varepsilon ^{\frac{1}{4}}\ \eta$, with $\eta$ is a definite quantity. Furthermore, the physical quantities appearing in the basic equations (1, 2, 3, 4, 5) are expanded as power series in $\varepsilon$ about their equilibrium values, viz

$$\begin{aligned} n_{d}= 1+\varepsilon n_{d1}+\varepsilon ^{\frac{3}{2}}n_{d2}+\varepsilon ^{2}n_{d3}+\cdots , \end{aligned}$$

(14a)

$$\begin{aligned} u_{d}= \varepsilon u_{d1}+\varepsilon ^{\frac{3}{2}}u_{d2}+\varepsilon ^{2}u_{d3}+\cdots , \end{aligned}$$

(14b)

$$\begin{aligned} \phi= \varepsilon \phi _{1}+\varepsilon ^{\frac{3}{2}}\phi _{2}+\varepsilon ^{2}\phi _{3}+\cdots \end{aligned}$$

(14c)

Substituting Eqs. (13, 14) into basic equations (1, 2, 3, 4, 5) and equating coefficients of powers of $\varepsilon$, the lowest order of $\varepsilon$ gives

$$\begin{aligned}&n_{d1}=\frac{q\ }{\lambda ^{2}}\phi _{1}, \end{aligned}$$

(15)

$$\begin{aligned}&u_{d1}=\frac{q\ }{\lambda }\phi _{1}. \end{aligned}$$

(16)

and the phase velocity is given by

$$\begin{aligned} \lambda =\sqrt{\frac{q^{2}}{\mu _{i}+\mu _{e}\sigma _{i}}}. \end{aligned}$$

(17)

The next order in $\varepsilon$ yields the following

$$\begin{aligned} {\frac{\partial n_{d1}}{\partial \tau }}-\lambda \frac{\partial n_{d2}}{ \partial \xi }+{\frac{\partial u_{d{2}}}{\partial \xi }}= 0, \end{aligned}$$

(18a)

$$\begin{aligned} {\frac{\partial u_{{d1}}}{\partial \tau }}-\lambda \frac{\partial u_{d2}}{ \partial \xi }+q\frac{\partial \phi _{2}}{\partial \xi }-\eta {\frac{ \partial ^{2}u_{d{1}}}{\partial {\xi }^{2}}}= 0, \end{aligned}$$

(18b)

$$\begin{aligned} \frac{\partial ^{3}\phi _{{1}}}{\partial {\xi }^{3}}+q\frac{\partial n_{d2}}{ \partial \xi }-\frac{q^{2}\ }{\lambda ^{2}}\frac{\partial \phi _{2}}{ \partial \xi }{+}2\mu _{i}b\left( -\phi _{{1}}\right) ^{\frac{1}{2}}\frac{ \partial \phi _{1}}{\partial \xi }= 0. \end{aligned}$$

(18c)

Solving this system with the aid of Eqs. (15, 16, 17) and eliminating the second-order perturbed quantities ($n_{d2}$, $u_{d2}$ and $\phi _{2 \text { }}$), we finally get the mKdV–Burgers equation as

$$\begin{aligned} \frac{\partial \phi _{1}}{\partial \tau }+A\left( -\phi _{{1}}\right) ^{ \frac{1}{2}}\frac{\partial \phi _{1}}{\partial \xi }+B\ \frac{\partial ^{3}\phi _{1}}{\partial \xi ^{3}}\ +C\ \frac{\partial ^{2}\phi _{1}}{ \partial \xi ^{2}}=0, \end{aligned}$$

(19)

where

$$\begin{aligned} A=\frac{\mu _{i}b\lambda ^{3}}{q^{2}},B=\frac{\lambda ^{3}}{2q^{2}}, C=- \frac{\eta }{2}. \end{aligned}$$

(20)

Let us introduce the variable $\chi =\xi -u_{0}\tau$ where $\chi$ is the transformed coordinate relative to a frame which moves with the velocity $u_{0}$. Integrating Eq. (19) with respect to the variable $\chi$, the reduced mKdV–Burgers equation leads to

$$\begin{aligned} \frac{\mathrm{d}^{2}\phi _{1}}{\mathrm{d}\chi ^{2}}+\frac{C}{B}\frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }-\frac{ 2A}{3B}\left( -\phi _{{1}}\right) ^{\frac{3}{2}}-\frac{u_{0}}{B}\phi _{1}=0. \end{aligned}$$

(21)

Owing to the presence of the Burgers term $\frac{C}{B}\frac{\mathrm{d}\phi _{1}}{ \mathrm{d}\chi }$, Eq. (21) describes homogeneous and dissipative dusty plasmas. Therefore, the phase paths of such equation are, in general, no longer level curves of an energy $H(\phi _{1},\frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi })$. So, in the dissipative case, it is reasonable to deal with $\frac{\mathrm{d}H}{\mathrm{d}\chi }$ rather than $H$. The mKdV–Burgers Eq. (21) can be written in the general form as

$$\begin{aligned} \frac{\mathrm{d}^{2}\phi _{1}}{\mathrm{d}\chi ^{2}}+h\left( \phi _{1},\frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi } \right) \frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }+G(\phi _{1})=0, \end{aligned}$$

(22)

where $h$ and $G$ are two functions that can be determined by comparing the Eqs. (21, 22).

In the conservative case ($h=0$), the total energy associated with Eq. (22) is

$$\begin{aligned} H=\frac{1}{2}\left( \frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }\right) ^{2}+V(\phi _{1}), \end{aligned}$$

(23)

where $V(\phi _{1})$ is the potential function and then

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}\chi }=\frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }\left( \frac{\mathrm{d}^{2}\phi _{1}}{ \mathrm{d}\chi ^{2}}+\frac{\mathrm{d}V}{\mathrm{d}\phi _{1}}\right) . \end{aligned}$$

(24)

If $\frac{\mathrm{d}V}{\mathrm{d}\phi _{1}}=G(\phi _{1})$ in addition to Eq. (22), the total derivative of $H$ will be

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}\chi }=-h\left( \phi _{1},\frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }\right) \left( \frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }\right) ^{2}, \end{aligned}$$

(25)

which is a decreasing function for the variable $\chi$ if $h>0$. This equation is very important for studying the stability of the system.

In the present study, the function $\frac{\mathrm{d}H}{\mathrm{d}\chi }$ corresponds to Burgers term in the mKdV–Burgers Eq. (21), as

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}\chi }=\frac{C}{B}\left( \frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }\right) ^{2}, \end{aligned}$$

(26)

which shows that the energy of the plasma system is not conserved and hence it is not easy to find out exact analytical solution for mKdV–Burgers equation.

In terms of the viscosity coefficient $\eta$, Eq. (26) can be written as

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}\chi }=-\frac{q^{2}\eta }{\lambda ^{3}}\left( \frac{\mathrm{d}\phi _{1}}{ \mathrm{d}\chi }\right) ^{2}, \end{aligned}$$

(27)

which is always a decreasing function since $q^{2}$, $\eta$ and $\lambda$ are positive quantities.

Bifurcation analysis and soliton solution

In the absence of the Burgers coefficient $\left( C=0\right)$, Eq. (21) becomes conservative and consequently $\frac{\mathrm{d}H}{\mathrm{d}\chi }=0$. Then, the total energy has the form

$$\begin{aligned} H=\frac{1}{2}\left( \frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }\right) ^{2}-\frac{u_{0}}{2B} \phi _{1}^{2}+\frac{4A}{15B}\left( -\phi _{1}\right) ^{\frac{5}{2}}, \end{aligned}$$

(28)

where the potential function $V(\phi _{1})$ is

$$\begin{aligned} V(\phi _{1})=-\frac{u_{0}}{2B}\phi _{1}^{2}+\frac{4A}{15B}\left( -\phi _{1}\right) ^{\frac{5}{2}}. \end{aligned}$$

(29)

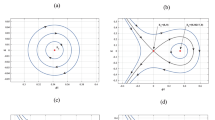
The bifurcation analysis is investigated via Eqs. (28, 29) under the condition $A>0$, $B>0$ and $u_{0}>0$. The potential function $V(\phi _{1})$ versus $\phi _{1}$ for different values of $\beta$ is shown graphically, Fig. 3, and it is clear that the potential well has one hump and a pit. These two points correspond to a saddle point at $(0,0)$ and a center point at $( -\left[ 3u_{0}/2A\right] ^{2},\ 0)$ in the phase portrait. From the topology of the phase portrait diagram, Fig. 4, one can see a family of periodic orbits at $( -\left[ 3u_{0}/2A\right] ^{2},\ 0)$, which refer to a family of periodic wave solutions. On the other hand, the homoclinic orbit at $(0,0)$ refers to one solitary wave solution. Moreover, Fig. 4 shows a series of bounded open orbits that corresponds to a series of breaking wave solutions.

Fig. 3

The variation of $V\left( \phi _{1}\right) \, \text {vs.}\,\phi _{1}$ for different values of $\beta$ for $\mu _{e}=1.4 , \mu _{i}=0.4,\sigma _{i}=0.2 , u_{0}=0.4, q=1$

Fig. 4

Phase portrait $\mathrm{d}\phi _{1}/ \mathrm{d}\chi\, \text { vs. }\, \phi _{1}$ for different $H$ for $\mu _{e}=1.4, \mu _{i}=0.4, \sigma _{i}=0.2, \beta =-0.05, u_{0}=0.4, q=1$

These trajectories that are shown in Fig. 4 refer to the existence of stable solitonic solution that should satisfy the following condition [2]

$$\begin{aligned} \left[ \frac{\mathrm{d}^{2}V}{\mathrm{d}\phi _{1}^{2}}\right] _{\phi _{1}=0}<0 \end{aligned}$$

which explains that there must exist a nonzero crossing point $\phi _{1}=\phi _{0}$ that $V(\phi _{1}=\phi _{0})=0$. In addition, there must exist a $\phi _{1}$ between $\phi _{1}=0$ and $\phi _{1}=\phi _{0}$ to make $V(\phi _{1})<0$. Obviously, from Eq. (28), the condition of existence of stable solitonic solution is satisfied, since

$$\begin{aligned} \left[ \frac{\mathrm{d}^{2}V}{\mathrm{d}\phi _{1}^{2}}\right] _{\phi _{1}=0}=-\frac{u_{0}}{B} <0, \end{aligned}$$

where the parameters $u_{0}$ and $B$ are positive. However, the corresponding stable solitonic solution is given by

$$\begin{aligned} \phi _{1}=-\phi _{0} {\mathrm{sech}}^{4}\left( \frac{\chi }{W}\right) , \end{aligned}$$

(30)

where $\phi _{0}=\left( \frac{15u_{0}}{8A}\right) ^{2}$ is the amplitude and $W=4\sqrt{\frac{B}{u_{0}}}$ is the width of the soliton solution in the absence of Burgers term. The behaviours of the obtained solution and its characterizing parameters (DA wave amplitude and its width) are presented in Figs. 5, 6, 7, and 8. Figure 5 shows the variation in $\phi _{1}$ with $\chi$ for different values of $\beta$ (the ratio of the free-ion temperature to the trapped-ion temperature). It emphasizes that the amplitude of the soliton wave increases with increasing of $\beta$. The single-pulse soliton solution $\phi _{1}$ is plotted versus $\xi$, and its propagation is shown at different time scales $\tau$ (Fig. 6).

Fig. 5

Evolution of $\phi _{1}\,\text { vs. }\,\chi$ for different values of $\beta$ for $\mu _{e}=1.4, \mu _{i}=0.4, \sigma _{i}=0.2,u_{0}=0.4, q=1$

Fig. 6

Evolution of $\phi _{1}\,\text { vs. }\,\xi$ for different values of $\tau \, \text {for }\,\mu _{e}=1.4, \mu _{i}=0.4, \sigma _{i}=0.2, \beta =-0.3, u_{0}=0.4, q=1$

The evolution of the amplitude $\phi _{0}$ with $\beta$ and $\sigma _{i}$ is presented in Fig. 7. It can be seen that the amplitude of the soliton wave increases with increasing the values of both $\beta$ and $\sigma _{i}$. However, the variation of the width $W$ with $u_{0}$ and $\sigma _{i}$ is graphed in Fig. 8, which shows that the soliton wave width increases with decreasing $u_{0}$ and $\sigma _{i}$.

Fig. 7

Evolution of $\phi _{0}\,\text { vs. }\,\left( \beta ,\sigma _{i}\right)$ for $\mu _{e}=1.4, \mu _{i}=0.4, u_{0}=0.4, q=1$

Fig. 8

Evolution of $W\,\text { vs. }\,\left( \sigma _{i}, u_{0}\right)$ for $\mu _{e}=1.4, \mu _{i}=0.4, q=1$

The soliton energy $E_{n}$ is obtained according to the integral

$$\begin{aligned} E_{n}=\int _{-\infty }^{\infty }u_{\mathrm{d}1}^{2}(\chi )\text { }\mathrm{d}\chi . \end{aligned}$$

(31)

Upon integrating (31), yields

$$\begin{aligned} E_{n}=\frac{45.2\ q^{2}u_{0}^{4}}{A^{4}\lambda ^{2}\sqrt{u_{0}/B}}. \end{aligned}$$

(32)

which, clearly, depends mainly on the plasma parameters via the coefficients $A$ and $B$. The variation of the soliton energy $E_{n}$ with $\sigma _{i}$ and $\beta$ is shown graphically in Fig. 9, which shows that the soliton energy increases with increasing the values of both $\sigma _{i}$ and $\beta$.

Fig. 9

Contour plot of $E_{n}\,\text { vs. }\,\left( \beta \text {, } \sigma _{i}\right)$ for $\mu _{e}=1.4, \mu _{i}=0.4, u_{0}=0.4, q=1$

Moreover, the associated electric field is obtained according to the relation

$$\begin{aligned} \mathbf {E}=-\varvec{\nabla }\phi _{1}, \end{aligned}$$

(33)

and then, the electric field has the expression

$$\begin{aligned} E=-\frac{225u_{0}^{2}\sqrt{u_{0}/B}}{64A^{2}} {\mathrm{sech}}^{4}\left( \frac{1 }{4}\sqrt{u_{0}/B}\chi \right) \tanh \left( \frac{1}{4}\sqrt{u_{0}/B}\chi \right) . \end{aligned}$$

(34)

The behaviour of the electric field $E$ is presented graphically as shown in Figs. 10, and 11. Figure 10 shows the variation of the electric field $E$ against $\chi$ for different values of $\beta$. Obviously, the electric field increases with the parameter $\beta$, whereas Fig. 11 represents the evolution of the electric field $E$ versus $\xi$ for different values of time $\tau$.

Fig. 10

Variation of $E\,\text { vs. }\,\chi$ for different values of $\beta$ for $\mu _{e}=1.4, \mu _{i}=0.4, \sigma _{i}=0.2, u_{0}=0.4, q=1$

Fig. 11

Evolution of $E\,\text { vs. }\,\xi$ for different values of $\tau$ for $\mu _{e}=1.4, \mu _{i}=0.4, \sigma _{i}=0.2, \beta =-0.3, u_{0}=0.4, q=1$

Shock wave solutions

In the presence of Burgers term, $C\ne 0$, the system of equations becomes dissipative and the total energy $H$ is not conservative. In this case, the exact solution of Eq. (21) cannot be easily constructed. Therefore, different mathematical methods [8–10, 12, 20] have arose to solve such types of these nonlinear differential equations. Among those, the tangent hyperbolic (tanh) method has been proved to be a powerful mathematical technique for solving nonlinear partial differential equations. Following the procedure of the tanh method [22], we consider the solution in the following form

$$\begin{aligned} \phi _{1}=\sum \limits _{n=0}^{N}a_{n}\tanh ^{n}(\chi ), \end{aligned}$$

(35)

where the coefficients $a_{n}$ and $N$ should be determined. Balancing the nonlinear and dispersion terms in Eq. (21), we obtain $N=4$. Substituting Eq. (35) into Eq. (21) and equating to zero the different coefficients of different powers of $\tanh (\chi )$ functions, one can obtain the following set of algebraic equations

$$\begin{aligned} -\frac{u_{0}}{B}a_{0}-\frac{2A}{3B}\left( -a_{0}\right) ^{\frac{3}{2}}+\frac{ C}{B}a_{1}+2a_{2}=0, \end{aligned}$$

(36a)

$$\begin{aligned} -2a_{1}-\frac{u_{0}}{B}a_{1}+\frac{A}{B}\sqrt{-a_{0}}a_{1}+\frac{2C}{B} a_{2}=0, \end{aligned}$$

(36b)

$$\begin{aligned} -\frac{C}{B}a_{1}-\frac{A}{3B}\frac{a_{1}^{2}}{\sqrt{-a_{0}}}-8a_{2}-\frac{ u_{0}}{B}a_{2}+\frac{A}{B}\sqrt{-a_{0}}a_{2}=0, \end{aligned}$$

(36c)

$$\begin{aligned} 2a_{1}-\frac{2C}{B}a_{2}-\frac{2A}{3B}\frac{a_{1}a_{2}}{\sqrt{-a_{0}}}=0, \text { and \ }6a_{2}-\frac{A}{3B}\frac{a_{2}^{2}}{\sqrt{-a_{0}}}=0. \end{aligned}$$

(36d)

Solving these set of algebraic equations, one gets

$$\begin{aligned} a_{0}= -\frac{\left( 12B+u_{0}\right) ^{2}}{A^{2}}, \end{aligned}$$

(37a)

$$\begin{aligned} a_{1}= -\frac{18C(12B+u_{0})}{5A^{2}}, \end{aligned}$$

(37b)

$$\begin{aligned} a_{2}= \frac{18B(12B+u_{0})}{A^{2}}, \end{aligned}$$

(37c)

$$\begin{aligned} C= 10B,\ \quad \text {and}\ \quad \ u_{0}=42B. \end{aligned}$$

(37d)

With the knowledge of the above coefficients, one can write down the explicit solution of the mKdV–Burgers equation (21) in terms of tanh function

$$\begin{aligned} \phi _{1}=\frac{(12B+u_{0})}{A^{2}}\left( 6B-u_{0}-\frac{18C}{5}\tanh (\chi )-18B {\mathrm{sech}}^{2}(\chi )\right) . \end{aligned}$$

(38)

This class of solution represents a particular combination of a solitary wave [(${\mathrm{sech}}^{2}(\chi )$ term on the right-hand side of Eq. (38)] with a Burgers shock wave [($\tanh (\chi )$ term]. The behaviour of this solution is shown graphically as in Figs. 12, 13, and 14. Figures 12, and 13 show the variation of $\phi _{1}$ with $\chi$ for different values of $\beta$ and $\sigma _{i}\,$, respectively, and indicate that the amplitude of the wave increases with increasing the values of both $\beta$ and $\sigma _{i}$. The variation of $\phi _{1}$ against $\xi$ due to the change of the time $\tau$ is plotted in Fig. 14. One can see from these figures that both soliton and shock structures are obtained due to the presence of both dispersive and dissipative coefficients.

Fig. 12

Variation of $\phi _{1}\text { vs. }\,\chi$ for different values of $\beta$ for $\mu _{e}=5, \mu _{i}=4, \sigma _{i}=0.15, \eta =0.3, u_{0}=0.4, q=1$

Fig. 13

Variation of $\phi _{1}\text { vs. }\,\chi$ for different values of $\sigma _{i}$ for $\mu _{e}=5, \mu _{i}=4, \beta =-0.3, \eta =0.3, u_{0}=0.4, q=1$

Fig. 14

Evolution of $\phi _{1}\text { vs. }\,\xi$ for different values of $\tau$ for $\mu _{e}=5, \mu _{i}=4, \sigma _{i}=0.15, \beta =-0.2, \eta =0.3, u_{0}=0.4, q=1$

Another type of solution can be obtained when the dissipation term is dominant over the dispersion term. In this case, Eq. (21) reduces to the following nonlinear first-order differential equation

$$\begin{aligned} \frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }=\frac{u_{0}}{C}\phi _{1}+\frac{2A}{3C}\left( -\phi _{{1}}\right) ^{\frac{3}{2}}, \end{aligned}$$

(39)

that admits the following solution

$$\begin{aligned} \phi _{1}=-\frac{9u_{0}^{2}\exp (\frac{u_{0}}{C}\chi )}{\left[ 1+2A\exp ( \frac{u_{0}}{2C}\chi )\right] ^{2}}. \end{aligned}$$

(40)

This type of solution actually describes monotonic shock wave.

On the other hand, another type of solution of special interest can be obtained if one considers the boundary condition $\chi \rightarrow \pm \infty \Rightarrow \frac{\mathrm{d}^{2}\phi _{1}}{\mathrm{d}\chi ^{2}}=\frac{\mathrm{d}\phi _{1}}{\mathrm{d}\chi }=0$. With this condition, one obtains the asymptotic solution

$$\begin{aligned} \phi _{c}=-\left( \frac{3u_{0}}{2A}\right) ^{2}, \end{aligned}$$

(41)

of the nonlinear mKdV–Burgers differential equation.

Using $\phi _{1} = \phi _{c} + \tilde{\phi }$ for $\mid \phi _{c}\mid \gg \mid \tilde{\phi }\mid$, Eq. (21) can be linearized to the second-order linear differential equation

$$\begin{aligned} \frac{\mathrm{d}^{2}\tilde{\phi }}{\mathrm{d}\chi ^{2}}+\frac{C}{B}\frac{\mathrm{d}\tilde{\phi }}{\mathrm{d}\chi }+ \frac{u_{0}}{2B}\tilde{\phi }=0. \end{aligned}$$

(42)

The solution of the linear differential equation (42) can be expressed in the exponential form $\tilde{\phi }=\exp (M\chi )$, where $M$ is defined by

$$\begin{aligned} M=\frac{C}{2B}\left[ -1\pm \sqrt{\left( 1-\frac{2u_{0}B}{C^{2}}\right) }\right] . \end{aligned}$$

(43)

For $C^{2}\ll$ $2u_{0}B$, the oscillatory shock wave solution is given by

$$\begin{aligned} \phi _{1}=\phi _{c}+\widetilde{K}\exp \left( -\frac{C}{2B}\chi \right) \cos \left( \sqrt{\frac{u_{0}}{2B}}\chi \right) , \end{aligned}$$

(44)

where $\widetilde{K}$ is an arbitrary constant. The behaviour of the obtained solution in terms of the coordinates $\xi$ and $\tau$ is shown graphically in Fig. 15. In addition to oscillatory shock wave, the mKdV–Burgers equation exhibits solitonic and monotonic shock wave due to the Burgers term that arises from the fluid viscosity.

Fig. 15

Evolution of $\phi _{1}\text { vs. }\,\xi$ for different values of $\tau$ for $\mu _{e}=2.5,\ \mu _{i}=1.5,\ \sigma _{i}=0.2,\ \beta =-0.4,\eta =0.1,u_{0}=0.4,q=1$

Conclusions

The linear and nonlinear properties of the DA waves in a system of homogeneous, unmagnetized, collisionless and dissipative dusty plasma consisted of extremely massive, micron-sized, negative dust grains, electrons obey a Boltzmann distribution and traped ions have been investigated. In the linear analysis, the normal mode method is used to reduce the basic set of fluid equations to a linear dispersion relation. Assuming $\omega =\omega _{r}+i\omega _{i}$, an expression for the damping rate $\omega _{i}$ is obtained and its behaviour with the plasma parameter (carrier wave number $k$, dust kinematic viscosity coefficient $\eta _{d}$, ratio of the ion to the electron temperatures $\sigma _{i})$ is shown graphically. Such graphs show that the instability damping rate decreases as the plasma parameters ($k$, $\eta _{d}$,$\sigma _{i}$) increase.

In the nonlinear analysis, the reductive perturbation method is used to reduce the basic set of fluid equations to the nonlinear partial differential mKdV–Burgers equation (19). Such nonlinear equation is not an integrable Hamiltonian system because the energy of plasma system is not conserved due to the dissipative Burgers term. This implies that finding exact solutions of mKdV–Burgers equation is a complicated task in general case. Therefore, in the absence of Burgers term, the equation becomes integrable and one can easily write down the explicit analytical solution. By solving the obtained mKdV–Burgers equation, we have succeeded to distinguish some interesting classes of analytical solutions due to Burgers coefficient $C$.

In the absence of the Burgers term ($C=0)$, i.e., the dissipation effect is negligible in comparison with that of the nonlinearity and dispersion, the topology of phase portrait and potential diagram is investigated as shown in Figs. 3, and 4. The advantage of using the phase portrait is that one may predict wide classes of the travelling wave solutions of mKdV–Burgers equation. One of these solutions is the soliton solution (30), whose behaviour is discussed in terms of plasma parameters ($\beta$, $\sigma _{i}$ , $u_{0}$, $\tau$) as shown in Figs. 5, 6, 7, and 8. In addition, the solitonic energy $E_{n}$ and the associated electric field $E$ are calculated and shown in Figs. 9, 10, and 11. It is obvious that the behaviour of the solitonic energy and the electric field depends crucially on the values of the parameters $\sigma _{i}\,$, $\beta$ and $\tau$.

In the presence of Burgers term ($C\ne 0$), the mKdV–Burgers equation admits some solutions of physical interest which are related to a combination between shock and soliton waves, monotonic and oscillatory shocks. The combination solution between shock and soliton waves is obtained explicitly using tanh method. In this case, both the dispersion and dissipation coefficients remain finite in comparison with each other and the profile of such case exhibits both shock and soliton waves for different values of $\beta$, $\sigma _{i}$ and $\tau$ as shown in Figs. 12, 13, and 14. The monotonic shock wave can exist when the dissipation term is dominant over the dispersion term. The oscillatory shock wave can exist when dispersion term is dominant over the dissipation term and its behaviour is presented in Fig. 15. However, the formation of these solutions depends crucially on the value of the Burgers term as well as the plasma parameters.

Finally, it is concluded that a plasma with dissipative and dispersive properties supports the existence of shock waves instead of solitons. Under appropriate conditions, shock waves can be propagated in the plasma medium. It is emphasized that the present investigation may be helpful in better understanding of waves propagation in the astrophysical plasmas as well as in inertial confinement fusion laboratory plasmas.