Introduction

Many phenomena in various field of the science, can be modeled very successfully by time-fractional differential equations. In this paper we focus on the following fractional diffusion-wave equation (FDWE) with damping [1]:

$$\begin{aligned} \frac{\partial ^q u(x,t)}{\partial t^q}+\frac{\partial u(x,t)}{\partial t}=\frac{\partial ^{2}u(x,t)}{\partial x^{2}}+h(x,t), \quad \quad 0<x<L,\quad 0<t<T, \end{aligned}$$
(1.1)

with the initial conditions:

$$\begin{aligned} u(x,0)=f_0(x), \quad \quad \frac{\partial u(x,0)}{\partial t}=f_1(x),\quad \quad 0\le x\le L, \end{aligned}$$
(1.2)

and the boundary conditions:

$$\begin{aligned} u(0,t)=g_0(t), \quad \quad u(L,t)=g_1(t), \quad \quad 0\le t\le T, \end{aligned}$$
(1.3)

where \(L>0, T>0, 1<q \le 2\) is the order of the fractional derivative in the Caputo sense, \(f_0, f_1, g_0\) and \(g_1\) are known and sufficiently smooth functions, while the function u is to be determined. In the case \(q=2\), this equation is named telegraph equation.

Recently, considerable amount of papers have been proposed methods for solving the FDWE [2–13]. Chen et al. [1] obtained the analytical solution by the method of separation of variables and proposed the numerical solution with finite difference method. In [2], Bhrawy et al. applied a spectral tau method based on the Jacobi operational matrix to solve the problem. Liu et al. [3] proposed the fractional predictor–corrector method to solve this problem. In [4], Mainardi derived the fundamental solutions for the FDWE. The combination of the compact difference method and alternating direction implicit method are used for solving two-dimensional fractional Cattaneo equation in [5]. A fully discrete difference scheme is recommended for a diffusion-wave system by Wess [6]. Heydari et al. [7] applied fractional operational matrix (FOM) of integration for the Legendre wavelets (LWs) to solve the problem. In [8] a compact finite-difference scheme is used for the fourth-order fractional diffusion-wave system. In [9] finite difference schemes of second-order are proposed for the time-fractional diffusion-wave equation. In [10], Hu and Zhang used finite-difference methods for fourth-order fractional diffusion-wave. Sumudu transform method for solving fractional differential equations and fractional diffusion-wave equation applied by Darzi et al. [11]. Hosseini et al. [12] employed the meshless local radial point interpolation method which is based on the Galerkin weak form and radial point interpolation approximation for solving FDWE.

The Ritz–Galerkin method is the method to transform a continuous problem to a discrete problem. Several partial differential equations are numerically solved by Ritz–Galerkin method, but using of the appropriate satisfier function in the Ritz–Galerkin method is taken into consideration recently, see for instance [14–20]. The satisfier function fulfills all the problem conditions. In conclusion, employing of it in Ritz–Galerkin method provides the facility to satisfy the problem conditions, also leads to a system of algebraic equations of smaller size and hence reduces the computation time.

In mathematical research, wavelet theory is a relatively new and growing area. It has been used in a wide range of engineering; for instance, wavelets are very successfully applied in signal analysis for waveform representations and segmentations [21]. Wavelets allow the accurate representation of many types of functions and operators [22, 23]. Furthermore, wavelets make a connection with fast numerical algorithms [24].

The shifted Legendre polynomials \(p_{n}(x), n=0,1,2,...\), that \(0 \le x \le 1\), are more efficient in approximation theory, among other orthogonal polynomials [25, 26]. The Bernoulli polynomials are not orthogonal functions. In [27], the superiority of Bernoulli polynomials \(\beta _n(x),\, n=0,1,2,...,\) so that \(0 \le x \le 1,\) to shifted Legendre polynomials in approximation of functions is proposed.

In this paper, we define two-dimensional BWs for the first time. Moreover, this is the first time the Ritz–Galerkin method in the two-dimensional BWs basis and with utilizing the satisfier function is employed to give an approximate solution of FDWE. We also compare our results with those results obtained by [3] and [7]. Comparison for the numerical examples shows the more accuracy and less computations of our scheme in comparison to other published methods.

This paper is separated in to the following sections: In Sect. 2, we introduce basic formulation of wavelets and the Bernoulli wavelets. In Sect. 3, we construct two different satisfier functions and apply the Ritz–Galerkin method in the two-dimensional BWs basis for numerically discretize the problem. Section 4 presents and discusses the numerical results for two test examples, whilst Sect. 5 includes the conclusions of this paper.

Properties of Bernoulli wavelets

Wavelets and Bernoulli wavelets

Dilation and translation of a function (mother wavelet) construct a family of functions called wavelets and is defined as follows [28]

$$\begin{aligned} \varphi _{a,b}(t)=\mid a\mid ^{\frac{-1}{2}}\varphi \left( \frac{t-b}{a}\right) , \quad a\ne 0, \end{aligned}$$

where \(a,b \in {\mathbb {R}}\) are dilation and translation parameters that vary continuously. The family of discrete wavelets that form a basis for \(L^{2}({\mathbb {R}})\) is defined as follows

$$\begin{aligned} \varphi _{k,n}(t)=\mid a_{0}\mid ^{\frac{k}{2}}\varphi (a_{0}^{k}t-nb_{0}), \end{aligned}$$

where n and k are positive integers and \(a_{0}>1, b_{0}>1\).

Bernoulli wavelets are obtained, when we choose Bernoulli polynomial \(\beta _{m}(t)\) as mother wavelet. BWs \(\varphi _{n,m}(t)=\varphi (k,{\hat{n}},m,t)\) have four arguments; \({\hat{n}}=n-1, n=1,2,4,...,2^{k-1}, m\) is the order for Bernoulli polynomials and k can assume any positive integer. They are defined on the interval [0, 1) for \(m=1,2,...,M-1\), that \(M>0\) is a fixed integer by [29]

$$\begin{aligned} \varphi _{n,m}(t)=\left\{ \begin{array}{lll} 2^{\frac{k-1}{2}}\frac{1}{\sqrt{\frac{(-1)^{m-1}(m!)^{2}}{(2m)!}\alpha _{2m}}}\beta _{m}(2^{k-1}t-{\hat{n}}), &{}\quad \frac{{\hat{n}}}{2^{k-1}}\le t< \frac{{\hat{n}}+1}{2^{k-1}},\\ 0, &{}\quad \hbox {otherwise}, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \varphi _{n,0}(t)=\left\{ \begin{array}{lll} 2^{\frac{k-1}{2}}, &{}\quad \frac{{\hat{n}}}{2^{k-1}}\le t< \frac{{\hat{n}}+1}{2^{k-1}},\\ 0, &{}\quad \hbox {otherwise}, \end{array}\right. \end{aligned}$$

where \(n=1,2,...,2^{k-1}\). The coefficient \(\frac{1}{\sqrt{\frac{(-1)^{m-1}(m!)^{2}}{(2m)!}\alpha _{2m}}}\) is applied to normalize the Bernoulli wavelets. Bernoulli polynomials form a complete basis over the interval [0, 1] [30] and are defined by [31]

$$\begin{aligned} \beta _m(t)=\sum \limits _{i = 0}^{m}{\left( \begin{array}{c} m\\ i \end{array}\right) } \alpha _{m-i} t^{i}, \end{aligned}$$
(2.1)

that \(\alpha _i,\,\,i=0,1,...,m\) are Bernoulli numbers.

For Bernoulli polynomials we have [32]

$$\begin{aligned} \int _{a}^{\tau }\beta _m(t)\mathrm{d}t= & {} \frac{\beta _{m+1}(\tau )-\beta _{m+1}(a)}{m+1}, \end{aligned}$$
(2.2)
$$\begin{aligned} \int _{0}^{1}\beta _{m_1}(t)\beta _{m_2}(t)\mathrm{d}t= & {} (-1)^{{m_1}-1}\frac{{m_1}!{m_2}!}{({m_1}+{m_2})!}\alpha _{{m_1}+{m_2}}, \quad {m_1},{m_2}\ge 1. \end{aligned}$$
(2.3)

Now, let

$$\begin{aligned} {\tilde{\beta }}_{m}(t)=\left\{ \begin{array}{lll} 1, &{}\quad m=0,\\ \frac{1}{\sqrt{\frac{(-1)^{m-1}(m!)^{2}}{(2m)!}\alpha _{2m}}}\beta _{m}(t), &{} \quad m>0.\\ \end{array}\right. \end{aligned}$$

We define, for the first time, the two-dimensional Bernoulli wavelets \(\varphi _{n_1m_1n_2m_2}(x,y)\) as

$$\begin{aligned} \left\{ \begin{array}{lll} 2^{\frac{(k_1-1)+(k_2-1)}{2}}{\tilde{\beta }}_{m_1}(2^{k_1-1}x-{\hat{n}}_1){\tilde{\beta }}_{m_2}(2^{k_2-1}y-{\hat{n}}_2), &{}\quad \hbox {for} \begin{array}{lll} \frac{{\hat{n}}_1}{2^{k_1-1}}\le x< \frac{{\hat{n}}_1+1}{2^{k_1-1}},\\ \frac{{\hat{n}}_2}{2^{k_2-1}}\le y< \frac{{\hat{n}}_2+1}{2^{k_2-1}}, \end{array} \\ 0, &{}\quad \hbox {otherwise} \end{array}\right. \end{aligned}$$

where \(m_1=0,1,2,...,M_1-1, m_2=0,1,2,...,M_2-1\). Here, \({\hat{n}}_1\) and \({\hat{n}}_2\) are defined similarly to \({\hat{n}}, k_1\) and \(k_2\) can be any positive integer, \({\tilde{\beta }}_{m_1}\) and \({\tilde{\beta }}_{m_2}\) are defined similarly to \({\tilde{\beta }}_{m}\) of order \(m_1\) and \(m_2\), respectively.

Function approximation

A function \(f(x,y)\in L^2([0,1)\times [0,1))\) may be expanded as in terms of two-dimensional Bernoulli wavelets as

$$\begin{aligned} f(x,y)=\sum \limits _{n=1}^{\infty } \sum \limits _{i=0}^{\infty } \sum \limits _{l=1}^{\infty } \sum \limits _{j=0}^{\infty } c_{nilj}\varphi _{nilj}(x,y). \end{aligned}$$
(2.4)

If the infinite series for f is truncated, then Eq. (2.4) can be written as

$$\begin{aligned} f(x,y)\simeq \sum \limits _{n=1}^{2^{k_1-1}} \sum \limits _{i=0}^{M_1-1} \sum \limits _{l=1}^{2^{k_2-1}} \sum \limits _{j=0}^{M_2-1} c_{nilj}\varphi _{nilj}(x,y)=C^T\Phi (x,y)=\Phi _1^T(x)F\Phi _2(y), \end{aligned}$$
(2.5)

where \(\Phi _1(x)\) and \(\Phi _2(y)\) are \(2^{k_1-1}M_1\times 1\) and \(2^{k_2-1}M_2\times 1\) matrices, respectively, given by

$$\begin{aligned} \Phi _1(x)= & {} [\varphi _{10}(x),\varphi _{11}(x),\ldots ,\varphi _{1M_1-1}(x),\varphi _{20}(x),\ldots ,\varphi _{2M_1-1}(x),\ldots ,\varphi _{2^{k_1-1}0}(x),\ldots ,\varphi _{2^{k_1-1}M_1-1}(x)]^T,\\ \Phi _2(y)= & {} [\varphi _{10}(y),\varphi _{11}(y),\ldots ,\varphi _{1M_2-1}(y),\varphi _{20}(y),\ldots ,\varphi _{2M_2-1}(y),\ldots ,\varphi _{2^{k_2-1}0}(y),\ldots ,\varphi _{2^{k_2-1}M_2-1}(y)]^T. \end{aligned}$$

In Eq. (2.5), F is a \(2^{k_1-1}M_1\times 2^{k_2-1}M_2\) matrix that can be calculated from [33]

$$\begin{aligned} F=D_1^{-1}<\Phi _1(x),<f(x,y),\Phi _2(y)>>D_2^{-1}, \end{aligned}$$

where \(\langle . \rangle\) denotes the inner product, \(D_1=\langle \Phi _1(x),\Phi _1(x) \rangle =\int _{0}^{1}\Phi _1(x)\Phi ^T_1(x)\mathrm{d}x\) and \(D_2=\langle \Phi _2(y),\Phi _2(y)\rangle =\int _{0}^{1}\Phi _2(y)\Phi ^T_2(y)\mathrm{d}y\) are \(2^{k_1-1}M_1\times 2^{k_1-1}M_1\) and \(2^{k_2-1}M_2\times 2^{k_2-1}M_2\) matrices, respectively.

Satisfier function

In the Ritz–Galerkin method with the two-dimensional BWs basis, the approximation \({\widetilde{u}}(x,t)\) of the solution u(x, t) in (1.1) is sought in the form of the truncated series

$$\begin{aligned} {\widetilde{u}}(x,t)=\sum _{n=1}^{2^{k_1-1}}\sum _{i=0}^{M_1-1}\sum _{l=1}^{2^{k_2-1}}\sum _{j=0}^{M_2-1}c_{nilj} \sigma _{nilj}(x,t)+ w(x, t), \quad (x, t)\in [0,L] \times [0, T], \end{aligned}$$
(3.1)

where \(\sigma _{nilj}(x,t)=x(x-L)t^2\varphi _{ni}(x)\varphi _{lj}(t)\) and w(x, t) is a satisfier function. The most important point in using the Ritz–Galerkin method is finding the satisfier function, which satisfies all the problem conditions [16]. Interpolation is one of the methods that is usually used to derive Satisfier functions. On the other hand, we have seen from experience, when in constructing of the satisfier function we use only the problem’s data, we get a satisfier function that is closer to the exact solution. Therefore, we obtain the cost-effective computational results [14, 16]. Here, we construct two different satisfier functions for the initial and boundary conditions:

$$\begin{aligned} u(x,0)= & {} f_0(x), \quad 0\le x \le L, \end{aligned}$$
(3.2)
$$\begin{aligned} \frac{\partial u(x,0)}{\partial t}= & {} f_1(x),\quad 0\le x \le L, \end{aligned}$$
(3.3)
$$\begin{aligned} u(0,t)= & {} g_0(t), \quad 0\le t\le T, \end{aligned}$$
(3.4)
$$\begin{aligned} u(L,t)= & {} g_1(t), \quad 0\le t\le T. \end{aligned}$$
(3.5)

It is worth pointing out that \(f_0(x), f_1(x), g_0(t)\) and \(g_1(t)\) satisfy the following compatibility conditions:

$$\begin{aligned} f_0(0)= & {} g_0(0),\quad f_0(L)=g_1(0), \end{aligned}$$
(3.6)
$$\begin{aligned} f_1(0)= & {} \acute{g_0}(0),\quad f_1(L)=\acute{g_1}(0) . \end{aligned}$$
(3.7)

The first technique for obtaining the satisfier function is as follows:

We set

$$\begin{aligned} w(x,t)=k_{1}(x)g_0(t)+k_{2}(x)g_1(t), \end{aligned}$$
(3.8)

then we construct \(k_{1}(x)\) and \(k_{2}(x)\), such that (3.8) fulfils the conditions (3.2)–(3.5).

Clearly, if \(k_{1}(x)\) and \(k_{2}(x)\) satisfy the following conditions:

$$\begin{aligned} k_{1}(0)= & {} k_{2}(L)=1,\quad k_{2}(0)=k_{1}(L)=0, \end{aligned}$$
(3.9)
$$\begin{aligned} k_{1}(x)g_0(0)+k_{2}(x)g_1(0)= & {} f_0(x),\quad k_{1}(x)\acute{g_0}(0)+k_{2}(x)\acute{g_1}(0)=f_1(x), \end{aligned}$$
(3.10)

then (3.8) can be a satisfier function for (3.2)–(3.5).

Equations (3.10) form a system of linear equations, which can be solved for \(k_{1}(x)\) and \(k_{2}(x)\) when \(g_0(0)\acute{g_1}(0)-g_1(0)\acute{g_0}(0)\ne 0\). By solving this system, we obtain

$$\begin{aligned} k_{1}(x)= & {} \frac{f_0(x)\acute{g_1}(0)-g_1(0)f_1(x)}{g_0(0)\acute{g_1}(0)-g_1(0)\acute{g_0}(0)}, \end{aligned}$$
(3.11)
$$\begin{aligned} k_{2}(x)= & {} \frac{f_1(x)g_0(0)-\acute{g_0}(0)f_0(x)}{g_0(0)\acute{g_1}(0)-g_1(0)\acute{g_0}(0)}. \end{aligned}$$
(3.12)

From compatibility conditions (3.6) and (3.7), it is easy to see that \(k_{1}(x)\) and \(k_{2}(x)\) have properties (3.9). Therefore, we introduce the satisfier function w(x, t) which satisfies the initial conditions (3.2) and (3.3), and the boundary conditions (3.4) and (3.5) when

$$\begin{aligned} g_0(0)\acute{g_1}(0)-g_1(0)\acute{g_0}(0)\ne 0, \end{aligned}$$

as:

$$\begin{aligned} w(x,t)=k_{1}(x)g_0(t)+k_{2}(x)g_1(t), \end{aligned}$$
(3.13)

where \(k_{1}(x)\) and \(k_{2}(x)\) are obtained from (3.11) and (3.12).

The second satisfier function is constructed as follows:

We firstly transform the nonhomogeneous boundary condition into a homogeneous boundary condition. Let

$$\begin{aligned} u(x,t)=v(x,t)+\phi (x,t), \end{aligned}$$

where

$$\begin{aligned} \phi (x,t)=\left( 1-\frac{x}{L}\right) g_0(t)+\frac{x}{L} g_1(t). \end{aligned}$$

The function v(x, t) then satisfies the problem with homogeneous boundary conditions:

$$\begin{aligned} v(x,0)= & {} F_0(x), \quad 0\le x \le L, \end{aligned}$$
(3.14)
$$\begin{aligned} \frac{\partial v(x,0)}{\partial t}= & {} F_1(x),\quad 0\le x \le L, \end{aligned}$$
(3.15)
$$\begin{aligned} v(0,t)= & {} 0, \quad 0\le t\le T, \end{aligned}$$
(3.16)
$$\begin{aligned} v(L,t)= & {} 0, \quad 0\le t\le T, \end{aligned}$$
(3.17)

that \(F_0(x)=f_0(x)-\phi (x,0),\) and \(F_1(x)=f_1(x)-\phi _{t}(x,0).\) From conditions (3.14)–(3.17), we drive compatibility conditions:

$$\begin{aligned} F_0(0)=F_0(L)=F_1(0)=F_1(L)=0. \end{aligned}$$

Therefore, \(W(x,t)=F_0(x)+t F_1(x)\) satisfies conditions (3.14)–(3.17) and eventually, we introduce the satisfier function for (3.2)–(3.5) as:

$$\begin{aligned} w(x,t)=W(x,t)+\phi (x,t). \end{aligned}$$
(3.18)

It is worth to mention that if \(g_0(0)\acute{g_1}(0)-g_1(0)\acute{g_0}(0)\ne 0\), we prefer the first attained satisfier function in (3.13), since in constructing of (3.13) we used only the problem’s data.

Returning now to the Ritz–Galerkin approximation (3.1), the expansion coefficients \(c_{nilj}\) are determined by the Galerkin equations:

$$\begin{aligned} \langle F({\widetilde{u}}) ,\varphi _{ni}(x)\varphi _{lj}(t) \rangle =0, \end{aligned}$$
(3.19)

where

$$\begin{aligned} F(u)=\frac{\partial ^q u(x,t)}{\partial t^q}+\frac{\partial u(x,t)}{\partial t}-\frac{\partial ^{2}u(x,t)}{\partial x^{2}}-h(x,t), \end{aligned}$$

and

$$\begin{aligned} \langle F({\widetilde{u}}) ,\varphi _{ni}(x)\varphi _{lj}(t) \rangle =\int _{0}^{L}\int _{0}^{T} F({\widetilde{u}})\varphi _{ni}(x)\varphi _{lj}(t)\mathrm{d}t\mathrm{d}x, \end{aligned}$$
(3.20)

where \(\varphi _{ni}(x),\varphi _{lj}(t)\) are BWs. Equations (3.19) form a linear system of equations which can be solved for the elements of \(c_{nilj}, n=1,...,2^{k_1-1}, i=0,...,M_1-1, l=1,...,2^{k_2-1}, j=0,...,M_2-1\) using mathematical softwares.

Numerical results and comparisons

In this section, we apply the numerical scheme in the previous section for finding the approximation solutions of two examples of FDWE. We compare our results with obtained results in [3] and [7]. In all examples the package of Mathematica ver. 10.4 has been used. The approximate norm-2 of absolute error is given as

$$\begin{aligned} \Vert e(x,t) \Vert _{L^2}^2 =\int _{0}^{L}\int _{0}^{T} e^2(x,t)\mathrm{d}t\mathrm{d}x=\int _{0}^{L}\int _{0}^{T} ( u(x,t)-{\widetilde{u}}(x,t) )^2\mathrm{d}t\mathrm{d}x \end{aligned}$$

Example 1

Notice the following FDWE [7]:

$$\begin{aligned} \frac{\partial ^q u(x,t)}{\partial t^q}+\frac{\partial u(x,t)}{\partial t}=\frac{\partial ^{2}u(x,t)}{\partial x^{2}}+h(x,t),\quad (x,t)\in [0,1]\times [0,1],\quad 1<q \le 2, \end{aligned}$$
(4.1)

with the homogenous initial and boundary conditions, and let

$$\begin{aligned} h(x,t)=\frac{2x(1-x)t^{2-q}}{\Gamma (3-q)}+2tx(1-x)+2t^2. \end{aligned}$$

Now, we apply the numerical method presented in this paper for \(k_1=k_2=1\) and \(M_1=M_2=3\). From Eq. (3.18) we have \(w(x,t)=0\) and from Eq. (3.19), for \(q=1.1, 1.3, 1.5, 1.7, 1.9\) we obtain

$$\begin{aligned} c_{1010}=-1,\quad c_{1i1j}=0,\quad i,j=1,2. \end{aligned}$$

Thus, from (3.1) we have

$$\begin{aligned} {\widetilde{u}}(x,t)=t^2x(1-x), \end{aligned}$$

which is the exact solution.

In [7], Heydari et al. used fractional operational matrix of integration for the LWs to solve this problem for \(q=1.1, 1.3, 1.5, 1.7, 1.9\). The best absolute error of the approximate solutions at some different points, in [7], with \(k_1=k_2=3\) and \(M_1=M_2=3\) is \(1.6695 \times 10^{-6}\).

Example 2

Consider the following FDWE [3, 7]:

$$\begin{aligned} \frac{\partial ^q u(x,t)}{\partial t^q}+\frac{\partial u(x,t)}{\partial t}=\frac{\partial ^{2}u(x,t)}{\partial x^{2}}+h(x,t),\quad (x,t)\in [0,1]\times [0,1],\quad 1<q \le 2, \end{aligned}$$
(4.2)

where

$$\begin{aligned} h(x,t)=\frac{6t^{3-q}e^x}{\Gamma (4-q)}+3t^2e^x-t^3e^x. \end{aligned}$$

The initial and boundary conditions are determined correspondingly to the exact solution \(u(x, t) =e^xt^3.\)

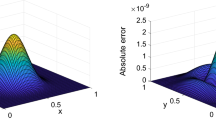
From (3.18), we obtain \(w(x,t)=t^3(1-x+ex)\), then apply the numerical method presented in this paper for \(k_1=k_2=1\) and \(M_1=M_2=3\). Tables 1 and 2 present, respectively, the absolute error and the \(L^2\) norm error for \(u(x,t)-{\widetilde{u}}(x,t)\) with different values of q. In Table 3, the absolute error of u(x, t) and CPU times for \(q = 1.5\) with \(k_1=k_2=1\) and different values of \(M_1=M_2\) are given. It is seen from Table 3 that, with increase in the number of the two-dimensional Bernoulli wavelets basis, the approximate values of u(x, t) converge to the exact solutions. In Figs. 1 and 2, the exact and approximate solutions, and also the absolute difference between exact and approximate solutions of u(x, t) with \(q=1.1\) and \(q=1.9\) are plotted, respectively. Also, the graphs of the absolute errors for \(q = 1.5\) at \(t = 0.5\) and \(x = 0.5\) are shown in Fig. 3.

Liu et al. [3] employed the fractional predictor–corrector method and solved this problem with \(q=1.85\) and different values of time and space step sizes. They obtained \(1.6341 \times 10^{-3}\) for the best maximum absolute error. Moreover, in Table 1 we compare our results with obtained results in [7]. These comparisons show the more accuracy and less computations of our technique in comparison to other published methods.

Table 1 Comparison of absolute errors of our scheme with scheme in [7], for Example 2
Full size table
Table 2 The \(L^2\) norm error, for Example 2
Full size table
Fig. 1
figure 1

The graphs of the Exact (blue) and approximate (red) solutions (left side) and the absolute error (right side) of u(x, t) in \(q=1.1\), for Example 2

Full size image
Table 3 Absolute error for different values of \(M_1\) and \(M_2\) in \(q=1.5\), for Example 2
Full size table
Fig. 2
figure 2

The graphs of the Exact (blue) and approximate (red) solutions (left side) and the absolute error (right side) of u(x, t) in \(q=1.9\), for Example 2

Full size image
Fig. 3
figure 3

The graphs of the absolute errors at \(t = 0.5\) (left) and \(x = 0.5\) (right) in \(q = 1.5\), for Example 2

Full size image

Conclusion

In this paper, the two-dimensional BWs was defined. Then the satisfier function in Ritz–Galerkin method with the two-dimensional BWs basis was successfully applied to solve the second-order time FDWE. Using of satisfier function in the Ritz–Galerkin method is an efficient tool to put on the initial and boundary conditions. Furthermore, a small number of basis elements were sufficient to derive accurate numerical solutions. Also, our results were compared with obtained results in [3] and [7]. Comparison for the numerical examples shows the more accuracy and less computations of the proposed method in comparison to other published methods.