Effect of geometric shape of micro-grooves on the performance of textured hybrid thrust pad bearing

Abstract

A numerical simulation is performed to investigate the synergizing influence of surface texture (micro-grooves) and electrically conducting lubricant on static and dynamic performance of hybrid thrust pad bearings operating under transverse magnetic field. Linear momentum and mass conservation equation are solved simultaneously to derive modified Reynolds equation for magnetohydrodynamic lubrication. Finite element approach has been used to obtain couple solution of modified Reynolds equation and restrictor (orifice) flow equation. A mass conserving algorithm (Jakobsson–Floberg–Olsson boundary condition) has been implemented to simulate cavitation phenomenon within micro-grooves. A parametric investigation (based on load-carrying capacity/fluid film pressure) is carried out to obtain optimum attributes for various micro-grooves shapes. Providing micro-groove on bearings surfaces results in a significant increase in load-carrying capacity, stiffness coefficient and reduction in frictional power loss of the bearing. Employing of electrically conducting lubricant is seen to be enhancing the load-carrying capacity and damping characteristics of the bearing.

Appendix

1.1 Derivation for modified Reynolds equation

Assumptions: steady-state flow$; \frac{\partial p}{\partial t} = 0$. Inertia and body forces (except Lorentz force) are assumed to be neglected. The momentum conservation equation and mass conservation equations are as follows:

$$ 0 = - \nabla p + \mu \left( {\nabla^{2} \vec{v}} \right) + \vec{F}_{\text{l}} $$

(12)

$$ \nabla \cdot \vec{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 $$

(13)

Here, $\vec{F}_{\text{l}}$ is a body force known as Lorentz force and defined as force felt by a charge particle passing through an external magnetic field (B_o). Mathematically, Lorentz force is expressed as cross-product of current density $\left( {\vec{J}} \right)$ and magnetic field $\left( {\vec{B}} \right)$, i.e. $\overrightarrow { F}_{\text{l}} = \left( {\vec{J} \times \vec{B}} \right)$; the current density is expressed as: $\vec{J} = \sigma \left( {\vec{E} + \left( {\vec{v} \times \vec{B}} \right)} \right)$. Navier–Stokes equation (12) along the three axes of Cartesian co-ordinate system is as follows:

$$ \mu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \sigma B_{o}^{2} u = \frac{\partial p}{\partial x} + \sigma E_{z} B_{o} $$

(14)

$$ \mu \frac{{\partial^{2} w}}{{\partial y^{2} }} - \sigma B_{o}^{2} w = \frac{\partial p}{\partial z} - \sigma E_{x} B_{o} $$

(15)

$$ \frac{\partial p}{\partial y} = 0 $$

(16)

$E_{z}$ and $E_{x}$ represent the magnitude of induced/generated electric field and the subscript denotes the direction. The bearing surfaces are assumed non-conducting. The magnitude of induced electric field can be obtained by setting net current flow to be zero, i.e.

$$ \mathop \smallint \limits_{0}^{h} \left( {E_{x} - wB_{o} } \right){\text{d}}y = 0 $$

(17)

$$ \mathop \smallint \limits_{0}^{h} \left( {E_{z} + uB_{o} } \right){\text{d}}y = 0 $$

(18)

Fluid film velocity profile is derived by using following Boundary conditions:

$$ {\text{At}}\;y = 0;\left( {u = U;w = W} \right)_{{{\text{No}}\;{\text{slip}} }} ;\quad v = \frac{\partial h}{\partial t} $$

(19)

$$ {\text{At}}\;y = h;\left( {u = 0;w = 0} \right)_{{{\text{No}}\;{\text{slip}} }} ;\quad v = 0 $$

(20)

The value of induced electric field (E_z and E_x) obtained by solving equations (17 and 18) is substituted into Eq. (14 and 15), and subsequently these equations are solved using boundary condition provided in Eqs. (19 and 20). The fluid film velocity profile along Cartesian axes x and z are governed by following expressions:

$$ \begin{aligned} &\left. {u_{i} = \frac{{U_{i} }}{2}\left\{ {1 - \frac{{\left[ {\sinh \left( {\frac{Hy}{{h_{0} }}} \right) - \sinh \left( {\frac{{H\left( {h - y} \right)}}{{h_{0} }}} \right)} \right]}}{{\sinh \left( {\frac{Hh}{{h_{0} }}} \right)}}} \right\}}\right. \\ &\quad \left.{- \frac{{h_{0} h}}{2\mu H}\left( {\frac{\partial p}{\partial n}} \right)_{i} \left\{ {\frac{{\left[ {\sinh \left( {\frac{Hh}{{h_{0} }}} \right) - \sinh \left( {\frac{Hy}{{h_{0} }}} \right) - \sinh \left( {\frac{{H\left( {h - y} \right)}}{{h_{0} }}} \right)} \right]}}{{\left[ {\cosh \left( {\frac{Hh}{{h_{0} }}} \right) - 1} \right]}}} \right\}} \right|_{i = 1,2} \end{aligned}$$

(21)

$$\begin{aligned} &i = 1;{\text{implies}} \left[ {u_{i} = u;U_{i} = U;\left( {\frac{\partial p}{\partial n}} \right)_{i} = \frac{\partial p}{\partial x}} \right]\;{\text{and}}\; \\ &i = 2;{\text{implies}} \left[ {u_{i} = w;U_{i} = W;\left( {\frac{\partial p}{\partial n}} \right)_{i} = \frac{\partial p}{\partial z}} \right] \end{aligned}$$

(22)

where H denotes Hartmann number, a non-dimensional parameter representing relative magnitude of electro-magnetic force to viscous force, i.e. $H = B_{o} h_{o} \left( {\sigma /\mu } \right)^{1/2}$; here, symbol $\sigma$ is used to represent lubricant electrical conductivity. Now, substituting the expression of fluid film velocity (21 and 22) in mass conservation Eq. (13) and performing integration w.r.t film thickness direction, modified Reynolds equation for electrically conducting lubricant can be obtained as follows:

$$\begin{aligned} &\frac{\partial }{\partial x}\left( {h^{3} \emptyset \left( {h,H} \right)\rho \frac{\partial p}{\partial x}} \right) + \frac{\partial }{\partial z}\left( {h^{3} \emptyset \left( {h,H} \right)\rho \frac{\partial p}{\partial z}} \right) \\ &\quad= 6\mu U\frac{\partial \rho h}{\partial x} + 6\mu W\frac{\partial \rho h}{\partial z} + 12\mu \frac{\partial \rho h}{\partial t} \end{aligned}$$

(23)

where $\emptyset \left( {h,M} \right) = \frac{{6h_{o}^{2} }}{{h^{2} H^{2} }}\left\{ {\left( {\frac{Hh}{{h_{o} }}} \right)coth\left( {\frac{Hh}{{2h_{o} }}} \right) - 2} \right\}$ is magnetohydrodynamic function.

The lubricant is fed in recess of the bearing by means of an orifice restrictor (compensating element). Under steady-state operation of bearing, the total lubricant input flow through the restrictor will be same as that of summation of lubricant flow rate through nodes located at recess boundary. The lubricant flow rate through orifice restrictor is governed by the following expression:

$$ \bar{Q}_{\text{R}} = \overline{\text{CS}}_{2} \left( {1 - \bar{p}_{\text{r}} } \right)^{1/2} = \bar{Q} $$

(24)

1.2 Cavitation parameters for JFO boundary conditions

Film zone/location	Boundary condition	Value of switch functions
Full film zone	$\bar{p} > 0$	$g = 1;\lambda = 1;\gamma = 1$	(25)
Film rupture location	$\bar{p} = 0;\left[ { \frac{{\partial \bar{p}}}{{\partial \bar{x}}} \& \frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right] = 0$	$g = 1;\lambda = 1;\gamma = 1$	(26)
Cavitation Zone	$\bar{p} < 0$	$g = 0;0 \le \lambda \le 1;\gamma = 0$	(27)
Film reformation location	$\bar{p} = 0; \left[ { \frac{{\partial \bar{p}}}{{\partial \bar{x}}} \& \frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right] > 0$	$g = 0;0 \le \lambda \le 1;\gamma = 0$	(28)

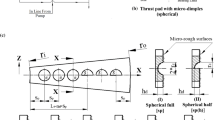
1.3 Fluid film thickness expression for groove having different cross-sectional shapes (Refer Fig. 1c)

Groove Shape	Fluid film expression	Domain	Eqs.
(I) Circular (Cir)	$\bar{h} = \bar{h}_{0} + \bar{d}_{\text{g}} \sqrt {1 - 4\left( {\frac{{\theta - \left( {\theta_{\text{gi}} + 0.5*\theta_{\text{g}} } \right)}}{{\theta_{\text{g}} }}} \right)^{2} }$	$\theta_{\text{gi}} \le \theta \le \theta_{\text{go}}$	(29)
(II) Rectangular (Rect)	$\bar{h} = \bar{h}_{0} + \bar{d}_{\text{g}}$	$\theta_{\text{gi}} \le \theta \le \theta_{\text{go}}$	(30)
(III) Triangular (Tri)	$\bar{h} = \bar{h}_{0} + 2*\bar{d}_{\text{g}} *\frac{{\left( {\theta - \theta_{\text{gi}} } \right)}}{{\theta_{\text{g}} }};$	$\theta_{\text{gi}} \le \theta < \left( {\theta_{\text{gi}} + 0.5*\theta_{\text{g}} } \right)$	(31)
	$\bar{h} = \bar{h}_{0} - 2*\bar{d}_{\text{g}} *\frac{{\left( {\theta - \left( {\theta_{\text{gi}} + \theta_{\text{g}} } \right)} \right)}}{{\theta_{\text{g}} }}$	$\left( {\theta_{\text{gi}} + 0.5*\theta_{\text{g}} } \right) \le \theta \le \theta_{\text{go}}$	(32)
(IV)Trapezoidal (Trap)	$\bar{h} = \bar{h}_{0} + 4*\bar{d}_{\text{g}} *\frac{{\left( {\theta - \theta_{\text{gi}} } \right)}}{{\theta_{\text{g}} }}$	$\theta_{\text{gi}} \le \theta < \left( {\theta_{\text{gi}} + 0.25*\theta_{\text{g}} } \right)$	(33)
	$\bar{h} = \bar{h}_{0} + \bar{d}_{\text{g}}$	$\left( {\theta_{\text{gi}} + 0.25*\theta_{\text{g}} } \right) \le \theta < \left( {\theta_{\text{gi}} + 0.75*\theta_{\text{g}} } \right)$	(34)
	$\bar{h} = \bar{h}_{0} - 4*\bar{d}_{\text{g}} *\frac{{\left( {\theta - \left( {\theta_{\text{gi}} + \theta_{\text{g}} } \right)} \right)}}{{\theta_{\text{g}} }}$	$\left( {\theta_{\text{gi}} + 0.75*\theta_{\text{g}} } \right) \le \theta < \theta_{\text{go}}$	(35)
Smooth surface	$\bar{h} = \bar{h}_{0} ;$	$\left( {\theta < \theta_{\text{gi }} } \right)\;{\text{or}}\; \left( {\theta > \theta_{\text{go}} } \right)$	(36)

1.4 Finite element formulation

Using approximation of fluid film pressure (Eq. 4) in Eq. 3, residue will be obtained:

$$\begin{aligned} & \frac{\partial }{{\partial \bar{x}}}\left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)g\frac{\partial }{{\partial \bar{x}}}\left\{ {\mathop \sum \limits_{j = 1}^{4} \left( {\bar{p}_{j} N_{j} } \right)} \right\}} \right)\\&\quad + \frac{\partial }{{\partial \bar{z}}}\left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)g\frac{\partial }{{\partial \bar{z}}}\left\{ {\mathop \sum \limits_{j = 1}^{4} \left( {\bar{p}_{j} N_{j} } \right)} \right\}} \right) \\ &\quad- \lambda \bar{u}\frac{{\partial \bar{h}}}{{\partial \bar{x}}} - \lambda \bar{w}\frac{{\partial \bar{h}}}{{\partial \bar{z}}} - \gamma \frac{{\partial \bar{h}}}{{\partial \bar{t}}} = R_{\text{es}} \end{aligned}$$

(37)

Integrating residue over fluid film domain (weak formulation)

$$ \mathop {\iint }\limits_{{\varOmega^{e} }}^{ } \left( {N_{j} *R_{\text{es}} } \right){\text{d}}\bar{x}{\text{d}}\bar{z} = 0 $$

(38)

Assembled global flow governing equation:

$$ \left[ {\bar{F}_{ij}^{e} } \right]\left\{ {\bar{p}} \right\} = \left\{ {\bar{Q}_{i}^{e} } \right\} + \left[ {\overline{\text{RH}}_{i}^{e} } \right]_{{\bar{u},\bar{w}}}^{ } + \bar{\dot{h}}\left[ {\overline{\text{RS}}_{i}^{e} } \right] $$

(39)

The matrix terms eth element in the above equation is expressed as follows:

Fluidity term matrix:

$$ \bar{F}_{ij}^{e} = \mathop {\iint }\limits_{{\varOmega^{e} }}^{ } g\left[ {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{{\partial N_{i} }}{{\partial \bar{x}}}\frac{{\partial N_{j} }}{{\partial \bar{x}}} + \bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{{\partial N_{i} }}{{\partial \bar{z}}}\frac{{\partial N_{j} }}{{\partial \bar{z}}}} \right]{\text{d}}\bar{x}{\text{d}}\bar{z} $$

(40)

Flow term matrix:

$$ \begin{aligned} \bar{Q}_{i}^{e} &= \mathop \smallint \limits_{{\varGamma^{e} }}^{ } g\left[ {\left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{\partial p}{{\partial \bar{x}}}} \right)n_{x} + \left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{\partial p}{{\partial \bar{z}}}} \right)n_{z} } \right]N_{i} {\text{d}}\varGamma^{e} \\ &\quad- \lambda \mathop \smallint \limits_{{\varGamma^{e} }}^{ } N_{i} \bar{h}\left( {\bar{u}n_{x} + \bar{w}n_{z} } \right){\text{d}}\varGamma^{e} \end{aligned}$$

(41)

Hydrodynamic term matrix

$$ \overline{\text{RH}}_{i}^{e} = \mathop {\iint }\limits_{{\varOmega^{e} }}^{ } \lambda \left[ {\bar{u}\bar{h}\frac{{\partial N_{i} }}{{\partial \bar{x}}} + \bar{w}\bar{h}\frac{{\partial N_{j} }}{{\partial \bar{z}}}} \right]{\text{d}}\bar{x}{\text{d}}\bar{z} $$

(42)

Squeeze term matrix:

$$ \overline{\text{RS}}_{i}^{e} = \mathop {\iint }\limits_{{\varOmega^{e} }}^{ } \gamma N_{i} {\text{d}}\bar{x}{\text{d}}\bar{z} $$

(43)

For obtaining dynamic characteristics, the local derivative of nodal pressure w.r.t film thickness and squeeze velocity is defined as:

$$ \frac{{\partial \bar{p}}}{{\partial \bar{h}}} = \left[ {\bar{F}} \right]^{ - 1} \left[ {\frac{{\partial \left\{ {\bar{Q}} \right\}}}{{\partial \bar{h}}} + \frac{{\partial \left[ {\overline{\text{RH}}_{ij}^{ } } \right]}}{{\partial \bar{h}}} + \bar{\dot{h}}\frac{{\partial \left[ {\overline{\text{RS}}_{ij}^{ } } \right]}}{{\partial \bar{h}}} - \left\{ {\bar{p}} \right\}\frac{{\partial \left[ {\bar{F}} \right]}}{{\partial \bar{h}}}} \right] $$

(44)

$$ \frac{{\partial \bar{p}}}{{\partial \bar{\dot{h}}}} = \left[ {\bar{F}} \right]^{ - 1} \left[ {\frac{{\partial \left\{ {\bar{Q}} \right\}}}{{\partial \bar{\dot{h}}}} + \frac{{\partial \left[ {\overline{\text{RH}}_{ij}^{ } } \right]}}{{\partial \bar{\dot{h}}}} + \left[ {\overline{\text{RS}}_{ij}^{ } } \right] + \bar{\dot{h}}\frac{{\partial \left[ {\overline{\text{RS}}_{ij}^{ } } \right]}}{{\partial \bar{\dot{h}}}} - \left\{ {\bar{p}} \right\}\frac{{\partial \left[ {\bar{F}} \right]}}{{\partial \bar{\dot{h}}}}} \right] $$

(45)

The numerical integration of aforementioned matrix terms (40–43) is obtained using Gauss–Legendre Quadrature. The shape function for four-noded isoparametric element is defined as:

$$ \hat{N}_{i} = \frac{1}{4}(1 + \xi_{i} \xi )(1 + \eta_{i} \eta ) $$

(46)

The derivative of shape function w.r.t $\xi$ and $\eta$ can be obtained using chain rule of partial differentiation

$$ \frac{{\partial N_{i} }}{\partial \xi } = \frac{{\partial N_{i} }}{{\partial \bar{x}}}\frac{{\partial \bar{x}}}{\partial \xi } + \frac{{\partial N_{i} }}{{\partial \bar{z}}}\frac{{\partial \bar{z}}}{\partial \xi };\quad \frac{{\partial N_{i} }}{\partial \eta } = \frac{{\partial N_{i} }}{{\partial \bar{x} }}\frac{{\partial \bar{x} }}{\partial \eta } + \frac{{\partial N_{i} }}{{\partial \bar{z}}}\frac{{\partial \bar{z}}}{\partial \eta } $$

(47)

The above partial derivatives in matrix form can be expressed as:

$$\begin{aligned} \left| {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{\partial \xi }} \\ {\frac{{\partial N_{i} }}{\partial \eta }} \\ \end{array} } \right| &= \left| {\begin{array}{*{20}c} {\frac{{\partial \bar{x}}}{\partial \xi }} & {\frac{{\partial \bar{z}}}{\partial \xi }} \\ {\frac{{\partial \bar{x} }}{\partial \eta }} & {\frac{{\partial \bar{z}}}{\partial \eta }} \\ \end{array} } \right|\left| {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{{\partial \bar{x}}}} \\ {\frac{{\partial N_{i} }}{{\partial \bar{z}}}} \\ \end{array} } \right| = \left[ J \right]\left| {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{{\partial \bar{x}}}} \\ {\frac{{\partial N_{i} }}{{\partial \bar{z}}}} \\ \end{array} } \right| \Rightarrow \left| {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{{\partial \bar{x}}}} \\ {\frac{{\partial N_{i} }}{{\partial \bar{z}}}} \\ \end{array} } \right| \\ &= J^{ - 1} \left| {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{\partial \xi }} \\ {\frac{{\partial N_{i} }}{\partial \eta }} \\ \end{array} } \right| = \left[ {\begin{array}{*{20}c} {J_{11}^{*} } & {J_{12}^{*} } \\ {J_{21}^{*} } & {J_{22}^{*} } \\ \end{array} } \right]\left| {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{\partial \xi }} \\ {\frac{{\partial N_{i} }}{\partial \eta }} \\ \end{array} } \right| \end{aligned}$$

(48)

where $\left[ J \right]$ represent Jacobian Matrix. Determinants of Jacobian Matrix are defined as: ${\text{d}}\bar{x}{\text{d}}\bar{z} = J{\text{d}}\xi {\text{d}}\eta$. Substituting the value of $\frac{{\partial N_{i} }}{{\partial \bar{x}}}$ and $\frac{{\partial N_{i} }}{{\partial \bar{z}}}$ from (48) in expression for $\overline{ F}_{ij}^{e}$

$$ \begin{aligned} \bar{F}_{ij}^{e} &= \mathop \smallint \limits_{ - 1}^{ + 1} \mathop \smallint \limits_{ - 1}^{ + 1} \bar{h}^{3} \emptyset \left( {\bar{h},H} \right)g\left\{ {\left( {J_{11}^{ *} \frac{{\partial N_{i} }}{\partial \xi } + J_{12}^{ *} \frac{{\partial N_{i} }}{\partial \eta }} \right)}\right.\\&\quad \times\left.{\left( {J_{11}^{ *} \frac{{\partial N_{j} }}{\partial \xi } + J_{12}^{ *} \frac{{\partial N_{j} }}{\partial \eta }} \right) + \left( {J_{21}^{ *} \frac{{\partial N_{i} }}{\partial \xi } + J_{22}^{ *} \frac{{\partial N_{i} }}{\partial \eta }} \right)}\right.\\&\quad \times\left.{\left( {J_{21}^{ *} \frac{{\partial N_{j} }}{\partial \xi } + J_{22}^{ *} \frac{{\partial N_{j} }}{\partial \eta }} \right)} \right\}\left| {\mathbf{J}} \right|{\text{d}}\xi {\text{d}}\eta \end{aligned}$$

(49)

Similarly the expression for $\left( { \overline{\text{RH}}_{i}^{e} } \right)$ and $\left( {\overline{\text{RS}}_{i}^{e} } \right)$ matrix terms for the eth element are described as

$$\begin{aligned} \overline{\text{RH}}_{i}^{e} &= \mathop {\iint }\limits_{{\varOmega^{e} }}^{ } \lambda \bar{h}\left[ {\bar{u}\frac{{\partial N_{i} }}{{\partial \bar{x}}} + \bar{w}\frac{{\partial N_{j} }}{{\partial \bar{z}}}} \right]{\text{d}}\bar{x}{\text{d}}\bar{z} \\ &= \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} \lambda \bar{h}\bar{u}\left( {J_{11}^{*} \frac{{\partial N_{i} }}{\partial \xi } + J_{12}^{*} \frac{{\partial N_{i} }}{\partial \eta }} \right)\left| J \right|{\text{d}}\xi {\text{d}}\eta \\ &\quad+ \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} \lambda \bar{h}\bar{w}\left( {J_{21}^{*} \frac{{\partial N_{i} }}{\partial \xi } + J_{22}^{*} \frac{{\partial N_{i} }}{\partial \eta }} \right)\left| J \right|{\text{d}}\xi {\text{d}}\eta \end{aligned}$$

(50)

$$ \overline{\text{RS}}_{i}^{e} = \mathop {\iint }\limits_{{{{\varOmega }}^{e} }}^{ } \gamma N_{i} {\text{d}}\bar{x}{\text{d}}\bar{z} = \mathop \int \limits_{ - 1}^{1} \mathop \int \limits_{ - 1}^{1} \gamma N_{i} \left| J \right|{\text{d}}\xi {\text{d}}\eta $$

(51)

Integrand for flow matric term ($\bar{Q}_{i}^{e}$) is expressed as

$$ \bar{Q}_{i}^{e} = \mathop \int \limits_{{\varGamma^{e} }}^{ } g\left[ {\left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{{\partial \bar{p}}}{{\partial \bar{x}}}} \right)n_{x} + \left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right)n_{z} } \right]N_{i} {\text{d}}\varGamma^{e} - \lambda \mathop \int \limits_{{\varGamma^{e} }}^{ } N_{i} \bar{h}\left( {\bar{u}n_{x} + \bar{w}n_{z} } \right){\text{d}}\varGamma^{e} $$

(52)

Using $n_{x} {\text{d}}\varGamma^{e} = {\text{d}}\bar{z}$ and $n_{z} {\text{d}}\varGamma^{e} = {\text{d}}\bar{x}$ in the above equation

$$ \begin{aligned} \bar{Q}_{i}^{e} &= \mathop \int \limits_{{\varGamma^{e} }}^{ } g\left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{{\partial \bar{p}}}{{\partial \bar{x}}}} \right)N_{i} {\text{d}}\bar{z} + \mathop \int \limits_{{\varGamma^{e} }}^{ } g\left( {\bar{h}^{3} \emptyset \left( {\bar{h},H} \right)\frac{{\partial \bar{p}}}{{\partial \bar{z}}}} \right)N_{i} {\text{d}}\bar{x} \\ &\quad- \lambda \mathop \int \limits_{{\varGamma^{e} }}^{ } N_{i} \bar{h}\bar{u}{\text{d}}\bar{z} - \lambda \mathop \int \limits_{{\varGamma^{e} }}^{ } N_{i} \bar{h}\bar{w}{\text{d}}\bar{x} \end{aligned} $$

(53)

The expression for flow term ${\bar{\mathbf{Q}}}_{i}^{e}$ is obtained by performing one-dimensional numerical integration as follows:

$$ \begin{aligned} \bar{\varvec{Q}}_{\varvec{i}}^{\varvec{e}} &= - {{\lambda }}\mathop \int \limits_{ - 1}^{ + 1} \bar{h}\hat{N}_{i} \bar{u}\left| {\bar{J}_{L2} } \right|{\text{d}}\eta - {{\lambda }}\mathop \int \limits_{ - 1}^{ + 1} \bar{h}\hat{N}_{i} \bar{w}\left| {\bar{J}_{L1} } \right|{\text{d}}\xi\\ &\quad + \mathop \int \limits_{ - 1}^{ + 1} \bar{h}^{3} \emptyset \left( {\bar{h},\bar{l},H} \right)g\frac{{\partial \bar{p}}}{{\partial \bar{x}}}\hat{N}_{i} \left| {\bar{J}_{L2} } \right|{\text{d}}\eta \\ &\quad+ \mathop \int \limits_{ - 1}^{ + 1} \bar{h}^{3} \emptyset \left( {\bar{h},\bar{l},H} \right)g\frac{{\partial \bar{p}}}{{\partial \bar{y}}}\hat{N}_{i} \left| {\bar{J}_{L1} } \right|{\text{d}}\xi \end{aligned} $$

(54)

where $\left| {\bar{J}_{L1} } \right| = \left| {\frac{{\partial \bar{x}}}{\partial \xi }} \right|, \left| {\bar{J}_{L2} } \right| = \left| {\frac{{\partial \bar{y}}}{\partial \eta }} \right|$

The expression in A.3.18 should be integrated over the nodes located at inner radius (r_i) or at outer radius (r_o) of thrust pad. This will provide lubricant flow rate through 1/32nd model of thrust pad. The total lubricant flow through entire bearing would be 32 times of this lubricant flow rate. The restrictor flow Eq. (24) should be coupled with the element system Eq. (39) to yield simultaneous solution of modified Reynolds equation for nodal pressure vector. Elemental matrix equation (39) is obtained for each element and is assembled to generate global system of equations, as expressed as follows:

$$ \left[ {\begin{array}{*{20}l} {\bar{F}_{11} } \hfill & {\bar{F}_{12} } \hfill & \ldots \hfill & {\bar{F}_{1j} } \hfill & \ldots \hfill & {\bar{F}_{1n} } \hfill \\ {\bar{F}_{21} } \hfill & {\bar{F}_{22} } \hfill & \ldots \hfill & {\bar{F}_{2j} } \hfill & \ldots \hfill & {\bar{F}_{2n} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\bar{F}_{i1} } \hfill & {\bar{F}_{i2} } \hfill & \ldots \hfill & {\bar{F}_{ij} } \hfill & \ldots \hfill & {\bar{F}_{in} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\bar{F}_{n1} } \hfill & {\bar{F}_{n2} } \hfill & \ldots \hfill & {\bar{F}_{nj} } \hfill & \ldots \hfill & {\bar{F}_{nn} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\bar{p}_{1} } \hfill \\ {\bar{p}_{2} } \hfill \\ \vdots \hfill \\ {\bar{p}_{i} } \hfill \\ \vdots \hfill \\ {\bar{p}_{n} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\bar{Q}_{1} } \hfill \\ {\bar{Q}_{2} } \hfill \\ \vdots \hfill \\ {\bar{Q}_{i} } \hfill \\ \vdots \hfill \\ {\bar{Q}_{n} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\overline{\text{RH}}_{1} } \hfill \\ {\overline{\text{RH}}_{2} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{i} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{n} } \hfill \\ \end{array} } \right] + \overline{{\dot{h}}} \left[ {\begin{array}{*{20}l} {\overline{\text{RS}}_{1} } \hfill \\ {\overline{\text{RS}}_{2} } \hfill \\ \vdots \hfill \\ {\overline{\text{RS}}_{i} } \hfill \\ \vdots \hfill \\ {\overline{\text{RS}}_{n} } \hfill \\ \end{array} } \right] $$

(55)

The above Eq. (55) has been used to compute nodal pressure vector, which depends on nodes coordinates, film thickness at a node and squeeze velocity. In order to obtained steady-state pressure, the squeeze velocity is set to zero. Thus, the above equation in steady state reduces to:

$$ \left[ {\begin{array}{*{20}l} {\bar{F}_{11} } \hfill & {\bar{F}_{12} } \hfill & \ldots \hfill & {\bar{F}_{1j} } \hfill & \ldots \hfill & {\bar{F}_{1n} } \hfill \\ {\bar{F}_{21} } \hfill & {\bar{F}_{22} } \hfill & \ldots \hfill & {\bar{F}_{2j} } \hfill & \ldots \hfill & {\bar{F}_{2n} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\bar{F}_{i1} } \hfill & {\bar{F}_{i2} } \hfill & \ldots \hfill & {\bar{F}_{ij} } \hfill & \ldots \hfill & {\bar{F}_{in} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\bar{F}_{n1} } \hfill & {\bar{F}_{n2} } \hfill & \ldots \hfill & {\bar{F}_{nj} } \hfill & \ldots \hfill & {\bar{F}_{nn} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\bar{p}_{1} } \hfill \\ {\bar{p}_{2} } \hfill \\ \vdots \hfill \\ {\bar{p}_{i} } \hfill \\ \vdots \hfill \\ {\bar{p}_{n} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\bar{Q}_{1} } \hfill \\ {\bar{Q}_{2} } \hfill \\ \vdots \hfill \\ {\bar{Q}_{i} } \hfill \\ \vdots \hfill \\ {\bar{Q}_{n} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\overline{\text{RH}}_{1} } \hfill \\ {\overline{\text{RH}}_{2} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{i} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{n} } \hfill \\ \end{array} } \right] $$

(56)

The numerical solution of hybrid thrust pad bearing requires coupling of the above-mentioned Eq. (56) with restrictor flow equation. This can be achieved by setting the value of nodal pressures, located on the recess radius (r_i) equal to recess pressure and algebraic sum of fluid flow rate (for 1/32nd model) through these nodes equal to flow through orifice restrictor.

$$ \begin{aligned} &\left[ {\begin{array}{*{20}l} {\bar{F}_{11} } \hfill & {\bar{F}_{12} } \hfill & \ldots \hfill & {\bar{F}_{1j} } \hfill & \ldots \hfill & {\bar{F}_{1n} } \hfill \\ {\bar{F}_{21} } \hfill & {\bar{F}_{22} } \hfill & \ldots \hfill & {\bar{F}_{2j} } \hfill & \ldots \hfill & {\bar{F}_{2n} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\bar{F}_{i1} } \hfill & {\bar{F}_{i2} } \hfill & \ldots \hfill & {\bar{F}_{ij} } \hfill & \ldots \hfill & {\bar{F}_{in} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\bar{F}_{n1} } \hfill & {\bar{F}_{n2} } \hfill & \ldots \hfill & {\bar{F}_{nj} } \hfill & \ldots \hfill & {\bar{F}_{nn} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\bar{p}_{1} } \hfill \\ {\bar{p}_{2} } \hfill \\ \vdots \hfill \\ {\bar{p}_{i} = \bar{p}_{r} } \hfill \\ \vdots \hfill \\ {\bar{p}_{n} } \hfill \\ \end{array} } \right] \\ &\quad= \left[ {\begin{array}{*{20}l} {\bar{Q}_{1} } \hfill \\ {\bar{Q}_{2} } \hfill \\ \vdots \hfill \\ {\bar{Q}_{R} } \hfill \\ \vdots \hfill \\ {\bar{Q}_{n} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\overline{\text{RH}}_{1} } \hfill \\ {\overline{\text{RH}}_{2} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{i} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{n} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\bar{Q}_{1} } \hfill \\ {\bar{Q}_{2} } \hfill \\ \vdots \hfill \\ {\frac{{\overline{\text{CS}}_{2} }}{32}*(1 - \bar{p}_{\text{r}} )^{1/2} } \hfill \\ \vdots \hfill \\ {\bar{Q}_{n} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\overline{\text{RH}}_{ 1} } \hfill \\ {\overline{\text{RH}}_{2} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{i} } \hfill \\ \vdots \hfill \\ {\overline{\text{RH}}_{n} } \hfill \\ \end{array} } \right] \end{aligned} $$

(57)