Skip to main content
SpringerLink
Log in

Complex period-1 motions of a periodically forced Duffing oscillator with a time-delay feedback

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

An Erratum to this article was published on 25 June 2014

Abstract

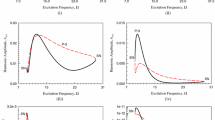
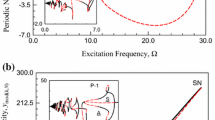
In this paper, complex period-1 motions in a periodically forced Duffing oscillator with a time-delay feedback are investigated, and the symmetric and asymmetric, complex period-1 motions exist in lower excitation frequency. The analytical solutions of complex period-1 motions in such a Duffing oscillator are obtained through the finite Fourier series, and the corresponding stability and bifurcations of complex period-1 motions are discussed by eigenvalue analysis. The frequency–amplitude characteristics of complex period-1 motions in the periodically forced Duffing oscillator with a time-delay feedback are discussed. Complex period-1 motions generated numerically and analytically are illustrated. As excitation frequency is close to zero, the complex period-1 motions need almost infinite harmonic terms in the Fourier series to express the analytical solutions. From this study, the initial time-delay in the time-delayed, nonlinear systems should be uniquely determined to achieve a specific periodic motion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Lagrange JL (1788) 1965 Mecanique Analytique, vol 2. edition Albert Balnchard, Paris

  2. Poincare H (1899) Methodes Nouvelles de la Mecanique Celeste, vol 3. Gauthier-Villars, Paris

    MATH  Google Scholar 

  3. van der Pol B (1920) A theory of the amplitude of free and forced triode vibrations. Radio Rev 1:701–710, 754–762

    Google Scholar 

  4. Fatou P (1928) Sur le mouvement d’un systeme soumis ‘a des forces a courte periode. Bull Soc Math 56:98–139

    Google Scholar 

  5. Krylov NM, Bogoliubov NN (1935) Methodes approchees de la mecanique non-lineaire dans leurs application a l’Aeetude de la perturbation des mouvements periodiques de divers phenomenes de resonance s’y rapportant. Academie des Sciences d’Ukraine, Kiev (in French)

  6. Bogoliubov NN, Mitropolsky YuA (1961) Asymptotic methods in the theory of nonlinear oscillations. Gorden and Breach, New York

    Google Scholar 

  7. Hayashi C (1964) Nonlinear oscillations in physical systems. McGraw-Hill Book Company, New York

    MATH  Google Scholar 

  8. Nayfeh AH (1973) Perturbation methods. Wiley, New York

    MATH  Google Scholar 

  9. Nayfeh AH, Mook DT (1979) Nonlinear oscillation. Wiley, New York

    Google Scholar 

  10. Coppola VT, Rand RH (1990) Averaging using elliptic functions: approximation of limit cycle. Acta Mech 81:125–142

    Article  MathSciNet  MATH  Google Scholar 

  11. Luo ACJ (2012) Continuous dynamical systems. Higher Education Press, Beijing/L&H Scientific, Glen Carbon

  12. Luo ACJ, Huang JZ (2012) Approximate solutions of periodic motions in nonlinear systems via a generalized harmonic balance. J Vib Control 18:1661–1871

    Article  MathSciNet  Google Scholar 

  13. Luo ACJ, Huang JZ (2012) Analytical dynamics of period-m flows and chaos in nonlinear systems. Int J Bifurcat Chaos 22, Article No. 1250093, 29 pp

  14. Luo ACJ, Huang J (2012) Analytical routines of period-1 motions to chaos in a periodically forced Duffing oscillator with twin-well potential. J Appl Nonlinear Dyn 1:73–108

    Article  MATH  Google Scholar 

  15. Luo ACJ, Huang J (2012) Unstable and stable period-m motions in a twin-well potential Duffing oscillator. Discontin Nonlinear Complex 1:113–145

    Article  MATH  Google Scholar 

  16. Tlusty J (2000) Manufacturing processes and equipment. Prentice Hall, Upper Saddle River

    Google Scholar 

  17. Hu HY, Wang ZH (2002) Dynamics of controlled mechanical systems with delayed feedback. Springer, Berlin

    Book  MATH  Google Scholar 

  18. Stepan G (1989) Retarded dynamical systems. Longman, Harlow

    MATH  Google Scholar 

  19. Sun JQ (2009) A method of continuous time approximation of delayed dynamical systems. Commun Nonlinear Sci Numer Simul 14(4):998–1007

    Article  MathSciNet  MATH  Google Scholar 

  20. Insperger T, Stepan G (2011) Semi-discretization for time-delay systems: stability and engineering applications. Springer, New York

    Book  Google Scholar 

  21. Hu HY, Dowell EH, Virgin LN (1998) Resonance of harmonically forced Duffing oscillator with time-delay state feedback. Nonlinear Dyn 15(4):311–327

    Article  MATH  Google Scholar 

  22. Wang H, Hu HY (2006) Remarks on the perturbation methods in solving the second order delay differential equations. Nonlinear Dyn 33:379–398

    Article  MATH  Google Scholar 

  23. MacDonald N (1995) Harmonic balance in delay-differential equations. J Sounds Vib 186(4):649–656

    Article  MathSciNet  MATH  Google Scholar 

  24. Liu L, Kalmar-Nagy T (2010) High-dimensional harmonic balance analysis for second-order delay-differential equations. J Vib Control 16(7–8):1189–1208

    MathSciNet  MATH  Google Scholar 

  25. Leung AYT, Guo Z (2012) Bifurcation of the periodic motions in nonlinear delayed oscillators. J Vib Control. doi:10.1177/1077546312464988

  26. Luo ACJ (2013) Analytical solutions of periodic motions in dynamical systems with/without time-delay. Int J Dyn Control 1:330–359

    Article  Google Scholar 

  27. Luo ACJ, Jin HX (2014) Bifurcation trees of period-m motion to chaos in a time-delayed, quadratic nonlinear oscillator under a periodic excitation. Discontin Nonlinear Complex 3:87–107

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Industrial Engineering, Southern Illinois University Edwardsville, Edwardsville, IL, 62026-1805, USA

    Albert C. J. Luo & Hanxiang Jin

Authors
  1. Albert C. J. Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hanxiang Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Albert C. J. Luo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luo, A.C.J., Jin, H. Complex period-1 motions of a periodically forced Duffing oscillator with a time-delay feedback. Int. J. Dynam. Control 3, 325–340 (2015). https://doi.org/10.1007/s40435-014-0091-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-014-0091-8

Keywords

Search

Navigation