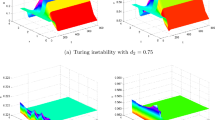Skip to main content
SpringerLink
Log in

Stationary patterns induced by self- and cross-diffusion in a Beddington–DeAngelis predator–prey model

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

The study of spatial pattern formation through diffusion-driven instability of reaction–diffusion models of interacting species has long been one of the fundamental problems in mathematical ecology. The present article is concerned with interacting predator–prey reaction–diffusion model with Beddington–DeAngelis type functional response. The essential conditions for Hopf and Turing bifurcations are derived on the spatial domain. The parameter space for Turing spatial structure is established. Based on the bifurcation analysis, the spatial pattern formation in Turing space through numerical simulations is carried out in order to study the evolution procedure of the proposed model system in the vicinity of coexistence equilibrium point. The consequences of the results obtained reveal that the effects of self- and cross-diffusion play significant role on the steady state spatiotemporal pattern formation of the reaction–diffusion predator–prey model system which concerns the influence of intra-species competition among predators. Finally, ecological implications of the present results obtained are discussed at length towards the end in order to validate the applicability of the model under consideration.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. May RM (2001) Stability and complexity in model ecosystems. Princeton University Press, Princeton

    MATH  Google Scholar 

  2. Murray JD (1993) Mathematical biology. Springer, Berlin

    Book  MATH  Google Scholar 

  3. Okubo A (1980) Diffusion and ecological problems: mathematical models. Springer, Berlin

    MATH  Google Scholar 

  4. Okubo A, Levin SA (2001) Diffusion and ecological problems: modern perspective. Springer, New York

    Book  MATH  Google Scholar 

  5. Dubey B, Das B, Hussain J (2001) A predator–prey interaction model with self and cross-diffusion. Ecol Model 141:67–76

    Article  Google Scholar 

  6. Kerner EH (1959) Further considerations on the statistical mechanics of biological associations. Bull Math Biophys 21:217–255

    Article  MathSciNet  Google Scholar 

  7. Shigesada N, Kawasaki K, Teramoto E (1979) Spatial segregation of interacting species. J Theor Biol 79:83–99

    Article  MathSciNet  Google Scholar 

  8. Turing AM (1952) The chemical basis of morphogenesis. Philos Trans R Soc Lond Ser B Biol Sci 237:37–72

    Article  MathSciNet  Google Scholar 

  9. Segel LA, Jackson JL (1972) Dissipative structure: an explanation and an ecological example. J Theor Biol 37:545–559

    Article  Google Scholar 

  10. Gierer A, Meinhardt H (1972) A theory of biological pattern formation. Kybernetik 12:30–39

    Article  MATH  Google Scholar 

  11. Levin SA, Segel LA (1976) Hypothesis for origin of planktonic patchiness. Nat Publ Group 259:659

    Google Scholar 

  12. Klausmeier CA (1999) Regular and irregular patterns in semiarid vegetation. Science 284:1826–1828

    Article  Google Scholar 

  13. Beddington JR (1975) Mutual interference between parasites or predators and its effect on searching efficiency. J Anim Ecol 44:331–340

    Article  Google Scholar 

  14. DeAngelis DL, Goldstein RA, O’neill RV (1975) A model for tropic interaction. Ecology 56:881–892

    Article  Google Scholar 

  15. Cosner C, DeAngelis DL, Ault JS, Olson DB (1999) Effects of spatial grouping on the functional response of predators. Theor Popul Biol 56:65–75

    Article  MATH  Google Scholar 

  16. Huisman G, De Boer RJ (1997) A formal derivation of the “Beddington” functional response. J Theor Biol 185:389–400

    Article  Google Scholar 

  17. Du P, Duan C, Liao X (2014) Dynamics behaviors of a reaction–diffusion predator–prey system with Beddington–DeAngelis functional response and delay. Appl Math 5:843–851

    Article  Google Scholar 

  18. Haque M (2011) A detailed study of the Beddington–DeAngelis predator–prey model. Math Biosci 234:1–16

    Article  MATH  MathSciNet  Google Scholar 

  19. He X, Zheng S (2015) Protection zone in a diffusive predator–prey model with Beddington–DeAngelis functional response. arXiv preprint arXiv:1505.06625

  20. Li H, Takeuchi Y (2011) Dynamics of the density dependent predator–prey system with Beddington–DeAngelis functional response. J Math Anal Appl 374:644–654

    Article  MATH  MathSciNet  Google Scholar 

  21. Sarwardi S, Haque M, Mandal PK (2014) Persistence and global stability of Bazykin predator–prey model with Beddington–DeAngelis response function. Commun Nonlinear Sci Numer Simul 19:189–209

    Article  MATH  MathSciNet  Google Scholar 

  22. Wang R, Jia Y (2016) Analysis on bifurcation for a predator–prey model with Beddington–DeAngelis functional response and non-selective harvesting. Acta Appl Math 143:15–27

    Article  MATH  MathSciNet  Google Scholar 

  23. Zhang XC, Sun GQ, Jin Z (2012) Spatial dynamics in a predator–prey model with Beddington–DeAngelis functional response. Phys Rev E 85:021924(1–14)

    Google Scholar 

  24. Hassell MP, Varley GC (1969) New inductive population model for insect parasites and its bearing on biological control. Nature 223:1133–1137

    Article  Google Scholar 

  25. Crowley PH, Martin EK (1989) Functional responses and interference within and between year classes of a dragonfly population. J North Am Benthol Soc 8:211–221

    Article  Google Scholar 

  26. Skalski GT, Gilliam JF (2001) Functional responses with predator interference: viable alternatives to the Holling type II model. Ecology 82:3083–3092

    Article  Google Scholar 

  27. Bazykin AD, Khibnik AI, Krauskopf B (1998) Nonlinear dynamics of interacting populations. World Scientific, Singapore, p 11

    Book  Google Scholar 

  28. Guin LN (2015) Spatial patterns through Turing instability in a reaction–diffusion predator–prey model. Math Comput Simul 109:174–185

    Article  MathSciNet  Google Scholar 

  29. Guin LN, Mandal PK (2014) Spatial pattern in a diffusive predator–prey model with sigmoid ratio-dependent functional response. Int J Biomath 7:1450047(1–26)

    Article  MATH  MathSciNet  Google Scholar 

  30. Guin LN, Mandal PK (2014b) Spatiotemporal dynamics of reaction-diffusion models of interacting populations. Appl Math Model 38:4417–4427

    Article  MathSciNet  Google Scholar 

  31. Haque M (2009) Ratio-dependent predator–prey models of interacting populations. Bull Math Biol 71:430–452

    Article  MATH  MathSciNet  Google Scholar 

  32. Haque M (2012) Existence of complex patterns in the Beddington–DeAngelis predator–prey model. Math Biosci 239:179–190

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgements

The final form of the paper owes much to the helpful suggestions of the anonymous referees, whose careful scrutiny we are pleased to acknowledge. The authors also gratefully acknowledge the financial support in part from Special Assistance Programme (SAP-III) sponsored by the University Grants Commission (UGC), New Delhi, India (Grant No. F.510/3/DRS-III/2015(SAP-I)).

Author information

Authors and Affiliations

  1. Department of Mathematics, Visva-Bharati, Santiniketan, West Bengal, 731 235, India

    Lakshmi Narayan Guin, Benukar Mondal & Santabrata Chakravarty

Authors
  1. Lakshmi Narayan Guin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Benukar Mondal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Santabrata Chakravarty
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Santabrata Chakravarty.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guin, L.N., Mondal, B. & Chakravarty, S. Stationary patterns induced by self- and cross-diffusion in a Beddington–DeAngelis predator–prey model. Int. J. Dynam. Control 5, 1051–1062 (2017). https://doi.org/10.1007/s40435-016-0281-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-016-0281-7

Keywords

Mathematics Subject Classification

Search

Navigation