1 Introduction

In 1773, Coulomb proposed a soil pressure theory of soil or rock failure, which is expressed by

$$\tau = c - \sigma \tan \phi ,$$
(1)

where τ and σ are respectively the shear strength and the normal stress (tensile stress is positive) in the shearing surface; c and ϕ are the cohesion and the angle of internal friction of soil or rock, respectively.

Later, Mohr developed the Coulomb failure condition into the law of shear failure, namely the Mohr–Coulomb (M–C for short hereinafter) yield criterion, that could be described in terms of the principal stresses (σ 1 ≥ σ 2 ≥ σ 3) as

$$F = \left( {\sigma_{1} - \sigma_{3} } \right) + \left( {\sigma_{1} + \sigma_{3} } \right)\sin \phi - 2c\cos \phi = 0 .$$
(2)

A large number of experiments have shown that the M–C yield criterion is able to reasonably depict the yield or failure behavior of soil and rock. In addition to Eq. (2), the M–C criterion can be expressed in many other forms, for example the following one in terms of stress invariants [1]:

$$F = \sigma_{\text{m}} \sin \phi + \bar{\sigma }\left( {\cos \theta - \frac{1}{\sqrt 3 }\sin \phi \sin \theta } \right) - c\cos \phi = 0 ,$$
(3)

where σ m is the average value of the three principal stresses; \(\bar{\sigma } = \sqrt {J_{2} }\), which is the equivalent stress; \(J_{2}\) is the second deviatoric stress invariant; and θ is the Lode angle ranging from −30° to 30°.

It is well known that the M–C yield criterion expresses a hexagonal pyramid surface in principal stress space, which has a flaw in numerical computation, i.e., the gradient discontinuities which occur at both the edges and the tip of the hexagonal pyramid surface. For that, researchers have ever presented the following three kinds of methods to overcome the flaw. Firstly, Drucker–Prager proposed the smooth circular conical surfaces, including the circumscribed, inscribed, and middle ones [2, 3], such that the ideal elasto-plastic constitutive model based on the Drucker–Prager criterion was one of the earliest models used for soil and rock and was embedded in some of the earliest commercial finite element programs, such as SAP, ADINA, ANSYS. Although the above circular conical surfaces overcome the numerical singularity of the original M–C model, they are significantly different in geometrical shape from the hexagonal pyramid of the M–C model, resulting in the advent of more or less errors [3] even if the equal area cone [4, 5] is employed while the above-mentioned programs are used. Secondly, the original M–C surface is viewed as six separate planar yield surfaces and the constitutive law is implemented as a multi-surface yield function using the formulation of Koiter [6] and Clausen et al. [7]. The third kind of methods, which is employed in this paper, is smoothing the vertices and approaching the M–C yield surface.

In order to sufficiently approach the original M–C yield surface, Abbo–Sloan [8] proposed a simple hyperbolic yield surface to eliminate the singularity of the M–C yield surface and presented two efficient FORTRAN 77 subroutines to illustrate how this yield surface is implemented in practice. However, they did not build an entire numerical constitutive model. Based on Abbo–Sloan function, a user-defined material subroutine (UMAT) was developed on the platform of ABAQUS by Jia et al. [9] using FORTRAN language.

Generally speaking, the M–C model can be reliably applied to stability analysis in geotechnical problems such as earth pressure [10, 11], slope stability [12, 13], and bearing capacity of foundation soil [14, 15]. ABAQUS is a well-known nonlinear finite element software, in which actually an embedded M–C model is included. And in the embedded M–C model the true M–C yield surface is used but the plastic potential function proposed by Menétrey–William [16] is employed, which presents a hyperbola in meridional plane and a closed smooth curve combined by three elliptic arcs in deviatoric plane, and it is the very inconsistency between the yield and potential functions so that the plastic flow rule of the model is always non-associated. Furthermore, this inconsistency is also a theoretical flaw of the embedded M–C model in ABAQUS. Jia’s UMAT model [9] has overcome this drawback, but it involves the second derivative of the plastic potential function, and the matrix inversion, resulting in not only the complexity of programming, but also the increases of the amount of calculation and the difficulty in numerical convergence, particularly when smoothed transition points are too close to the edges of the hexagonal pyramid surface. For that, a simplified method and the programming of new user-defined material subroutines will be introduced in this paper, and note that in the following text, UMAT only refers to the new subroutines. And in order to test and verify the UMAT, firstly, the indoor conventional triaxial compression and uniaxial tensile tests were numerically replicated with the UMAT and compared with the results of the embedded M–C model and analytical or Mohr circle-drawing approaches. Then a typical two-dimensional homogeneous soil slope [17] was simulated with the UMAT and compared in detail with the results of the embedded M–C model.

2 Brief introduction of Abbo–Sloan yield function

The hyperbolic yield function F proposed by Abbo–Sloan [8] is smooth in both meridional and deviatoric planes and can be expressed as

$$F = \sigma_{\text{m}} \sin \phi + \sqrt {\bar{\sigma }^{2} K^{2} \left( \theta \right) + a^{2} c^{2} \cos^{2} \phi } - c\cos \phi = 0 ,$$
(4)

where

$$K\left( \theta \right) = \left\{ \begin{aligned}\begin{array}{ll} A - B\sin 3\theta&\quad \, \left| \theta \right| >\theta_{\text{T}} \hfill \\ \cos \theta - \frac{1}{\sqrt 3 }\sin \phi \sin \theta &\quad\, \left| \theta \right| \le \theta_{\text{T}} \hfill \\\end{array} \end{aligned} \right.,$$
(5)

where

$$\begin{aligned} A = \frac{1}{3}\cos \theta_{\text{T}} [3 + \tan \theta_{\text{T}} \tan 3\theta_{\text{T}} \,+ \hfill \\ \, \frac{1}{\sqrt 3 } \times {\text{sign}}\left( \theta \right)\left( {\tan 3\theta_{\text{T}} - 3\tan \theta_{\text{T}} } \right)\sin \phi ], \hfill \\ \end{aligned} $$
(6)
$$B = \frac{1}{{3\cos 3\theta_{\text{T}} }}\left( {{\text{sign}}\left( \theta \right)\sin \theta_{\text{T}} + \frac{1}{\sqrt 3 }\cos \theta_{\text{T}} \sin \phi } \right),$$
(7)

where

$${\text{sign}}\left( \theta \right) = \left\{ \begin{aligned} + 1 \quad \theta \ge 0^{ \circ } \hfill \\ - 1 \quad \theta { < 0}^{ \circ } \hfill \\ \end{aligned} \right. ,$$
(8)

in above relevant expressions, K(θ) is used to control the shape of the yield surface in deviatoric plane; θ T is the transition angle ranging from 0° to 30°, and the greater the value of θ T, the better fitting the M–C cross section in deviatoric plane, but θ T should not be too close to 30° in order to avoid ill-conditioning of the approximation. A typical value of θ T is 25° as suggested by Abbo–Sloan [8] and Jia et al. [9]. In Ref. [8], the negative branch of the hyperbola has been chosen, which takes into account the tensile strength of soil through parameter a. In fact, parameter a is somewhat similar to the meridional eccentricity ε included in the potential function of the embedded M–C model [18], and the Abbo–Sloan yield function (Eq. 4) can closely model the M–C yield function (Eq. 3) by changing the magnitude of a and will theoretically be degraded as the latter if a is zero. The M–C yield surface and some sections of various smooth hyperbolic surfaces in a deviatoric plane are plotted in Fig. 1. Evidently, with the decrease of parameter a, the Abbo–Sloan yield surface gradually approaches the M–C yield surface. However, to avoid the ill-conditioning of numerical calculation, a is not allowed to be zero just as there is a limitation of the allowable minimum of 0.1 for the meridional eccentricity ε in the embedded M–C model [18]. Several meridional sections of the hyperbolic yield surfaces with different a values as well as θ = 0° and ϕ = 30° are plotted in Fig. 2 [8]. One can infer that the hyperboloid is an approximation to the M–C yield surface in the meridional plane. Obviously, a value has a significant influence on the shape of the hyperbolic surface. When a = 0.05 and θ T = 25°, the hyperbolic surface almost approaches the M–C yield surface with the maximum difference of less than 0.15% [8].

Fig. 1
figure 1

M–C yield surface in 3D principal stress space and Abbo’s rounded yield surface in deviatoric plane

Full size image
Fig. 2
figure 2

Abbo’s hyperbolic approximation to M–C meridional section [8]

Full size image

From Fig. 2, it is shown that for a specific value of a, error always becomes less and less with the increase of the minor principle stress toward the direction of compression stress. Meanwhile, if assuming θ T = 29°, as suggested by Owen and Hinton [19], the closer results to smooth the edges of the M–C hexagonal yield surface pyramid will be obtained. And the examples in this paper will show that fast convergence can still be achieved and the higher precisions than those of Abbo–Sloan [8] and Jia et al. [9] can be obtained as well.

Theoretically, making the potential function similar to the yield function is reasonable, and only by this way, the associated flow rule can be achieved possibly. In this paper, the potential function G was assumed to have the same form as the hyperbolic yield function F. The only difference is that the angle of internal friction ϕ was replaced with the dilation angle ψ (always ψ ≤ ϕ). If ψ = ϕ, the associated flow rule is adopted, otherwise the non-associated flow rule is used. Thus, the mathematical expression of G is

$$G = \sigma_{\text{m}} \sin \psi + \sqrt {\bar{\sigma }^{2} K^{2} \left( \theta \right) + a^{2} c^{2} \cos^{2} \psi } - c\cos \psi = 0 .$$
(9)

Obviously, the geometrical shape of the potential surface is similar to the yield surface in Fig. 1, but the inclination angle (dilation angle) in the strain meridional plane (similar to the stress meridional plane shown in Fig. 2) is always less than or equal to the angle of internal friction. Note that for an ideal elasto-plastic model, the yield surface is fixed but the plastic potential surface may move outwards with the increase of plastic strain.

3 First derivative used in UMAT

Differentiation of the yield and potential functions with respect to stress may respectively obtain the flow vectors n and n′, which are used for the stress adjustment after yielding and are consistent with Refs. [8, 9, 20]; for example, the flow vector n is defined as

$${\user2{n}} = \frac{\partial F}{\partial \sigma } = C_{1} \frac{{\partial \sigma_{\text{m}} }}{\partial \sigma } + C_{2} \frac{{\partial \bar{\sigma }}}{\partial \sigma } + C_{3} \frac{{\partial J_{3} }}{\partial \sigma } ,$$
(10)

where

$$C_{1} = \sin \phi ,\;C_{2} = \alpha \left( {K - \tan 3\theta \frac{{{\text{d}}K}}{{{\text{d}}\theta }}} \right) ,$$
$$C_{3} = \alpha \left( { - \frac{\sqrt 3 }{{2\cos 3\theta \bar{\sigma }^{2} }}\frac{{{\text{d}}K}}{{{\text{d}}\theta }}} \right) ,$$
$$\alpha = \frac{{\overline{\sigma } K}}{{\sqrt {\bar{\sigma }^{2} K^{2} + a^{2} c^{2} \cos^{2} \phi } }} ,$$
$$\frac{{{\text{d}}K}}{{{\text{d}}\theta }} = \left\{ \begin{aligned}\begin{array}{ll} - 3B\cos 3\theta \quad \left| \theta \right| > \theta_{\text{T}} \hfill \\ - \sin \theta - \frac{1}{\sqrt 3 }\sin \phi \cos \theta \quad \left| \theta \right| \le \theta_{\text{T}} \hfill \\ \end{array}\end{aligned} \right.,$$
$$\frac{{\partial \sigma_{\text{m}} }}{\partial \sigma } = \frac{1}{3}\left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 0 & 0 & 0 \\ \end{array} } \right]^{\text{T}} ,$$
$$\frac{{\partial \bar{\sigma }}}{\partial \sigma } = \frac{1}{{2\overline{\sigma } }}\left[ {\begin{array}{*{20}c} {s_{x} } & {s_{y} } & {s_{z} } & {2\tau_{xy} } & {2\tau_{xz} } & {2\tau_{yz} } \\ \end{array} } \right]^{\text{T}} ,$$
$$\frac{{\partial J_{3} }}{\partial \sigma } = \left\{ {\begin{array}{*{20}c} {s_{y} s_{z} - \tau_{yz}^{2} } \\ {s_{x} s_{z} - \tau_{xz}^{2} } \\ {s_{x} s_{y} - \tau_{xy}^{2} } \\ {2\left( {\tau_{yz} \tau_{xz} - s_{z} \tau_{xy} } \right)} \\ {2\left( {\tau_{xy} \tau_{yz} - s_{y} \tau_{xz} } \right)} \\ {2\left( {\tau_{xz} \tau_{xy} - s_{x} \tau_{yz} } \right)} \\ \end{array} } \right\} + \frac{{\bar{\sigma }^{2} }}{3}\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\} .$$

Since the potential function G has the same form as the yield function F, its differentiation with respect to stress (n′) is similar to n, except the angle of internal friction ϕ must be replaced with the dilation angle ψ.

As can be seen from the formulas listed above, when |θ| = 30°, C 2 and C 3 are infinite values, resulting in the singularity of numerical calculation, and therefore, in the UMAT they are set to be zero when |θ| is greater than the transition angle θ T.

4 Stress adjustment in UMAT

During incremental loading, stresses at some Gaussian integration points in a model may exceed yield stresses, accompanied with plastic strains, but the stresses of these points must be adjusted to the yield surface to meet the yield criterion and constitutive law. Thus, the backward Euler integral regression algorithm was adopted in the paper. The flowchart of the UMAT is shown in Fig. 3. Yield stress σ y varies with different yield criterions, and in the M–C model it is defined as

$$\sigma_{{y}} = \sigma_{y}^{0} + H'{\text{d}}\bar{\varepsilon }_{\text{p}} = c\cos \phi + H'{\text{d}}\bar{\varepsilon }_{\text{p}} ,$$
(11)

where \({\text{d}}\bar{\varepsilon }_{\text{p}}\) is the effective plastic strain; H′ is the first derivative of hardening function H. Since no hardening or softening is considered in ideal elasto-plastic model, H = H′ = 0, and σ y is constant.

Fig. 3
figure 3

Flowchart of the UMAT

Full size image

Assuming that the stress vector of a Gaussian point is σ r−1 after the (r − 1)th iteration, there are the following two cases on the adjustment of yield stress.

4.1 First case

As shown in Fig. 4, point B has already yielded after the (r − 1)th iteration—that is to say, point B is on the yield surface F = 0 at this moment. Then at the rth iteration the elastic trial stress \(\sigma^{r}_{e} = \sigma^{r - 1} + {\text{d}}\sigma^{r}_{e}\) is calculated as segment OA. In other words, point B moves to point A due to obtaining the elastic stress increment calculated by \({\text{d}}\sigma^{r}_{e} = D_{e} {\text{d}}\varepsilon^{r}\) (segment BA in Fig. 4) at the rth iteration, in which D e is the elastic matrix. Point A has been beyond the yield surface, but actually it is a stress point that an ideal elasto-plastic material cannot reach. Therefore, to meet the yield criterion and constitutive relationship, point A must be adjusted to point D′ on the yield surface. Point A cannot move back to point B because a point can only move on the yield surface at yield state with the accompanying of plastic strain.

Fig. 4
figure 4

Schematic of stress adjustment in the first case [19]

Full size image

According to the vector diagram in Fig. 4, the stress calculation formula after adjustment is

$$\sigma^{r} = \sigma^{r - 1} + {\text{d}}\sigma_{e}^{r} - {\text{d}}D_{e} {\text{d}}\lambda,$$
(12)

where dλ is the differential increment of the plastic multiplier λ, which can be expressed as

$${\text{d}}\lambda = \frac{1}{{H + {\user2{n}}^{\rm T} {\mathbf{d}}D_{e} }}{\user2{n}}^{\text{T}} D_{e} {\text{d}}\varepsilon,$$
(13)

where dD e  = D e n′.

By Eq. (13), point A can only be adjusted to point D (see Fig. 4) that may still deviate from point D′. In order to move to point D′, one may have

$$OD \prime = k \cdot OD,$$
(14)

where the adjustment coefficient k is given by

$$k = \frac{{\sigma_{y}^{0} + H'\bar{\varepsilon }_{\text{p}}^{r} }}{{\bar{\sigma }^{r} }} ,$$
(15)

where \(\bar{\varepsilon }_{\text{p}}^{r}\) is the effective plastic strain after the rth iteration; \(\bar{\sigma }^{r}\) is the effective stress given by

$$\bar{\sigma }^{r} = \sigma_{\text{m}} \sin \phi + \sqrt {\bar{\sigma }^{2} K^{2} \left( \theta \right) + a^{2} c^{2} \sin^{2} \phi } .$$
(16)

4.2 Second case

As shown in Fig. 5, a Gaussian point, for example point C, does not yield after the (r − 1)th iteration but it does at the rth iteration. At the (r − 1)th iteration, point C is inside the yield surface and in elastic state, but the elastic trial stress at the rth iteration makes it move to point A, and CA intersects with the yield surface at point B. The elastic stress increment calculated by \(\sigma^{r}_{e} = D_{e} {\text{d}}\varepsilon^{r}\) (segment CA) at the rth iteration involves two segments, i.e., CB and BA, of which CB is still inside the yield surface but BA outside. Therefore, only segment BA needs to be adjusted. That is to say, point A must be adjusted back to D′. From Fig. 5, one can see the stress value that needs to be adjusted is \(R{\text{d}}\sigma^{r}_{e}\), in which the adjustment factor R is

$$R = \frac{BA}{CA} = \frac{{\bar{\sigma }_{{e}}^{r} - \sigma_{y} }}{{\bar{\sigma }_{{e}}^{r} - \bar{\sigma }_{{e}}^{r - 1} }} ,$$
(17)

where σ y  = σ 0 = c · cosϕ.

Fig. 5
figure 5

Schematic of stress adjustment in the second case [19]

Full size image

Equation (12) may still be used in stress adjustment. Similarly, point A can merely be adjusted to point D. In order to move to point D′, Eqs. (14) and (15) may still be used.

To sum up, in the process of finite element computation, stress adjustments are only conducted for yield Gaussian points in above two cases. Meanwhile, as is generally known, for those yield points, plastic strains accompanied with them can be calculated by the following orthogonal flow rule:

$$\text{d}\varvec{\varepsilon }^{{\mathbf{p}}} = {\text{d}}\lambda \frac{\partial G}{{\partial\varvec{\sigma}}} .$$
(18)

Obviously, from Eq. (18), one can see that the flow direction of plastic strains is associated with the plastic potential function G. If the same dilation angle is considered, comparisons of the plastic potential surfaces determined by Eq. (9) in this paper and the potential surface proposed by Menétrey–William [16] and employed in the embedded M–C model in ABAQUS are shown in Fig. 6. One can see that for any of the same strain Lode angle θ ε except θ ε = ±30°, the flow directions of plastic strains are different due to the difference of geometrical shapes of the two kinds of potential surfaces. Therefore, even if under the same loading condition after yielding, the total amount of plastic strains for both surfaces might be equal, each plastic strain component is not equal yet, such that the plastic shear and volumetric strains are different as well. Apparently, the potential surface used in this paper is a better approximation to the M–C yield surface in shape, meaning that it is more reasonable than the one employed by the embedded M–C model.

Fig. 6
figure 6

Comparisons of plastic potential surfaces in π plane in principal strain space

Full size image

Based on the above theories, the UMAT subroutines were developed and their reliability will be validated in the following section by comparing with the embedded M–C model in ABAQUS (hereafter refer to as ABAQUS) and the analytical solutions of the M–C criterion.

5 UMAT verification and application

5.1 Laboratory simulation tests

A standard 3D model of a cylindrical soil specimen with a diameter of 39.1 mm and a height of 80 mm was built to numerically simulate the indoor conventional triaxial compression and uniaxial tensile tests. The model and its discretization are shown in Fig. 7. The cylindrical coordinates and C3D20R element type were adopted. The bottom in Z-axial direction and the side in R-axial direction were constrained, and the top was free. Self-weight stress was not considered in this modeling. The mechanical parameters of the clay were cited from Ref. [21], including the elastic modulus E = 2,300 kPa, the Poisson ratio v = 0.4, the cohesion of the soil \(c\) = 21.43 kPa, the angle of internal friction ϕ = 17.13°, and the unit weight γ = 17.8 kN/m3.

Fig. 7
figure 7

3D finite element model and meshes of a standard specimen

Full size image

In the triaxial compression simulation, the model was loaded with a confining pressure of 63 kPa, and a downward displacement of 16 mm was applied on its top while in the uniaxial tensile simulation, without confining pressure, only an upward displacement of 5 mm was applied on its top.

Comparisons of the triaxial compression and uniaxial tests between the UMAT and ABAQUS model are shown in Figs. 8 and 9, respectively. It shows that in both the UMAT and ABAQUS model, the yield stresses are not affected by the magnitude of ψ. That is to say, the shear and tensile strengths of soil or rock are irrelevant to the associated and non-associated flow rules because the dilation angle ψ does not occur to the yield functions, i.e., Eqs. (3) and (4), at all.

Fig. 8
figure 8

Stress–strain curves of numerical simulations of triaxial compression

Full size image
Fig. 9
figure 9

Stress–strain curves of numerical simulations of uniaxial tension

Full size image

As a matter of fact, the theoretical strengths for the triaxial compression and uniaxial tests can also be obtained by Eq. (2) or by drawing the Mohr circles (respectively see the biggest one and the first one on the right side of the τ-axis in Fig. 10), which are 110.667 and 31.64 kPa, respectively. Almost the same results, i.e., 110.645 and 31.638 kPa, were respectively obtained by ABAQUS. It proves that the M–C criterion is precisely replicated in the embedded M–C model in ABAQUS. Accordingly, when a = 0.05, slightly less results, i.e., 109.674 and 31.506 kPa (with the relative errors of 0.9% and 0.4% or so), were obtained by the UMAT, respectively. This is because the yield surface of Abbo–Sloan function is inside the M–C yield surface, as can be seen in Figs. 1 and 2. However, evidently, when a is less than or equal to 0.05, the UMAT already can depict the M–C criterion with a rather reliable precision. Despite of that, from Figs. 8 and 9, one can see that with the increase of a, the relative errors increase, particularly in the uniaxial tensile tests. And this law is still decided by the Abbo–Sloan hyperbolic yield function—the closer the maximum principal stress away from the tip of the M–C yield surface, the greater the relative error.

Fig. 10
figure 10

Mohr circles corresponding to various stress states of soil

Full size image

Figure 10 also shows several special Mohr circles, such as the uniaxial compression (σ 1 > 0, σ 2 = σ 3 = 0), pure shear (σ 1 > 0, σ 2 = σ 3 < 0, |σ 1| = |σ 2| = |σ 3|), and triaxial tension circles (σ 1 > σ 2≥σ 3 > 0). Note that the triaxial tension is one of the Mohr circles approaching the tip (point O′) of the M–C yield envelope. In line with the theory of the M–C criterion—Eq. (1), the possible maximum tensile stress σ tmax can be

$$\sigma_{\text{tmax}} = \frac{c}{\tan \phi } .$$
(19)

That is to say, when σ 1 = σ 2 = σ 3 = σ tmax = 69.53 kPa (see Fig. 10), a stress point will reach point O′ as far as this clay is concerned. To test the actual tensile strength, using the improved triaxial apparatus, Bishop and Garga had ever conducted the triaxial drained tension tests of the London clay [22], showing that under the low confining pressure range, i.e., σ 3 = −21 to −70 kPa, the tensile strength of the London clay is σ 1 = σ tmax = 27–34 kPa, which is much less than the theoretical strength determined by Eq. (19). Obviously, the loading conditions of their tests are similar to the two Mohr circles of tension under low confining pressures as shown in Fig. 11. It is easy to understand that without confining pressure, i.e., under the uniaxial tension, the tensile strength of clay should be less than those with low confining pressures and cannot reach the following theoretical strength expressed as Eq. (20):

$$\sigma_{\text{t}} = \frac{2c\cos \phi }{1 + \sin \phi },$$
(20)

derived from the M–C shear criterion—Eq. (2), which is 31.64 kPa exactly as far as the clay previously simulated is concerned. It is more impossible for clay to reach the maximum theoretical tensile strength determined by Eq. (19). In other words, the M–C shear yield criterion overestimates tensile strengths of soil and rock. Actually, when the major principal stress at a point of a soil or rock mass is positive or becomes tensile and exceeds the tensile strength of the soil or rock, the tensile rather than shear yield or failure will occur at this point.

Fig. 11
figure 11

Mohr circle analyses of tensile strengths of a soil

Full size image

For this reason, the tension cutoff can be considered by defining the uniaxial tensile strength of soil or rock when using the M–C model embedded in ABAQUS. Jia’s comment (Ref. [9]) on that the tensile strengths of soil and rock are not considered in the embedded M–C model is not pertinent. For the UMAT in this paper, tensile strength can be reflected by simply defining the magnitude of parameter a. That is to say, the value of a decides not only the similarity between the Abbo–Sloan and M–C yield surfaces, but also the uniaxial tensile strength of soil or rock. As far as this clay is concerned, given a = 0.2 or 0.5, actually the uniaxial tensile strength was let be 30.802 or 26.584 kPa, and θ = − 30°, of course, these two strength values can be obtained by Eq. (4) as well. Obviously, respectively specifying these two values to be the tension cutoff strengths, the precise numerical simulations can be realized by ABAQUS (see Fig. 9). If the uniaxial tensile strength of the soil is known or given by the Mohr circle of the hypothetical uniaxial tension as indicated in Fig. 11, then parameter a can be calculated by Eq. (4).

5.2 Stability analysis of a typical slope

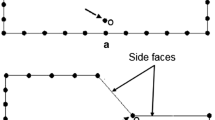
A homogeneous two-dimensional soil slope [17, 23, 24] was cited herein. The sizes and discretization of the model are shown in Fig. 12. The quadrilateral element with full integration (CPE4) was adopted to discretize the model. The grid density is completely consistent with those of Dawson et al. [17] and Fei and Zhang [24]. The mechanical parameters of the soil are the unit weight γ = 20 kN/m3, the cohesion c = 12.38 kPa, and the internal friction angle ϕ = 20°. With these soil parameters, the stability safety factor of the slope is exactly 1.00 according to the limit analysis solution of Chen [23].

Fig. 12
figure 12

Model sizes and meshes of a typical slope

Full size image

Over the last two decades or so, the finite element strength reduction technique has been widely used in slope stability analysis. But there is still a controversy on what judgment criterion should be adopted when determining the factor (F s) of safety. Generally, three judgment criteria were used: the non-convergence of numerical calculation (criterion 1), the plastic penetration (criterion 2), and the displacement mutation (criterion 3) [25–27]. Usually, the computed results by criteria 2 and 3 are not significant, and they are close to the results of the limit equilibrium or limit analysis methods. In this paper, the numerical analyses of the slope using criteria 1 and 2 were performed. When using the UMAT, the associated flow with ψ = ϕ=20° and non-associated flow rules with ψ = 0.5ϕ = 10° or with ψ = 0.1° (approximately 0°, which is tantamount to no consideration of dilation because ψ is not allowed to equal zero in both ABAQUS and the UMAT to avoid numerical singularity) were adopted respectively. And let parameter a be 0.05, 0.5, and 0.99, respectively. Actually, when a = 0.5 or 0.99, it means the uniaxial tensile strength is 7.11 or around 0 kPa according to Eq. (4). Here, two cases were considered. One is the conventional method that parameter a of the whole soil mass is 0.5 or 0.99. Usually, tensile stresses merely occur in the shallow layer near the top of a slope, so in the second case, for the deep layer, let a be 0.05, and for the shallow soil layer like the top three rows of elements in Fig. 12, let a be 0.5 or 0.99. Correspondingly, when using ABAQUS, firstly the maximum allowable dilation angle is ψ = 17.831° to keep its potential surface convex and similar in shape to the M–C yield surface. Then, when ψ = 10 or 0.1°, similar analyses were performed with the tension cutoff of 7.11 and 0.01 kPa (approximately 0 kPa because it is not allowed to equal zero in ABAQUS to avoid numerical singularity). Only when the tension cutoff was considered, criterion 3 was adopted to determine the factors of safety because plastic penetration zone cannot be obtained. All the factors of safety are listed in Table 1.

Table 1 Computed factors of safety F s
Full size table

From Table 1, the following conclusions can be drawn:

  1. 1.

    The factor of safety increases with the dilation angle, and it reaches the minimum (even less than 1.00) or maximum (greater than 1.00), respectively, when zero dilation or full dilation (associated flow rule) is considered.

  2. 2.

    When criterion 1 is used without tension cutoff, the computed factors of safety with respect to the three dilation angles by ABAQUS are respectively 15%, 14%, and 6% greater than the exact factor of safety of 1.00; when criterion 2 is used without tension cutoff, they are respectively 8%, 3% greater or 2% less than 1.00. Similar results are obtained by the UMAT. Moreover, for both ABAQUS and the UMAT, the factors of safety by criterion 1 often deviate from 1.00 farther than those of by criterion 2.

  3. 3.

    When criterion 1 is used with tension cutoff, the computed factor of safety by ABAQUS obviously decreases but its variation with the dilation angle is unremarkable; when criterion 2 is used with the tension cutoff, ABAQUS is unable to show the plastic penetration zone so that no values are listed in those columns in Table 1, and in this case, criterion 3 was adopted to determine the factors of safety, which actually are around 0.94 for both tensile strengths σ t = 7.11 and 0.01 kPa and for all three dilation angles.

    At this point, it shows that the computed results by ABAQUS in consideration of tension cutoff are not satisfying.

  4. 4.

    For the UMAT, when a = 0.05 for the whole slope, which means that tensile yield is not considered, the factors of safety with criterion 2 are less than those by ABAQUS and closer to 1.00. The differences between the results from UMAT and ABAQUS are caused by the different potential functions.

  5. 5.

    The tensile strength of clay may be considered by the UMAT through changing the magnitude of parameter a, but comparisons show that merely in the potential tensile stress zone, a set to be the value matched with the tensile strength is more reasonable, and if in slope stability analysis, a is set to be 0.99, that actually means no tensile but shear strength is considered.

Given the non-associated flow rule with no dilation (ψ = 0.1°), without considering the tensile strength of this clay, Figs. 13 and 14 show the contours of the magnitude of equivalent plastic strains (PEMAG in ABAQUS or defined as SDV9 in the UMAT) and the contours of displacements in critical plastic penetration state, respectively, obtained by ABAQUS (σ t = not set) and the UMAT (a = 0.05). Evidently, the contour distributions and displacement magnitudes obtained by ABAQUS and the UMAT are quite similar or close. The slight differences between them are attributed to the different potential functions. Likewise, without considering shear dilation but considering a uniaxial tensile strength of 7.11 kPa (i.e., σ t = 7.11 kPa in ABAQUS or for the whole slope, a = 0.5 in the UMAT), the same comparisons are shown in Figs. 15 and 16. One can see that no plastic penetration zone is shown by ABAQUS even if non-convergence occurred, but it can still be revealed by the UMAT. To save the space, the contour comparison of other cases were not provided here.

Fig. 13
figure 13

Contours of PEMAG and displacements (ABAQUS, σ t = not set)

Full size image
Fig. 14
figure 14

Contours of PEMAG and displacements (UMAT, a = 0.05)

Full size image
Fig. 15
figure 15

Contours of PEMAG and displacements (ABAQUS, σ t = 7.11 kPa, \(\psi = 0.1^\circ\))

Full size image
Fig. 16
figure 16

Contours of PEMAG and displacements (UMAT, a = 0.5, \(\psi = 0.1^\circ\))

Full size image

6 Conclusions

The modified Mohr–Coulomb model in this paper can approach the hexagonal pyramid surface when θ T = 29° and a ≤ 0.05. The methods of stress adjustment after yielding avoid solving the second derivative of the plastic potential function and inverse matrix, and therefore, a fully implicit backward Euler integral regression algorithm was adopted in the UMAT and proved to be highly efficient in numerical convergence.

The examples of the numerical simulations on the triaxial compression and uniaxial tension tests show that both ABAQUS and the UMAT can obtain the solutions consistent with the analytical solutions. The magnitude of dilation angle does not affect the yield strength of soil or rock.

Theoretical analysis shows that the plastic flow direction is related to the potential function. Therefore, even if the total plastic strains are the same, the plastic strain components such as the plastic shear strain and the plastic volumetric strain may still be different due to different potential functions, which have been proven by comparisons of the contours of equivalent plastic strains and displacements obtained by ABAQUS and the UMAT.

Comparisons of the typical soil slope stability analyses by ABAQUS and the UMAT show that the differences are not remarkable when only the shear yield and the plastic penetration criterion are considered. The results by the UMAT are slightly less than that by ABAQUS and closer to the theoretical results. Therefore, the UMAT is more reliable than the embedded Mohr–Coulomb model.

The factor of safety of a slope is influenced by the dilation angle. The larger the dilation angle, the greater the factor of safety, and the factor of safety reaches its maximum when the associated flow rule (the dilation angle equals to the angle of internal friction of soil or rock) is adopted by the UMAT. Usually, the limit equilibrium method and limit analysis method cannot fully consider the influence of the dilation of soil and rock. Consequently, if the accurate value of the dilation angle of soil or rock can be obtained by test, the results by the UMAT or ABAQUS will be definitely more reliable than those of the limit equilibrium and limit analysis methods.

When the tensile strength of soil or rock is considered, it seems the factor of safety by ABAQUS is not so reliable because it is not sensitive to the magnitude of tensile strength. The relatively accurate results, however, can still be obtained by the UMAT through setting parameter a in the potential tensile stress zone of a slope to be the value matched with the tensile strength.