1 Introduction

The railway-induced ground and building vibrations have been extensively analysed by measurements and detailed models. In the German research work [1, 2], the knowledge about railway vibrations had to be condensed in a prediction programme which could be used by experts as well as by non-experts. The challenge was to generate similar results as detailed models do, but with much less computer time and detailing. This is quite contrary to the usual task of programming complex and more complex models. This task is, nevertheless, as difficult, because complex models must be calculated and the results must be understood. Finally, approximating models must be found which are physically meaningful rather than black box approximations. It must be pointed out that the simple prediction methods could not be developed without detailed models, for example three-dimensional finite-element models. The results of many detailed models serve as a guide for finding proper approximations.

At the beginning, railway-induced ground vibrations have been analysed by experiments. A prediction was based on measurements at a different situation and on the experience and the intuition of the engineer how to transfer the results to the new situation. This method can be structured in a prediction software where only certain influencing factors are allowed and can be derived statistically from an experimental database [3,4,5,6]. Another purely experimental method uses impact measurements on the site and train measurements on another site to predict the train vibrations at the site [7].

On the other side, theoretical methods have been developed for the wave propagation through the soil and the soil–structure interaction. Basic work has been done in the 1980s and early 1990s by SNCF [8], British Rail Research [9] and BAM [10]. The wave propagation through layered soils can be calculated by wavenumber integrals [11,12,13]. Tracks on the soil can also be solved by wavenumber domain methods [8, 9, 14,15,16]. Many alternatives for track–soil interaction have been developed. Large three-dimensional finite-element regions are possible with transmitting boundaries [17,18,19]. The combined finite-element boundary-element method has been used for the track–soil [20] and the building–soil interaction [21]. Finite-element and boundary-element methods across the track can be combined with the wavenumber method along the track yielding the so-called 2.5-dimensional method [22,23,24,25,26].

All these detailed methods are very time-consuming. If a larger area needs many predictions, so-called scoping predictions have been developed [27, 28]. They use neural networks [29, 30] or other methods of artificial intelligence [31] to represent the results of many time-consuming calculations.

Scoping predictions have also been found for buildings [32], where only the relevant building modes are used in a fast computation. Many simplifications of building vibrations have been used, so far. In [33], the calculations of detailed models have been used to find simple explicit building transfer functions. Simplified building models have been achieved by considering infinitely long buildings [34, 35], infinitely high buildings [36] and infinitely high buildings with flexible floors [37]. Simple finite structures composed of columns and floors have been used, in [38] a single column and infinitely large floors, and in [39] multi-column and multi-floor bay models.

Buildings have been often calculated without the underlying soil or with a very stiff soil [33, 38,39,40,41,42]. The soft soil, however, yields an amplitude reduction with increasing frequency, modifies the resonance frequencies and mode shapes and provides a strong radiation damping. Without the soil, many resonance peaks appear in the solution which are not present for the building model with the soil. The building–soil interaction should be included in the building analysis even if the propagation through the soil and the response of the building is calculated separately.

In the same way, the track–soil interaction should be included in the excitation analysis even if the propagation through the soil is analysed in the next step [18, 43, 44]. The coupling of the track (the excitation step) and the soil (the propagation step) can be done by the total force on the soil. This way of coupling is used in this article as it has some advantages if mitigation measures at track are analysed, and it represents better the excitation than any displacement quantity. Coupled (substructure) models have also been used for the full three stage prediction, for example [40,41,42].

A single track–soil model for the emission and transmission has often been used, for example [15, 19, 45]. A single model for all three parts of the prediction, the track, the soil and the building need time-consuming computations and are rarely found [17, 21, 46]. More examples of detailed models can be found in the state-of-the-art articles [47,48,49].

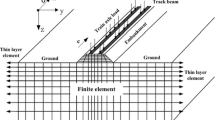
The present article describes a fast prediction of all three parts (Fig. 1), emission (excitation by rail traffic), transmission (propagation through the soil) and immission (response of buildings). Physical models are used for all parts. The track–soil model is calculated by transfer matrices of the rail, rail pad, sleeper, ballast, soil and all possible elastic elements for mitigation. The building model of a column/wall and adjacent floors is also calculated by transfer matrices. The approximating model of the layered half-space is a homogeneous half-space with a frequency-dependent wave velocity. These prediction methods are fast in computation, the response follows within a second, but also simple in handling, as only a minimum of parameters is needed as the input. The prediction methods have been derived from several detailed methods, such as the thin-layer method, different finite-element methods, the boundary-element method, wavenumber integrals and wavenumber domain methods for the calculation of tracks. At the same time, many measurements (in 50 buildings, at 40 ground vibration sites and at 30 railway tracks) have been performed which have been used to thoroughly test the prediction methods. This article presents some comparison of the prediction methods with detailed numerical methods and with some measurements which demonstrate that this comprehensive prediction is theoretically well-founded and of practical value.

Fig. 1
figure 1

The prediction of railway-induced vibration and its part a emission from the train, b transmission through the soil, and c immission into the building

Full size image

This article is organised as follows. Sections 2, 4 and 6 present the complete set of formula for each part of the prediction emission (excitation of railway vibration), transmission (propagation of waves through the soil) and immission (response of the building). Each section with the formula is followed by a section (Sects. 3, 5, 7) including some example results, the comparison with detailed numerical models and with measurements which shows the good theoretical agreement and the practical relevance of the prediction methods. The article ends with the conclusions.

2 Emission: excitation forces from vehicle–track interaction

The excitation forces are calculated from the vehicle and track irregularities and the vehicle–track interaction. By that, the excitation forces can be predicted, but also the mitigation effect of any mitigation measure at track (such as rail pads, sleeper pads and ballast mats) can be determined.

2.1 Vehicle and track irregularities

The main causes of train-induced ground vibrations are irregularities of the vehicle and the track. The amplitudes s of the different irregularities depend on the condition of the vehicle and track, but the following general rules for the third-of-octave band spectra have been found [2, 50]:

$$ \begin{aligned} & {\text{track}}\,{{\text{alignment:}}} \\ & s(\lambda ) \sim \lambda^{1.5-2}, \quad \lambda > 1.2\,{\text{m},}\;\;{{s(}}\lambda = 2\,{\text{m) = 0}} . {0 1 7}\!{-}\!0. 1 7\,{\text{mm;}} \\ & {\text{wheel}}\,{\text{out-of-roundness:}} \\ & s(\lambda ) \sim \lambda^{0.5-1}, \quad 0.3\,{\text{m < }}\lambda < 3\,{\text{m},}\;\;{{s(}}\lambda = 1\,{\text{m) = 0}} . {0 0 5}\!{-}\!0. 0 1 5\,{\text{mm;}} \\ & {\text{wheel}}\,{\text{roughness:}} \\ & s(\lambda ) \sim \lambda^{0.5}, \quad \lambda < 0.3\,{\text{m}},\;\;s(\lambda = 0.25\,{\text{m}})\, = {0.002}\!{-}\!0.007\,{\text{mm}}; \\ & {\text{rail}}\,{\text{roughness:}} \\ & s(\lambda ) \sim \lambda^{0.5-1}, \quad \lambda < 0.5\,{\text{m}},\;\;s(\lambda = 0.2\,{\text{m}})\, = {0.001}\!{-}\!0.005\,{\text{mm}}. \\ \end{aligned}. $$
(1)

The irregularities are given as a function of the wavelength λ, but this can also be translated to a function of the frequency f depending on the train speed vT according to f = vT/λ. The track yields long-wavelength (low frequency) alignment irregularities and short-wavelength (high-frequency) roughness irregularities. The wheel irregularities include the out-of-roundness at mid-frequencies (the first and second out-of-roundnesses are single peaks) and the roughness for higher frequencies (short wavelengths). The irregularities s increase with the wavelength λ, strongest for the track alignment, and this means a decrease with frequency f, s(λ) ~ λq means s(f) ~ f −q.

The spectrum of the combined track and vehicle irregularities is the starting point of a complete prediction of railway vibrations. Within the above limits, simplified spectra for good, medium and bad vehicle and track conditions are provided [2].

2.2 Simple vehicle and multi-beam-on-Winkler-support track models

The dynamic stiffness KV of the vehicle can be approximated by the inertia of the wheelset:

$$ K_{{\text{V}}} \left( \omega \right) = - m_{\rm W} {\omega}^{2} ,$$
(2)

where mW is the mass of the wheelset and ω = 2πf is the circular frequency of excitation. The minor effects of the low-frequency rigid and elastic vibrations of the carbody and bogies have been proved in [51].

Many track systems have been calculated by the combined finite-element boundary-element method [20], and the results have been used to derive a faster multi-beam-on-Winkler-support track model (Fig. 2). This track model consists of n beams which represent the rails and track slabs and which are described by the bending stiffness EIj and the mass per length mj′, and by support elements representing rail pads, sleepers, the ballast and any isolation element. The multi-beam system fulfils the following set of differential equations for the displacements u and the load FT

$$ \varvec{EI}\frac{{\partial^{4} {\user2{u}}}}{{\partial y^{4} }} + \varvec{M}\frac{{\partial^{2} {\user2{u}}}}{{\partial t^{2} }} + \varvec{C}^{\prime } \frac{{\partial {\user2{u}}}}{\partial t} + \varvec{K}^{\prime } \varvec{u} = \varvec{F}_{\text{T}}^{\prime }. $$
(3)
Fig. 2
figure 2

Model of the track: multi-beam on support or multi-beam on soil system

Full size image

This equation transformed into the frequency–wavenumber domain reads

$$ (\xi ^{4} \user2{EI} - \omega ^{2} \user2{M} + {i}\omega \user2{C}^{\prime } + \user2{K}^{\prime } )\user2{u} = (\xi ^{4} \user2{EI} + \user2{K}_{{{\text{TS}}}} ^{\prime } (\omega ))\user2{u} = \user2{F}_{{\text{T}}} ^{\prime } (\omega ), $$
(4)

where \({\varvec{K}}_{\text{TS}}^{{\prime}}\)(ω) is the dynamic track–soil stiffness matrix which is calculated by transfer matrices for each support element.

Transfer matrices T relate the state (F force and u displacement) of the bottom and the top of each support element as

$$ \left[ {\begin{array}{*{20}c} {F_{1} } \\ {u_{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{2} } \\ {u_{2} } \\ \end{array} } \right]. $$
(5)

The forces point to the element and F1 and u1 have the same direction. An elastic spring element (stiffness k, for example a rail pad, a sleeper pad or a ballast mat) yields

$$ \varvec{T}_{\text{E}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ {1/k} & 1 \\ \end{array} } \right]. $$
(6)

The spring–damper element for the Winkler soil reads similarly

$$ \varvec{T}_{\text{S}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ {1/\left( {k + ci{\omega}} \right)} & 1 \\ \end{array} } \right]. $$
(7)

A mass element (mass m, for example the sleeper) would yield

$$\user2{T}_{{\text{M}}} = \left[ {\begin{array}{*{20}c} 1 & { - m\omega ^{2} } \\ 0 & 1 \\ \end{array} } \right].$$
(8)

The transfer matrix of a column, which is used for the ballast, reads

$$ \varvec{T}_{\text{C}} = \left[ {\begin{array}{*{20}c} {{ \cos\, }a} & { - { \sin\,}a \cdot k_{\text{B}} a} \\ {{ \sin }\,a /k_{\text{B}} a} & {{ \cos\,}a} \\ \end{array} } \right], $$
(9)

with the static stiffness kB = EBAB/hB, the area AB, the height hB, the longitudinal wave velocity vB of the ballast and a = ωhB/vB a non-dimensional wave parameter. This transfer matrix allows wave propagation through the ballast at high frequencies.

The transfer function of a support section is achieved by multiplying the transfer functions of all support elements (for example rail pad, sleeper, ballast and soil, see Fig. 2) as

$$ \varvec{T} = \varvec{T}_{\text{E}} \varvec{T}_{\text{M}} \varvec{T}_{\text{B}} \varvec{T}_{\text{S}} . $$
(10)

The transfer matrix T is transformed to the stiffness matrix K as

$$ \left[ {\begin{array}{*{20}c} {F_{1} } \\ { - F_{2} } \\ \end{array} } \right] = \frac{1}{{T_{21} }}\left[ {\begin{array}{*{20}c} {T_{11} } & { - { \det }\varvec{T}} \\ { - 1} & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] = \frac{1}{{T_{21} }}\left[ {\begin{array}{*{20}c} {T_{11} } & { - 1} \\ { - 1} & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] = \varvec{Ku}, $$
(11)

where det T = 1 for passive systems, and the sign definition is different for F2; and the stiffness matrix K is added to the system Eq. (4).

A strong simplification is a Winkler soil where the load and displacement are proportional at every point of the soil surface. It has been found that an acceptable approximation FS/uS = kS + cSiω can be established which can be used for the dynamic compliance of the track–soil system under the axle load.

The dynamic track stiffness KT(ω) at the wheel-rail contact can be calculated as the wavenumber integral

$$ \frac{1}{{K_{T} \left( \omega \right)}} = \frac{{u_{{\text{R}}} }}{{F_{T} }}\left( \omega \right) = \frac{1}{2}\mathop \int \nolimits_{{ - \infty }}^{\infty } \user2{e}_{1} ^{{\text{T}}} \left({\xi} {^{4} \user2{EI} + \user2{K}_{{{\text{TS}}}} ^{{\mathbf{\prime }}} \left( \omega \right)} \right)^{{ - 1}} \user2{e}_{1} {\text{d}}{\xi}, $$
(12)

where the base vectors \( \varvec{e}_{1} \) indicate the components of the matrix, \( \left( {\xi^{4} \varvec{EI} + \varvec{K}_{\text{TS}}^{\prime } \left( \omega \right)} \right)^{ - 1} \) the compliance in wavenumber domain according to Eq. (4), and the spatial constant FT is the wavenumber transform of the point load. The force transfer from top to bottom of the track follows as

$$ H_{\text{T}} \left( \omega \right) = \frac{{F_{\text{S}} \left( \omega \right)}}{{F_{\text{T}} \left( \omega \right)}} = \mathop \int \limits_{ - \infty }^{\infty } \frac{{F_{\text{S}}^{\prime } \left( {y,{\omega}} \right)}}{{F_{\text{T}} \left( {\omega} \right)}}{\text{d}}y = \frac{{F_{\text{S}}^{\prime } \left( {\xi = 0,} \right)}}{{F_{\text{T}} \left( {\omega} \right)}} = \varvec{K}_{\text{S}}^{\prime } \left( {\xi = 0,\omega} \right)\varvec{e}_{2}^{\text{T}} \varvec{K}_{\text{TS}}^{\prime - 1} \left( {\xi = 0,{\omega}} \right)\varvec{e}_{1} ,$$
(13)

where \( \varvec{K}_{\text{S}}^{\prime } \) is the stiffness matrix of the soil, \( \varvec{K}_{\text{S}}^{\prime } \left( {\xi ,\omega } \right)\varvec{e}_{2}^{\text{T}} \varvec{K}_{\text{TS}}^{\prime - 1} \left( {\xi ,\omega } \right) \) the force transfer from top to bottom in wavenumber domain, and its integral along the track can be evaluated by its value at ξ = 0 [16].

2.3 The vehicle–track transfer functions

The dynamic stiffness KT(ω) of the track is coupled with the dynamic stiffness KV(ω) of the vehicle to analyse the combined vehicle–track system. The force FT(ω) that acts on the track is calculated as

$$ F_{\text{T}} \left( \omega \right) = - \frac{{K_{\text{V}} \left( \omega \right)K_{\text{T}} \left( \omega \right)}}{{K_{\text{V}} \left( \omega \right) + K_{\text{T}} \left( \omega \right)}}s\left( \omega \right) = H_{\text{V}} \left( \omega \right) s\left( \omega \right), $$
(14)

for the vehicle–track irregularities s.

The influence of the track mass must be introduced by the force transfer function HT(ω) from top to bottom of the track (Eq. (13)) which can be simply evaluated from the support chain [52]. Finally, the force FS(ω) on the soil, which excites the ground vibration, can be calculated as

$$ F_{\rm{S}} \left( \omega \right) = H_{\text{T}} \left( \omega \right)F_{\text{T}} \left( \omega \right) = H_{\text{T}} \left( \omega \right)H_{\text{V}} \left( \omega \right)s\left( \omega \right), $$
(15)

The force FS(ω) on the soil is the final result of the emission part of the prediction.

3 Examples for the emission of train-induced vibrations

At first, the dynamic stiffness KT(ω) of the track is presented for three different models in Fig. 3, a finite-element boundary-element model [20], a multi-beam-on-continuous-soil model [16] and a multi-beam-on-Winkler-soil approximation. All results are in the range of 108–109, and the stiffness increases from the low static to the higher dynamic values. The agreement between the approximate and the exact calculations is quite good and well acceptable for the prediction.

Fig. 3
figure 3

Dynamic stiffness of the track–soil system: a three-dimensional finite-element boundary-element model: b two-dimensional model on continuous soil; c two-dimensional model on Winkler support with rail pad kR = 300 × 106 N/m and ballast vB = 600 m/s

Full size image

Next, the most important vehicle–track–soil transfer function FS/s(ω) = HT(ω)HV(ω) is presented for some vehicle and track parameters (Table 1). The vehicle–track–soil transfer function is strongly influenced by the unsprung mass of the vehicle, the wheelset mass (Fig. 4a). The dynamic axle-loads are proportional to the wheelset mass for frequencies up to 60 Hz or even higher. For this frequency range, the transfer function increases with FS/s ~ ω 2. The higher frequency range is determined by the stiffness of the track and the soil which is demonstrated by the variation of the ballast stiffness (the longitudinal wave velocity of the ballast) in Fig. 4b. The stiffer ballast results in a higher vehicle–track resonance frequency up to 200 Hz. The high-frequency transfer function is almost constant where the highest values are reached for the stiffest ballast.

Table 1 Parameters of the emission part (per one sleeper)
Full size table
Table 2 Parameters of the immission part
Full size table
Fig. 4
figure 4

Transfer function FS/s between the irregularities s and the force FS on the soil: a for different wheelset masses (rail pad kR = 300 × 106 N/m, ballast vB = 400 m/s and soil vS = 200 m/s); b for different ballast (rail pad kR = ∞ and soil vS = 500 m/s); c for different rail pads (ballast vB = 600 m/s and soil vS = 300 m/s); d for different sleeper pads (rail pad kR = 300 × 106 N/m, ballast vB = 600 m/s and soil vS = 300 m/s)

Full size image

If soft track elements are introduced in the track, the vehicle–track resonance frequency is lower and the high-frequency transfer values are correspondingly reduced. Soft rail pads yield resonance frequencies down to 40 Hz (Fig. 4c), and soft sleeper pads have resonance frequencies between 20 and 64 Hz (Fig. 4d). The dynamic axle-loads can thus be reduced to less than one tenth of the values of a standard ballast track.

Now, the experimental results of emission are shown in Figs. 5 and 6 for an almost homogeneous site with a shear wave velocity of vS = 270 m/s. An irregularity spectrum has been specified (Fig. 5a) which includes a strongly decreasing alignment error, a weakly decreasing roughness of the rail and wheel, the sleeper passing component (0.012 mm) and a first out-of-roundness of the wheel (0.1 mm). These irregularities are shifted in frequency according to the train speeds of vT = 63 to 160 km/h. For these irregularities, the forces acting on the track (and ground) have been calculated (Fig. 5b). The strongly decreasing irregularities (together with the strongly increasing transfer functions) yield almost constant forces which lie around 1 kN, a value which can be used as a first approximation. The forces have a weak maximum at 90 Hz due to the vehicle–track resonance frequency. The increasing train speeds yield strongly increasing force amplitudes at low frequencies and a weaker increase at high frequencies. Finally, axle-box measurements are presented for this case in Fig. 6a [53]. All characteristics of the predicted forces can well be found in the measurement results, mainly the almost constant spectra, the strong increase with train speed at low frequencies, and the shift in frequency for the singular components of the out-of-roundness (6–16 Hz) and the sleeper passage (32–80 Hz). If the wheelset accelerations are multiplied by the wheelset mass of 1500 kg, the amplitudes of the excitation force can be confirmed.

Fig. 5
figure 5

Vehicle–track interaction for different train speeds: a wheel and track irregularities s and b force on the track FT

Full size image
Fig. 6
figure 6

Measured wheelset accelerations for different train speeds: a at a ballast track and b at a slab track

Full size image

Figure 6b shows a similar measurement result for a slab track. The slab track has soft rail pads which yield a lower vehicle–track resonance at 64 Hz and a stronger resonance amplitude because of the reduced track damping. So, the vehicle–track resonance can be clearly seen for the slab track, whereas the sleeper passage frequency can better be followed for the ballast track. By these measurements, the prediction of forces as a result from irregularities is confirmed.

4 Transmission: approximate methods for the prediction of train-induced ground vibration

The prediction of “transmission” means to calculate the response of the soil (particle velocity spectra) at different distances from the track due to the excitation force spectrum which has been calculated in the emission part. The transfer function of the soil is calculated for a fixed load (as in the US standard [7]). Thus, any moving load effect is excluded and the rare case of trans-Rayleigh trains is not covered by this prediction method. The transfer functions of layered soils are calculated by the “frequency-dependent half-space model”, that is a homogeneous half-space of which the stiffness varies with frequency. This concept is based on the fact that the dominant Rayleigh wave reaches down to a certain portion of its wavelength, and this means down to a frequency-dependent depth. The prediction of the transmission consists of the following three steps:

  1. 1.

    the calculation of the approximate dispersion for the layered soil,

  2. 2.

    the calculation of the frequency-dependent point-load solutions,

  3. 3.

    and the superposition of point loads to get the train load.

4.1 Approximative dispersion of a layered soil

The exact dispersion curves of layered, multi-layered and continuously layered soils have been used to derive an approximate calculation of the Rayleigh wave dispersion vR(f) from the soil profile vS(z). It is based on the approximated dispersion of a layer on a stiffer half-space with the wave velocities of the Rayleigh waves vR1 and vR2, as

$$ v_{\text{R}} \left( f \right) = v_{{{\text{R}}1}} + \left( {v_{{{\text{R}}2}} - v_{{{\text{R}}1}} } \right)0.5\left( {1 + { \cos }\frac{\uppi }{2}\frac{f}{{f_{1} }}} \right)\quad {\text{with}}\quad f_{1} = \frac{{v_{{{\text{S}}1}} }}{{3h_{1} }}, $$
(16)

which is extended to a multi-layered situation. A correction for each layer is added to the wave speed vR1 of the top layer

$$ v_{\rm{R}} \left( f \right) = v_{{\rm{R}1}} + \sum\limits_{{i = 1}}^{{n - 1}} {\left( {v_{{\rm{R}}i}{ + 1} - v_{{\rm{R}}i} } \right)} 0.5\left( {1 + \cos \frac{\uppi }{2}\frac{f}{{f_{i} }}} \right)\quad {\text{with}}\quad f_{i} = \frac{{v_{{\rm{S}}i} }}{{3h_{i} }}, $$
(17)

where hi is the depth where the layer i ends. For very low frequencies, the wave speed of the underlying half-space can be reached.

4.2 Approximative transfer function of a point load

The amplitudes of a homogeneous soil can be approximated by the asymptotes

$$ H_{\rm{P}} \left( {r,f} \right) = \frac{v}{F}\left( {r,f} \right) = \frac{{f\left( {1 - \nu } \right)}}{{Gr}}\exp \left( { - Dr^{*} } \right)\left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad {\text{for~}}\quad ~r^{*} \le r_{0} ^{*} } \hfill \\ {\sqrt {r{\text{/}}r_{0} ^{*} } } \hfill & {\quad {\text{for~}}\quad r^{*} > r_{0} ^{*} } \hfill \\ \end{array} } \right.\quad {\text{with}}\quad r^{*} = \frac{{2\uppi fr}}{{v_{\text{S}} }} .$$
(18)

The upper part of Eq. (18) describes the static solution which can be used for the near-field and the low-frequency response. At r* = r*0  ≈ 2.7 starts the lower part of Eq. (18), the far field which is dominated by the Rayleigh wave.

The amplitudes of a homogeneous soil can be used to calculate the wave field of an inhomogeneous soil. The amplitudes of the inhomogeneous soil with its dispersion vR(f) are approximated by the amplitudes of a homogeneous half-space, but for each frequency the half-space has a different wave speed—the wave speed vR(f). This method works very well for a soil with continuously increasing stiffness.

If this method is applied to a clearly layered situation, the following modifications must be included. A frequency-dependent resonance amplification

$$ V = \frac{1}{{1 + {i}2D\eta -\eta^{2} }} ,$$
(19)

can be introduced, where

$$ \eta = \left\{ {\begin{array}{*{20}l} {f{\text{/}}f_{1} } \hfill & {\quad {\text{for}}\quad ~f \le f_{1} } \hfill \\ {2 - f{\text{/}}f_{1} ~} \hfill & {\quad ~{\text{for}}\quad f > f_{1} } \hfill \\ \end{array} } \right.,\quad f_{1} = \frac{{v_{{\rm{S}1}} }}{{3h_{1} }},\quad {\text{and}}\quad D = \frac{2}{\uppi }\frac{{\rho _{1} v_{{{\text{S}}1}} }}{{\rho _{2} v_{{{\text{S}}2}} }} , $$
(20)

are used for the normalized frequency η, the resonance frequency f1, and the damping D is calculated according to the one-dimensional wave theory.

The effect of soft top layers on the low-frequency near-field and the effect of stiff deeper layers on the high-frequency far field are included by a general procedure. Normally at a certain frequency f, the half-space amplitudes of the corresponding wave velocity vR(f) are calculated. Corrections of the transfer functions are made if deeper and stiffer soil material yields greater half-space amplitudes, or softer top layers yield greater “layer amplitudes” which are approximated by AL = AHe−ar/h, according to the low frequency behaviour of a layer on a rigid base. The greatest amplitude is always chosen as the correct transfer function. The method can be improved if the dispersion is shifted one-third of octave to lower frequencies, and if the resonance damping in Eq. (19) is always D ≥ 0.1.

4.3 Approximative transfer function of a train load

The frequency-dependent effect of the track width of b = 2.6 m is approximated by modifying the force spectrum [54]

$$\frac{{F^{*} }}{F}\left( f \right) = \left\{ {\begin{array}{*{20}l} {{\text{sin}}(b^{*} /2)/b^{*} /2} \hfill & {\quad {\text{for}}\quad ~b^{*} \le \uppi } \hfill \\ {2/b^{*} } \hfill & {\quad {\text{for}}\quad ~b^{*} > \uppi } \hfill \\ \end{array} } \right.\quad {\text{with}}\quad ~b^{*} = ~\frac{{2\uppi fb}}{{v_{{\text{R}}} }} ,$$
(21)

where vR is the velocity of the Rayleigh wave.

The response to a train load is calculated by adding the responses of all n axle loads along the train length L which are considered fixed at their places and as random independent sources

$$ v\left( {x,f} \right) = \sqrt[{}]{{\mathop \sum \limits_{j = 1}^{n} H_{\rm{P}}^{2} \left( {\sqrt[{}]{{x^{2} + y_{j}^{2} }},f} \right)}}F^{*} \left( f \right), $$
(22)

where n = 40 and L = 250 m are used as standard values. It has been found by numerical tests that this train length already yields the response of an infinitely long train for normal soils with material damping and for normal distances up to 100 m. That means that the ground vibration amplitudes which are predicted for trains longer than 250 m are the same as those of a standard train of L = 250 m.

5 Examples for the transmission of train-induced ground vibrations

Results are presented for two layered sites, one site with soft soils and one site with stiff soils. The soil parameters have been established from wave velocity measurements [55] as

  • vS1 = 125 m/s, vS2 = 350 m/s, h = 4 m, D = 2.5% soft site,

  • vS1 = 325 m/s, vS2 = 850 m/s, h = 5 m, D = 2.5% stiff site.

The mass density and the Poisson’s ratio are assumed as ρ = 2000 kg/m3 and ν = 0.33. At first, Fig. 7a–d shows the transfer functions v/F between the excitation force F and the ground vibration amplitudes v at different distances. The exact point-load solutions (Fig. 7a, b) which are calculated by an infinite wavenumber integral [13] are compared with the approximate solution (Fig. 7c, d). Both solutions show the strong difference between the soft and the stiff soil. The amplitudes of the soft soil are almost a factor 10 higher than the amplitudes of the stiff soil. For each site, the low-frequency amplitudes are low and increasing with frequency. The high-frequency amplitudes are not so increasing in the near field and decreasing in the far field. Big differences between the near and the far field occur, thus yielding a strong attenuation with distance. The far field spectra have a maximum in the mid-frequency range which is characteristic for the layering of the soil. The maximum is at 16 Hz for the soft soil and at 32 Hz for the stiff soil. All these details of the point-load transfer function are in good agreement between the time-consuming, exact and the fast, approximate solution.

Fig. 7
figure 7

Ground vibration at a soft layered site (a, c, e, g) and at a stiff layered site (b, d, f, h) at different distances: a, b exact point-load transfer functions; c, d approximated point-load transfer functions; e, f train-load transfer functions; g, h measured train-induced ground vibrations

Full size image

For the prediction of train-induced ground vibration, many of these point-load transfer functions have been superposed to get the train-load transfer functions in Fig. 7e, f. The train-load transfer functions are closer together than the point-load transfer function. That means that the train-induced ground vibration has less attenuation with distance. The train-induced far field amplitudes are higher than the point-load amplitudes. The high-frequency train-induced amplitudes are reduced so that the near field is almost constant with frequency and the far field has a stronger reduction with frequency. At the end, if the soft and stiff soil are compared, the soft soil has much higher amplitudes at low frequencies, but similar amplitudes as the stiff soil at high frequencies.

Finally, some passages of passenger trains with train speeds trains between 100 and 160 km/h are presented in Fig. 7g, h from a measurement campaign in Switzerland [53]. The train-induced spectra are very similar to the transfer functions. This good agreement between measurement and prediction means that a wheelset force of 1 kN per third of octave band is a suitable assumption for the prediction. Train specific components can be found in the measurements. At frequencies below 8 Hz, the amplitudes measured at 4 m are higher than the measured ones (the quasi-static response), and at 50 Hz in Fig. 7h and at 80 Hz in Fig. 7g, a peak can be observed which is caused by the passage of the wheels over the equally spaced sleepers. The train-induced spectra represent all the characteristics of the soft and stiff layered soils. These examples demonstrate the necessity to evaluate soil-dependent predictions.

6 Immission: the building response to the free-field vibrations

A simplified building model has been established which consists of the foundation stiffness, the rising structure (column or wall) and the floors at each storey (Fig. 8). The model captures the important effects of soil–structure interaction, of floor resonances and of deformable walls and columns. This simple model can be applied for the whole building, giving average results, or to a regular vertical section of the building. Buildings are very complex structures so that a detailed model should be calculated if possible, for example when a new building is planned near a railway line (see some examples in [58]).

Fig. 8
figure 8

Simplified building model consisting of the soil, a wall or column and the floors

Full size image
Fig. 9
figure 9

Soil–building transfer functions of a four-storey apartment building: a, b wall; c, d floors; a, c one-dimensional prediction model; b, d three-dimensional finite-element model

Full size image

6.1 The dynamic foundation stiffness (soil–structure interaction)

The soil is represented by a spring and a damper element. The spring and damper parameters for a rigid circular foundation on a homogeneous soil are

$$ k \approx 3.4G\sqrt {A_{\text{S}} } \quad {\text{and}}\quad c \approx 1.6\sqrt {G\rho } A_{\text{S}} = 1.6 \rho v_{\text{S}} A_{\text{S}}, $$
(23)

with foundation area AS, shear modulus G, mass density ρ and shear wave velocity vS of the soil. These parameters are used as a standard. They can be checked against detailed calculations [56]. These soil elements are excited by the free-field vibrations u0 at their lower ends (see Fig. 8).

6.2 Floor vibrations and their feedback on the building structure

The floor with mass mF, damping D and eigenfrequency fF is described by two transfer functions of frequency f between the wall displacement uW at the floor support and the displacement uF at mid-span and the support force FW:

$$ \frac{{u_{\text{F}} }}{{u_{\text{W}} }} = 1 +\alpha \frac{{f^{2} }}{{\left( {1 + 2Di} \right)f_{\text{F}}^{2} - f^{2} }}, $$
(24)
$$ \frac{{F_{\text{W}} }}{{u_{\text{W}} }} = \left( {2\uppi f} \right)^{2} m_{\text{F}} \left( {1 + \frac{{f^{2} }}{{\left( {1 + 2Di} \right)f_{\text{F}}^{2} - f^{2} }}} \right). $$
(25)

The transfer functions are given for the first mode v of the floor, and the parameters follow as [57]

$$ \alpha= \frac{{v\left( {x_{\rm{F}} } \right)\int v{\text{d}}m}}{{\int v^{2} {\text{d}}m}}, $$
(26)
$$ \mu = \frac{{\left( {\int v{\text{d}}m} \right)^{2} }}{{m_{\rm{F}} \int v^{2} {\text{d}}m}}. $$
(27)

The values α and μ vary with the mode shape v(x). For a square floor area, the values are given in Table 3 for different boundary conditions. In the order 4 sides clamped, 4 sides hinged, 2 sides clamped, 2 sides hinged, 4 corners clamped, 4 corners hinged, the mass ratio μ is increasing and displacement factor α is decreasing or almost constant.

Table 3 Parameters of square floors
Full size table

6.3 Transfer matrix of a wall-, floor- and soil-element

Transfer matrices describe the transfer of the displacement and force from the bottom to the top of a building element

$$ \left[ {\begin{array}{*{20}c} {F_{1} } \\ {u_{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{2} } \\ {u_{2} } \\ \end{array} } \right] .$$
(28)

The transfer matrix of a wall element with the storey height h and the cross section AW is

$$ \varvec{T}_{\text{W}} = \left[ {\begin{array}{*{20}c} {{ \cos }\, a} & { - { \sin\, }a \cdot k_{\text{W}} a} \\ {{ \sin } \, a/k_{\text{W}} a} & {{ \cos } \, a} \\ \end{array} } \right], $$
(29)

with the static stiffness kW = EAW/h, the dimensionless wave parameter a = ωh/vL, and the longitudinal wave velocity vL of the wall. This transfer matrix results in considerable wave propagation along the height of the building. The transfer matrix for a rigid or flexible floor is

$$ \varvec{T}_{\text{R}} = \left[ {\begin{array}{*{20}c} 1 & { - m^{2} } \\ 0 & 1 \\ \end{array} } \right]\quad \varvec{T}_{\text{F}} = \left[ {\begin{array}{*{20}c} 1 & {F_{\text{W}} /u_{\text{W}} } \\ 0 & 1 \\ \end{array} } \right], $$
(30)

and the transfer matrix of the soil element is

$$ \varvec{T}_{\rm{S}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ {1/\left( {k + ci\omega} \right)} & 1 \\ \end{array} } \right]. $$
(31)

The whole building (for example a four-storey building) is represented by the matrix chain

$$ \varvec{T}_{\rm{B}} = \varvec{T}_{\rm{S}} \varvec{T}_{\rm{F}} \varvec{T}_{\rm{W}} \varvec{T}_{\rm{F}} \varvec{T}_{\rm{W}} \varvec{T}_{\rm{F}} \varvec{T}_{\rm{W}} \varvec{T}_{\rm{F}} \varvec{T}_{\rm{W}} \varvec{T}_{\rm{F}} . $$
(32)

The boundary condition F = 0 at the roof is used to evaluate the foundation force F0 = TB12/TB22u0, and all response quantities at walls and floors can then be calculated by the free-field excitation u0, F0, the transfer matrices and the transfer function uF/uW (Eq. (24)) of the floor.

7 The vibration response for different types of buildings

Some building examples have been analysed by this simple prediction method and by the three-dimensional finite-element method [58] for comparison, some column-type office buildings of four to twenty storeys and a wall-type apartment building. The material and geometric parameters of these buildings are given in Table 2.

7.1 A four-storey apartment building

A four-storey apartment building with masonry walls and concrete floors has been analysed on a medium stiff soil. The transfer functions between the free field and the building components are shown in Fig. 9. These transfer functions show some general characteristics. All freefield-building transfer functions start with V = 1 at zero frequency and usually end below V < 1 at 50 Hz. That means that the free field is not modified by the building at low frequencies whereas the free field is reduced by the building at high frequencies. In between, amplifications of the free field can occur due to several reasons. At 10 Hz, the resonance of the building on the compliant soil can be found with amplitudes of V = 5 to 6. This building-soil resonance frequency is determined by the stiffness k of the soil and the mass m of the building as \(f_{\rm{s}} = \sqrt{k/m}\). As a consequence, the building-soil resonance frequency should be proportional to the shear wave velocity of the soil \(f_{\rm{s}} \sim V_{\rm{s}}= \sqrt{G/\rho}\) and indirectly proportional to the square root of the number of storeys \(f_{{\text{s}}} \sim\sqrt{n}\).

Next at 25 Hz, some smaller amplifications can be found which are due to the floor resonances. The floor resonance frequencies are ruled by the width (5 m × 5 m), the thickness (0.2 m) and the support conditions (clamped–clamped) of the floor (Fig. 10a). Finally, another characteristic behaviour can be observed at 37 Hz where the floors and the walls are vibrating in anti-phase (Fig. 10b). The results for the finite-element model are also given in Figs. 9c, d. The agreement of the one-dimensional prediction model with the three-dimensional finite-element model is very good.

Fig. 10
figure 10

Vibration modes of the apartment building at a 24 Hz and b 37 Hz

Full size image

7.2 A twenty-storey office tower

The twenty-storey office tower presents another characteristic of building vibration. Figure 11 shows a vibration mode where the amplitudes increase with increasing storey number. This vibration mode is called the column mode because the deformation of the columns is the main reason of this vibration. The column frequency is determined by the wave velocity vL of the columns (and floors) and the height H of the building fC = vL/4H. The column frequency indicates an amplification of the amplitudes with height and a resonance in case of a stiff soil. The column frequency of the office tower is fC = 6 Hz, and the soil–building resonance is also at 6 Hz. So, both modes (the soil and the column mode) work together, amplifying each other and resulting in a basic building resonance at 4 Hz which can be found for the prediction as well as for the finite-element model (Fig. 12a, b). The office tower has the lowest resonance frequency and the highest resonance amplitudes of all building examples, but at the same time all amplitudes above 10 Hz are quite small, below V = 1.

Fig. 11
figure 11

Vibration mode of the office tower at 4 Hz

Full size image
Fig. 12
figure 12

Soil–building transfer functions of the office tower: a prediction model and b finite-element model

Full size image

It should be noted that the apartment building of the preceding section has also a relevant column (wall) frequency at fC = 19 Hz because of the softer masonry material. Due to the soft material, the low-rise apartment building has a low wall frequency and the deformations of the wall have an influence on the basic building resonance shifting it from 12 to 10 Hz (Fig. 9a).

7.3 Some parameter variations for office buildings

The office buildings are built with concrete columns of cross section 0.6 m × 0.6 m and concrete floors of dimensions 6 m × 6 m × 0.2 m. A four-storey office building is shown in Fig. 13 with its soil–building transfer functions. The basic building resonance at 9 Hz is dominant. Some small floor resonances can be observed at 12 Hz. At the same frequency, the column amplitudes are clearly reduced. More office buildings on different soils and with different number of storeys are presented in Fig. 14 with average column and floor transfer functions. The floor resonances are at quite low frequencies around 12 Hz for the column-type office buildings. Therefore, the floor vibrations have an influence on the basic building resonance and reduce its resonance frequency which lies between 7 Hz for the softest soil and 10 Hz for the stiffest soil (Fig. 14a–d). The same presentation is given in Fig. 14e–h for the variation of the number of storeys. The calculated basic building resonance frequency can be compared with the theoretical soil, floor and column frequencies where the closest theoretical frequencies have the strongest influence. The four-storey building has a calculated basic building resonance frequency of fB = 9 Hz which is influenced by the soil frequency of fS = 14.4 Hz and the floor frequency of fF = 13.7 Hz. The twelve-storey building has a basic frequency of fB = 6 Hz which is influenced by the soil frequency of fS = 8.8 Hz and the column frequency of fC = 10.3 Hz. To conclude, all interactions of floor, column and soil modes in all building models are well represented by the simple building model in good agreement with the three-dimensional finite-element model.

Fig. 13
figure 13

Soil–building transfer functions of the four-storey office building: a, b column; c, d floors; a, c prediction model; b, d finite-element model

Full size image
Fig. 14
figure 14

Averaged soil–column (a, b, e, f) and soil–floor (c, d, g, h) transfer functions of office buildings with a–d different soils, and with e–h different number of storeys (VS = 200 m/s)

Full size image

7.4 Measurement results

Finally, two measurement examples are shown in Fig. 15 [59]. Both buildings have a column-type structure. The first building is a four-storey concrete building, and the second building is a six-storey steel-frame construction. Both buildings show some floor resonances, the first building at 12.5 Hz, the second building between 15 and 20 Hz. Most typical, both column-type buildings have a dominant first resonance at 7.5 Hz and 10 Hz, respectively. The amplitudes are increasing with the number of storeys which can clearly be observed in Fig. 15b. For the four-storey building (Fig. 15a), this difference can also be seen between the first and the third storey, but also the influence of the amplified floors can be seen. The first building resonance is therefore clearly identified as a combination of the column mode and the floor mode. For frequencies higher than the building and the floor resonance frequencies, the amplitudes are clearly reduced. The measured reduction is stronger than the calculated reduction for the detailed and the simple models. The reason for the stronger reduction may be a softer soil in the measurements or a higher building mass for example of the non-bearing members which are not included in the models. In general, these building examples offer proof for the practical relevance of the investigated phenomena of column-type buildings.

Fig. 15
figure 15

Measured soil–building transfer functions of two office buildings: a a four-storey concrete building; b a six-storey steel-frame building

Full size image

8 Conclusions

A simple and fast prediction scheme has been presented for train-induced ground and building vibrations. All formula for the vehicle–track, soil and building models have been given in this article. It has been demonstrated that the results of all simple models can well represent the behaviour of more detailed models, three-dimensional finite-element boundary-element track models, wavenumber integrals for layered soil models, and three-dimensional finite-element building models. Moreover, measurement examples have been given for the emission (two track examples measured from axle boxes), transmission (two-layered soil examples) and immission (two multi-storey column-type office buildings) which underline the practical value of the prediction. The characteristic behaviour of the different components has been demonstrated by example predictions.

  • The strongly decreasing irregularity spectra and the strongly increasing vehicle–track transfer function lead to almost constant excitation forces.

  • Elastic track elements shift the vehicle–track–soil resonance frequency and yield a reduction in the excitation force.

  • The wave propagation through layered soils is strongly frequency dependent. The deeper stiff soil yields small low-frequency amplitudes, whereas the softer top layer yields greater high-frequency amplitudes. Moreover, a clear difference between a soft and a stiff site has been calculated and measured. Therefore, a site-specific prediction of train-induced ground vibration is absolutely essential.

  • Floor, column and soil modes have been observed in apartment and office buildings. The analysis of different number of storeys and different stiffnesses of the soil shows the coupling between these modes which leads to lower resonance frequencies and higher resonance amplitudes. These phenomena are in a very good agreement between the simple one-dimensional prediction model and the three-dimensional finite-element model.