1 Introduction

The voltage and frequency of the power systems vary depending on the demand of consumers. Therefore, these changes should be kept within a certain limits to supply quality energy to consumers [1]. Especially, the frequency is one of the dominant parameters in power quality. And it becomes a primary control parameter in power systems.

Load frequency control (LFC) of conventional power systems is performed with three different control loops [2, 3], which loops are primary, secondary and tertiary control loops. The primary control loop provides active power balance, and the secondary control loop minimizes the steady-state error in the control loop frequency formed at the end of the primary control loop. The tertiary control loop is the central loop that regulates the system frequency error and includes measures performed by verbal instructions in case primary and secondary loops are insufficient. Linear models including primary and secondary control loops are suggested to analyze the frequency control of the systems [3,4,5]. However, there is also a time delay caused by phasor measurement units (PMUs) as well as communication links. The time delay affects performances of these control loops in the power systems and it is approximately in the range of 5–15 s [4, 6]. Also the time delay may reduce the damping performance of the control system and even cause the instability if it exceeds the delay margin [7,8,9]. In fact, this value is the delay time which makes the system marginally stable. Therefore, the time delay must be considered for both analysis and design of a power system. For this purpose, linear models including time delay have been proposed [3,4,5].

The proportional integral/ proportional integral derivative (PI/PID) controllers which are commonly used in the industry [10] are also used for the LFC systems [5, 11,12,13,14]. In the analysis of LFC systems, time delay is taken into account, and it is important to obtain the delay margin where the system is marginally stable. Various methods are used to determine the delay margin of a system with time delay. These methods may be either frequency [15,16,17,18] or time domain based methods [5]. The direct method is one of the frequency domain based methods [15]. This method transforms the transcendental characteristic equation to a polynomial form by eliminating the exponential function, and it facilitates calculation of delay margin. Delay margin of delayed LFC system with integer-order PI controller has been computed delayed LFC system for different controller parameters for single and two areas [13].

Although the history of fractional calculus dates back to three centuries ago, the usage of fractional-order controllers in control systems has rapidly increased in the last twenty years [19,20,21,22,23,24]. The research results show that fractional-order controllers are more flexible than integer-order controllers. Also, the fractional-order controllers are used in LFC without time delay and their effectiveness is proven [25,26,27,28,29,30]. In addition to these studies, analog and digital implementation of fractional-order controller has been recently studied [31,32,33,34,35]. Therefore, it is significant to determine the effects on the systems theoretically before the implementation of fractional controllers. So far, no study has investigated effects of fractional-order PI controller on the stability and performance of the delayed LFC system.

The system stability is the most significant issue in all control systems [36]. This statement is also available for delayed LFC system. The instability in delayed LFC system causes to collapse and this result reveals difficulties which are hard to compensate [30]. Controller and system parameters affect the stability in delayed LFC systems. Since the delayed LFC system has a delay-dependent stability, the system stability should be analyzed in terms of time delay, and controllers which are provided to extend the value of delay margin should be proposed. For a fixed time delay, the usage of fractional-order PI controller in the delayed LFC system is provided with significant improvement on system stability according to controller parameters [24]. In this study, the improvement effect of fractional-order PI on delay margin is investigated in a single-area delayed LFC system. Although the single-area power system is simple, the stability analysis is complex because of a fractional integrator and time delay in the system. Thus a single-area delayed LFC system is chosen to show the effect of the fractional-order PI controller. In addition, because of the similarity to microgrids [37,38,39,40], this is a preliminary study for them.

For this purpose, the gain parameters of fractional-order PI are as fixed and delay margin analysis is performed according to the fractional integral order of fractional-order PI. The delay margin analysis of delayed LFC system has been realized by using the direct method. In addition, the system stability has been determined graphically, by the generalized modified Mikhailov (GMM) criterion given in [41]. The results obtained are compared with results of the integer-order controller.

After the introduction, mathematical model of the fractional-order PI controller, block diagram of a time-delay single-area LFC system with fractional-order PI controller, and GMM criterion have been given in Section 2. In Section 3, delay margin of the system have been computed for different fractional integral orders by using the direct method, and stability analysis of the delayed LFC system with fractional-order PI controller has been performed by using the GMM criterion. The results have been validated with results of time domain simulations in Section 4, and conclusions are presented in Section 5.

2 Materials and methods

2.1 Fractional-order PI controller

After fractional calculus was suggested for the first time in 1695, Liouville, Riemann, and Holmgren have carried out the first studies systematically about the fractional calculus [42, 43]. Many approaches have been proposed for the fractional-order integral and derivative operators in these studies [42]. However, controllers defined by fractional calculus have been applied intensively in control systems in the last two decade. The controller types which have the fractional-order integral or derivative operator are called as fractional-order controllers.

The fractional-order PI controller, which is one of the fractional-order controllers, is defined with the transfer function expressed in the following form [44].

$$G_{c}^{f} (s) = K_{p} + \frac{{K_{i} }}{{s^{\alpha } }}\begin{array}{*{20}c} {} & {} & {K_{p} ,K_{i} \ge 0} \\ \end{array}$$
(1)

where Ki is integral gain constant of controller; Kp is proportional gain constant of the controller.

Here, α is fractional integral order and a real number (0 < α < 2), and Kp and Ki are the proportional and integral gains, respectively. If Kp or Ki is chosen as negative, the controller could be a non-minimum phase. In this case a minimum phase system can transform into non-minimum phase. Therefore, Kp and Ki have been chosen as positive real number. Figure 1 shows the illustration of the integer-order and the fractional-order PI controller on the α-axis.

Fig. 1
figure 1

Integer-order PI and fractional-order PI on α axis

Full size image

Note that the integer-order controller is defined by two points on the α-axis, whereas the fractional-order PI controller can be defined by infinite number of points indicated in the range of (0, 2) with bold line on the α-axis. This means that fractional-order PI controller has more flexibility than integer-order controller.

2.2 Single-area delayed LFC system with fractional-order PI controller

In a power system, frequency depends on the active power balance. The change in active power demand in the system causes a change in the frequency affecting the entire system.

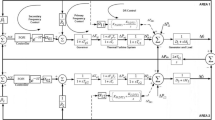
Therefore, the purpose of the LFC system is to secure the desired frequency against these changes [2, 3]. The block diagram for a single-area delayed LFC system given in [14] is modified for the single-area delayed LFC system with fractional-order controller as shown in Fig. 2.

Fig. 2
figure 2

Block diagram of one-area fractional-order delayed LFC system

Full size image

As can be seen in Fig. 2, the block diagram contains primary and secondary control loops. ΔPm is change of turbine output; ΔPv is change of governor output; λ is fractional order of the integrator; and ACE is an area control error. Moreover, the power system is turned to a fractional-order structure due to the usage of a fractional-order controller. The transfer functions given in the block diagram are defined as:

  1. 1)

    Fractional-order PI controller: \(G_{c}^{f} (s) = K_{p} + K_{i} /s^{\alpha }\)

  2. 2)

    Governor: \(G_{g} (s) = 1/T_{g} s + 1\)

  3. 3)

    Turbine: \(G_{ch} (s) = 1/T_{ch} s + 1\)

  4. 4)

    Power system: \(G_{M} (s) = 1/Ms + D\)

In Fig. 2, the system parameters are assigned as similar to those in [14].

$$\frac{\Delta f(s)}{{\Delta P_{d} (s)}} = \frac{{ - Rs^{\alpha } (T_{g} s + 1)(T_{ch} s + 1)}}{{s^{\alpha } [R(T_{g} s + 1)(T_{ch} s + 1)(Ms + D) + 1] + \beta R(K_{p} s^{\alpha } + K_{i} ){\text{e}}^{ - s\tau } }}$$
(2)

where τ is the time delay; M is generator inertia constant; R is governor speed regulation; Tch is time constant of turbine; Tg is time constant of governor; β is frequency bias parameter; Δf is system frequency deviations; and D is damping coefficient.

According to (2), the transcendental fractional-order characteristic equation of the system is determined as:

$$\left \{\begin{aligned} & \Delta (s,\tau ) = P(s) + Q(s){\text{e}}^{ - s\tau } = 0 \\ & P(s) = s^{\alpha } (p_{4} s^{3} + p_{3} s^{2} + p_{2} s + p_{1} ) \\ & Q(s) = q_{1} s^{\alpha } + q_{0} \end{aligned}\right.$$
(3)

where \(p_{1} = RD + 1\), \(p_{2} = RM + RDT_{g} + RDT_{ch}\), \(p_{3} = RMT_{g} + RMT_{ch} + RDT_{g} T_{ch}\), \(p_{4} = RMT_{g} T_{ch}\), \(q_{1} = \beta RK_{p}\), \(q_{0} = \beta RK_{i}\).

Fractional-order transcendental characteristic (3) will be used for both computing delay margin and obtaining GMM plot.

2.3 Generalized modified Mikhailov criteria

Using graphical methods based on frequency domain can simplify the stability analysis of the fractional-order time delay systems. The graphical procedures of Mikhailov use the similar approach to the Nyquist for the relative-stability problem [45]. While Nyquist approach is based on the (−1, 0) point in the complex plane, Mikhailov approach is based on the origin. The GMM stability criterion is a graph-based method used to analyze fractional-order linear systems with time delay [41]. This method is also used to analyze fractional-order delayed non-linear systems [46]. Because the GMM stability criterion provides closed curves in polar plane, the stability analysis of the system will be simplified.

Consider a linear fractional-order system with delays described by a transfer function:

$$T(s^{\alpha } ) = \frac{{\Delta_{N0} (s^{\alpha } ) + \sum\limits_{j = 1}^{{y_{2} }} {\Delta_{Nj} (s^{\alpha } ){\text{e}}^{{ - \tau_{j} s}} } }}{{\Delta_{D0} (s^{\alpha } ) + \sum\limits_{i = 1}^{{y_{1} }} {\Delta_{Di} (s^{\alpha } ){\text{e}}^{{ - \tau_{i} s}} } }} = \frac{{\Delta_{N} (s^{\alpha } )}}{{\Delta_{D} (s^{\alpha } )}}$$
(4)

where τi is the time delay, and fractional-order polynomials ΔDi(sα) and ΔNj(sα) with real coefficients have the form:

$$\Delta_{{D_{i} }} (s^{\alpha } ) = \sum\limits_{k = 1}^{n} {r_{ik} s^{{\alpha_{Dk} }} } \quad\quad i = 0,1, \ldots ,y_{1}$$

and

$$\Delta_{Nj} (s^{\alpha } ) = \sum\limits_{k = 1}^{m} {z_{jk} s^{{\alpha_{Nk} }} } \quad\quad j = 0,1, \ldots ,y_{2}$$

where αDk and αNk are real non-negative numbers and r0n≠ 0, z0m≠ 0. The system described by the transfer function (4) is a commensurate order if αDk = kα (k = 0,1,…,n) and αNk = kα (k = 0,1,…,m). Otherwise, the system is a non-commensurate order. The fractional-order characteristic function of the system (4) has the form:

$$\Delta_{D} (s^{\alpha } ) = \Delta_{D0} (s^{\alpha } ) + \sum\limits_{i = 1}^{{y_{1} }} {\Delta_{Di} (s^{\alpha } )\text{e}^{{ - \tau_{i} s}} }$$
(5)

By generalization of the Mikhailov theorem for the fractional-order characteristic function (5), the following theorem is obtained.

Theorem 1

[41] The fractional characteristic (5) of commensurate order is stable if and only if:

$$\mathop {\Delta \arg }\limits_{0 \le \omega < \infty } D(({\text{j}}\omega )^{\alpha } ) = n\frac{\uppi }{2}$$
(6)

where n is the number of the system’s poles located in the left half of the s-plane and π/2 is one quadrant of complex plane. The plot of function ΔD((jω)α) is called Mikhailov plot. The plot of ΔD((jω)α) runs in positive direction by n quadrants of the complex planes when ω grows from 0 to +∞. ΔD((jω)α) has the infinite number of roots due to the time-delay terms in ΔD((jω)α). Therefore, it generates an infinite number of spirals on complex plane and the origin of this plane is missing as ω grows to +∞, and it is difficult to confirm the condition of Theorem 1. To avoid this difficulty, the following rational function has been proposed instead of the fractional characteristic function (5):

$$\psi (s) = \frac{{\Delta_{D} (s^{\alpha } )}}{{w_{r} (s)}}$$
(7)

where wr(s) is stable and can be chosen in the form:

$$w_{r} (s) = a_{0} (s + c)^{\alpha } \begin{array}{*{20}c} {} & {c > 0} \\ \end{array}$$
(8)

where a0 is the coefficient of the first term ΔD0(sα) in (5). Note that (8) is stable for c > 0.

Theorem 2

[41]. The fractional characteristic function (5) of commensurate or non-commensurate order is stable if and only if:

$$\mathop {\Delta \arg }\limits_{ - \infty \le \omega < \infty } \mathop {\psi ({\text{j}}\omega ) = 0}\limits_{{}}$$
(9)

The plot of function ψ(jω) is called GMM plot. Equation (9) holds if and only if the GMM plot ψ(jω) does not encircle the origin of the complex plane as ω grows to ± ∞.

3 Computation delay margin and stability analysis of delayed LFC system with fractional-order PI controller

The delay margin of the system can be obtained by using the characteristic equation of the system given in Fig. 2. Systems without time delay is called as a delay free system and their stability is determined by the roots of P(s) + Q(s) polynomial given in (3). Otherwise, the time delay is effective on the stability of the system. Various methods are used to find in the frequency and time domain roots of transcendental polynomials as given in (3) [15,16,17,18]. The frequency based direct method reduces the complexity of characteristic equation from transcendental to polynomial structure through the elimination of exponential expression and simplifies the solution. In order to compute the delay margin of the system, the critical frequency ωc where poles of the system intersect jω axis should be obtained. If this value is not equal to zero, these poles are complex conjugate. In this case, fractional-order transcendental characteristic equation is provided for s1 = jωc and s2 = –jωc. Characteristic equations are given for two polar values as shown below:

$$\left\{\begin{aligned} &P({\text{j}}\omega_{c} ) + Q({\text{j}}\omega_{c} ){\text{e}}^{{ - {\text{j}}\omega_{c} \tau_{c} }} = 0 \hfill \\ &P( - {\text{j}}\omega_{c} ) + Q( - {\text{j}}\omega_{c} ){\text{e}}^{{{\text{j}}\omega_{c} \tau_{c} }} = 0 \hfill \\ \end{aligned} \right.$$
(10)

If the exponential expression is eliminated in (10), the following is obtained:

$$W(\omega_{c} ) = P({\text{j}}\omega_{c} )P( - {\text{j}}\omega_{c} ) - Q({\text{j}}\omega_{c} )Q( - {\text{j}}\omega_{c} ) = 0$$
(11)

which is turned into a fractional polynomial depending on ωc only:

$$\begin{aligned} W(\omega_{c} ) = m_{5} \omega^{6 + 2\alpha } + m_{4} \omega^{4 + 2\alpha } + m_{3} \omega^{2 + 2\alpha } \hfill \\ \quad \quad \quad \quad +\,m_{2} \omega^{2\alpha } + m_{1} \omega^{\alpha } + m_{0} = 0 \hfill \\ \end{aligned}$$
(12)

where \(m_{5} = p_{4}^{2}\); \(m_{4} = p_{3}^{2} - 2p_{2} p_{4}\); \(m_{3} = p_{2}^{2} - 2p_{1} p_{3}\); \(m_{2} = p_{1}^{2} - q_{1}^{2}\); \(m_{1} = - 2q_{0} q_{1} \cos \left( {\alpha \pi /2} \right)\); \(m_{0} = - q_{0}^{2}\).

Positive real roots of W polynomial (12) give the frequency where the system intersects the jω-axis. The delay margin is obtained from the following expression for this frequency:

$$\tau_{c} = \frac{1}{{\omega_{c} }}\arccos \left( {\text{Re} \left\{ { - \frac{{P({\text{j}}\omega_{c} )}}{{Q({\text{j}}\omega_{c} )}}} \right\}} \right)$$
(13)
$$\begin{aligned} \tau_{c} = \frac{1}{{\omega_{c} }}{{\arccos \frac{{\omega_{c}^{\alpha } (n_{5} \omega_{c}^{3} + n_{4} \omega_{c}^{2 + \alpha } + n_{3} \omega_{c}^{2} + n_{2} \omega_{c}^{\alpha } + n_{1} \omega_{c}^{{}} + n_{0} )}}{{d_{2} \omega_{c}^{2 + \alpha } + d_{1} \omega_{c}^{\alpha } + d_{0} }}}} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{2k\uppi }{{\omega_{c} }}\quad \quad k{ = 0,1,2} \hfill \\ \end{aligned}$$
(14)

where \(n_{5} = - p_{4} q_{0} \sin \left( {\alpha \uppi /2} \right)\); \(n_{4} = p_{3} q_{1}\); \(n_{3} = p_{3} q_{0} \cos \left( {\alpha \uppi /2} \right)\); \(n_{2} = - p_{1} q_{1}\); \(n_{1} = p_{2} q_{0} \sin \left( {\alpha \uppi /2} \right)\); \(n_{0} = - p_{1} q_{0} \cos \left( {\alpha \uppi /2} \right)\); \(d_{2} = q_{1}^{2}\); \(d_{1} = - q_{0} q_{1} \cos \left( {\alpha \uppi /2} \right)\); \(d_{0} = q_{0}^{2}\).

Delay margin values for α = 0.8, 1, and 1.2 are obtained for system parameters by utilizing (14) as shown in Tables 1, 2, and 3, respectively.

Table 1 Delay margin values for α = 0.8 and different controller gains
Full size table
Table 2 Delay margin values for α = 1 and different controller gains
Full size table
Table 3 Delay margin values for α = 1.2 and different controller gains
Full size table

Delay margin values in Tables 1, 2 and 3 marked as the bold and italic will be used as simulation parameters in Sect. 4. These time delays ensure that system poles are on the jω-axis. The system is marginal stable for these delay times and they are representing a specific boundary. However, there is no information about system stability at the outside of this boundary. This means that the system is stable for delays either greater or lower than these values. If GMM criterion is used to test stability of the system, a rational function should be defined as given in (15) and (16). Therefore, the GMM plot can be obtained by using the characteristic equation of the fractional-order LFC system.

$$\psi (s,\tau ) = \frac{\Delta (s,\tau )}{{w_{r} (s)}}$$
(15)
$$w_{r} (s) = a_{0} (s + c)^{\alpha } \begin{array}{*{20}c} {} &\, {c > 0} \\ \end{array}$$
(16)

Since all roots of polynomial, \(a_{0} = p_{4} s^{3} + p_{3} s^{2} + p_{2} s + p_{1}\) is in the left half s-plane for the given values, the stability analysis is performed depending on the enclosing of the origin by the GMM plot. In this analysis, the values between 0 and 1000 rad/s are assigned to ω for obtaining the GMM plot. The GMM plot is drawn for time delays either greater or smaller than the delay margins for α = 0.8 and α = 1.2 in Figs. 3 and 4, respectively.

Fig. 3
figure 3

GMM plot of the delayed one area LFC system for α  = 0.8, Kp = 1 and Ki = 0.6

Full size image
Fig. 4
figure 4

GMM plot of the delayed single-area LFC system for α = 1.2, Kp = 1 and Ki = 0.6

Full size image

As shown in Figs. 3 and 4, the system becomes unstable for the time delays which are greater than the delay margins. On the other hand, it becomes stable for the delays below the delay margin since the plot does not encircle the origin. The system is marginally stable for the values of delay margin as expected and in this case, GMM plot intersects the origin according to these results given in the Tables 1 and 3, the delay margin increases at low Kp–Ki gains. Conversely, for the bigger value than α = 1, the delay margin relatively increases at high controller gains. The delay time is given as 5–15 s in the LFC systems [4, 6]. If the delay margin is taken as 5 s for these systems, the stable controller gains are expanded as the fractional integral order gets lower. This means that the stability of the system becomes more flexible according to integer-order controller with low gain values. In addition to that, the usage of fractional-order controller in LFC system is more robust than integer-order controller.

The delay margin surface according to Tables 1, 2, and 3 for α = 0.8, 1, and 1.2 are shown in Figs. 5, 6, and 7 respectively.

Fig. 5
figure 5

Delay margin surface obtained from Table 1 (α = 0.8)

Full size image
Fig. 6
figure 6

Delay margin surface obtained from Table 2 (α = 1.0)

Full size image
Fig. 7
figure 7

Delay margin surface obtained from Table 3 (α = 1.2)

Full size image

In Figs. 5, 6, and 7, this surface represents a stability boundary. In this case, the system is marginally stable for a point at the surface, it is stable for a point under the surface, and it is unstable for a point above the surface.

4 Numerical results

In this section, time domain simulation results of the single-area delayed LFC system with fractional-order PI controller is presented in order to verify the results obtained in the previous section. The load change is ΔPd= 0.1 p.u. in all simulations, and this load is started up at t = 5 s.

The time response of the system for α = 0.8, Kp= 1, Ki= 0.6, and delay margin τc = τ2 = 0.372 s, which is given as italic in Table 1, is obtained in Fig. 8. Additionally, time domain simulations obtained for τc> τ1 = 0.3 s and τc< τ3 = 0.4 s values are also given in the same figure.

Fig. 8
figure 8

Frequency deviation with respect to time for three different values of time delay (α = 0.8, Kp = 1 and Ki = 0.6)

Full size image

As expected, the system is marginally stable when the time delay is equal to delay margin, it is stable when the time delay is smaller than delay margin and it is unstable when the time delay is larger than delay margin. Similarly, the time responses of the system for α = 0.8, Kp = 0.2, and Ki = 0.4, and delay margin τc = τ2 = 5.315 s, which is given as bold in Table 1, τc> τ1 = 5 s and τc< τ3 = 6 s are obtained in Fig. 9.

Fig. 9
figure 9

Frequency deviation with respect to time for three different values of time delay (α = 0.8, Kp = 0.2 and Ki = 0.4)

Full size image

Note that similar results are also obtained in the case of equal, smaller, and larger values of delay margin. Also, time domain simulations are given in Figs. 10 and 11 for Table 2 and they are given in Figs. 12 and 13 for Table 3 in a similar way.

Fig. 10
figure 10

Frequency deviation with respect to time for three different values of time delay (α = 1, Kp = 1 and Ki = 0.6)

Full size image
Fig. 11
figure 11

Frequency deviation with respect to time for three different values of time delay (α = 1, Kp = 0.2 and Ki = 0.4)

Full size image
Fig. 12
figure 12

Frequency deviation with respect to time for three different values of time delay (α = 1.2, Kp = 1 and Ki = 0.6)

Full size image
Fig.13
figure 13

Frequency deviation with respect to time for three different values of time delay (α = 1.2, Kp = 0.2 and Ki = 0.4)

Full size image

The simulations prove the results obtained analytically. Finally, the time response of the system for values α = 1.2, Kp= 1, Ki= 0.6, and τc = 0.603 s that make the system marginally stable is given in Fig. 14, and about one period of time response is also given in this figure.

Fig. 14
figure 14

Frequency deviation with respect to time for delay margin value (α = 1.2, Kp= 1, Ki = 0.6, and τc = 0.603 s)

Full size image

The critical frequency ωc, which was obtained with the solution of (11), is the undamped oscillation frequency and this value is ωc= 2.2607 rad/s. And the period of oscillation is calculated as Tc= 2.779 s. In Fig. 14, it is shown that the period of the time response has been correctly calculated from (11).

5 Conclusion

In this study, the fractional-order PI controller has been proposed for controlling a single-area delayed LFC system. In this case, we aim to present the effects of the fractional integral order on the delay margins for controller gains, and they have been computed by using the direct method. The delay margin surfaces have also been obtained for different fractional-orders by using delay margin values. These results have shown that fractional integral order provides much more flexibility about system stability. That is, the fractional-order controller makes the system more robust than integer-order controller in term of delay margin parameter. Clearly, this allows formation of different delay margin surfaces for different α values and presents potential of solving stability problems caused by time delay.

In addition, the GMM criterion has been used to test whether the system is stable for delays either above or below the delay margins. The system which is analyzed in this paper has been determined as stable for the values below delay margins. Finally, the results obtained have been confirmed by the time domain simulations.

Also, the following observations and comments can be made from the results:

  1. 1)

    The direct method can be used as an effective tool to compute the delay margin and the frequency of undamped oscillations for fractional-order delayed systems.

  2. 2)

    For the fractional-order system which is analyzed, the delay margin increases at low Kp–Ki gains. Conversely, for the bigger value than α = 1, the delay margin relatively increases at high controller gains.

  3. 3)

    The GMM criterion is found to be quite effective for stability analysis of the fractional-order delayed power system.

As a result, the fractional-order PI controller has an obvious effect on the delay margins depending on the fractional integral order, which is the third controller parameter. If effective calculation methods or tools are determined, it is planned to carry out a delay-marginal analysis of the two and multi-area LFC system as a next study.