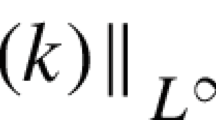1 Introduction

Rogue Waves in the ocean are often defined as waves larger than twice the significant wave height, \(2H_\mathrm{s}\), loosely speaking waves “much larger than the waves around them”. Following dramatic direct and indirect evidence for the existence and impact of Rogue Waves in the last 30 years, a consensus has emerged that although they are rare events, they are much more common than the statistics of “usual” waves would lead us to expect (Dysthe et al. 2008). More recently, Rogue Waves have been identified in many different noisy nonlinear wave systems (Chabchoub et al. 2015; Onorato et al. 2013b), including Bose–Einstein condensates (He et al. 2014) and optics (Dudley et al. 2014).

There is intense debate on the modelling of Rogue Waves, especially on the mechanisms responsible for their emergence. Numerous studies link them with breathers (Chabchoub et al. 2012; Dudley et al. 2014; Kibler et al. 2015; Onorato et al. 2013) or other special solutions of nonlinear Schrödinger equations.

Many authors point out that Benjamin–Feir instabilities of focusing nonlinear waves must play a key role in the formation of Rogue Waves (Chabchoub et al. 2015; Kibler et al. 2015; Onorato et al. 2013b). In this work, we quantify for the first time how a continuous superposition of Benjamin–Feir-type instabilities can create a highly localized, rapidly growing perturbation of a noisy wave background. A key novelty of our analysis is that it can be applied to any background Fourier spectrum, not just plane waves. Another key point is that we quantify how spatially-periodic Benjamin–Feir-type modes can combine to yield persistently localized unstable modes, and what are the fundamental lengthscales and timescales of this localization.

To achieve this, we study the Wigner transform of the nonlinear Schrödinger equation, and then carry out a linear stability analysis of the resulting exact, nonlinear Wigner equation in phase space. On the technical level, we adapt tools originally invented by Penrose for the study of the Vlasov–Poisson equation (Penrose 1960).

Finally, it must be mentioned that our approach can be applied to a large family of nonlinear pseudodifferential equations (including in particular realistic Whitham operators). This is due to the pseudodifferential calculus available for the Wigner transform (Athanassoulis et al. 2011; Gérard et al. 1997).

1.1 Nonlinear Schrödinger equations and the role of the functional framework

Nonlinear Schrödinger equations (NLS) of the form

$$\begin{aligned} i\partial _t u + \frac{p}{2} \Delta u + q |u|^{2} u =0 \end{aligned}$$
(1)

are used to model a wide variety of nonlinear wave phenomena including water waves, see (Chabchoub et al. 2015; Mei et al. 2005; Onorato et al. 2013, 2013b; Segur et al. 2005; Sulem and Sulem 1999; Zakharov 1968) and the references therein. A key dichotomy in this class lies between the focusing and defocusing cases: if \(pq<0\), then we have the defocusing NLS, and strong stability results and a priori estimates are available. On the other hand, if \(pq>0\), then we have the focusing NLS, and much more unstable behaviour is possible.

In the context of ocean waves with a central wavenumber \(k_0\), the envelope can be seen to satisfy a focusing NLS of the form (1) with (Mei et al. 2005, Eqs. (13.2.45), (13.2.61))

$$\begin{aligned} p=\frac{-\sqrt{g}}{ 4 k_0^{\frac{3}{2}}}, \quad q=-\frac{\sqrt{g}}{2} k_0^{\frac{5}{2}}. \end{aligned}$$
(2)

In this paper, we will use the forced and damped focusing NLS

$$\begin{aligned} i\partial _t u +\frac{p}{2} \Delta u +q |u|^2 u + \frac{i}{2} D u =f \end{aligned}$$
(3)

for the envelope u as a basic model for the unidirectional propagation of narrowband ocean waves (Slunyaev et al. 2015; Segur et al. 2005). The envelope u(x, t) and the physical sea surface elevation \(\eta (x,t)\) (on an appropriate frame of reference) are related by Mei et al. (2005), Onorato et al. (2013), Segur et al. (2005) and Zakharov (1968)

$$\begin{aligned} \eta (x,t) = {\text {Re}}\left[ u(x,t) e^{i(k_0 \cdot x - \omega _0 \cdot t)} \right] . \end{aligned}$$
(4)

Thus, the Fourier spectrum for \(\eta \) usually has a peak at \(k=k_0\), while the Fourier spectrum for the corresponding envelope u is translated to have a peak at \(k=0\). The wavenumber \(k_0\) will be called interchangeably the central, carrier or modal wavenumber. The central frequency \(\omega _0=\omega (k_0)\) is determined by virtue of the deep water dispersion relation, \(\omega ^2 = g k\) (Mei et al. 2005, Eq. (13.2.20b)).

The parameter \(D>0\) models dissipation (Slunyaev et al. 2015; Segur et al. 2005), which in most cases is very small, but physically present. The right hand side term f models applied pressure (e.g., by the wind) (Bühler et al. 2016; Maleewong et al. 2005), wave breaking (Cousins and Sapsis 2014), and other processes.

While modified NLS equations with additional terms have been proposed to model accurately higher order effects (Trulsen and Dysthe 1996; Trulsen et al. 2000), in many cases, the basic model (3) contains the most fundamental physics of the problem. Indeed, we will see that key mechanisms and scalings generating localized instabilities are already contained in Eq. (3). This is consistent with the consensus that Rogue Waves are a generic phenomenon of nonlinear dispersive waves (Chabchoub et al. 2015; Dudley et al. 2014; He et al. 2014; Kibler et al. 2015; Onorato et al. 2013b), and thus, they do not originate from some peculiar term arising only in a very specific context.

A mathematical aspect of Eq. (3) that is sometimes physically underestimated is that of the boundary conditions or, in other words, of the behaviour at infinity. A “harmless” assumption like \(u(t=0) \in L^2_x\) means that the wavefunction has to decay to zero at infinity—an assumption seemingly inappropriate for ocean waves. Indeed, the mathematical study of focusing Schrödinger equations with non-vanishing behaviour at infinity indicates that it is much more unstable than the vanishing case, and this aspect seems to play a role in the formation of Rogue Waves. One realization of this effect is the formation of breathers, long linked with Rogue Waves (Chabchoub et al. 2012; Dudley et al. 2014; Kibler et al. 2015; Onorato et al. 2013). However, breathers grow out of a plane wave background; the object of our analysis is to capture the first stages of a breather-like solution growing out of a background consistent with a realistic Fourier spectrum, in particular not an exact plane wave.

1.2 The Wigner transform and phase-space modelling

Given a wavefunction u(x, t), its Wigner transform (WT) is defined as

$$\begin{aligned} W(x,k,t)=W[u(t)](x,k) {=} \int \limits _y e^{-2\pi i k y} u(x{+}\frac{y}{2},t) \overline{u}(x{-}\frac{y}{2},t) \mathrm{d}y. \end{aligned}$$

Observe that W[u(t)](x, k) is real valued for any complex valued function u(x, t).

The WT keeps track of how much “wave action” can be found in each wavenumber k, at every point x and every moment in time t (Cohen 1976; Rubinstein and Wolansky 2005; Mallat 1999; Lions and Paul 1993).

Broadly speaking, the advantage of working with W(x, k, t) as opposed to u(x, t) is that it can be used as a tool for homogenization: in a problem with a large number of individual waves N, it will take at least O(N) degrees of freedom to meaningfully represent (in a non-parametric way) u(x, t). In contrast, W(x, k, t) plays the role of a phase-space energy density, and its complexity does not grow with N; in fact, in many problems, the WT “cleans up” for large N. Thus, the WT offers a way to coarse-grain the problem. It has been extensively used in many linear problems, including the semiclassical limit of quantum mechanics (Athanassoulis 2008; Athanassoulis et al. 2009; Lions and Paul 1993; Gérard et al. 1997) and the simulation of graphene (Fermanian-Kammerer and Méhats 2016).

A particularity of the WT is that, since it is essentially a second moment of u, in nonlinear problems, you do not obtain automatically an exact, closed Wigner equation. However, for the NLS equation a closed, exact Wigner equation derived by exploiting the correct marginal property

$$\begin{aligned} |u(x)|^2 = \int \limits _k W[u](x,k) \mathrm{d}k \end{aligned}$$

effectively as a moment closure. This control of the magnitude of point values of u(x, t) is also instrumental in describing localized instabilities quantitatively.

We directly compute the WT of Eq. (3) in Sect. 2.2. The same ideas can be used to derive the exact, closed nonlinear Wigner equation corresponding to a wide range of nonlinear dispersive equations, including the MMT equation (Majda et al. 1997; Cousins and Sapsis 2014), Ginzburg–Landau models (Aranson and Kramer 2002), Hartree equations (Athanassoulis et al. 2011), and the Szegö equation (Pocovnicu 2011). In particular, the Whitham pseudodifferential operator (Whitham 1967) can be treated in the place of the Laplacian, so that fully realistic dispersion is used.

It must be noted that if u is thought of as a stochastic process \(u=u(x,t;\beta )\), the Wigner spectrum

$$\begin{aligned}&\langle {W}(x,k,t) \rangle _\beta \\&\quad := E_\beta \left[ \int \limits _y e^{-2\pi i k y} u(x+\frac{y}{2},t;\beta ) \overline{u}(x-\frac{y}{2},t;\beta ) \mathrm{d}y \right] , \end{aligned}$$

i.e., the average Wigner transform, can also be used for the analysis of u. This has been used in the context of signal processing for non-stationary random processes (Martin and Flandrin 1985) and for the propagation of waves in random media (Bal et al. 2003; Ryzhik et al. 1996; Erdös and Yau 2000). In the context of water waves, Alber (1978) used the Wigner spectrum to study the directional stability of solutions of the two-dimensional Davey–Stewartson equations in a narrowband setting. The Alber equation was derived under a Gaussianity assumption, and it has since been studied in the context of directional stability, as well as numerically (Ribal et al. 2013; Crawford et al. 1980; Stiassnie et al. 2008; Regev et al. 2008; Dysthe et al. 2003).

1.3 Structure of the paper

In Sect. 2.1, some key properties of the WT are revisited, and in Sect. 2.2, the exact, nonlinear equation governing the WT of the NLS (3), Eq. (11), is derived. In Sect. 2.2, it is checked that, in the absence of forcing, i.e., for \(f=0,\) any homogeneous initial data \(W_0(x,k)=P(k)\) give rise a time-decaying homogeneous solution of the Wigner equation, \(W(x,k,t) = e^{-Dt} P(k)\). Indeed, since there is dissipation in Eq. (3), the absence of forcing any solution would have to decay in time. However, the combination of dissipation and forcing can create solutions that are homogeneous as well as stationary. We call this combination the Deterministic Balanced Wigner (DBW) equation, cf. Eq. (12). That way we recover the setting widely observed in ocean waves, namely, of wavefields that appear to be homogeneous and stationary, at least for timescales of a few hours, and space scales of several kilometers. These are exactly the scales, where the emergence of extreme events is most interesting.

Crucially, by virtue of the WT, we can work with any observed Fourier spectrum P(k), despite the lack of explicit representations for realistic u(x, t) or f(x, t). The merit of this is that now, we can perform a linear stability analysis for the Fourier spectrum P(k), with dynamics equivalent to the NLS Eq. (3). In Sect. 3.1, we proceed to investigate small perturbations of P(k) by denoting \(W(x,k,t)=P(k)+\epsilon w(x,k,t)\), \(\epsilon \ll 1\), and obtaining a linearized equation for the evolution of the perturbation w(x, k, t), namely, Eq. (14).

This linearization is grounded on smallness of \(\epsilon w(x,k,t)\); that is, this is a weakly non-stationary, weakly non-homogeneous regime. In particular, we do not introduce any additionalFootnote 1 smallness assumptions for the amplitude of the background waves, which is controlled by \(\int \limits P(k) \mathrm{d}k\).

Following an approach Penrose devised for the classical Vlasov–Poisson equation (Penrose 1960; Bardos and Besse 2013), we introduce the ansatz

$$\begin{aligned} w_\zeta (x,k,t) = F_\zeta (k) e^{i\zeta (x - 2\pi (\alpha _\zeta +i \beta _\zeta ) t)} \end{aligned}$$
(5)

for solutions of the linearized Eq. (14). Should such a solution exist, \(\zeta \) is its wavenumber, \(2\pi \alpha _\zeta \) its velocity, and \(2\pi \zeta \beta _\zeta \) its exponential rate of growth or decay, depending on its sign. If \(\zeta \beta _\zeta >0\) we say the mode is unstable. (The k-profile \(F_\zeta (k)\) plays only a secondary role.) We will also use the notation \(\Omega _\zeta =\alpha _\zeta +i\beta _\zeta \) for the complex “Penrose frequency”. Plugging the ansatz (5) in the linearized equation, we obtain the Penrose condition

(6)

If the denominator becomes singular, the integral should be interpreted in the Cauchy principal value sense (it becomes essentially a Hilbert transform). This connection will become apparent when looking into some more detailed questions in Sect. 5.3.

Observe that Eq. (6) is a system of two real-valued equations (real and imaginary part) for three real unknowns (\(\zeta ,\alpha ,\beta \)), hence in general we expect the solution set to be a (union of) curve(s) in \(\mathbb {R}^3\). Every solution \((\zeta ,\alpha ,\beta )\) of the Penrose condition leads to a Penrose mode, which automatically is a solution of Eq. (14). However, the interesting Penrose modes are the unstable ones, i.e., the ones with \(\zeta \beta _\zeta >0\). To work with these unstable modes systematically, we will call the set of all \(\zeta \in \mathbb {R}\) for which there are unstable Penrose modes the set of resonant Penrose numbers, denoted by

$$\begin{aligned} \mathbb {P}= & {} \{ \zeta \in \mathbb {R}\,\, | \,\, \exists \Omega _\zeta \in \mathbb {C} \text{ so } \text{ that } \text{ Eq. } (6)\, \text {is satisfied},\nonumber \\&\text {and} \,\zeta {\text {Im}}\Omega _\zeta >0 \}. \end{aligned}$$
(7)

Unstable Penrose modes generalize Benjamin–Feir sidebands. Indeed, it is checked in Sect. 4.2 that when u is a plane wave, our approach is an equivalent construction of the standard modulation instability. The advantage of Penrose stability analysis though is that it can be carried out for any background Fourier spectrum P(k), as opposed to around plane waves only.

Moreover, since the linearized Eq. (14) is by construction linear in w, we can create more interesting solutions by superpositions of unstable Penrose modes

$$\begin{aligned} w(x,k,t)=\int G(\zeta ) \,w_\zeta (x,k,t)\mathrm{d}\zeta \end{aligned}$$

for various weights \(G(\zeta )\). In Sect. 3.2, we demonstrate that such composite solutions can be highly localized— in contrast to the spatially periodic Penrose modes. Moreover, we observe that their key scalings (how sharply localized they can become, how fast they grow) are controlled by the Penrose condition (6), and not the weight \(G(\zeta )\), which seems to not play an essential role. This is elaborated with the help of numerical results in Sect. 4.3.

A key finding is that for each observed Fourier spectrum P(k), the Penrose bandwidth \(|\mathbb {P}|\), i.e., the Lebesgue measure of the set \(\mathbb {P}\) of unstable Penrose numbers, is controlling how sharply localized any instabilities of Eq. (3) can become. Localized unstable modes can be interpreted as a concentration of energy from the homogeneous background into small regions; in this context, a linearly unstable mode localized over a single typical wavelength, \(\lambda _0=\frac{2\pi }{k_0}\), will be interpreted as the emergence of a Rogue Wave. Moreover, we find that the timescale \(\tau \) at which the linearly unstable modes grow, measured in wave periods \(T_0=\frac{2\pi }{\omega _0},\) does not depend on \(k_0\). In particular, we find that within \(\approx 40\) wave periods, the perturbation grows from \({\approx }1\%\) to \({\approx }1\). This is consistent with state-of-the-art numerical results for the prediction of Rogue Waves in the NLS, (Cousins and Sapsis 2016).

In Sect. 4, we work explicitly the narrowband limit \(P(k)\approx A^2 \delta (k-k_0).\) This allows an explicit comparison with the standard modulation instability and a systematic investigation of the emergence of localized instabilities with the benefit of some explicit results. In Sect. 5, a numerical scheme for the resolution of the Penrose condition (6) is formulated. It is then applied to a realistic Ochi–Hubble spectrum. It is found that as the spectrum becomes broader, if \(H_s\) remains the same, then the localization of unstable modes deteriorates. In that sense, our analysis can be used to quantify the trade-off between the size of the support of the Fourier spectrum and the wave height, i.e., the “stabilization through spectral broadening”. That would essentially amount to a Benjamin–Feir index which takes fully into account the shape of the Fourier spectrum. A semi-analytic technique to determine whether there are solutions of the Penrose condition is presented in Sect. 5.3, along with some resulting characterisations of symmetric unimodal spectra.

2 Wigner transform and the DBW equation

2.1 The Wigner transform

The Wigner transform (WT) is a sesquilinear transform

$$\begin{aligned} W: u,v \mapsto W[u,v](x,k) = \int \limits _{y \in \mathbb {R}^n} e^{-2\pi i k y}u\left( x{+}\frac{ y}{2}\right) \bar{v}\left( x-\frac{y}{2}\right) \mathrm{d}y. \end{aligned}$$

When \(u=v\), i.e., in the quadratic version of the Wigner transform, the notation can be simplified to

$$\begin{aligned} W[u] := W[u,u]= \int \limits _y e^{-2\pi i k y} u\left( x+\frac{y}{2}\right) \overline{u}\left( x-\frac{y}{2}\right) \mathrm{d}y. \end{aligned}$$
(8)

Lemma 2.1

The following correct marginal properties

$$\begin{aligned} \int \limits _k W[u](x,k) \mathrm{d}k = |u(x)|^2, \quad \int \limits _x W[u](x,k) \mathrm{d}x = |\widehat{u}(k)|^2, \end{aligned}$$
(9)

and the operational properties

$$\begin{aligned}&W[u,v] = \overline{W[v,u]}, \quad W [xu,v] = \left( x-\frac{1}{4\pi i} \partial _k \right) W[u,v], \nonumber \\&W[ \partial _x u,v] = \left( 2\pi i k + \frac{1}{2} \partial _x \right) W[u,v] \end{aligned}$$
(10)

hold true.

Proof

The proofs follow from direct computations (Athanassoulis 2008; Gérard et al. 1997). \(\square \)

Lemma 2.2

(Wigner transform of plane waves) The plane wave \(u(x,t)=Ae^{2\pi i (\xi x - \omega t)},\) \(A,\xi \in \mathbb {R},\) \(\omega \in \mathbb {C},\) has WT given by

$$\begin{aligned} W[u(t)](x,k)= A^2e^{4\pi {\text {Im}}\omega t}\delta (k-\xi ). \end{aligned}$$

Proof

By direct computation, we obtain

$$\begin{aligned}&W[Ae^{2\pi i (\xi x - \omega t)}](x,k) = |A|^2 e^{4\pi {\text {Im}}\omega t} \\&\qquad \int \limits _y e^{-2\pi i k y} e^{2\pi i \xi \left( x+\frac{y}{2}\right) - 2\pi i \xi \left( x-\frac{y}{2}\right) } \mathrm{d}y\\&\quad =|A|^2 e^{4\pi {\text {Im}}\omega t} \int \limits _y e^{-2\pi i y (k-\xi )} \mathrm{d}y = A^2 e^{4\pi {\text {Im}}\omega t} \delta (k-\xi ). \end{aligned}$$

\(\square \)

Finally, we will also use the following computation:

Lemma 2.3

Let \(V:\mathbb {R}\rightarrow \mathbb {R}\), \(u:\mathbb {R}\rightarrow \mathbb {C}\). Then

$$\begin{aligned} W[Vu,u] - W[u,Vu]= & {} \int \limits _{y} e^{-2\pi i k y} \frac{V\left( x-\frac{y}{2}\right) -V\left( x+\frac{y}{2}\right) }{y} \mathrm{d}y \, *_k \nonumber \\&\times \frac{\partial _k}{2\pi i} W[u](x,k), \end{aligned}$$

where \(*_k\) denotes convolution in the k variable only.

Proof

We will normalize the Fourier transform as

$$\begin{aligned} \mathcal {F}_{x\rightarrow k}[f(x)](k) = \widehat{f}(k) = \int \limits _{x\in \mathbb {R}} e^{-2\pi i k \cdot x} f(x) \mathrm{d}x. \end{aligned}$$

Then, one readily checks that

$$\begin{aligned}&W[Vu,u] - W[u,Vu]=\int \limits _y e^{-2\pi i k y} \Big [ V\left( x+\frac{y}{2}\right) \nonumber \\&\qquad \qquad -\, V\left( x+\frac{y}{2}\right) \Big ] u\left( x+\frac{y}{2}\right) \overline{u}\left( x-\frac{y}{2}\right) \mathrm{d}y\\&\quad =\mathcal {F}_{y\rightarrow k} \left[ \frac{V\left( x+\frac{y}{2}\right) - V\left( x-\frac{y}{2}\right) }{y} y u\left( x+\frac{y}{2}\right) \overline{u}\left( x-\frac{y}{2}\right) \right] \nonumber \\&\quad = \mathcal {F}_{y\rightarrow k} \left[ \frac{V\left( x+\frac{y}{2}\right) -V\left( x-\frac{y}{2}\right) }{y} \right] *_k \frac{\partial _k}{-2\pi i} W[u](x,k)\\&\quad =\int \limits _{\lambda ,y} e^{-2\pi i \lambda y} \frac{V\left( x-\frac{y}{2}\right) {-}V\left( x{+}\frac{y}{2}\right) }{y} \mathrm{d}y \frac{\partial _k}{2\pi i} W[u](x,k{-}\lambda ) \mathrm{d}\lambda . \end{aligned}$$

\(\square \)

2.2 DBW equation and stationary and homogeneous solutions

The derivation of the Wigner equation corresponding to (3) is known (Athanassoulis et al. 2009). However, for the sake of completeness, we outline it here: let u satisfy Eq. (3), and \(W=W[u(t)](x,k)\); then

$$\begin{aligned} \partial _t W= & {} W[\partial _t u, u] + W[u,\partial _t u] =\frac{i}{2} \Big ( W[p \Delta u,u] - W[u,p\Delta u] \Big ) \nonumber \\&+\, iq \Big (W[|u|^2u,u] - W[u,|u|^2u] \Big ) - D W + W[f], \end{aligned}$$

leading to the exact Wigner equation

(11)

by virtue of Lemmas 2.1 and 2.3. Observe that as long as \(V(x,t) = \int \nolimits _\xi W(x,\xi ,t) d\xi \) is differentiable (e.g., either \(C^1\) or \(H^1\)), then \(\frac{V(x-\frac{y}{2},t)-V(x+\frac{y}{2},t)}{y}\) makes sense for almost all y;  in particular, for \(|y|\ll 1\), it simply looks like \(\partial _x V(x,t).\) Thus, the dy integral in Eq. (11) makes sense as a Fourier transform under simple differentiability conditions.

At first glance, any homogeneous wave spectrum P(k) can be seen as a time-decaying solution of the unforced Wigner equation (11): indeed, if \(f=0\), the Wigner equation (11) with homogeneous initial data, \(W_0(x,k)=P(k)\), has the homogeneous solution:

$$\begin{aligned} W(x,k,t)=e^{-D t} P(k) \end{aligned}$$

since

The conclusion now follows by solving an ODE.

However, the time-decaying solutions described above do not correspond to what is usually observed in the ocean. Indeed, forcing terms describing wind, wave breaking, etc are crucial in explaining why certain stationary spectra are common, and some are almost never observed. To observe a given stationary spectrum P, the dissipation term DW has to cancel out the effective forcing.Footnote 2 This situation can be captured as follows: if \(W_0(x,k)=P(k)\) and \(W[f]=D P(k)\), then the deterministic balanced Wigner equation

(12)

has the stationary and homogeneous solution:

$$\begin{aligned} W(x,k,t)= P(k). \end{aligned}$$

Indeed, one readily checks that

We call Eq. (12) the deterministic balanced Wigner equation, because it contains effective forcing and damping terms, in addition to the free evolution terms.

3 Penrose stability analysis

3.1 Linearization, unstable Penrose modes, and the Penrose condition

We investigate small perturbations of the stationary and homogeneous solution \(W(x,k,t)=P(k)\) of Eq. (12), and whether such perturbations can grow arbitrarily. More specifically, we look for solutions of Eq. (12) of the form

$$\begin{aligned} W(x,k,t) = P(k) + \epsilon w(x,k,t), \end{aligned}$$
(13)

and particularly whether w can grow rapidly, so that \(\epsilon w(x,k,0)\) is negligible at \(t=0\) but \(\epsilon w(x,k,T)\) becomes comparable to the background waves over some meaningfulFootnote 3 timescale T. Using Eq. (13) to rewrite the problem for the perturbation w(x, k, t) only, Eq. (12) becomes

Dropping the quadratic term, we are led to the linearized DBW equation:

(14)

The driving question now becomes; are there solutions w of Eq. (14) that can grow rapidly in time? To answer this question, we will use an idea originally introduced by Penrose for the stability of plasmas (Penrose 1960), namely, the introduction of an appropriate ansatz for the solutions of Eq. (14). In the process, we will also recover the timescales and other qualitative features of linearly unstable modes.

We will seek solutions of the linearized DBW equation (14) as in Eq. (5). Such solutions will be called Penrose modes of wavenumber \({\zeta }\). The first question is, for which \(\zeta \), \(F_\zeta (k)\), and \(\Omega _\zeta \) do Penrose modes exist? In addition, second, are there Penrose modes with \({\text {Im}}\big (\zeta \Omega _\zeta \big )>0\)? If solutions with \({\text {Im}}\big (\zeta \Omega _\zeta \big ) >0\) exist, these correspond to perturbations of P(k) that grow arbitrarily, and they will be called unstable Penrose modes.

Of course, once the perturbation grows sufficiently, the linearized equation should no longer be expected to approximate well the nonlinear problem; however, the question we focus on is whether the growth of such perturbations is possible in the first place.

Plugging the ansatz (5) in Eq. (14), we get

which finally leads to

$$\begin{aligned} \frac{ F_{\zeta }(k)}{\int \nolimits _{\xi } F_\zeta (\xi ) \mathrm{d}\xi } = \frac{q}{2\pi p \zeta } \frac{ P(k-\frac{\zeta }{4\pi }) - P(k+\frac{\zeta }{4\pi })}{k-\frac{1}{p}\Omega -i\frac{D}{2\pi p\zeta }} \end{aligned}$$
(15)

for the admissible k profile of a Penrose mode. Moreover, upon integrating Eq. (15) in k, obtain the Penrose condition, i.e., Eq. (6).

Thus, if there are solutions \(\zeta \in \mathbb {R},\) \(\Omega _\zeta \in \mathbb {C}\) for the Penrose condition (6), then the linearized DBW equation (14) has a solution given by the Penrose mode:

$$\begin{aligned} w_\zeta (x,k,t) = \frac{ P(k+\frac{\zeta }{4\pi }) - P(k-\frac{\zeta }{4\pi }) }{ \zeta k-\frac{\zeta }{p} \Omega _\zeta -i\frac{D}{2\pi p}} e^{i\zeta (x - 2\pi \Omega _\zeta t)}. \end{aligned}$$
(16)

Since Eq. (14) is a linear equation, applying scalar factors or taking real parts is possible.

3.2 Superposition of unstable modes and localized instabilities

So far, we have seen how solving the Penrose condition (6) can lead to the construction of spatially periodic unstable modes for a given spectrum. However, physical extreme events—including oceanic Rogue Waves—are typically due to localized wavepackets, and not spatially periodic patterns. Here, we will see how our construction can describe localized instabilities as well. While our mathematical approach is completely different, physically, our results are reminiscent of (Kibler et al. 2015).

Fig. 1
figure 1

Numerical evaluation of \(\epsilon n(x,t)\) for \(A=5.3,\) \(k_0=0.24\) and different weights \(G(\zeta )\) and times t. Time is measured in timescales \(\tau ,\) cf. Eq. (22). Top left plot for \(G(\zeta )=\frac{1}{3},\) \(t=1\tau .\) Top right plot for \(G(\zeta )=\frac{1}{3},\) \(t=7\tau .\) Bottom left plot for \(G(\zeta )=-i\zeta (\zeta ^2-\zeta _\mathrm{max}^2)e^{-\frac{4\zeta ^2}{\zeta _\mathrm{max}^2}},\) \(t=1\tau .\) Bottom right plot for \(G(\zeta )=-i\zeta (\zeta ^2-\zeta _\mathrm{max}^2)e^{-\frac{4\zeta ^2}{\zeta _\mathrm{max}^2}},\) \(t=7\tau \)

Full size image

Assume that for a given background spectrum P(k), we have resolved the Penrose condition, i.e., we have found all \(\Omega _\zeta =\alpha _\zeta +i \beta _\zeta \), so that Eq. (6) holds and \(\zeta \beta _\zeta >0\). This of course means that we know all unstable Penrose modes, by virtue of Eq. (16). Then, due to the linearity of Eq. (14), superpositions of Penrose modes

$$\begin{aligned}&w(x,k,t) = { \frac{q}{2\pi p}} {\text {Re}}\nonumber \\&\qquad \times \int \limits _{\zeta \in \mathbb {P}} G(\zeta ) \, \frac{ P(k+\frac{\zeta }{4\pi }) - P(k-\frac{\zeta }{4\pi })}{ \zeta k-\frac{\zeta }{p} \Omega _\zeta -i\frac{D}{2\pi p}} e^{i\zeta (x - 2\pi \Omega _\zeta t)} \, \mathrm{d}\zeta \nonumber \\ \end{aligned}$$
(17)

are also solutions of Eq. (14) for any weight \(G(\zeta )\). Recall also that the whole point of Eq. (14) is that, for \(\epsilon \ll 1\), \(P(k) + \epsilon w(x,k,t) \approx W(x,k,t)\), where W(x, k, t) is the solution of the nonlinear Wigner equation (12), at least until some time when w becomes too large in an appropriate sense. By virtue of the marginal property of the Wigner transform, Lemma 2.1, \(P(k) + \epsilon w(x,k,t) \approx W(x,k,t)\) implies

$$\begin{aligned} |u(x,t)|^2= & {} \int \limits _k W(x,k,t) \mathrm{d}k \approx \int \limits _{k} \big [ P(k) + \epsilon w(x,k,t) \big ] \mathrm{d}k\nonumber \\= & {} A ^2 +\epsilon \int \limits _k w(x,k,t)\mathrm{d}k, \end{aligned}$$
(18)

where \(A^2:=\int \nolimits _k P(k)\mathrm{d}k\) is the zero moment of the background Fourier spectrum. Therefore, the quantity

$$\begin{aligned} n(x,t) := \int \limits _k w(x,k,t) \mathrm{d}k \end{aligned}$$
(19)

controls the x, t localization of instability in the sense that

$$\begin{aligned} |u(x,t)| \approx \sqrt{ |A|^2 + \epsilon n(x,t)} \end{aligned}$$
(20)

as long as the linearization (14) provides an acceptable approximation of (12).

Moreover, it can be seen that

$$\begin{aligned} n(x,t)= & {} \int \limits _k w(x,k,t) \mathrm{d}k \nonumber \\= & {} \frac{q}{2\pi p} {\text {Re}}\int \limits _{\zeta \in \mathbb {P}} \int \limits _{k\in \mathbb {R}} \frac{ P(k+\frac{\zeta }{4\pi }) - P(k-\frac{\zeta }{4\pi })}{ \zeta k-\frac{\zeta }{p} \Omega _\zeta -i\frac{D}{2\pi p}}\nonumber \\&\times \,\mathrm{d}k \, G(\zeta ) e^{i\zeta (x - 2\pi \Omega (\zeta ) t)} \mathrm{d}\zeta \nonumber \\= & {} {\text {Re}}\int \limits _{\zeta \in \mathbb {P}} G(\zeta ) e^{i\zeta (x - 2\pi \alpha _\zeta t)+2\pi \zeta \beta _\zeta t} \mathrm{d}\zeta . \end{aligned}$$
(21)

The finding here is that the dk integral is exactly the one controlled by the Penrose condition; hence, it can be carried out explicitly and the result does not depend on \(\zeta \).

The behaviour of this expression depends more on \(\mathbb {P}\), \(\alpha _\zeta ,\) \(\beta _\zeta \) than on the weight \(G(\zeta )\), cf. Fig. 1. In fact, Eq. (21) becomes very powerful once we have found all \((\zeta ,\alpha ,\beta )\) satisfying the Penrose condition, as we will see in detail in Sect. 4.3.

A related question that we can address here is that of timescales: since we have been working with a linearized equation, for how long can we trust this linearization to be qualitatively correct? The answer is determined by the fastest rate of growth of any unstable Penrose mode.

Thus, the timescale

$$\begin{aligned} \tau = \frac{1}{\sup \limits _{\zeta \in \mathbb {P}} 2\pi \zeta \beta _\zeta } \end{aligned}$$
(22)

appears.

4 Case study for a prototypical narrowband spectrum

4.1 Finding the unstable Penrose modes

To see precisely what the previous computation mean physically, it is instructive to apply them to the simplest narrowband, stationary solution of the NLS, namely

$$\begin{aligned} P(k)=A^2\delta (k-0). \end{aligned}$$

This is the case of the Fourier spectrum for the envelope u,  concentrated at \(k=0.\) It is equivalent with a Fourier spectrum of \(A^2\delta (k-k_0)\) for the sea surface elevation \(\eta \). The analysis that follows can be applied to either spectrum; the difference between the two is a question of normalization, not dynamics.

In this prototypical case, the Penrose condition (6) becomes

$$\begin{aligned}&A^2 \int \limits _{k\in \mathbb {R}} \frac{\delta (k-\frac{\zeta }{4\pi })-\delta (k+\frac{\zeta }{4\pi })}{k - \frac{\Omega }{p} - i \frac{D}{2\pi p \zeta }} \mathrm{d}k = \frac{2\pi p \zeta }{q} \nonumber \\&\quad \Leftrightarrow \quad \frac{1}{\frac{p\zeta }{4\pi } - \Omega - i \frac{D}{2\pi \zeta }} - \frac{1}{-\frac{p\zeta }{4\pi } - \Omega - i \frac{D}{2\pi \zeta }} = \frac{2\pi \zeta }{q A^2} \end{aligned}$$

finally leading to

$$\begin{aligned} \Omega _\zeta = -i\frac{D}{2\pi \zeta } \pm \frac{\sqrt{p^2 \zeta ^2 - 4pq A^2}}{4\pi }. \end{aligned}$$
(23)

In particular, as long as

$$\begin{aligned} \zeta ^2< 4 \frac{q}{p} A^2, \end{aligned}$$
(24)

we have the purely imaginary solutions:

$$\begin{aligned} \Omega _\zeta= & {} \beta _\zeta = -i\frac{D}{2\pi \zeta } \pm \frac{\sqrt{p^2 \zeta ^2 - 4pq A^2}}{4\pi }\nonumber \\= & {} -i\frac{D}{2\pi \zeta } \pm i \frac{\sqrt{4pq A^2-p^2 \zeta ^2 }}{4\pi }. \end{aligned}$$
(25)

This leads to the Penrose mode

$$\begin{aligned} w_\zeta (x,k,t)= & {} \frac{ P(k+\frac{\zeta }{4\pi }) - P(k-\frac{\zeta }{4\pi }) }{ \zeta \left( k\pm \frac{i}{ 4\pi } \sqrt{2k_0^3A^2-\zeta ^2}\right) }\nonumber \\&\times \, e^{i\zeta x} e^{ \left( -D \pm \zeta \frac{\sqrt{4pq A^2-p^2 \zeta ^2 }}{2} \right) t}, \quad \zeta ^2< 8 k_0^4 A^2.\nonumber \\ \end{aligned}$$
(26)

This form represents an unstable mode as long as the exponential rate of growth in time is positive, i.e., as long as

$$\begin{aligned} -D + |\zeta | \frac{\sqrt{4pq A^2-p^2 \zeta ^2 }}{2} > 0. \end{aligned}$$

This is the case if and only if

$$\begin{aligned} \frac{4D^2}{\zeta ^2} + p^2\zeta ^2 < 4pq A^2. \end{aligned}$$

This in turn is at all possible if and only if the bi-quadratic equation in \(\zeta ^2\)

$$\begin{aligned} p^2\zeta ^4 - 4pq A^2 \zeta ^2 + 4D^2 = 0 \end{aligned}$$
(27)

has two distinct roots, i.e., positive discriminant

$$\begin{aligned} A^4 > \frac{D^2}{q^2}. \end{aligned}$$
(28)

Thus, if Eq. (28) holds, then for \(\zeta \) in the nonempty set \(\mathbb {P}=\{ \zeta \,\,|\,\, \frac{4D^2}{\zeta ^2} + p^2\zeta ^2 < 4pq A^2\}\), exactly, one of the Penrose modes of Eq. (26) is unstable. We can work out \(\mathbb {P}\) explicitly; indeed, if

$$\begin{aligned} \zeta _\mathrm{min}:= & {} \sqrt{2\frac{q}{p} \left( A^2 -\sqrt{A^4-\frac{D^2}{q^2}}\right) }, \\ \zeta _\mathrm{max}:= & {} \sqrt{2\frac{q}{p} \left( A^2 +\sqrt{A^4-\frac{D^2}{q^2}}\right) }, \end{aligned}$$

then

$$\begin{aligned} \mathbb {P} =(-\zeta _\mathrm{max},-\zeta _\mathrm{min}) \,\, \bigcup \,\, (\zeta _\mathrm{min},\zeta _\mathrm{max}). \end{aligned}$$

In particular, observe that if \(D=0,\) then

$$\begin{aligned} \zeta _\mathrm{min} = 0, \quad \zeta _\mathrm{max} = 2 A \sqrt{\frac{q}{p}} = 2 \sqrt{2} A k_0^2. \end{aligned}$$
(29)

4.2 Comparison with the modulation instability

It is instructive to compare our results with the classical Benjamin–Feir (modulation) instability (Mei et al. 2005). The appropriate setting would be the linear stability analysis of the plane wave solution

$$\begin{aligned} u_0(x,t) = A e^{i\left[ \xi _0\cdot x - (\frac{p \xi _0^2}{2}-qA^2)t\right] } \end{aligned}$$

of the NLS

$$\begin{aligned} i\partial _t u +\frac{p}{2} \Delta u +q |u|^2 u + \frac{i}{2} D u =\frac{D}{2} A e^{i\left[ \xi _0\cdot x - \left( \frac{p \xi _0^2}{2}-qA^2\right) t + \frac{\pi }{2}\right] } \end{aligned}$$
(30)

which is of the same type as Eq. (3). For brevity, we will treat in full detail the case \(D=0\), cf. Eq. (1). Moreover, without loss of generality (i.e., by choosing an appropriate frame of reference), \(\xi _0=0\).

Thus, we start from

$$\begin{aligned} u_0(t) = A_0 e^{iqA^2 t}, \end{aligned}$$

and consider small perturbations thereof, namely

$$\begin{aligned} u(x,t) = A_0 e^{iq A^2 t} (1+\delta (x,t)). \end{aligned}$$
(31)

Inserting the ansatz (31) in the NLS equation (1), we obtain

$$\begin{aligned}&u_0 \left( i\delta _t + \frac{p}{2}\Delta \delta +qA_0^2 (\delta + \overline{\delta }) +qA_0^2 (\delta + \overline{\delta }) \delta \right. \nonumber \\&\quad \left. +\, qA_0^2 |\delta |^2 (1+\delta ) \right) =0 \end{aligned}$$
(32)

for \(\delta \). To proceed, we divide by \(u_0\) and drop terms that are high order in \(\delta \). Thus, we arrive to the linearized equation

$$\begin{aligned} i\delta _t + \frac{p}{2}\Delta \delta +qA_0^2 (\delta + \overline{\delta }) =0; \end{aligned}$$
(33)

upon separating real and imaginary parts \(\delta = c + i d\), it becomes a system

$$\begin{aligned} c_t + \frac{p}{2} \Delta d=0,\quad d_t - \frac{p}{2} \Delta c - 2q A_0^2c=0, \end{aligned}$$
(34)

and finally, by cross differentiation, we can eliminate d to obtain

$$\begin{aligned} c_{tt}+ \frac{p^2}{4} \Delta ^2 c +p q A_0^2 \Delta c = 0. \end{aligned}$$
(35)

One readily checks that the plane wave

$$\begin{aligned} c(x,t) = {\text {Re}}\left( C e^{i\widetilde{\zeta }( x - 2\pi \widetilde{\Omega } t)} \right) = {\text {Re}}\left( C e^{i\widetilde{\zeta }( x - 2\pi {\text {Re}}\widetilde{\Omega } t)} e^{2\pi \widetilde{\zeta } {\text {Im}}\widetilde{\Omega } t} \right) \end{aligned}$$
(36)

is a solution of Eq. (35) for any \(C \in \mathbb {C}\) as long as

$$\begin{aligned} -4\pi ^2 \widetilde{\zeta }^2 \widetilde{\Omega }^2 + \frac{p^2 \widetilde{\zeta }^4}{4} -pq A^2 \widetilde{\zeta }^2 =0 \end{aligned}$$
(37)

This mirrors exactly Eq. (23).

A similar (but substantially lengthier) calculation is possible for \(D>0\) as well. In agreement with (Segur et al. 2005), Eq. (28) implies that for strong enough dissipation (equivalently small enough amplitude of the background waves), the modulation instability completely vanishes, i.e., no linearly unstable modes exist.

In conclusion, using Penrose stability analysis on a \(\delta \) spectrum, we recover exactly the well-known modulation instability. The main point, however, is that Penrose stability analysis can be applied to any background spectrum, something that is not possible on the level of the wavefunction u. We proceed to treat some realistic Fourier spectra of ocean waves in Sect. 5; however, first, we need to introduce some more concepts related to the emergence of sharply localized instabilities.

4.3 Emergence of Rogue Waves

In Sect. 4.1, we completely resolved the Penrose condition for a \(\delta \) spectrum. Now, we can exploit Eq. (21) to extract quantitative information possible about Rogue Wave phenomena emerging from a very narrow spectrum.

Lemma 4.1

(Localization bound in the absence of dissipation) Let \(P(k)=A^2\delta (k-0)\) be the background Fourier spectrum for the wave envelope u, \(k_0\) be the central wavenumber, and \(D=0.\) Then, no superposition of unstable Penrose modes can be spatially localized in a region smaller than

$$\begin{aligned} \frac{4}{\zeta _\mathrm{max}}= \frac{4}{\sqrt{8k_0^4 A^2}}. \end{aligned}$$

More specifically, for any weight \(G(\zeta )\), consider the superposition of unstable Penrose modes with weight \(G(\zeta )\), cf. Eq. (17). This will give rise to

$$\begin{aligned} |u(x,t)|\approx & {} \sqrt{A^2 + \epsilon n(x,t)},\nonumber \\ n(x,t)= & {} \int \limits _s g(x-s,t) \frac{\sin ( s \sqrt{8k_0^4 A^2} )}{s \sqrt{8k_0^4 A^2}} \mathrm{d}s \end{aligned}$$
(38)

where g is depends explicitly on G and the parameters of the problem.

Remark 4.2

In fact, this result is valid more generally, namely, when the solutions of the Penrose condition are of the form \((\zeta ,\alpha _0,\beta (\zeta )),\) where \(\zeta \in (-\zeta _\mathrm{max},\zeta _\mathrm{max}){\setminus }\{0\},\) and \(\zeta \beta (\zeta )> 0.\) This turns out to be the case for other spectra as well.

Proof

By virtue of Eq. (21)

$$\begin{aligned} n(x,t)= & {} {\text {Re}}\int \limits _{|\zeta |< 2 \sqrt{\frac{q}{p}} A} G(\zeta ) e^{i\zeta (x - 2\pi \Omega (\zeta ) t)} \mathrm{d}\zeta \nonumber \\= & {} {\text {Re}}\int \limits _{|\zeta |< 2 \sqrt{2} A k_0^2} G(\zeta ) e^{i\zeta x + 2\pi |\zeta | \frac{\sqrt{4pq A^2-p^2 \zeta ^2 }}{4\pi } t} \mathrm{d}\zeta \\= & {} {\text {Re}}\int \limits _{|\zeta |< 2 \sqrt{2} A k_0^2} G(\zeta ) e^{i\zeta x + |\zeta | \frac{\sqrt{\frac{g}{2} k_0 A^2-\frac{g}{16 k_0^3} \zeta ^2 }}{2} t} \mathrm{d}\zeta . \end{aligned}$$

Now, denoting \(\widetilde{G}_t(\zeta ):= G(\zeta ) e^{ |\zeta | \frac{\sqrt{\frac{g}{2} k_0 A^2-\frac{g}{16 k_0^3} \zeta ^2 }}{2} t},\) we get

$$\begin{aligned} n(x,t)= & {} {\text {Re}}\int \limits _{|\zeta |< 2 \sqrt{2k_0^3} A} \widetilde{G}_t(\zeta ) e^{i\zeta x} \mathrm{d}\zeta \nonumber \\= & {} {\text {Re}}\int \limits _{\zeta \in \mathbb {R}} e^{i\zeta x} \widetilde{G}_t(\zeta ) \chi _{[- 2 \sqrt{2} A k_0^2, 2 \sqrt{2} A k_0^2]}(\zeta ) \mathrm{d}\zeta \\= & {} 2\pi {\text {Re}}\int \limits _{\zeta \in \mathbb {R}} e^{2\pi i\frac{\zeta }{2\pi } x} \widetilde{G}_t\left( 2\pi \frac{\zeta }{2\pi }\right) \chi _{[- \frac{\sqrt{2} A k_0^2}{\pi }, \frac{\sqrt{2} Ak_0^2}{\pi }]}\left( \frac{\zeta }{2\pi }\right) \frac{\mathrm{d}\zeta }{2\pi } \nonumber \\= & {} 2\pi {\text {Re}}\mathcal {F}^{-1}_{\zeta \rightarrow x} \left[ \widetilde{G}_t(2\pi \zeta ) \chi _{[- \frac{\sqrt{2} A k_0^2}{\pi }, \frac{\sqrt{2} A k_0^2}{\pi }]}(\zeta ) \right] \\= & {} 2\frac{\sqrt{2} A k_0^2}{\pi }\mathcal {F}^{-1}_{\zeta \rightarrow x} \left[ \widetilde{G}_t\right] \left( \frac{x}{2\pi }\right) *\frac{\sin ( x 2\sqrt{2} A k_0^2 )}{x 2\sqrt{2} A k_0^2}. \end{aligned}$$

In other words, however, we choose \(G(\zeta ),\) n(x, t) will always be of the form:

$$\begin{aligned} n(x,t) = {\text {Re}}\int \limits _{s\in \mathbb {R}} g(x-s,t) \frac{\sin ( s 2\sqrt{2} A k_0^2 )}{s 2\sqrt{2} A k_0^2} \mathrm{d}s \end{aligned}$$

where of course \(g(x) = 2\frac{\sqrt{2} A k_0^2}{\pi }\mathcal {F}^{-1}_{\zeta \rightarrow x} [G(\zeta ) e^{2\pi |\zeta | \frac{\sqrt{\frac{g}{2} k_0 A^2-\frac{g}{16 k_0^3} \zeta ^2 }}{4\pi } t}] (\frac{x}{2\pi })\).

As is well known, \(\frac{\sin (xL)}{(xL)}\) has a main lobe supported over a region of size roughly \(\frac{4}{L}\). The proof is complete. \(\square \)

In Fig. 1, we see the profiles of the perturbation \(\epsilon n(x,t)\) for two different weights \(G(\zeta ),\) measured in timescales \(\tau .\) As was seen in Eq. (38), \(\epsilon n(x,t)\) should be compared with \(A^2\); in this case, \(A^2=28.09\). Once the values of the perturbation become comparable with \(A^2,\) we can no longer trust our linearization as describing accurately the dynamics. It is clear that the qualitative behaviour of the perturbations does not depend on \(G(\zeta ),\) but mainly on \(\zeta _\mathrm{max},\) which controls the lengthscale of persistent localization, and on \(\tau .\) Crucially, in Fig. 1, we observe that the perturbation of \(A^2\) increases from approximately \(1\%\) of the background wave to comparable to the background wave within approximately \(7 \tau .\)

Thus, we can use Lemma 4.1 to formulate a criterion for the appearance of localized unstable modes which does not depend on \(G(\zeta ).\)

Definition 4.3

(Rogue Wave criterion) We will say that a superposition of unstable Penrose modes can lead to a Rogue Wave if its effective support is small enough to be comparable to a single wavelength: \(\lambda _0=\frac{2\pi }{k_0}.\)

  1. (i)

    If we stay in the setting of Lemma 4.1 (i.e., no dissipation, very narrow spectrum), this can be formalized as

    $$\begin{aligned} \frac{2\pi }{k_0} \geqslant \frac{4}{2\sqrt{2} A k_0^2} \quad \Leftrightarrow \quad A \geqslant \frac{1}{k_0 \sqrt{ 2} \pi }. \end{aligned}$$
    (39)

    This leads to a scaling of \(A_0 \approx \frac{1}{k_0 \pi \sqrt{ 2}} \approx 0.2251 \cdot k_0^{-{1}} \) as the smallest amplitude for which instabilities localized within a single wavelength are expected to arise for \(\eta (x,t)\) with Fourier spectrum \(P(k)=A^2 \delta (k-k_0)\).

  2. (ii)

    More generally, if we have unstable Penrose modes with \(\zeta \in \mathbb {P}=(-\zeta _\mathrm{max},\zeta _\mathrm{max}){\setminus }\{0\},\) \(\alpha \approx \alpha _0,\) and \(\zeta \beta (\zeta )>0\) for all \(\zeta \in \mathbb {P},\) then the criterion becomes

    $$\begin{aligned} \zeta _\mathrm{max} > \frac{2k_0}{\pi }, \end{aligned}$$

    irrespectively of P(k).

In particular, the existence of linearly unstable modes leads to Rogue Waves only if there is a sufficiently large collection of unstable modes, which, by superposition, can create instabilities localized over regions small enough to be comparable to a single wavelength.

Since the wavelengths \(\lambda _0\) of ocean waves are roughly in the range 5–200 m, the corresponding wavenumbers \(k_0\) are roughly in the range 1–0.01. Equation (39) means that longer waves need to have larger amplitudes to trigger localized enough instabilities to be considered Rogue Waves. Moreover, by virtue of Eqs. (22) and (25), the timescales for the emergence of these instabilities are given by

$$\begin{aligned} \tau = \frac{1}{\max \limits _{\zeta \in \mathbb {P}} 2\pi \zeta \beta _\zeta } = \frac{2}{\sqrt{g} A^2 k_0^{\frac{5}{2}}}. \end{aligned}$$

Given that the period \(T_0\) for a wave of wavenumber \(k_0\) is given by

$$\begin{aligned} T_0 = \frac{2\pi }{\sqrt{g k_0}}, \end{aligned}$$

the timescale for the emergence of the instability, measured in wave periods, is

$$\begin{aligned} \frac{\tau }{T_0} = \frac{\frac{2}{\sqrt{g} A_0^2 k_0^{\frac{5}{2}}}}{\frac{2\pi }{\sqrt{g k_0}}} = \frac{ 1}{\pi A^2 k_0^2}. \end{aligned}$$
(40)

Now, if we combine this with Eq. (39) for amplitudes close to the critical value \(A_0\), it follows that the time (measured in wave periods) it takes for an instability to arise for the critical amplitude \(A_0\) does not depend on \(k_0\), since

$$\begin{aligned} A_0\approx \frac{1}{k_0 \pi \sqrt{2}}, \quad \frac{\tau }{T_0} \approx \frac{ 1}{\pi A_0^2 k_0^2} \quad \Rightarrow \quad \frac{\tau }{T_0} \approx 2\pi . \end{aligned}$$
(41)

Thus, for any \(k_0,\) the timescale at which localized instabilities emerge should be measured in wave periods \(T_0\). Furthermore, within approximately \(7\tau = 14 \pi T_0\) wave periods, a \(1\%\) perturbation becomes comparable to the background, cf. Fig. 1. This is in close agreement with the numerical study of emergence of Rogue Waves in Cousins and Sapsis (2016). It is also broadly in agreement with Birkholz et al. (2015).

An observation is in order with respect to moving towards a more realistic setting than that of Lemma 4.1: if the dissipation term \(\frac{i}{2}Du\) in Eq. (3) does describe reasonably well the effective dissipation, then values of D as small as \(O(10^{-3})\) can have an O(1) impact on the formation of Rogue Waves. Indeed, Eq. (28) means that, in the presence of dissipation, there are no unstable modes at all unless

$$\begin{aligned} A^2 > \frac{D^2}{\frac{g}{4} k_0^3}. \end{aligned}$$

More generally, as long as the two sides of this inequality are comparable, the effect of dissipation will be noticeable. For \(k_0\approx 10^{-2}\), \(A_0\approx 0.2251 k_0;\) this means that D as small as \(D\approx 0.00237\) would have an O(1) effect in our analysis, and thus require noticeably larger amplitude A before sufficiently localized instabilities could be observed.

The results of this section, and in particular, the criterion of Eq. (39) can only be considered indicative: for example, if \(A= \frac{0.95}{k_0 \pi \sqrt{2}}\) our Rogue Wave criterion is not satisfied, but of course, we would still get an unstable mode localized in a region very nearly as small as a single wavelength. The main point here is that the scalings we recover look reasonable in realistic contexts.

Furthermore, it is desirable to apply our analysis to more general background Fourier spectra P(k) and not only \(\delta \) spectra. This requires the numerical resolution of the Penrose condition. A numerical scheme for this is developed and implemented in the next section.

5 Investigation of the Penrose condition for general spectra and applications

As was repeatedly emphasized, the advantage of our approach is that it can be applied to problems with continuous spectra. Before we proceed to the presentation of concrete results, it is worth discussing the modelling side of this investigation. We work in a setting comparable to (Cousins and Sapsis 2016); namely, we work with the deterministic problem of Eq. (3), using a given Fourier spectrum P(k) as a proxy for a quasi-stationary, quasi-homogeneous u(x, t). In Cousins and Sapsis (2016), the reconstruction of such a wavefunction was carried out numerically. Here, we do not need to generate a u(x, t) that would be consistent with P(k),  because we only need its Wigner transform. By virtue of the quasi-homogeneity and quasi-stationarity of u(x, t)

$$\begin{aligned} W[u(t)](x,k)= & {} \int \limits _y e^{-2\pi i k y} u(x+\frac{y}{2},t) \overline{u}(x-\frac{y}{2},t) \mathrm{d}y\\\approx & {} P(k) \end{aligned}$$

for any x, t. This is a modelling step which allows the treatment of wavefunctions that are empirically observed to be approximately homogeneous and stationary in terms only of partial (or “coarse-grained”) spectral information.

As a physical case study, in Sect. 5.2, we will study numerically wave trains consistent with the Ochi–Hubble spectrum with central wavenumber \(k_0,\) shape parameter \(\sigma \), and significant wave height \(H_s\) (Ochi and Hubble 1977). Physical spectra for ocean waves are often resolved over frequencies

$$\begin{aligned} S(\omega ) = \frac{(4\sigma +1)^\sigma }{4^{\sigma +1} \Gamma (\sigma )} \frac{(H_s)^2}{\omega _0} \left( \frac{\omega _0}{\omega } \right) ^{4\sigma +1} e^{-\frac{4\sigma +1}{4} \left( \frac{\omega _0}{\omega }\right) ^4}, \end{aligned}$$
(42)

where of course, \(\omega _0\) is the central frequency. To express this in terms of wavenumbers, we will use the deep water dispersion relation \(\omega (k) = \sqrt{g k}\) and conservation of energy (Ochi 1998):

$$\begin{aligned} P(k)= & {} \frac{(4\sigma +1)^\sigma }{4^{\sigma +1} \Gamma (\sigma )} \frac{(H_s)^2}{\sqrt{g k_0}} \left( \frac{\sqrt{g k_0}}{\sqrt{g k}} \right) ^{4\sigma +1} e^{-\frac{4\sigma +1}{4} \left( \frac{\sqrt{g k_0}}{\sqrt{g k}}\right) ^4} \nonumber \\ \frac{\partial \omega }{\partial k}= & {} \frac{H_s^2}{k_0} \frac{(\sigma +\frac{1}{4})^\sigma }{8\Gamma (\sigma )} \left( \frac{k_0}{k}\right) ^{2\sigma +1} e^{-\frac{4\sigma +1}{4} \frac{ k_0^2}{ k^2}}. \end{aligned}$$
(43)

The shape parameter \(\sigma \) affects how broadband the spectrum is (larger \(\sigma \) leads to more peaked spectrum, smaller \(\sigma \) leads to less pronounced peaks).

Now, using P(k) of this form, a Penrose condition can be formulated. In Sect. 5.1, a numerical method for the numerical resolution of the Penrose condition is presented, and applied to the Ochi–Hubble spectrum in Sect. 5.2.

A related question is to formulate a robust and computable criterion for whether the Penrose condition has a solution at all. This is formulated in Sect. 5.3 for the case without dissipation, and is based on ideas from Bardos and Besse (2013); Penrose (1960). Some useful ramifications are explored in a case study for a Gaussian spectrum.

Finally, let us recall some basic facts about extracting information for waves from a continuous spectrum. In the case of a plane wave \(u(x,t) = Ae^{i (k_0\cdot x - \omega _0 \cdot t)}\), the Fourier spectrum is \(A^2 \delta (k-k_0)\) and the amplitude is plainly A. However, when we have a more realistic wavefield, which includes waves of different wave amplitudes, there are different notions of amplitude that can be associated with the wavefield. The most important one is the significant wave height, \(H_s,\) which is related with \(m_0 = \int P(k)dk\) through \(H_s=4\sqrt{m_0}\) (Ochi 1998). Similarly, an estimate of the slope associated with a given Fourier spectrum with central wavenumber \(k_0\) is Huang et al. (1989)

$$\begin{aligned} \beta _p = \frac{\sqrt{m_0}}{\lambda _0} = \frac{H_s k_0}{8\pi }. \end{aligned}$$
(44)

Slopes larger than 0.0505 are considered unphysical, and a common value is 0.01 (Huang et al. 1989); this will provide an additional way to check the physical plausibility of our results.

5.1 A numerical scheme for the investigation of the Penrose condition

We describe a practical scheme for the numerical investigation of the Penrose condition (6) given a background Fourier spectrum P(k).

We assume that the given spectrum is piecewise constant

$$\begin{aligned} P(k) = \sum \limits _{j=1}^N P_j \chi _{[y_j,y_{j+1})}(k). \end{aligned}$$
(45)

Of course, any spectrum can be well approximated by one of the form (45) for N large enough. Indeed, measurements are noisy, and in many cases, the error in this approximation by a histogram would be within measurement error anyway.

Now, we can carry out the integrals appearing in the Penrose condition explicitly. First of all, we write separately the imaginary and real parts of the Penrose condition:

(46)

and

(47)

respectively. Now, the left hand side of Eq. (46) becomes

(48)

At this point, denote for brevity

$$\begin{aligned} \widetilde{\beta }:=\beta +\frac{D}{2\pi \zeta }; \end{aligned}$$
(49)

then we have

$$\begin{aligned} \mathcal {I}_{im}= & {} \frac{1}{p\widetilde{\beta }} \sum \limits _{j=1}^N P_j \left[ \arctan \left( \frac{\widetilde{\beta }(py_{j+1}-py_j)}{\widetilde{\beta }^2 + (py_{j+1}+\frac{p\zeta }{4\pi }-\alpha )(py_{j}+\frac{p\zeta }{4\pi }-\alpha )} \right) \right. \nonumber \\&\left. - \arctan \left( \frac{\widetilde{\beta }(py_{j+1}-py_j)}{\beta ^2 + (py_{j+1}-\frac{p\zeta }{4\pi }-\alpha )(py_{j}-\frac{p\zeta }{4\pi }-\alpha )} \right) \right] . \end{aligned}$$
(50)

Similarly, if we work on the left hand side of Eq. (47), we have

(51)

Now, we can reformulate the Penrose condition as

and in terms of the fitness function \(\mathbb {F}_P\) as

$$\begin{aligned} \mathbb {F}_{P}:= & {} \left| \frac{1}{p\widetilde{\beta }} \sum \limits _{j=1}^N P_j \left[ \arctan \left( \frac{\widetilde{\beta }(py_{j+1}-py_j)}{\widetilde{\beta }^2 + (py_{j+1}+\frac{p\zeta }{4\pi }-\alpha )(py_{j}+\frac{p\zeta }{4\pi }-\alpha )} \right) \right. \right. \nonumber \\&\left. \left. - \arctan \left( \frac{\widetilde{\beta }(py_{j+1}-py_j)}{\widetilde{\beta }^2 + (py_{j+1}-\frac{p\zeta }{4\pi }-\alpha )(py_{j}-\frac{p\zeta }{4\pi }-\alpha )}\right) \right] \right| \nonumber \\&+\, \left| \sum \limits _{j=1}^N P_j \log \left( \frac{ \left[ \widetilde{\beta }^2+({py_{j+1}+\frac{p\zeta }{4\pi }-\alpha })^2 \right] \left[ \widetilde{\beta }^2+({py_{j}-\frac{p\zeta }{4\pi }-\alpha })^2 \right] }{ \left[ \widetilde{\beta }^2+({py_{j}+\frac{p\zeta }{4\pi }-\alpha })^2 \right] \left[ \widetilde{\beta }^2+({py_{j+1}-\frac{p\zeta }{4\pi }-\alpha })^2 \right] } \right) -\frac{4\pi p\zeta }{q} \right| =0. \end{aligned}$$
(52)

In this form, it is straightforward to look for iso-surfaces of the fitness function being close to zero

$$\begin{aligned} \mathbb {F}_{P}(\zeta ,\alpha ,\beta ) = \varepsilon \end{aligned}$$
(53)

for various small values of \(\varepsilon \). If there are exact solutions of the Penrose condition, they will be outlined by the iso-surfaces. We can use this scheme to approximate the solution set \(\mathbb {P}\) of the Penrose condition for any background spectrum. It must be noted that an analogous scheme based on the approximation of a general spectrum by a sum of \(\delta \) functions, i.e., working with \(P(k) = \sum \nolimits _{j=1}^N P_j \delta (k - k_j)\) was presented in Ribal et al. (2013).

Table 1 Summary of the case studies of Section 5.2
Full size table

5.2 Case study for the Ochi–Hubble spectrum

Now, we can use Eq. (53) as a practical way to look for solutions of the Penrose condition in \((\zeta ,\alpha ,\beta )\) space for general spectra P(k). In particular, we can investigate the formation of localized instabilities out of a background wave train consistent with an Ochi–Hubble spectrum. We investigate the case with central wavenumber \(k_0=0.24\,\mathrm{m}^{-1}\) (corresponding to wavelengths \(\lambda _0=26.18\,\mathrm{m}\)) and negligible dissipation, \(D=10^{-8}\). By virtue of Sect. 4, we can resolve completely the Penrose condition and the localized unstable Penrose modes for a \(\delta \) spectrum. Therefore, first, we compare the \(\delta \)-spectrum results with a narrow Ochi–Hubble spectrum with \(H_s=5\,\mathrm{m}\), \(\sigma =76.5,\) and check that the observed \(\zeta _\mathrm{max}\approx 0.165\), cf. Table 1. For a broader Ochi–Hubble spectrum, \(\sigma =66.5\), we observe that for the same \(H_s=5\,\mathrm{m}\), poorer localization of the unstable mode is found, as evidenced by \(\zeta _\mathrm{max}\approx 0.13\). The iso-surfaces of the fitness function \(\mathbb {F}_P\), which serve as an approximate solution of the Penrose condition, are presented in Figs. 2 and 3. The results are summarised in Table 1.

The first qualitative finding is that, for the narrow Ochi–Hubble spectrum, we find a single branch of solutions of the Penrose condition, effectively of the form \((\zeta ,\alpha _0,\pm \beta _\zeta )\), for \(\zeta = (-\zeta _\mathrm{max},\zeta _\mathrm{max}) {\setminus } \{ 0 \}\) (similar to the \(\delta \) spectrum). Thus, the analysis of Lemma 4.1 applies, and since \(\zeta _\mathrm{max}\approx 0.165>\frac{2k_0}{\pi }\approx 0.1528\), Rogue Waves are expected. Using Eq. (44), we see that this regime corresponds to a reference slope \(\beta _p\approx 0.0477\), i.e., a large but physically possible sea.

Fig. 2
figure 2

Top left a narrow Ochi–Hubble Fourier spectrum for \(\eta ,\) Eq. (43), with \(H_s=5m,\) \(k_0=0.24m^{-1},\) \(\sigma =76.5,\) and its piecewise constant approximation, cf. Eq. (45), with 79 intervals. Top right Projection on the \(\alpha ,\beta \) plane of the iso-surface \({\mathbb {F}_{P}(\zeta ,\alpha ,\beta )} = \frac{1}{1,322,314} \max \nolimits _{(\zeta ',\alpha ',\beta ')\in \mathbb {B}} \mathbb {F}_{P}(\zeta ',\alpha ',\beta '),\) where \(\mathbb {B}=[0.021,0.2]_\zeta \times [-1.605,-1.597]_\alpha \times [0.000015,0.037]_\beta \) is the parallelepiped spanned by the axes of the plots. The number of points used is \(453\times 451\times 455\). We work for \(\zeta >0\), since the situation is essentially symmetric for \(\zeta <0\). Bottom The same surface projected on the \(\zeta ,\alpha \) and \(\zeta ,\beta \) planes

Full size image
Fig. 3
figure 3

Same as Fig. 2, but \(\sigma =66.5\) and the iso-surface plotted is defined by \({\mathbb {F}_{P}(\zeta ,\alpha ,\beta )} = \frac{1}{1,186,513} \max \limits _{(\zeta ',\alpha ',\beta ')\in \mathbb {B}} \mathbb {F}_{P}(\zeta ',\alpha ',\beta ').\) Apart from the main line, several small lines of isolated solutions are observed

Full size image

If we set \(\sigma =66.5\), we have a less peaked spectrum. While the approximate solutions of the Penrose condition still contain a recognizable main branch, isolated solutions account for a larger percentage of the \(\zeta \) bandwidth. In addition, we find poorer localization of instabilities, in terms of smaller \(\zeta _\mathrm{max}\approx 0.13\). Technically, in this case, we do not have Rogue Waves (understood as instabilities localized within a single wavelength), although just barely.

If we were to further decrease \(\sigma \) below 66.5,  keeping \(H_s\) fixed, the set of solutions of the Penrose condition becomes contained in a strip \(|\zeta |\ll 0.13\) and more irregular (breaks up to many disconnected pieces). To reach \(\zeta _\mathrm{max}\approx 0.15\) for small \(\sigma ,\) larger \(H_s\) is required. Eventually, this requirement becomes unphysical, in terms of the slope constraint \(\frac{H_s k_0}{8\pi } \leqslant 0.0505.\)

Moreover, for \(\sigma \) small enough (and keeping \(H_s=5m\) fixed), it seems that there will be no solutions whatsoever of the Penrose condition, i.e., no unstable modes. Thus, we find a trade-off between \(H_s\) (or equivalently \(m_0\)) and the effective support of the spectrum. Note that this outlines a trade-off between spectral spread and \(H_s\) reminiscent of the Benjamin–Feir index (Serio et al. 2005), and is consistent with the findings of Gibbs and Taylor (2005). Using the scheme of Sect. 5.1, we can investigate this trade-off taking fully into account the shape of a given spectrum.

5.3 On the solvability of the Penrose condition

Let \(P(k)=A^2 \sigma S(\sigma (k-k_0))\) be a given background spectrum, where S(k) is a probability density function, \(S(k)\geqslant 0,\) \(\int \nolimits _k S(k)\mathrm{d}k=1,\) which is smooth enough and with fast enough decay (e.g., a Schwarz test function, \(S\in \mathcal {S}(\mathbb {R})\)). The parameter \(A^2>0\) controls the amplitude of the background waves, while \(\sigma > 0\) controls how broad the spectrum is (larger \(\sigma \) leads to more sharply localized spectrum). Without loss of generality, we will assume \(k_0=0\) in the remainder of this section.

Now, if we neglect dissipation, \(D=0,\) the Penrose condition becomes

$$\begin{aligned}&\frac{ 2\pi }{ q} = \int \limits _{k\in \mathbb {R}} \frac{ P(k-\frac{\zeta }{4\pi }) - P(k+\frac{\zeta }{4\pi })}{ \zeta (pk-\Omega )} \mathrm{d}k \nonumber \\&\quad \Leftrightarrow \frac{2\pi p}{A^2q\sigma ^2}= \int \limits _{k\in \mathbb {R}} { \frac{ S(k-\sigma \frac{\zeta }{4\pi }) - S(k+\sigma \frac{\zeta }{4\pi }) }{\sigma \zeta }}\frac{1}{ k-\sigma \frac{\Omega }{p}} \mathrm{d}k.\nonumber \\ \end{aligned}$$
(54)

Denoting

$$\begin{aligned}&F_{\zeta ,\sigma }(k):= \frac{ S(k-\frac{\sigma \zeta }{4\pi })-S(k+\frac{\sigma \zeta }{4\pi })}{ \sigma \zeta }, \\&\quad \mathbb {F}_{\zeta ,\sigma }(\Omega ) = p.v. \int \limits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k-\frac{\sigma \Omega }{p}}\mathrm{d}k, \end{aligned}$$

the Penrose condition now can be reformulated as

$$\begin{aligned} \text{ given } \sigma >0, \quad \zeta \in \mathbb {R }, \quad \text{ is } \text{ there } \Omega \text{ such } \text{ that } \mathbb { F}_{\zeta ,\sigma }(\Omega ) {=} \frac{2\pi p}{A^2 q \sigma ^2 } \text{? }\nonumber \\ \end{aligned}$$
(55)

As before, \(\zeta {\text {Im}}\Omega >0\) is required for instability.

Remark 5.1

The divided difference \(F_{\zeta ,\sigma }(k)\) has the properties \(F_{\zeta ,\sigma }(k)=F_{-\zeta ,\sigma }(k)\) and \(\lim \nolimits _{\zeta \rightarrow 0}F_{\zeta ,\sigma }(k)=-\frac{1}{8\pi }S'(k).\)

The merit of the formulation (55) is that complex-analytic function machinery can be readily adapted from (Bardos and Besse 2013; Penrose 1960) to yield the following

Lemma 5.2

(Conditions for solvability of the Penrose condition) Given \(\zeta ,\sigma \) there is a solution \(\Omega \) of Eq. (55) in the upper complex half plane if and only if the closed curve

$$\begin{aligned} \left\{ z^+(t)= p.v. \int \limits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k-t}dk + i \pi \frac{\sigma }{|p|} F_{\zeta ,\sigma }(t), \quad t\in \mathbb {R} \right\} \end{aligned}$$

on the complex plane encloses the real point \(\frac{2\pi p}{A^2 q \sigma ^2}\).

Similarly, there is a solution \(\Omega \) of Eq. (55) in the lower complex half plane if and only if the closed curve

$$\begin{aligned} \left\{ z^-(t)= p.v. \int \limits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k-t}\mathrm{d}k - i \pi \frac{\sigma }{|p|} F_{\zeta ,\sigma }(t), \quad t\in \mathbb {R} \right\} \end{aligned}$$

on the complex plane encloses the real point \(\frac{2\pi p}{A^2 q \sigma ^2}\).

Proof

First of all, observe that \(\mathbb {F}_{\zeta ,\sigma }\) is a bounded analytic function in each of the upper and lower half planes, vanishing at infinity (Bardos and Besse 2013). Moreover, the boundary values are well defined on the real axis, although they exhibit a jump across it. Indeed, for \(x\in \mathbb {R}\)

$$\begin{aligned}&\lim \limits _{\varepsilon \rightarrow 0^+} \mathbb {F}_{\zeta ,\sigma }(x\pm i \varepsilon ) = \lim \limits _{\varepsilon \rightarrow 0^+} p.v. \int \limits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k) }{k-\frac{\sigma }{p} (x\pm i \varepsilon )}\mathrm{d}k\\&\quad = \lim \limits _{\varepsilon \rightarrow 0^+} p.v. \int \limits _{k\in \mathbb {R}} F_{\zeta ,\sigma }(k) \frac{ k + \frac{\sigma }{p} x \mp i \frac{\sigma }{p} \varepsilon }{(k+\frac{\sigma }{p}x)^2 +\frac{\sigma ^2}{p^2}\varepsilon ^2}\mathrm{d}k\\&\quad =\mathbb {F}_{\zeta ,\sigma }(\frac{\sigma }{p}x) \pm i \lim \limits _{\varepsilon \rightarrow 0^+} \int \limits _{k\in \mathbb {R}} F_{\zeta ,\sigma }(k) \frac{ \frac{\sigma }{|p|} \varepsilon }{(k+i \frac{\sigma }{p}x)^2 +\frac{\sigma ^2}{p^2}\varepsilon ^2}\mathrm{d}k, \end{aligned}$$

where in the last step, we passed into the limit for the real part and took into account the fact that \(p<0.\) We complete the computation by observing that, for any \(f\in \mathcal {S}(\mathbb {R}),\) \(X\in \mathbb {R},\)

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0^+} \int \limits _{-\infty }^{+\infty } f(\xi -X) \frac{\varepsilon }{\xi ^2+\varepsilon ^2} \mathrm{d}\xi = \pi f(X). \end{aligned}$$

Thus, we recover a kind of Sokhotsky–Plemelj formula (King 2009, Section 3.7) for our problem, namely

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0^+} \mathbb {F}_{\zeta ,\sigma } (x\pm i \varepsilon ) = \mathbb {F}_{\zeta ,\sigma } (x) \pm i \pi \frac{\sigma }{|p|} F_{\zeta ,\sigma }(x). \end{aligned}$$

In particular, the limit values at the real axis, either from above or from below, are bounded and continuous.

Without loss of generality, we will carry out the rest of the proof for \(\Omega \) in the upper half plane only. Indeed, by virtue of the argument principle, a value \(Z_0\) is attained \(Z_0=\mathbb {F}_{\zeta ,\sigma }(\Omega )\) for some \({\text {Im}}\Omega >0\) if and only if the curve \(\mathbb {F}_{\zeta ,\sigma }(\mathbb {R}+i 0)\) has positive winding number around \(Z_0.\)

While the structure of the nonlinearity is different here, the overall proof is in the spirit of Bardos and Besse (2013); Penrose (1960). The proof is complete. \(\square \)

Lemma 5.3

(Radial unimodal spectra) Let S be even, \(S(k)=S(-k)\), and decreasing away from zero \(S'(k)<0\) \(\forall k>0\). Then, there exist unstable Penrose modes for the spectrum S if and only if

$$\begin{aligned} p.v. \int \limits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k}\mathrm{d}k > \frac{2\pi p}{A^2 q\sigma ^2} \end{aligned}$$
(56)

Proof

We will need to break the proof up in several steps:

Claim

\(F_{\zeta ,\sigma }(k)=0\) if and only if \(k=0.\)

Proof of the claim:

First of all,

$$\begin{aligned} F_{\zeta ,\sigma }(0) = \frac{S(-\frac{\sigma \zeta }{4\pi })-S(\frac{\sigma \zeta }{4\pi })}{\sigma \zeta }=0. \end{aligned}$$

Moreover, observe that our assumptions imply that the restriction \(S:[0,\infty )\rightarrow \mathbb {R}\) is one-to-one. Now, we can compute

$$\begin{aligned} F_{\zeta ,\sigma }(k)= & {} 0 \quad \Rightarrow \quad S\left( k-\frac{\sigma \zeta }{4\pi }\right) =S\left( k+\frac{\sigma \zeta }{4\pi }\right) \\\Rightarrow & {} \quad k-\frac{\sigma \zeta }{4\pi } = \pm \left( k+\frac{\sigma \zeta }{4\pi }\right) \quad \Rightarrow \quad \left\{ \begin{array}{l} \zeta =0, \text{ or }\\ k=0. \end{array} \right. \end{aligned}$$

Since \(\zeta =0\) is unphysical and we exclude it, the claim follows.

Claim

Each of the curves \(z^\pm (t)\) tends to 0 or \(t\rightarrow \pm \infty .\)

Proof of the claim

$$\begin{aligned}&\lim \limits _{t\rightarrow \infty } z^+(t)= \lim \limits _{t\rightarrow \infty } \left( p.v. \int \limits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k-t}\mathrm{d}k + i \pi \frac{\sigma }{|p|} F_{\zeta ,\sigma }(t)\right) \\&\quad = \lim \limits _{t\rightarrow \infty } p.v. \int \limits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k-t}\mathrm{d}k =0 \end{aligned}$$

by the standard results on the Hilbert transform (King 2009). In fact, since \(F_{\zeta ,\sigma }(k)\) has zero mean, the Hilbert transform \(p.v. \int \nolimits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k-t}\mathrm{d}k\) inherits from \(F_{\zeta ,\sigma }(k)\) the superpolynomial decay in t (King 2009, Section 4.7). The other cases follow similarly.

The proof of the claim is complete.

To complete the proof, we need to extract the geometry encoded in these claims. The only points where the curve \(z^+(t)\) intersects the real axis are \(t=0,\) where \(z^+(t)=p.v. \int \nolimits _{k\in \mathbb {R}} \frac{F_{\zeta ,\sigma }(k)}{k-t}\mathrm{d}k,\) and in the limit \(t\rightarrow \pm \infty ,\) where \(z^+(+\infty )=z^+(-\infty )=0\). Thus, the only way the real number \(\frac{2\pi p}{A^2 q \sigma ^2}\) is enclosed in the curve, is if it lies between 0 and \(z^+(0).\) Moreover, this does not depend on whether \(\Omega \) belongs in the upper or lower half plane. Cf. Fig. 4.

The proof is complete. \(\square \)

Fig. 4
figure 4

Vizualization of Lemma 5.2 for a Gaussian envelope spectrum, \(P(k)=A^2 \frac{\sigma }{\sqrt{\pi }} e^{-\sigma ^2 k^2}.\) The black point in the third plot is the real number \(\frac{2\pi p}{A^2 q \sigma ^2}\). Observe that this curve looks like a reflection along the imaginary axis of the corresponding curve for the defocusing Vlasov–Poisson equation (Penrose 1960). This is due to the focusing character of the problem here, leading to (large enough) unimodal profiles being in general unstable

Full size image

By substituting \(S(k)=\frac{1}{\sqrt{\pi }} e^{-k^2}\) in Lemma 5.3, we obtain the following

Corollary 5.4

(Gaussian spectra) There are unstable modes for the Gaussian spectrum \(P(k){=}A^2\frac{\sigma }{\sqrt{\pi }} e^{-\sigma ^2k^2}\) if and only if

$$\begin{aligned} \int \limits _{k=0}^\infty \frac{e^{-(k-\frac{\sigma \zeta }{4\pi })^2}-e^{-(k+\frac{\sigma \zeta }{4\pi })^2}}{\sigma \zeta k} \mathrm{d}k > \frac{\pi ^{\frac{3}{2}} p}{A^2 q \sigma ^2} \end{aligned}$$

Fixing all parameters and taking A large enough, one quickly sees that eventually (i.e., for A large enough), there will be unstable Penrose modes irrespective of the precise values of \(\sigma ,\zeta .\) Similarly, fixing all parameters and taking \(\zeta \) large enough, one sees that the inequality eventually cannot hold. In other words, the unstable Penrose numbers have to be contained in a bounded interval.

6 Conclusions

In this paper, we construct a methodology to compute Benjamin–Feir-type linearly unstable modes growing out of any background Fourier spectrum. These are spatially periodic modes which grow exponentially in time, and their parameters are obtained by resolving the Penrose condition, Eq. (6). Localized unstable modes can arise by superposition of the spatially periodic ones, cf. Lemma 4.1. It turns out that the \(\zeta \) bandwidth of different spatially periodic modes controls the sharpest possible localization. This computation leads naturally to the description of Rogue Waves as unstable modes, localized in a region not larger than a single wavelength, Definition 4.3. In other words, appropriate superposition of unstable Penrose modes, when they exist, hints towards the existence of breather-like solutions emerging out of homogeneous backgrounds with spectrum P(k). Thus, linear instability and the emergence of Rogue Waves are clearly distinguished; the former is a necessary but not sufficient condition for the latter.

This is illustrated in a simple case, where analytic calculations are possible (narrowband limit). In more complicated settings, we can use the numerical scheme of Eq. (53) to resolve the Penrose condition. It is found that for narrow spectra, generation of Rogue Waves seems to be within the physically realistic region of parameters. As the spectrum becomes broader (keeping \(H_s\) fixed), the localization of unstable modes deteriorates, and beyond a certain threshold, it is completely destroyed. This is natural in the sense that breather-like solutions can emerge from “any narrowband enough” spectrum P(k);  however, once the background spectrum becomes broadband enough, these breathers disappear. In particular, we find a “stabilization via spectral broadening” trend, which will be more precisely quantified with further work. It is worth noting that similar trends have been identified in Gibbs and Taylor (2005) through detailed fine-scale computations using nonlinear numerical simulations.

It must also be mentioned that the localized instabilities we find seem to grow over a few wave periods \(T_0\) uniformly in \(k_0\); this is both physically reasonable and in agreement with other studies in the topic Birkholz et al. (2015); Cousins and Sapsis (2016). It is desirable to understand better the nonlinear evolution of these localized instabilities, which seem to correspond to breathers emerging from an almost periodic background.

Finally, let us comment on the numerical scheme of Sect. 5.1 for the resolution of the Penrose condition. It amounts essentially to solving a nonlinear system of equations with a spanning method. While it does give reasonable approximations for the loci of possible solutions, it is not completely satisfactory as a stand-alone solver; in particular, it cannot reliably determine whether solutions exist (as opposed to near solutions). It is complemented by a semi-analytic method for determining the existence of solutions, elaborated in Sect. 5.3. This latter method uses adapted Sokhotsky–Plemelj formulas to come up with a geometric criterion for the solvability of the Penrose condition for given \(\zeta ,\) and involves only quadrature errors in the computation of certain integrals. Under additional assumptions on the shape of the spectrum, it can yield compact criteria, shedding some light in the tradeoffs between power \(m_0\) and the effective width of the spectrum. In particular, all symmetric spectra decreasing away from the peak wavenumber have unstable Penrose modes for high enough power, cf. Lemma 5.3.