Introduction

Zadeh [1] introduced the uncertainty theory which is very useful to cope with imprecise data in many real-life problems. There are certain situations in real life where we tend to find the maximum or minimum, optimum solutions for existing problems. However, in most of the cases, the data to be handled are uncertain, imprecise and inconsistence, the obtained results are not consistent, and, therefore, uncertainty theory came into existence. During the last few decades, the topic of fuzzy optimization has achieved substantial popularity among researchers because of its widespread applications in different branches of network flow problem [2], production [3], shortest path problem [4,5,6,7,8], pick up delivery problem [9], travel salesman problem [10], traffic assignment problem [11].

Transportation problems play a significant role in many real-life applications. This problem aims to maintain the supply from source to destination. Traditionally, it has been generally assumed that transversal costs of supply/demand are expressed in terms of crisp numbers. However, these values are generally imprecise or vague. Consequently, various attempts have been made by researchers for different types of transportation problems in the fuzzy environment. In 1984, Chanas et al. [12] suggested fuzzy transportation problems. Since then many authors test the transportation problems in various fuzzy environments such as integer fuzzy [13], multi-objective [14, 15], type-2 fuzzy [16,17,18,19], interval-valued fuzzy fractional [20], interval integer fuzzy [21], interval-valued intuitionistic fuzzy [22]. Moreover, we noticed that there are numerous methods to solve this transportation problem such as extension principle [23], ranking function [24], modified Vogel’s approximation method [25], Simplex type algorithm [26], fuzzy linear programming [27], fuzzy Russell’s method [28], modified best candidate method [29], zero point and zero suffix methods [30] and so on. However, the fuzzy set takes only a membership function. Here, the degree of the non-membership function is just a compliment of the degree of the membership function. There may be a situation where the sum of the membership function and non-membership function is greater than one. Thus, Yager [31, 32] recently introduced another class of non-standard fuzzy subset, i.e., Pythagorean fuzzy set (PFS), where the square sum of the membership and the non-membership degrees sum is equal to or less than one. There are various methods in the field of PFS to solve multi-criteria decision-making problems such as: extension of TOPSIS [33], Similarity measure [34], Weighted geometric operator [35], alternative queuing method [36], analytic hierarchy process (AHP) [37], Hamacher operation [38], Einstein operations [39, 40], Maclaurin symmetric mean operator [41, 42], extended TODIM methods [43], Bonferroni mean [44], correlation coefficients [45], confidence level [46], improved score function [47, 48], and so on; see also [49,50,51,52,53].We have tabulated all those important influences of different researchers who have introduced these real-life applications under the Pythagorean fuzzy environment in Table 1.

Table 1 Important influences of different researchers: real-life applications of operators for decision making
Full size table

Table 2 charts some significant influences towards transportation problem (TP). Based on the previous discussions on TP and currently available data, there are no existing methods which are available for TP under Pythagorean fuzzy environment. Therefore, there is a need to establish a new algorithm for Pythagorean fuzzy transportation problem.

Table 2 Significance influences of the different authors towards TP under various environment
Full size table

To the nice of our facts, there are no optimization models in literature for TP under Pythagorean fuzzy environment. This complete scenario has motivated us to come up with a new method for solving TP with the Pythagorean fuzzy range which are formulated and solved with the use of the proposed algorithm for the first time.

Pythagorean set theory is documented technique to manage uncertainty in the optimization problem. The most contributions of this paper are as follows.

  • This approach helps to resolve a new set of problem with the Pythagorean fuzzy number.

  • We define the TP problem below normal Pythagorean fuzzy surroundings and recommend an efficient solution to locate the corresponding crisp valued.

  • Within the literature of Pythagorean fuzzy set, we tend to introduce a scoring approach in conjunction with the proposed method.

This paper is organized as follows: in the next section, some basic knowledge, concepts on Pythagorean fuzzy set theory and arithmetic operation on Pythagorean Fuzzy Numbers (PFNs) are presented. The following section includes the existing method under crisp and fuzzy transportation problems. In the next following section, the proposed method for solving the transportation problem is discussed. In section before conclusion, a few numerical examples are given to reveal the effectiveness of the proposed model. Finally, some conclusions are provided in the last section.

Preliminaries

Definition 2.1

[31, 71] Let X is a fixed set, a Pythagorean fuzzy set (PFS) is an object having the form

$$ P = \left\{ {\left\langle {x,\left( {\theta_{P} (x),\delta_{P} (x)} \right)} \right\rangle \left| {x \in X} \right.} \right\}, $$
(1)

where the function \( \theta_{P} (x){:}\, X \to \left[ {0,1} \right] \) and \( \delta_{P} (x){:}\,X \to \left[ {0,1} \right] \) are the degree of membership and non-membership of the element \( x \in X \) to \( P \), respectively. Also for every \( x \in X, \) it holds that

$$ \left( {\theta_{P} (x)} \right)^{2} + \left( {\delta_{P} (x)} \right)^{2} \le 1 $$
(2)

Definition 2.2

[31, 71] Let \( \tilde{a}_{1}^{P} = \left( {\theta_{i}^{P} ,\delta_{s}^{P} } \right) \) and \( \tilde{b}_{1}^{P} = \left( {\theta_{o}^{P} ,\delta_{f}^{P} } \right) \) be two Pythagorean Fuzzy Numbers (PFNs).Then the arithmetic operations are as follows:

  1. (i)

    Additive property: \( \tilde{a}_{1}^{P} \oplus \tilde{b}_{1}^{P} = \left( {\sqrt {\left( {\theta_{i}^{P} } \right)^{2} + \left( {\theta_{o}^{P} } \right)^{2} - \left( {\theta_{i}^{P} } \right)^{2} \cdot \left( {\theta_{o}^{P} } \right)^{2} } ,\delta_{s}^{P} \cdot \delta_{f}^{P} } \right) \)

  2. (ii)

    Multiplicative property: \( \tilde{a}_{1}^{P} \otimes \tilde{b}_{1}^{P} = \left( {\theta_{i}^{P} \cdot \theta_{o}^{P} ,\sqrt {\left( {\delta_{s}^{P} } \right)^{2} + \left( {\delta_{f}^{P} } \right)^{2} - \left( {\delta_{s}^{P} } \right)^{2} \cdot \left( {\delta_{f}^{P} } \right)^{2} } } \right) \)

  3. (iii)

    Scalar product: \( k \cdot \tilde{a}_{1}^{P} = \left( {\sqrt {1 - \left( {1 - \theta_{i}^{P} } \right)^{k} } ,\left( {\delta_{s}^{P} } \right)^{k} } \right),{\text{where }}k{\text{ is nonnegative const}} . { } . {\text{i}} . {\text{e}} . { }k \succ 0 \)

Definition 2.3

[31, 71] (Comparison of two PFNs) Let \( \tilde{a}_{1}^{P} = \left( {\theta_{i}^{P} ,\delta_{s}^{P} } \right) \) and \( \tilde{b}_{1}^{P} = \left( {\theta_{o}^{P} ,\delta_{f}^{P} } \right) \) be two PFNs such that the score and accuracy function are as follows:

  1. (i)

    Score function: \( S\left( {\tilde{a}_{1}^{P} } \right) = \frac{1}{2}\left( {1 - \left( {\theta_{i}^{P} } \right)^{2} - \left( {\delta_{s}^{P} } \right)^{2} } \right) \)

  2. (ii)

    Accuracy function: \( H\left( {\tilde{a}_{1}^{P} } \right) = \left( {\theta_{i}^{P} } \right)^{2} + \left( {\delta_{s}^{P} } \right)^{2} \)

Then the following five cases arise:

Case 1:

\( \tilde{a}_{1}^{P} \succ \tilde{b}_{1}^{P} {\text{ iff }}S\left( {\tilde{a}_{1}^{P} } \right) \succ S\left( {\tilde{b}_{1}^{P} } \right) \)

Case 2:

\( \tilde{a}_{1}^{P} \prec \tilde{b}_{1}^{P} {\text{ iff }}S\left( {\tilde{a}_{1}^{P} } \right) \prec S\left( {\tilde{b}_{1}^{P} } \right) \)

Case 3:

\( if \, S\left( {\tilde{a}_{1}^{P} } \right) = S\left( {\tilde{b}_{1}^{P} } \right)\quad{\text{and }}H\left( {\tilde{a}_{1}^{P} } \right) \prec H\left( {\tilde{b}_{1}^{P} } \right)\quad{\text{then }}\tilde{a}_{1}^{P} \prec \tilde{b}_{1}^{P} \)

Case 4:

\( if \, S\left( {\tilde{a}_{1}^{P} } \right) = S\left( {\tilde{b}_{1}^{P} } \right)\quad{\text{and }}H\left( {\tilde{a}_{1}^{P} } \right) \succ H\left( {\tilde{b}_{1}^{P} } \right)\quad{\text{then }}\tilde{a}_{1}^{P} \succ \tilde{b}_{1}^{P} \)

Case 5:

\( if \, S\left( {\tilde{a}_{1}^{P} } \right) = S\left( {\tilde{b}_{1}^{P} } \right)\quad{\text{and }}H\left( {\tilde{a}_{1}^{P} } \right) = H\left( {\tilde{b}_{1}^{P} } \right)\quad{\text{then }}\tilde{a}_{1}^{P} = \tilde{b}_{1}^{P} \)

Existing model in the crisp transportation environment

Let us consider “m” sources and “n” destinations. In the transportation problem, the objective is to minimize the cost of distributing a product from these sources to the destinations, but the demand and supply of the product with the following assumptions and constraints are crisp:

\( m \) :

The total number of sources existing in the network

\( n \) :

The total number of destination nodes

\( i \) :

The source index for all m

\( j \) :

The destination index for all n

\( x_{ij} \) :

The number of unit of product transported from source to destination

\( c_{ij}^{P} \) :

The Pythagorean fuzzy cost of one unit quantity transported from ith source to jth destination

\( c_{ij} \) :

The crisp cost of one unit of quantity

\( a_{ij} \) :

The available supply quantity in the crisp environment from each source

\( a_{ij}^{P} \) :

The available supply quantity in the Pythagorean fuzzy environment from each source

\( b_{ij} \) :

The market demand quantity in the crisp environment from each destination

\( b_{ij}^{P} \) :

The market demand quantity in the Pythagorean fuzzy environment from each destination.

Then, the crisp transportation problem is as follows:

$$ {\text{Min }}Z = \sum\limits_{i = 0}^{m} {\sum\limits_{j = 0}^{n} {x_{ij} \cdot c_{ij} } } $$
(3)

Subject to

$$ \sum\limits_{j = 0}^{n} {x_{ij} } = a_{i} = {\text{supply}},{\text{ where }}i = 1, \ldots ,m $$
$$ \sum\limits_{i = 0}^{m} {x_{ij} } = b_{i} = {\text{demand}},{\text{ where }}j = 1, \ldots ,m $$
$$ x_{ij} \ge 0 \,\quad \forall \, i,j. $$

Furthermore, if we replaced the parameter \( c_{ij} \) from Eq. (3) into Pythagorean fuzzy (PyF) parameters, i.e., \( c_{ij}^{P} \), then the new LP model obtained is called as Type I Pythagorean fuzzy transportation (T1PyFT) problem, and it is shown as the following:

$$ {\text{Min }}Z = \sum\limits_{i = 0}^{m} {\sum\limits_{j = 0}^{n} {x_{ij} \cdot c_{ij}^{P} } } . $$
(4)

Subject to

$$ \sum\limits_{j = 0}^{n} {x_{ij} } = a_{i} = {\text{supply}},{\text{ where }}i = 1, \ldots ,m $$
$$ \sum\limits_{i = 0}^{m} {x_{ij} } = b_{i} = {\text{demand}},{\text{ where }}j = 1, \ldots ,m $$
$$ x_{ij} \ge 0 \quad \forall \, i,j. $$

Again, if the decision maker will not be sure about the unit transportation supply and demand units, we replace the parameters \( a_{ij} \) and \( b_{ij} \) into PyF parameters. Then this type of problem is known as Type II Pythagorean fuzzy transportation (T2PyFT) problem and it is shown in the below model:

$$ {\text{Min }}Z = \sum\limits_{i = 0}^{m} {\sum\limits_{j = 0}^{n} {x_{ij} \cdot c_{ij} } } . $$
(5)

Subject to

$$ \sum\limits_{j = 0}^{n} {x_{ij} } = a_{i}^{P} , $$
$$ \sum\limits_{i = 0}^{m} {x_{ij} } = b_{j}^{P} , $$
$$ x_{ij} \ge 0 \quad \forall \, i,j. $$

Lastly, if the decision maker will not be sure about the transportation cost, supply and demand unit, we replace the parameter \( c_{ij} , \) \( a_{ij} \) and \( b_{ij} \) into PyF parameters. Then this type of problem is known as Type III Pythagorean fuzzy transportation (T3PyFT) problem and it is shown in the following model:

$$ {\text{Min }}Z = \sum\limits_{i = 0}^{m} {\sum\limits_{j = 0}^{n} {x_{ij} \cdot c_{ij}^{P} } } . $$
(6)

Subject to

$$ \sum\limits_{j = 0}^{n} {x_{ij} } = a_{i}^{P} , $$
$$ \sum\limits_{i = 0}^{m} {x_{ij} } = b_{j}^{P} , $$
$$ x_{ij} \ge 0 \quad \forall \, i,j. $$

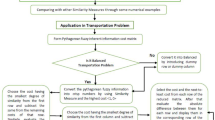
Proposed algorithms for solving three different types of PyF transportation models

In this section, we propose a new algorithm (Main Algorithm) to solve all types of TP under Pythagorean fuzzy environment. This method contains two sub-algorithms. The first sub-algorithm (Algorithm 1) presents a method to find an initial basic feasible solution for TP and the second sub-algorithm (Algorithm 2) is an existing optimality method for calculation of the cost of transportation. These algorithms are as follows:

figure a
figure b
figure c

Illustrative example

In this section, some examples are provided to illustrate the potential application of the proposed method.

Example 5.1 (T1PyFN model)

Consider a transportation problem with the conditions of Table 3.

Table 3 Input data for Pythagorean transportation problem of type-I
Full size table

Step 1 Calculate the score value of each PFN cost, replace all them by its score value and obtain a crisp transportation problem. This step is shown in Table 4.

Table 4 The defuzzified Pythagorean fuzzy transportation problem of Example 5.1
Full size table

Step 2 To check the balance of transportation we execute:

$$\begin{aligned} \sum {a_{i} } &= 26 + 24 + 30 = 80\;{\text{and}}\\ \sum {b_{i} } &= 17 + 23 + 28 + 12 = 80.\end{aligned} $$

Therefore, it is a balanced transportation problem.

Step 3 Now to find an initial basic feasible solution, we proceed with Algorithm 1 as it mentions in the main algorithm. After maximum allotting in the cell (2, 3) we get a new table. Table 5 shows the first allotment with penalties (Tables 6, 7, 8).

Table 5 First allotment with penalties in Example 5.1
Full size table
Table 6 Second allotment with penalties in Example 5.1
Full size table
Table 7 Third allotment with penalties in Example 5.1
Full size table
Table 8 Complete allotment in Example 5.1
Full size table

Table 9 shows the initial basic feasible solution of Example 5.1.

Table 9 The initial basic feasible solution of Example 5.1
Full size table

Hence, the initial basic feasible solution (IBFS) is as follows:

$$\begin{aligned} (O_{1} ,D_{1} ) &= x_{11} = 17,\;(O_{1} ,D_{2} ) = x_{12} = 9,\\ (O_{2} ,D_{3} ) &= x_{23} = 24,\;(O_{3} ,D_{2} ) = x_{32} = 14,\\ (O_{3} ,D_{3} ) &= x_{33} = 4,\;{\text{and}}\;(O_{3} ,D_{4} ) = x_{34} = 12.\end{aligned} $$

Also, the minimum cost of IBFS is obtained as follows:

$$ Min = 17 \times 0.335 + 9 \times 0.545 + 24 \times 0.26 + 14 \times 0.815 + 4 \times 0.6 + 12 \times 0.9 = 41.45. $$

Steps 4–5 Now, we test the optimality of the transportation problem. Since the m + n − 1 = 6, it is a degenerate solution, and we need to proceed to test the optimality. To obtain the optimality, we use Lingo software. Therefore, the optimal solution is as follows:

$$\begin{aligned} (O_{1} ,D_{1} ) &= x_{11} = 17,\;(O_{1} ,D_{2} ) = x_{12} = 9,\\ (O_{2} ,D_{3} ) &= x_{23} = 24,\;(O_{3} ,D_{2} ) = x_{32} = 14,\\ (O_{3} ,D_{3} ) &= x_{33} = 4,\;{\text{and}}\;(O_{3} ,D_{4} ) = x_{34} = 12.\end{aligned} $$

Step 6 Now put all \( x_{ij} \) in the above equation; so we get:

$$ {\text{Min}} = 17 \times 0.335 + 9 \times 0.545 + 24 \times 0.26 + 14 \times 0.815 + 4 \times 0.6 + 12 \times 0.9. $$

Minimum cost = 41.45.

Example 5.2 (T2PyFN model)

Consider type-II PyFN problem with the conditions of Table 10 where the costs are crisp, but the demand and supply are PFN. The supplies are denoted as Pythagorean fuzzy numbers, i.e.,

$$\begin{aligned} \tilde{s}_{1}^{P} &= \left( {\theta^{P} ,\delta^{P} } \right) \approx \left( {0.7, \, 0.1} \right),\;\tilde{s}_{2}^{P} \approx \left( {0.8, \, 0.1} \right),\\ \tilde{s}_{3}^{P} &\approx \left( {0.9, \, 0.1} \right).\end{aligned} $$
Table 10 Input data for Pythagorean transportation problem of type-II
Full size table

Similarly, the demands are also denoted as Pythagorean fuzzy numbers, respectively. We note that \( \theta^{P} ,\delta^{P} \) represent the maximum degree of the membership (i.e., the degree of acceptance of quantity) and the non-membership (i.e., the degree of rejection of quantity) respectively. Moreover, they will also satisfy the inconsistence information under these conditions, i.e., \( 0 \le \theta^{P} \le 1, \) \( 0 \le \delta^{P} \le 1, \) \( 0 \le \left( {\theta^{P} } \right)^{2} + \left( {\delta^{P} } \right)^{2} \le 1 \).

Solution

After executing the steps 1–3, we get the initial basic feasible solution as follows:

$$\begin{aligned} (O_{1} ,D_{1} ) &= x_{11} = 0.3350,\;(O_{1} ,D_{2} ) = x_{12} = 0.405,\\ (O_{2} ,D_{3} ) &= x_{23} = 0.8150,\;(O_{3} ,D_{2} ) = x_{32} = 0.295,\;{\text{and}}\\ (O_{3} ,D_{4} ) &= x_{34} = 0.6050.\end{aligned} $$

Also, the minimum cost of an initial basic feasible solution is

$$ Min = 0.0335 \times 0.3350 + 0.0545 \times 0.405 + 0.295 \times 0.0815 + 0.026 \times 0.8150 + 0.07 \times 0.6050 = 0.132978. $$

Again, execute the steps 4–6, we get the optimum solution, i.e.:

$$\begin{aligned} (O_{1} ,D_{1} ) &= x_{11} = 0.3350,\;(O_{1} ,D_{2} ) = x_{12} = 0.405,\\ (O_{2} ,D_{3} ) &= x_{23} = 0.8150,\;(O_{3} ,D_{2} ) = x_{32} = 0.295,\;{\text{and}}\\ (O_{3} ,D_{4} ) &= x_{34} = 0.6050.\end{aligned} $$
$$ Min = 0.0335 \times 0.3350 + 0.0545 \times 0.405 + 0.295 \times 0.0815 + 0.026 \times 0.8150 + 0.07 \times 0.6050, $$

Minimum cost = \( 0.132978. \)

Example 5.3

Consider type-III PyFN problem with the conditions of Table 11. Here, the supplies are denoted as Pythagorean fuzzy. Similarly, the demands are also denoted as Pythagorean fuzzy numbers \( \left( {\theta^{P} ,\delta^{P} } \right) \), respectively. We note that \( \theta^{P} ,\delta^{P} \) represent the maximum degree of the membership (i.e., the degree of acceptance of quantity) and the non-membership (i.e., the degree of rejection of quantity), respectively. The cost values are also in Pythagorean fuzzy numbers where \( C^{P} \approx (C_{a}^{P} ,C_{r}^{P} ) \) represents the degree of acceptance and rejection of cost.

Table 11 Input data for Pythagorean transportation problem of type-III
Full size table

Solution

After executing the steps 1–3, we get the initial basic feasible solution as follows.

After executing the step 1–3, we get the initial basic feasible solution, i.e., \( (O_{2} ,D_{1} ) = x_{21} = 0.335, \) \( (O_{1} ,D_{2} ) = x_{12} = 0.135, \) \( (O_{2} ,D_{2} ) = x_{22} = 0.48, \) \( (O_{2} ,D_{3} ) = x_{23} = 0.085, \) \( (O_{3} ,D_{3} ) = x_{33} = 0.815, \) and \( (O_{1} ,D_{4} ) = x_{14} = 0.6050; \) so the minimum IBFS cost is 0.322775.

Again, by steps 4–6, we get the optimum solution i.e., \( (O_{2} ,D_{1} ) = x_{21} = 0.335, \) \( (O_{1} ,D_{2} ) = x_{12} = 0.22, \) \( (O_{2} ,D_{2} ) = x_{22} = 0.48, \) \( (O_{3} ,D_{4} ) = x_{34} = 0.085, \) \( (O_{3} ,D_{3} ) = x_{33} = 0.815, \) and \( (O_{1} ,D_{4} ) = x_{14} = 0.52, \), that the minimum cost is 0.31895.

Results and discussion

In Example 5.1, it is clear that the PyFN transportation cost of IBFS is 41.45 which is same as the optimum transportation cost of PyFN transportation problem. Hence, this shows that the optimal value is not more than the IBFS and in Example 5.2, the PyFN transportation cost of IBFS is 0.132978 which is the same as the optimum transportation cost of PyFN transportation problem. Again we observe that the optimum value is not more than the IBFS. However, in Example 5.3 the optimum transportation cost of PyFN transportation problem is 0.31895, which is less than the transportation cost of IBFS i.e. 0.322775. Therefore, we can say that the proposed method produces lower optimum values when compared with IBFS. The logical comparison for all the above three discussed examples is shown in Table 12. In this table, we can see that the optimal value of PyFN transportation problem is either equal or less than the IBFS solution.

Table 12 Logical comparison of IBFS with optimum value
Full size table

Therefore, we can conclude that our proposed algorithm is a new way to handle the uncertainty in the crisp environment.

Conclusions

In this paper, the fuzzy Pythagorean transportation problem has been investigated. At that point, we proposed another arrangement approach for understanding whole number esteemed Pythagorean fuzzy transportation problem. Moreover, we study three different models in the Pythagorean fuzzy environment. The existing arithmetic operations on the Pythagorean fuzzy numbers and a score function are employed to find the optimum solutions. The proposed algorithm is a new way to handle the uncertainty in the crisp environment. In the future, the proposed method can be applied to real-world problems in the field of assignment, job scheduling, shortest path problem, and so on.