Modeling and analysis of a predator–prey type eco-epidemic system with time delay

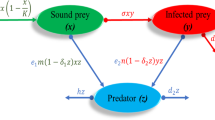
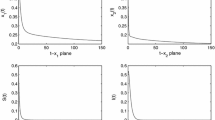
Abstract

In this research work, a delay-induced eco-epidemic model using a reconstructed Leslie–Gower-type growth rate is formulated and analyzed. An extended qualitative nature of the solutions of the model system like boundedness, strong uniform persistence, and permanence is examined to secure the longstanding viability of the system. The stability of the system is investigated at different stationary points, and sufficient conditions are obtained for the local as well as global stability. The dynamics of the delay-induced model system, including the Hopf bifurcation phenomenon, is rigorously studied around the coexisting equilibrium using the normal form method and center manifold theorem. Also, the length of the delay to preserve the stability of the coexisting equilibrium is evaluated. It is observed that the effect of infection on the total harvest is negligible, but the effort to harvest can reduce the infection and preserve the system’s stability. The results may help to determine the point of reference for disease persistence and extinction. Based on our analytical results, several numerical simulations are also performed.

Appendices

Appendix A

Let $x$ be the amount of susceptible prey that are contaminated by some infectious disease and $\tau$ be the time to become infected from susceptible after contamination. This $x$ amount does not increase the biomass of the infected class. There are some losses due to external hazards within the time delay $\tau$. Let $\gamma$ be the decay rate of that loss at any instant t. Then, after one unit of time, it would be $x - \gamma x = \left( {1 - \gamma } \right)x$. After two unit time, it would be $\left( {1 - \gamma } \right)x - \gamma \left( {1 - \gamma } \right)x = \left( {1 - \gamma } \right)^{2} x$, and that will be $\left( {1 - \gamma } \right)^{\tau } x$ after $\tau$ units of time. If the decay rate is calculated section wise by two times in one unit of time, then after $\tau$ times, it would be $\left( {1 - \frac{\gamma }{2}} \right)^{2\tau } x$. If the decay rate is calculated section wise by three times in one unit of time, then after $\tau$ times, it would be $\left( {1 - \frac{\gamma }{3}} \right)^{3\tau } x$. Similarly, if the decay rate is calculated section wise by $m$ times in one unit of time, then after $\tau$ times, it would be $\left( {1 - \frac{\gamma }{m}} \right)^{m\tau } x$. Thus, letting $m \to \infty$, we get continuous compounding amounts as $\mathop {\lim }\limits_{m \to \infty } \left( {1 - \frac{\gamma }{m}} \right)^{m\tau } x = e^{ - \gamma \tau } x$.

Here, $x = \frac{{\beta I\left( {t - \tau } \right)S\left( {t - \tau } \right)}}{{\left( {S\left( {t - \tau } \right) + I\left( {t - \tau } \right) + M} \right)}}$, and hence, $e^{ - \gamma \tau } x = e^{ - \gamma \tau } \frac{{\beta I\left( {t - \tau } \right)S\left( {t - \tau } \right)}}{{\left( {S\left( {t - \tau } \right) + I\left( {t - \tau } \right) + M} \right)}}$.

Appendix B (proof of positivity)

From the system (1), and using the initial conditions, we have:

$$S\left( t \right) = S\left( 0 \right)\exp \left( {\int\limits_{0}^{t} {\aleph_{1} {\text{d}}u} } \right) > 0,$$

$$I\left( t \right) = I\left( 0 \right)\exp \left( {\int\limits_{0}^{t} {\aleph_{2} {\text{d}}u} } \right) > 0,$$

and $P\left( t \right) = P\left( 0 \right)\exp \left( {\int\limits_{0}^{t} {\aleph_{3} {\text{d}}u} } \right) > 0$

where $\aleph_{1} = r - r\frac{S\left( u \right) + I\left( u \right)}{K} - \frac{\beta I\left( u \right)}{S\left( u \right) + I\left( u \right) + M} - \frac{\alpha P\left( u \right)}{a + S\left( u \right)} - q_{1} E$,

$$\aleph_{2} = \frac{{e^{ - \gamma \tau } \beta S\left( {u - \tau } \right)I\left( {u - \tau } \right)}}{{\left( {S\left( {u - \tau } \right) + I\left( {u - \tau } \right) + M} \right)I\left( u \right)}} - \sigma P\left( u \right) - d - q_{2} E,$$

and $\aleph_{3} = s - \frac{sP\left( u \right)}{\eta S\left( u \right) + \omega I\left( u \right) + L} - q_{3} E.$

Therefore, all the solutions of the system (1) are positive. Hence, the desired result is obtained.

Appendix C (Proof of Proposition 3.1):

First, we state a result due to Chen (2005) as follows:

Lemma C.1

If $a > 0,b > 0$ and $\dot{x}(t) \ge ( \le )x(t)(b - ax^{\alpha } (t))$, ($\alpha > 0$), then for $t \ge 0$ and $x\left( 0 \right) > 0$, we have $x\left( t \right) \ge \left( \le \right)\left( {\frac{b}{a}} \right)^{{\frac{1}{\alpha }}} \left[ {1 + \left( {\frac{{bx^{ - \alpha } \left( 0 \right)}}{a} - 1} \right)e^{ - b\alpha t} } \right]^{{ - \frac{1}{\alpha }}}$.

Now, using the first equation of (1), we have for all $t > 0$:

$$\dot{S}\left( t \right) < S\left( t \right)\left( {r - q_{1} E - \frac{rS\left( t \right)}{K}} \right).$$

According to the Lemma C.1, we get $\mathop {\lim \sup }\limits_{t \to + \infty } S\left( t \right) \le \frac{{K\left( {r - q_{1} E} \right)}}{r} = Q_{1}$ (say).

Thus, we may conclude that, for any $\varepsilon > 0$, $\exists$ $T_{1} > 0$, such that:$S\left( t \right) < Q_{1} + \varepsilon ,\quad t > T_{1}$.

From the second equation of (1), we can write, $\dot{I}\left( t \right) \ge - \left( {d + q_{2} E} \right)I\left( t \right)$.

Integrating between $t - \tau$ to $t$, we have $I\left( {t - \tau } \right) \le I\left( t \right)e^{{\left( {d + q_{2} E} \right)\tau }}$.

Now, from Eq. (1), using the above inequality, we find:

$$\dot{I}(t) \le (\beta e^{{(d + q_{2} E - \gamma )\tau }} - (d + q_{2} E))I(t).$$

Now, if we assume that $\left( {d + q_{2} E} \right) > \beta e^{{\left( {d + q_{2} E - \gamma } \right)\tau }}$, then for any $\varepsilon > 0$, $\exists$ $T_{2} > T_{1} > 0$ and $Q_{2} > 0$, such that $I\left( t \right) < Q_{2} + \varepsilon ,\quad t > T_{2}$, where $\mathop {\lim \sup }\limits_{t \to + \infty } I\left( t \right) \le Q_{2}$.

Again, from the last equation of (1), we have:

$$\dot{P}\left( t \right) \le P\left( t \right)\left( {\left( {s - q_{3} E} \right) - \frac{P\left( t \right)}{{\left( {\eta Q_{1} + \omega Q_{2} + L} \right)}}} \right).$$

Following Lemma C.1, we obtain $\lim \sup_{t \to + \infty } P(t) \le (s - q_{3} E)(\eta Q_{1} + \omega Q_{2} + L) = Q_{3}$.

Therefore, for any $\varepsilon > 0$, $\exists$ $T_{3} > T_{2} > 0$, such that $P\left( t \right) < Q_{3} + \varepsilon ,\quad t > T_{3}$.

Furthermore, from the first equation of (1), we have:

$$\dot{S}\left( t \right) = S\left( t \right)\left( {r\left( {1 - \frac{S\left( t \right) + I\left( t \right)}{K}} \right) - \frac{\beta S\left( t \right)I\left( t \right)}{S\left( t \right) + I\left( t \right) + M} - \frac{\alpha P\left( t \right)}{a + S\left( t \right)} - q_{1} E} \right)$$

$$\ge S\left( t \right)\left( {r\left( {1 - \frac{{S\left( t \right) + Q_{2} }}{K}} \right) - \frac{{\beta Q_{1} Q_{2} }}{M} - \frac{{\alpha Q_{3} }}{a} - q_{1} E} \right)$$

$$\ge S\left( t \right)\left( {\left( {r - \frac{{rQ_{2} }}{K} - \frac{{\beta Q_{1} Q_{2} }}{M} - \frac{{\alpha Q_{3} }}{a} - q_{1} E} \right) - \frac{rS\left( t \right)}{K}} \right).$$

By Lemma C.1, we can conclude that:

$$\mathop {\lim \inf }\limits_{t \to + \infty } S\left( t \right) \ge \frac{K}{r}\left( {r - \frac{{rQ_{2} }}{K} - \frac{{\beta Q_{1} Q_{2} }}{M} - \frac{{\alpha Q_{3} }}{a} - q_{1} E} \right) = R_{1} \left( {\text{say}} \right).$$

Then, we can say that, for any $\varepsilon > 0$, there exists $T_{4} > T_{3} > 0$, such that: $S(t) > R_{1} + \varepsilon ,\quad t > T_{4}$.

From second equation of (1), we have, $\dot{I}(t) > - (\sigma Q_{3} + d + q_{2} E)I(t)$.

Since $(\sigma Q_{3} + d + q_{2} E) > 0$ always, so we can say for any $\varepsilon > 0$, there exists $T_{5} > T_{4} > 0$ and $R_{2} > 0$, such that, $I(t) > R_{2} + \varepsilon ,\quad t > T_{5}$, where $\lim \inf_{t \to + \infty } I(t) \ge R_{2}$.

Finally, from last equation of (1), we find $\dot{P}\left( t \right) \ge P\left( t \right)\left( {\left( {s - q_{3} E} \right) - \frac{P\left( t \right)}{{\eta R_{1} + \omega R_{2} + L}}} \right)$.

Following Lemma C.1, we obtain $\mathop {\lim \inf }\limits_{t \to + \infty } P\left( t \right) \ge \left( {s - q_{3} E} \right)\left( {\eta R_{1} + \omega R_{2} + L} \right) = R_{3}$.

Therefore, it can be said that, for any $\varepsilon > 0$, there exists $T_{6} > T_{5} > 0$, such that $P\left( t \right) > R_{3} + \varepsilon ,\quad t > T_{6}$.

Hence, the theorem.

Appendix D: Permanence (Proof of the Theorem 3.2)

It is obvious that $\lim \inf < \lim \sup$.

Therefore, $\hbox{min} \left( {\lim \inf } \right) < \hbox{max} \left( {\lim \sup } \right)$ which implies that $\nu < \vartheta$.

Meanwhile, we have established that for the persistence of the system, that all the constants $Q_{i} ,R_{i} (i = 1,2,3)$ are greater than zero.

Therefore, $\hbox{min} \left\{ {R_{1} ,R_{2} ,R_{3} } \right\} \ge 0$ and $\hbox{max} \left\{ {Q_{1} ,Q_{2} ,Q_{3} } \right\} \ge 0$.

Hence, the desired results are done automatically. Therefore, the system is permanent.

Appendix E (stability of infection-free equilibrium)

One eigenvalue of the Jacobian matrix at $E^{3} (S_{3} ,0,P_{3} )$ is given as $\lambda_{1} = \frac{{\beta S^{*} (S^{*} + M)}}{{(S^{*} + M)^{2} }} - \sigma P^{*} - \tilde{d}$.

Now, $\lambda_{1}$ will be negative if (i)$\beta S^{*} (S^{*} + M) < (\sigma P^{*} + \tilde{d})(S^{*} + M)^{2} .$

The other two eigenvalues are obtained from the following matrix:

$$J_{3} = \left( {\begin{array}{*{20}c} {\tilde{r} - \frac{{2rS^{*} }}{K} - \frac{{a\alpha P^{*} }}{{(a + S^{*} )^{2} }}} & {\frac{{ - \alpha S^{*} }}{{(a + S^{*} )}}} \\ {\frac{{s\eta P^{*2} }}{{(\eta S^{*} + L)^{2} }}} & {\tilde{s} - \frac{{2sP^{*} }}{{(\eta S^{*} + L)}}} \\ \end{array} } \right).$$

The two characteristic roots of $J_{3}$ will have negative real parts if $Tr\left( {J_{1} } \right) < 0$ and $\det \left( {J_{1} } \right) > 0$. Now, the above two conditions will be satisfied if the following two inequalities hold:

(2) $\tilde{r} + \tilde{s} < \frac{{2rS^{*} }}{K} + \frac{{a\alpha P^{*} }}{{(a + S^{*} )^{2} }} + \frac{{2sP^{*} }}{{(\eta S^{*} + L)}}$

(3) $\tilde{r}\tilde{s} + \frac{{2sP^{*} }}{{(\eta S^{*} + L)}}\left( {\frac{{2rS^{*} }}{K} + \frac{{a\alpha P^{*} }}{{(a + S^{*} )^{2} }}} \right) + \frac{{\alpha s\eta S^{*} P^{*2} }}{{(\eta S^{*} + L)(a + S^{*} )}} > \frac{{2s\tilde{r}P^{*} }}{{(\eta S^{*} + L)}} + \tilde{s}\left( {\frac{{2rS^{*} }}{K} + \frac{{a\alpha P^{*} }}{{(a + S^{*} )^{2} }}} \right)$.

Hence, following the Routh–Hurwitz criteria, we may conclude that the system will be LAS at the infection-free stationary state if the inequalities (1), (2), and (3) are satisfied.