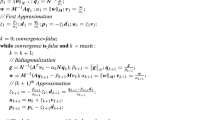Skip to main content
SpringerLink
Log in

Numerical Solution for Nonlinear Klein–Gordon Equation via Operational Matrix by Clique Polynomial of Complete Graphs

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

This article has been updated

Abstract

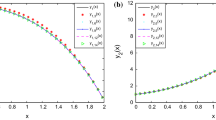
This study introduced a generalized operational matrix using Clique polynomials of a complete graph and proposed the latest approach to solve the nonlinear Klein–Gordon (KG) equation. KG equations describe many real physical phenomena in fluid dynamics, electrical engineering, biogenetics, tribology. By using the properties of the operational matrix, we transform the nonlinear KG equation into a system of algebraic equations. Unknown coefficients to be determined by Newton’s method. The present technique is applied to four problems, and the obtained results are compared with another method in the literature. Also, we discussed some theorems on convergence analysis and continuous property.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Change history

  • 04 August 2023

    The original article was updated for removal of unnecessary hyphens present in the text.

Abbreviations

\(\alpha\) :

Real number

\(P\left( y \right)\) :

A nonlinear term in Eq. (1.1)

\(y\left( {x,t} \right)\) :

The wave displacement at \(x\) and \(t\)

\(A\left( x \right)\) :

Wave kinks

\(V\left( G \right)\) :

The vertex set of \(G\)

\(E\left( G \right)\) :

Edge set of \(G\)

\(S\left( {G;x} \right)\) :

Clique polynomials of a graph \(G\)

\(K_{n}\) :

Complete graph

References

  1. Rashidinia, J., Mohammadi, R.: Tension spline approach for the numerical solution of nonlinear Klein-Gordon equation. Comput. Phys. Commun. 181, 78–91 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  2. Raza, N., Rashid Butt, A., Javid, A.: Approximate Solution of Nonlinear Klein-Gordon Equation Using Sobolev Gradients, Hindawi Publishing Corporation. J. Funct. Sp. Vol. 2016, Article ID 1391594, 01–07

  3. Fukang, Y., Tian, T., Song, J., Zhu, M.: Spectral methods using Legendre wavelets for nonlinear Klein/Sine-Gordon equations. J. Comput. Appl. Math. 275, 321–334 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  4. Rashidinia, J., Ghasemia, M., Jalilian, R.: Numerical solution of the nonlinear Klein/Gordon equation. J. Comput. Appl. Math. 233, 1866–1878 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  5. Khuri, S.A., Sayfy, A.: A spline collocation approach for the numerical solution of a generalized nonlinear Klein-Gordon equation. Appl. Math. Comput. 216, 1047–1056 (2010)

    MathSciNet  MATH  Google Scholar 

  6. Chowdhury, M.S.H., Hashim, I.: Application of Homotopy perturbation method to Klein–Gordon and sine-Gordon equations. Chaos, Solitons Fractals 39, 1928–1935 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Rashidinia, J., Jokar, M.: Numerical solution of nonlinear klein-gordon equation using polynomial wavelets. Adv. Intell. Syst. Comput. 441, 199–214 (2016)

    Google Scholar 

  8. Dehghan, M., Shokri, A.: Numerical solution of the nonlinear Klein-Gordon equation using radial basis functions. J. Comput. Appl. Math. 230, 400–410 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. El-Sayed, S.M.: The decomposition method for studying the Klein-Gordon equation. Chaos Solitons Fractals 18(5), 1025–1030 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kanth, A.R., Aruna, K.: Differential transform method for solving the linear nonlinear Klein-Gordon equation. Comput. Phys. Commun. 180, 708–711 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  11. Shiralashetti, S.C., Kumbinarasaiah, S.: Laguerre wavelets collocation method for the numerical solution of the Benjamina Bona Mohany, equations. J. Taibah Univ. Sci. 13(1), 9–15 (2019)

    Article  Google Scholar 

  12. Shiralashetti, S.C., Kumbinarasaiah, S.: CAS wavelets analytic solution and Genocchi polynomials numerical solutions for the integral and integrodifferential equations. J. Interdiscip. Math. 22(3), 201–218 (2019)

    Article  Google Scholar 

  13. Shiralashetti, S.C., Kumbinarasaiah, S.: Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems. Alexandria Eng. J. 57(4), 2591–2600 (2018)

    Article  Google Scholar 

  14. Shiralashetti, S.C., Kumbinarasaiah, S.: Theoretical study on continuous polynomial wavelet bases through wavelet series collocation method for nonlinear lane-Emden type equations. Appl. Math. Comput. 315, 591–602 (2017)

    MathSciNet  MATH  Google Scholar 

  15. Mohammadi, A., Aghazadeh, N., Rezapour, S.: Haar wavelet collocation method for solving singular and nonlinear fractional time dependent Emden-Fowler equations with initial and boundary conditions. Math. Sci. 13, 255–265 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  16. Heydari, M.H., Hooshmandasl, M.R., Malek Ghaini, F.M., Fereidouni, F.: Two dimensional Legendre wavelets for solving fractional Poisson equation with Dirichlet boundary conditions. Eng. Anal. Boundary Elem. 37, 1331–1338 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  17. Diudea, M. V., Gutman, I., Lorentz, J.: Molecular Topology 1999.

  18. Harary, F.: Graph Theory, Addison Wesley, Reading 1969.

  19. Hoede, C., Li, X.: Clique polynomials, and independent set polynomials of graphs. Discrete Math. 125, 219–228 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  20. Ganji, R.M., Jafari, H., Baleanu, D.: A new approach for solving multivariable orders differential equations with Mittag Leffler kernel. Chaos Solitons Fractals 130, 109405 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  21. Srinivasa, K., Rezazadeh, H.: Numerical solution for the fractional order one dimensional telegraph equation via wavelet technique. Int. J. Nonlinear Sci. Numer. Simulation (2020). https://doi.org/10.1515/ijnsns-2019-0300

    Article  MATH  Google Scholar 

  22. Ganji, R.M., Jafari, H.: Numerical solution of variable order integro differential equations. Adv. Math. Models Appl. 4(1), 64–69 (2019)

    Google Scholar 

  23. Ganji, R.M., Jafari, H.: A new approach for solving nonlinear Volterra integrodifferential equations with Mittag-Leffler kernel. Proc. Inst. Math. Mech. 46(1), 144–158 (2020)

    MathSciNet  MATH  Google Scholar 

  24. Ganji, R. M., Jafari, H., Nemati, S.: A new approach for solving integro differential equations of variable order, J. Comput. Appl. Math. 112946 (2020).

  25. Shiralashetti, S.C., Kumbinarasaiah, S.: Cardinal B-spline wavelet based numerical method for the solution of generalized Burgers-Huxley equation. Int. J. Appl. Comput. Math. 4, 73 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  26. Shiralashetti, S.C., Kumbinarasaiah, S.: New generalized operational matrix of integration to solve nonlinear singular boundary value problems using Hermite wavelets. Arab J. Basic Appl. Sci. 26(1), 385–396 (2019)

    Article  Google Scholar 

  27. Shiralashetti, S.C., Kumbinarasaiah, S.: Laguerre wavelets exact parseval frame based numerical method for the solution of system of differential equations. Int. J. Appl. Comput. Math. 6, 101 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  28. Srinivasa, K., Rezazadeh, H., Adel, W.: Numerical investigation based on Laguerre wavelet for solving the hunter saxton equation. Int. J. Appl. Comput. Math. 6, 139 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  29. Kumbinarasaiah, S.: A new approach for the numerical solution for the nonlinear Klein-Gordon equation. SeMA 77, 435–456 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  30. Islam, M.S., Akbar, M.A., Khan, K.: Analytical solutions of nonlinear Klein-Gordon equation using the improved F expansion method. Opt. Quant. Electron. 50, 224 (2018)

    Article  Google Scholar 

  31. Kurulay, M.: Solving the fractional nonlinear Klein-Gordon equation by means of the Homotopy analysis method. Advances in Difference Equations 2012, 187 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  32. Chaudry, M.K., Anjan, B.: Analysis of nonlinear Klein-Gordon equations using Lie symmetry. Appl. Math. Lett. 23(11), 1397–1400 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  33. Necdet, B., Sinan, D.: New approximate solutions to the nonlinear Klein-Gordon equations using perturbation iteration techniques. Discrete Contin. Dyn. Syst. S 13(3), 503–518 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Deniz, S., Konuralp, A., De la Sen, M.: Optimal perturbation iteration method for solving fractional model of damped Burgers’ equation. Symmetry 12, 958 (2012)

    Article  Google Scholar 

  35. Duan, J.S., Rach, R., Bulean, D., Wazwaz, A.M.: A review of the Adomian decomposition method and its applications to fractional differential equations. Commun. Fract. Calc. 3(2), 73–99 (2012)

    Google Scholar 

  36. Bildik, N., Deniz, S.: A new efficient method for solving delay differential equations and a comparison with other methods. Eur. Phys. J. Plus 132, 51 (2017)

    Article  Google Scholar 

  37. Deniz, S., Bildik, N.: A new analytical technique for solving Lane - Emden type equations arising in astrophysics. Bull. Belg. Math. Soc. Simon Stevin 24(2), 305–320 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  38. Khaled, M.S., Deniz, S., Dumi̇tru, B.: On a new modified fractional analysis of Nagumo equation. Int. J. Biomath. 12(3), 1950034 (2019)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Bangalore University, Bengaluru, India

    S. Kumbinarasaiah

  2. Department of Mathematics, Karnatak University, Dharwad, India

    H. S. Ramane & K. S. Pise

  3. Department of Mathematics, SASTRA University, Tanjore, India

    G. Hariharan

Authors
  1. S. Kumbinarasaiah
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. S. Ramane
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. S. Pise
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. G. Hariharan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Kumbinarasaiah.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumbinarasaiah, S., Ramane, H.S., Pise, K.S. et al. Numerical Solution for Nonlinear Klein–Gordon Equation via Operational Matrix by Clique Polynomial of Complete Graphs. Int. J. Appl. Comput. Math 7, 12 (2021). https://doi.org/10.1007/s40819-020-00943-x

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-020-00943-x

Keywords

Mathematics Subject Classification

Search

Navigation