Modeling the Dynamics of COVID-19 in Nigeria

Abstract

To understand the dynamics of COVID-19 in Nigeria, a mathematical model which incorporates the key compartments and parameters regarding COVID-19 in Nigeria is formulated. The basic reproduction number is obtained which is then used to analyze the stability of the disease-free equilibrium solution of the model. The model is calibrated using data obtained from Nigeria Centre for Disease Control and key parameters of the model are estimated. Sensitivity analysis is carried out to investigate the influence of the parameters in curtailing the disease. Using Pontryagin’s maximum principle, time-dependent intervention strategies are optimized in order to suppress the transmission of the virus. Numerical simulations are then used to explore various optimal control solutions involving single and multiple controls. Our results suggest that strict intervention effort is required for quick suppression of the disease.

Introduction

Resulting from severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), the coronavirus disease (COVID-19) has become a major public health concern throughout the globe. Guidelines from Chinese health authorities described human-to-human transmission via droplets transmission, aerosol transmission and contact transmission as the main transmission routes for the disease [24, 25]. Symptomatic treatment and supportive care are being given to COVID-19 patients as there are no specific antiviral treatments [5, 13].

In Nigeria, the index case was confirmed on the 27th of February, 2020. The Nigeria Center for Disease Control (NCDC) responded by activating a multi-sectoral Emergency Operations Centre (EOC) which is the highest emergency level in the country. 11,516 cases were confirmed including 323 death cases as of 4th of June, 2020 [26]. However, Adegboye et al. [2] reported that the outbreak could be worse than it is actually being disclosed as a result of poor disease surveillance and inadequate quality health care facilities.

To better understand the dynamics of COVID-19, researchers have proposed several models. A mathematical model incorporating presence of infectious undetected cases, sanitizing conditions of hospitalized cases and fraction of detected cases was proposed in [17]. The model estimated the number of cases that could have been infected in China including cases that have gone undetected. Yang and Wang [48] proposed a SEIR model which incorporated environment-to-human and human-to-human transmission routes. The findings suggested that adequate efforts should be put in place to fight the virus for a longer time duration so as to reduce the endemic burden and potentially eradicate the disease totally. Rong et al. [36] investigated the effect of delay in diagnosis on the disease transmission with a deterministic model. The authors reported that increasing the proportion of timely diagnosis and reducing the waiting time for diagnosis is not sufficient for the eradication of COVID-19 but can effectively reduce the transmission risk.

A mathematical model for the investigation of the impact of mask use by the general, asymptomatic public was presented in [9]. A risk structure model which divides the population into two groups (masked group and unmasked group) was developed and analysed. Their results suggested that the use of face masks by the general public is of high value in suppressing the transmission of the disease when adoption is nearly nation-wide and compliance level is high. Moreover the positive impact of the use of face mask will be greatest when face masks are used together with other non-pharmaceutical practices (such as social-distancing).

A mathematical model incorporating virus reservoir was proposed and discussed in [44]. Basic reproduction number $(R_0)$ was expressed and the values of $R_0$ are estimated from reservoir to human being as well as starting individual to individual. It was demonstrated that the spreading of COVID-19 is superior to the Middle-East pulmonary inrmity during the Middle-East nationals, analogous to harsh sensitive pulmonary inrmity, but inferior to Middle-East pulmonary inrmity within the Republic of Korea. In [43], a mathematical model for the spread and control of the coronavirus disease was developed. Real-life data was used to estimate the basic reproduction number. The author then proposed a study of the impact of the percentage of recognition of cases and obtained that the magnitude of the epidemic can be signicantly reduced when increasing this percentage.

Ibrahim and Oladipo [15] developed an auto regressive integrated moving average (ARIMA) using R software to predict the spread of COVID-19 in Nigeria using available data from NCDC. The dataset used spanned from February 27, 2020 to April 26, 2020 and contained both laboratory confirmed and clinically diagnosed cases. A non-stationary time series forecasting approach was applied on the obtained data which totaled 1120 cases. The result of data analysis using the model showed a steep growth of the spread of the virus whose peak cannot be said to have been reached within the selected time frame. In conclusion, the government was advised to take adequate steps in curbing the spread of the disease apart from measures that have already been put in place.

An opinion on COVID-19 pandemic in Nigeria was given in [12]. The author reported that Nigeria may suffer a major outbreak of the disease if necessary precautions were not taken. Enahoro et al. [14] developed a Kermack-McKendrick-type compartmental epidemic model for understanding the transmission dynamics and control of COVID-19 in Nigeria. It was predicted that if social-distancing, lockdown and other community transmission reduction measures are not implemented, Nigeria would have recorded a high COVID-19 mortality by April 2021. It was, however, shown that COVID-19 elimination is feasible in Nigeria if the public face masks use strategy is complemented with a social-distancing strategy. It was also noted that relaxing, or fully lifting, the lockdown measures sooner, in an effort to re-open the economy or the country, may trigger a deadly second wave of the pandemic.

In this work, a mathematical model which captures the key compartments and parameters regarding COVID-19 in Nigeria is formulated. Then the basic reproduction number is obtained which is used to analyze the stability of the model. Following are the research objectives:

• (i) The first of objective of the this work is to obtain the values of the key parameters that describe the dynamics of COVID-19 in Nigeria. Key parameters in the dynamics of COVID-19 in Nigeria have been estimated in [14, 29]. The predictions, using these parameter values, were well overestimated. Thus the parameter values in [14, 29] are not applicable to discuss the present situation of COVID-19 pandemic in Nigeria. We therefore carry out data fitting to estimate the key parameters of the model and forecast the trend of the pandemic.

• (ii) The second objective is to investigate the influence of each parameter on the dynamics of the disease using Latin hypercube sampling with partial rank correlation coefficient index, (LHS-PRCC).

• (iii) 10,898 out of 22,570 quarantined individuals, $(48.3\%)$, were discharged by NCDC on the 03/08/2020. There was a repeat of this on 20/09/2020 where 3316 out of 10,960 quarantined individuals $(30.3\%)$, were discharged. Discharging such a high percentage in a day could pose a danger to the containment of the disease because that an hospitalized individual tested negative to COVID-19 does not mean (s)he has fully recovered [6]. Such individual becomes asymptomatic and contributes to the spread of the disease. We therefore investigate the impact of incomplete recovery on the spread of the virus.

• (iv) To investigate the impacts of three containment measures—compliance to preventive guidelines, contact tracing and mass diagnosis of the citizens on the spread of COVID-19 in Nigeria. This is done in optimal control framework using Pontryagin’s maximum principle

The rest of this article is organized as follows: A deterministic model is formulated and analyzed in section “Baseline Model” and disease free stationary solution of the model is analyzed in section “Model Analysis”. Key parameters of the model are estimated by data fitting and sensitivity analysis is carried out in section “Parameter Estimation”. Analysis is carried out for time-dependent controls in section “Optimal Control” while the effects of intervention strategies are investigated in section “Simulation and Discussions”.

Baseline Model

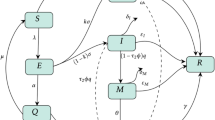
Following previous models [29, 38, 40], compartments relevant to the dynamics of COVID-19 in Nigeria is incorporated into a general SEIR model. The population is divided into the following compartments: susceptible (S), exposed (E), quarantined (Q), asymptomatic infectious (A), symptomatic infectious (I) and recovered (R). It is assumed that disease transmission only occur when susceptible individuals come in contact with infectious individuals. We consider disease related deaths only for quarantined and symptomatic infectious populations. As of June 2020, up to 812 healthcare workers have contracted the disease due to inadequate protective equipments [35]. We therefore include the transmission route from quarantined individuals. We also assume that the disease is transmitted faster in symptomatic population than asymptomatic and quarantined populations and thus include a variability factors $\eta _A$, $\eta _Q$. We consider disease related deaths only for quarantined and symptomatic populations.

Susceptible individuals become exposed when they come in contact with infectious individuals at the transmission rate $\beta$. Through contact tracing, exposed individuals become quarantined at the rate $q_E$, become infectious (symptomatic or asymptomatic) after an incubation period of $\frac{1}{\sigma }$. A fraction a of the exposed individuals become asymptomatic A while the remaining fraction $(1-a)$ become symptomatic infectious I. Due to mass/random testing, symptomatic and asymptomatic individuals are tested for the virus and quarantined (at home, isolation centre or hospital) at the rate $q_I$ and $q_A$ respectively. Recovery rates for symptomatic, asymptomatic and quarantined are taken as $\rho _I$, $\rho _A$, $\rho _Q$. That an hospitalized individual tested negative to COVID-19 does not mean (s)he has fully recovered [6]. Such individual becomes asymptomatic and contributes to the spread of the disease. We therefore take $\kappa$ to represent the fraction of the quarantined individuals with incomplete recovery and are moved to asymptomatic compartment. We consider disease related deaths only for quarantined and symptomatic populations. See Fig. 1 for the epidemic interactions among the human compartments and see Table 1 for definitions of parameters.

Fig. 1

Epidemic interactions among the human compartments

The model is therefore given as the following system of equations:

$$\begin{aligned} \frac{dS}{dt}= & {} - \frac{\beta (t) S (I+\eta _A A+ \eta _Q Q)}{N} , \end{aligned}$$

(1)

$$\begin{aligned} \frac{dE}{dt}= & {} \frac{\beta (t) S (I+\eta _A A+ \eta _Q Q)}{N} - (q_E+\sigma ) E, \end{aligned}$$

(2)

$$\begin{aligned} \frac{dA}{dt}= & {} \sigma a E - (\rho _A + q_A ) A + \kappa \rho _Q Q , \end{aligned}$$

(3)

$$\begin{aligned} \frac{dI}{dt}= & {} \sigma (1-a) E - (\rho _I + q_I +\delta _I) I , \end{aligned}$$

(4)

$$\begin{aligned} \frac{dQ}{dt}= & {} q_EE +q_A A+q_I I - (\rho _Q(t) +\delta _Q) Q , \end{aligned}$$

(5)

$$\begin{aligned} \frac{dR}{dt}= & {} (1-\kappa )\rho _Q(t) Q + \rho _A A +\rho _I I, \end{aligned}$$

(6)

as $N(t)=S(t)+E(t)+A(t)+I(t)+Q(t)+R(t)$.

Table 1 Summary of the parameters

Model Analysis

The following result gives the feasible region of the model (1)–(6):

Theorem 3.1

Let $N(0)=N_0$ and let the initial data for (1)–(6) be $S(0)>0$, $E(0)\ge 0$, $A(0)\ge 0$, $I(0)\ge 0$, $Q(0)\ge 0$, and $R(0)\ge 0$. Then the solutions (S(t), E(t), A(t), I(t), Q(t), R(t)) of the model will remain non-negative for all time $t>0$. Furthermore if $S(0)+E(0)+I(0)+Q(0)+R(0)= N_0$, then the feasible region of solution is defined by

$$\begin{aligned} \varOmega= & {} \left\{ (S(t),E(t),A(t),I(t),Q(t),R(t))\in \right. {\mathbb {R}}^{6}_+ S(t)\\&\quad \left. +E(t)+A(t)+I(t)+Q(t)+R(t) \le N_0 \right\} , \end{aligned}$$

Proof

It can be seen from (1) that

$$\begin{aligned}\frac{dS}{S}=- \frac{\beta (t) (I+\eta _A A+ \eta _Q Q)}{N} dt,\end{aligned}$$

it then follows that

$$\begin{aligned} S(t)=S(0)\exp \left( -\int _{0}^{t} \frac{\beta (s) (I(s)+\eta _A A(s)+ \eta _Q Q(s))}{N(s)} ds \right)>0 \qquad \text{ for } \; t>0. \end{aligned}$$

(7)

Following a similar argument, it can be established that

$$\begin{aligned} E(t)\ge 0,\;A(t)\ge 0,\;I(t)\ge 0,\;Q(t)\ge 0,\;R(t)\ge 0. \end{aligned}$$

(8)

Now, adding (1) through (6),

$$\begin{aligned} \frac{dN}{dt}=-(\delta _II(t)+\delta _QQ(t)). \end{aligned}$$

This implies

$$\begin{aligned} N(t)=N(0)-\int _{0}^{t}(\delta _II(s)+\delta _QQ(s))\; ds\; \le \; N(0) \qquad \text{ for } \; t>0. \end{aligned}$$

(9)

Theorem 3.1 follows from (7)–(9). $\square$

System (1)–(6) has a disease-free equilibrium (DFE) given by

$$\begin{aligned} \varepsilon _0 = (S^\star ,E^\star ,A^\star ,I^\star ,Q^\star ,R^\star ) = \left( N_0, \;0,\;0, \;0, \;0, \;0\right) . \end{aligned}$$

(10)

Using the next generation operator approach of [7], the basic reproduction number is calculated for the special case when $\beta (t)=\beta _1$, $\rho _Q(t)=\rho _Q^1$. The associated next generation matrices F and V for the new infection terms and the transition terms are, respectively,

$$\begin{aligned} F=\left[ \begin{array}{cccc} 0 &{} \eta _A\beta _1&{} \beta _1&{} \eta _Q\beta _1 \\ 0 &{} 0&{} 0&{} 0 \\ 0 &{} 0&{} 0&{} 0 \\ 0 &{} 0&{} 0&{} 0 \\ \end{array} \right] \end{aligned}$$

and

$$\begin{aligned} V= \left[ \begin{array}{cccc} q_E+\sigma &{} 0&{} 0&{} 0 \\ -a\sigma &{} \rho _A+q_A&{} 0&{} -\kappa \rho _Q^1\\ -(1-a)\sigma &{} 0&{} \rho _I+q_I+\delta _I&{} 0\\ -q_E &{} -q_A&{} -q_I&{} \rho _Q^1+\delta _Q\\ \end{array} \right] . \end{aligned}$$

${\mathfrak {R}}_0$ is the spectral radius of $FV^{-1}$ and is given as

$$\begin{aligned} {\mathfrak {R}}_0 = {\mathfrak {R}}^1_0+{\mathfrak {R}}^2_0+{\mathfrak {R}}^3_0+{\mathfrak {R}}^4_0+{\mathfrak {R}}^5_0+{\mathfrak {R}}^6_0, \end{aligned}$$

(11)

where

$$\begin{aligned} {\mathfrak {R}}^1_0= & {} \frac{\beta _1 (1-a)\sigma (\rho _A + q_A)(\rho _Q^1 +\delta _Q)}{(q_E+\sigma )(\rho _I+q_I+\delta _I)((\rho _A + q_A)(\rho _Q^1 +\delta _Q)-\kappa \rho _Q^1 q_A)} \\ {\mathfrak {R}}^2_0= & {} \frac{\beta _1 \eta _A a\sigma (\rho _Q^1 + \delta _Q)}{(q_E+\sigma )((\rho _A + q_A)(\rho _Q^1 +\delta _Q)-\kappa \rho _Q^1 q_A)} \\ {\mathfrak {R}}^3_0= & {} \frac{\beta _1\eta _Q(\rho _A + q_A)q_E }{(q_E+\sigma )((\rho _A + q_A)(\rho _Q^1 +\delta _Q)-\kappa \rho _Q^1 q_A)} \\ {\mathfrak {R}}^4_0= & {} \frac{a\beta _1\eta _Q \sigma q_A}{(q_E+\sigma )((\rho _A + q_A)(\rho _Q^1 +\delta _Q)-\kappa \rho _Q^1 q_A)} \\ {\mathfrak {R}}^5_0= & {} \frac{(1-a)\beta _1\eta _Q \sigma q_I(\rho _A + q_A)}{(q_E+\sigma )(\rho _I+q_I+\delta _I)((\rho _A + q_A)(\rho _Q^1 +\delta _Q)-\kappa \rho _Q^1 q_A)} \\ {\mathfrak {R}}^6_0= & {} \frac{\beta _1\kappa }{(q_E+\sigma )((\rho _A + q_A)(\rho _Q^1 +\delta _Q)-\kappa \rho _Q^1 q_A)} \left[ \eta _A q_E + \frac{\sigma (1-a)(\eta _A q_I-q_A)}{\rho _I + q_I +\delta _I} \right] . \end{aligned}$$

The basic reproduction number ${\mathfrak {R}}_0$ is a measure of the average number of new infections generated by a single infected person during his or her infectious period through an immunologically naive population. The basic reproduction number is a significant indicator in detecting the transmission risks of an infectious disease and its control. ${\mathfrak {R}}^1_0$, ${\mathfrak {R}}^2_0$ and ${\mathfrak {R}}^3_0-{\mathfrak {R}}^5_0$ represent the contributions of symptomatic infectious class, asymptomatic infectious class and quarantined class, respectively, to the spread of the virus while incomplete recovery contributes to ${\mathfrak {R}}^j_0$, $(j=1,\ldots ,6)$.

Following the local stability result of [8], we have

Theorem 3.2

Taking $\beta (t)=\beta _1$ and $\rho _Q(t)=\rho _Q^1$, the disease-free equilibrium $\varepsilon _0$ of (1)–(6) is locally stable in $\varOmega$ if ${\mathfrak {R}}_0<1$.

Proof

The Jacobian matrix of the system (2.1)–(2.6) evaluated at disease-free equilibrium point $\varepsilon _0$ is obtained as

$$\begin{aligned} J({\varepsilon _0}) = \left( \begin{array}{cccccc} 0 &{} 0 &{} \beta _1\eta _A &{} \beta _1 &{} \beta _1\eta _Q &{} 0\\ 0 &{} -(q_E + \sigma ) &{} -\beta _1\eta _A &{} -\beta _1 &{} -\beta _1\eta _Q &{} 0\\ 0 &{}\sigma a &{} -(\rho _A + q_A) &{} 0 &{} \kappa \rho ^1_Q&{} 0\\ 0 &{} \sigma (1-a) &{} 0 &{} - (\rho _I + q_I + \delta _I) &{} 0 &{} 0\\ 0 &{} q_E &{} q_A &{} q_I &{} - (\rho ^1_Q + \delta _Q) &{} 0\\ 0 &{} 0 &{} \rho _A &{} \rho _I &{} (1-\kappa )\rho ^1_Q &{} 0 \end{array}\right) , \end{aligned}$$

(12)

and we need to show that all the eigenvalues of $J(\varepsilon _0)$ are negative or zero. As the first and sixth columns contain only the diagonal terms which form the two zero eigenvalues $\lambda _1 = \lambda _6 = 0$, the other four eigenvalues can be obtained from the sub-matrix, $J_1(\varepsilon )$, formed by excluding the first and sixth rows and columns of $J(\varepsilon _0)$. For simplicity, we take $\kappa =0$ and obtain

$$\begin{aligned} J_1({\varepsilon _0}) =\left( \begin{array}{cccc} -(q_E + \sigma ) &{} -\beta _1\eta _A &{} -\beta _1 &{} -\beta _1\eta _Q \\ \sigma a &{} -(\rho _A + q_A) &{} 0 &{} 0\\ \sigma (1-a) &{} 0 &{} - (\rho _I + q_I + \delta _I)&{} 0 \\ q_E &{} q_A &{} q_I &{} - (\rho ^1_Q + \delta _Q) \end{array}\right) . \end{aligned}$$

The eigenvalues of the matrix $J_1({\varepsilon _0})$ are the roots of the characteristic equation

$$\begin{aligned} \lambda ^4 + a_3\lambda ^3 + a_2\lambda ^2 + a_1\lambda + a_0 = 0, \end{aligned}$$

(13)

where

$$\begin{aligned} a_3= & {} C_1+C_2+C_3+C_4, \end{aligned}$$

(14)

$$\begin{aligned} a_2= & {} C_1C_2+C_1C_3+C_1C_4+C_2C_3+C_2C_4+C_3C_4 - (1-a)\beta _1\sigma -a\eta _A\beta _1\sigma \nonumber \\&- \beta _1\eta _Q q_E, \end{aligned}$$

(15)

$$\begin{aligned} a_1= & {} C_1C_2C_3+C_1C_2C_4+C_1C_3C_4+C_2C_3C_4 - (1-a)\beta _1\sigma (C_2+C_4) \nonumber \\&- a\eta _A\beta _1\sigma (C_3+C_4)- (1-a)\eta _Q\beta _1\sigma q_I- a\eta _Q\beta _1\sigma q_A - \eta _Q\beta _1q_E(C_2+C_3), \end{aligned}$$

(16)

$$\begin{aligned} a_0= & {} C_1C_2C_3C_4 - (1-a)\beta _1\sigma C_2C_4 - a\eta _A \beta _1\sigma C_3C_4 - (1-a)\eta _Q\beta _1\sigma q_I C_2 \nonumber \\&- a\eta _Q\beta _1\sigma q_A C_3 - \eta _Q\beta _1 q_E C_2C_3, \end{aligned}$$

(17)

$$\begin{aligned} C_1=q_E+\sigma , \quad C_2=\rho _A+q_A, \quad C_3=\rho _I+q_I+\delta _I, \quad C_4=\rho ^1_Q+\delta _Q. \end{aligned}$$

We employ the Routh-Hurwitz criterion, see [23], which states that all roots of polynomial (13) have negative real parts if and only if $a_i>0$, for $i=1,\ldots ,4$ and

$$\begin{aligned}\qquad H_2 =\left| \begin{array}{cc} a_3 &{} 1 \\ a_1 &{} a_2 \end{array}\right|> 0,\qquad H_3 = \left| \begin{array}{ccc} a_3 &{} 1 &{} 0 \\ a_1 &{} a_2 &{} a_3\\ 0 &{} a_0 &{} a_1\\ \end{array}\right| >0.\end{aligned}$$

Simplifying (14)–(17), we have

$$\begin{aligned} a_3= & {} C_1+C_2+C_3+C_4, \\ a_2= & {} C_1C_3\left( 1-{\mathfrak {R}}^1_0 \right) +C_1C_2\left( 1-{\mathfrak {R}}^2_0 \right) +C_1C_4\left( 1-{\mathfrak {R}}^3_0 \right) + C_2C_3+ C_2C_4+ C_3C_4 , \\ a_1= & {} C_1C_2C_3\left( 1-{\mathfrak {R}}^1_0-{\mathfrak {R}}^2_0 \right) +C_1C_2C_3\left( 1-{\mathfrak {R}}^2_0-{\mathfrak {R}}^3_0-{\mathfrak {R}}^4_0 \right) \\&+ C_1C_3C_4\left( 1-{\mathfrak {R}}^1_0-{\mathfrak {R}}^3_0-{\mathfrak {R}}^5_0 \right) + C_2C_3C_4, \\ a_0= & {} C_1C_2C_3C_3C_4\left( 1 -{\mathfrak {R}}_0 \right) . \end{aligned}$$

Clearly $a_i>0$ $(i=1,\ldots ,4)$ when ${\mathfrak {R}}_0<1$. Now, for $H_2$, we obtain (after a simple calculation)

$$\begin{aligned} H_2= & {} C_1C_3(C_1+C_3)\left( 1-{\mathfrak {R}}^1_0 \right) +C_1C_2(C_1+C_2)\left( 1-{\mathfrak {R}}^2_0 \right) +C_1C_4(C_1+C_4)\left( 1-{\mathfrak {R}}^3_0 \right) \\&+\; (1-a)\beta _1\sigma \eta _Qq_I + a\beta _1\sigma \eta _Qq_A+ C_4(C_2+C_3)^2+2C_1C_2C_3 \\&+\; (C_2+C_3)(2C_1C_4+C_2C_3+C^2_4) \; > \;0 \qquad \text{ whenever } \; {\mathfrak {R}}_0<1. \end{aligned}$$

$H_3>0$ can be established similarly. Therefore, the disease-free equilibrium point is locally stable since all the eigenvalues of the Jacobian matrix (12) are either zero or have negative real parts when ${\mathfrak {R}}_0 < 1$. $\square$

Parameter Estimation

Using the cumulative “death cases” data provided by NCDC from 27/02/2020 to 17/05/2020, Enahoro et al. [14] estimated the basic reproduction number for COVID-19 dynamics in Nigeria as $2.05 \le {\mathfrak {R}}_0\le 2.301$. Using the “active cases” data provided by NCDC from 16/03/2020 to 02/05/2020, Okuonghae and Omame [29] estimated the basic reproduction number for COVID-19 dynamics in Lagos (the epicentre of COVID-19 in Nigeria) as $2.006 \le {\mathfrak {R}}_0\le 2.1074$. It was also predicted that cumulative active cases of the disease in Lagos will be 160,000 in mid August, whereas the data provided by NCDC shows that there were 2751 active cases in Lagos as of 11/08/2020. Part of the causes in the discrepancy in the predicted and reality is the fact that the Government of Nigeria has implemented certain containment measures such as regular hand washing with alcohol-based sanitizer, use of face masks in public, social distancing, movement restrictions etc. This reduces the transmission rate and consequently the basic reproduction number. Another cause of the discrepancy is the fact that only one compartment was used for model fitting and parameter estimation. The unused data may be the source of error in the estimated values. In this work, three compartments are used simultaneously for model fitting. Therefore giving us better parameter values. For this purpose, we add two new compartments - confirmed cases (C) and death cases (D) to model (1)–(6).

$$\begin{aligned} \frac{dD}{dt}= \delta _I I + \delta _Q Q. \end{aligned}$$

(18)

$\text{ Confirmed } \text{ cases }=\text{ Quarantined } \text{ individuals }+\text{ Known } \text{ recovered } \text{ individuals }+\text{ Death } \text{ cases }$. Therefore

$$\begin{aligned} \frac{dC}{dt} = q_EE +q_A A+q_I I + \delta _I I. \end{aligned}$$

(19)

We use the COVID-19 data provided by Nigeria Centre for Disease Control (NCDC) from 27/02/2020 through 07/10/2020 (222 days) which is publicly available at [26] for our model fitting. The quarantined compartment (Q) is fitted to the cumulative “active cases”, death compartment is fitted to the cumulative “death cases” while confirmed cases compartment is fitted to the cumulative “confirmed cases” data. Nigeria is roughly a 200,000,000 population country, we therefore set $S(0)=199,999,998$, $I(0)=1$, $Q(0)=1$, and other variables set to zero initially. Our simulation was carried out using “lsqcurvefit” package by MATLAB.

“lsqcurvefit” package by MATLAB solves nonlinear data-fitting problems in the least-square sense. That is, given input data tdata (which could be matrices or vectors) and the observed output data ydata (which could be matrices or vectors), we find coefficients x that best fit the equation

$$\begin{aligned} \min _{x}\Vert F(x,tdata)-ydata\Vert ^2_2= \min _x\sum _{i}(F(x,tdata_i)-ydata_i)^2, \end{aligned}$$

where F(x, tdata) is a matrix-valued or vector-valued function of the same size as ydata [21].

The transmission rate is not constant as it is affected by individuals and government’s response to COVID-19 containment measures. In order to accommodate the fact that the transmission rate changes with time, we follow [39] and assume that the transmission rate $(\beta )$ takes the form

$$\begin{aligned} \beta =\left\{ \begin{array}{cc} \beta _0, &{} 0\le t\le t_0 \\ \beta _{\min } + (\beta _0-\beta _{\min })\exp (-\varsigma (t-t_0)), &{} t_0\le t\le t_1 \\ \beta _1&{} t>t_1 \end{array} \right. , \end{aligned}$$

where $\beta _1=\beta _{\min } + (\beta _0-\beta _{\min })\exp (-\varsigma (t_1-t_0))$ and $\varsigma$ is the rate at which contact decreases. It is also assumed that the recovery rate for the quarantined individuals $(\rho _Q)$ takes the form

$$\begin{aligned} \rho _Q=\left\{ \begin{array}{cc} \displaystyle \rho ^1_Q\left( \frac{t}{t_1}\right) ^3 , &{} 0\le t\le t_1 \\ \rho ^1_Q&{} t>t_1 \end{array} \right. . \end{aligned}$$

This assumption is necessary to accommodate the sudden discharge of 10898 out of 22570 quarantined individuals.

Lock-down was initiated in states with cases of COVID-19 from 30/03/2020 (31 days after the incidence of COVID-19). We therefore take $t_0=31$. We also assume that $\kappa =0$.

$\beta _0$, $\beta _{\min }$ and $\beta _1$ are estimated as 1.66, 0.107 and 0.109 respectively while the basic reproduction number is estimated as 0.675 with 99% confidence interval [0.669, 0.680]. Table 2 shows the estimated parameter values while Fig. 2a–c show the plot of the real-life data and the fitted curves. As shown in Fig. 2d, our model estimates the spread of the virus reached its peak in July, 2020. It was also estimated that by the end of 07/10/2020, about 88,000 individuals are exposed to the virus, 80,000 are symptomatic but undiscovered and 83,000 are asymptomatic but undiscovered. For subsequent simulation, we take $\beta =\beta _1$ and $\rho _Q=\rho ^1_Q$. If the trend in Fig. 2 continues, the virus will remain in the human population beyond two hundred days (see Fig. 5)

Table 2 Summary of the parameter values

Fig. 2

a–c Data and simulated figures from 27/02/2020 through 07/10/2020. c Simulated trajectories of undiscovered infected individuals (Exposed individuals (E), asymptomatic individuals (A) and symptomatic individuals (I))

Uncertainty and Global Sensitivity Analysis

Uncertainty analysis (UA) delineates the relationship between the uncertainty in the outcomes of a model and the uncertainty in the model inputs [16]. While sensitivity analysis helps us to recognize important parameters in the dynamics of infection being studied [37]. As a measure of uncertainty in our parameter estimation, we estimate confidence interval for each parameter. This is then used to estimate the confidence interval for the basic reproduction number. There are different techniques for SA - variance-based methods, global screening methods, sampling-based methods. See [47] for comparisons between these methods. Since our focus is to quantify the impact of each parameter on the basic reproduction number (${\mathfrak {R}}_0$) and to determine which parameters are important in contributing uncertainty to the predictions of our model, we adopt a sampling-based method called Latin hypercube sampling with partial rank correlation coefficient index, (LHS-PRCC). For a comprehensive description of this method, we refer to [4, 20].

Sensitivity indices of the basic reproduction number relative to model parameters are derived. LHS/PRCC method with 5000 samples from a uniform distribution of each parameter range are generated and used as simulation inputs. The PRCC for the model parameters are displayed pictorially in Fig. 3. The size of PRCC shows the influence of the parameter in the dynamics of the disease. Thus a slight change in a highly influential parameter is likely to cause a significant change to the disease dynamics. The PRCC sign (+ or -) shows the qualitative relationship between the input parameter and the output variables. Scatter plot showing the relationship of parameters with great impacts on the basic reproduction number are also shown in Fig. 4.

Figure 3 indicates that recovery rates for symptomatic infected, $\rho _I$ as well as asymptomatic infected, $\rho _A$ and infectious-susceptible transmission rate, $\beta$, are critical for precisely forecasting and controlling the number of COVID-19 cases. Uncertainty in any of these three parameters is an important contributor to uncertainty in prevalence of the disease. While the recovery rates for symptomatic infected individuals, $\rho _I$ and asymptomatic infected, $\rho _A$ should be increased, infectious-susceptible transmission rate, $\beta$, should be decreased in order to curtail the transmission of the virus. It can also be seen in Fig. 3 that, with the present situation of the pandemic in Nigeria, the influence of incomplete recovery $\kappa$ is negligible. This is further demonstrated in Fig. 5. Figure 5 also shows that the virus will remain in the human population beyond 25/04/2021 (200 days from 07/10/2020).

Next, we seek to reduce the virus in the human population and eradicate the disease within the shortest possible period.

Fig. 3

PRCC of the influence of each parameter on the basic reproduction number

Fig. 4

Scatter plot showing the relationship of parameters $\beta$, $\rho _I$ and $\rho _A$ on the basic reproduction number

Fig. 5

Effect of incomplete recovery on a cumulative confirmed cases, b cumulative death cases, c quarantined d infectious individuals (I) and e asymptomatic infected individuals (A)

Optimal Control

In this section, we assume that a fraction $\xi$ of the general population abide by the WHO prevention guidelines such as the use of face mask, regular hand washing using hand sanitizer, physical distancing etc with success of compliance $\phi (t)$. It is worth mentioning that $\phi (t)$ incorporates the level of compliance and efficacy of the guidelines. Other control parameters are rate of contact tracing, r(t), and rate of mass/random diagnosis of citizens.

We therefore consider the system

$$\begin{aligned} \frac{dS}{dt}= & {} - \frac{(1-\xi \phi (t))\beta _1 S (I+\eta _A A+ \eta _Q Q)}{N} , \end{aligned}$$

(20)

$$\begin{aligned} \frac{dE}{dt}= & {} \frac{(1-\xi \phi (t))\beta _1 S (I+\eta _A A + \eta _Q Q)}{N} - (q_E+r(t)+\sigma ) E, \end{aligned}$$

(21)

$$\begin{aligned} \frac{dA}{dt}= & {} \sigma a E - (\rho _A + q_A+\omega _A(t) ) A+ \kappa \rho _Q^1 Q , \end{aligned}$$

(22)

$$\begin{aligned} \frac{dI}{dt}= & {} \sigma (1-a) E - (\rho _I + q_I+\omega _I(t) +\delta _I) I , \end{aligned}$$

(23)

$$\begin{aligned} \frac{dQ}{dt}= & {} (q_E+r(t))E + (q_A+\omega _A(t)) A+(q_I+\omega _I(t)) I - (\rho _Q^1 +\delta _Q) Q , \end{aligned}$$

(24)

$$\begin{aligned} \frac{dR}{dt}= & {} (1-\kappa )\rho _Q^1 Q +\rho _A A +\rho _I I, \end{aligned}$$

(25)

as $N(t)=S(t)+E(t)+A(t)+I(t)+Q(t)+R(t)$.

We follow [22, 45] in this section. We optimize the control variables $\phi (t)$, r(t), $\omega _A(t)$ and $\omega _I(t)$ which are assumed to be at least Lebesgue measurable on [0, T]. The control set is defined as

$$\begin{aligned} \varGamma= & {} \left\{ (\phi (t),r(t),\omega _A(t),\omega _I(t)) \;|\; 0\le \phi (t)\le \phi ^{\max },\; 0\le r(t)\le r^{\max },\right. \\&\ \qquad \left. 0\le \omega (t)\le \omega _A^{\max }, 0\le \omega (t)\le \omega _I^{\max } \right\} , \end{aligned}$$

where $\phi ^{\max }$, $r^{\max }$, $\omega _A^{\max }$ and $\omega _I^{\max }$ denote the upper bounds for the citizens’ success of compliance, contact tracing and mass COVID-19 testing rates for asymptomatic and symptomatic patients respectively. These bounds set limitations on the maximum control rates in a given time period.

It is desired to minimize the total number of infections as well as the costs of controls over the time interval [0, T]. Let parameters $c_{j}$, $(j = 1,2,3,4)$, with appropriate units, be the appropriate costs associated with these controls. The objective function is given as

$$\begin{aligned}&J(\phi , r, \omega _A, \omega _I)\nonumber \\&\quad = \min _{\phi ,r,\omega _A,\omega _I\; \in \;\varGamma } \int _{0}^{T} \left[ E(t)+I(t)+ A(t)\right. \nonumber \\&\quad \left. + \frac{1}{2}\left( c_{1}\phi ^2(t) +c_{2}r^2(t)+c_{3}\omega _A^2(t) +c_{4}\omega _I^2(t)\right) \right] dt. \end{aligned}$$

(26)

We incorporate quadratic terms to indicate nonlinear costs potentially arising at high intervention levels [22, 45]. (26) is subject to the state equations (20)–(25).

The following theorem establishes the existence of optimal control.

Theorem 5.1

There exists $\phi (t)$, r(t), $\omega _A(t)$, $\omega _I(t)$ such that the objective functional (26) is minimized.

Proof

The control set $\varOmega$ is closed, convex, bounded and time-invariant. The integrand of the objective functional in (26) and the right hand side of (20)–(25) are continuously differentiable. Hence, the conditions for the existence of global optimal control are satisfied based on the standard optimal control theorem [11, Theorem 2, page 66]. $\square$

We apply Pontryagin’s Maximum Principle (PMP) [32] to determine the necessary conditions for the optimal control of the disease. By introducing the adjoint functions and representing the optimal control $\phi ^*$, $r^*$, $\omega _A^*$, $\omega _I^*$ in terms of the state and adjoint functions, PMP changes the problem of minimizing the objective functional, subject to the state equations, into that of minimizing the Hamiltonian with respect to the controls.

$$\begin{aligned} \begin{array}{rcl} {\mathcal {L}} &{}=&{}\displaystyle E(t)+I(t)+ A(t) + \frac{1}{2}\left( c_{1}\phi ^2(t) +c_{2}r^2(t)+c_{3}\omega _A^2(t) +c_{4}\omega _I^2(t)\right) \\ &{}&{}\displaystyle + \lambda _S \left\{ - \frac{1}{N}(1-\xi \phi (t))\beta _1 S (I+\eta _A A+ \eta _Q Q)\right\} \\ &{}&{}\displaystyle + \lambda _E \left\{ \frac{1}{N}(1-\xi \phi (t))\beta _1 S (I+\eta _A A + \eta _Q Q) - (q_E+r(t)+\sigma ) E\right\} \\ &{}&{}\displaystyle + \lambda _A \{ \sigma a E - (\rho _A + q_A+\omega _A(t) ) A + \kappa \rho _Q^1 Q\} \\ &{}&{}\displaystyle + \lambda _I \{\sigma (1-a) E - (\rho _I + q_I+\omega _I(t) +\delta _I) I\} \\ &{}&{}\displaystyle + \lambda _Q \{(q_E+r(t))E + (q_A+\omega _A(t)) A+(q_I+\omega _I(t)) I - (\rho _Q^1 +\delta _Q) Q\} \\ &{}&{}\displaystyle + \lambda _R \{ (1-\kappa )\rho _Q^1 Q +\rho _A A +\rho _I I \}. \end{array} \end{aligned}$$

(27)

where the $\lambda _S, \lambda _E, \lambda _Q, \lambda _A, \lambda _I, \lambda _H, \lambda _R$ are the adjoint variables or co-state variables. Applying Pontryagin’s Maximum Principle [32], we obtain the following theorem.

Theorem 5.2

Given an optimal control $(\phi ^*, r^*, \omega _A^*, \omega _I^*)$ and solutions $S^*, E^*, A^*, I^*, Q^*, R^*$ of the corresponding (20)–(25) that minimizes $J(\phi , r, \omega _A, \omega _I)$ over $\varOmega$. Then there exists adjoint variables $\lambda _S, \lambda _E, \lambda _A, \lambda _I, \lambda _Q, \lambda _R$ satisfying

$$\begin{aligned} \left. \begin{array}{lllllll} \displaystyle - \frac{d\lambda _S}{dt} &{}=&{} \displaystyle \frac{\partial {\mathcal {L}}}{\partial S} = \frac{1}{N^2}(1 - \xi \phi (t))\beta _1(I+\eta _A A+ \eta _Q Q)(N-S)(\lambda _E-\lambda _S) \\ \displaystyle - \frac{d\lambda _E}{dt} &{}=&{} \displaystyle \frac{\partial {\mathcal {L}}}{\partial E} = 1 + \left[ \frac{(1 - \xi \phi (t))\beta _1 S(I+\eta _A A+ \eta _Q Q)}{N^2} \right] (\lambda _S - \lambda _E) + (\lambda _Q-\lambda _E)(q_E+r(t))\\ &{}&{} -\sigma \lambda _E+ \sigma a\lambda _A+ \sigma (1-a)\lambda _I \\ \displaystyle - \frac{d\lambda _A}{dt} &{}=&{}\displaystyle \frac{\partial {\mathcal {L}}}{\partial A} =\displaystyle 1 + \frac{1}{N^2}(1-\xi \phi (t))\beta _1S(\lambda _S-\lambda _E) (I + \eta _A (A-N)+\eta _QQ) ) \\ &{}&{} +(q_A+\omega _A(t))(\lambda _Q-\lambda _A) + \rho _A(\lambda _R-\lambda _A)\\ \displaystyle - \frac{d\lambda _I}{dt} &{}=&{}\displaystyle \frac{\partial {\mathcal {L}}}{\partial I} =\displaystyle 1 + \frac{1}{N^2}(1-\xi \phi (t))\beta _1S(\lambda _S-\lambda _E) (I-N + \eta _A A+\eta _QQ) ) \\ &{}&{} +(q_I+\omega _I(t))(\lambda _Q-\lambda _I) + \rho _I(\lambda _R-\lambda _I) - \delta _I\lambda _I\\ \displaystyle - \frac{d\lambda _Q}{dt} &{}=&{} \displaystyle \frac{\partial {\mathcal {L}}}{\partial Q} =\displaystyle \frac{1}{N^2}(1-\xi \phi (t))\beta _1S(\lambda _S-\lambda _E) (I + \eta _A A+\eta _Q(Q-N)) ) \\ &{}&{} + \rho _Q^1(1-\kappa )(\lambda _R-\lambda _Q) + \kappa \rho _Q^1(\lambda _A-\lambda _Q) - \delta _Q\lambda _Q\\ \displaystyle - \frac{d\lambda _R}{dt} &{}=&{}\displaystyle \frac{\partial {\mathcal {L}}}{\partial R} = \frac{1}{N^2}(1 - \xi \phi (t))\beta _1 S(I+\eta _AA+\eta _QQ) (\lambda _S - \lambda _E)\nonumber \end{array} \right\} \\ \end{aligned}$$

(28)

and with transversality conditions $\lambda _S(T) = \lambda _E(T) = \lambda _I(T) = \lambda _Q(T) = \lambda _R(T) = 0$ and the control $\phi ^*, r^*$ and $\omega ^*$ satisfy the optimality condition

$$\begin{aligned} \left. \begin{array}{llll} \phi ^* &{}=&{}\displaystyle \max \left( 0, \min \left( \frac{(\lambda _E - \lambda _S)\xi \beta _1 S(I+\eta _AA+\eta _QQ) }{c_1N}, \; \phi ^{\max }\right) \right) \\ r^* &{}=&{} \displaystyle \max \left( 0, \min \left( \frac{(\lambda _E - \lambda _Q)E}{c_{2}}, \; r^{\max }\right) \right) \\ \omega _A^* &{}=&{}\displaystyle \max \left( 0, \min \left( \frac{(\lambda _A - \lambda _Q) A }{c_{3}}, \; \omega _A^{\max }\right) \right) \\ \omega _I^* &{}=&{}\displaystyle \max \left( 0, \min \left( \frac{(\lambda _I - \lambda _Q) I }{c_{4}}, \; \omega _I^{\max }\right) \right) \end{array} \right\} \end{aligned}$$

(29)

Proof

The differential equations (28) that govern the adjoint variables are obtained by differentiation of the Hamiltonian function (27), evaluated at the optimal control and with transversality conditions

$$\begin{aligned} \lambda _S(T) = \lambda _E(T) = \lambda _A(T)= \lambda _I(T) = \lambda _Q(T) = \lambda _R(T) = 0. \end{aligned}$$

On the interior of the control set, where $0< \phi < \phi ^{\max }$, $0< r < r^{\max }$, $0< \omega < \omega ^{\max }$, we have

$$\begin{aligned} 0= & {} \frac{\partial {\mathcal {L}}}{\partial \phi } = c_{1}\phi (t) + \frac{\xi \beta S(I+\eta _AA+\eta _QQ)}{N} (\lambda _S - \lambda _E) \\ \displaystyle \phi (t)= & {} \frac{(\lambda _E - \lambda _S)\xi \beta _1 S(I+\eta _AA+\eta _QQ) }{c_1N} \\ 0= & {} \frac{\partial {\mathcal {L}}}{\partial r} = c_{2}r(t) + (\lambda _Q - \lambda _E)E \\ r(t)= & {} \frac{(\lambda _E - \lambda _Q)E}{c_{2}} \\ 0= & {} \frac{\partial {\mathcal {L}}}{\partial \omega _A} = c_{3}\omega _A(t) - A\lambda _A + A\lambda _Q \\ \omega _A(t)= & {} \frac{(\lambda _A - \lambda _Q) A }{c_{3}} \\ 0= & {} \frac{\partial {\mathcal {L}}}{\partial \omega _I} = c_{4}\omega _I(t) - I\lambda _I + I\lambda _Q \\ \displaystyle \omega _I(t)= & {} \frac{(\lambda _I - \lambda _Q) I }{c_{4}}. \end{aligned}$$

(29) follows immediately. $\square$

Simulation and Discussions

In this section, the effects of the optimal control strategies on the dynamics of the disease are investigated numerically. The state equations (20)–(25) are solved forward marching in time, with an initial guess for the control variables. Then, the adjoint equations (10) are solved backward in time using the solutions of the state equations. The control is updated with new values of the state and adjoint solutions. The process is repeated until convergence of solution is attained.

The parameter values in Table 2 are used to carry out the numerical simulation. As of August, 2020, the probability of detecting an infectious individual in random testing is 0.17 [26]. This implies many testing kits were used for uninfected individuals. It is therefore assumed that the cost of random/mass diagnosis to detect infectious patient is very high. The following set of values are assigned to the cost parameters:

$$\begin{aligned} c_{1} = 200, \; c_{2} = 2000, \; c_{3} = 3500, \; c_{4} = 3000 . \end{aligned}$$

Figure 5 shows the infection curves for the model without controls. Next we investigate the impacts of each control measure in curtailing the spread of the virus. We seek optimal combination of the control measures to eradicate the disease within 50 days of the initiation of the control measure (ie $T=100$ days).

Strategy 1: Compliance to WHO Guidelines

Recommended preventive measures for COVID-19 include frequent washing of hands with soap and water for at least 20 seconds, use of alchohol based hand sanitizer, avoid touching of eyes, nose, or mouth with unwashed hands, practice of good respiratory etiquette (including covering coughs and sneezes), maintaining physical distance from other people, wearing a face mask in public , stay home if sick, travel restrictions, Personal Protective Equipment for health workers.

Insecurity, high poverty level and lack of government outreach affected the level of compliance of people to the lockdown and other restrictions imposed by the government [1, 41]. Physical distancing is somewhat difficult to observe in some geographical areas and particular locations in Nigeria [1, 31]. Face masks are not 100% effective [9] and there are also cases of misuse and abuse of mask [27]. Due to all these challenges, it is reasonable to assume 50% as the strict effectiveness level of individual compliance to the prevention guidelines (ie $\phi ^{\max } =0.5$) and 50% as the highest possible fraction of the population initially abiding by the WHO prevention guidelines.

Fig. 6

Model predictions considering the impact of compliance to the prevention guidelines. a Cumulative confirmed cases, b cumulative death cases, c confirmed cases in quarantine (Q) d unconfirmed symptomatic infected (I), e unconfirmed asymptomatic infected (A), and f control profile at optimum level

We set $r(t)=\omega _A(t)=\omega _I(t)=0$ and investigate the impact of the control $\phi (t)$. When individuals comply with the WHO guidelines, COVID-19 transmission rate is lowered and less people contract the virus. This is the situation in Fig. 6 where our simulation shows a significant reduction on the spread of the virus with the introduction of the control in optimal setting. Figure 6f shows that the success level of the containment measure ($\phi$) as well as the proportion of the population abiding by the guidelines ($\xi$) must be at the maximum level throughout the implementation period of the intervention. Figure 6d, e suggest that this intervention strategy is not sufficient for the removal of the infected population from the entire population within 100 days of initiation of the intervention strategy.

Strategy 2: Contact Tracing Followed by Quarantine and Isolation

Contact tracing involves locating and quarantining individuals exposed to the virus. Contact tracing has setbacks in that (i) some people see it as an inversion of privacy and therefore not willing to divulge information, (ii) due to the high level of insecurity in the country, contacts become suspicious of contact tracers and unwilling to divulge information, (iii) NCDC is understaffed as each tracer can have more than sixty people to monitor daily, and this can be logistically challenging [42]. Also there have been cases where quarantined individuals left the isolation centre [33, 34]. In the face of these challenges, it is reasonable to assume that contact tracing rate $r\in [0,0.5]$ Next we assume other intervention strategies are at zero level and simulate the optimal control model.

Fig. 7

Model predictions considering contact tracing as control measure. a Cumulative confirmed cases, b cumulative death cases, c confirmed cases in quarantine (Q) d unconfirmed symptomatic infected (I), e unconfirmed asymptomatic infected (A), and f control profile at optimum level

Figure 7 shows the impact of contact tracing in suppressing the spread of the disease. With contact follow up followed by quarantined as the only intervention strategy, there is a drastic reduction in disease classes. Although the implementation of the intervention has to be maintained for close to 100 days (see Fig. 7f), this intervention strategy appears to be effective. Although the population of quarantined individuals reduces greatly, it first increases and attains a peak value of about 70,000 individuals. Figure 7a therefore shows that this intervention strategy places a heavy burden on the health care facilities to contain the too many isolated infected individuals. Due to its high cost implication, maintaining a high level of surveillance for a long period of time is difficult. Due to the fact that the estimated value of $\delta _Q$ is greater than the estimated value of $\delta _I$ (see Table 2), this strategy tend to increase the death of the infected individuals. It is necessary to note that the estimated value of $\delta _I$ may not be correct as the death cases reported in NCDC data may be flawed (see section “Conclusion”).

Strategy 3: Mass Testing

It was shown in Fig. 3 that recovery rates for symptomatic infected individuals, $\rho _I$ and asymptomatic infected, $\rho _A$ are significant parameters and should be increased in order to quickly suppress the spread of the disease. Unfortunately, unconfirmed asymptomatic carriers are not available for treatment and therefore not easy to monitor. Thus, reducing the population of unconfirmed infectious individuals is necessary. This could be achieved by mass testing of the populace. The parameters $\omega _A$ and $\omega _I$ measures the rate at which asymptomatic and symptomatic individuals are randomly tested for the virus. We assume that the minimum waiting time to test an individual for the virus is 3 days (ie $\omega ^{\max }_A=\omega ^{\max }_I=1/3$). This is because the health system is weak, there is unequal access to testing, as well as challenges to access some areas of the country [41]. Another challenge facing the diagnosis of the virus is the slowdown in global manufacturing of medical supplies against a high demand which has made procurement of diagnostic reagents difficult [46].

Fig. 8

Simulation showing the influence of random diagnosis on the dynamics of COVID-19. a Cumulative confirmed cases, b cumulative death cases, c confirmed cases in quarantine (Q) d unconfirmed symptomatic infected (I), e unconfirmed asymptomatic infected (A), and f control profile at optimum level

Figure 8 shows that random testing of asymptomatic and symptomatic individuals who were not discovered by contact tracing will help in mitigating the spread of the virus. The populations of asymptomatic and symptomatic individuals reduce greatly however, isolation centers as well as bed space would be increased as the population of quarantined individuals first increases and attains a peak value of about 120,000 individuals.

Strategies 1–3

The combine effects of the three strategies is very rewarding as can be seen in Fig. 9. However, Fig. 9c shows that heavy burden will be placed on the health care facilities. It is therefore necessary for government to improve on the health care system by building more isolation centre with up-to-date facilities if this strategy is to be effective.

Fig. 9

Model predictions considering the impact of the three strategies. a Unconfirmed symptomatic infected (I), b unconfirmed asymptomatic infected (A), c confirmed cases in quarantine (Q) and d–f control profiles at optimum level

Cost Effectiveness Analysis

Controlling the spread of diseases in a community can be labor and capital intensive. Hence, the need for cost effectiveness analysis to determine the most cost-effective strategy to use. In this section, the cost effectiveness analysis will be implemented using two approaches; namely, the infection averted ratio (IAR) and the average cost-effectiveness ratio (ACER).

Infection Averted Ratio (IAR)

The infection averted ratio (IAR) is stated as:

$$\begin{aligned} \text{ IAR }=\frac{\text{ Number } \text{ of } \text{ infection } \text{ averted }}{\text{ Number } \text{ of } \text{ recovered }} . \end{aligned}$$

The number of infection averted is the difference between the total infectious individuals over the simulation period in the absences of control and the total infectious individuals with control. The strategy with the highest ratio is the most cost-effective [3].

The IAR for each intervention strategy is given in Table 3. According to this cost-effectiveness analysis method, the combination of three control strategies is the most cost-effective strategy. The use of control strategy 1 only is the least cost-effective.

Average Cost-Effectiveness Ratio (ACER)

The ACER is calculated as

$$\begin{aligned} \text{ ACER }=\frac{\text{ Total } \text{ cost } \text{ produced } \text{ by } \text{ the } \text{ intervention }}{\text{ Total } \text{ number } \text{ of } \text{ infection } \text{ averted }}. \end{aligned}$$

The total cost produced by the intervention is estimated using the objective function

$$\begin{aligned}\begin{array}{r} \displaystyle \frac{1}{2} \int _{0}^{T} \left( c_{1}(\phi ^\star )^2 +c_{2}(r^\star )^2+c_{3}(\omega ^\star _A)^2 +c_{4}(\omega ^\star _I)^2\right) \; dt. \end{array}\end{aligned}$$

The strategy with the lowest ratio is the most cost-effective.

Based on this cost-effectiveness approach, the most cost-effective strategy is Strategy 1, followed by the combination of the three strategies. The least cost-effective strategy is Strategy 2 (see Table 3).

Table 3 ICER of COVID-19 averted by control measures

Conclusion

In this study, a deterministic model which captures the dynamics of COVID-19 in Nigeria is proposed. The disease-free equilibrium solution is found to be locally stable when ${\mathfrak {R}}_0<1$. This implies that imposing the conditions that makes ${\mathfrak {R}}_0<1$ will lead to the suppression of the spread of the disease. A significant part of this work is the parameter estimation which was obtained by fitting the model to three sets of real-life data simultaneously. The basic reproduction number is estimated and sensitivity analysis is done to reveal the influence of the parameters in containing the disease. Pontryagin’s maximum principle is used to investigate cost-effective solutions for time-dependent controls to suppress the transmission of the virus within a specific period.

The basic reproduction number is estimated to be between [0.669, 0.680]. This implies that the spread of the disease is declining (as of the compilation of this work) and the disease will vanish however, our prediction shows that it will take more than 200 days to achieve a virus-free population. By sensitivity analysis, it is shown that recovery rates for symptomatic infected as well as asymptomatic infected and infectious-susceptible transmission rate are critical for precisely forecasting and controlling the number of COVID-19 cases. It is also shown that with the present situation of the pandemic in Nigeria, the influence of incomplete recovery is negligible.

It is shown that strict population wide compliance to WHO guidelines (strategy 1), effective contact tracing (strategy 2) and testing the population for COVID-19 (strategy 3), containment of the disease within a specific period of time could be achieved (see Table 3). However, the capacity of health care facilities should be increased greatly to accommodate the peak value of the quarantined individuals.

Our result further suggests that intervention strategies involving identifying and isolating the infectious individuals is more effective. Since asymptomatic carriers show no clinical symptoms, it is difficult to identify them therefore, in order to capture the asymptomatic individuals who escape contact tracing, screening of individuals with history of travel to or living in COVID-19 epidemic areas could be done, or population-wide testing should be conducted. However, due to limited amount of testing kits [46], maintaining mass testing of the populace for a long period of time seems difficult.

Due to high poverty level, low level of education, lack of access to health care, easy availability of over the counter drugs in markets and poor drug regulatory practices in Nigeria, many Nigerians prefer using over-the-counter drugs to going to the hospital for medical attention. In some instances, especially in rural areas, there are no doctors and so the people are left to their own devices [28, 30]. Therefore, many Nigerians sick of COVID-19 must have died of the virus unnoticed to the government. This is a pointer to the fact that the death cases reported in NCDC data is flawed. This flaw also accounts for the very small disease induced death rate for the infectious population $(\delta _I)$ as estimated in Table 2. Thus the estimated values of the parameters in Table 2 and the results of this work should be interpreted or used with caution.