The Space–Time Coupled Fractional Cattaneo–Friedrich Maxwell Model with Caputo Derivatives

Abstract

In the current article, we have thoroughly investigated the collective impact of mixed convection with thermal radiation and chemical reaction on MHD flow of viscous and electrically conducting fluid (Cattaneo–Friedrich Maxwell-CFM model) over a permeable surface embedded in a porous medium. Here we have utilized the Caputo time-fractional derivatives and mechanical laws (generalized shear stress constitutive equation and generalized Fourier’s and Fick’s laws) are being used to fractionalize the presented model. The effects of radiative heat flux, Ohmic dissipation, and internal absorption are presented through generalized Fourier’s law while Fick’s law or mass transfer equation offers the effects of first order chemically reactive species. The finite element method and finite difference method are being utilized to numerically solve the nonlinear coupled differential equations. It is established, through compression of numerical and analytical solutions, that the presented model is convergent. Further, error analysis of the subject model is also carried out. Moreover, for better illustration of results, we have also offered a graphical and tabular presentation of impacts of the parameters of interest on velocity, temperature, concentration profile, local skin friction coefficient, and heat and mass transfer. It is evident from the obtained results that velocity near and away from the surface increases with the enhancement of fractional derivative parameter whereas an opposite trend is observed in the case of temperature. Furthermore, it is noticed that temperature shows a decreasing behavior for the value ${\Lambda }_{\theta }<2$ and ${\Lambda }_{\phi }<2$, on the other hand entirely opposite trend is witnessed for ${\Lambda }_{\theta }\ge 3$ and ${\Lambda }_{\phi }\ge 3$. From an engineering perspective, we have acquired comprehensive outcomes such that the heat transfer offers an increasing trend in the case of T_R and thermal fractional parameter $\beta_{1}$ . Additionally, the chemical reaction parameter and Sc significantly contribute towards the mass transfer rate. Since, in literature, one cannot refer to such results with non-integer Caputo fractional derivatives thus the results obtained through the current assessment hold significance for future research avenues. Moreover, the numerical inferences of the subject study may contribute to an advanced thermal processing method in the food industry to swiftly increase the temperature for cooking or sterilization drives.

Introduction

Most physical phenomena in the natural environment are developed in the combination of initial and boundary value problems in time and space respectively. To interpret the long-term behavior and attitude of solutions with reference to time, the equations that characterize adaptation in time (named as initial value problems) are significant. We need stable solutions which are either bound by initial conditions or any physical constraint for these time-dependent equations. From the point of view of fluid dynamics, fluid flows that exhibit viscoelastic nature is of great importance. Moreover, viscoelastic fluid flow is a complicated phenomenon and due to the challenging non-linearity associated with governing equations (Navier–Stokes equations), it is difficult to analyze the entire flow field. In this respect, boundary layer approximations offer comprehensive knowledge regarding the solutions without solving the complete equations of Navier–Stokes throughout the whole domain [21] yet not sacrificing the consistency of the solutions. Here we have considered boundary layer viscoelastic non-Newtonian liquids because of significant advancement in different sectors such as geothermal engineering, meteorological, observational astronomy bio-fluid, and oil manufacturing companies. Due to its adaptable existence, many fundamental associations of non- Newtonian fluids are taken into consideration. Non-Newtonian fluids have earned the consideration of professionals and researchers due to their advanced and manufacturing implementations, i.e., passing on paper, manufacturing of plastic products, metals industry, food processing, cables, and surface coating and ecological fluid growth, etc. It has been established through experimental data that blood may be handled as non-Newtonian fluid at low shear concentrations in small blood vessels. Numerous physiological processes are designed for biological tissues as porous layers. To understand the behavior of such bioliquids, many non-Newtonian liquid models exist. Maxwell fluid model is the simplest of all existing non-Newtonian fluid models. Recently heat transfer analysis of fractional Maxwell fluid together with radiation and chemical reaction effects are considered by [14]. They thoroughly study the impact of the MHD and fractional parameters on the fluid flow. They have found that fractional derivatives improve the fluid velocity while the opposite trend was noticed for the relaxation and magnetic effect. Effects of electrically conductive Maxwell fluid combined with free convection and chemical reaction over a stretched surface embedded with porous medium are analyzed [18]. They used the analytical technique to get the results for flow parameters. They noticed remarkable effects of thermal radiation on thermal profiles. A semi-analytical solution for the fractional Maxwell fluid model together with MHD effects is studied by [7]. The main finding of the article is when the Reynolds number enhances, they directly affect the viscosity and fluid motion. Further, they notice the opposite effects for Pr and Sc numbers on concentration and temperature profile. One can find in the literature that many scholars have studied Maxwell fluid through multiple mechanical and thermal boundary conditions [8, 16, 19, 39, 43]. Convective flow with simultaneous heat and mass transfer, under the involvement of an electromagnetic essence and chemical reaction, has gained significant interest from scholars since this phenomenon occurs in man disciplines of engineering and innovative technologies. In several fields, including but not limited to freezing of nuclear power plants and hydromagnetic (MHD) power generators in the chemical industry, potential embodiments of this form of flow can be observed. The flow of free convection also exists in a natural environment. It happens not only because of the temperature variations but due to the variation in concentration or the mixture of these two. In industrial applications in which simultaneous heat and mass transfer occur as a result of the cumulative buoyancy impact of the diffusion of chemical reactions, numerous transportation processes occur. Free convection flows in chemical reaction porous structures have widespread applicability in the technologies of geothermal and petroleum reservoirs, and also in highly porous chemical reactors. Besides, substantial concern in radioactive interference with chemical reaction and convection for heat and mass transport in liquids has already been shown. This is due to the crucial role of solar radiation in the transmission of surface heat if convection heat transfer is prohibited, specifically in the situations of free convection having absorption-emitting liquids. Very recently, the study of axisymmetric convection fractional Maxwell viscoelastic fluid combined with velocity and temperature jump effects as demonstrated by [26]. They find a significant impact of velocity and temperature jump on velocity and temperature. Transport of heat and mass of free convection fractional Maxwell fluid model between two parallel plates are analyzed by [46]. They find the closed-form solutions of the Maxwell fluid model by using the Laplace method. The impact of chemical reactions on MHD Maxwell fluid induced by a stretched surface is investigated by [36]. They find the analytical solution by using HAM and notices that Deborah and Biot's numbers play a significant role in heat transfer. Further, they notice a remarkable improvement in concentration profile for the Archimedes number. For more refs see [17, 25, 37, 48].

Low cost/ economical raw structures have to encounter chemical reactions in all manufacturing chemical procedures to convert into potentially high manufactured goods. In a reactor design, that have certain toxic chemical transitions take place. The reactor plays a key role to bring reactants into intimate contact and provides a suitable atmosphere to extract the final product. We are therefore highly interested in situations where diffusion and chemical reaction happen at approximately the same velocity. Thus, in connection with many physical problems, such as liquids experiencing exothermic or endothermic chemical reactions, the analysis of heat generation or absorption impacts in fluid transport holds significant importance. In several manufacturing methods, which involve flow and mass transport past a variable sheet, the diffusing species may be produced or consumed due to chemical reaction with the atmospheric liquid which can significantly influence the flow and accordingly the characteristics and quality of the end product. The mechanisms employing mass transfer impact have recently been accepted as significant mainly in chemical processing equipment. Physical properties of heat and mass transfer over a stretched surface embedded with porous medium are considered by [27]. Different impacts on fluid-like chemical reactions and thermal radiation are taken into consideration. They used a numerical Keller box approach to analyze the fluid parameters. The effects of thermal radiation and chemical reaction on a nonlinear stretched surface embedded with the permeable medium are studied by [45]. They used the FEM method to get the numerical solution of the considered heat and mass transfer flow of nanofluid. They concluded from their finding that velocity and temperature are greatly affected by Brownian motion while the opposite trend for concentration profile. For more literature, the author suggests [30, 33, 44].

Keeping in view the assumption that time-fractional operators are satisfactory methods for differentiation, conventional derivatives are substituted by fractional derivatives in several physio-mathematical natural phenomena. Convolutions of the fractional operator kernels and ordinary local derivatives form the basis to formulate these fractional operators. In literature, one can find a vast variety of kernels to construct fractional operators yet in [15] Caputo is applied on time derivatives to formulate a fractional operator. Here it is pertinent to mention that fractional operators enjoy diverse applicability in relaxation processes, viscoelasticity, diffusion, and electrochemistry. Recently, many researchers are dedicatedly doing efforts to generalize classic dynamical systems to fractional dynamical systems. In this regard [2, 47] and [20] perform pioneering work on fractional calculus for different rheological problems. Fractional derivatives have recently identified the complex patterns of viscoelastic materials in different physical and industrial fields, particularly cryptographic products, planer system plastic liquid extruding, crystalline substances, metal plate deflation, exotic oils, fiberglass processing, and plastic blowing [12, 22]. It was confirmed by [32] that it was For the Maxwell model with standard derivatives, it is unsatisfactory to acquire adequately innovative data due to the varying spectrum of frequencies. Recently [3] performed numerical analysis for the Covid-19 model using the fractional calculus approach. For more interesting numerical studies on Covid-19 applications for instance see [1, 10]. Several methods are used to get the solutions of fractional derivatives like analytical and semi-analytical see [11, 24, 31, 35]. To study the hyperchaotic attractors and harmonic oscillator with position-dependent mass using fractional calculus approach is investigated [13, 41]. The numerical study of optimal control theory using the fractional calculus approach is analyzed by [23, 34]. In this article, we will use a stable numerical method to find solutions to the aforementioned models. Several researchers have applied a numerical technique to solved FDEs [4,5,6, 42].

Owing to potential applications in technology and industry and having broader intuition in comprehending the basic physics of the problems, fundamental flows are of significant importance. In practice, such flow geometries can be witnessed in several instances such as extrusion process, journal bearing, respiratory and circulatory systems. In literature, we have enough indication to deduce that the effects of Ohmic heating along with chemical reaction and thermal radiation are not studied by considering Caputo fractional derivatives. The problem under consideration is coupled in heat mass transfer by taking into account the effect of a magnetic field. Nevertheless, adopting a real approach, the Ohmic effect is being included to investigate the effect of thermal transport in magnetized boundary layer flow. For two-dimensional non-Newtonian flow, the impact of electrified and magnetized mixed convection heat transport has been analyzed [18]. Further, [9] offered an exact analysis of the free convection flow of the viscoelastic Jeffery fluid model with the latest Caputo-Fabrizio fractional derivative of the non-singular kernel. Hence in the current study, we have presented a collective analysis of Simultaneous upward force or buoyancy force impacts and first-order homogeneous chemical reaction in one-dimensional MHD flow, heat, and mass transfer of a fractional viscoelastic non-Newtonian fluid over a moving permeable surface embedded in a porous medium by considering exothermic and endothermic reaction, ohmic dissipation and thermal radiation. The acceleration of the moving plate is altered by changing the exponent n over the time interval $[0,T]$. In order to have a stable solution for the system of governing equations, finite element discretization and finite difference discretization (FED and FDD) are used for space and time variables, respectively. Moreover, we have offered a comparative analysis of the exact and numerical solutions of the system of equations in addition to carrying out error analysis to validate the numerical methods. At last, we have given a graphical and tabular view of the impacts of several physical parameters on velocity, temperature, and concentration profiles as well as local Nusselt and Sherwood numbers. The current article may significantly contribute to comprehend the characteristics of the boundary layer flow of Caputo fractional viscoelastic fluids. The layout plan of this study is as follows: The problem under consideration is mathematically modeled in Sect. 2. Sections 4, 6 deal with deriving transformation solutions methodology/ homogeneous model for the governing equations. In Sect. 78 and 9, finite element and finite difference method (FEM and FDM) are being utilized with the help of MATLAB oriented code to solve the system of principal equations, and the main results obtained through the subject computational scheme are presented through flow charts while error analysis in respect of subject scheme is also performed. Section 11 is mainly about the results and discussion followed by conclusions. Finally, the right-hand side term appears in the model equation, and the transformation used for the homogeneous model is presented in Sect. 13.

Mathematical Modeling of Physical Process

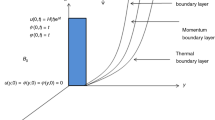
Unidirectional boundary layer flow of a viscous incompressible electrically conducting and radiating fluid over an accelerating moving surface immersed with a uniform permeable material subjected to thermal and concentration resilience impacts are considered. Moving surface acceleration varies with the flow exponent of n. The entire flow environment is steady at the initial time after $t>0$ the flow motion starts. The wall is retained at a steady temperature $({T}_{0})$ and concentration $({C}_{0})$ (depending on t and y) higher than the atmospheric temperature and concentration, respectively. Fluid flow heat and mass propagation regulation is accomplished along with other physical parameters by fractional time derivatives $\alpha ,{\beta }_{1} \mathrm{and} {\gamma }_{1}.$ It is also presumed that there is a heat generation/absorption interaction among the diffusing species and the liquid together with a first-order homogeneous chemical reaction with a rate constant of ${k}_{1}$. The Caputo fractional time derivative [15] is employed for mathematical formulation in this paper. The interpretation of the Caputo fractional time derivative is defined by

$$ {\text{C}}_{{\text{F}}} {\mathbf{D}}^{{{\varvec{\upeta}}}} q\left( t \right) := \frac{1}{{{\Gamma }\left( {p - \eta } \right)}}\mathop \smallint \limits_{0}^{t} \frac{{q^{n} \left( \tau \right)}}{{\left( {p - \tau } \right)^{\eta + 1 - p} }}d\tau p - 1 < \eta < p \in {\mathbb{N}} $$

(1)

where $\Gamma \left(\cdot \right)$ signifies Gamma function. Under the aforementioned premises, the boundary layer free convection flow with mass transfer, generalized Ohm’s and Fick’s laws ${\mathbf{J}}_{c}=\sigma \left({\mathbf{E}}_{\mathbf{F}}+\mathbf{U}\times {\mathbf{B}}_{\mathbf{F}}\right)$ and fractional Maxwell’s equations [20] are given by [8, 28].

$$ \begin{aligned} & \partial _{t} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right): = \nu \left( {1 + {{\Lambda }}_{2}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\partial _{{yy}} u + \sigma \rho ^{{ - 1}} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\left( {{\mathbf{E}}_{M} {\varvec{B}_{M}} + {\mathbf{B}}_{M}^{2} } \right) - \nu K^{{ - 1}} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)u \\ & \quad + g_{a} \beta _{{TE}} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\left( {T - T_{0} } \right) + g_{a} \beta _{{CE}} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\left( {C - C_{0} } \right), \\ & \partial _{t} \left( {1 + \frac{{\tau _{2}^{{\beta _{1} }} }}{{{{\Gamma }}\left( {1 + \beta _{1} } \right)}}{\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right): = \left( {\alpha _{1} + \frac{{16\sigma ^{*} T_{0}^{3} }}{{3k^{*} \rho c_{p} }}} \right)\partial _{{yy}} T + \sigma \rho ^{{ - 1}} C_{p}^{{ - 1}} \left( {1 + \frac{{\tau _{2}^{{\beta _{1} }} }}{{{{\Gamma }}\left( {1 + \beta _{1} } \right)}}{\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right)\left( {{\mathbf{E}}_{M} {\varvec{B}_{M}} -{\varvec{u}}} \right)^{2} - \frac{{Q_{0} }}{{\rho c_{p} }}\left( {T - T_{0} } \right), \\ & \partial _{t} \left( {1 + \frac{{\tau _{3}^{{\gamma _{1} }} }}{{{{\Gamma }}\left( {1 + \gamma _{1} } \right)}}{\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\gamma }}_{1} }} } \right)C: = D\partial _{{yy}} C - k_{1} \left( {1 + \frac{{\tau _{3}^{{\gamma _{1} }} }}{{{{\Gamma }}\left( {1 + \gamma _{1} } \right)}}{{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\gamma }}_{1} }} } \right)\left( {C - C_{0} } \right).~ \\ \end{aligned} $$

(2)

Form the above equations $\alpha ,\rho ,{\Lambda }_{1}, {\Lambda }_{2},T,C,{K}_{1},{Q}_{0},{c}_{p}$ memory effect, the density of fluid, relaxation time, retardation time, temperature, concentration, permeability parameter, heat generation/absorption coefficient, and specific heat of constant pressure, respectively. Further, we have ${g}_{a}$ gravitational acceleration, ${\beta }_{TE},{\beta }_{CE}$ are the thermal and concentration expansion coefficients, D is the molecular diffusivity,${\mathbf{B}}_{\mathbf{F}}=\left(0,{\mathbf{B}}_{\mathbf{M}},0\right)$ shows magnetic field intensity, B_M magnetic field coefficient, E_F electric field intensity, and J_c is the current density. The continuity equation is identically satisfied for the proposed model. In contrast with other chemical species, the concentration of diffusing species is quite small, and far away from the wall is incredibly small. Chemical reactions occur in the flow and all thermo-physical characteristics are supposed to be unchanged in the linear momentum equation, which is estimated as per the Boussinesq interpretation, apart from density involve in upthrust or buoyancy terms. Near the solar radiation and concentration buoyancy impact, a uniform electric and magnetic field of magnitude B_M, E_F is implemented. The permeable material is considered to be homogeneous and exists throughout in the local thermodynamic stability.

The appropriate boundary conditions (ICs and BCs) for the above dimensional model (2) as given below:

$$ \begin{aligned} & u\left( {0,t} \right): = u_{0} \left( {\nu l^{{ - 2}} } \right)^{n} ,~~~u\left( {l,T} \right): = 0, \\ & T\left( {0,t} \right): = T_{0} \left( {l^{4} + \nu ^{2} t^{2} } \right)l^{{ - 4}} ,\quad and~~~~T\left( {l,t} \right): = T_{0} \left( {l^{2} } \right)l^{{ - 2}} ,~~~t > 0 \\ & C\left( {0,t} \right): = C_{0} \left( {l^{4} + \nu ^{2} t^{2} } \right)l^{{ - 4}} ,~\quad and~~~~~~~C\left( {l,T} \right): = C_{0} \left( {l^{2} + \nu t} \right)l^{{ - 2}} ,~~~~t > 0 \\ & u\left( {y,0} \right): = 0: = u_{y} \left( {y,0} \right),~~T\left( {y,0} \right): = T_{0} ,~~~C\left( {y,0} \right): = C_{0} , \\ & T_{t} \left( {y,0} \right): = l^{{ - 3}} \left( {T_{0} \nu } \right)y: = C_{t} \left( {y,0} \right),~~~~~~~\left| y \right| \le l. \\ \end{aligned} $$

(3)

Here ${u}_{0}$ and $\nu$ indicates dimensional constant and kinematic viscosity. The current flow domain is described by the flow conditions are given in (3).

Engineering Aspects Physical Parameters

The physical quantities of interest are the surface heat flux and surface mass flux. Concentration gradients are used by many cells to complete a wide variety of tasks. There is energy stored in the concentration gradient because the molecules want to reach equilibrium. So, this energy can be utilized to accomplish tasks. In particular, the thermal gradient is very significant for the production reliability of the final goods in manufacturing processes. In thermal and mass flux estimation at the boundaries, the Nusselt number and Sherwood number play a very important role. In the present situation, Nusselt and Sherwood numbers are specified as

$$ \begin{aligned} & \left( {1 + \frac{{\tau _{2}^{{\beta _{1} }} }}{{{{\Gamma }}\left( {1 + \beta _{1} } \right)}}{\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right)Nu_{1} : = \frac{{ - l\left( {T_{y} } \right)_{{y = 0}} }}{{T_{{sl}} - T_{0} }} \\ & \left( {1 + \frac{{\tau _{3}^{{\gamma _{1} }} }}{{{{\Gamma }}\left( {1 + \gamma _{1} } \right)}}{\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\gamma }}_{1} }} } \right)Sh_{1} : = \frac{{ - l\left( {C_{y} } \right)_{{y = 0}} }}{{C_{{sl}} - C_{0} }} \\ \end{aligned} $$

At y = 0, T_s1 and C_s1 are upper surface temperature and concentration respectively. Moreover, for upper surface y: = l we have heat and mass transfer rate are

$$ \begin{aligned} & \left( {1 + \frac{{\tau _{2}^{{\beta _{1} }} }}{{{{\Gamma }}\left( {1 + \beta _{1} } \right)}}{\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right)Nu_{2} : = \frac{{ - l\left( {T_{y} } \right)_{{y = l}} }}{{T_{{sl}} - T_{0} }},~~ \\ ~ & \left( {1 + \frac{{\tau _{3}^{{\gamma _{1} }} }}{{{{\Gamma }}\left( {1 + \gamma _{1} } \right)}}{\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\gamma }}_{1} }} } \right)Sh_{2} : = \frac{{ - l\left( {C_{y} } \right)_{{y = l}} }}{{C_{{sl}} - C_{0} }} \\ \end{aligned} $$

(4)

temperature and concentration at the upper surface $\left( {y: = l} \right)\;{\text{are}}~\;T_{{s2}} \;~{\text{and}}\;~C_{{s2}}$.

Non-dimensional Caputo Fractional Flow Equations

To find the solutions of the above EQs (2–3) we have to convert the model's equations into dimensionless form. To simplify the model in the context of parameters, certain suitable units less quantities are incorporated:

$$ \widehat{{y^{*} }}~: = yl^{{ - 1}} ,~~~\widehat{{t^{*} }}~: = \left( {\nu t} \right)l^{{ - 2}} ,~~~\widehat{{u^{*} }}: = uu_{0}^{{ - 1}} ,~~\widehat{{\theta ^{*} }}: = \frac{{T - T_{0} }}{{T_{0} }},~~~\widehat{{\phi ^{*} }}: = \frac{{C - C_{0} }}{{C_{0} }}.$$

(5)

Utilizing Eq. (5) the IBVP (2)-(3) (for simplicity “$\widehat{{.}^{*}}'' \text{is excluded})$ can be turned into

$$ \begin{aligned} & \partial _{t} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)u~: = ~\left( {1 + {{\Lambda }}_{2}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)u_{{yy}} + M_{N} E_{f} - \left( {M_{N} + P_{m} } \right)\left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)u + {{\Lambda }}_{{{\theta }}} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\theta \\ & \quad + {{\Lambda }}_{\phi } \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\phi , \\ & Pr\partial _{t} \left( {1 + {{\Lambda }}_{{{{r\theta }}}} {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right)\theta ~: = \left( {1 + T_{R} } \right)\theta _{{yy}} + PrEc_{n} M_{N} \left( {1 + {{\Lambda }}_{{{{r\theta }}}} {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right)\left( {u - E_{f} } \right)^{2} - PrE_{T} \theta ,~ \\ & Sc\partial _{t} \left( {1 + {{\Lambda }}_{{{{r}}\phi }} {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\gamma }}_{1} }} } \right)\phi ~: = \phi _{{yy}} - ScC_{{rs}} \phi .~ \\ \end{aligned} $$

(6)

The ICs and BCs are below

$$ \left\{ {\begin{array}{*{20}l} {u\left( {0,~t} \right): = t^{n} ,~~~~u\left( {1,~t} \right): = 0,~~~\theta \left( {0,~t} \right): = t^{2} ,~~~\theta \left( {1,~t} \right): = t~: = ~\phi \left( {1,t} \right)} \\ {u\left( {y,0} \right): = 0: = \partial _{y} u\left( {y,~0} \right),~~\theta \left( {y,~0} \right): = 0: = \phi \left( {y,~0} \right),~~\partial _{y} \theta \left( {y,0} \right): = y~: = \partial _{y} \phi \left( {y,~0} \right).~~~} \\ \end{array} } \right. $$

(7)

In the above, $\Lambda$ is momentum relaxation time parameter, ${\Lambda }_{2}$ refers retardation time parameter, ${M}_{N}, {M}_{T}$ and ${E}_{f}$ signifies magnetic field, electric and exothermic/ endothermic parameters respectively, ${P}_{\nu r}$ stand for porosity variable, ${\Lambda }_{\theta },{\Lambda }_{\phi }$ are convection and diffusion parameters, Pr is the Prandtl number, $E{c}_{n}$ stand for Eckert number, ${\beta }_{r\theta }$ stands for thermal relaxation time parameter, ${T}_{R}$ shows thermal radiation parameter, $Sc \mathrm{and} {C}_{rs}$ are Schmidt number and chemical reaction parameter respectively, and ${\Lambda }_{r\phi }$ denotes the concentration relaxation time parameter. All the above non-dimensionless parameters are mathematically written as follow:

$$ \begin{aligned} {{~}} & {{\Lambda }}_{\theta } ~: = ~\frac{{g_{a} l^{2} \beta _{{TE}} T_{0} }}{{u_{0} \nu }},~~~{{\Lambda }}_{\phi } : = ~\frac{{g_{a} l^{2} \beta _{{CE}} C_{0} }}{{u_{0} \nu }},~~~P_{{\nu r}} : = \frac{K}{{\nu l}},~{{\Lambda }}_{{r\theta }} : = \frac{{\tau _{2}^{{\beta _{1} }} \nu ^{{\beta _{1} }} }}{{{{\Gamma }}\left( {1 + \beta _{1} } \right)l^{{2\beta _{1} }} }},~ \\ ~ & {{\Lambda }}_{{r\theta }} : = \frac{{\tau _{3}^{{\gamma _{1} }} \nu ^{{\gamma _{1} }} }}{{{{\Gamma }}\left( {1 + \gamma _{1} } \right)}}l^{{2\gamma _{1} }} ,~~~M_{N} ~: = \frac{{\sigma {\mathbf{B}}_{M}^{2} l^{2} }}{\mu },~~~ \\ & E_{f} ~: = \frac{{{\varvec{E}_{M} }}}{{{\varvec{B}_{M} u_{0} }}},~\Pr : = \frac{\nu }{{\alpha _{1} }},~Sc~: = \frac{\nu }{D},~~~Ec_{n} ~: = \frac{{u_{0}^{2} }}{{c_{p} T_{0} }},~~~T_{R} ~: = \frac{{16\sigma ^{*} T_{0}^{3} }}{{3k^{*} \mu c_{p} }},~~~C_{{rs}} ~: = \frac{{k_{1} l^{2} }}{\nu },~E_{T} ~: = \frac{{Q_{0} l^{2} }}{{\mu c_{p} }}.~ \\ \end{aligned} $$

(8)

Heat and mass transfers rate in the dimensionless form are given by

$$ \begin{aligned} & \left( {1 + {{\Lambda }}_{{r\theta }} {{C}}_{{{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right)\frac{{Nu_{1} }}{{Re^{{2~}} }}~: = - \left( {\partial _{y} \theta } \right)_{{y = 0}} \quad ~and~~\left( {1 + {{\Lambda }}_{{r\theta }} {{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\beta }}_{1} }} } \right)\frac{{Nu_{2} }}{{Re}}~: = - \left( {\partial _{y} \theta } \right)_{{y = 1}} ,~ \\ & \left( {1 + {{\Lambda }}_{{r\phi }} {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\gamma }}_{1} }} } \right)\frac{{Sh_{1} }}{{Re^{{2~}} }}~: = - \left( {\partial _{y} \phi } \right)_{{y = 0}} ~\quad ~~and~~\left( {1 + {{\Lambda }}_{{r\phi }} {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{{\gamma }}_{1} }} } \right)\frac{{Sh_{2} }}{{Re}}~: = - \left( {\partial _{y} \phi } \right)_{{y = 1}} ~~~~~~~~~~~~~ \\ \end{aligned} $$

(9)

Here $Re :=\frac{{u}_{0}L}{\nu }$ stands for Reynold’s number.

Fractional Homogenous Model

Equations (2–3) reflect a set of dimensionless PDEs that cannot be easy to get the solution in closed form however these types of equations can easily tackle numerically. Hence, we will use the finite element (FEM) as well as the (FDM) finite difference method. For the sake of convenience, we will first convert the above PDEs into homogeneous boundary condition by choosing the appropriate transformation given in (13) and the converted homogeneous model along with boundary conditions as follows

$$ \begin{aligned} & \partial _{t} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right): = \left( {1 + {{\Lambda }}_{2}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)w_{{yy}} + M_{N} E_{f} - \left( {M_{N} + P_{{\nu r}} } \right)\left( {1 + {{\Lambda }}^{\alpha } {{C}}_{{{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)w \\ & \quad + {{\Lambda }}_{\theta } \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\bar{\theta } + {{~~\Lambda }}_{\phi } \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\bar{\phi } + {\mathbb{F}}_{{1u}} \left( {y,t} \right), \\ \end{aligned} $$

$$Pr{\partial }_{t}\left(1+{{\Lambda }_{{r\theta }}\text{C}}_{\text{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\overline{\theta } =\left(1+{T}_{R}\right)\overline{{\theta }_{yy}}+PrE{c}_{n}{M}_{N}\left(1+{{\Lambda }_{{r\theta }}\text{C}}_{\text{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right){\left(w\right)}^{2}-Pr{Ec}_{n}{M}_{N}{t}^{n}cos\left(\frac{\pi }{2}\right)y\left(1+{{\Lambda }_{{r\theta }}\text{C}}_{\text{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\left(w\right)+wPrE{c}_{n}{M}_{N}cos\left(\frac{\pi }{2}\right)y\left({t}^{n}+\frac{{\Lambda }_{{r\theta }}\Gamma \left(n+1\right){t}^{n-{\beta }_{1}}}{\Gamma \left(n+1-{\beta }_{1}\right)}\right)-2PrE{c}_{n}{M}_{N}{E}_{f}\left(1+{{\Lambda }_{{r\theta }}\text{C}}_{\text{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\left(w\right)-Pr{E}_{T}\left(1+{{\Lambda }_{{r\theta }}\text{C}}_{\text{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\theta +{\mathbb{F}}_{2\theta }\left(y,t\right),$$

$$ Sc\partial_{t} \left( {1 + {\Lambda }_{{{{r}}\phi }} {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\upgamma }_{1} }} } \right)\overline{\phi } : = \overline{\phi }_{yy} - ScC_{rs} \overline{\phi } + {\mathbb{F}}_{3\phi } \left( {y,t} \right). $$

together with homogeneous Dirichlet BCs and ICs we have

$$\left\{ {\begin{array}{*{20}l} {w\left( {0, t} \right)0: = w\left( {1,t} \right), \overline{\theta }\left( {0, t} \right)0: = \overline{\phi }\left( {0, t} \right), \overline{\theta }\left( {1, t} \right)0: = \overline{\phi }\left( {1, t} \right)} \\ {w\left( {y, 0} \right)0: = \partial_{y} w\left( {y,0} \right), \overline{\theta }\left( {y, 0} \right)0: = \overline{\phi }\left( {y, 0} \right), \partial_{y} \overline{\theta }\left( {y, 0} \right)0: = \partial_{y} \overline{\phi }\left( {y, 0} \right) \left( {10} \right)} \\ {, } \\ \end{array} } \right. $$

(10)

Solution Methodology for Numerical Simulations

The finite-element (FEM) and finite-difference (FDM) algorithm is proposed together with suitable time-fractional operators is utilized to discretize the considered flow model equations. After getting the aforementioned model to discretize form, we have numerically solved the below nonlinear algebraic equations [29, 40]

$${\mathcal{M}}_{1}^{i} {\mathcal{L}}_{k}^{\alpha + 1 } \left[ {{\mathbf{W}}_{{\mathbf{h}}}^{{\mathbf{i}}} } \right] + {\mathcal{T}}_{1}^{i} {\mathcal{H}}_{k}^{\alpha } \left[ {{\mathbf{W}}_{{\mathbf{h}}}^{{\mathbf{i}}} } \right] - \left( {M_{N} - P_{\nu r} } \right){\mathcal{M}}_{1}^{i} {\mathcal{L}}_{k}^{\alpha } \left[ {{\mathbf{W}}_{{\mathbf{h}}}^{{\mathbf{i}}} } \right] - {{ \Lambda }}_{\theta } {\mathcal{M}}_{1}^{i} {\mathcal{L}}_{k}^{\alpha } \left[ {{{\varvec{\Theta}}}_{{\mathbf{h}}}^{{\mathbf{i}}} } \right] - {\Lambda }_{\phi } {\mathcal{M}}_{1}^{i} {\mathcal{L}}_{k}^{\alpha } \left[ {{{\varvec{\Phi}}}_{{\mathbf{h}}}^{{\mathbf{i}}} } \right]\overline{{K_{1} }}^{i} . $$

$$Pr{\mathcal{M}}_{2}^{i} {\mathcal{L}}_{k}^{{\beta_{1} + 1}} \left[ {{\Theta }_{h}^{i} } \right] + {\mathcal{T}}_{2}^{i} \left[ {{\Theta }_{h}^{i} } \right] - 2\Pr Ec_{n} M_{N} {\mathcal{N}}_{1}^{i} \left[ {W_{{k - 1_{h} }}^{i} } \right]{\mathcal{L}}_{k}^{{\beta_{1} }} \left[ {W_{kh}^{i} } \right] - t_{k - 1n}^{n} M_{N} {\mathcal{D}}_{1} {\mathcal{L}}_{k}^{{\beta_{1} }} \left[ {{\mathbf{W}}_{h}^{i} } \right] - PrEc_{n} M_{N} \left( {t^{n} + \frac{{{\Lambda }_{{{{r\theta }}}} {\Gamma }\left( {n + 1} \right)t^{{n - \beta_{1} }} }}{{{\Gamma }\left( {n + 1 - \beta_{1} } \right)}}} \right){\mathcal{D}}_{1} \left[ {{\mathbf{W}}_{{\mathbf{h}}}^{{\mathbf{i}}} } \right] + 2PrEc_{n} E_{f} M_{N} {\mathcal{M}}_{2}^{i} {\mathcal{L}}_{k}^{{\beta_{1} }} \left[ {{\mathbf{W}}_{{\mathbf{h}}}^{{\mathbf{i}}} } \right]\overline{{K_{2} }}^{i} $$

$${ \mathcal{M}}_{3}^{i} {\mathcal{L}}^{{\gamma_{1} + 1}} \left[ {{{\varvec{\Phi}}}_{{\varvec{h}}}^{{\varvec{i}}} } \right] + {\mathcal{T}}_{3}^{i} \left[ {{{\varvec{\Phi}}}_{{\varvec{h}}}^{{\varvec{i}}} } \right] - ScC_{rs} {\mathcal{M}}_{3}^{i} {\mathcal{L}}^{{\gamma_{1} }} \left[ {{{\varvec{\Phi}}}_{{\varvec{h}}}^{{\varvec{i}}} } \right]\overline{{K_{3} }}^{i} . \left( {11} \right) $$

(11)

Solution Technique

The nonlinear system of coupled equations (11) with the associated boundary conditions (10) are numerically solved for the velocity, temperature, and concentration distributions. In order to have a precise and efficient solution to the considered initial and boundary value problem, we have utilized the finite element method and finite difference method. The basic steps involved in the approach are given below:

Discretization of the Domain

In the first step, we discretized the entire domain into a finite number of sub-domains such as a method or process called domain discretization. In the discretized domain each sub-domain is named a finite element. The collection of all subdomain or elements is assigned to the finite element grid.

The Equation Derivation

The below main three steps required for the derivation of the finite element method, i.e., algebraic equations contained the unknown parameters during the finite element approximation:

• At the first step, we developed a variational formulation for the given system of equations.

• Presume the approximate solution form over a conventional finite element.

• At the last, we put the considered approximate solutions into constructed variational form and get the required finite element system of equations.

Assembling the Elements Equations

By implementing the conditions of inter-element continuity, we acquired the algebraic equations are assembled. This comprises a broad number of algebraic equations that govern the entire flow domain.

Boundary Conditions Implementation

After performing the above steps the specified boundary conditions are imposed on the assembled equation.

The Final Solution of the Assembled Form

For the numerical solutions of the final matrix, we construct a finite element base code by implementing a P₂ element. For seeking the convergence and stability of our implemented numerical scheme we slightly change the values of u, $\theta$, and $\phi$ and add $\epsilon$ in the source terms and change the value of an added term $\epsilon$ no significant change was observed in the values of u, $\theta$, and $\phi$. And in the solutions, we find no disruption. The applied numerical methodology is thus robust and convergent.

Flowchart of Computational Scheme

Validation of Numerical Solutions

Before running real simulations, verification of the numerical scheme is essential. We, therefore, computed estimates of numerical error and made comparisons with theoretical error estimates. We claimed that the model being investigated was fulfill the following definitions of error:

$$ \begin{aligned} & \vartheta _{h} \left( {t_{k} } \right) - \vartheta _{{ext}} \left( {t_{k} } \right){\mathcal{L}}_{2} \left( {{\Omega }} \right) \le {\mathcal{C}}_{1}^{*} \left( {h_{1}^{{r + 1~}} + \widehat{{\tau ^{*} }}} \right) \\ & \vartheta _{h} \left( {t_{k} } \right) - \vartheta _{{ext}} \left( {t_{k} } \right){\mathcal{H}}^{1} \left( {{\Omega }} \right) \le {\mathcal{C}}_{2}^{*} \left( {h_{1}^{{r~}} + \widehat{{\tau ^{*} }}} \right)~~~~~ \\ \end{aligned} $$

(12)

where the constants ${\mathcal{C}}_{2}^{*}>0$ and ${\mathcal{C}}_{1}^{*}>0$ are free of step sizes ${h}_{1} and \widehat{{\tau }^{*}}$, see [38].

$$ \begin{aligned} & \partial _{t} \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)w: = \left( {1 + {{\Lambda }}_{2}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)w_{{yy}} + M_{N} E_{f} - \left( {M_{N} + P_{{\nu r}} } \right)\left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)w \\ & \quad + {{~~~\Lambda }}_{\theta } \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\bar{\theta } + {{~~\Lambda }}_{\phi } \left( {1 + {{\Lambda }}^{\alpha } {\text{C}}_{{\text{F}}} {\mathbf{D}}_{{\mathbf{t}}}^{{{\alpha }}} } \right)\bar{\phi } + {\mathbf{f}}_{1} \left( {y,t} \right), \\ \end{aligned} $$

$$Pr{\partial }_{t}\left(1+{{\Lambda }_{{r\theta }}\mathrm{C}}_{\mathrm{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\overline{\theta } :=\left(1+{T}_{R}\right)\overline{{\theta }_{yy}}+PrE{c}_{n}{M}_{N}\left(1+{{\Lambda }_{{r\theta }}\mathrm{C}}_{\mathrm{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right){\left(w\right)}^{2}-Pr{Ec}_{n}{M}_{N}{t}^{n}cos\left(\frac{\pi }{2}\right)y\left(1+{{\Lambda }_{{r\theta }}\mathrm{C}}_{\mathrm{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\left(w\right)+wPrE{c}_{n}{M}_{N}cos\left(\frac{\pi }{2}\right)y\left({t}^{n}+\frac{{\Lambda }_{{r\theta }}\Gamma \left(n+1\right){t}^{n-{\beta }_{1}}}{\Gamma \left(n+1-{\beta }_{1}\right)}\right)-2PrE{c}_{n}{M}_{N}{E}_{f}\left(1+{{\Lambda }_{{r\theta }}\mathrm{C}}_{\mathrm{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\left(w\right)-Pr{E}_{T}\left(1+{{\Lambda }_{{r\theta }}\mathrm{C}}_{\mathrm{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upbeta }_{1}}\right)\theta +{\mathbf{f}}_{2}\left(y,t\right),$$

$$Sc{\partial }_{t}\left(1+{{\Lambda }_{{r\phi }}\mathrm{C}}_{\mathrm{F}}{\mathbf{D}}_{\mathbf{t}}^{{\upgamma }_{1}}\right)\overline{\phi } :={\overline{\phi }}_{yy}-Sc{C}_{rs}\overline{\phi }+{\mathbf{f}}_{3}\left(y,t\right).$$

Validation of numerical solutions is verified by introducing source terms f₁(y, t), f₂(y, t), and f₃(y, t) in the momentum, energy, and concentration equations. Which are given as follows:

$$ \begin{aligned} & {\mathbf{f}}_{1} \left( {y,~t} \right): = 2ty\left( {1 - y} \right) + {{\Lambda }}^{\alpha } y\left( {1 - y} \right)\frac{{2t^{{1 - \alpha }} }}{{{{\Gamma }}\left( {2 - \alpha } \right)}} + 2t^{2} + \frac{{4t^{{2 - \alpha }} {{\Lambda }}_{2}^{\alpha } }}{{{{\Gamma }}\left( {3 - \alpha } \right)}} - M_{N} E_{f} \\ & \quad + \left( {M_{N} + P_{{\nu r}} } \right)\left( {t^{2} y\left( {1 - y} \right) + {{\Lambda }}^{\alpha } y\left( {1 - y} \right)\frac{{2t^{{2 - \alpha }} }}{{{{\Gamma }}\left( {3 - \alpha } \right)}}} \right) - {{\Lambda }}_{{{\theta }}} \left( {t^{2} sin2\left( {2\pi y} \right) + {{\Lambda }}^{\alpha } {{sin}}\left( {2\pi y} \right)\frac{{2t^{{2 - \alpha }} }}{{{{\Gamma }}\left( {3 - \alpha } \right)}}} \right) \\ & \quad - {{\Lambda }}_{\phi } \left( {t^{2} sin\left( {2\pi y} \right) + {{\Lambda }}^{\alpha } {{sin}}\left( {2\pi y} \right)\frac{{2t^{{2 - \alpha }} }}{{{{\Gamma }}\left( {3 - \alpha } \right)}}} \right) -{\mathbb{F}}_{{1u}} , \\ \end{aligned} $$

$${\mathbf{f}}_{2}\left({\varvec{y}},{\varvec{t}}\right)\boldsymbol{ }:={\varvec{P}}{\varvec{r}}\left(2tsin\left(2\pi y\right)+{\Lambda }_{{r\theta }}\mathrm{sin}\left(2\pi y\right)\frac{2{t}^{1-{\beta }_{1}}}{\Gamma \left(2-{\beta }_{1}\right)}\right)+\left(1+{T}_{R}\right){\left(2\pi t\right)}^{2}\mathrm{sin}\left(2\pi y\right)+2\mathrm{sin}\left(2\pi y\right)PrE{c}_{n}{M}_{N}{E}_{f}{t}^{2}+\frac{4\mathrm{sin}\left(2\pi y\right){\Lambda }_{r\theta }PrE{c}_{n}{M}_{N}{E}_{f}}{\Gamma \left(3-{\beta }_{1}\right)}{t}^{n-{\beta }_{1}}-\mathrm{sin}\left(2\pi y\right)Pr{E}_{T}{t}^{2}-\frac{2\mathrm{sin}\left(2\pi y\right){\Lambda }_{r\theta }Pr{E}_{T}}{\Gamma \left(3-{\beta }_{1}\right)}{t}^{n+2-{\beta }_{1}}-PrE{c}_{n}{M}_{N}\left[{t}^{4}{\mathrm{sin}}^{2}\left(2\pi y\right)+\frac{24{\mathrm{sin}}^{2}\left(2\pi y\right){\Lambda }_{r\theta }}{\Gamma \left(5-{\beta }_{1}\right)}{t}^{4-{\beta }_{1}}\right]-{t}^{2}\mathrm{sin}\left(2\pi y\right)cos\left(\frac{\pi y}{2}\right)PrE{c}_{n}{M}_{N}\left[{t}^{n}+\frac{\Gamma \left(n+1\right){\Lambda }_{r\theta }}{\Gamma \left(n+1-{\beta }_{1}\right)}{t}^{n-{\beta }_{1}}\right]$$

$$ \begin{aligned} {\mathbf{f}}_{3} \left( {y,t} \right)&: = Sc2tsin\left( {2\pi y} \right) + \frac{{2sin\left( {2\pi y} \right){{\Lambda }}_{{r\phi }} }}{{{{\Gamma }}\left( {2 - \gamma _{1} } \right)}}t^{{1 - \gamma _{1} }} + \left( {2\pi t} \right)^{2} \sin \left( {2\pi y} \right) \\ & \quad + ScC_{{rs}} \sin \left( {2\pi y} \right)t^{2} + \frac{{2sin\left( {2\pi y} \right){{\Lambda }}_{{r\phi }} }}{{{{\Gamma }}\left( {3 - \gamma _{1} } \right)}}t^{{2 - \gamma _{1} }} -{\mathbb{F}}_{{3\phi }} ~ \\ \end{aligned} $$

(13)

Here ${\mathbb{F}}_{1}, {\mathbb{F}}_{2} \mathrm{and} {\mathbb{F}}_{3}$ are the right term of the solutions. With the same initial and boundary conditions

$$ \left\{ {\begin{array}{*{20}l} {w\left( {0,t} \right): = 0: = w\left( {1,t} \right),~~\bar{\theta }\left( {0,t} \right): = 0: = \bar{\phi }\left( {0,t} \right),~~~\bar{\theta }\left( {1,t} \right): = 0: = \bar{\phi }\left( {1,t} \right)~~~~~~~~~~~~~~~~~~~~~} \\ {w\left( {y,0} \right): = \partial _{y} \left( {w,0} \right),~\bar{\theta }\left( {y,0} \right): = 0: = \bar{\phi }\left( {y,0} \right),~~~\partial _{y} \bar{\theta }\left( {y,0} \right): = 0: = \partial _{y} \bar{\phi }\left( {y,0} \right)~~} \\ \end{array} } \right. $$

(14)

The exact solutions can be obtained as follows

$$ w_{{ex}} \left( {y,~t} \right): = t^{2} y\left( {1 - y} \right)~\quad {\text{and}}~~\theta _{{ex}} \left( {y,t} \right): = t^{2} \sin \left( {\pi y} \right): = ~\phi _{{ex}} \left( {y,t} \right) $$

Figure 1 shows the velocity and temperature distribution of the fluid along the y-direction obtained by the numerical solution and the analytical solution. It can be found that the numerical solutions agree well with the analytical solutions. Similarly, we found the results for concentrations equations also agreed with an analytical solution. The results demonstrate that the numerical method developed in this study is reliable to be used in solving the fractional Maxwell model along with Fourier and Fick’s Laws of heat conduction and concentrations. Moreover, in the logarithmic scales, in Fig. 2a–c, approximate error estimates are illustrated by assigning eight separate values for the space discretization phase h. It is essential to mention that the slope of the $\left({L}_{2}(\Omega )\right)$ error curve will be almost 3 and that of the $\left({H}^{1}(\Omega )\right)$ error curve is approximately 2. Theoretically, error slopes should be roughly equal to $r+1$ and $r$ respectively for the Lagrange polynomial degree of $r=$. Since degree two polynomials from Lagrange are utilized in this method. Therefore, the estimates of numerical errors are considered to be in reasonable agreement with the theoretical estimates. This guarantees that the method is convergent and appears to agree with theoretical errors.

Fig. 1

Compression of Exact and Approximate Solutions for velocity and Temperature

Fig. 2

${L}_{2}\left(\Omega \right) and {H}^{1}(\Omega )$ Error for velocity (a), Temperature (b) and Concentration (c)

Discussion

Numerical results/findings for velocity, temperature, and concentrations governing Eqs. (11) with ICs and BCs (10) are achieved in the current analysis using the approach of finite element and finite difference. In this assessment, we analyze the electrically conducted mixed convection boundary layer flow in the existence of Joule heating and thermal radiation over an accelerated surface. The fractional parameters i.e. ($\alpha ,{\beta }_{1} and {\gamma }_{1})$ influence on velocity, temperature, and concentration field were also calculate and analyzed. In a graphical and tabular manner, the simulated results are demonstrated. We have obtained fascinating knowledge about the impact of all the physical parameters that govern the model problem.

Figure 3a illustrates the fractional parameter (α) impact on the velocity profile u (y, t). As the (α) values rise, the velocity gradient significantly increases and thus the thickness of the momentum boundary layer improves. The velocity boundary layer has a maximal spike for (α = 15%), while the fluid has no memory implications for (α = 0%). This ensures that the fractional parameter regulates the boundary layer of momentum. The greater the fractional stress parameter (α) is for a fixed value of Y, the better the elastic behavior and the higher the velocity magnitude. This is based on the assumption that the thickness of the velocity boundary layer improves with the improvement in the elastic function. We noticed that the velocity boundary-layer reduces its thickness as Λ increases in Fig. 3b. The relaxation time at 15% maximal level although we have recorded minimal relaxation at 0.0% or no relaxation time. We say from this result that the fluid’s viscoelasticity increases but there is more gap in recovery. The buoyancy ratio parameter ${\Lambda }_{\theta }$ represents the ratio between mass and thermal buoyancy forces. When = ${\Lambda }_{\theta }$0 or less than 3 there is no mass transfer or less mass transfer in the fluid domain and the buoyancy force is due to the thermal diffusion only. This indicates that the mass buoyancy force behaves in almost the same direction as the thermal buoyancy force for (${\Lambda }_{\theta }$> 0) or (> 3). In Fig. 3c, the role of (${\Lambda }_{\theta }$) on the velocity profile can be seen. An identify trends of (Λ_θ), which raises the velocity profile, is displayed in the figure. It happens when the buoyancy force raises, which leads to an increased in the velocity of the fluid and an improvement in the thickness of the boundary layer. The optimum velocity for a higher value of (${\Lambda }_{\theta }$) near the upper surface. From Fig. 3d we can see the effect of solutal Grashof number (Λ_φ) on velocity. The improvement in (Λ_φ) is expected to enhance the velocity in the momentum boundary layer. Besides that, it is observed that the maximum value of velocity increases dramatically near the upper surface and declines in the vicinity of the bottom surface as the value of (Λ_φ). Figure 4a for the case when permeable permeability value is continued to increase. Initially when (P_vr = 0) no pore resistance to the fluid after increasing the value of porosity parameter from (0.0 to 0.9) pore provide more resistance to the fluid. We can therefore note that the impact of maximizing the value of (P_vr) is to reduce the effect of the velocity component in the boundary layer due to undergo degradation or significantly increases the friction of the fluid by increasing the value of the porous permeability on the fluid flow, resulting the velocity reduces. The same pattern has been observed in Fig. 4b. The velocity begins from the highest value of the upper surface and declines unless it hits the maximum level or holds significant friction and afterward the flow pressure reduces before it exceeds the required value at the end of the boundary layer. It is significant to mention that the strength of the magnetic fields in the boundary layer is to diminish the value of the velocity profile. We notice that, with an enhancement in the strength of the magnetic field, the maximal strength decreases significantly, since the involvement of an MHD in an electrified fluid generates a resisting force that we call the Lorentz force which operates against the liquid if, as in the present problem, the magnetic field is implemented in the normal direction. As seen in this figure, this kind of opposing force delays the fluid velocity drop. The moving number n and the final time properties are specified in Fig. 4c, d. Rises in the moving number n the velocity u(y, t) enhance over the interval [0, 1.5] shows in 4(c). In particular, an improvement in (n) generating velocity of flow rate increases over [0, 1.5], which leads to an increase in flow rate. Likewise, it is inferred that the velocity rises for the fixed moving number (n = 1) by continuing to increase the final time (t), see Fig. 4d. Implications of the fractional parameter (β₁) on the ($\theta (y,t)$) presented in 5(a). As the surface temperature increases, the continuous pattern of the temperature gradient declines, and the thickness of the thermal boundary layer tends to increase as values of (β₁) raise. It indicates that in the thermal boundary layer, (β₁) plays a significant role. We concluded in Fig. 5b that the thermal field variable is affected by the magnetic field variable (M_N) in the domain [0, 2] and the dual tendency of the dimensionless temperature profiles is witnessed to enhance the value of the domain in the specified domain. When (${\Lambda }_{\theta }$< 2), the temperature is a declining (M_N) function. This is because the longitudinal magnetic field gives rise to a resistive force defined as the Lorentz force of an electrically conducting fluid. This force allows the liquid to encounter friction by growing the resistance among the layers and thereby reducing its temperature. Whereas the adverse attitude of the (M_N) on the ($\theta (y,t)$) is noticed when = ${\Lambda }_{\theta }$4. In this situation, when (M_N) is enhanced, we realized that the thermal boundary layer thickness is raised, thus the temperature rises. Figure 5c demonstrates the influence on ($\theta (y,t)$) for an electric field variable. The heat transfer rate declines as the electric field increases. Because of the Lorentz strength, the electric field accelerates the fluid temperature. This result gives enhancement in the thermal boundary layer thickness and temperature field. The improvement in the temperature distribution with the increment of the (${\Lambda }_{\theta }$) is depicted in 5(d). It is acknowledged that with the rise of Y over the interval [0, 2], the temperature profile significantly reduces. Changing the thermal relaxation parameter (${\Lambda }_{\theta }$) takes more time for viscoelastic material to shift heat energy from insulated to non-insulated molecules, resulting in a reduction in the temperature profile for higher values of Y. The result on the ($\theta (y,t)$) of the Eckert number (Ec_n) can be seen in Fig. 6a. For increasing values of Eckert number (Ec_n), the temperature profile ($\theta (y,t)$) is evaluated. The thermal boundary layer thickness remains thicker and the temperature distribution rises as the (Ec_n) increases. This contributes significantly to a low heat transfer rate on the surface. An exothermic reaction is a chemical process that, that releases energy in the form of light and heat. It is the reverse of an endothermic response. It provides energy to its surroundings. The energy required for the reaction to proceed is far less or significantly higher than the overall endothermic or exothermic reaction energy released, accordingly. The alteration of heat generation/absorption (E_T) on the non-dimensional temperature profile ($\theta (y,t)$) is shown in Fig. 6b. (E_T > 0) leads to the generation of heat and (E_T < 0) corresponds to the heat absorption. It was acknowledged that, in comparison to heat absorption, the temperature profile and thickness of the thermal layer are progressed for heat generation. As the variable of heat generation continues to rise, the temperature and thickness of the thermal layer start rising while an opposite trend is seen in the case of heat absorption. Enough heat is generated by the heat generation method, contributing to temperature field improvement. The significant importance of the thermal conductivity to the thermal radiation exchange is described by the radiation parameter. The growing influence of (T_R) on temperature is shown in Fig. 6c. It is evident that an improvement in the radiation parameter in the flow environment increases with an increase in temperature. Attributed to the higher thermal radioactive effect, the rate of heat transport at the surface decreases. With substantial radiation parameters, elevated temperatures and thicker thermal boundary layer thickness are connected. Increasing radiation variable values contribute to a weak heat transport rate at the surface since the temperature of the liquid is strengthened. The impact of the Prandtl number (Pr) over the dimensionless temperature $\theta (y,t)$ is shown in Fig. 6d. Because of its increasing values over the non—dimensional liquid temperature, the Prandtl number has a diminishing impact and the thermal boundary layer thickness is also decreased. This is because the low thermal conductivity of relatively high Prandtl number fluid decreases conduction and thus decreases the thermal boundary layer thickness boundary layer. The influence of the reaction rate variable (C_rs) on generative chemical reaction species concentration profiles is included in Fig. 7a. The analysis indicates that the influence of maximizing the value of the chemical kinetics variable (C_rs) on the (φ(y, t)) in the boundary layer is indicated. From this figure, it is specifically concluded that the magnitude of species concentration declines from (0 to 1.5). Besides, it is recognized that a higher amount of the (C_rs) reduces the concentration of species in the boundary layer, attributed to the reason that the boundary layer declines with an increase in the value of (C_rs), i.e., the chemical reaction in this system results in the chemical accumulation and thus causes a decrease in the concentration profile. In the circumstance where the Schmidt number (Sc) is enhanced as shown in Fig. 7b, comparable findings are shown with the last figure. It can also be ascertained from this result that for significantly greater values of (Sc), the influence of the Schmidt number (Sc) on concentration distribution declines gradually. As can be predicted, as (Sc) continues to increase with all other parameters set, the mass transfer rate rises, i.e., an increment in (Sc) causes a decline in the thickness of the concentration boundary layer, correlated with the decrease in the concentration profiles. Higher the value of (Sc) implies decreasing molecular diffusion by (D). The species concentration is thus significantly greater for relatively small (Sc) values and reduces for larger (Sc) values. Tables 1 and 2 shows the computational values of Nusselt and Sherwood numbers for different values of coupled nonlinear fluid problem. It notices from Table 1 the presence of thermal radiation and the fractional derivative parameter is to increase Nusselt number at the upper surface. Further, it is found from Table 2 the increasing influence of chemical reaction parameter (C_rs) and concentration relaxation time parameter decreases the values of the Sherwood number.

Fig. 3

Fractional number $\alpha ,$ relaxation time $\Lambda ,$ thermal buoyancy ratio parameter ${\Lambda }_{\theta }$ and solutal buoyancy ratio parameter ${\Lambda }_{\phi }$ on velocity profile when ${\beta }_{1}={\Lambda }_{r\theta }={\gamma }_{1}=0.95, {\Lambda }_{r\phi }=0.7, {\Lambda }_{2}=0.5, {\mathcal{M}}_{\mathcal{N}}=0.1={E}_{f}, n=2.0, {P}_{vr}=0.3,{C}_{rs}=0.5, {T}_{R}=E{c}_{n}=Sc=0.4, Pr=1.2.$

Fig. 4

Porosity variable P_vr, Magnetic number M_N, moving exponent n and final time on velocity profile when β₁ = α = Λ_rθ = γ₁ = 0.95, Λ₁ = 0.1,, C_rs = E_f = 0.5, Λ_rφ = 0.1, Sc = T_R = Ec_n = E_T = 0.2, Pr = 1.2

Fig. 5

Thermal memory parameter β₁, Magnetic parameter M_N, Electric parameter E_f and Thermal relaxation time parameter Λ_rθ, on temperature profile when α = γ₁ = 0.95, Λ_θ = 4 = Λ_φ, Λ_rφ = 0.1, n = 2.0, _R = 0.1, Sc = E_T = 0.5

Fig. 6

Eckert parameter Ec_n, Heat generation/absorption parameter E_T, Thermal Radiation parameter T_R and Prandtl number Pr on temperature profile when α = β₁ = γ₁ = 0.95, Λ = Λ₂ = 0.1, M_N = E_f = 0.5, n = 2.0, Λ_rφ = P_vr = Λ_rθ = 0.1, Λ_φ = Λ_θ = 4 Sc = 0.5

Fig. 7

Chemical reaction parameter C_rs, and Schmidt number Sc on Concentration profile when α = β₁ = γ₁ = 0.95, Λ = Λ₂ = 0.4, M_N = E_f = 0.5,Pr = 1.0, Ec_n = 0.5 = E_T, n = 2.0, Λ_rφ = P_vr = Λ_rθ = 0.1, = ${\Lambda }_{\phi }$Λ_θ = 4, T_R = 0.5

Table 1 Numerical values for heat transfer rate (Lower and Upper surface) for different values of coupled nonlinear fluid model parameters when $\alpha =0.1, n=1.0, {T}_{R}={E}_{T}=\Lambda =0.5, {\Lambda }_{\theta }={\Lambda }_{\phi }=0.1, {P}_{vr}=0.5.$

Table 2 Numerical values for mass transfer rate (Lower and Upper surface) for different values coupled nonlinear fluid model parameters when $\alpha =0.1, n=1.0,\Lambda =0.5,Pr=0.4, {\Lambda }_{\theta }={\Lambda }_{\phi }=0.1,{P}_{vr}=0.5.$

Final Remarks

The current study offers a detailed overview regarding the effects of solar radiation (T_R) and magnetic field (M_N ) on the unstable heat and mass transport of an electrically conducting fluid by mixed convection beside a moving surface where homogeneous first-order chemical reaction with the influence of Ohmic heating and exothermic and endothermic reactions are taken into consideration. The Cattaneo-Friedrich fractional technique is being utilized to formulate the principal equations of the subject flow problem. After modeling the problem, the very well-known techniques named finite element and finite difference method are utilized to have a numerical solution of the problem. Three fractional parameters α, β₁ and γ₁ are introduced in momentum, energy, and concentration equations. The numerical scheme presented by us is being validated by performing an error analysis of the same. In order to have a pictorial view, the quantities of interest like velocity, temperature, and concentration profile as well as Nusselt and Sherwood numbers are presented through graphs and tables. The physical variables that have been observed to influence the different fields under discussion are the relaxation time parameters (Λ, Λ_rθ, Λ_rφ ), fractional parameter (α, β₁, γ₁), magnetic parameter (M_N ), porosity parameter (P_vr), electric parameter (E_f ), thermal and solutal Grashof number (Λ_θ, Λ_φ), chemical reaction parameter (C_rs), radiation parameter (T_R), Prandtl number (Pr), Schmidt number (Sc) and heat absorption parameter(E_T ). The following inferences can be deducted from the above discussion and numerical computations:

• The velocity field is greatly influenced by the relaxation time parameters and the fractional derivative. One can observe that corresponding to an increase in the fractional derivative and relaxation time parameter, the thickness of the momentum boundary layer becomes thinner. Moreover, increasing fractional derivative and relaxation parameters increase the velocity near and away from the surface (upper and lower surface).

• A higher magnetic resistance is observed which cause a reduction in the velocity through dual trend is observed for temperature in (case 1) temperature shows decreasing behavior for (Λ_θ < 2) whereas in (case 2) increasing trend is witnessed in temperature for (Λ_θ ≥ 2) which is due to thermal buoyancy frictional force. However, this trend cannot be generalized as other parameters of interest also contribute to determining this trend.

• Thermal gradient behaves like a decreasing function for β₁ and Pr, whereas an increasing trend is noticed for T_R and Ec_n where the temperature is a quadratic function of time at the heated boundary.

• It is also observed that the existence of thermal radiation and the fractional derivative parameter contributes to the increment of Nusselt number at the upper surface. On the other hand, the effect of thermal radiation on Nusselt number at the lower surface is almost negligible. Further, one can observe that fractional derivative parameters greatly affect heat transfer.

Furthermore, the value of the Nusselt number increases on both surfaces due to the existence of a heat source.

An increment in chemical reaction parameter and concentration relaxation time parameter results in a decrease in the value of Sherwood number whereas as opposite behavior is witnessed in case of the upper surface.

Appendices

Appendix

Transformation for Homogeneous model

$$ \left\{ {\begin{array}{*{20}l} {w\left( {y,t} \right): = u\left( {x,t} \right) - t^{n} cos\left( {\frac{{\pi y}}{2}} \right),} \\ {\bar{\theta }\left( {y,t} \right): = \theta \left( {y,t} \right) - \left( {t^{2} \left( {1 - y} \right) + ty} \right),} \\ {\bar{\phi }\left( {y,t} \right): = \phi \left( {y,t} \right) - \left( {t^{2} \left( {1 - y} \right) + ty} \right),} \\ \end{array} } \right. $$

Right hand side term

$$ \begin{aligned} & {\mathbb{F}}_{{1{u}}} : = - {nt}^{{{n} - 1}} cos\left( {\frac{{\pi y}}{2}} \right) - cos\left( {\frac{{\pi y}}{2}} \right)\frac{{{{\Lambda }}^{\alpha } {{\Gamma }}\left( {n + 1} \right)}}{{{{\Gamma }}\left( {n - \alpha } \right)}}t^{{n - \alpha - 1}} - \left( {\frac{\pi }{2}} \right)^{2} cos\left( {\frac{{\pi y}}{2}} \right)\left( {t^{n} + \frac{{{{\Lambda }}_{2}^{\alpha } {{\Gamma }}\left( {n + 1} \right)}}{{{{\Gamma }}\left( {n + 1 - \alpha } \right)}}t^{{n - \alpha }} } \right) \\ & \quad - cos\left( {\frac{{\pi y}}{2}} \right)\left( {M_{N} + P_{{vr}} } \right)\frac{{{{\Gamma }}\left( {n + 1} \right)}}{{{{\Gamma }}\left( {n + 1 - \alpha } \right)}}t^{{n - \alpha }} - cos\left( {\frac{{\pi y}}{2}} \right)\left( {M_{N} + P_{{vr}} } \right)t^{n} + \frac{{2{{\Lambda }}_{\theta } {{\Lambda }}\left( {1 - y} \right){{~~}}}}{{{{\Gamma }}\left( {3 - \alpha } \right)}}t^{{2 - \alpha }} \\ & \quad + {{\Lambda }}_{\theta } t^{2} + \frac{{{{\Lambda }}_{\theta } y}}{{{{\Gamma }}\left( {2 - \alpha } \right)}}t^{{1 - \alpha }} + {{\Lambda }}_{\theta } t + \frac{{2{{\Lambda }}_{\phi } \left( {1 - y} \right)}}{{{{\Gamma }}\left( {3 - \alpha } \right)}}t^{{2 - \alpha }} + {{\Lambda }}_{\phi } t^{2} + \frac{{{{\Lambda }}_{\phi } y}}{{{{\Gamma }}\left( {2 - \alpha } \right)}}t^{{1 - \alpha }} {{\Lambda }}_{\phi } t, \\ \end{aligned} $$

$${\mathbb{F}}_{2{\varvec{\theta}}}:=PrE{c}_{n}{M}_{N}{t}^{n}cos{\left(\frac{\pi y}{2}\right)}^{2}\left[{t}^{n}+\frac{{\Lambda }_{{r\theta }}\Gamma \left(n+1\right)}{\Gamma \left(n+1-{\beta }_{1}\right)}{t}^{n-{\beta }_{1}}\right]+PrE{c}_{n}{M}_{N}{E}_{f}^{2}-2PrE{c}_{n}{M}_{N}{E}_{f}{t}^{n}cos\left(\frac{\pi y}{2}\right)-2PrE{c}_{n}{M}_{N}{E}_{f}\left[\frac{{\Lambda }_{{r\theta }}\Gamma \left(n+1\right)}{\Gamma \left(n+1-{\beta }_{1}\right)}{t}^{n-{\beta }_{1}}cos\left(\frac{\pi y}{2}\right){t}^{n-{\beta }_{1}}\right]+Pr{E}_{T}\left[{t}^{2}\left(1-y\right)+ty+\frac{2{\Lambda }_{{r\theta }}\left(1-\mathrm{y}\right){\mathrm{t}}^{2-{\upbeta }_{1}}}{\Gamma \left(3-{\beta }_{1}\right)}+\frac{{\Lambda }_{{r\theta }}{\mathrm{yt}}^{1-{\upbeta }_{1}}}{\Gamma \left(2-{\beta }_{1}\right)}\right]-2tPr\left(1-y\right)-\frac{{\Lambda }_{{r\theta }}\mathrm{Pr}\left(1-\mathrm{y}\right)}{\Gamma \left(2-{\beta }_{1}\right)}{\mathrm{t}}^{1-{\upbeta }_{1}}-Pry-\frac{{\Lambda }_{{r\theta }}\mathrm{Pry}}{\Gamma \left(1-{\beta }_{1}\right)}{\mathrm{t}}^{-{\upbeta }_{1}},$$

$${\mathbb{F}}_{3\phi } := -Sc{C}_{rs}{t}^{2}\left(1-y\right)+Sc2t\left(1-y\right)-Sc\left(\frac{2\left(1-y\right){\Lambda }_{r\phi }}{\Gamma \left(2-{\gamma }_{1}\right)}{t}^{1-{\gamma }_{1}}+\frac{y{\Lambda }_{r\phi }}{\Gamma \left(1-{\gamma }_{1}\right)}{t}^{-{\gamma }_{1}}\right)-Scy-Sc{C}_{rs}$$