Fractional Model and Numerical Algorithms for Predicting COVID-19 with Isolation and Quarantine Strategies

Abstract

In December 2019, a new outbreak in Wuhan, China has attracted world-wide attention, the virus then spread rapidly in most countries of the world, the objective of this paper is to investigate the mathematical modelling and dynamics of a novel coronavirus (COVID-19) with Caputo-Fabrizio fractional derivative in the presence of quarantine and isolation strategies. The existence and uniqueness of the solutions for the fractional model is proved using fixed point iterations, the fractional model are shown to have disease-free and an endemic equilibrium point.We construct a fractional version of the four-steps Adams-Bashforth method as well as the error estimate of this method. We have used this method to determine the numerical scheme of this model and Matlab program to illustrate the evolution of the virus in some countries (Morocco, Qatar, Brazil and Mexico) as well as to support theoretical results. The Least squares fitting is a way to find the best fit curve or line for a set of points, so we apply this method in this paper to construct an algorithm to estimate the parameters of fractional model as well as the fractional order, this model gives an estimate better than that of classical model.

Introduction

In December 2019, an unidentified virus was found in Wuhan, Hubei province, China. The responsible virus was later confirmed as a new coronavirus [23]. The World Health Organization (WHO) temporarily named the virus as the novel coronavirus 2019 (2019-nCoV), and the disease as coronavirus disease 2019 (COVID-19) on 11 February 2020. The first confirmed case of the virus was discovered on 17 November 2019 in Hubei. As of 5 July 2020, more than 11.1 million cases have been reported in 188 countries in the world, which resulted in more than 528,000 deaths. Over 6.03 million people recovered [57].

The progress of fractional calculus in the last few years has been very rapid due to its applicability in many fields, such as physical problems [15, 23, 51, 58], engineering mechanics [9], epidemiological models [6, 14, 17, 18, 26, 29, 44, 45, 47], image processing [28, 59], chaos theory [10, 52] and others. There are in the literature several definitions of the fractional derivative, the most famous of these is the definition of Caputo, Riemann-Liouville, Grünwald–Letnikov and Hadamard derivative, the new operators with non-singular kernels appear in this domain of mathematics, namely the Caputo-Fabrizio derivative [19] and the Atangana-Baleanu-Caputo derivative [8].

A number of epidemiological models with fractional derivative have been developed to understand the transmission dynamics of COVID-19 and other infectious diseases outbreak from various aspects. We mention them, Kumar et al. [33] have been studied fractional SIRS-SI model describing the transmission of malaria disease by using the Caputo–Fabrizio fractional operator. Tuan et al. [53] studied a mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Singh et al. [49] studied the numerical solution of SEIAR model with Grünwald-Leitnikov derivative. Abdo et al. [1] have investigated the mathematical model of novel coronavirus (COVID-19) depending of fourteen nonlinear FDEs with Atangana-Baleanu-Caputo fractional derivative. Peter et al. [42] investigated a fractional order mathematical model of COVID-19 in Nigeria using Atangana-Aaleanu derivative. Ahmad et al. [2] Studied the fractional model and dynamics of COVID-19 in Pakistan using Atangana Baleanau operators. Nisar et al. [41] Proposed a SIRD model of COVID-19 with Caputo fractional derivative. Rezapour et al. [44] presented a new mathematical model for the transmission of Zika virus between humans as well as between humans and mosquitoes using Caputo derivative. Baleanu et al. [16] proposed a new fractional model for human liver involving Caputo– Fabrizio derivative. Rezapour et al. [43] studied the fractional-order model for the anthrax disease between animals based on the Caputo–Fabrizio derivative. Dokuyucu and Dutta [26] examined the Ebola virus model using the fractional derivative and the integral operator proposed by Caputo and Fabrizio. Area et al. [6] have been studied the classical and Caputo fractional order SEIR (susceptible, exposed, infections, removed) Ebola epidemic model and its comparison with real data. Tulu et al. [54] developed the Caputo fractional mathematical model of the Ebola virus with a quarantine strategy and the presence of the vaccine, using both the Euler method and one of the top ten most influential algorithms known as Markov Chain Monte Carlo (MCMC) method. Singh et al. [48] have been studied the fractional epidemiological model for computer viruses using Caputo-Fabrizio fractional derivative. Singh et al. [47] studied the diabetes model and its complications with the CF-fractional derivative. Mohammadi et al. [38] used Caputo–Fabrizio fractional derivative to model hearing loss in children caused by the mumps virus. Higazy [30] suggested a SIDARTHE model for COVID-19 pandemic by using Caputo fractional derivative. Zhang et al. [63] applied the fractional SEIRD Model to the real data of the COVID-19 for China using Caputo fractional derivative. Some other outstanding studies of COVID-19 by fractional derivative have been made in [4, 5, 7, 24, 31, 34, 37, 46, 60, 62].

Always when a new virus appears, researchers look for effective ways to control the virus, including vaccination, isolation, and quarantine. In the absence of the vaccine, the isolation and quarantine strategies remain effective to mitigate and eliminate the impact of the virus (see [12, 20,21,22, 27, 64]). In this current study, we modify the general SEIR epidemiological model for the effects of isolation and quarantine strategies on COVID-19 transmission, to become a fractional order model of type Caputo-Fabrezio fractional derivative. The main objective in this work is to provide a new discussion and new tools for developing epidemiological models with Caputo-Fabrizio derivative, this work is motivated by all these results that prove the efficiency of fractional derivative, to our best knowledge, such problem has never been studied previously for the fractional case. We will start this article in the theoretical part by proving the existence and uniqueness of the solutions, then we will determine the equilibrium and the basic reproduction number of the model. We construct a fractional version of the four-steps Adams-Bashforth method as well as the error estimate of this method.

In machine learning, the Least squares fitting is a way to find the best fit curve or line for a set of points, so we apply this method in this paper to construct an algorithm to estimate the parameters of fractional model as well as the fractional order, this model gives an estimate better than that of classical model. The paper is organized as follows. In Section 2, we present the basic theory of the Caputo-Fabrizio derivative. The clasical and fractional model are formulated in Section 3. The basic roprodoction number and the disease-free equilibrium are given in Section 4. The fixed point iterations is applied to prove existence and uniqueness results in Section 5. Using fractional m-step Adams-Bashforth scheme with $\mathrm {CF}$ derivative, the numerical solution of the proposed model is obtained in Section 6. Simulation results are presented in Section 7. Finally, the present work is concluded in Section 8.

Preliminaries

Recalled here some background material for the Caputo-Fabrizio fractional derivatives, see [3, 19, 32] for details.

Definition 1

([19]) Let $u \in H^{1}(a, b), b>a, 0<\alpha <1,$ the time fractional Caputo-Fabrizio fractional differential operator is defined by

$$\begin{aligned} ^{C F} D_{t}^{\alpha } u(t)=\frac{M(\alpha )}{(1-\alpha )} \int _{\mathrm {a}}^{t} \exp \left[ -\frac{\alpha (t-x)}{1-\alpha }\right] u^{\prime }(x) dx, \quad t \ge 0. \end{aligned}$$

where M is a normalization function which depends on $\alpha$ and gives $M(0) =M(1) =1$, where $^{C F} D_{t}^{\alpha } u(t)=0,$ if u is a constant function. The definition is also written if the function does not belong to $\mathrm {H}^{1}(a, b)$

$$\begin{aligned} ^{CF} D_{\mathrm {t}}^{\alpha }(u(t))=\frac{\alpha M(\alpha )}{1-\alpha } \int _{\mathrm {a}}^{\mathrm {t}}(u(t)-u(x)) \exp \left[ -\frac{\alpha (t-x)}{1-\alpha }\right] d x. \end{aligned}$$

The corresponding integral was described by Jorge and Juan [32].

Definition 2

([32]) Let 0 $<\alpha < 1$, then the CF fractional integral operator of order $\alpha$ given by

$$\begin{aligned} ^{C F} I_{t}^{\alpha } u(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} u(t) +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} u(s) ds, \quad t \ge 0. \end{aligned}$$

Model Formulation

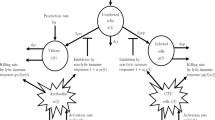
In more detail, we have studied a fractional SEIR epidemiological model with quarantine and isolation strategies. The total population is divided into seven groups, namely susceptible (S), exposed (E), infectious but not yet symptomatic, infectious with symptoms (I) and recovered (R) compartments, as well as quarantined susceptible $(S_{q}),$ quarantined exposed $(E_{q})$ and isolated infected $(I_q)$ compartments. Where susceptible individuals can be quarantined at a rate of $\delta _s$ and then returned to the pool of susceptible individuals once it is determined they are uninfected at a rate of $\delta _q$. The unquarantined susceptible individuals, if infected, move to the compartment E at a rate of $\beta (I+qE)$ where $\beta$ is the transmission incidence rate and q is the fraction of transmission rate for exposed, also the exposed individuals develop symptoms at a rate $\sigma _0$ and are assumed to be quarantined at a rate $\sigma _{1},$ not only-but also the exposed quarantined individuals can be isolated at rate $q_e$ they also recover after isolation at rate $q_i$. Likewise the infected symptomatically individuals develop symptoms and can be isolated at rate $\gamma _1$, in addition they recover from the disease at rates $\gamma _0$, finally $\varLambda$ is the recruitment rate, $\mu$ represent natural death rate and $\mu _I$ show the death rate of infected human individuals with the coronavirus disease 2019.

Fig. 1

Schematic diagram of the model compartments and parameters

The transfer diagram for this model is described by Fig. 1 and the classical version of this model formulated by the following system of ODEs:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm {d} S}{\mathrm {d} t}=\varLambda -\beta S(I+qE)+\delta _q S_q -(\delta _s+\mu ) S ,\\ \frac{\mathrm {d} E}{\mathrm {d} t}=\beta S(I+qE)-(\sigma _0+\sigma _1+\mu )E, \\ \frac{\mathrm {d} I}{\mathrm {d} t}=\sigma _0 E-(\gamma _0+\gamma _1+\mu +\mu _I)I, \\ \frac{\mathrm {d} R}{\mathrm {d} t}=\gamma _0I+q_i I_q-\mu R, \\ \frac{\mathrm {d} S_q}{\mathrm {d} t}=\delta _sS-(\delta _q+\mu )S_q, \\ \frac{\mathrm {d} E_q}{\mathrm {d} t}=\sigma _1E-(q_e+\mu )E_q, \\ \frac{\mathrm {d} I_q}{\mathrm {d} t}=q_eE_q+\gamma _1I-(q_i+\mu +\mu _I)I_q, \\ \end{array}\right. } \end{aligned}$$

(1)

Fractional Model

Now replacing the classical derivative in (1) by Caputo-Fabrizio derivative we obtain by moment closure, the following system of fractional ODEs :

$$\begin{aligned} {\left\{ \begin{array}{ll} D_t^{\alpha }S=\varLambda -\beta S(I+qE)+\delta _q S_q-(\delta _s +\mu )S ,\\ D_t^{\alpha }E=\beta S(I+qE)-(\sigma _0 +\sigma _1 +\mu )E ,\\ D_t^{\alpha }I=\sigma _0 E-(\gamma _0 +\gamma _1 +\mu +\mu _I )I ,\\ D_t^{\alpha }R=\gamma _0 I+q_i I_q-\mu R ,\\ D_t^{\alpha }S_q=\delta _s S-(\delta _q +\mu )S_q, \\ D_t^{\alpha }E_q=\sigma _1 E-(q_e +\mu )E_q ,\\ D_t^{\alpha }I_q=q_e E_q+\gamma _1 I-(q_i +\mu +\mu _I )I_q, \\ \end{array}\right. } \end{aligned}$$

(2)

with the initial conditions $S(0)=S_0 \geqslant 0, E(0)=E_0 \geqslant 0, I(0)=I_0 \geqslant 0; R(0)=R_0 \geqslant 0,$ $S_{q}(0)=S_{q0} \geqslant 0, E_{q}(0)=E_{q0} \geqslant 0, I_{q}(0)=I_{q0} \geqslant 0$ and $D^\alpha _t$ is the Caputo-Fabrizio fractional operator of order $\alpha$.

The total population $S(t)+E(t)+I(t)+R(t)+S_q(t)+E_q(t)+I_q(t)=N(t)$. Then

$$\begin{aligned} D_t^{\alpha }N(t)= & {} D_t S(t)+D_t E(t)+D_t I(t)+D_t R(t)+D_t S_q(t)+D_t E_q(t)+D_t I_q(t) ,\\\Rightarrow & {} D_t^{\alpha }N(t)=\varLambda -\mu N(t) -\mu _{I} \left( I+I_{q}\right) . \end{aligned}$$

In the absence of the disease, $D_t^{\alpha }N(t)=\varLambda -\mu N(t)$, this shows that the population size $\mathrm {N}$ tends to carrying capacity

$$\begin{aligned} \frac{\varLambda }{\mu } \text { as } t \rightarrow \infty . \end{aligned}$$

Quarantine Reproductive Number and Existence of Equilibrium

The epidemic model (2) has a family of disease-free equilibrium, obtained by setting the right hand side of the equations in (2) to zero, given by

$$\begin{aligned} DFE=\left( S^{0}, E^{0}, I^{0}, R^{0}, S_q^{0}, E_{q}^{0}, I_{q}^{0}\right) , \end{aligned}$$

where $E^{0}=I^{0}= R^{0}=E_{q}^{0}= I_{q}^{0}=0$ and

$$\begin{aligned} S^{0}=\frac{\varLambda (\delta _q +\mu )}{\mu (\mu +\delta _q +\delta _s )} \quad ,\quad S_q^{0}=\frac{\varLambda \delta _s }{\mu (\mu +\delta _q +\delta _s )}. \end{aligned}$$

(3)

Now using the notation in [56], the non-negative matrix, F, for the new infection terms and the non-singular M -matrix, V, for the remaining transfer terms are given by

$$\begin{aligned} F&=\left( \begin{array}{llll} q\beta S &{}\quad \beta S &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array}\right) . \end{aligned}$$

(4)

$$\begin{aligned} V&=\left( \begin{array}{llll} \sigma _0 +\sigma _1 +\mu &{}\quad 0&{}\quad 0 &{}\quad 0 \\ -\sigma _0 &{}\quad \gamma _0 +\gamma _1 +\mu +\mu _I &{}\quad 0 &{}\quad 0 \\ -\sigma _1 &{}\quad 0 &{}\quad q_e +\mu &{}\quad 0\\ 0 &{}\quad -\gamma _1 &{}\quad -q_e &{}\quad q_i +\mu +\mu _I \end{array}\right) . \end{aligned}$$

(5)

Thus

$$\begin{aligned} FV^{-1}=\left( \begin{array}{llll} A&{}\quad B&{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array}\right) . \end{aligned}$$

(6)

where

$$\begin{aligned} A=\frac{q\beta S^{0}}{\sigma _0 +\sigma _1 +\mu } +\frac{\beta S^{0} \sigma _0 }{(\sigma _0 +\sigma _1 +\mu ) (\gamma _0 +\gamma _1 +\mu +\mu _I )}\quad \text { and } B=\frac{\beta S^{0}}{\gamma _0 +\gamma _1 +\mu +\mu _I }. \end{aligned}$$

The effective reproduction number (or quarantine-isolation reproduction number), denoted by ${\mathcal {R}}_{e},$ is given by ${\mathcal {R}}_{e}=\rho \left( F V^{-1}\right)$ where $\rho$ denotes the spectral radius. It follows that

$$\begin{aligned} {\mathcal {R}}_{e} =\frac{\beta S^{0} [q(\gamma _0 +\gamma _1 +\mu +\mu _I) +\sigma _0 ]}{(\sigma _0 +\sigma _1 +\mu )(\gamma _0 +\gamma _1 +\mu +\mu _I )}. \end{aligned}$$

(7)

The system (2) has a unique endemic steady state

$$\begin{aligned} ESS=\left( S^{*}, E^{*}, I^{*}, R^{*}, S_q^{*}, E_{q}^{*}, I_{q}^{*}\right) , \end{aligned}$$

where

$$\begin{aligned}&S^{*}=\frac{S^0}{R_e},\quad S_q =\frac{\delta _s }{\delta _q +\mu }S^{*},\quad E^{*} =\frac{\varLambda (\delta _q +\mu )-\mu (\mu +\delta _s +\delta _q )}{(\sigma _0 +\sigma _1 +\mu ) (\delta _q +\delta _s +\mu )}\frac{\varLambda }{R_e},\\&E_q=\frac{\sigma _1 }{q_e +\mu }E^{*},\quad I^{*} =\frac{\sigma }{(\gamma _0 +\gamma _1 +\mu +\mu _I )}E^{*};\\&I_q^{*}=\frac{q_e \sigma _1 (\gamma _0 +\gamma _1 +\mu +\mu _I ) +\gamma _1 \sigma _0 (q_e +\mu )}{(q_i +\mu + \mu _I )(q_e +\mu ) (\gamma _0 +\gamma _1 +\mu +\mu _I )}E^{*}. \end{aligned}$$

Existence and Uniqueness of a System of Solutions

In this section, we prove the existence of the system of solutions by applying the fixed-point theorem.

Let ${\mathcal {H}}=(C(J))^7$, and C(J) be a Banach space of continuous $J\subset {\mathbb {R}} \rightarrow {\mathbb {R}}$ valued functions on the interval J with the norm

$$\begin{aligned} \Vert (S, E, I, R,S_q, E_q, I_q)\Vert =\Vert S\Vert +\Vert E\Vert +\Vert I\Vert +\Vert R\Vert +\Vert S_q\Vert +\Vert E_q\Vert +\Vert I_q\Vert , \end{aligned}$$

where $\Vert .\Vert$ denote the supremum norm in C(J).

Now using the integral operator of fractional order introduced by Losada and Nieto Jorge and Juan [32] on the system (2), we get

$$\begin{aligned} S(t)-S(0)&= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )}\{\varLambda -\beta S(t)(I(t) +qE(t))+\delta _q S_q(t)-(\delta _s +\mu )S(t)\} \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\{\varLambda -\beta S(x)(I(x)+qE(x)) +\delta _q S_q(x)-(\delta _s +\mu )S(x)\} d x ,\\ E(t)-E(0)&= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left\{ \beta S(t)(I(t)+qE(t))-(\sigma _0 +\sigma _1 +\mu )E(t) \right\} \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left\{ \beta S(x)(I(x)+qE(x))-(\sigma _0 +\sigma _1 +\mu )E(x)\right\} d x, \\ I(t)-I(0)&= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left\{ \sigma _0 E(t)-(\gamma _0 +\gamma _1 +\mu +\mu _I )I(t)\right\} \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left\{ \sigma _0 E(x)-(\gamma _0 +\gamma _1 +\mu +\mu _I )I(x)\right\} d x ,\\ R(t)-R(0)&= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left\{ \gamma _0 I(t)+q_i I_q(t)-\mu R(t) \right\} ,\\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left\{ \gamma _0 I(x)+q_i I_q(x)-\mu R(x) \right\} d x ,\\ S_q(t)-S_q(0)&= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left\{ \delta _s S(t)-(\delta _q +\mu )S_q(t)\right\} \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left\{ \delta _s S(x)-(\delta _q +\mu )S_q(x)\right\} d x, \\ E_q(t)-E_q(0)&= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left\{ \sigma _1 E(t)-(q_e +\mu )E_q(t) \right\} \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left\{ \sigma _1 E(x)-(q_e +\mu )E_q(x) \right\} d x ,\\ I_q(t)-I_q(0)&= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left\{ q_e E_q(t)+\gamma _1 I(t)-(q_i +\mu +\mu _I )I_q(t) \right\} \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left\{ q_e E_q(x)+\gamma _1 I(x)-(q_i +\mu +\mu _I )I_q(x) \right\} d x .\\ \end{aligned}$$

For simplicity,

$$\begin{aligned}&\varPhi _1(t,S)=\varLambda -\beta S(t)(I(t)+qE(t))+\delta _q S_q(t)-(\delta _s +\mu )S(t),\\&\varPhi _2(t,E)=\beta S(t)(I(t)+qE(t))-(\sigma _0 +\sigma _1 +\mu )E(t) , \\&\varPhi _3(t,I)= \sigma _0 E(t)-(\gamma _0 +\gamma _1 +\mu +\mu _I )I(t) , \\&\varPhi _4(t,R)= \gamma _0 I(t)+q_i I_q(t)-\mu R(t) , \\&\varPhi _5(t,S_q)=\delta _s S(t)-(\delta _q +\mu )S_q(t) , \\&\varPhi _6(t,E_q)=\sigma _1 E(t)-(q_e +\mu )E_q(t) , \\&\varPhi _7(t,I_q)=q_e E_q(t)+\gamma _1 I(t)-(q_i +\mu +\mu _I )I_q(t). \end{aligned}$$

To prove the following theorems, we will assume that $\Vert S(t)\Vert \le c_{1},\Vert E(t)\Vert \le c_{2},\Vert I(t)\Vert \le c_{3},\Vert R(t)\Vert \le c_{4},$ $\Vert S_q(t)\Vert \le c_{5},\Vert E_q(t)\Vert \le c_{6},$ and $\Vert I_q(t)\Vert \le c_{7}$ where $c_{i}, i=1,\ldots ,7$, are some positive constants. Denote

$$\begin{aligned}&L_{1}=\beta c_3+q\beta c_2+\delta _s +\mu ,\quad L_{2}=q\beta c_1 +\sigma _0 +\sigma _{1} +\mu ,\\&L_{3}=\gamma _0 +\gamma _{1} +\mu +\mu _I ,\quad L_{4}=\mu ,\quad L_{5}=\delta _s +\mu , \quad L_{6}=q_e +\mu ,\quad L_{7}=q_i +\mu +\mu _I . \end{aligned}$$

Theorem 3

The kernels $\varPhi _{i}$ $(i=1,\ldots ,7)$, satisfy the Lipschitz condition and contraction if the inequality given below holds

$$\begin{aligned} 0\leqslant L_i<1, \text { for }i=1,\ldots 7. \end{aligned}$$

(8)

Proof

Let $S_{1}$ and $S_{2}$ be two functions, then

$$\begin{aligned} \left\| \varPhi _{1}\left( t, S_{1}\right) -\varPhi _{1}\left( t, S_{2}\right) \right\|&=\left\| \left( -\beta I(t)-q\beta E(t)-(\delta _s +\mu ) \right) \left( S_{1}-S_{2}\right) \right\| \\&\leqslant \left[ \beta \left\| I\right\| +q\beta \left\| E\right\| +\left( \delta _s +\mu \right) \right] \left\| S_{1}(t)-S_{2}(t) \right\| \\&\leqslant \left( \beta c_3+q\beta c_2+\delta _s +\mu \right) \left\| S_{1}(t)-S_{2}(t) \right\| . \end{aligned}$$

Thus

$$\begin{aligned} \left\| \varPhi _{1}\left( t, S_{1}\right) -\varPhi _{1}\left( t, S_{2}\right) \right\| \leqslant L_1\left\| S_1(t)-S_2(t)\right\| . \end{aligned}$$

(9)

Hence, for $\varPhi _{1}$ the Lipschitz condition is obtained. Similarly for $\varPhi _{2},\varPhi _{3},\varPhi _{4},\varPhi _{5},\varPhi _{6}$, and $\varPhi _{7}$ the Lipschiz condition can be easily verified and given below:

$$\begin{aligned}&\left\| \varPhi _{2}(t, E_1)-\varPhi _{2}(t, E_{2})\right\| \leqslant L_{2} \left\| E_1(t)-E_2(t) \right\| ,\\&\left\| \varPhi _{3}(t, I_1)-\varPhi _{3}(t, I_{2})\right\| \leqslant L_{3} \left\| I_1(t)-I_2(t) \right\| , \\&\left\| \varPhi _{4}(t, R_1)-\varPhi _{4}(t, R_{2})\right\| \leqslant L_{4} \left\| R_1(t)-R_2(t) \right\| , \\&\left\| \varPhi _{5}(t, S_{q1})-\varPhi _{5}(t, S_{q2})\right\| \leqslant L_{5} \left\| S_{q1}(t)-S_{q2}(t) \right\| , \\&\left\| \varPhi _{6}(t, E_{q1})-\varPhi _{6}(t, E_{q2})\right\| \leqslant L_{6} \left\| E_{q1}(t)-E_{q2}(t) \right\| , \\&\left\| \varPhi _{7}(t, I_{q1})-\varPhi _{7}(t, I_{q2})\right\| \leqslant L_{7} \left\| I_{q1}(t)-I_{q2}(t) \right\| , \\ \end{aligned}$$

$\square$

Now we write the system (2) in the following recursive form:

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{n}(t)= \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )}\varPhi _{1} \left( t, S_{n-1}\right) +\frac{2\alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \varPhi _{1}\left( x, S_{n-1}\right) \mathrm {d} x ,\\ E_{n}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \varPhi _{2} \left( t, E_{n-1}\right) +\frac{2\alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \varPhi _{2}\left( x, E_{n-1}\right) \mathrm {d} x ,\\ I_{n}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \varPhi _{3} \left( t, I_{n-1}\right) +\frac{2\alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \varPhi _{3}\left( x, I_{n-1}\right) \mathrm {d} x, \\ R_{n}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \varPhi _{4} \left( t, R_{n-1}\right) +\frac{2\alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \varPhi _{4}\left( x, R_{n-1}\right) \mathrm {d} x, \\ S_{q,n}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \varPhi _{5} \left( t, S_{q,n-1}\right) +\frac{2\alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \varPhi _{5}\left( x, S_{q,n-1}\right) \mathrm {d} x, \\ E_{q,n}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \varPhi _{6} \left( t, E_{q,n-1}\right) +\frac{2\alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \varPhi _{6}\left( x, E_{q,n-1}\right) \mathrm {d}x,\\ I_{q,n}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \varPhi _{7} \left( t, I_{q,n-1}\right) +\frac{2\alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \varPhi _{7}\left( x, I_{q,n-1}\right) \mathrm {d} x .\\ \end{array}\right. } \end{aligned}$$

(10)

The initial conditions are

$S_{0}(t)=S(0)$, $E_{0}(t)=E(0)$, $I_{0}(t)=(0)$, $R_{0}(t)=R(0)$, $S_{q,0}(t)=S_q(0)$, $E_{q,0}(t)=E_q(0)$ and $I_{q,0}=I_q(0).$

Then we get the following expressions for the difference between the successive terms:

$$\begin{aligned} W^1_{n}(t)&= S_{n}(t)-S_{n-1}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{1}\left( t, S_{n-1}\right) -\varPhi _{1}\left( t, S_{n-2}\right) \right) \nonumber \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left( \varPhi _{1} \left( x, S_{n-1}\right) -\varPhi _{1}\left( x, S_{n-2}\right) \right) d x , \end{aligned}$$

(11)

$$\begin{aligned} W^2_{n}(t)&= E_{n}(t)-E_{n-1}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{2}\left( t, E_{n-1}\right) -\varPhi _{2}\left( t, E_{n-2}\right) \right) \nonumber \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left( \varPhi _{2} \left( x, E_{n-1}\right) -\varPhi _{2}\left( x, E_{n-2}\right) \right) d x , \end{aligned}$$

(12)

$$\begin{aligned} W^3_{n}(t)&= I_{n}(t)-I_{n-1}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{3}\left( t, I_{n-1}\right) -\varPhi _{3}\left( t, I_{n-2}\right) \right) \nonumber \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left( \varPhi _{3} \left( x, I_{n-1}\right) -\varPhi _{3}\left( x, I_{n-2}\right) \right) d x , \end{aligned}$$

(13)

$$\begin{aligned} W^4_{n}(t)&= R_{n}(t)-R_{n-1}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{4}\left( t, R_{n-1}\right) -\varPhi _{4}\left( t, R_{n-2}\right) \right) \nonumber \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left( \varPhi _{4} \left( x, R_{n-1}\right) -\varPhi _{4}(x, R_{n-2})\right) d x , \end{aligned}$$

(14)

$$\begin{aligned} W^5_{n}(t)&= S_{q,n}(t)-S_{n-1}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{5}\left( t, S_{q,n-1}\right) -\varPhi _{5}\left( t, S_{q,n-2}\right) \right) \nonumber \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left( \varPhi _{5} \left( x, S_{q,n-1}\right) -\varPhi _{5}(x, S_{q,n-2})\right) d x , \end{aligned}$$

(15)

$$\begin{aligned} W^6_{n}(t)&= E_{q,n}(t)-E_{q,n-1}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{6}\left( t, E_{q,n-1}\right) -\varPhi _{6}(t, E_{q,n-2})\right) \nonumber \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left( \varPhi _{6} \left( x, E_{q,n-1}\right) -\varPhi _{6}\left( x, E_{q,n-2}\right) \right) d x , \end{aligned}$$

(16)

$$\begin{aligned} W^7_{n}(t)&= I_{q,n}(t)-I_{q,n-1}(t)=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{7}\left( t, I_{q,n-1}\right) -\varPhi _{7}\left( t, I_{q,n-2}\right) \right) \nonumber \\&+\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left( \varPhi _{7}\left( x, I_{q,n-1}\right) -\varPhi _{7}\left( x, I_{q,n-2}\right) \right) d x. \end{aligned}$$

(17)

Taking the norm on both side of the Eq. (11), applying triangular inequality and using the Lipschitz condition proved in (9) we obtained

$$\begin{aligned} \left\| W_{n}^{1}(t)\right\|&= \left\| S_{n}(t)-S_{n-1}(t)\right\| \\&\leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{1} \left\| S_{n-1} -S_{n-2}\right\| + \frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{1} \int _{0}^{t} \left\| S_{n-1}-S_{n-2}\right\| d x. \end{aligned}$$

Then, we have

$$\begin{aligned} \left\| W_{n}^{1}(t)\right\| \leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{1} \left\| W_{n-1}^{1}(t)\right\| +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{1} \int _{0}^{t}\left\| W_{n-1}^{1}(x)\right\| dx. \end{aligned}$$

(18)

Similarly, for the remaining equations of the system, we obtain the following results:

$$\begin{aligned}&\left\| W_{n}^{2}(t)\right\| \leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{2} \left\| W_{n-1}^{2}(t)\right\| +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{2} \int _{0}^{t}\left\| W_{n-1}^{2}(x)\right\| dx, \end{aligned}$$

(19)

$$\begin{aligned}&\left\| W_{n}^{3}(t)\right\| \leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{3} \left\| W_{n-1}^{3}(t)\right\| +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{3} \int _{0}^{t}\left\| W_{n-1}^{3}(x)\right\| d x, \end{aligned}$$

(20)

$$\begin{aligned}&\left\| W_{n}^{4}(t)\right\| \leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{4} \left\| W_{n-1}^{4}(t)\right\| +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{4} \int _{0}^{t} \left\| W_{n-1}^{4}(x)\right\| d x, \end{aligned}$$

(21)

$$\begin{aligned}&\left\| W_{n}^{5}(t)\right\| \leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{5} \left\| W_{n-1}^{5}(t)\right\| +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{5} \int _{0}^{t} \left\| W_{n-1}^{5}(x)\right\| d x, \end{aligned}$$

(22)

$$\begin{aligned}&\left\| W_{n}^{6}(t)\right\| \leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{6} \left\| W_{n-1}^{6}(t)\right\| +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{6} \int _{0}^{t} \left\| W_{n-1}^{6}(x)\right\| d x, \end{aligned}$$

(23)

$$\begin{aligned}&\left\| W_{n}^{7}(t)\right\| \leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{7} \left\| W_{n-1}^{7}(t)\right\| +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{7} \int _{0}^{t} \left\| W_{n-1}^{7}(x)\right\| d x, \end{aligned}$$

(24)

Immediately, in view of the above results, we state the following theorem.

Theorem 4

The solution of the CF—fractional model given in (2) will exist and be unique if we can find some $t_{0}$ such that

$$\begin{aligned} \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{i}+\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )}L_{i}<1,\text { for }i=1,2, \ldots , 7. \end{aligned}$$

(25)

Proof

As the functions $S(t), E(t), I(t), R(t), S_q(t),I_q(t)$ and $E_q(t)$ are bounded and fulfill Lipschitz condition. So, by considering Eqs. (18)–(24), we obtain the following relations:

$$\begin{aligned}&\left\| W_{n}^{1}(t)\right\| \le \left\| S_{n}(0)\right\| \left[ \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{1} +\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} L_{1}\right] ^{n}, \\&\left\| W_{n}^{2}(t)\right\| \le \left\| E_{n}(0)\right\| \left[ \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{2} +\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} L_{2} \right] ^{n}, \\&\left\| W_{n}^{3}(t)\right\| \le \left\| I_{n}(0)\right\| \left[ \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{3} +\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} L_{3}\right] ^{n}, \\&\left\| W_{n}^{4}(t)\right\| \le \left\| R_{n}(0)\right\| \left[ \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{4} +\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} L_{4}\right] ^{n}, \\&\left\| W_{n}^{5}(t)\right\| \le \left\| S_{q,n}(0)\right\| \left[ \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{5} +\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} L_{5}\right] ^{n},\\&\left\| W_{n}^{6}(t)\right\| \le \left\| E_{q,n}(0)\right\| \left[ \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{6} +\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} L_{6}\right] ^{n},\\&\left\| W_{n}^{7}(t)\right\| \le \left\| I_{q,n}(0)\right\| \left[ \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{7} +\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} L_{7}\right] ^{n}. \end{aligned}$$

Thus, the proof the existence and continuity of the solutions is completed. To show that the above functions are solutions of system (2), we set as follows:

$$\begin{aligned} S(t)-S(0)&=S_{n}(t)-B^{1}_{ n}(t), \\ E(t)-E(0)&=E_{n}(t)-B^{2}_{ n}(t), \\ I(t)-I(0)&=I_{n}(t)-B^{3 }_{n}(t), \\ R(t)-R(0)&=R_{n}(t)-B^{4}_{ n}(t), \\ S_{q}(t)-S_{q}(0)&=S_{q,n}(t)-B^{5 }_{n}(t), \\ E_{q}(t)-E_{q}(0)&=E_{q,n}(t)-B^{6 }_{n}(t),\\ I_{q}(t)-I_{q}(0)&=S_{q,n}(t)-B^{7}_{n}(t). \end{aligned}$$

Therefore, we have

$$\begin{aligned} \left\| B^{1}_{n}(t)\right\|&\leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )}\left\| \left( \varPhi _{1}(t, S)-\varPhi _{1}\left( t, S_{n-1}\right) \right) \right\| \nonumber \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t}\left\| \left( \varPhi _{1}(y, S) -\varPhi _{1}\left( y, S_{n-1}\right) \right) \right\| d y ,\nonumber \\&\leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{1} \left\| S-S_{n-1}\right\| +\frac{2 \alpha t}{(2-\alpha ) M(\alpha )}L_{1} \left\| S-S_{n-1}\right\| . \end{aligned}$$

(26)

On using this process recursively, it yields

$$\begin{aligned} \left\| B^{1}_{n}(t)\right\| \le \left( \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )}+\frac{2 \alpha }{(2-\alpha ) M(\alpha )} t\right) ^{n+1} L_{1}^{n+1} c_1. \end{aligned}$$

where $c_1$ is a positive constant. Then at $t_{0},$ we have

$$\begin{aligned} \left\| B^{1}_{n}(t)\right\| \le \left( \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )}+\frac{2 \alpha t_{0}}{(2-\alpha ) M(\alpha )} \right) ^{n+1} L_{1}^{n+1} c_1. \end{aligned}$$

Now taking the limit as n tends to infinity, we get

$$\begin{aligned} \left\| B^{1}_{n}(t)\right\| \rightarrow 0. \end{aligned}$$

Repeating the same procedure we obtain

$$\begin{aligned} \left\| B^{i}_{n}(t)\right\| \rightarrow 0,\text { for }i=2,\ldots ,7. \end{aligned}$$

Hence, proof of existence is verified.

Next to show the uniqueness of the solution of the model (2), suppose on the contrary that there exists another set of solutions $S_{1}(t)$, $E_{1}(t)$, $I_{1}(t)$, $R_{1}(t)$, $S_{q,1}(t)$, $E_{q,1}(t)$ and $I_{q,1}(t)$ then

$$\begin{aligned} S(t)-S_{1}(t)&=\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left( \varPhi _{1}(t, S)-\varPhi _{1}\left( t, S_{1}\right) \right) \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left( \varPhi _{1}(y, S)-\varPhi _{1}\left( y, S_{1}\right) \right) d y. \end{aligned}$$

Applying norm in the above equation, we get

$$\begin{aligned} \left\| S(t)-S_{1}(t)\right\|&\leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} \left\| \varPhi _{1}(t, S)-\varPhi _{1}\left( t, S_{1}\right) \right\| \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} \int _{0}^{t} \left\| \left( \varPhi _{1}(y, S)-\varPhi _{1}\left( y, S_{1}\right) \right) \right\| d y. \end{aligned}$$

By employing the Lipschitz condition of kernel, we have

$$\begin{aligned} \left\| S(t)-S_{1}(t)\right\|&\leqslant \frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{1}\left\| S(t)-S_{1}(t)\right\| \\&\quad +\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{1} t\left\| S(t)-S_{1}(t)\right\| . \end{aligned}$$

It gives

$$\begin{aligned} \left\| S(t)-S_{1}(t)\right\| \left( 1-\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{1}-\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{1} t\right) \leqslant 0. \end{aligned}$$

Clearly $S(t)=S_1(t)$ if

$$\begin{aligned} 1-\frac{2(1-\alpha )}{(2-\alpha ) M(\alpha )} L_{1} -\frac{2 \alpha }{(2-\alpha ) M(\alpha )} L_{1} t> 0. \end{aligned}$$

(27)

Employing the same procedure, we get

$E(t)=E_{1}(t), I(t)=I_{1}(t), R(t)=R_{1}(t),S_q(t)=S_{q,1}(t),E_q(t)=E_{q,1}(t)$ and $I_q(t)=I_{q,1}(t) .$

Hence the solution is unique if condition (25) is satisfied. $\square$

Numerical Scheme

In this Section, we present a numerical solution of the fractional order model (2). Then The numerical simulations are obtained using the proposed scheme for Adams-Bashforth. For this purpose we use the fractional m-step Adams Bashforth method to approximate the CF-fractional integral operator and to obtain an iterative scheme,

Consider the Caputo-Fabrizio fractional differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{C F} D_{t}^{\alpha }(x(t))=f(t, x(t)), \quad 0<\alpha <1,\\ x(0)=x_0. \end{array}\right. } \end{aligned}$$

(28)

Now applying the fractional integral to system (28) we get:

$$\begin{aligned} x(t)-x(0)=\frac{1-\alpha }{M(\alpha )} f(t, x(t))+\frac{\alpha }{M(\alpha )} \int _{0}^{t} f(\tau , x(\tau )) d \tau . \end{aligned}$$

At $t = t_{n+1}$, and $t=t_n$ for $n =1, 2,3, . . .$, we have

$$\begin{aligned} x\left( t_{n+1}\right) -x(0)=\frac{1-\alpha }{M(\alpha )} f \left( t_{n}, x\left( t_{n}\right) \right) +\frac{\alpha }{M(\alpha )} \int _{0}^{t_{n+1}} f(\tau , x(\tau )) d \tau , \end{aligned}$$

(29)

and

$$\begin{aligned} x\left( t_{n}\right) -x(0)=\frac{1-\alpha }{M(\alpha )} f \left( t_{n-1}, x\left( t_{n-1}\right) \right) +\frac{\alpha }{M(\alpha )} \int _{0}^{t_{n}} f(\tau , x(\tau )) d \tau . \end{aligned}$$

(30)

Subtracting (30) from (29), the following equation obtained

$$\begin{aligned} x\left( t_{n+1}\right) -x\left( t_{n}\right) =\frac{1-\alpha }{M(\alpha )} \left\{ f\left( t_{n}, x\left( t_{n}\right) \right) -f\left( t_{n-1}, x_{n-1}\right) \right\} +\frac{\alpha }{M(\alpha )} \int _{t_n}^{t_{n+1}} f(t, x(t)) d t. \end{aligned}$$

Fig. 2

Graphical representation of numerical solution for susceptible S(t) and Exposed E(t) at various fractional order of the considered model. Parameter values used are as given in Table 1

Fig. 3

Graphical representation of numerical solution for Infected I(t) and Recovered R(t) at various fractional order of the considered model. Parameter values used are as given in Table 1

Fig. 4

Graphical representation of numerical solution for Susceptible quarantined $S_q(t)$ and Exposed quarantined $E_q(t)$ at various fractional order of the considered model. Parameter values used are as given in Table 1. The initial conditions are the same of the Section 7.2

Fig. 5

Graphical representation of numerical solution for Infected isolated $I_q(t)$ at various fractional order of the considered model. Parameter values used are as given in Table 1. The initial conditions are the same of the Section 7.2

The function $f\left( t, x(t)\right)$ can be approximated over $\left[ t_{n}, t_{n+1}\right] ,$ for $n=0,1,2,...,$ and $h=t_{n+1}-t_{n}$ using the interpolation polynomial of Lagrange of degree m, we have

$$\begin{aligned} f\left( t, x(t)\right) \approx P(t,x(t)) =\sum _{j=n-m}^{n}L_{j}(t) f\left( t_{j}, x_{j}\right) , \end{aligned}$$

where $L_j$ are the Lagrange functions on the $(m+1)$ points $\{t_{n-m},....,t_{n-1},t_n \}$ and given by

$$\begin{aligned} L_{j}(t)=\prod _{\begin{array}{c} k=n-m \\ k \ne j \end{array}}^{n} \frac{t-t_{k}}{t_{j}-t_{k}}, \end{aligned}$$

Therefore, the integral becomes

$$\begin{aligned} \int _{t_{n}}^{t_{n+1}} f(t,x(t)) dt&\approx \int _{t_{n+s-1}}^{t_{n+s}} P(t,x(t)) d t \\&=\int _{t_{n}}^{t_{n+1}} \sum _{j=n-m}^{n}L_{j}(t) f\left( t_{j}, x_{j}\right) d t \\&=\sum _{j=n-m}^{n} f\left( t_{j}, x_{j}\right) \int _{t_{n}}^{t_{n+1}} L_{j}(t) dt. \end{aligned}$$

Thus

$$\begin{aligned} x\left( t_{n+1}\right) -x\left( t_{n}\right)&=\frac{1-\alpha }{M(\alpha )} \left\{ f\left( t_{n}, x\left( t_{n}\right) \right) -f\left( t_{n-1}, x_{n-1}\right) \right\} \\&\quad +\frac{\alpha }{M(\alpha )} \sum _{j=n-m}^{n} f\left( t_{j}, x_{j}\right) \int _{t_{n}}^{t_{n+1}} L_{j}(t) dt. \end{aligned}$$

This method is known as m-step Adams–Bashforth method, for $m=1$ we obtain the CF-fractional second-order Adams-Bashforth method (see also [11])

$$\begin{aligned} x_{n+1}=x_{n}+\frac{2-2\alpha +3\alpha h}{2M(\alpha )}f\left( t_{n}, x_{n}\right) +\frac{2-2\alpha +\alpha h}{2M(\alpha )} f\left( t_{n-1}, x_{n-1}\right) . \end{aligned}$$

For $m=2$ we obtain the CF-fractional three-order Adams-Bashforth method (see also Moore et al. [39])

$$\begin{aligned} x_{n+1}&=x_{n}+\left( \frac{1-\alpha }{M(\alpha )}+\frac{23\alpha h}{12M(\alpha )}\right) f\left( t_{n}, x_{n}\right) -\left( \frac{1-\alpha }{M(\alpha )} +\frac{16\alpha h}{12M(\alpha )} \right) f\left( t_{n-1}, x_{n-1}\right) \\&\quad +\frac{5\alpha h}{12M(\alpha )}f\left( t_{n-2}, x_{n-2}\right) . \end{aligned}$$

For $m=3$ we obtain the CF-fractional four-order Adams-Bashforth method

$$\begin{aligned} x_{n+1}&=x_{n}+\left( \frac{1-\alpha }{M(\alpha )}+\frac{55\alpha h}{24M(\alpha )}\right) f\left( t_{n}, x_{n}\right) -\left( \frac{1-\alpha }{M(\alpha )} +\frac{59\alpha h}{24M(\alpha )} \right) f\left( t_{n-1}, x_{n-1}\right) \\&\quad +\frac{37\alpha h}{24M(\alpha )}f\left( t_{n-2}, x_{n-2}\right) -\frac{9\alpha h}{24M(\alpha )}f\left( t_{n-3}, x_{n-3}\right) . \end{aligned}$$

It should be noted that when $\alpha = 1$ this method reduces to the classical Adams–Bashforth m-step method.

The truncation error for the m-step formula can be estimated by using the error estimate for the Lagrange interpolating polynomial, namely,

$$\begin{aligned}&f(t,x(t))=P_{m}(t)+E_{m}(t) \quad \text { where }\\&E_{m}(t)=\prod _{j=n-m}^{n}\left( t-t_{j}\right) \frac{f^{(m+1)}(\xi _n,x(\xi _n))}{(m+1) !}; \quad \xi _n\in [t_{n-m},t_{n}]. \end{aligned}$$

Then we have

$$\begin{aligned} \int _{t_{n}}^{t_{n+1}} E_{m}(t) d t= \frac{f^{(m+1)}(\xi _n,x(\xi _n))}{(m+1) !} \int _{t_{n}}^{t_{n+1}}\prod _{j=n-m}^{n}\left( t-t_{j}\right) d t \end{aligned}$$

a simple calculation shows that the last quantity is bounded by

$$\begin{aligned} C_m=\frac{ch^{m+2}}{(m+1)!}. \end{aligned}$$

where c is a constant only depends on f and m.

Table 1 Parameter of the model used in the simulation

Fig. 6

Contour shows the variation of $R_e$ for different parameter values: a shows the variation of $R_0$ for different values for $\beta$ and $\delta _s$, b shows the variation of $R_0$ for different values for $\beta$ and $\sigma _1$ and the lower heat map c shows the variation of $R_0$ for different values for $\beta$ and $\gamma _{1}$

Fig. 7

Illustration of the impact of quarantine rate $\delta _s$ on the dynamics of the infected (I) for two values of $\alpha$. All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2

Fig. 8

Illustration of the impact of quarantine rate $\delta _s$ on the dynamics of the infected quarantined ($I_q$) for two values of $\alpha$. All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2

Fig. 9

Illustration of the impact of quarantine rate $\sigma _1$ on the dynamics of the infected (I) for two values of $\alpha$. All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2

Fig. 10

Illustration of the impact of quarantine rate $\sigma _1$ on the dynamics of the infected quarantined ($I_q$) for two values of $\alpha$. All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2

Fig. 11

Illustration of the impact of isolation rate $\gamma _1$ on the dynamics of the infected (I) for two values of $\alpha$. All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2

Fig. 12

Illustration of the impact of isolation rate $\gamma _1$ on the dynamics of the infected quarantined ($I_q$) for two values of $\alpha$. All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2

Fig. 13

Fitting model to data in Morocco, Qatar, Brazil and Mexico (Real data source: WHO report of COVID-19)

Now using 4-step fractional Adams–Bashforth scheme to obtain numerical solutions of the fractional model (2) we get for the first equation in (2) the following scheme:

$$\begin{aligned} S_{n+1}&=S_{n}+\tilde{h}_1(\alpha ) \varPhi _1\left( t_{n}, S_{n}\right) +\tilde{h}_2(\alpha ) \varPhi _{1}\left( t_{n-1}, S_{n-1}\right) +\tilde{h}_3(\alpha ) \varPhi _{1}\left( t_{n-2}, S_{n-2}\right) \\&\quad +\tilde{h}_4(\alpha ) \varPhi _{1}\left( t_{n-3}, S_{n-3}\right) . \end{aligned}$$

where

$$\begin{aligned}&\tilde{h}_1(\alpha ) = \frac{1-\alpha }{M(\alpha )}+\frac{55\alpha h}{24M(\alpha )} ; \quad \tilde{h}_2(\alpha ) =-\frac{1-\alpha }{M(\alpha )}-\frac{59\alpha h}{24M(\alpha )};\nonumber \\&\tilde{h}_3(\alpha ) = \frac{37\alpha h}{24M(\alpha )}\text {and} \quad \tilde{h}_4(\alpha ) = -\frac{9\alpha h}{24M(\alpha )}. \end{aligned}$$

(31)

similarly for the other equations, thus, desired numerical approach is obtained for CF-fractional model.

Numerical Simulation and Calibration of the Model

In this Section, we illustrate the numerical results for the fractional model (2) for different values of fractional order $\alpha$ to analyze the influence of fractional order on the disease dynamics. Some numerical simulations with the Caputo–Fabrizio operator for the fractional COVID-19 virus model are presented using the fractional version of Adams-Bashforth four-step method.

Estimation of Model Parameters and Best Fit of Fractional Orders

The model calibration problem seeks to estimate the model parameters which, to some extent, make the model response as close as possible to the observed values (real data), for that using the Least Squares method to predict the model parameters.

We consider the model solution $u(t)=(S(t), E(t), I(t), R(t), S_q(t),E_q(t), I_q(t)),$ depending on the vector of parameters $\theta =(\delta _s,\delta _q,\beta ,q,\sigma _0,\gamma _0,\sigma _1 ,\gamma _1,q_e,q_i,\mu _{I})$ excepting $\mu , \varLambda$ and N,  which are kept fixed, and the vector X of the observation data at given times $t_{i}, i=1, \ldots n .$ Let $\varPsi (u, \theta ,\alpha )$ be the function computing the numerical solution u of the fractional differential system (2), the vector of parameters is restricted to be on the convex set of admissible values $\varTheta =\{(\theta ,\alpha ) \in {\mathbb {R}}^{12} / \text { lb } \le \theta \le \text { ub }\text { and } 0<\alpha \le 1\},$ such as lb and ub are lower and upper vector bounds for the model parameter $\theta$ respectively.

The estimation of the parameter $\theta$ is obtained by solving the following non linear least squares problem by finding a vector of parameter $\theta ^{*}$ such that:

$$\begin{aligned} (\theta ^{*},\alpha ^*)=\underset{(\theta ,\alpha ) \in \varTheta }{\arg \min } \left\{ \sum _{j=1}^{n}\left| X_{j}-\varPsi (u_j,\theta ,\alpha )\right| ^{2}\right\} . \end{aligned}$$

The aim is to minimize the objective function

$$\begin{aligned} J(\theta ,\alpha )=\Vert X-\varPsi (u,\theta ,\alpha )\Vert ^{2} =\sum _{j=1}^{n}\left| X_j-\varPsi (u_j,\theta ,\alpha )\right| ^{2}. \end{aligned}$$

subject to $(\theta ,\alpha ) \in \varTheta$ and Equation (2) to obtain the best estimate of parameters and the fractional order $\alpha$. For more details about least squares method, see for example [25, 36]. Now using 4-steps Adams-Bashforth method we get the optimization problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \left( J(\theta ,\alpha )=\sum _{j=1}^{n} \left| X_j-\varPsi (u_j,\theta ,\alpha )\right| ^{2}\right) ,\\ \text {subject to } (\theta ,\alpha ) \in \varTheta ,\\ \varPsi (u_0,\theta ,\alpha )=(S_0,E_0,I_0,R_{0},S_{q,0},E_{q,0},I_{q,0}),\\ \varPsi (u_{1},\theta ,\alpha )=\varPsi (u_{0},\theta ,\alpha )+(K_1(\alpha )+K_2(\alpha )) f\left( t_{0}, \varPsi (u_{0},\theta ,\alpha ) \right) , \\ \varPsi (u_{2},\theta ,\alpha )=\varPsi (u_{0},\theta ,\alpha )+K_1(\alpha ) f\left( t_{0}, \varPsi (u_{0},\theta ,\alpha )\right) +K_2(\alpha ) f\left( t_{1}, \varPsi (u_{1},\theta ,\alpha ) \right) , \\ \varPsi (u_{3},\theta ,\alpha )=\varPsi (u_{1},\theta ,\alpha ) +K_1(\alpha )f\left( t_{1}, \varPsi (u_{1},\theta ,\alpha )\right) +K_2(\alpha ) f\left( t_{2}, \varPsi (u_{2},\theta ,\alpha ) \right) , \\ \text {for } j = 4 \text { until n calculate}\\ \varPsi (u_j,\theta ,\alpha ) =\varPsi (u_{j-1},\theta ,\alpha )+\tilde{h}_1(\alpha ) f\left( t_{j-1},\varPsi (u_{j-1},\theta ,\alpha )\right) \\ +\tilde{h}_2(\alpha ) f\left( t_{j-2}, \varPsi (u_{j-2},\theta ,\alpha )\right) +\tilde{h}_3(\alpha ) f\left( t_{j-3}, \varPsi (u_{j-3},\theta ,\alpha )\right) \\ +\tilde{h}_4(\alpha ) f\left( t_{j-4}, \varPsi (u_{j-4},\theta ,\alpha )\right) . \end{array}\right. } \end{aligned}$$

(32)

to obtain the best estimate of parameters and the vector of fractional orders $\alpha$, where

$$\begin{aligned} K_1(\alpha )=\frac{2-2\alpha +3\alpha h}{2M(\alpha )}, \quad K_2(\alpha )=\frac{2-2\alpha +\alpha h}{2M(\alpha )} , \end{aligned}$$

the values of $\tilde{h}_i(\alpha ), i=1,2,3,4$ are given in (31) and the function f is the right-hand side of the model (2).

Impact of Fractional Order Derivative

Based on numerical scheme derived in Section 6, we present the graphical results of the proposed CF fractional model (2) in Figs. 2, 3, 4 and 5 to analyze the influence of fractional order. We have considered the initial conditions $N=3500001$, $S(0)=3500000$, $I(0)=1$ and $E(0)=R(0)=S_q(0)=E_q(0)=I_q(0)=0$.

From the analysis of the obtained graphs, we notice that the population of the infected class decreases significantly by decreasing the order of the fractional derivative and the endemic state of the disease goes to the disease-free state in all the cases studied. In addition, the graphical results of the CF-derivative model reveal that this operator is more significant in exploring the dynamics of the model and providing more biologically feasible results.

Impact of Quarantined and Isolation Parameters

It is well known that the effective reproduction number $(R_e)$ of the fractional model is a very important parameter in the infectious disease, which determines whether the could spread. In our model, $R_e$ is determined by the parameters given in (3) and (7). In order to identify the impacts of these parameters on COVID-19 transmission and prevalence, we will discuss the change in the number of infected individuals with the COVID-19 virus when we change the values of the controlled parameters, transmission rate ($\beta$), quarantine rate of susceptible ($\delta _s$), isolation rate of infected individuals ($\gamma _1$) and quarantine rate of exposed ($\sigma _1$). All parameter values for the simulation in this section are given in Table 1.

Firstly, to determine the dependence of the attack rate on the controllable model parameters, fixing two of $\delta _s, \sigma _1$ and $\gamma _1$ at the specific value (given in Table 1) and varying the other two parameters (one of the previous four parameters with $\beta$), the contour plots of the quarantine reproduction number are illustrated in Fig. 6.

Figure 6a and 6b show that higher quarantine rate $\delta _s$ and $\sigma _1$ will reduce $R_0$, then will help bring $R_0< 1$, thus prevent the outbreak from happening. On the other hand Fig. 6c shows that the isolation rate is effective when the transmission rate is high, this is natural since infected people are those who carry the virus and transmit it to other people in the population.

In order to compare the effectiveness of quarantine and isolation to reduce the spread of a virus COVID-19, the model is simulated the impact of using quarantine only as well as isolation interventions only for a range of values of quarantine and isolation parameters.

Figures 7,8, 9 and 10 show the effectiveness of the quarantine strategy, similarly Figs. 11 and 12 show the effectiveness of the isolation of infected cases to control the evolution of viruses.

Table 2 Different values of quarantine reproduction number according to quarantine rate of susceptible individuals

Table 3 Different values of quarantine reproduction number according to quarantine rate of exposed individuals

Fitting Model to Real Data

In this present section we have estimated the important model parameters and the fractional order $\alpha$ using the infection cases (that are found on the WHO web-page) in Morocco, Qatar, Brazil and Mexico. The initial conditions used are given in the Table 4, we estimated the value of the fractional order $\alpha$ for the four countries and we found 0.9533 for the Morocco model, 0.9418 for Qatar, 0.9906 for Brazil and 0.822 for Mexico. These values show the importance of the fractional order in the COVID-19 considered model and its influence to decrease the error of the of least squares method. In addition to making the proposed model more realistic and obtaining the average values of the acceptable parameters.

Now by analyzing the curves presented in Fig. 13, the importance role of quarantine and isolation in Morocco and Qatar in reducing the impact of the COVID-19, whilst Mexico and Brazil did not succeed in applying the quarantine well, which caused an increase in the number of people infected with the virus. Finally these values are kept low compared to potential values in the absence of a quarantine and isolation strategy (see Fig. 6, Tables 2 and 3 )

Table 4 Initial values using in Fig. 13

Conclusion

In this manuscript, a Caputo–Fabrizio fractional differential equation model for COVID-19 with quarantine (of susceptible and exposed cases) and isolation (of symptomatic cases) has been investigate and the effect of each of them was studied. The existence and uniqueness of the system of solutions of the Caputo-Fabrizio model are established using a fixed-point theorem and an Picard iterative method. The m-step Adams-Bashforth approach is proposed to numerically approximate the solutions of the fractional model. We have compared the numerical simulations with respect to different values of the fractional order $\alpha$. Finally, The Method of Least Squares is used to determine the best fit to real data (real data for Morocco, Qatar, Brazil and Mexico). The paper gives an example of the use of the Caputo–Fabrizio fractional derivative as a model for real world problems (especially epidemiological problems).