Introduction

Despite prohibitions in some Indian states, the utilization of plastic products such as polyethylene bags, bottles, containers and packaging strips etc., is increasing day by day. As a consequence, the landfills are continuously filled up with this valuable resource. In many regions, waste plastic is now being collected for recycling and reuse. At present, only a fraction of total waste plastic is used for recycling purposes in India. The remaining plastic wastes will remain in the landfills or environment for centuries, maybe thousands, of years. The estimated urban municipal solid waste production in India up to the year 2000 was of the order of 39 million metric tons per year. This number is likely to reach 160 million tons per year by the year 2040 [1]. The typical percentage of plastic in the municipal solid waste produced in India is 9 % [2] at present. Researchers [3, 4] have presented through experimental studies that this valuable resource can be used to improve the properties or behaviour of sands. But conducting experiments and generating data are invariably an expensive proposal. Building up a mathematical model is an alternative approach where major variables are calibrated to fit the experimental results to understand the relationships among the participating variables. The capability of storing the learning experience and the power to capture the inherent complex relationship without any prior assumptions about the geotechnical engineering problem makes the neural network a suitable choice for modeling. Past studies [5–11] have demonstrated that neural network-based prediction models can be used in predicting the soil properties or behaviour. With the above in view, in the present study, a feed forward neural network based predictive model from the consolidated drained triaxial test data has been developed. The input variables in the developed neural network models were strip content, tensile strength of strip, thickness of the strip, elongation at failure of the strip, aspect ratio; dry unit weight of the composite specimen, confining pressure and strain at failure of the composite specimen and the output was the deviator stress. Sensitivity analysis relating the variables affecting the deviator stress has been performed. A comparison of the developed neural network model is made with the model derived from multiple regression analysis. Finally, a model equation has been presented based on the connection weight.

Material Used and Experimental Procedure

The investigation was carried out on Badarpur sand which is a medium grained, uniform quarry, sand having sub-angular particles of weathered quartzite. It had a specific gravity of 2.66, maximum particle size of 1.20 mm, minimum particle size of 0.07 mm, mean particle diameter (D 50) of 0.42 mm, coefficient of uniformity (C u) of 2.11 and a coefficient of curvature (C c) of 0.96. Minimum and maximum void ratios were 0.56 and 1.12 while the corresponding dry unit weights were 16.70 and 12.30 kN/m3 respectively. The sand was classified as SP-SW. The reinforcement consisted of two types of plastic waste. For the first one (designated as Type I) used plastic carry bags of LDPE having a mass per unit area of 30 gsm and a thickness of 0.05 mm were chosen. From these, 12 mm wide strips were cut. Further, these strips were cut into pieces of 24 and 12 mm length. The resulting strips of size 24 × 12 mm are designated as Type I A (Fig. 1a) and 12 × 12 mm strips are designated as Type I B (Fig. 1b). The second material studied was used packaging strips made of HDPE (designated as Type II) having a breadth of 12 mm, and a thickness of 0.45 mm and a volume of 3.8 g/m. These were cut into lengths of 24 mm (designated as Type II A (Fig. 1c) and 12 mm (designated as Type II B (Fig. 1d) lengths. Type I strips (with a width of 12 mm) had an ultimate tensile strength of 0.011 kN and the percent elongation at failure was 20 %. The ultimate tensile strength of Type II (with a width of 12 mm) strip was 0.32 kN and percent elongation at failure was 25 %. It may be noted that 1 % of Type II A inclusions resulted in 280 strips whereas 0.15 % of Type I A contained 276 strips. This is attributed to the difference in their thickness. The units (pieces) of the strips were manually counted corresponding to each percentage. A standard triaxial apparatus was used for testing unreinforced and reinforced sand. The specimen was of 100 mm diameter and 200 mm high. To ensure uniform distribution of strips in the mixture, the dry sand and the required percentage of waste plastic strips (0.05–0.15 % for LDPE and 0.25–2 % for HDPE, both strips having aspect ratios of 1 and 2) were weighed and divided into three equal parts respectively. One part of sand and one part of the weighed strip were mixed together manually in dry condition in a random arrangement. The sand-strip mixture was then soaked. The soaked sand-strip mixture was then deposited into the rubber membrane inside a split mould former as a first layer. The requisite number of blows was given to the first layer through tamping with a rubber tamper consisting of a round disk attached to an aluminium rod to reach the required density. The similar procedure was repeated for the second and the third layer. The specimen was compacted in three layers. The density of the sand specimen with Type I and Type II inclusions was maintained at 15.08 ± 0.18  and 14.88 ± 0.42 kN/m3 respectively for different samples. Conventional consolidated drained triaxial tests were then conducted at a deformation rate of 1.016 mm/min under a confining pressure varying from 34.5 to 276 kPa.

Fig. 1
figure 1

Photograph of a LDPE strips Type I A b LDPE strips Type I B c HDPE strips Type II A d HDPE strips Type II B

Full size image

Stress–Strain Behaviour

The stress–strain behaviour of unreinforced sand is illustrated in Fig. 2a. It can be mostly determined from this figure that with an increase in confining pressure, the peak stress increases and corresponding axial strain, generally remains constant. For example, at σ3 = 276 kPa sand exhibits a maximum deviator stress of 894 kPa at an axial strain of 4.54 %, whereas at σ3 = 34.5 kPa these values are 100 kPa and 4.84 % respectively. Typical stress–strain curves in the sand reinforced with 0.15 % Type I A and 2 % Type II A strips at a confining pressure of 34.5 kPa are shown in Fig. 2b, c respectively. These figures indicate that strip inclusion in sand improves the performance of the sand specimen. This matter is essentially due to the increase in confinement. Moreover, as shown in Fig. 2b, c improvement in performance of reinforced specimen is more pronounced for a greater percentage of strips. A quick summary of the deviator stress at failure, strain at failure, dry unit weight of the composite along with details of the strips is given in Table 1.

Fig. 2
figure 2

Stress–strain-volume change curves for a unreinforced sand b sand with strip Type I A at 34.5 kPa c sand with strip Type II A at 34.5 kPa

Full size image
Table 1 Summary of the variables and results of triaxial tests
Full size table

Neural Network Model

The aim of this work is to model the neural network architecture for the sand reinforced with waste plastic strips based on the consolidated drained triaxial test results. The various input variables used in the developed neural network models are strip content, tensile strength of strip, thickness of the strip, elongation at failure of the strip, aspect ratio, dry unit weight of the composite specimen, confining pressure and strain at failure of the composite specimen.

Optimal NN Model Selection

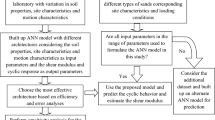
The performance of neural network model is basically dependent on the network architecture and parameter settings. To find the optimal network architecture in a neural network is the most difficult task and determining numbers of optimal layers and neurons in the hidden layers is generally carried out by trial and error approach. The performance of the neural network to a great extent is influenced by the assignment of initial weights and other related parameters. Further, there is no well-defined procedure to get an optimal network architecture and parameter settings. Hence, a time consuming trial and error method still remains valid.

Selection of Neural Network Structure

Past studies by Boger and Guterman [12] has reported that the performance of the neural network relies on the structure of the network. But, there is no well-defined procedure to obtain the structure of the network. Hence, the researchers resort to a time consuming trial and error method. There will always be a complexity in choosing the number of hidden layers and the number of neurons present in each hidden layer in case of multilayer feed -forward network. The nodes in the hidden layer should be decided prior to the selection of number of hidden layers. There is no specific formula by which one can arrive at the specific architecture of neural networks. However, researchers have come to the conclusion that broadly some thumb rules can be adopted to start with. Boger and Guterman [12] have suggested that the number of hidden layer neurons can be 2/3 (or 70 %) of the size of the input layer. They further reported that, If the number of hidden layer neurons is insufficient then number of output layer neurons can be added later on. Berry and Linoff [13] have reported that the number of hidden layer neurons should be less than twice of the number of neurons in the input- layer, whereas Blum [14] have reported that the size of the hidden layer neurons will be between the input layer size and the output layer size. Keeping the above in view, the number of neurons in the hidden layers was determined using the thumb rules proposed by Boger and Guterman [12]. A similar approach is advocated by other researchers [15, 16]. Multiple hidden layers are employed in applications where accuracy is the main concern for researchers. In order to select the optimal structure of the network, the number of hidden layers and the number of neurons in the hidden layer were fixed. For the successful application of the neural network model, the major problem is when to stop training. Excessive training of the neural network results in noise, whereas insufficient training of the neural network leads to poor predictions. Therefore generalization of the network will not be there for a new set of data. Hence, the numbers of iterations of the training and testing data set were changed using trial and error method. The mean square error between the actual and the predicted value for different iterations were computed. The iteration, which gives the least mean square error, is chosen for identifying the neural network structure. The training is stopped when the average-error function becomes small. Further, iterations beyond this point result in an overfitting effect. This is attributed to induction of noise with the decreasing ability of generalization of the neural network models. These observations are consistent with the literature [17, 18]. Keeping the above in view, the number of iterations chosen was 3000. Therefore, the neural network model chosen for our experiment has the structure of 8-6-1 for the constitutive modeling.

Data Set

This work presents an application of neural network for constitutive modelling of the deviator stress for the sand-waste plastic strip mixtures based on the consolidated drained triaxial test data. The experimental data used in this study include 60 records, which were taken from the experiments reported by Dutta and Rao [4] and a summary of the same is given in Table 1. For constitutive modeling, the experimental results were randomly selected for the training and testing which is required in order to check the generalization capability of the neural network model using testing data set. The variables are continuing one and hence the choosing of the percentage of training and the testing data sets does not affect the model. Further, for training 64 % of the total records were taken and the remaining 36 % were used for testing the model.

Activation Function Selection

Each neuron in a neural network has an activation function. The activation function specifies the output of a neuron corresponding to a given input. Further, activation functions also scale the output of the neural network into proper ranges and serve to introduce nonlinearity into it which makes the neural network powerful. A large number of activation functions are in use in artificial neural networks. The transfer functions are the most common choice among the activation functions for neural network application due to its amenable mathematical properties in the realm of approximation theory, the function’s and its derivative’s fast computability and boundedness in the unit interval. The aim of this study is to analyze the performance of different neural network architectures using different activation functions for the neurons of hidden and output layers. For experimental comparisons, linear, sigmoid, sigmoid stepwise, sigmoid symmetric, Gaussian, Gaussian symmetric, Elliot, Elliot symmetric, linear piece, linear piece symmetric, sin, sin symmetric, cos symmetric functions were used. These functions are supported in the open source Agiel neural network software. By trial and error method, the predicted deviator stress at 3000 number of iterations gives the value equal to the targeted deviator stress for both the training and testing data set. The learning rate is used to determine how aggressive training should be (default learning rate is 0.7) for the algorithm chosen. Maximum iteration basically refers to the maximum number of trials to be conducted. The bigger the value of maximum iteration should give the longer running time.

Performance Measures

After the model is identified, it is now required to check its performance in predicting the deviator stress using test data set. For the choice of the best measure for the prediction, there is no consensus among researchers. Hence accuracy is considered as one of the criteria in evaluating the quality of the prediction. This can be achieved after minimizing the error [15–18]. Therefore, mean absolute percentage error (MAPE), root mean square error (RMSE), mean absolute error (MAE), and mean square error (MSE), was selected as these parameters measure the magnitude of the prediction errors. MAE measures an overall accuracy and gives an indication of the degree of spread. In calculating MAE, all errors are assigned an equal weight. MAE is zero for the good fitment of data and large for the poor fitment of data. Thus, comparisons between the prediction methods is made and the one is selected for which MAE is minimum. In calculating MSE which also provides measures of accuracy and indications of the degree of spread, the large errors were assigned additional weights. MSE considers the squared difference between the predicted and actual observed data and quantify the difference between predicted and actual observed data, whereas RMSE is simply a root of MSE, and has the advantage of being measured in the same unit as the predicted variable. MAE is also measured in the same unit as the prediction, but provides less weight to large prediction errors than the MSE and RMSE. MSE heavily penalizes large errors in comparison to MAE. MAPE is a useful measure to compare the accuracy of prediction among different methods as it measures relative performance. If the calculated MAPE is less than 10 % between 10 and 20 %, between 20 and 50 % and over 50 %, it is interpreted as an excellent accurate prediction, good prediction, acceptable prediction and inaccurate prediction respectively. MAPE provide measurement of the prediction quality which is independent of the unit of measurement of the variable. The MSE, RMSE, MAE, and MAPE provide the measurement of the magnitude of the prediction errors. Smaller values for these statistics will indicate better models. RMSE and MSE are popular historically, due to their theoretical relevance in statistical modeling whereas some researcher recommend against their use in predictive accuracy evaluation, as they are more sensitive to outliers than MAE. Further, MAE and the RMSE can be used together to diagnose the variation in the error in a set of prediction. RMSE will always be larger or equal to the MAE. The greater the difference between RMSE and MAE, greater will be the variance in the individual error in the data set. Further, when RMSE is equal to MAE (both can range from 0 to ∞), then all the errors are going to be of the same magnitude. They are negative-oriented scores: lower values are better. Further, MAE can be viewed as a ‘robust’ measure of predictive accuracy. MAE tends to prefer predictive procedures that produce occasional large prediction failures, while they are reasonably good on average, whereas MSE tends to prefer predictive procedures that avoid large prediction failures, even though they produce a less satisfactory fit otherwise. Usually, estimation procedures are based on least-squares criteria, an emphasis on the MAE may involve a slight logical inconsistency. The best class of models is then selected according to a criterion that is different from the one that selects among the different members of an individual model class. Selection of an error measure has an important effect on the conclusions about which of a set of predictive methods are most accurate. Further, the performance of neural network model is generally evaluated in terms of the coefficient of correlation (r) and coefficient of determination (R 2) only. This approach suffers from biased evaluation. Therefore other unbiased statistical criteria should be used along with the coefficient of correlation (r) and coefficient of determination (R 2). The various statistical parameters and error models used are given in Table 2 for the prediction of the deviator stress. For this, using different activation functions in the hidden and output neuron, the correlation coefficient (r), coefficient of determination (R 2), MSE, RMSE, MAE and the MAPE for the training and testing data were determined for eight input neurons and hidden hidden neurons and one output neuron for 3000th iterations in the network setup. The best activation function of the structure of the network is chosen by selecting the best correlation coefficient (r), coefficient of determination (R 2), least mean square error, RMSE, MAE and MAPE among all the activation functions. The values of r, R 2, MSE, RMSE, MAE and MAPE for the activation function Elliot symmetric is the least both for training and testing data among all other activation functions studied and are shown in Table 3. The plot between the target and neural network predicted deviator stress using Elliot symmetric activation functions is shown in Fig. 3. For the Elliot symmetric activation function, the calculated value of R 2 was found to be 0.992 (Fig. 3) indicating the model accuracy of the constructed neural network. Figure 3 also depicts good correlation between the targeted deviator stress and neural network predicted deviator stress, suggesting the accuracy of the neural network predictability for the nonlinear systems. From the above, it is recommended that the neural network model be designed using an Elliot symmetric function to obtain the predicted deviator stress closer to the targeted one.

Table 2 Various statistical parameters and error models
Full size table
Table 3 Statistical values for the training and testing data for the best activation function
Full size table
Fig. 3
figure 3

Predicted and target deviator stress for sand reinforced with waste plastics in the training and testing data set using Elliot symmetric activation function with 8-6-1 topology

Full size image

Sensitivity Analysis on Elliot symmetric function based Model

Sensitivity analysis was carried out in order to study the contribution of individual variables on the deviator stress using a method reported by Garson [19] which was based on weight configuration. But method reported by Garson [19] had own limitations because it measures the absolute value of the weights. Olden and Jackson [20] have suggested a method to overcome the limitations of the method reported by Garson [19]. Keeping the above in view, the method reported by Olden and Jackson [20] has been used for the sensitivity analysis. This method calculates the sum of the product of final weights of the connection from input neuron to hidden neurons with the connection from hidden neurons to output for all input neurons. The variable contribution of a given input variable is defined by Eq. (1).

$${\text{RI}}_{j} \, = \,\mathop \sum \limits_{k = 1}^{h} w_{jk} \, \times \,w_{k}$$
(1)

where, w jk is the connection weight between jth input variable and kth neuron of the hidden layer, \(w_{k}\) is the connection weight between kth neuron of hidden layer and the single output neuron, RI j is the relative importance of the jth neuron of input layer and h is the number of neurons in the hidden layer.

This paper involves eight input variables and their influence on the deviator stress was studied on the basis of weights obtained in the optimal feed-forward back-propagation neural network model. The final weights between the input and hidden neuron as well as between hidden and output neuron generated in the Elliot symmetric function are given in Table 4. The relative importance of individual variable considered in Elliot symmetric function based neural network architecture is shown in Fig. 4. Study of Fig. 4 reveals that the CP is found to be the most important parameter followed by ε, AR, εts and SC as per the method reported by Olden and Jackson [20]. Further, it can be seen from Fig. 4 that the inputs CP, ε, AR, εts and SC have a positive contribution to the deviator stress, whereas \(\gamma\)d, ST and TS have negative effects on the deviator stress. Thus, it is inferred that CP, ε AR, εts and SC are directly and \(\gamma\)d, ST and TS are indirectly proportional to the deviator stress. Therefore, the connection weight approach reported by Olden and Jackson [20] matches the physical meaning for the deviator stress. From the above, it can be seen that sensitivity analysis is an effective method of indicating the physical relationship between inputs with the output.

Table 4 Final weights between the input neuron and hidden neuron as well as hidden neuron and output neuron
Full size table
Fig. 4
figure 4

Relative importance of individual variable on the output deviator stress

Full size image

Revised Neural Network Architecture

Sensitivity analysis perceived that the inclusion of strip thickness, tensile strength of the strip and the dry unit weight of the composite specimen in the neural network model leads to low degree of generalization. Keeping the above in view, the neural network structure was revised. The inputs considered in the revised neural network structure were SC, εts, AR, CP, ε and the output was the deviator stress. The variable involved in the problem has been reduced to five and so that the input layer in the neural network model has the number of neurons equal to the number of variables. The number of neurons in the hidden layer was obtained using the thumb rule reported by Boger and Guterman [12]. Hence, the topology of the revised neural network model was 5-4-1 as shown in Fig. 5. The revised structure of the network was set up in the Agiel neural network software and the network was analysed with the same training and testing data set used in the previous model having 8-6-1 topology. The parameter settings in the neural network model such as number of iterations, activation functions and learning rate are kept as same as in the previous model. The final weights between the input and hidden neuron as well as between hidden and output neuron generated in the revised Elliot symmetric function are given in Table 5. The output obtained in the revised model and the model obtained before the sensitivity analysis was compared using performance measures and the results for the training and testing data set are shown in Table 6. The graph between the target deviator stress and the neural network predicted deviator stress for the training and testing data set in the revised neural network model are represented in Fig. 6. Study of Table 6 reveals that the coefficient of correlation (r) for the revised neural network model in the training data set has the value of 0.999 whereas the coefficient of correlation (r) for the previous model in the training data set was 0.996. There was an increase of 0.22 % in the coefficient of correlation with respect to the previous model. Further, for the testing data set, the coefficient of correlation for the revised neural network model with 5-4-1 topology was 0.999 which increased by 0.16 % with respect to the previous model with 8-6-1 topology. The next comparison was made with a coefficient of determination (R 2). The R 2 was increased by 0.53 and 0.45 % with respect to the previous neural network model for the training and testing data set respectively. Further, the performance measure such as mean squared error of the revised neural network model was compared with the previously obtained neural network model with 8-6-1 topology. The MSE of the training and testing data set was reduced by 73.42 and 72.56 %, respectively, with respect to the previous neural network model. RMSE of the training and testing data set was reduced by 48.23 and 47.27 % respectively with respect to the previous neural network model. MAE of the training and testing data set was reduced by 44.17 and 38.54 % respectively with respect to the previous neural network model. MAPE of the training and testing data set is reduced by 28.23 and 37.25 % respectively with respect to the previous neural network model. The above results reveal that the revised neural network model with 5-4-1 topology shows a good prediction with respect to previous model having 8-6-1 topology for the training and testing data set. Further, the authors of this paper are of the view that the revised neural network model was proposed for a specific type of sandy soil reinforced with two types of plastic strips. Further, study is required for generalization of the neural network model for different type’s sands and reinforcing strips.

Fig. 5
figure 5

Revised neural network architecture for the deviator stress

Full size image
Table 5 Final weights between the input neuron and hidden neuron as well as hidden neuron and output neuron for the revised neural network having topology 5-4-1
Full size table
Table 6 Statistical values for the training and testing data for the revised topology
Full size table
Fig. 6
figure 6

Predicted and target deviator stress for sand reinforced with waste plastics in the training and testing data set using Elliot symmetric activation function with 5-4-1 topology

Full size image

Comparison

Multiple regression analysis was carried out for the training data set used in the development of neural network model. The input variables considered were SC, εts, AR, CP, ε and the output was the deviator stress for the multiple regression analysis. These input variables have been chosen based on the sensitivity analysis carried out for the neural network model having 8-6-1 topology. Multiple regression model obtained from the training data set is shown in Eq. (2).

$$\sigma {\text{d}}p = 26.942\, \times \,{\text{SC}}\, + \,0.704\, \times \,\varepsilon {\text{ts}}\, + \,26.519\, \times \,{\text{AR}}\, + \,3.538\, \times \,{\text{CP}}\, + \,24.717\, \times \,\varepsilon \,{-}\,159.965$$
(2)

where, \(\sigma\) dp is the predicted deviator stress in kPa, SC is the strip content in  %, εts is the strip elongation at failure in  %, AR is the aspect ratio, CP is the confining pressure in kPa, ε is the strain at failure of the composite specimen in  %.

The various performance measures obtained for the training and testing data set using multiple regression analysis are shown in Table 7. Comparison of the revised neural network model having 5-4-1 topology and the one obtained using multiple regression analysis was carried out using performance measures. The input variables of the testing data set were substituted in Eq. (2) and the output deviator stress was obtained. The plot between the target deviator stress and the predicted deviator stress of the training and testing data set using multiple regression analysis are shown in Fig. 7. Study of Table 7 reveals that the coefficient of correlation (r) and Coefficient of determination (R 2) of the training and testing data set was increased by 0.68 and 0.94 and 1.34 and 1.92 % respectively in comparison to the multiple regression analysis. The MSE, RMSE, MAE and MAPE of the training and testing data set was reduced by 87 & 91.16, 64.56 & 70.26, 71.72 & 66.56 and 70.36 & 61.27 % respectively in comparison to the multiple regression analysis. The statistical comparison as shown in Table 7 revealed that the revised neural network model having 5-4-1 topology is superior to the one obtained using multiple regression analysis in predicting the output deviator stress. The poor prediction of the output deviator stress using multiple regression analysis is attributed to non-linearity involved in the problem.

Table 7 Comparison of statistical coefficients between revised neural network model having 5-4-1 topology and multiple regression analysis
Full size table
Fig. 7
figure 7

Predicted and target deviator stress for sand reinforced with waste plastics in the training and testing data set using multiple regression analysis

Full size image

Model Equation for the Deviator Stress Based on Revised Neural Network Architecture

The fundamental equation of the neural network model relating the input variables to the output can be formulated as

$$\sigma {\text{dpn}}\,{ = }\, \, f \, \left\{ {b_{\text{o}} + \,\mathop \sum \limits_{k = 1}^{h} \left[ {w_{k} \, \times \,f \left( {b_{hk} + \, \mathop \sum \limits_{j = 1}^{m} w_{jk} \, \times \,X_{j} } \right)} \right]} \right\}$$
(3)

where \(\sigma\) dpn is the normalized (in the range −1–1 in this case) \(\sigma\) dp value; b o is the bias at the output layer; w k is the connection weight between kth neuron of hidden layer and the single output neuron; b hk is the bias at the kth neuron of hidden layer; h is the number of neurons in the hidden layer; m is the number of neurons in the input layer; w jk is the connection weight between jth input variable and kth neuron of hidden layer; X j is the normalized input variable j in the range [−1, 1] and f is the activation function.

Therefore, the equation for the output deviator stress can be formulated based on the trained weights and biases of the neural network model. The model equation for the sand reinforced with waste plastic strips on drained triaxial compression test was established using the values of the weights and biases shown in Table 5 as per the following expressions.

$$A \, = \, - 8.604 \, \, + \,0.616\, \times \,{\text{SC}}\, + \,0.106\, \times \,\varepsilon {\text{ts}}\, + \,0.741\, \times \,{\text{AR}}\, + \,8.153\, \times \,{\text{CP}}\, + \,1.275\, \times \,\varepsilon$$
(4)
$$B \, = \, 4.430\, - \,0.539\, \times \,{\text{SC}}\, + \,0.323\, \times \,\varepsilon {\text{ts}}\, - \,0.387\, \times \,{\text{AR}}\, - \,3.902\, \times \,{\text{CP}}\, - \,1.115\, \times \,\varepsilon$$
(5)
$$C \, = \, 1.628\, - \,0.322\, \times \,{\text{SC}}\, - \,0.076\, \times \,\varepsilon {\text{ts}}\, - \,0.166\, \times \,{\text{AR}}\, + \,2.510\, \times \,{\text{CP}}\, - \,0.491\, \times \,\varepsilon$$
(6)
$$D \, = \, 1.158 \, + \, 0.019 \, \times {\text{ SC }} + \, 0.26\, \times \, \varepsilon {\text{ts }} - \, 0.125 \, \times \,{\text{AR }} - \, 3.143 \, \times {\text{ CP }} - \, 0.378 \, \times \, \varepsilon$$
(7)
$$E \, = 7.107\, + \, 9.015\, \times \, \frac{A\, \times \,0.5}{{1 + \left| { A\, \times \,0.5 } \right|}}\, - 2.94 \, \times \,\frac{B\, \times \,0.5}{{1 + \left| { B\, \times \,0.5 } \right|}}\, + \, 3.422\, \times \,\,\frac{C\, \times \,0.5}{{1 + \left| { C\, \times \,0.5 } \right|}}\, + \, 2.218\, \times \,\frac{D\, \times \,0.5}{{1 + \left| { D\, \times \,0.5 } \right|}}$$
(8)
$$\sigma {\text{dpn}}\, = \,\frac{E\, \times \,0.5}{{1 + \left| { E\, \times \,0.5 } \right|}}$$
(9)

The \(\sigma {\text{dpn}}\) value as obtained from Eq. (9) is in the range [−1, 1] and this needs to be denormalized as

$$\sigma {\text{dp}}\, = \,0.5\, \times \,(\sigma {\text{dpn }} + \, 1)\, \times \,(\sigma {\text{dpmax}}\,{-}\,\sigma {\text{dpmin}})\, + \,\sigma {\text{dpmin}}$$
(10)

where, \(\sigma\)dpmax and \(\sigma\)dpmin is the maximum and the minimum value of predicted deviator stress in kPa respectively.

Conclusions

Modelling of deviator stress of a mixture of two or more materials is a complex phenomenon. For this, an alternative approach using neural network is adopted to overcome this complexity. Over the past couple of years, applications of neural networks in geotechnical engineering are being explored globally. In this paper, an application of neural network for the modeling of the deviator stress for the sand-waste plastic strip mixtures based on experimental data obtained through consolidated drained triaxial tests is presented. The model is developed for the data set of 60 records of deviator stress. The results indicate that the 8-6-1 topology of the neural network architecture is fairly capable of predicting the deviator stress with acceptable accuracy. Further, the proposed neural network model has been evaluated on a comprehensive performance measures. From the performance measure analysis, it was evident that the proposed neural network model predicted the deviator stress closer to the one obtained experimentally through consolidated drained triaxial tests with acceptable accuracy. Sensitivity analysis revealed that the contribution of the input variables such as strip thickness, tensile strength of the strip and dry unit weight does not have much impact on the output deviator stress. The revised model having 5-4-1 topology gives a better prediction of the output deviator stress than the previous model with 8-6-1 topology. Further, the revised neural network model having 5-4-1 topology is superior to the one obtained using multiple regression analysis in predicting the output deviator stress. Finally a model equation is presented based on trained weights in the revised neural network. More studies are required to be conducted to validate the results obtained using other variants of neural network models. In general, the neural network models have the limitation in giving explanations and reasoning behind the model so obtained. In future, suitability of alternative techniques such as support vector machines, particle swarm optimization or genetic programming, may also be explored.