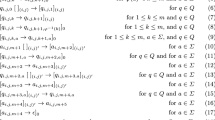1 Introduction

P systems with active membranes, introduced in [23], are among the most investigated variants of P systems. Using the polarizations of the membranes and the possibility of dividing elementary (or even non-elementary) membranes these systems can solve computationally hard problems efficiently. More precisely, with elementary membrane division they can solve \({\mathbf {NP}}\)-complete problems [12, 23, 28, 33], while with non-elementary membrane division they can solve even \({\mathbf {PSPACE}}\)-complete problems in polynomial time [1, 30]. Solving computationally hard problems with P systems with active membranes has a huge literature in Membrane Computing, see, e.g. [2, 5, 7, 21, 22, 27, 29, 31], and the references therein.

It is also widely investigated how certain restrictions on P systems with active membrane affect the computation power of these systems (see for example [6, 8, 9, 11, 13, 14, 16, 17, 19, 20, 25]). Probably, the most investigated question in this research line is whether these P systems are still powerful enough to solve hard problems in polynomial time when the polarizations of the membranes are not used. In the case when non-elementary membrane division is allowed the answer to this question is positive since in [3] the \({\mathbf {PSPACE}}\)-complete QSAT problem was solved in polynomial time without polarizations. On the other hand, no polynomial-time solutions for hard problems exist when neither polarization nor non-elementary membrane division is allowed. In fact, Gh. Păun conjectured already in 2005 that without polarization and non-elementary membrane division P systems with active membranes cannot solve \({\mathbf {NP}}\)-complete problems in polynomial time [24]. Păun’s conjecture, often called the P conjecture, has not been proven yet although there are some partial solutions for it (see, e.g. [10, 15, 18, 32]). A direct attempt to calculate efficiently all the elementary membranes of a computation of a P system with active membranes fails as in general, the number of these membranes can grow exponentially and, moreover, these membranes can contain pairwise different multisets. However, it was discovered in [10] that if dissolution rules are not allowed to use, then there is no need to simulate all the elementary membranes to determine the result of a computation. Instead, it is enough to consider a certain graph, called the dependency graph [4] of the P system. Roughly, this graph describes how the rules of the P system can evolve and move objects through the membranes. To determine the result of a computation in this case it is enough to check whether a distinguished object is reachable from certain objects in the dependency graph. Using dependency graphs it was shown in [10] that polarizationless P systems with active membranes using no dissolution rules and working in polynomial time can solve only problems in \(\mathbf {P}\).

If dissolution rules are also allowed, then things become much more complicated. Consider a P system \(\varPi\) with active membranes and assume, for example, that \(\varPi\) contains a membrane sub-structure \([[a\,\,b]_2]_1\). Assume moreover that a can dissolve membrane 2 but b cannot. Then \(\varPi\) dissolves membrane 2 using a and b releases to membrane 1 without directly being involved in any application of a rule. Notice that in this case b immediately “knows” that \(\varPi\) contained an occurrence of a in the membrane with label 2. This way the objects can send information to each other, and this kind of behaviour cannot be captured by dependency graphs.

Using generalizations of dependency graphs the P conjecture was already proved in some special cases where the P systems were allowed to use dissolution rules as well. In [32], for example, the P conjecture was proved using object division graphs in the case where the initial membrane structure of the P system is a linearly nested sequence of membranes and the system can employ only dissolution and elementary membrane division rules. In [15] the P conjecture was proved in another case using a generalization of dependency graphs. Here the P systems are deterministic, can use all types of rules except send-in communication rules, and the membrane structure is such that the skin contains only elementary membranes. In these papers the authors used these generalizations of dependency graphs to simulate a reasonable small part of the configurations in a computation of the investigated P systems.

In this paper we propose a new method to address Păun’s conjecture. With this method we are able to simulate efficiently an entire computation of a P system. More precisely, we can compute in polynomial time the multiset content of the skin membrane at the end of certain computations of a P system. To make our ideas as clear as possible, we give our method only for a rather restricted variant of P systems, called halting simple divide-dissolve P systems. The computations of these P systems always terminate, initially they have only one elementary membrane in the skin, and they can employ only membrane division and membrane dissolution rules (see Definition 1 for further properties of these P systems). Moreover, we simulate only particular computations of these P systems, where, for example, division rules have priority over dissolution rules. We will call these computations division-driven computations (see Definition 2 for further details).

Our approach can be roughly described as follows. Consider a halting simple divide-dissolve P system \(\varPi\), its input multiset \(\omega _1\), and a division-driven computation \({\mathcal {C}}\) of \(\varPi\). First, based on the concept of object division graphs, we define object division polynomials (Definition 3). The object division polynomial of an object a describes which and how many objects can be created from a using only division rules of \(\varPi\). Then, we consider a polynomial \(P_{\omega _1}\) which is, roughly, the multiplication of the object division polynomials of objects in \(\omega _1\) (Definition 5). After that, we show that there is a strong relationship between the monomials of \(P_{\omega _1}\) and the numbers of certain membranes and their contents in \({\mathcal {C}}\) (Lemma 3). Then, using \(P_{\omega _1}\), we show how to calculate in polynomial time which and how many objects are released to the skin membrane in each step of \({\mathcal {C}}\) (Theorem 1). Using this we conclude that the multiset content of the skin membrane in the last configuration of \({{\mathcal {C}}}\) can be computed in polynomial time (Corollary 1).

We believe that our method can be extended to more general variants of P systems. In particular, a generalization to P systems having also send-out communication rules and a more general initial membrane structure seems to be achievable as it is discussed in the Conclusions section.

2 Preliminaries

Here we recall the necessary notions used later. Nevertheless, we assume that the reader is familiar with the basic concepts of membrane computing techniques (for a comprehensive guide see, e.g. [26]).

\(\mathbb {N}\) denotes the set of natural numbers including zero and, for every \(i,j\in \mathbb {N}\), \(i\le j\), [i, j] denotes the set \(\{i,\ldots ,j\}\). If \(i=1\), then [i, j] is denoted by [j]. We will use polynomials with coefficients in \(\mathbb {N}\). A polynomial of the form \(p=cx_1^{j_1}\ldots x_n^{j_n}\) where \(c,n,j_1,\dots ,j_n\in \mathbb {N}\) and \(x_1,\dots ,x_n\) are variables is called a monomial and c is called the coefficient of p. An \(n\times m\)matrix\(\mathbf {M}\) has n rows and m columns. We will consider matrices with entries in \(\mathbb {N}\). \(({\mathbf {M}})_{ij}\) denotes the jth element of the ith row of \({\mathbf {M}}\). By a vector\({\mathbf {v}}\) we mean an \(n\times 1\) matrix, for some \(n\ge 1\). \(\mathbf {v}^T\) denotes the transpose of \(\mathbf {v}\), and instead of \(({\mathbf {v}})_{j1}\) and \(({\mathbf {v}}^T)_{1j}\)\((j\in [n])\) we will write simply \(({\mathbf {v}})_j\) and \(({\mathbf {v}}^T)_j\), respectively. If a vector \({\mathbf {v}}\) has n entries, for some \(n\ge 1\), then \({\mathbf {v}}\) is called an n-dimensional vector or just an n-vector.

Next, we define a variant of polarizationless P systems with active membranes.

Definition 1

A simple divide-dissolve P system (sdd P system, for short) is a polarizationless P system with active membranes having the following properties. \(\varPi\) is of the form \(\varPi =(O,H,\mu ,\omega _{1}, R)\), where

  • O is the alphabet of objects,

  • \(H=\{1,s\}\) is the set of labels of the membranes,

  • \(\mu =[[\,\,]_{1}]_{s}\) is the initial membrane structure containing two membranes labelled with 1 and s, respectively, s being the skin membrane,

  • \(\omega _1\in O^*\) is the initial multiset of objects placed in the membrane with label 1 (initially, the skin membrane is empty), and

  • R is a finite set of rules defined as follows:

    • \([a]_1\rightarrow a\), where \(a \in O\)

      (membrane dissolution rules; in reaction with an object, a membrane can be dissolved, the objects of a dissolved membrane remain in the region surrounding it) and

    • \([a]_{1}\rightarrow [b]_{1} [c]_{1}\), where \(a, b, c \in O\)

      (division rules for elementary membranes; in reaction with an object, the membrane is divided into two membranes with the same label; the object specified in the rule is replaced in the two new membranes by possibly new objects; all other objects are duplicated in the two new copies of the membrane).

Moreover, for every \(a\in O\), R has at most one division rule of the form \([a]_1\rightarrow [b]_1[c]_1\). \(\varPi\) is called halting, if each of its computations halts.

As it is usual in membrane computing, sdd P systems work in a maximally parallel manner: at each step the system first nondeterministically assigns appropriate rules to the objects of the system such that the assigned multiset S of rules satisfies the following properties: (i) at most one rule from S is assigned to any object of the system, (ii) a membrane can be the subject of at most one rule in S, and (iii) S is maximal among the multisets of rules satisfying (i) and (ii).

Let \(\varPi =(O,\{1,s\},[[\,\,]_{1}]_{s},\omega _{1},R)\) be a halting sdd P system. For any rule r of the form \(u\rightarrow v\), u (resp. v) is called the left-hand side (resp. the right-hand side) of r. We call membranes with label 1 working membranes (notice that as the skin cannot be divided or dissolved, the objects in the skin remain unchanged during all computations of \(\varPi\), that is, only objects in working membranes can be changed). An object \(a\in O\) is called a divider if a can divide working membranes, that is, R contains a division rule with left-hand side \([a]_1\). Likewise, an object \(a\in O\) is called a dissolver if R contains a dissolution rule with left-hand side \([a]_1\).

3 Results

In this paper we consider only halting sdd P systems. In the rest of this section \(\varPi\) is always a halting sdd P system of the form \(\varPi =(O,\{1,s\},[[\,\,]_1]_s,\omega _1,R)\), where \(O=\{a_1,\ldots ,a_n\}\)\((n\in \mathbb {N})\) and \(\omega _1=a_{i_1}\ldots a_{i_m}\) (\(m\ge 1\) and \(i_1,\ldots ,i_m\in [n]\)).

In this section we show that the multiset content of the skin membrane of \(\varPi\) at the end of so-called division-driven computations can be computed in polynomial time in nm. In a division-driven computation division rules have priority over dissolution rules and there is a certain order between the division rules too. To specify these computations precisely we need some preparation.

Consider a halting computation \({{\mathcal {C}}}:C_0\Rightarrow C_1\Rightarrow \cdots \Rightarrow C_t\) of \(\varPi\). We first assign to each occurrence of an object occurring in a working membrane a label defined inductively as follows. The label of an object \(a_{i_\ell }\)\((\ell \in [m])\) in \(\omega _1\) in \(C_0\) is \(\ell\). Now, let M be a working membrane in \(C_i\), for some \(i\in [0,t-1]\), and consider an occurrence of an object a in M with label \(\ell\)\((\ell \in [m])\). Then we have exactly one of the following three cases: (i) this occurrence of a is not involved in the application of any rule, or (ii) it is involved in the application of a division rule \(r:[a]_1\rightarrow [b]_1[c]_1\), or (iii) it is involved in the application of a dissolution rule during \(C_i\Rightarrow C_{i+1}\). In Case (i) the same occurrence of a occurs in \(C_{i+1}\) too. Then let the label of this occurrence of a in \(C_{i+1}\) be \(\ell\). In Case (ii) r divides M into two new membranes in \(C_{i+1}\). Then let the label of the occurrences of b and c introduced by r in these two new membranes be \(\ell\). In Case (iii) no objects are introduced in the working membranes by the considered occurrence of a, thus no labelling is necessary in this case. If a is an object with label \(\ell\), then we will often denote this by \(a^{(\ell )}\).

Notice that the multiset content of a working membrane in \({{\mathcal {C}}}\) always has the form \(a_{j_1}^{(1)}\ldots a_{j_m}^{(m)}\), for some \(j_1,\ldots ,j_m\in [n]\). Using the labels of the objects we can define now division-driven computations as follows.

Definition 2

Let \(\varPi\) be a halting sdd P system with object alphabet \(O=\{a_1,\ldots ,a_n\}\) and initial multiset \(\omega _1=a_{i_1}\ldots a_{i_m}\). A halting computation \({\mathcal {C}}\) of \(\varPi\) is called division-driven if the following conditions hold.

  1. 1.

    If \(\varPi\) can apply both division and dissolution rules to a membrane in \({{\mathcal {C}}}\), then \(\varPi\) applies a division rule, and

  2. 2.

    when a division rule is applied to a membrane M in \({{\mathcal {C}}}\) with an object \(a_i^{(\ell )}\) on the left-hand side \((i\in [n],\ell \in [m])\), then M contains no dividers with label \(\ell '<\ell\).

Intuitively, in a division-driven computation \({\mathcal {C}}\) of \(\varPi\) the computation goes as follows. Assume that the labels of those objects in \(\omega _1\) that can divide working membranes are \({\ell _1}<\cdots <\ell _k\), for some \(k\in [m]\). Then first objects with label \(\ell _1\) are used to divide working membranes, then those objects which have label \(\ell _2\), and so on until at the end those objects are used which have label \(\ell _k\). Then those objects are used which can dissolve working membranes, and if no more working membranes can be dissolved, the computation terminates. Notice that if a non-divider object with label \(\ell\) occurs in a working membrane, then this object remains unchanged until the computation halts.

Example 1

Let \(\varPi _{ex}=(\{a_1,a_2,a_3,a_4\},\{1,s\},[[\,\,]_1]_s,a_1^{(1)}a_1^{(2)},R)\), where

$$\begin{aligned} R=\{[a_1]_1\rightarrow [a_2]_1[a_3]_1, [a_2]_1\rightarrow [a_4]_1[a_4]_1, [a_4]_1\rightarrow a_4\}. \end{aligned}$$

Figure 1 shows a division-driven computation of \(\varPi _{ex}\). Recall that the numbers in parentheses are the labels of the corresponding objects. Notice that each working membrane contains two objects with label 1 and 2, respectively. One can see that this computation is indeed a division-driven one. In the first step, \(a_1^{(1)}\) is used to divide the working membrane. Then, in the second step the upper working membrane is divided by \(a_2^{(1)}\) and the other working membrane is divided by \(a_1^{(2)}\) (no dividers with label 1 are present in this membrane). In the third step, the upper two working membranes are divided by \(a_1^{(2)}\), the working membrane containing \(a_3^{(1)}a_2^{(2)}\) is divided by \(a_2^{(2)}\), and the remaining working membrane is unchanged. Then, the computation continues according to the definition of division-driven computations: dividers have priority over dissolvers and dividers (resp. dissolvers) with label 1 have priority over dividers (resp. dissolvers) with label 2. \(\square\)

Fig. 1
figure 1

A division-driven computation of \(\varPi _{ex}\) from Example 1. Grey areas are the working membranes. Working membranes appearing closer to each other are results of a membrane division

Full size image

As it is mentioned in the introduction, our work is based on the concept of object division polynomials. To define this concept precisely we first define object division trees similarly as object division graphs were defined, for example, in [32]. Let \(\varPi\) be a halting sdd P system with object alphabet \(O=\{a_1,\ldots ,a_n\}\). The object division tree of \(a_i\) (\(i\in [n]\)), denoted by \({\mathrm {odt}}_{a_i}\), is the smallest binary tree satisfying the following conditions:

  • the root of \({\mathrm {odt}}_{a_i}\) is labelled by \(a_i\), and

  • if a node N of \({\mathrm {odt}}_{a_i}\) is labelled by \(a_j\) (\(j\in [n]\)) and \([a_j]_1\rightarrow [a_k]_1[a_l]_1\)\((k,l\in [n])\) is a rule of \(\varPi\), then N has exactly two children with labels \(a_k\) and \(a_l\), respectively.

Since \(\varPi\) is an sdd P system, it does not have different division rules with the same left-hand side. Thus \({\mathrm {odt}}_{a_i}\) is well defined. Notice that in \({\mathrm {odt}}_{a_i}\) a subtree with a root labelled by an object \(a_j\)\((j\in [n])\) is equal to \({\mathrm {odt}}_{a_j}\). The height of\({\mathrm {odt}}_{a_i}\), denoted by \(h({\mathrm {odt}}_{a_i})\), is defined inductively as follows. If \({\mathrm {odt}}_{a_i}\) is a single node labelled by \(a_i\), then \(h({\mathrm {odt}}_{a_i})=0\). Otherwise let \(h_{max}\) be the maximum of the heights of subtrees of the root in \({\mathrm {odt}}_{a_i}\). Then \(h({\mathrm {odt}}_{a_i})=h_{max}+1\).

Example 2

Consider again \(\varPi _{ex}\) from Example 1. The tree \({\mathrm {odt}}_{a_1}\) can be seen in Fig. 2. Notice that \({\mathrm {odt}}_{a_2}\) and \({\mathrm {odt}}_{a_3}\) are equal to the first and second subtrees of \({\mathrm {odt}}_{a_1}\), respectively, and \({\mathrm {odt}}_{a_4}\) is equal, for example, to the first subtree of \({\mathrm {odt}}_{a_2}\). \(\square\)

Fig. 2
figure 2

The tree \({\mathrm {odt}}_{a_1}\) from Example 2

Full size image

Next we show a useful property of object division trees.

Lemma 1

Let\(\varPi\)be a halting sdd P system with object alphabet\(O=\{a_1,\ldots ,a_n\}\)and initial multiset\(\omega _1\). Let\(i\in [n]\)such that\(a_i\)occurs in\(\omega _1\). Then\(h({\mathrm {odt}}_{a_i})<n\).

Proof

We give an indirect proof. Assume that \(h({\mathrm {odt}}_{a_i})\ge n\). Then there exists a path P in \({\mathrm {odt}}_{a_i}\) with length at least n. Due to the pigeonhole principle, there exists \(j\in [n]\) such that \(a_j\) occurs at least twice in P. Let \(N_1\) and \(N_2\) be the first two nodes of P (counted from the root) labelled by \(a_j\). Let \(t_1\) and \(t_2\) be the subtrees of \({\mathrm {odt}}_{a_i}\) with roots \(N_1\) and \(N_2\), respectively. Clearly, \(t_2\) is a proper subtree of \(t_1\). Moreover, by our above note \(t_1=t_2={\mathrm {odt}}_{a_j}\). This implies that \({\mathrm {odt}}_{a_i}\) is infinite, which further implies that a division-driven computation will never halt. However, this contradicts to the fact that \(\varPi\) is a halting sdd P system, proving our statement. \(\square\)

Every object division tree defines an object division polynomial as follows.

Definition 3

Consider a halting sdd P system \(\varPi\) with object alphabet \(O=\{a_1,\ldots ,a_n\}\). Let \(V=\{x_{i}\mid i\in [n]\}\cup \{x\}\) be a set of variables. Let moreover \(i\in [n]\) and \(l=h({\mathrm {odt}}_i)\). The object division polynomial of \(a_i\) (\({\mathrm {odp}}_{a_i}\) for short) is a polynomial with variables in V defined as follows:

$$\begin{aligned} {\mathrm {odp}}_{a_i}=\sum \limits _{j\in [0,l],k\in [n]}m_{jk}\cdot x_{k}\cdot x^j, \end{aligned}$$

where \(m_{jk}\) is the number of leaves in \({\mathrm {odt}}_{a_i}\) at depth j labelled by \(a_k\).

Example 3

Consider \(\varPi _{ex}\) from Example 1 and the object division trees considered in Example 2. The corresponding object division polynomials are as follows:

  • \({\mathrm {odp}}_{a_1}=2x_4x^2+x_3x\),

  • \({\mathrm {odp}}_{a_2}=2x_4x\),

  • \({\mathrm {odp}}_{a_3}=x_3\),

  • \({\mathrm {odp}}_{a_4}=x_4.\)

\(\square\)

Next we show that object division polynomials can be calculated in polynomial time.

Lemma 2

Consider a halting sdd P system\(\varPi\)with object alphabet\(O=\{a_1,\ldots ,a_n\}\)and let\(i\in [n]\). Then the object divisionpolynomial of\(a_i\)can be computed in polynomial time inn.

Proof

Let \(l=h({\mathrm {odt}}_{a_i})\) and, for every \(j\in [0,l]\), let \({\mathbf {v}}_j\) be an n-vector such that \(({\mathbf {v}}_j)_k\)\((k\in [n])\) is the number of nodes labelled by \(a_k\) on the \(\mathrm {j}\)th level of \({\mathrm {odt}}_{a_i}\). Let \(ndiv=\{j\in [n]\mid a_j \text { is a non-divider}\}\). As the set of labels of leaves in \({\mathrm {odt}}_{a_i}\) is included in the set \(\{a_j\mid j\in ndiv\}\), we get that

$$\begin{aligned} {\mathrm {odp}}_{a_i}=\sum \limits _{j\in [0,l],k\in [n]}{\mathbf {v}}_j{\mathbf {e}}_k x_k x^j, \end{aligned}$$

where \({\mathbf {e}}_k\)\((k\in [n])\) is an n-vector defined as follows:

$$\begin{aligned} (e_k)_\xi = {\left\{ \begin{array}{ll} 1&{} \text {if}\, \xi =k \, \text {and}\, k\in ndiv \\ 0&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

To compute \({\mathbf {v}}_j\)\((j\in [0,l])\) let us define, for every \(k\in [n]\), the n-vector \({\mathbf {m}}_{k}\) as follows: for every \(\xi \in [n]\), if there is a rule r of \(\varPi\) with \(a_\xi\) on the left- and \(a_k\) on the right-hand side, then let \(({\mathbf {m}}_{k})_\xi\) be the number of occurrences of \(a_k\) on the right-hand side of r. If there is no such rule of \(\varPi\), then let \(({\mathbf {m}}_{k})_\xi\) be 0. It can be clearly seen that if we multiply \({\mathbf {v}}_j^T\)\((j\in [0,l-1])\) with \({\mathbf {m}}_{k}\)\((k\in [n])\), we get the number of occurrences of \(a_k\) on the \((\mathrm {j}+1)\)th level of \({\mathrm {odt}}_{a_i}\). Thus, for every \(j\in [0,l-1]\), \({\mathbf {v}}_{j+1}^T={\mathbf {v}}_j^T {\mathbf {M}}\), where \({\mathbf {M}}\) is the \(n\times n\) matrix whose kth column \((k\in [n])\) is \({\mathbf {m}}_{k}\). Since matrix multiplication is associative, we get that \({\mathbf {v}}_j^T={\mathbf {v}}_0^T{\mathbf {M}}^j\)\((j\in [l])\). This implies that

$$\begin{aligned} {\mathrm {odp}}_{a_i}=\sum \limits _{j\in [0,l],k\in [n]}{\mathbf {v}}_0^T{\mathbf {M}}^j{\mathbf {e}}_k x_k x^j. \end{aligned}$$

Notice that since the 0th level of \({\mathrm {odt}}_{a_i}\) contains only the root of \({\mathrm {odt}}_{a_i}\), \(({\mathbf {v}}_0)_k=1\) if \(k=i\), and \(({\mathbf {v}}_0)_k=0\) otherwise. Therefore, the coefficient of a factor \(x_k x^j\) in \({\mathrm {odp}}_{a_i}\) is \(({\mathbf {M}}^j)_{ik}\). Thus, we only have to compute \({\mathbf {M}}^j\) for every \(j\in [0,l]\). Since every row in \({\mathbf {M}}\) contains at most two non-zero elements and the sum of these elements is two, it is easy to see that the largest value in \({\mathbf {M}}^j\) is at most \(2^j\). So these values can be stored using n bits and thus computing one entry of \({\mathbf {M}}^{j+1}\) can be done in \({\mathcal {O}}(n)\) steps. Since \({\mathbf {M}}\) is an \(n\times n\) matrix, computing every necessary value can be done in polynomial time in n. \(\square\)

Example 4

Consider \({\mathrm {odp}}_{a_1}\) and \({\mathrm {odp}}_{a_2}\) given in Example 3. According to the proof of Lemma 2, we can compute these polynomials as follows. We will use \({\mathbf {e}}_i\)\((i\in [4])\) and \({\mathbf {M}}^j\)\((j\in [0,2])\) in the computation of each polynomial. These have the following values: \({\mathbf {e}}_1^T={\mathbf {e}}_2^T=\begin{bmatrix} 0&0&0&0 \end{bmatrix}, {\mathbf {e}}_3^T=\begin{bmatrix} 0&0&1&0 \end{bmatrix}, {\mathbf {e}}_4^T=\begin{bmatrix} 0&0&0&1 \end{bmatrix},\) and

$$\begin{aligned} {\mathbf {M}}^0=\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix},\quad {\mathbf {M}}^1=\begin{bmatrix} 0&1&1&0\\ 0&0&0&2\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix},\quad {\mathbf {M}}^2=\begin{bmatrix} 0&0&0&2\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix}. \end{aligned}$$

Moreover, in the case of \({\mathrm {odp}}_{a_1}\)\({\mathbf {v}}_0^T=[1\,\,0\,\,0\,\,0]\) and \(l=2\). Clearly,

$$\begin{aligned}&\sum \limits _{j\in [0,2],k\in [4]}{\mathbf {v}}_0^T{\mathbf {M}}^j{\mathbf {e}}_k x_k x^j \\&\quad = \sum \limits _{k\in [4]}{\mathbf {v}}_0^T{\mathbf {M}}^0{\mathbf {e}}_k x_k + \sum \limits _{k\in [4]}{\mathbf {v}}_0^T{\mathbf {M}}^1{\mathbf {e}}_k x_k x + \sum \limits _{k\in [4]}{\mathbf {v}}_0^T{\mathbf {M}}^2{\mathbf {e}}_k x_k x^2. \end{aligned}$$

Thus, in the case of \({\mathrm {odp}}_{a_1}\) we get that

$$\begin{aligned}&\sum \limits _{j\in [0,2],k\in [4]}{\mathbf {v}}_0^T{\mathbf {M}}^j{\mathbf {e}}_k x_k x^j \\&\quad = \sum \limits _{k\in [4]}[1\,\,0\,\,0\,\,0]{\mathbf {e}}_k x_k + \sum \limits _{k\in [4]}[0\,\,1\,\,1\,\,0]{\mathbf {e}}_k x_k x \\&\qquad +\sum \limits _{k\in [4]}[0\,\,0\,\,0\,\,2]{\mathbf {e}}_k x_k x^2 = (0x_1 + 0x_2 + 0x_3 + 0x_4) \\&\qquad +(0x_1x + 0x_2x + 1x_3x + 0x_4x) \\&\qquad + (0x_1x^2 + 0x_2x^2 + 0x_3x^2 + 2x_4x^2)\\&\quad = 2x_4x^2 + x_3x = {\mathrm {odp}}_{a_1}. \end{aligned}$$

On the other hand, in the case of \({\mathrm {odp}}_{a_2}\)\({\mathbf {v}}_0^T=[0\,\,1\,\,0\,\,0]\) and \(l=1\). Thus we get the following calculation.

$$\begin{aligned}&\sum \limits _{j\in [0,1],k\in [4]}{\mathbf {v}}_0^T{\mathbf {M}}^j{\mathbf {e}}_k x_k x^j\\&\quad = \sum \limits _{k\in [4]}[0\,\,1\,\,0\,\,0]{\mathbf {e}}_k x_k + \sum \limits _{k\in [4]}[0\,\,0\,\,0\,\,2]{\mathbf {e}}_k x_k x \\&\quad =(0x_1 + 0x_2 + 0x_3 + 0x_4) \\&\qquad + (0x_1x + 0x_2x + 0x_3x + 2x_4x) \\&\quad = 2x_4x = {\mathrm {odp}}_{a_2}. \end{aligned}$$

\(\square\)

Let \(\varPi\) be a halting sdd P system with object alphabet \(O=\{a_1,\ldots ,a_n\}\) and initial multiset \(\omega _1=a_{i_1}\ldots a_{i_m}\). Consider a division-driven computation \({{\mathcal {C}}}:C_0\Rightarrow C_1\Rightarrow \cdots \Rightarrow C_t\) of \(\varPi\). First we specify certain working membranes of \({{\mathcal {C}}}\), then show how to use object division polynomials to calculate the multiset contents of these working membranes.

Let M be a working membrane in \({\mathcal {C}}\) and \(\ell \in [m]\). If M contains no dividers with label \(\ell '\le \ell\), then M is called \(\ell\)-divider-stable. Moreover, m-divider-stable working membranes are called non-dividing. Consider an \(\ell\)-divider-stable membrane M in \(C_i\)\((\ell \in [m], i\in [t])\). M is called primary if either \(i=0\) or the following holds. Let N be that membrane in \(C_{i-1}\) from which \(\varPi\) derives M. Then N is not \(\ell\)-divider-stable.

Example 5

Let \(\varPi _{ex}\) be the P system given in Example 1 and consider the working membrane M containing \(a_3^{(1)}a_2^{(2)}\) in \(C_2\). Then M is 1-divider-stable, as the only object in M having label 1 or less is \(a_3\) which is a non-divider. However, this M is not 2-divider-stable, since it contains \(a_2\) having label 2 and \(a_2\) is a divider. M is neither primary, as M is derived from the working membrane N in \(C_1\) containing \(a_3^{(1)}a_1^{(2)}\), but N is 1-divider-stable too. However, N is primary, since it is derived from the working membrane in \(C_0\) containing \(a_1^{(1)}a_2^{(2)}\), which is not 1-divider-stable.

The only working membrane in \(C_5\) is non-dividing, as it is 2-divider-stable, and 2 is the greatest label in this example. Notice that non-dividing working membranes are those which do not contain dividers. \(\square\)

Let \({{\mathcal {C}}}\) be a division-driven computation of \(\varPi\). To calculate the multiset contents of primary non-dividing working membranes of \({\mathcal {C}}\), we extend first the definition of object division polynomials to objects having labels.

Definition 4

Consider a halting sdd P system \(\varPi\) with object alphabet \(O=\{a_1,\ldots ,a_n\}\) and initial multiset \(\omega _1=a_{i_1}\ldots a_{i_m}\). Let \(i\in [n]\), \(\ell \in [m]\), and consider the object division polynomial \({\mathrm {odp}}_{a_{i}}=\sum \nolimits _{j\in [0,l],k\in [n]}m_{jk} x_{k} x^j\) of \(a_i\).

The labelled object division polynomial of \(a_i^{(\ell )}\) (\({\mathrm {lodp}}_{a_{i}^{(\ell )}}\) for short) is the polynomial \(\sum \nolimits _{j\in [0,l],k\in [n]}m_{jk} x_{\ell k} x^j\) (that is, we added \(\ell\) to the indices of certain variables of \({\mathrm {odp}}_{a_{i}}\), referring this way to the label of the corresponding object).

Next we define a product of labelled object division polynomials of objects in \(\omega _1\).

Definition 5

Let \(\varPi\) be a halting sdd P system with object alphabet \(O=\{a_1,\ldots ,a_n\}\) and initial multiset \(\omega _1=a_{i_1}\ldots a_{i_m}\). The \(\omega _1\)-product of\(\varPi\) is

$$\begin{aligned} P_{\omega _1}=\prod \limits _{\ell \in [m]}{\mathrm {lodp}}_{a^{(\ell )}_{i_\ell }}. \end{aligned}$$

It is easy to see that all monomials in \(P_{\omega _1}\) have the form \(\alpha x_{1 j_1}\ldots x_{m j_m}x^j\), for some \(\alpha ,j\in \mathbb {N}\) and \(j_1,\ldots ,j_m\in [n]\). Using the next lemma we can determine the multiset contents of primary non-dividing working membranes of the computation \({\mathcal {C}}\) by calculating the monomials of \(P_{\omega _1}\).

Lemma 3

Let\(\varPi\)be a halting sdd P system with object alphabet\(O=\{a_1,\ldots ,a_n\}\)and initial multiset\(\omega _1=a_{i_1}\ldots a_{i_m}\). Consider the\(\omega _1\)-product\(P_{\omega _1}\)and adivision-driven computation\({{\mathcal {C}}}:C_0\Rightarrow C_1\Rightarrow \cdots \Rightarrow C_t\)of\(\varPi\). Let moreover\(j_1,\ldots ,j_m\in [n]\)and\(j\in [0,t]\). Then the coefficient of\(x_{1 j_1}\ldots x_{m j_m}x^j\)in\(P_{\omega _1}\)equals to thenumber of those primary non-dividing working membranes in\(C_j\)which contain\(a^{(1)}_{j_1}\ldots a^{(m)}_{j_m}\).

Proof

We show the statement by induction on m. If \(m=1\), then \(P_{\omega _1}={\mathrm {lodp}}_{a^{(1)}_{i_1}}\). Then, by Definitions 3 and 4, \(P_{\omega _1}\) contains a monomial \(m_{jk} x_{1k}x^j\) if and only if the number of leaves in \({\mathrm {odt}}_{a_1}\) at depth j labelled by \(a_{k}\) is \(m_{jk}\). Thus, the number of those non-dividing working membranes in \(C_j\) which contain \(a^{(1)}_{k}\) equals to the coefficient of \(x_{1k}x^j\) in \(P_{\omega _1}\). Then the statement follows taking into consideration that every non-dividing working membrane in \({\mathcal {C}}\) is primary.

Now assume that the statement holds if \(m=m'\), for some \(m'\ge 1\). We show it for \(m=m'+1\). Let \(\alpha\) be the coefficient of a monomial \(x_{1 j_1}\ldots x_{m j_m}x^j\) in \(P_{\omega _1}\). Let moreover \({\hat{\alpha }}\) be the number of those primary m-divider-stable working membranes in \(C_j\) which contain \(a^{(1)}_{j_1}\ldots a^{(m)}_{j_m}\). We show that \(\alpha ={\hat{\alpha }}\).

Let \(\omega _1'=a_{i_1}\ldots a_{i_{m'}}\) and \(P_{\omega _1'}=\prod \nolimits _{\ell \in [m']}{\mathrm {lodp}}_{a^{(\ell )}_{i_\ell }}\). Clearly, \(P_{\omega _1}=P_{\omega _1'} {\mathrm {lodp}}_{a^{(m)}_{i_m}}\). Let us denote by \(\alpha _{j'}\) and \(\beta _{j''}\)\((j',j''\in [t])\) the coefficients of \(x_{1 j_1}\ldots x_{m' j_{m'}}x^{j'}\) in \(P_{\omega _1'}\) and \(x_{mj_m}x^{j''}\) in \({\mathrm {lodp}}_{a^{(m)}_{i_m}}\), respectively. One can see that \(\alpha\) can be calculated by summing up the products \(\alpha _{j'}\beta _{j''}\), for every \(j',j''\in [t]\) with \(j'+j''=j\).

On the other hand, let \(j',j''\in [t]\) and denote \({\hat{\alpha }}_{j'}\) the number of those primary \(m'\)-divider-stable working membranes in \(C_{j'}\) which contain \(a^{(1)}_{j_1}\ldots a^{(m')}_{j_{m'}}\). Denote, moreover, \({\hat{\beta }}_{j''}\) the number of leaves labelled by \(a_{j_m}\) in \({\mathrm {odt}}_{a_{i_m}}\) at depth \(j''\). Consider now a membrane M in \(C_j\) containing \(a^{(1)}_{j_1} \ldots a^{(m)}_{j_{m}}\). One can see that the only way for \(\varPi\) to create M is the following. First \(\varPi\) creates a membrane N containing \(a^{(1)}_{j_1}\ldots a^{(m')}_{j_{m'}} a^{(m)}_{i_m}\) in \(j'\) steps (\(j'\in [t]\)) using only dividers having labels \(m'\) or less. Then, using dividers with label m, \(\varPi\) creates M in \(j''=j-j'\) steps. Thus \({\hat{\alpha }}\) can be calculated by summing up the products \({\hat{\alpha }}_{j'}{\hat{\beta }}_{j''}\), for every \(j',j''\in [t]\) with \(j'+j''=j\).

By induction hypothesis, \(\alpha _{j'}={\hat{\alpha }}_{j'}\), for every \(j'\in [t]\). Moreover, by the definition of object division polynomials, \(\beta _{j''}={\hat{\beta }}_{j''}\), for every \(j''\in [t]\). Thus we have that

$$\begin{aligned} \alpha =&\sum \limits _{\begin{array}{c} j',j''\in [t],\\ j'+j''=j \end{array}} \alpha _{j'} \beta _{j''} = \sum \limits _{\begin{array}{c} j',j''\in [t],\\ j'+j''=j \end{array}} {\hat{\alpha }}_{j'} {\hat{\beta }}_{j''} = {\hat{\alpha }}, \end{aligned}$$

which finishes the proof of the lemma. \(\square\)

We show now through an example how to use the \(\omega _1\)-product \(P_{\omega _1}\) to calculate multiset contents of primary non-dividing working membranes.

Example 6

Consider \(\varPi _{ex}\) from Example 1 and the computation \({\mathcal {C}}\) given in Fig. 1. From Example 3 we know that \({\mathrm {odp}}_{a_1}=2x_4x^2+x_3x\). Thus \({\mathrm {lodp}}_{a^{(1)}_1}=2x_{14}x^2+x_{13}x\) and \({\mathrm {lodp}}_{a^{(2)}_1}=2x_{24}x^2+x_{23}x\). As \(P_{a_1^{(1)}a_1^{(2)}}={\mathrm {lodp}}_{a^{(1)}_1}{\mathrm {lodp}}_{a^{(2)}_1}\) we get that

$$\begin{aligned}&P_{a_1^{(1)}a_1^{(2)}}=(2x_{14}x^2+x_{13}x)(2x_{24}x^2+x_{23}x)\\&\quad = 4x_{14}x_{24}x^4+2x_{14}x_{23}x^3+2x_{13}x_{24}x^3+x_{13}x_{23}x^2. \end{aligned}$$

Figure 3 shows the correspondence between the monomials of \(P_{a_1^{(1)}a_1^{(2)}}\) and the primary non-dividing working membranes of \({\mathcal {C}}\). Notice that the variables \(x_{ij}\)\((i\in [2],j\in [4])\) correspond to objects \(a_j^{(i)}\), the coefficient of a monomial corresponds to the number of the corresponding membranes, and the power of x shows the index of the corresponding configuration. \(\square\)

Fig. 3
figure 3

Representing primary non-dividing working membranes of \(\varPi _{ex}\) by monomials

Full size image

Consider a halting sdd \(\varPi\), the \(\omega _1\)-product \(P_{\omega _1}\) of \(\varPi\), and a division-driven computation \({{\mathcal {C}}}\) of \(\varPi\). As we have seen, the multiset content of the primary non-dividing working membranes of \({\mathcal {C}}\) can be calculated by determining the monomials of \(P_{\omega _1}\). Clearly, if we know these multisets, then we can tell which and how many objects are released to the skin (by applying membrane dissolution rules) in each step of \({\mathcal {C}}\). However, the size of \(P_{\omega _1}\) can be exponential in nm, which means that we cannot use \(P_{\omega _1}\) directly to calculate efficiently the number of these objects. Instead, we will use another polynomial yielded by using the next definition.

Definition 6

Consider a halting sdd P system \(\varPi\) with object alphabet \(O=\{a_1,\ldots ,a_n\}\) and initial multiset \(\omega _1=a_{i_1}\ldots a_{i_m}\). Let P be a polynomial over the variables \(V=(\{x_{\ell k}\mid \ell \in [m], k\in [n]\}\cup \{x\})\). Let moreover \(i\in [n]\) and y be a new variable not occurring in V. The i-reduction ofP is the polynomial \(P^{\langle i\rangle }\) which we get from P using the following operations. First, for every \(\ell \in [m],k\in [n]\) with \(k\not =i\), we substitute \(x_{\ell k}\) in P with z, where

$$\begin{aligned} z= {\left\{ \begin{array}{ll} y, \text { if}\, a_k^{(\ell )}\, \text {can dissolve working membranes, and }\\ 1, \text { otherwise.} \end{array}\right. } \end{aligned}$$

Let the given new polynomial be \(P'\) and let \(P^{\langle i\rangle }\) be the polynomial created from \(P'\) by substituting \(x_{\ell i}\) with \(x_i\), for every \(\ell \in [m]\).

Example 7

The i-reductions (\(i\in [4]\)) of \(P_{a_1^{(1)}a_1^{(2)}}\) given in Example 6 are as follows:

  • \(P^{\langle 1\rangle }_{a_1^{(1)}a_1^{(2)}}=4yyx^4+2y1x^3+2\cdot 1yx^3+1\cdot 1x^2=4y^2x^4+4yx^3+x^2\),

  • \(P^{\langle 2\rangle }_{a_1^{(1)}a_1^{(2)}}=4yyx^4+2y1x^3+2\cdot 1yx^3+1\cdot 1x^2=4y^2x^4+4yx^3+x^2\),

  • \(P^{\langle 3\rangle }_{a_1^{(1)}a_1^{(2)}}=4yyx^4+2yx_3x^3+2x_3yx^3+x_3x_3x^2=4y^2x^4+4yx_3x^3+x_3^2x^2\),

  • \(P^{\langle 4\rangle }_{a_1^{(1)}a_1^{(2)}}=4x_4x_4x^4+2x_41x^3+2\cdot 1x_4x^3+1\cdot 1x^2=4x_4^2x^4+4x_4x^3+x^2\).

Lemma 4

Let\(\varPi\)be a halting sdd P system with object alphabet\(O=\{a_1,\ldots ,a_n\}\)and initial multiset\(\omega _1=a_{i_1}\ldots a_{i_m}\). Consider the\(\omega _1\)-product\(P_{\omega _1}\)of\(\varPi\). Let moreover\(i\in [n]\). Then thei-reduction of\(P_{\omega _1}\)canbe calculated in polynomial time innm.

Proof

One can see using basic properties of polynomials that

$$\begin{aligned} P^{\langle i\rangle }_{\omega _1}=\prod \limits _{\ell \in [m]}{\mathrm {odp}}^{\langle i\rangle }_{a_{i_\ell }}, \end{aligned}$$

where \(P^{\langle i\rangle }_{\omega _1}\) and \({\mathrm {odp}}^{\langle i\rangle }_{a_{i_\ell }}\) denote the i-reductions of \(P_{\omega _1}\) and \({\mathrm {lodp}}_{a^{(\ell )}_{i_\ell }}\), respectively. By Lemma 2, we can compute \({\mathrm {odp}}_{a_{i_\ell }}\), and in turn \({\mathrm {odp}}^{\langle i\rangle }_{a_{i_\ell }}\) as well, in polynomial time in n. Moreover, \({\mathrm {odp}}^{\langle i\rangle }_{a_{i_\ell }}\) contains only at most three variables, \(x_i, x\), and y, for every \(\ell \in [m]\). Thus, multiplying these polynomials can be done in polynomial time in nm. \(\square\)

Using the i-reduction of \(P_{\omega _1}\) we can compute which and how many objects are released to the skin membrane during a division-driven computation of \(\varPi\) as follows.

Theorem 1

Let\(\varPi\)be a halting sdd P system with object alphabet\(O=\{a_1,\ldots , a_n\}\)and initial multiset\(\omega _1=a_{i_1}\ldots a_{i_m}\). Consider a division-drivencomputation\({{\mathcal {C}}}:C_0\Rightarrow C_1\Rightarrow \cdots \Rightarrow C_t\)of\(\varPi\). Let moreover\(i\in [n], j\in [0,t-1]\)and denote\(N_{ij}\)the number of copies of\(a_i\)released to the skin membrane by dissolutions of elementarymembranes during the step\(C_j\Rightarrow C_{j+1}\). Then\(N_{ij}\)can be computed in polynomial time innm.

Proof

Let \(P_{\omega _1}\) be the \(\omega _1\)-product of \(\varPi\) and \(P^{\langle i\rangle }_{\omega _1}\) be the i-reduction of \(P_{\omega _1}\). Clearly, \(P^{\langle i\rangle }_{\omega _1}\) can be written in the form

$$\begin{aligned} P^{\langle i\rangle }_{\omega _1}=\sum \limits _{\begin{array}{c} \mu ,\nu \in [0,m],\mu +\nu \le m\\ j\in [0,mn] \end{array}}m_{\mu \nu j} x_{i}^{\mu }y^{\nu }x^j. \end{aligned}$$

Using Lemma 3 and the definition of i-reductions, we get the following. A monomial \(m_{\mu \nu j}x_i^\mu y^\nu x^j\) in \(P^{\langle i\rangle }_{\omega _1}\) represents that there are \(m_{\mu \nu j}\) primary m-divider-stable membranes in \(C_j\) containing \(\mu\) copies of \(a_i\) and \(\nu\) copies of such objects different from \(a_i\) which can dissolve the membrane. Distinguishing between the cases whether \(a_i\) is a dissolver or not, we get the following equations.

$$\begin{aligned} N_{ij}=\sum \limits _{\begin{array}{c} \mu ,\nu \in [0,m],\nu \ge 1\\ \mu +\nu \le m \end{array}} m_{\mu \nu j} \mu , \end{aligned}$$
(1)

if \(a_i\) is a non-dissolver, and

$$\begin{aligned} N_{ij}=\sum \limits _{\begin{array}{c} \mu ,\nu \in [0,m]\\ \mu +\nu \le m \end{array}} m_{\mu \nu j} \mu \end{aligned}$$
(2)

otherwise. As we have seen in Lemma 4, \(P^{\langle i\rangle }_{\omega _1}\) can be computed in polynomial time in nm. Thus, the corresponding (polynomial number of) coefficients of the monomials in the sums (1) and (2) can be calculated in polynomial time in nm as well. \(\square\)

Example 8

Consider Example 1 and the computation shown in Fig. 1. Let, for every \(i\in [4],j\in [0,4]\), \(N_{ij}\) be the value defined in Theorem 1. Then \(N_{ij}=0\), for \(i\in [2],j\in [0,4]\) and \(i\in [3,4],j\in [0,2]\). Moreover, \(N_{33}=N_{43}=4\), \(N_{34}=0\), and \(N_{44}=8\).

We show that these values can be calculated using the i-reductions given in Example 7 and the equations (1) and (2) given in the proof of Theorem 1. If \(i\in [2]\), then \(a_i\) is a non-dissolver, thus we have to use Eq. (1) in this case. However, the monomials in \(P^{\langle i\rangle }_{a_1^{(1)}a_1^{(2)}}\) do not contain \(x_i\), hence in this case \(\mu\) is 0, for each monomial. Therefore the sum equals to 0, for every \(j\in [0,4]\). Now let \(i=3\). Since \(a_3\) is a non-dissolver, we should use again Eq. (1) in this case. Now the only monomial which contains both \(x_3\) and y is \(4yx_3x^3\), which means that \(N_{33}=4\cdot 1=4\) and \(N_{3j}=0\), for every \(j\in \{0,1,2,4\}\). Lastly, let \(i=4\). Since \(a_4\) is a dissolver, we should use Eq. (2) in this case. Now the monomials that contain \(x_4\) are \(4x_4^2x^4\) and \(4x_4x^3\). Therefore \(N_{44}=4\cdot 2=8\), \(N_{43}=4\cdot 1=4\), and \(N_{4j}=0\), for every \(j\in [0,2]\). \(\square\)

From Theorem 1 we immediately get the following result.

Corollary 1

Let\(\varPi\)be a halting sdd P system with object alphabet\(O=\{a_1,\ldots ,a_n\}\)and initial multiset\(\omega _1=a_{i_1}\ldots a_{i_m}\). Consider a division-driven computation\({{\mathcal {C}}}:C_0\Rightarrow C_1\Rightarrow \ldots \Rightarrow C_t\)of\(\varPi\). Then the multiset content of the skin in\(C_t\)can becomputed in polynomial time innm.

Proof

Let \(i\in [n]\). It can be clearly seen that the number \(N_i\) of occurrences of \(a_i\) in the skin membrane in \(C_t\) is \(\sum \nolimits _{j\in [0,t-1]}N_{ij}\), where \(N_{ij}\) is the number defined in Theorem 1. By Theorem 1, \(N_{ij}\) can be calculated in polynomial time in nm. Thus, to see the statement it is enough to show that \(t\le nm\).

On the one hand, \(\omega _1\) contains m objects. On the other hand, by Lemma 1, for every \(\ell \in [m]\), \(h({\mathrm {odt}}_{a_{i_\ell }})<n\). This means that there are at most \(n-1\) steps in \({{\mathcal {C}}}\) where objects with label \(\ell\) are used to divide working membranes. Thus there are at most \(m(n-1)\) steps where division rules are applied, and there is at most one step, where only dissolution rules are applied. Thus, \(t\le m(n-1)+1\le mn\). \(\square\)

4 Conclusions

In this paper we proposed a polynomial-time method for calculating the number of each object occurring in the skin membrane at the end of a division-driven computation of a halting sdd P system \(\varPi\). To calculate these numbers we used multiplications of certain polynomials which were created from the object division polynomials of the objects initially contained in the working membrane of \(\varPi\).

Although our method considers only division-driven computations of halting sdd P systems, we can use it to simulate recognizer P systems too. Recognizer P systems [28] are common tools in membrane computing to solve decision problems with P systems. They have only halting computations and they are confluent, which means that all of their computations yield the same result. That is, a division-driven computation gives the same result as that of the other computations.

By definition, sdd P systems have no different rules with the same left-hand side. In fact, we can safely assume that a recognizer P system having only dissolution and division rules possesses this property, too. To see this consider such a recognizer P system \(\varPi\). If \(\varPi\) has two different rules \(r_1\) and \(r_2\) with the same left-hand side, then there is a computation of \(\varPi\) where in each situation when \(r_2\) is applicable, \(\varPi\) applies \(r_1\) instead (clearly, if \(r_2\) is applicable, then \(r_1\) should be applicable, too). That is, if we remove \(r_2\) from \(\varPi\), then the remaining part of \(\varPi\) will still compute the same result as before.

Concerning the future work, we would like to extend our method to P systems having other types of rules or different initial membrane structures. The method can easily be extended to the case when the dissolution rules can have arbitrary objects in their right-hand sides. Indeed, in this case we only need to change the calculation of the value \(N_{ij}\) in the proof of Theorem 1 accordingly.

It seems that we can extend our method to send-out communication rules too. To this end, we need to extend the definition of division-driven computations, for example such that send-out communication rules have less priority than that of dissolution rules. Moreover, in the calculation of \(N_{ij}\) in the proof of Theorem 1 we should add a case where \(a_i\) is a non-dissolver but can trigger a send-out communication rule. Notice that a working membrane can contain more than one occurrence of such an object a which can trigger send-out communication rules. However, during one step only one a can be used by a rule. Therefore, in the computation of \(N_{ij}\) we might need to consider such monomials too which contain \(x^{j'}\), for some \(j'<j\).

Moreover, our method seems to be suitable for generalisation to such P systems which initially have more than one working membranes (possibly with different labels). On the other hand, to extend it to such P systems where the initial membrane structure is deeper than one is not so trivial. Consider for example a P system \(\varPi\) having an initial membrane structure of the form \([\ldots [\,[\,\,]_1\,]_2\ldots ]_n\), where \(n\ge 3\) and n is the skin. Assume also that the other properties of \(\varPi\) correspond to those of the sdd P systems. Since membranes with label \(i>1\) cannot be divided until membranes with label 1 are present, we could use our method to calculate the number of objects in the regions of \(\varPi\) until the last membrane with label 1 is dissolved. Assume that at this point the elementary membrane has label i, for some \(i\in [2,n]\). We can use our method again to calculate the number of objects in the regions of \(\varPi\) until the last membrane with label i is dissolved. Continuing this way the application of our method, we can calculate the number of objects occurring in the skin membrane when the computation of \(\varPi\) halts. However, we cannot assume that the above-described computation is efficient because of the following reasons. Consider that point of the computation when the last membrane with label 1 is dissolved and the new elementary membrane is the one with label i. Then this membrane can contain exponentially many objects, which means that to apply our method we should multiply exponentially many polynomials. Nevertheless, it is more or less clear that if \(\varPi\) works in polynomial time, then only a polynomially large number of these objects are used by \(\varPi\) during the computation. This means that we can apply our method taking into consideration only a polynomially large number of objects.