Introduction

Malaria causes around 230 million infections and more than 400.000 deaths each year [1] – although it is preventable and treatable. Medications containing derivatives of artemisinin, a secondary metabolite of the plant Artemisia annua, show high efficacy against the disease and cause only low side effects, making these treatments a key in this global effort. Due to their high price, however, especially the people, who suffer most of the disease – the population in the sub-Saharan region – do not have full access to artemisinin-based combination therapies (ACTs).

Until today, artemisinin is mainly produced by extraction of the plant A. annua [2]. As an alternative, semi-synthetic processes for artemisinin production were developed [3, 4] and applied in industrial scale [5, 6] starting from fermentation with genetically engineered yeasts. The final production step is the reaction from dihydroartemisinic acid (DHAA) to artemisinin. DHAA is a biological precursor to artemisinin and obtained as major byproduct from the extraction. By applying a similar reaction step as in the semi-synthetic production, it can be utilized as an additional source for artemisinin [7] increasing the yield of artemisinin retrieved from the plant.

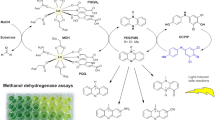
In both approaches the synthesis from DHAA to artemisinin plays a crucial role. Thus, a good understanding of the reaction mechanism and the main factors of influence is of large interest. The partial synthesis starting from DHAA (Fig. 1) proceeds via an initial photooxygenation forming a tertiary hydroperoxide as main intermediate [8, 9]. In the presence of strong acids, this hydroperoxide (PO1) undergoes a Hock-cleavage, a second oxidation and subsequent cyclization reactions forming artemisinin as main product [10, 11]. The first step, the photooxygenation, is initiated by formation of singlet oxygen in situ. Photosensitization requiring light irradiation and a matching dye is widely applied at lab- and industrial-scale [5, 6, 12] for this purpose due to its reduced need for reactants and higher selectivity. To achieve a fast and selective conversion of DHAA to artemisinin, the reactor system and the reaction conditions need to provide high mass transfer of oxygen, strong mixing and efficient irradiation within the reactor volume. These requirements were met by applying small-scaled reactor systems operated under slug flow conditions [13, 14] as displayed in Fig. 1.

Fig. 1
figure 1

Partial synthesis of artemisinin starting from dihydroartemisinic acid: Illustration of mass transfer, photon transfer and reaction kinetics

Full size image

To obtain an optimal overall process of artemisinin production, the partial synthesis step needs to be designed with respect to all upstream and downstream units. For this task, model-based tools have been proven essential in academia and the pharmaceutical industry [15, 16] to facilitate system understanding and control [17]. The description of the process chain constitutes a highly complex mathematical problem with multiple process variables, degrees of freedom and at the same time various constraints, e.g. on product quality and process safety. For each unit within the process, a model is required, which predicts the units’ behaviors well but is also simple to enable joint optimization of all involved units [18]. To the best of our knowledge, a comprehensive model is not available for the artemisinin partial synthesis so far [19]. To be predictive, the model needs to describe the major characteristics and phenomena of the process. However, multi-phase flow and photon emission in chemical reactors are 3D phenomena that can be described either based on first principles yielding complex models or by reducing the complexity with simplifications limiting the model applicability [20,21,22,23].

The aim of this contribution is to provide a first quantitative model for the reaction kinetics of the photooxidation of dihydroartemisinic acid to the intermediate tertiary hydroperoxide PO1. The model combines a detailed description of the reaction kinetics with mass and photon transfer. Focus in the model development was to obtain a model structure, which is reliable but at the same time as simple as possible, to allow for analysis of the production process, its limitation and model-based optimization. The model was parameterized by steady-state experiments of the photooxygenation in a continuous photo-flow reactor. The ferrioxalate actinometer was utilized to quantify the incident photon flux in the reactor – an essential quantity in the reaction kinetics of the photooxygenation. The challenging identification of the kinetic parameters was supported by an iterative strategy applying model-based experimental design to ensure large parameter sensitivities and reduce the experimental workload [24]. In the following, we first introduce the reaction mechanism and the experimental setup we used to study the kinetics. We explain the mathematical tools and how they are combined based on the applied experimental setting to yield a predictive model with reliable kinetic constants for the photooxidation of DHAA. To demonstrate the potential of the model, we use it in the end to derive promising experimental regimes for future lab and industrial implementation of the photooxygenation.

Reaction network of the photooxygenation of dihydroartemisinic acid

The photooxygenation of dihydroartemisinic acid (DHAA) to hydroperoxides proceeds via two main reaction steps (Fig. 2):

  1. 1.

    photosensitized formation of singlet oxygen and

  2. 2.

    ene-type reaction to an hydroperoxide.

In photosensitization, a photoactive molecule, the photosensitizer, absorbs light of a corresponding wavelength and transfers that energy to an oxygen molecule exciting it in its singlet state [12]. In this study we used 9,10-dicyanoanthracene (DCA), which is a widely applied photosensitizer due to its high efficiency, strong chemical stability and absorbance in the visible spectrum [25].

Fig. 2
figure 2

Simplified reaction network of the photooxygenation of dihydroartemisinic acid (DHAA) to the desired hydroperoxide PO1 – the key intermediate in the artemisinin partial synthesis. 9,10-Dicynanoanthracene (DCA) serves as photosensitizer in the in situ formation of singlet oxygen

Full size image

After absorption of light in the blue region (400–500 nm) DCA is excited to a singlet state following a complex network of different quenching processes [26, 27]. In the main pathway, singlet state DCA is quenched by triplet oxygen forming one molecule of singlet oxygen. The residual triplet state allows the formation of another molecule of singlet oxygen reducing DCA to its ground state. Parallel quenching processes, e.g. fluorescence or phosphorescence, lead to deactivation of DCA without forming singlet oxygen. Depending on the solvent, the dissolved oxygen concentration and the presence of additional quenchers, the overall quantum yield of singlet oxygen formation with DCA might vary significantly [27]. A maximum quantum yield of singlet oxygen is reported in the range of 1.56–1.71 in benzene extrapolated to indefinite oxygen concentration [27,28,29].

Once singlet oxygen is formed, it either reacts with DHAA or it is quenched back to its triplet state. The reaction of DHAA with singlet oxygen proceeds via 1,5-sigmatropic H-shift matching an ene-type reaction mechanism known as Schenk-reaction [30]. In the range of the double bond, H-atoms in three different positions can be abstracted forming three different hydroperoxides. Due to the cis-effect of the ene-type reaction, the tertiary hydroperoxide PO1 is the main product. PO1 is also the intermediate to artemisinin and so the desired product of the photooxygenation. All formed hydroperoxides are semi-stable species which undergo several rearrangement and degradation reactions leading to total decomposition within several weeks [11].

Kinetic steady-state experiments in a photo-flow reactor

The photooxygenation of dihydroartemisinic acid (DHAA) requires efficient irradiation of the reactant solution and sufficient supply of oxygen to investigate the kinetics of the reaction steps. Milli-scaled flow reactors in Taylor flow mode offer high surface area between gas and liquid phase and efficient irradiation of the substrate due to the small channel depths. This makes this type of reactors suitable to study the kinetics of photoreactions [31,32,33]. The experimental conditions including toluene as solvent, 9,10-dicyanoanthracene (DCA) as photosensitizer and a temperature of -20 °C were adapted from [14] due to the optimal yields for artemisinin observed in this study. To exclude dynamics from the kinetic analysis, the reactor has to enter a steady-state before sampling or evaluating online-measurement data.

In the following, the applied reactor setup and the procedure of the photooxygenation experiments are introduced briefly. For details on materials, the equipment and sample analysis, the interested reader is referred to the Supporting Information (SI).

Continuous photo-flow reactor system

The photooxygenation of DHAA was investigated in an in-house-made tubular reactor system, Fig. 3. The photoreactor consisted of wrapped transparent tubing (FEP, ID 0.8 mm) immersed in a cooling liquid connected to a thermostat. The length of the photoreactor (2–10 m) was chosen according to the residence time range of interest. Two LED modules emitting blue light (417 nm) irradiated the photoreactor from both sides in all experiments. The irradiation intensity was set relative to the maximum emitted optical power of the LED modules (21 W per module) by adjusting the current in the power supply. In the following we refer to this setting as LED power PLED.

Fig. 3
figure 3

Continuous photo-flow reactor setup applied for the kinetic investigation of the photooxygenation of dihydroartemisinic acid. The liquid and gas feed are pumped at Taylor flow conditions through the reaction line (ID: 0.8 mm) kept at -20 °C and irradiated by blue LED light (417 nm)

Full size image

The liquid and the gas feed were dosed continuously by a syringe pump and mass flow controllers, respectively. Both feed streams were contacted in a T-mixer and then entered the photoreactor. After irradiation, the gas and liquid phase are split in a membrane phase separator. The residual gas stream is measured with a flow meter. The liquid stream is collected and analyzed offline. The pressure in the reaction line was controlled by two back-pressure regulators at the gas and the liquid side.

Steady-state experiments for the photooxygenation of DHAA in Taylor flow conditions

The feed solution consisting of DHAA and DCA dissolved in toluene was connected to the reactor system and dosed together with a gas stream containing either pure oxygen or oxygen/nitrogen mixtures through the reactor system. In all experiments, the gas/liquid ratio was set to 4:1 (v/v) - equal to a gas holdup of β = 0.8. The total flow rate was varied between 1–2 ml/min at 7 bar absolute system pressure, ensuring Taylor flow conditions in all experiments. The photoreactor was operated at -20 °C, while all the up- and downstream equipment was kept at room temperature.

To ensure steady-state operation of the reactor system, one set of experimental conditions was kept for a duration of at least 5 times of the estimated residence time in the whole reactor before sampling the liquid effluent at the end of the reaction line. The concentrations of DHAA and the formed hydroperoxides were determined by quantitative 1H-NMR.

Measurement of the provided photon flux by chemical actinometry

The initial step of the photooxygenation of DHAA is the light-induced formation of singlet oxygen, where photons must be considered as stoichiometric reagent. Chemical actinometry is a well-established tool to investigate the incident photon flux in complex reactor geometries, where other methods as radiometry are not easily applicable [34]. It is an integral method yielding an average value of the incident photon flux over the irradiation period.

In this study, we used potassium ferrioxalate as actinometer – also known as the Hatchard-Parker-Actinometer [35] – to characterize the photon flux reaching the reactor in our experimental setup. This actinometer is the most established one [36] and used also for characterization of flow reactors [37, 38] due to its wide range of absorption in the UV and visible spectrum, easy preparation and handling. As Roibu et al. [39] showed, the absorbed amount of photons differs depending on the set flow conditions. To mimic the radiation conditions in the photooxygenation experiments, all actinometric measurements shown in this study were performed in continuous mode in Taylor flow conditions. The procedure of measurements with ferrioxalate and their analysis were adapted from Wriedt et al. [38].

Experimental procedure of actinometric measurements

A 0.15M solution of ferrioxalate was prepared freshly on the day of the experiment. The actinometer solution was pumped together with nitrogen as inert phase in slug flow pattern through the irradiated reactor at 7 bar system pressure. The gas holdup β was 0.8 in all experiments – equal to the flow conditions in the photooxygenation experiments. The two-phase-flow was pumped through the photoreactor resulting in a residence time of 6–12 s in the irradiated section (2 m length). After achieving stable flow conditions for at least 5 min, 3 samples of the liquid effluent stream were collected.

Each sample was diluted 25-fold with 0.05M sulfuric acid before combining it with a buffer solution of 0.1% phenanthroline solution in 0.05M sulfuric acid containing 0.06M sodium acetate. After 30 min the absorption of the sample was measured at 510 nm with a UV/Vis spectrometer to determine the formed amount of Fe(II) oxalate and calculate the actinometer conversion. In addition, samples of the reactor effluent without irradiation were collected and processed likewise to the irradiated samples to determine actinometer conversion due to ambient light.

Details on materials, sample workup and analysis are given in the SI.

Determination of the incident photon flux

The conversion of ferrioxalate XAct in the linear region of the actinometer only depends on the constant quantum yield ΦAct at the irradiation wavelength of 417 nm, the optical path length lopt and the volumetric incident photon flux Lp during irradiation in the photoreactor with a residence time τ. Following the procedure and the model introduced in Wriedt et al. 2018 [38], Lp is obtained by solving Eq. 1 numerically, based on the known residence time and the measured actinometer conversion,

$$ \frac{\mathrm{d} X^{\text{Act}}}{\mathrm{d}\tau} = \frac{{{\varPhi}}^{\text{Act}}_{417 \text{nm}}}{[\text{Act}]_{0}} L_{\mathrm{p}} \left( 1-e^{-\kappa_{417 \text{nm}}^{\text{Act}}[\text{Act}]_{0} (1-X^{\text{Act}}) l_{\text{opt}}}\right). $$
(1)

The quantum yield ΦAct and the Napierian absorption coefficient \(\kappa _{417 nm}^{\text {Act}}\) of ferrioxalate at irradiation wavelength are given in the SI – together with details on the calculation of the actinometer conversion and the determination of the incident photon flux. The relation of absorbed and incident photon flux based on the Lambert-Beer law is introduced in the following section on model development for the photooxygenation of DHAA.

Process model for the photooxygenation of dihydroartemisinic acid

The difficulty in obtaining reliable reaction kinetics for the photooxygenation of dihydroartemisinic acid (DHAA) lies in the interaction of the chemical reaction network with photon and mass transfer processes. Both phenomena are complex to describe and depend strongly on the reactor system applied. Accordingly, the identified process model is assembled from two main parts. The kinetic model describes the (photo-induced) chemical reactions and is independent of the process setup. The reactor model, instead, reproduces the fluid dynamics of the two-phase flow, including the interfacial transfer equations, and is dependent on the photo-flow reactor system used. Both components of the process model, that integrates the kinetics into the reactor model, are introduced in the following subsections. In the end, a short theoretical background on how we identified the process model and estimated and assessed its model parameters is outlined.

The interested reader is referred to the Supporting Information (SI) for a more thorough motivation and derivation of the reactor model. Likewise, more details on the strategy leading to the identified process model can be found in the SI.

Kinetic rate equations for the photooxygenation

The reaction scheme of the kinetic model is shown in Fig. 2. The tertiary hydroperoxide PO1 is the species of interest, i.e., it is further converted to artemisinin. The two secondary hydroperoxides PO2 and PO3 are lumped together to the byproduct species POy. In the conducted photooxygenation experiments, the recovery of the measured products PO1 and POy make up around 95 % of the total amount of reacted DHAA. The missing 5 % are attributed to rearrangement and degradation products formed between sampling and NMR analysis (Section 6). To cover these additional and presently chemically unidentified products and the respective reactions, an additional species POx is introduced, which is produced from PO1 and POy. Identical reaction rate constants are assumed. This approach is motivated by the lack of data on species and reactions, as it allows to lump the unknown and unquantifiable reactions and side products. This approach may be replaced by a more detailed mechanism once more is known on the side reactions. Alternatively, separate loss reactions might lead to additional complications during the identification of their reaction constants and would therefore make a physical interpretation difficult. Hence, the chemical reaction network is

$$ \begin{array}{@{}rcl@{}} \text{DHAA} {+}^{1}&\text{O}_{2} \xrightarrow{{k_{\text{PO}}}_{1}}& \text{PO}_{1}, \\ \text{DHAA} {+}^{1}&\text{O}_{2} \xrightarrow{{k_{\text{PO}}}_{\text{y}}}& \text{PO}_{\text{y}}, \\ &{~}^{1}\text{O}_{2} \xrightarrow{1/\tau_{{{\varDelta}}}}& {~}^{3}\text{O}_{2}, \\ &\text{PO}_{1} \xrightarrow{{k_{\text{PO}}}_{\text{x}}}& \text{PO}_{\text{x}}, \\ &\text{PO}_{\text{y}} \xrightarrow{{k_{\text{PO}}}_{\text{x}}}& \text{PO}_{\text{x}}, \end{array} $$
(2)

with kinetic rate constants ki, i ∈{PO1,POy,POx}, and the lifetime of singlet oxygen τΔ. The corresponding reaction rates are expressed as elementary reactions [40], resulting in the following rates of formation:

$$ \begin{array}{@{}rcl@{}} r_{\text{PO}_{1}} &=& k_{\text{PO}_{1}} [\text{DHAA}][{~}^{1}{\text{O}}_{2}], \end{array} $$
(3a)
$$ \begin{array}{@{}rcl@{}} r_{\text{PO}_{\text{y}}} &=& k_{\text{PO}_{\text{y}}} [\text{DHAA}][{~}^{1}{\text{O}}_{2}], \end{array} $$
(3b)
$$ \begin{array}{@{}rcl@{}} r_{\text{PO}_{\text{x}}} &=& k_{\text{PO}_{\text{x}}} ([\text{PO}_{1}]+[\text{PO}_{\text{y}}]). \end{array} $$
(3c)

Since singlet oxygen is a very reactive and short-lived species, the steady-state-assumption is applied,

$$ \frac{\mathrm{d} [{~}^{1}{\text{O}}_{2}]}{\mathrm{d} z} \overset{!}{\cong}0 \cong r_{{~}^{1}{\text{O}}_{2}} - (k_{\text{PO}_{1}}+k_{\text{PO}_{\text{y}}}) [\text{DHAA}][{~}^{1}{\text{O}}_{2}] - \frac{1}{\tau_{{{\varDelta}}}}[{~}^{1}{\text{O}}_{2}], $$
(4)

where \(r_{{~}^{1}{\text {O}}_{2}}\) is the formation rate of singlet oxygen. Combining (??) with (4), yields

$$ \begin{array}{@{}rcl@{}} r_{\text{PO}_{1}} &=& r_{{~}^{1}{\text{O}}_{2}} \frac{\tilde{k}_{\text{PO}_{1}} [DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}, \end{array} $$
(5a)
$$ \begin{array}{@{}rcl@{}} r_{\text{PO}_{\text{y}}} &=& r_{{~}^{1}{\text{O}}_{2}} \frac{\tilde{k}_{\text{PO}_{\text{y}}} [DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}, \end{array} $$
(5b)
$$ \begin{array}{@{}rcl@{}} r_{\text{PO}_{\text{x}}} &=& k_{\text{PO}_{\text{x}}} ([\text{PO}_{1}]+[\text{PO}_{\text{y}}]), \end{array} $$
(5c)

with the kinetic constants normalized to the lifetime of singlet oxygen

$$ \tilde{k}_{i} = k_{i} \tau_{{{\varDelta}}}, i\in\{\text{PO}_{1},\text{PO}_{\text{y}}\}. $$
(6)

The lifetime of singlet oxygen in toluene τΔ is 33.2 μ s at -20°, extrapolated from available data in the range from 5 to 90° [41].

Photosensitized formation of singlet oxygen

In photosensitized processes, expressions for reaction rates are either empirically derived, thus having limited scope, or mechanistically motivated [42]. The mechanistic justification lies in the fact that “in a single photon absorption process, the rate of the photosensitizer activation step (primary event) is proportional to the rate of energy absorbed” [42]. The formation rate of singlet oxygen might be expressed as

$$ r_{{~}^{1}{\text{O}}_{2}} = {{\varPhi}}_{{~}^{1}{\text{O}}_{2}} L_{\mathrm{p}}^{\mathrm{a}}, $$
(7)

with the local volumetric rate of photon absorption \(L_{\mathrm {p}}^{\mathrm {a}}\) and the quantum yield of singlet oxygen \({{\varPhi }}_{{~}^{1}{\text {O}}_{2}}\), i.e., the number of singlet oxygen molecules formed divided by the number of absorbed photons.

Different mechanistic networks for the formation of singlet oxygen by DCA in various solvents have been derived in literature [26, 27]. Here, we neglect implications on the quantum yield by extraneous species, e.g. solvent quenching, as they are unknown and would encompass the unfavorable situation that the quantum yield does not tend to zero with vanishing oxygen concentration [21, 26, 27]. The quantum yield of singlet oxygen can then be stated as

$$ {{\varPhi}}_{{~}^{1}{\text{O}}_{2}} = \frac{[\text{O}_{2}]}{k_{\mathrm{l}1}[\text{O}_{2}] + k_{\mathrm{l}2}}, $$
(8)

where kl1 and kl2 are lumped kinetic parameters that combine diverse rate constants [27]. The concentration of triplet oxygen concentration in Eq. 8 has been replaced by the concentration of dissolved oxygen as singlet oxygen occurs merely in trace quantities [21, 33].

Connecting the reaction kinetics to the rate of photon absorption

The interaction between radiative transfer and reaction kinetics is visualized in Fig. 4. The

Fig. 4
figure 4

Interaction between radiative transfer and reaction kinetics; Lp: local volumetric incident photon flux, \(L_{\mathrm {p}}^{\mathrm {a}}\): local volumetric rate of photon absorption, c: vector holding concentrations of present species

Full size image

reaction rates in Eqs. 6 and 7 depend on the local volumetric rate of photon absorption \(L_{\mathrm {p}}^{\mathrm {a}}\) that results from the radiative transfer equation (RTE). The \(L_{\mathrm {p}}^{\mathrm {a}}\), in turn, depends on the concentrations of the chemical species c. A common assumption is that photons are predominantly absorbed by the photosensitizer, i.e. c = (cDCA)⊤, leading to the substantial simplification that the RTE and the chemical kinetics are decoupled and can therefore be solved independently. However, the \(L_{\text {p}}^{\text {a}}\) remains a complex function of position and time, that is highly dependent on the individual reactor geometry, the physical properties of the participating media and the flow conditions [43].

If nontransient light intensity is assumed, an averaged \(L_{\mathrm {p}}^{\mathrm {a}}\) is derived from the Beer-Lambert law [44],

$$ \langle L_{\mathrm{p}}^{\mathrm{a}}\rangle = L_{\mathrm{p}} (1-\exp{[-\kappa c_{\text{DCA}} l_{\text{opt}}]}), $$
(9)

with the the local volumetric incident photon flux Lp, the Napierian absorption coefficient of the absorbing species κ, the photosensitizer concentration cDCA, and the optical path length lopt. The concentration of DCA was assumed to be constant throughout the whole reactor. Please note that Eq. 9 does not explicitly include the irradiation from two sides as the here used reactor setup would suggest. Due to the symmetric configuration of the capillary reactor, however, the superposition of the light emission from two sides is implicitly alleviated in Lp. In addition, an error resulting from this simplified description is balanced by considering the optical path length as one of the parameters to be estimated, Eq. 21.

The local volumetric incident photon flux Lp is defined as the absolute incident photon flux q0 related to the irradiated volume of the reaction solution Vl:

$$ L_{\mathrm{p}} = \frac{q_{0}}{V_{\text{l}}}. $$
(10)

In complex reactor geometries, the local rate of photon absorption might differ significantly within the reactor volume altering the local reaction rates. In this study, \(L_{\mathrm {p}}^{\mathrm {a}}\) was assumed to be constant. The assumption of homogeneous illumination is commonly made in microreactor modelling, resulting in good model-data fits [45]. This includes that the effect of a decreasing gas holdup due to reaction progress on the average path length [39] is neglected. The reaction kinetics are therefore related to the averaged \(L_{\mathrm {p}}^{\mathrm {a}}\), which is constant over the whole reactor length. Accordingly, the actinometric measurements used to characterize the irradiation conditions in the reactor also provide an average value of the incident photon flux over the reactor length, see Eq. 1.

Reactor model

The reactor model connects the intrinsic reaction rates with the physical phenomena occurring within the reactor line, namely the specific flow conditions and mass transfer. The key assumptions for the description of the reactor behavior are stated in Table 1. In a reliable reactor model, the gas and liquid phase as well as the mass transfer between them need to be quantified. In the following, we first derive the balance equations for each phase separately based on the two-fluid model, and subsequently describe the interfacial mass transfer between the gas and the liquid phase.

Table 1 Summary of key assumptions applied to describe the reactor behavior
Full size table

Description of fluid dynamics with the two-fluid model

The core idea of the two-fluid model (indices g and l for gas and liquid phase, respectively) is to balance each phase individually and close their balances by interfacial transfer equations. A more detailed motivation for the two-fluid model can be found in the SI, Section 5.1.2.

Resulting from the simplifications in Table 1, the material balance of a species i in the liquid phase in terms of concentration ci along the reactor coordinate z becomes

$$ \frac{\text{d}{c_{i}}}{\text{d}{z}} = \frac{1}{u_{\text{l}}} (r_{i} + \delta_{i} j_{\text{O}_{2}}), \quad \delta_{i} = \begin{cases} 1, &i=\text{O}_{2} \\ 0, &\text{else} \end{cases}, $$
(11)

where ul is the liquid phase velocity, ri is the net rate of reaction and \(j_{\text {O}_{2}}\) is the transfer of oxygen from the gas to the liquid phase. The species i is in the set {DHAA,PO1,POy,POx,O2}. The delta function δi ensures that the oxygen transfer is solely active in the balance for dissolved oxygen.

For the gas phase, a material balance over oxygen and the total gas flow \(\dot {V}_{\text {g}}\) is considered. The former in terms of molar fraction \(\textsf {x}_{\text {O}_{2}}\) is

$$ \frac{\text{d}\textsf{x}_{\text{O}_{2}}}{\text{d}{z}} = -\frac{RT}{p\dot{V}_{\text{g}}} (1-\alpha)A j_{\text{O}_{2}} (1-\textsf{x}_{\text{O}_{2}}), $$
(12)

and the material balance over the total gas flow reads

$$ \frac{\text{d}\dot{V}_{\text{g}}}{\text{d}z} = - \frac{RT}{p} (1-\alpha)A j_{\text{O}_{2}}. $$
(13)

In Eqs. 12 and 13, R is the universal gas constant, T temperature, p total pressure, and A the known cross-sectional area of the channel. The gas fraction α is a key characteristic of the two-fluid model, which assigns a relative area to any of the phases:

$$ \alpha = \frac{A_{\text{g}}}{A},\quad 1-\alpha = \frac{A_{\text{l}}}{A}, \quad\text{and } A=A_{\text{g}}+A_{\text{l}}, $$
(14)

where Ag and Al are the unspecified cross-sectional areas covered by the gas phase flow \(\dot {V}_{\text {g}}\) and the liquid phase flow \(\dot {V}_{\mathrm {l}}\), respectively. The phase velocities can then be expressed as

$$ u_{\text{g}} = \frac{\dot{V}_{\text{g}}}{A_{\text{g}}} = \frac{\dot{V}_{\text{g}}}{\alpha A},\quad u_{\text{l}} = \frac{\dot{V}_{\mathrm{l}}}{A_{\text{l}}} = \frac{\dot{V}_{\mathrm{l}}}{(1-\alpha)A}. $$
(15)

To solve the material balances in Eqs. 11, 12 and 13, the unknown gas fraction α must be determined. To this end, we utilize an established simplification of the two-fluid model – the drift flux model [46, 47] (further details in SI, Sec. 5.1.3). Its constitutive equation relates α to the known gas holdup β,

$$ \alpha = \frac{1}{C_{0}} \beta, $$
(16)

with

$$ \beta = \frac{\dot{V}_{\text{g}}}{\dot{V}} = \frac{\dot{V}_{\text{g}}}{\dot{V}_{\text{g}}+\dot{V}_{\mathrm{l}}}. $$
(17)

The distribution factor C0 might be taken from literature or experimentally determined. In this study, C0 was estimated by measurement of the residence time after tracer injection (SI, Sec. 6.1).

Interfacial oxygen transfer

Mass transfer of oxygen from the gas into the liquid phase is modeled according to

$$ j_{\text{O}_{2}} = k_{\text{l}} a ([\text{O}_{2}]^{\infty} - [\text{O}_{2}]), $$
(18)

where \([\text {O}_{2}]^{\infty }\) is the saturation concentration of oxygen in the liquid phase and kla is the volumetric transfer coefficient based on the specific gas-liquid interfacial surface area a. The saturation concentration is calculated by Henry’s law (SI, Sec. 5.1.4) and is taken from literature [48]. The mass transfer coefficient kla in Eq. 18 is affected by several reactor-dependent and fluid properties, that are summarized in a contribution from the Taylor bubble caps and a contribution from the liquid film between reactor wall and Taylor bubble [49]. The contribution by the film was observed to be dominant [49], leading to \(k_{\text {l}} a \propto \sqrt {D_{\text {O}_{2}} u_{\text {g}}^{\mathrm {s}} / L_{\text {UC}}} /d\) with the diffusion coefficient of oxygen \(D_{\text {O}_{2}}\) and the length of a unit cell LUC consisting of the gas bubble and the liquid slug [50]. For no information about the geometry of the unit cell is readily available, we simply consider a dependence of the mass transfer coefficient on the superficial gas velocity:

$$ k_{\text{l}} a = \widetilde{k_{\text{l}} a} \sqrt{u_{\text{g}}^{\mathrm{s}}}, $$
(19)

introducing a constant \(\widetilde {k_{\text {l}} a}\).

The process model: Combining the kinetics with the reactor model

The integration of the chemical kinetics, Eq. ??, and the mass transfer relation, Eq. 18, into the material balances (11), (12) and (13) provides the governing equations of the process model for both the liquid and the gas phase:

$$ \begin{array}{@{}rcl@{}} \frac{\text{d}[\text{DHAA}]}{\text{d}z} &=& \frac{\left( 1-\frac{\beta}{C_{0}}\right)A}{\dot{V}_{\mathrm{l}}} \left( -\frac{[\text{O}_{2}]}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}} \frac{(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]} \right.\\ &&\left. L_{\mathrm{p}} (1-\exp{[-\kappa c_{\text{DCA}} l_{\text{opt}}]}) \vphantom{ -\frac{[\text{O}_{2}]}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}} \frac{(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}}\right), \\ \frac{\text{d}[\text{PO}_{1}]}{\text{d}z} &=& \frac{\left( 1-\frac{\beta}{C_{0}}\right)A}{\dot{V}_{\mathrm{l}}} \left( \frac{[\text{O}_{2}]}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}} \frac{\tilde{k}_{\text{PO}_{1}}[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]} \right.\\ &&\left. L_{\mathrm{p}} (1-\exp{[-\kappa c_{\text{DCA}} l_{\text{opt}}]}) - k_{\text{PO}_{\text{x}}} [\text{PO}_{1}]\vphantom{ -\frac{[\text{O}_{2}]}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}} \frac{(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}} \right), \\ \frac{\text{d}[\text{PO}_{\text{y}}]}{\text{d}z} &=& \frac{\left( 1-\frac{\beta}{C_{0}}\right)A}{\dot{V}_{\mathrm{l}}} \left( \frac{[\text{O}_{2}]}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}} \frac{\tilde{k}_{\text{PO}_{\text{y}}}[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]} \right.\\ &&\left. L_{\mathrm{p}} (1-\exp{[-\kappa c_{\text{DCA}} l_{\text{opt}}]}) - k_{\text{PO}_{\text{x}}} [\text{PO}_{\text{y}}] \vphantom{ -\frac{[\text{O}_{2}]}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}} \frac{(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}}\right), \\ \frac{\text{d}[\text{PO}_{\text{x}}]}{\text{d}z} &=& \frac{\left( 1-\frac{\beta}{C_{0}}\right)A}{\dot{V}_{\mathrm{l}}} k_{\text{PO}_{\text{x}}} ([\text{PO}_{1}] + [\text{PO}_{\text{y}}]), \\ \frac{\text{d}[\text{O}_{2}]}{\text{d}z} &=& \frac{\left( 1-\frac{\beta}{C_{0}}\right)A}{\dot{V}_{\mathrm{l}}} \left( -\frac{[\text{O}_{2}]}{k_{\mathrm{l}1}[\text{O}_{2}] + k_{\mathrm{l}2}} \frac{(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]} \right.\\ && \left. L_{\mathrm{p}} (1-\exp{[-\kappa c_{\text{DCA}} l_{\text{opt}}]}) + \widetilde{k_{\text{l}} a} \sqrt{u_{\text{g}}^{\mathrm{s}}} ([\text{O}_{2}]^{\infty} - [\text{O}_{2}]) \vphantom{ -\frac{[\text{O}_{2}]}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}} \frac{(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[DHAA]}}\right), \\ \frac{\text{d}x_{\text{O}_{2}}}{\text{d}z} &=& - \frac{RT}{p\dot{V}_{\text{g}}} \left( 1- \frac{\beta}{C_{0}}\right) A (1-{x}_{\text{O}_{2}})\widetilde{k_{\text{l}} a} \sqrt{u_{\text{g}}^{\mathrm{s}}} ([\text{O}_{2}]^{\infty} - [\text{O}_{2}]), \\ \frac{\text{d}\dot{V}_{\text{g}}}{\text{d}z} &=& - \frac{RT}{p}\left( 1- \frac{\beta}{C_{0}}\right) A \widetilde{k_{\text{l}} a} \sqrt{u_{\text{g}}^{\mathrm{s}}} ([\text{O}_{2}]^{\infty} - [\text{O}_{2}]), \end{array} $$
(20)

with initial conditions

$$ \begin{array}{@{}rcl@{}} ([\text{DHAA}], [\text{PO}_{1}], [\text{PO}_{\text{y}}], [\text{PO}_{\text{x}}], [\text{O}_{2}], [\textsf{x}_{\text{O}_{2}}], [\dot{V}_{\text{g}}])^{\top}(0) \\ = ([\text{DHAA}]_{0}, 0, 0, 0, [\text{O}_{2}]^{\infty}, \textsf{x}_{\text{O}_{2},0}, \dot{V}_{\text{g},0})^{\top}. \end{array} $$

The vector of unknown model parameters of the process model, that needs to be identified, is

$$ (\widetilde{k_{\text{l}} a},k_{\mathrm{l}1},k_{\mathrm{l}2},\tilde{k}_{\text{PO}_{1}},\tilde{k}_{\text{PO}_{\text{y}}},k_{\text{PO}_{\text{x}}},l_{\text{opt}})^{\top}. $$
(21)

Identification of the model parameters by Model-based Design of Experiments

Identifying a reliable process model is a challenging problem, particularly in (bio-)chemical engineering where often reaction kinetics are not known a priori. Even if the stoichiometries have been established, the mathematical rate laws might not be readily revealed [40]. For the identification of a reliable mathematical model, a systematic procedure is therefore key [53, 54]. One major tool in this process is the model-based design of experiments (MBDoE). MBDoE facilitates model identification by planning experiments with high informative output under the consideration of the formulated model candidates, thereby reducing development time and cost [55,56,57].

In the study case at hand, we primarily used MBDoE for the enhanced precision of parameter estimates. Here, MBDoE aims at minimizing the covariance matrix of the model parameters, a measure for the quantification of the parametric uncertainties, by maximizing the parameter sensitivities on the measured outputs [58]. Having collected the measurement data of the optimally planned experiment, the parameters of the proposed model candidate(s) were estimated. Parameter estimation was performed using the maximum likelihood approach to obtain a match between model outputs and the experimental data. Next to an evaluation of the model-data fit, the model parameters and their estimates were assessed by checking their identifiability and by the calculation of confidence intervals. Identifiability of parameters ensures that the model parameters can be uniquely determined from the available measurement data [58, 59], and is therefore a necessity for a reliable interpretation of parameter values. We used the profile likelihood approach that yields improved confidence intervals for the model parameters besides conclusions about parameter identifiability [60, 61]. More information about the MBDoE and the profile likelihood approach is outlined in the SI.

Results and Discussion

In the following first part, the experimental data is shown, which was later on used to parameterize the developed process model. Here, the actinometric measurements are discussed, which yielded a relation for the incident volumetric photon flux Lp – a key parameter in the model to disentangle kinetic parameters from reactor-dependent influences. Subsequently, the reaction behaviour of the photooxygenation is analyzed qualitatively on the basis of the experimental data.

In the second part, the experimental data is used to identify the kinetic model parameters and assess the suitability of the previously made assumptions. The parameterized model is finally applied to understand and identify the rate-determining effects in dependence on the reaction conditions offered.

Quantification of the incident volumetric photon flux L p

Relation between L p and the set LED power

The actinometric measurements with ferrioxalate were performed in Taylor flow conditions as the later presented photooxygenation experiments. In Fig. 5a, the obtained actinometer conversions are depicted. The experimental operation window of LED settings and residence time in the irradiated section was limited to a narrow range of 6–12 s and 10–25%LED by physical and technical constraints [38]. Precipitation occurred in all samples obtained at LED settings higher than 25%LED. Therefore, these data were excluded from further analysis. The conversions obtained without precipitation show an expected linear dependence on the residence times.

Fig. 5
figure 5

Results of actinometric measurements at two-phase slug flow conditions: a Actinometer conversion in dependence on set LED power PLED and residence time in the irradiated section of the photoreactor, b Volumetric incident photon absorption determined based on measured actinometer conversion (lopt = 0.8 mm)

Full size image

Based on the obtained actinometer conversion and the known quantum yield of ferrioxalate, the volumetric incident photon flux (Lp) was determined separately for each data point based on Eq. 1. The optical path length was assumed to be equal to the channel diameter of 0.8 mm. The average values for each LED setting are depicted in Fig. 5b.

The incident photon flux shows a strong linear dependence on the LED power at lower set values. The measured incident photon fluxes deviate from that dependence due to the aforementioned observed precipitation during the experiment. The linear behavior is a known property of LEDs and also given in the reference data-sheet of the LED modules applied. Therefore, a linear relation is used to connect the volumetric incident photon flux with the LED power as additional model equation introducing \( \tilde {L}_{\text {p}}\) as proportionality factor,

$$ L_{\mathrm{p}} = \tilde L_{\mathrm{p}} \cdot P_{\text{LED}}. $$
(22)

Relation between L p and the unknown optical path length

The determination of the incident photon flux from actinometric measurements strongly depends on the value set for the optical path length lopt, which either has to be estimated or measured to take partial absorption into account, Eq. 9. In our actinometric data set shown above, the path length was found to be insensitive. That is, for each path length assumed (e.g. 0.8 mm as shown above), values for the incident photon flux and the resulting proportionality factor \( \tilde {L}_{\text {p}}\) could be found, which fit the experimental actinometric data equally well.

The complex irradiation geometry of our applied reactor (Fig. 3), however, also makes it difficult to predict the path length from theoretical considerations due to the combination of a wide emission angle of the LED modules, illumination from two sides, reflection within the photoreactor casing and Taylor flow conditions.

As an alternative, the optical path length can be set as an additional parameter to be estimated based on the experimental data of the photooxygenation of DHAA. A relation between incident photon flux and path length is developed from the actinometric measurements and then used as additional model equation in the analysis of the photooxygenation.

The absorbed and the incident volumetric photon flux are connected by Beer-Lambert law, as shown in Eq. 23. The relation contains two unknown parameters; \(\tilde L_{\mathrm {p}}^{\mathrm {a}}\) as the proportionality factor between the the absorbed volumetric photon flux and the set LED power and \([\overline {\text {Act}}]\). \([\overline {\text {Act}}]\) can be interpreted as an average concentration of the ferrioxalate during irradiation. Both parameters were estimated by first determining \(\tilde {L}_{\text {p}}\) for various assumed lengths of the optical path (as in Fig. 5 for 0.8 mm) from experimental data and then by fitting the exponential expression of Eq. 23 to these obtained values of \(\tilde {L}_{\text {p}}\) (details are given in SI):

$$ \begin{array}{@{}rcl@{}} L_{\mathrm{p}} &=& \frac{L_{\mathrm{p}}^{\mathrm{a}}}{1-e^{- \kappa_{\text{Act}} [\overline{\text{Act}}] l_{\text{opt}}}} = \underbrace{\frac{\tilde L_{\mathrm{p}}^{\mathrm{a}}}{1-e^{- \kappa_{\text{Act}} [\overline{\text{Act}}] l_{\text{opt}}}}}_{\tilde L_{\mathrm{p}}} P_{\text{LED}} , \end{array} $$
(23)
$$ \begin{array}{@{}rcl@{}} \tilde L_{\mathrm{p}} &=& \frac{8.893 \cdot 10^{-5} \frac{\text{mol}}{\mathrm{L s \%LED}}}{1-e^{-23.935 \text{cm}^{-1} \cdot l_{\text{opt}}}}. \end{array} $$
(24)

The parameterized relation in Eq. 24 was used in the model to link the knowledge from the actinometric measurements with the photooxygenation experiments.

Qualitative assessment of the reaction behaviour of the photooxygenation

The main goal of this contribution is to provide a kinetic model for the photooxygenation of dihydroartemisinic acid to the desired intermediate hydroperoxide PO1. In the following, a subset of the experimental data is shown to illustrate qualitative trends of the reaction behavior in Fig. 6.

Fig. 6
figure 6

Behavior of the photooxygenation of dihydroartemisinic acid to the desired hydroperoxide PO1 at varied reaction conditions (incl. initial concentration of DHAA): a Concentration of DHAA, the formed hydroperoxides and the observed reactant recovery in dependence on the superficial residence time b Dependence of PO1 formation on provided light intensity c Effect of varied photosensitizer concentration and gas phase composition at the inlet at constant superficial residence time

Full size image

Due to the applied model-based design of experiments, the kinetics were studied selectively at conditions that assured highest sensitivity of the kinetic parameters to be estimated. That is why the experimental conditions of the data shown in Fig. 6 change between the subplots.

Each data point is the result of a separate experiment in steady-state. The experimental results are compared based on the superficial residence time defined by the initial gas and liquid flow rates:

$$ \begin{array}{@{}rcl@{}} \tau^{\mathrm{s}} = \frac{V_{\mathrm{r}}}{\dot{V}_{\mathrm{l}}+\dot{V}_{\mathrm{g,0}}}. \end{array} $$
(25)

The superficial residence time underestimates the real residence time in the system: Due to O2 consumption, the gas flow rate decreases with the increasing conversion of DHAA. Therefore, the real residence time does not only depend on the initial flow settings but also on the reaction progress. To compare the amount of unknown products formed in the photooxygenation, an additional quantity, the recovery, is introduced, which is defined as the ratio of known components of the reaction mixture and the initially added amount of DHAA:

$$ \begin{array}{@{}rcl@{}} \mathit{Recovery} = \frac{[\text{DHAA}]+[\text{PO}_{1}]+[\text{PO}_{\text{y}}]}{[\text{DHAA}]_{0}} \cdot 100 \%. \end{array} $$
(26)

The photooxygenation of DHAA is a fast reaction reaching full DHAA conversion in less than 5 min residence time in the irradiated section (Fig. 6a). The desired tertiary hydroperoxide PO1 reaches a yield of 85 %, while the secondary hydroperoxides are formed with a yield of 8 %. These obtained numbers are in accordance with previous studies, which observed a yield of PO1 up to 90 % [7, 14] under comparable conditions. The concentration-time-profiles agree in shape with the mixed zero and first reaction order, which was proposed in the model. The recovery of the reactant decreased from 100 % at short residence time to 92 % when full conversion was reached. We assume that this decrease is caused by rearrangement and degradation reactions of the formed hydroperoxides as observed in previous mechanistic studies by Brown et al. [8, 9, 11]. This non-detectable amount of formed products was treated as additional species POx in the model in order to close the overall mass balance.

When the light intensity increases, the reaction accelerates without affecting the final yields (Fig. 6b). This is in correspondence with the proposed reaction network since the incident photon flux affects only the formation of singlet oxygen. The ratio of the reaction rates of PO1 and POx is constant and equal to the ratio of the corresponding rate constants kPO1 and kPOX. The constant recovery in respect to light intensity indicates that the consecutive rearrangement and degradation of PO1 and POx are independent of irradiation.

Based on the model structure, the reaction rate is supposed to increase linearly with the incident photon flux. Doubling the LED power from 50% to 100%, however, results only in an 1.5 fold increase of the effective initial rate PO1 formation (from 0.174 mol/l/min to 0.257 mol/l/min at τs= 0.55 min). That is, at the high irradiation intensities, the proposed linearity is not observed in our experimental data. The effect may result from oxygen mass transfer between gas and liquid phase, which is slower than the high reaction rates under strong irradiation and thus limit the overall observed reaction rate.

In Fig. 6c, the photosensitizer concentration and gas phase composition was varied while the superficial residence time was kept constant. Again both parameters only influence the reaction rate while the total recovery was unaffected. A 3-fold increase of the catalyst concentration yielded a 2-fold increase in PO1 concentration formed. Assuming an optical path length equal to the channel diameter of 0.8 mm, an approx. 3-fold rise in light absorption and, thus, in the reaction rate is expected according to Beer-Lambert law. The lower increase observed in the experiments might indicate that the light passes the reactor on a longer path length resulting in high absorption and thus lower sensitivity on the catalyst concentration. A decrease in O2 content in the gas phase results in approx. 20% lower yield of PO1 at otherwise similar reaction conditions. Based on this data, it cannot be concluded yet if that significant decrease is caused by a lower \({~}^{1}{\text {O}}_{2}\) quantum yield or by slower mass transfer due to reduced equilibrium concentration of oxygen in the liquid phase. For this conclusion, the quantitative analysis based on a parameterized and validated model of the photooxygenation is required.

Identification of the process model parameters and quantitative assessment of the model-data fit

The process model developed to describe the photooxygenation behaviour contains seven unknown parameters to be identified with experimental data, Eq. 21. Two of the parameters, the mass transfer coefficient \(\widetilde {k}_{\text {l}} a\) and the optical path length lopt, are related to the applied reactor setup. The other five parameters are kinetic rate constants, which are independent of the experimental setup.

During the model identification process, a local sensitivity analysis revealed (SI) that the kinetic parameters of the chemical reactions forming the intermediate hydroperoxides, \(\tilde {k}_{{\text {PO}_{1}}}\) and \(\tilde {k}_{\text {PO}_{\text {y}}}\), are heavily correlated with the kl1 parameter of the quantum yield relation for singlet oxygen, Eq. 8. Thus, it becomes impractical to uniquely determine the involved parameters with the measurement information at hand. A potential reduction of the correlation by MBDoE did not predict to significantly disentangle the strong connection between the parameters. One related problem lies in the mathematical structure of the quantum yield relation. Its parameters are theoretically identifiable, but cannot be determined properly if noisy data is utilized, i.e. different parameter sets can explain the outcome equally well [62]. Accordingly, parameter estimation runs showed that physically reasonable values of the quantum yield of singlet oxygen, i.e., values below 2, could not be retrieved. Consequentially, the unknown quantum yield parameters were set to literature values, taken from [27] for DCA in benzene: kl1 = 0.641 and kl2 = 0.0119mol/L.

Hence, five parameters to be estimated were left: The mass transfer coefficient \(\widetilde {k}_{\text {l}} a\), the three chemical kinetic constants \(\tilde {k}_{\text {PO}_{1}}\), \(\tilde {k}_{\text {PO}_{\text {y}}}\) and \(k_{\text {PO}_{\text {x}}}\), and the optical path length lopt. The results of the parameter estimation and of the subsequent quantitative assessment of the derived model parameters and the model-data fit are summarized in Table 2. The measurement error variance estimated from regression statistics (SI) \(\hat \sigma ^{2}\)= 2.73e-4 mol2/L2 is satisfactorily low. Correspondingly, the relative deviation between the predicted and measured concentration of the key intermediate PO1 is 7.09 %. The good model-data fit is visualized in the parity plots in Fig. 7 which show a good match between experimental results and simulated data over the whole range of investigated superficial residence times. Exemplarily, the data points appearing in Fig. 6a are marked in Figs. 7a, b and c accordingly. In contrast to DHAA and PO1, the key chemical species on the route towards artemisinin, the data of POy is less matched because for two reasons. On the one hand, the optimizer tends to favor higher concentrations per definition of the objective function, i.e., the likelihood function. On the other hand, the POy concentrations are closer to zero, where the signal-to-noise ratio is increased.

Fig. 7
figure 7

Match of experimental data with simulated results based on the parametrized process model for all quantities measured at the reactor outlet. The grey scale illustrates the superficial residence time in the photoreactor of each data point. Triangle, diamond and square markers represent data from Fig. 6a. The dashed lines mark 20 % deviations

Full size image
Table 2 Goodness of fit and estimated parameter values and spreads, Eq. 21, for the developed process model, Eqs. 20. The confidence intervals are based on the profile likelihood (SI)
Full size table

To further assess the quality of the identified model, relative deviations of PO1 over four important process parameters, that is, the initial DHAA concentration, the LED light power, the photosensitizer concentration, and the molar fraction of oxygen, were investigated (SI). The results suggest that the existent deviations are mainly caused by measurement noise and errors that inherently occur during the measurement procedure but not by systematic model discrepancy.

Following the profile likelihood approach, all five estimated parameters in the developed process model are identifiable (SI). Next to a coefficient of dispersion (COD) 95 % confidence intervals (CI) for the estimated parameters are stated in Table 2.

It can be noted that the chemical kinetic constants have larger COD s and are, loosely spoken, more uncertain in their estimates than the mass transfer coefficient and the optical path length. On the whole, each of the parameters shows an acceptable spread suggesting that their expected values can be reliably used for further model-based investigation.

The rate constants for the formation of the desired hydroperoxide PO1 and the byproducts were normed, Eq. 6, to ease the parameter estimation process. Based on the known life time of singlet oxygen in toluene (33.2 μ s at -20° [41]) the absolute rate constants of the reactions of DHAA with \({~}^{1}{\text {O}}_{2}\) to the hydroperoxides, Eq. ??, can be obtained:

$$ \begin{array}{@{}rcl@{}} k_{\text{PO}_{1}} &= 2.15 \cdot 10^{5} \text{L mol}^{-1}s^{-1},\\ k_{\text{PO}_{\text{y}}} &= 0.19 \cdot 10^{5} \text{L mol}^{-1}s^{-1}. \end{array} $$

Both values are in the same order of magnitude as rate constants published for other investigated ene-type reactions [33, 63, 64]. The reaction to the desired hydroperoxide is about 10-fold faster than the reaction to the byproducts. This matches with the favored selectivity of PO1 observed in the photooxygenation experiments.

For Taylor flow fluid dynamics and mass transfer in microchannels, there are various relations for the mass transfer coefficient available that vary substantially among each other [65]. In the study case at hand, initial superficial velocities between 120 cm/min and 350 cm/min appear, resulting in volumetric mass transfer coefficients of approximately 12 min− 1 to 20 min− 1. These values lie within the range of kla values predicted from correlations available in the literature [65].

Intuitively, the length of the optical path lopt = 0.178 cm seems to be large at first sight as it is greater than twice the tube diameter of 0.08 cm. In a single circular tube geometry with perpendicular irradiation, the optical path length can be assumed to be between channel diameter d as upper boundary and the ratio A/d as lower boundary depending on the collimation of the incident light [66]. Both boundaries, however, are based on the hypothesis that light enters the tubing from one side and is lost after leaving it. In the considered photoreactor instead, two light sources are installed in a closed box of stainless steel, resulting in reflection of the light beam back to the reactor. Furthermore, as the reactor itself is symmetric (compare with Fig. 3), leaving light beams on one side can re-enter the reactor tubing on the other side. In particular in the tube convolutions around the poles in the reactor box, optical path lengths significantly exceeding twice the tube diameter are very plausible.

In conclusion, the model developed to describe the photooxygenation of DHAA provides a good fit with the experimental data. All model parameters are identifiable and their estimates are in plausible ranges. The required simplification on fluid dynamics and photon transfer, namely the application of the two-fluid model and the neglect of absorption rate distribution, offers a good description of the observed process behavior.

Albeit, we want to emphasize that for a reliable utilization and interpretation of the identified process model the following aspects need to be taken into account. Neglecting the distribution of the local volumetric rate of photon absorption is a strong simplification affecting the reaction system on various levels. In particular, a gradient in the absorbed photon flux will cause a non-uniform distribution of the rate of singlet oxygen production within the liquid slug, resulting in a potential diffusion limitation of the overall reaction rate. The absorbed photon flux itself is influenced by the gas holdup and photosensitizer concentration. Both quantities decrease with reaction time due to oxygen consumption and photobleaching and therefore affect the absorbed photon flux. We also want to point to the fact that a reliable description of the two-phase flow is essential. A global sensitivity analysis of important model parameters (details in SI) showed, that the distribution parameter C0, that links the relative motion of the different phases, Eq. 16, is highly sensitive. A variation of C0 in the model induces a considerable change in the simulated PO1 concentration. Lastly, the identified model and all parameters are only valid for a temperature of -20 °C. Studying the complex influence of temperature on the reaction system including the mass transfer and flow conditions is beyond the scope of this paper and a task for future studies.

Exploitation of the process model to analyse different operating regimes

The identified and fully-parameterized model can now be used to understand the process behavior and identify optimal operation windows. In the following, three characteristic operating situations are illustrated that differ in the cause that limits or partially limits the process dynamics: light irradiance, substrate DHAA or mass transfer. The possible fourth operating regime – the kinetically controlled domain without any other limitation – does not occur under the investigated conditions.

In Figs. 8 and 9, the dynamic behavior of the system’s key quantities, product concentrations, gas flow rate and gas phase composition are drawn over the reactor length. The thin vertical line marks the exit of the photoreactor and thus the end of light irradiance. The discontinuities in the curves at the reactor exit are induced by a temperature jump from reactor to ambient temperature. Experimental data are plotted at the sampling position downstream to the photoreactor exit.

Fig. 8
figure 8

Propagation of concentrations, oxygen molar fraction and gas flow along the reactor coordinate showing no mass transfer limitations (conditions: [DHAA]0 = 0.23 mol l− 1, [DCA] = 0.85 mmol l− 1, PLED = 100% LED, x\(_{\text {O}_{2},0}\)= 1). The thin vertical line marks the reactor outlet

Full size image
Fig. 9
figure 9

Propagation of concentrations, oxygen molar fraction and gas flow along the reactor coordinate showing mass transfer limitations (conditions: [DHAA]0 = 0.48 mol l− 1, [DCA] = 0.60 mmol l− 1, PLED = 100% LED, x\(_{\text {O}_{2},0}\)= 0.51). The thin vertical line marks the reactor outlet

Full size image

In the first case example, the gas phase consists solely of oxygen, as can be observed in Fig. 8b. The volumetric gas flow decreases along the reaction line in the photoreactor since oxygen is consumed in the liquid phase due to the chemical reactions and continuously supplied from the gas phase, Fig. 8b. The negative slope of the PO1 concentration curve after reaching its maximum concentration, Fig. 8a, is owed to the consecutive loss reactions, Eq. 2, that also continue to go on downstream of the reactor in contrast to the photo-induced reactions. The further discontinuity downstream leading to an even higher negative slope is caused by a slow down of the reaction medium due to a diameter jump of the tubing. Noteworthy is the behaviour of the dissolved oxygen in Fig. 8b. The dissolved oxygen is rapidly consumed at the inlet of the photoreactor as reaction rates are large in the beginning, see Fig. 8a, but is recovered with decreasing reaction rate values. Obviously, mass transfer does not substantially hinder the process dynamics. In contrast, both the light-limiting and the substrate-limiting regime can be observed in Fig. 8a. Here, a pseudo-inflection point might be determined that describes the transition between the two regimes that are often observed in photoredox catalysis [21]. At the inflection point, the reaction switches from a pseudo-zero-order reaction with the reaction rate at its maximum to a first-order reaction. Mathematically, the inflection point is defined as the half-maximum kinetic reaction rate. Accordingly, with \(\frac {1}{2} \overset {!}{=} r_{\text {PO}} = r_{\text {PO}_{1}} + r_{\text {PO}_{\text {y}}}\), Eq. ??, the light-limiting regime is controlled by

$$ (\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[\text{DHAA}] \gg 1:\quad r_{\text{PO}} = {{\varPhi}}_{{~}^{1}{\text{O}}_{2}} L_{\mathrm{p}}^{\mathrm{a}} = r_{\text{PO}}^{\max}, $$
(27)

and the substrate-limited regime by

$$ (\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[\text{DHAA}] \ll 1:\quad r_{\text{PO}} = {{\varPhi}}_{{~}^{1}{\text{O}}_{2}} L_{\mathrm{p}}^{\mathrm{a}} (\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[\text{DHAA}]. $$
(28)

In this study, the inflection point is therefore at [DHAA] ≈ 0.129mol/L. In the DHAA graph in Fig. 8a this inflection point is passed shortly beyond the intersection between the DHAA and the PO1 curve. To the left of it, it follows zero-order kinetics, and to the right of the inflection point, it approaches first order kinetics.

A complementary process characteristic is shown in Fig. 9. In this case, the gas phase consists of both oxygen and nitrogen; see the molar concentration of oxygen in Fig. 9b. From the curve of dissolved oxygen in Fig. 9b, it readily can be observed that the system quickly runs into mass transfer limitations. The level of dissolved oxygen settles down to an equilibrium stage that continuously decreases as the molar fraction of oxygen in the gas phase drops and therefore correspondingly the solubility limit of oxygen that is determined by Henry’s law. Note that despite the elevated temperature beyond the photoreactor, the dissolved oxygen concentration does not reach again the initial dissolved oxygen concentration because of the decreased molar fraction of oxygen. Along the whole reactor line, the process runs above the inflection point, i.e. above [DHAA] ≈ 0.129 mol/L, see Fig. 9a. This implicates that the DHAA curve in the same figure follows pseudo-zero-order kinetics. The additional bending of the actual straight line is caused by the low availability of oxygen in the liquid phase that affects the quantum yield of singlet oxygen, Eq. 8, and reduces the maximum reaction rate, Eq. 27. Thus, here, the process is partially limited by mass transfer, i.e. the mass transfer rate is approximately equal to the rate of the bulk kinetics, preventing a more efficient conversion of DHAA.

Identification of mass transfer limited regimes for the photooxygenation of dihydroartemisinic acid

The analysis for the process behavior so far was linked to the applied reactor setup. The identified kinetic constants for the photooxygenation can also be used to predict suitable operation regimes for other process settings to prevent that mass transfer of oxygen limits the overall reaction rate. Such a classification can be stated with the Hatta number. Based on the two-film theory, the Hatta number relates the rate of chemical reaction in the liquid phase to the diffusion rate across the phase boundary [67]. The higher the Hatta number, the faster is the reaction in comparison to diffusion, which causes the chemical reaction to take place only at the phase boundary. Critical Hatta values are

$$ \begin{array}{@{}rcl@{}} \textit{Ha} &\geq& 3,~~~~~\text{strong mass transfer limitation},\\ \textit{Ha} &\leq& 0.3, ~~\text{kinetic regime, no limitation by mass transfer}. \end{array} $$

In the study case at hand, the Hatta number [68] is defined as (SI)

$$ Ha = \frac{1}{k_{\text{l}}} \sqrt{D_{\text{O}_{2}} L_{\mathrm{p}}^{\mathrm{a}} \frac{1}{k_{\mathrm{l}1} [\text{O}_{2}] + k_{\mathrm{l}2}}\frac{(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[\text{DHAA}]}{1+(\tilde{k}_{\text{PO}_{1}}+\tilde{k}_{\text{PO}_{\text{y}}})[\text{DHAA}]}}. $$
(29)

The diffusion coefficient of oxygen in toluene may be taken from [69] and has a value of 2.4860e− 09 m2 s− 1 at − 20°C. The limits of the Hatta regimes are drawn as contours in Fig. 10.

Fig. 10
figure 10

Prediction of mass transfer limited regimes for the photooxygenation of DHAA. The Hatta number is given in dependence on the provided volumetric rate of photon absorption Lp and the mass transfer coefficent for different O2 concentrations (contour lines, in mol L− 1) and for DHAA = 0.5 mol L− 1. The grey rectangle approximately covers the experimental space explored in this article

Full size image

Generally speaking, with decreasing DHAA concentrations all contour lines move towards the ordinate. As observed in the previous section, the conducted experiments, visualized as the grey rectangle, lie around the lower Hatta limit where behaviors from dynamics partially limited by mass transfer to dynamics not limited by mass transfer appear.

Conclusion

In this study we provide a mechanistic kinetic model for the photooxygenation of dihydroartemisinic acid – the important initial step in the partial synthesis to artemisinin. The experimental study on the reaction kinetics was conducted in a continuous flow photoreactor utilizing Taylor flow. The reaction kinetics are combined with a simplified process model taking photon and mass transfer into account. To characterize the light input of the reactor, the photooxygenation experiments were complemented by actinometric measurements yielding a relation between the incident photon flux and the unknown optical path length, which was integrated in the process model.

The model achieves a good fit between the model outputs and the experimental results from steady-state experiments for a wide range of different critical process parameters. Therefore, the made assumptions and the simplifications, including the two-fluid-model provide a suitable description for the main process characteristics. Nevertheless, assuming a spatially independent rate of photon absorption within the reactor is a strong simplification of the reaction system applied, considering its geometrical complexity and the large value obtained for the average path length. Thus, extending the model by more detailed descriptions of the photon transport inside the reactor as well as of the fluid dynamics might improve the predictability of the model.

By analyzing the process behavior, different regimes of operation were identified where the process is limited by either absorbed photon flux, substrate concentration or mass transfer. Due to is potential to describe the main photooxygenation characteristics, the developed model is seen as an essential building block for future investigations on the partial synthesis of arteminsinin. It provides a good starting point for kinetic studies of the subsequent acid-catalyzed reaction sequence finally yielding artemisinin. The model can be used also as a valuable building block in optimizing the whole process chain from extraction or fermentation to artemisinin purification in the end.