Bayes Factors for Mixed Models

Abstract

Although Bayesian linear mixed effects models are increasingly popular for analysis of within-subject designs in psychology and other fields, there remains considerable ambiguity on the most appropriate Bayes factor hypothesis test to quantify the degree to which the data support the presence or absence of an experimental effect. Specifically, different choices for both the null model and the alternative model are possible, and each choice constitutes a different definition of an effect resulting in a different test outcome. We outline the common approaches and focus on the impact of aggregation, the effect of measurement error, the choice of prior distribution, and the detection of interactions. For concreteness, three example scenarios showcase how seemingly innocuous choices can lead to dramatic differences in statistical evidence. We hope this work will facilitate a more explicit discussion about best practices in Bayes factor hypothesis testing in mixed models.

In a typical response time experiment, multiple participants complete multiple trials in multiple conditions. For example, in a lexical decision task (Meyer & Schvaneveldt, 1971), 30 participants may be instructed to decide as quickly and accurately as possible whether or not 100 individually presented letter strings are words (e.g., FISH) or nonwords (e.g., DRAPA). A possible experimental manipulation may concern the type of motor effector — on half of the trials participants have to press the response buttons with their thumbs, and on the other half they have to use their index fingers.

In such two-condition within-participant designs, researchers are generally interested in the effect of the experimental manipulation. As a first step, researchers often address the question of whether or not the manipulation may be said to have had an effect, for instance, whether or not response times (RTs) differ when people respond with their thumbs rather than with their index fingers.¹ Several statistical methods are available to test for such a difference between conditions and the choice among them cannot be based on statistical considerations alone—each of these approaches instantiates a different interpretation of the main question of interest.

The oldest and most common analysis approach is to conduct a repeated measures (RM) analysis of variance (ANOVA), which in the case of two conditions is equivalent to a paired-samples t-test. In the scenario above, participants’ RTs for individual trials are first averaged within each condition, resulting in two average RTs per participant, one for each condition. We term this averaging process aggregation. Following aggregation, participants’ average RTs are then subjected to a one-way RM ANOVA.

This method accounts for the correlation between the averaged observations that is caused by some participants generally being faster or slower than others (i.e., the presence of baseline differences or random intercepts). This is in contrast to a between participants ANOVA, which is not designed to account for correlated observations. Nonetheless, both types of ANOVA have in common that they are applied to observations averaged across multiple trials. Aggregating individual response times loses information and limits the questions that can be addressed. For example, aggregated RM ANOVA cannot be used to assess whether the experimental manipulation affects all participants alike, or whether the effect of the manipulation differs per participant.

In contrast, mixed effects models (also referred to as hierarchical or multilevel models) make use of the full (i.e., unaggregated) data set. These models typically account for the nested data structure by modelling baseline differences in general response speed across participants (as in RM ANOVA) as well as differences in the magnitude of the condition effect across participants (i.e., random slopes). By modelling individual RTs, mixed effects models enable researchers to ask more specific questions. As in RM ANOVA, mixed effects models estimate the average effect of condition (i.e., the fixed effect), but additionally they can be used to examine the extent to which the effect of condition differs between participants (i.e., the random effect).

The example given here can be generalized in two ways. First, while condition is a categorical variable, the same framework can be applied to continuous predictor variables. Second, the random effects grouping factor (in the example above, “participant” is the grouping factor) can be any categorical variable in the design for which there are multiple observations. For instance, instead of modelling differences between individual participants, we could model a difference in the effect of the manipulation for different groups of people (e.g., two different geographical regions). Furthermore, in the case of multiple grouping factors, the random effects can either be nested or crossed. In the case of nested random effects, not all levels of one grouping factor are measured for the other grouping factor. For example, if both “participant” and “region” are used as grouping factors, the structure is nested, because each participant will be either from one region or the other. In the case of crossed random effects, all levels of one grouping factor are measured for the other grouping factor. For example, if both “participant” and “item” are used as grouping factors, the structure is crossed when all participants complete all items, because for each participant, there are observations for each item (for more examples, see Baayen et al., 2008; Quené & Van den Bergh 2008; Singmann & Kellen, 2019).

Although alluded to by (Fisher, 1935) and (Yates, 1935), the first explicit definition of random intercepts was given by Jackson (1939), who proposed to account for individual differences in intelligence in order to more accurately assess the reliability of mental tests.

Since their introduction, mixed effects models have seen an increase in statistical development (e.g., Scheffe 1956; Kempthorne 1975; Efron and Morris 1977; Nelder 1977; Lindstrom & Bates 1990), and arguably rank among the most important statistical ideas of the last 50 years (Gelman & Vehtari, 2020). The application of mixed effects models has been particularly stimulated by software implementations (e.g., lme4, Bates et al. (2015b); nlme, Pinheiro and Bates (2000) and Pinheiro et al. (2020); and afex, Singmann et al., 2020) and tutorial papers (e.g., Baayen et al., 2008; Judd et al., 2012, 2017; Singmann and Kellen 2019).

Here we focus on Bayesian inference for mixed effects models, and specifically on Bayes factor hypothesis tests (e.g., Rouder et al., 2012; Clyde et al., 2011).² Despite the availability of Bayesian tutorials (Shiffrin et al., 2008; Rouder et al., 2013; Sorensen et al., 2016) and software alternatives (e.g., Morey & Rouder 2018; Carpenter et al., 2017; Goodrich et al., 2020; Bürkner 2017; Thalmann & Niklaus2018; JASP Team 2020), there remains a lack of clarity and consensus about how to best conduct Bayesian model comparison when considering mixed effects.

Examining the effect of a manipulation requires the specification of both a null model, which assumes no effect of the manipulation, and an alternative model. In the frequentist framework, a well-cited recommendation for the specification of the alternative mixed effects model of the full data is to specify a “maximal” model (i.e., the model that includes all fixed and random effects justified by the study design). In particular, failure to include random slopes can inflate Type 1 or Type 2 error probabilities (Bates et al., 2015a; Matuschek et al., 2017, but see Barr et al., 2013b; Berkhof & Kampen 2004; Schielzeth & Forstmeier 2008; Heisig & Schaeffer 2019). Despite the fact that there are multiple suitable null models that the maximal model can be compared to, the appropriate specification of the null model is much less discussed. This is problematic because the choice of the null model (just like the alternative model) defines the question we ask about the condition effect.

Several decisions need to be made when testing for the effect of a manipulation in an experimental within-participant designs: Which model comparisons are both suitable and sensible, whether or not to aggregate, how to quantify effects, and how to set prior distributions. The aim of the current paper is to list the available options and demonstrate their impact on inference. We hope our exposition provides a common starting ground for a discussion among experts in the field of Bayes factor model comparison. We further hope that this discussion will foster the development of a much needed set of guiding principles for the applied researcher who ventures into the realm of Bayesian mixed models.

The outline of this paper is as follows. We start by defining the possible models that can be compared when random effects are considered. Then, we present a simple synthetic data set to illustrate the differences in model comparisons, as well as the effect of aggregating the data. The second example demonstrates how the different mixed model comparisons behave when analyzing data sets with either few accurate measurements or many noisy measurements. As a third example, we present a real-life data set that underscores these modelling questions, and highlights the added complexity of having multiple independent variables of interest. Table 1 below provides the main research questions that are explored, including the relevant examples for each question.

Table 1 Summary of the different modeling questions faced when conducting a Bayes factor mixed model comparison

The Candidate Models

In this section we define the candidate models for a one-factorial design. Suppose I participants each observe M trials in each of J conditions. For this research scenario, there are the following six candidate models (Fig. 1), each with different theoretical underpinnings:

• Model 1. Intercept (μ) only, no fixed effect of condition and no random effects for participants. With subscript i for the i^th participant, j for the j^th condition, and m for the m^th trial, the model for the observed values Y_ijm can be written as a function of the grand mean μ and the error variance $\sigma _{\epsilon }^{2}$. We give this definition below, and then expand it for each subsequent model:

  $$ Y_{ijm} \sim \mathrm{N}(\mu,\sigma_{\epsilon}^{2}). $$

  (1)

• Model 2. Fixed effect ν of condition, but no random effects for participants. The term x_j is a design element that encodes condition (i.e., $x_{1}= -\frac {1}{2}$, $x_{2} = \frac {1}{2}$ if J = 2), which ensures the sums-to-zero constraint for the fixed effects (Rouder et al., 2012).³ The resulting model can be written as follows:

  $$ Y_{ijm} \sim \mathrm{N}(\mu+x_{j}\nu,\sigma_{\epsilon}^{2}). $$

  (2)

• Model 3. No fixed effect of condition, but random intercepts α_i specific to the i th participant. In contrast to Models 1 and 2, this model includes baseline differences. The random intercepts are distributed normally around the grand mean μ, with standard deviation σ_α. Random intercepts can also be understood as a main effect of participant. When σ_α is 0, Model (3) reduces to Model (1). In one-way RM ANOVA, this model is typically used as the null model. Since this model includes neither fixed nor random effect of condition, we refer to this model as the Strict null. The model can be written as follows:

  $$ \begin{aligned} Y_{ijm} &\sim \mathrm{N}(\alpha_{i},\sigma_{\epsilon}^{2}),\\ \alpha_{i} &\sim \mathrm{N}(\mu,\sigma_{\alpha}^{2}). \end{aligned} $$

  (3)

• Model 4. Fixed effect ν of condition and random intercepts α_i for participants. In one-way RM ANOVA, this model is used as the alternative model. The model can be written as follows:

  $$ \begin{aligned} Y_{ijm} &\sim \mathrm{N}(\alpha_{i}+x_{j}\nu,\sigma_{\epsilon}^{2}),\\ \alpha_{i} &\sim \mathrm{N}(\mu,\sigma_{\alpha}^{2}). \end{aligned} $$

  (4)

• Model 5. No fixed effect, but random intercepts α_i and slopes θ_i specific to the i th participant. The random slopes are distributed normally around 0, with standard deviation σ_θ. In general, random slopes can also be understood as an interaction effect between condition and participant (Nelder, 1977). When σ_θ is 0, Model (5) reduces to Model (3). In essence, this model postulates that there is an effect of condition in each participant, but that it varies across participants in a perfectly balanced way, such that the average effect is 0 across participants. We therefore refer to this model as the Balanced null. The model can be written as follows:

  $$ \begin{aligned} Y_{ijm} &\sim \mathrm{N}(\alpha_{i}+x_{j}\theta_{i},\sigma_{\epsilon}^{2})\\ \alpha_{i} &\sim \mathrm{N}(\mu,\sigma_{\alpha}^{2})\\ \theta_{i} &\sim \mathrm{N}(0,\sigma_{\theta}^{2}) \end{aligned} $$

  (5)

• Model 6. The full model, with fixed effect ν of condition, random intercepts α_i, and random slopes θ_i for participants. All previous models are restrictions of this model. For mixed models in the frequentist framework, this is the often-recommended alternative model (Barr, 2013a). The model can be written as follows:

  $$ \begin{aligned} Y_{ijm} &\sim \mathrm{N}(\alpha_{i}+x_{j}\theta_{i},\sigma_{\epsilon}^{2})\\ \alpha_{i} &\sim \mathrm{N}(\mu,\sigma_{\alpha}^{2})\\ \theta_{i} &\sim \mathrm{N}(\nu,\sigma_{\theta}^{2}) \end{aligned} $$

  (6)

We do not entertain all possible combinations of parameters (e.g., models with random slopes but no random intercepts, or models without a grand mean), because we consider them both theoretically and statistically inappropriate in the current mixed modeling setting. Additionally, in the remainder of this article we do not discuss explicitly modeling the correlation between the random slopes and random intercepts. Failure to account for correlated random effects can lead to misleading results, for instance in the context of ceiling effects, where participants with high intercepts will be inherently limited in their effect.

For all models, $\sigma _{\epsilon }^{2}$ denotes the error variance, which is the variance in the data left unexplained by the model. The explained variance of a mixed model is the sum of the variance induced by the fixed effect, the variance of the random intercepts $\sigma _{\alpha }^{2}$, and the variance of the random slopes $\sigma _{\theta }^{2}$ (Rights & Sterba, 2019). Together the explained variance and $\sigma _{\epsilon }^{2}$ make up the total variance of the data y. Random effects are a source of systematic variation that, if unaccounted for in the model, may be incorrectly attributed to the explained variance of a fixed effect, or the error variance, leading to conclusions about the fixed effect that are either overly permissive, or overly conservative, respectively (Barr et al., 2013b).

Fig. 1

A graphical representation of the postulations for the six models, in the case where I = 3 participants each observe M = 1 trial in each of J = 2 conditions. The models in the left column postulate no fixed effect of condition, whereas the models in the right column postulate a fixed effect of condition. The models in the top row postulate no random effects, the models in the middle row postulate random intercepts only, and the models in the bottom row postulate random intercepts and random slopes. The arrows indicate the nested structure of these six models, where each model on the left is nested in the model on the right, and each model is nested in the model that is located below

The Model Comparisons

With the series of six models defined, we can use model comparisons to assess whether or not there is an effect of condition. Between the six models under consideration we can make $\frac {n (n-1)}{2} = 15$ model comparisons that can be applied to either the full data or the aggregated data. The models differ from each other with respect to the three parameters of interest: ν,σ_α, and σ_θ. The appropriate model comparison depends on the research question at hand, since each comparison answers a different question. Specifically, the combined choice of the null and alternative model constitute different definitions of what it means for a manipulation to have an effect: Model (4) posits that the fixed effect manifests in every participant, whereas Model (6) posits that the fixed effect is the average of participant-specific effects that vary in magnitude. Below, we consider three model comparisons that we consider to be primarily relevant to the current scenario.

We start by outlining the popular RM ANOVA procedure, which compares Model (3) to Model (4). This procedure uses one observation per participant and per level of each factor (i.e., M = 1). In cases where M > 1, the observations are typically aggregated first, even though aggregation is not strictly required.⁴ The aggregation discards information about the distribution of each participants’ observations within each condition. As a consequence, it becomes impossible to distinguish between systematic random slope variance and random error variance (i.e., aggregation confounds the random slopes variance with the residual variance). However, a benefit of aggregation is that it greatly reduces the impact of random slopes in the inference for a fixed effect and therefore eliminates the inflation of Type 1 and Type 2 error rates that ignoring random slopes typically entails (see Examples 1 & 2 for a demonstration). Comparing Model (3) to Model (4) on the full data, on the other hand, does suffer from this inflation, and we therefore do not consider it appropriate. The comparison of Model (3) to Model (4) on the full data might be applicable under the strict assumption that there are no random slopes. In the remainder of this manuscript, we focus on scenarios where random slopes cannot be excluded a priori.

We now outline the comparisons of models that contain random slopes. In the frequentist framework, it is often recommended to use the maximal mixed model justified by the design (Barr, 2013a). The presence of the fixed effect ν is typically tested by means of a t- or F-test. This procedure implicitly compares the full model (Model (6)) to the full model without the fixed effect (Model (5)).

Since random slopes are in fact an interaction effect between the fixed effect of condition and the random effect of participant, specifying a model that includes random slopes without the corresponding fixed effect (i.e., Model (5)) can be seen as conceptually problematic. Specifically, Rouder et al. (2016) argues that a model containing an interaction effect without the main effect is only plausible when the exact levels of each factor are picked such that the true main effects perfectly cancel, which in most practical applications seems implausible. If we accept this argument while still accounting for random slopes, the implied model comparison is between the full model (Model (6)) and the model with only the random intercepts (Model (3)). However, this model comparison comes with its own set of challenges: The increase in model validity coincides with a loss of diagnostic specificity: when Model (6) outperforms Model (3), we can only conclude that the data offer support for the presence of a fixed effect, random effect, or both a fixed and random effect.

Note that, for aggregated data, Models (5) and (6) are not identified.⁵ We therefore only consider model comparisons involving Models (5) and (6) when applied to the full data.

Thus, based on different considerations, we identify three possible model comparisons, where the last two comparisons are named after the null model that is being used:

• 1. The RM ANOVA comparison: Model (3) vs Model (4) using the aggregated data

• 2. The Balanced null comparison: Model (5) vs Model (6) using the full data

• 3. The strict null comparison: Model (3) vs Model (6) using the full data

Examples

Although all three comparisons outlined in the previous section can be viable options in an applied setting, they may lead to dramatically different conclusions. In order to illustrate the different behaviors of the three comparisons, we now discuss three data examples. We follow each example with several concrete questions that we hope will serve as useful starting points for discussion.

All Bayes factors presented below are computed using the BayesFactor package (Morey and Rouder, 2018), using the default settings for the multivariate Cauchy prior distributions (scale set to 0.5 and 1 for fixed effects and random effects, respectively). The BayesFactor package specifies Jeffreys’s prior on the grand mean and error variance (i.e., $f(\mu , \sigma ^{2}) \propto \frac {1}{\sigma ^{2}}$) and does not explicitly model correlations between random slopes and intercepts. Each example also includes a reference to the analysis code in the Online Supplementary Material.

Example 1: The Effect of Aggregation

We start with a relatively simple scenario, where I = 20 participants complete M = 15 trials in each of J = 2 conditions for a total of 600 observations.⁶ The purpose of this example is to illustrate the effect of random slopes on the different model comparisons, and how each comparison reacts to the process of aggregation. Figure 2 shows both the full data and the aggregated data, where each color corresponds to a different participant. The data were simulated with a medium fixed effect (ν = 0.5), random intercepts ($\sigma _{\alpha }^{2} = 0.5$), and random slopes ($\sigma _{\theta }^{2} = 1$). The difference between the top-left and top-right panels clearly underscores the process of aggregating, where a lot of information is discarded. The random slopes are evidenced by the different orientations of the lines in the plots in the bottom row: some participants exhibit an increase from condition 1 to condition 2, while for other participants this effect is reversed. To further demonstrate the effect of aggregation, we present the results for all three comparisons, for both the full and aggregated data.

Fig. 2

Synthetic data for Example 1: the effect of aggregation. The top-left panel presents the full data set, and the top-right panel the aggregated data, where the average value is taken per participant, per condition. The different point colors correspond to different participants. The bottom row presents the full data for five example participants, including their condition means. Some participants display an increase as a result of the manipulation, whereas other participants display a decrease. Note that the overall and participant-specific condition means are exactly the same for both versions of the data

The different model comparisons yield widely different Bayes factors. For comparison purposes we report the natural logarithm of the Bayes factor throughout this manuscript. When $\log \left (\text {BF}_{A,N}\right ) > 0$, Model A is preferred; when $\log \left (\text {BF}_{A,N}\right ) < 0$, Model N is preferred. Note that $\log \left (\text {BF}_{A,N}\right ) = 3$ corresponds to $\left (\text {BF}_{A,N}\right ) \approx 20$. First, consider the results for the full data set:

• 1. The RM ANOVA comparison: $\log \left (\text {BF}_{4,3}\right ) = 10.81$

• 2. The Balanced null comparison: $\log \left (\text {BF}_{6,5}\right ) = 0.04$

• 3. The strict null comparison: $\log \left (\text {BF}_{6,3}\right ) = 65.5$

The RM ANOVA comparison on the full data highlights why it is important to include random slopes whenever possible. The true difference between the condition means is modest, and so is the sample size — yet this model comparison yields overwhelming evidence in favor of a fixed effect of condition, a result caused by the presence and pronounced influence of the random slopes. This behavior aligns with the inflation of Type 1 error probabilities in the frequentist framework as demonstrated by Barr et al. (2013b), who therefore advised against performing the RM ANOVA comparison on the full data. Since the Balanced null comparison controls for random slopes by including the random slopes term in both models, it does not suffer from the overconfidence displayed in the RM ANOVA comparison. The Strick null comparison yields extreme evidence in favor of Model (6), but based on this comparison alone it is impossible to conclude whether this evidence is due to the random slopes, the fixed effect, or both.

Now, consider the results for the aggregated data:

• 1. The RM ANOVA comparison: $\log \text {BF}_{4,3} = 0.2$

• 2. The Balanced null comparison: $\log \text {BF}_{6,5} = 0.16$

• 3. The strict null comparison: $\log \text {BF}_{6,3} = -0.21$

For the two comparisons where only one or none of the models include a random slope (i.e., the Strict null comparison and the RM ANOVA comparison, respectively), aggregation greatly impacts the Bayes factor. For both comparisons, the previously overwhelming Bayes factor plummets to around 0, leaving it undecided about which model best predicted the data. This demonstrates that aggregation eliminates the presence of random slopes: for the Strick null comparison, there is no longer any evidence for the alternative model, and for the RM ANOVA comparison there is no longer the inflation of the evidence in favor of a fixed effect.

In contrast, the Balanced null comparison appears relatively stable and is barely in favor of Model (6) in both cases, since the two rival models both include the random slopes. However, we should stress that conducting the Balanced null and Strick null comparisons on aggregated data is unorthodox (i.e., the random slopes estimates are entirely informed by the prior distribution), and that we present these two Bayes factors merely as an illustration.

Taken together, these results suggest that there are two valid methods to test for the presence of a fixed effect, and only the fixed effect, of condition in the presence of random slopes: either performing the Balanced null comparison on the full data, or performing the RM ANOVA comparison on the aggregated data. In order to avoid the demonstrated inflation of the fixed effect when performing the RM ANOVA comparison on the full data, we therefore only consider the this comparison for the aggregated data and not the full data in the remainder of this manuscript.

The considerations above motivate the following questions:

• 1. What are the relevant model comparisons for a one-factorial design?

  • (a) When is aggregation an appropriate procedure?

• 2. Should more models be considered than the ones described here?

• 3. If strictly interested in the fixed effect only, when should the RM ANOVA comparison be used instead of the Balanced null comparison?

Example 2: The Effect of Measurement Error

For the second example, we again consider RTs of I = 20 participants in J = 2 conditions. However, the measurements are done with an instrument that can either measure quickly but inaccurately, or measure accurately but slowly. Thus, there is a trade-off between the measurement error and the number of trials that can be measured in the experiment. If this trade-off is perfectly balanced (i.e., the observed condition means, observed participant means within each condition, and the within-participant standard errors of the condition means are identical) does it matter which setting we choose? In other words, can a noisy measurement instrument be compensated for by collecting many data points per participant? The purpose of this example is to demonstrate how the different model comparisons behave as both the measurement error and number of trials decrease.

In order to implement the trade-off between number of trials and measurement error, we can start with the data set that has 100 trials per participant, per condition. Then, the average RT can be taken of every 10 trials a participant completes. This results in 10 scores per participant, per condition. For both of these data sets, the participant means for each condition and the within-participant standard errors for the fixed effect of condition in a hierarchical model are identical. The difference between these data sets lies in the trial level variance (i.e., the residual variance). Multiple data sets can be created this way by using different numbers of trials to average across. Doing so illustrates how the different model comparisons develop as the number of trials decreases, but the accuracy of those measurements increases. When the number of averages equals 100, the full data is used; when the number of averages equals 1, we obtain the fully aggregated data set. We also create intermediate data sets by taking 50, 10, 5, and 2 averages per participant, per condition. Since the RM ANOVA comparison is performed on the aggregated data and would remain identical, we consider only the Balanced null and Strick null comparisons for these different versions of the data.

Figure 3 shows how each Bayes factor changes as the number of trials decreases and the accuracy of each individual trial increases. The three panels correspond to three different models that generated the data. In the first panel, data were simulated under the model without a fixed effect or random slopes (i.e., Model (3)). In the second panel, data were simulated for a fixed effect only (i.e., Model (4)). In the third panel, data were simulated under a fixed effect and random slopes (i.e., Model (6)). The code for the data generation and analysis is available at https://osf.io/jsgm3/.

Fig. 3

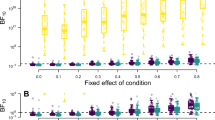
Bayes factors for Example 2 across the various comparisons, for different levels of aggregation. The y-axis shows $\log (\text {BF}_{A, N})$, where A refers to the alternative model, and N refers to the null model of that specific comparison. The lower x-axis denotes how many averages are taken; 100 indicates the use of the full data, and 1 indicates the use of the aggregated data. The upper x-axis denote the measurement error, which decreases as the number of trials decreases. The Strick null comparison is highly influenced by the presence or absence of random slopes, although this sensitivity dramatically decreases as the number of trials decreases. The Balanced null comparison remains relatively stable around values of − 1.5 and 5 in the top and bottom panels, respectively

The effect of decreasing the number of trials in the data is the most pronounced in the strict null comparison, where the log Bayes factor gets less decisive (i.e, closer to 0) as the data set goes towards full aggregation in all three settings. As was illustrated in Example 1, the process of aggregation confounds the random slope variance with residual variance. This results in a less decisive Bayes factor for the Strick null comparison, as only one of the two models being compared includes the random slopes term.

In the top panel, the data were generated under the null model of the strict null comparison, and in the bottom panel the data were generated under the alternative model of that comparison. For these settings, it is not surprising that those models receive the most support in their favor, although the magnitudes of the Bayes factors seem too extreme in light of the relatively low sample sizes.

Surprisingly, the middle panel still depicts overwhelming evidence in favor of the alternative model (i.e., model 6), even though the data generating model did not include random effects. The Balanced null comparison in the middle panel also depicts evidence in favor of model 6, but to a much lesser extent than the Strick null comparison. Since both comparisons have the same alternative model, this difference in behavior is due to the null model. It seems that the null model in the Balanced null comparison (i.e., model 5) is able to model the data better than the null model in the Strick null comparison (i.e., model 3). This suggests that a random slopes term can, to some degree, account for a fixed effect in the data. Moreover, by definition, adding a random effect inherently increases a models robustness to the added variance induced by extreme values in the tails of the distribution.

The Balanced null comparison is relatively stable in the top and bottom panels, which confirms the balance between the number of trials and their accuracy. Since this comparison is between two models that both contain the random slopes factor, these Bayes factors do not reflect the effect of averaging on the random slope variance. Combined with the results from Section 1, this suggests that the process of aggregation mainly affects those model comparisons where only one of the models under consideration includes random slopes. However, the Balanced null comparison is not entirely stable across the different levels of averaging.

We suspect that the (relatively minor) instability of the Balanced null comparison is largely due to a component of Bayesian mixed modeling that we have not addressed so far: the prior distribution. Until now, we have used the default settings for the scale settings of the multivariate Cauchy prior distributions, which are 0.5 and 1 for the fixed effects and random effects, respectively. The widths of these distributions reflect which standardized effect sizes are to be expected under each model. The standardization of the effect sizes is influenced by the measurement error, since observing the same mean difference between conditions, but with a smaller measurement error, results in a larger effect size. Thus, the prior distribution ought to reflect information about the expected measurement error: when this error is small, we can expect larger effect sizes and the prior distribution should be wider, and vice versa.

We suspect that using the same prior distribution for each level of aggregation is in part what leads to the extreme levels of evidence obtained for the full data sets in the Strict null comparisons, which seems overly sensitive to the presence of absence of random slopes in the data. In the case where there is only a fixed effect and no random slopes (middle panel of Fig. 3), the Strick null comparison yields far more decisive Bayes factors than the Balanced null comparison, which does not seem desirable. We therefore wish to underscore the importance of having a sensible prior specification (i.e., accounting for the trial level variance) when random slopes are considered in only one of the two models under consideration.

Finally we focus on the difference between the Strict null and the Balanced null comparisons. In the former comparison, the null model (Model (3)) postulates that none of the participants is affected by condition, whereas the alternative model (Model (6)) postulates that participants are affected differently. For the Balanced null comparison, both the null model (Model (5)) and the alternative model (Model (6)) postulate that participants are affected differently by condition, but only the latter model postulates an overall effect. When there are more observations per participant, the error variance and the random slope variance can be disentangled more easily. Since the Strick null comparison focuses more on individual differences than the Balanced null comparison, collecting more data points will lead to more decisive Bayes factors in the Strick null comparison than in the Balanced null comparison.

The above considerations motivate the following questions:

• 1. How should the prior distributions for the fixed and random effect be constructed?

  • (a) How can we construct an effect size that is meaningfully standardized? In other words, what variance should we standardize by?

• 2. Since there is overlap of the predictive space of Model 4 (fixed effect, but no random slopes) and Model 5 (random slopes, but no fixed effect), there is a certain degree of model mimicry: random slopes in a model account for variations due to a fixed effect (e.g., see also the middle panel of Fig. 3, where Model 6 receives far more support in the Strick null than in the Balanced null due to the random slopes in Model 5). Can we therefore meaningfully disentangle a fixed effect and random slopes, both statistically and theoretically?

Example 3: A Random Interaction Effect

Up to now, our discussion on mixed models has only dealt with the relatively simple case of a single independent variable of interest (e.g., condition).

The purpose of the present example is to highlight how mixed model comparisons are affected by the presence of multiple independent variables of interest, and to explore which models to consider when testing for the presence of an interaction effect. Due to the addition of a second independent variable of interest, the possibility emerges to test for an interaction effect between the two variables that, just like a main effect, can have a fixed and a random component. Just as for the main effects, each cell of the interaction (i.e., each combination of levels from each factor) requires multiple measurements within each participant for the random interaction effect to be identifiable.

To demonstrate the decisions that arise when testing for an interaction effect, we consider a real world example by Lukács et al. (2020).⁷ In this scenario, the hold-duration of a response button was measured in I = 116 participants, who completed an item recognition task where they used either thumb or index finger (factor A, with two levels) to respond to either a probed or irrelevant item (factor B, with two levels). For the RM ANOVA comparison, we can consider the aggregated case with one observation per participant, per cell of the design (i.e., per level of A, per level of B). For instance, the aggregated data contains one observation for the hold-duration of participant 4, where they responded with their thumb to an irrelevant item. Figure 4 presents these aggregated data.

Fig. 4

Aggregated data for Example 3, where we consider only the average observation per participant, per cell of the design. Each point in the plot represents one aggregated hold-duration. The left panel has factor A on the x-axis and factor B indicated by the colors of the points. The right panel has factor B on the x-axis and factor A indicated by the colors of the points. The lines connect the condition means in order to illustrate whether or not there is an interaction effect. If the two lines are not parallel, this is an indication of an interaction effect. There appears to be a main effect of factor A (i.e., responses made with the thumb are faster than those made with the index finger)

For aggregated data, the analysis of choice is typically a RM ANOVA, where only the fixed effects of A, B, and A×B are considered. However, despite of the aggregation, it is possible to fit random slopes for A and B, because there are 2 observations for each level of A, and 2 observations for each level of B, for each participant. On the other hand, the aggregation prevents the calculation of random slopes for the interaction effect as there is only one observation for each combined cell of A×B.⁸ Considering the full data instead of the aggregated data enables the fitting of random slopes for main and interaction effects. Figure 5 presents the full data that contains multiple observations per cell of the research design.

Fig. 5

Full data for Example 3, where we consider all observations per participant, per cell of the design. The distributions of hold-duration for five example participants for each combination of conditions A and B are shown in two rows. The top row shows factor A on the x-axis, and indicates factor B with the different colors. The bottom row shows factor B on the x-axis, and indicates factor A with the different colors. The points indicate the participant means for level of A and B. The lines are drawn between the points to indicate the change in hold-duration. If these two lines are not parallel, this is an indication of an interaction effect. A random interaction effect then means that different participants exhibit varying degrees of the two lines not being parallel

In this example, we are interested in whether there is an interaction effect A×B, as the original authors postulated that participants might keep the response button pressed for a longer period of time when responding to an irrelevant probe (factor B), and that this difference in hold-duration might differ per response mechanism (factor A). Because we previously defined the models in a scenario with only a single variable of interest, we will alter the models under consideration. We list the models under consideration in Table 2, and below we describe the process of constructing these models.

Table 2 Model definitions for a 2 × 2 design when analyzing an interaction effect

We start with the commonalities. Previously, this was only μ and σ_𝜖, but now this includes all parameters that are essential: the main effects of A and B (due to marginality; see also Wagenmakers et al., 2018, and references therein), and the random intercepts for each participant (due to the repeated measures design). This defines a new version of Model (1). Next, we add the fixed interaction effect of the two factors, A×B, and create a new version of Model (2).

However, these two models can also include random slopes for the main effect of A and B, since these are now identifiable. Thus, we can define Model 3 and 4, which are similar to the updated Models 1 and 2, but with added random slopes for A and B. Finally, we can add the random slopes for the interaction effect to these newly defined models 3 and 4, and create the updated versions of models (5) and (6), respectively.

With the updated models, we can consider the different model comparisons again. The RM ANOVA comparison, which is based on the aggregated data, can be either between Model 1 and Model 2 or between Model 3 and Model 4, based on whether or not the random effects for A and B are included. We will refer to the former comparison as the “minimal” RM ANOVA comparison, as it includes no random slopes at all. As before, both versions of the RM ANOVA take the approach of minimizing the random effects through aggregation, in order to focus on the fixed effect at hand. The Balanced null comparison (Model 5 vs Model 6), on the other hand, accounts for the random effect by including it in both models that are compared, such that the only difference between the models is the fixed effect of interest. The Strick null comparison (Model 3 vs Model 6) makes a different statement. Analogous to the earlier examples, the difference between the two models under consideration is the combination of both the fixed and random effect. It therefore quantifies evidence for the presence or absence of a general effect of condition.

The differences between these four comparisons are again reflected in the diverging Bayes factors:⁹

• 1. The minimal RM ANOVA comparison: $\log \text {BF}_{2,1} = -1.75$

• 2. The RM ANOVA: $\log \text {BF}_{4,3} = 2.26$

• 3. The Balanced null comparison: $\log \text {BF}_{6,5} = -1.59$

• 4. The Strict null comparison: $\log \text {BF}_{6,3} = -34.35$

The RM ANOVA comparison is the only case where there is evidence in favor of an interaction effect. Interestingly, there is a discrepancy between the two RM ANOVA comparisons, which means that including the random effects for A and B has consequences for the interaction effect. A possible explanation for this is the presence of a strong random and fixed effect for A. This result stands in contrast to the frequentist results in Barr (2013a), who demonstrated that excluding the non-critical random slopes yields similar results to the approach that does include the non-critical slopes.

The Balanced null comparison agrees with the minimal RM ANOVA comparison and provides moderate evidence against the presence of a fixed interaction effect. The Strict null comparison also agrees but yields a much stronger Bayes factor, which implies that there is also no evidence for a random interaction effect. Table 3 shows all possible Bayes factor comparisons between the 6 models outlined here, for both the full and aggregated data. From these comparisons, it is clear that there is evidence in favor of random effects of A and/or B, because of the overwhelming Bayes factors comparing Models 3, 4, 5, and 6 (i.e., the models with the random effects of A and B) to Models 1 and 2 (i.e., the models without the random effects of A and B). For instance, while Model 1 is marginally better than Model 2 for the full data ($\log (\text {BF}_{1,2})$ = 1.03), Model 1 is heavily outperformed by Model 3 ($\log (\text {BF}_{1,3}) = -4286.09$). Based on the table, Model 4 (i.e., the model with the random and fixed main effects) performed the best for both versions of the data: all the Bayes factors in row 4 are positive, indicating that there is at least moderate support for Model 4 compared to the model in the column, for both aggregated and full data.

Table 3 Bayes factors for all pairs of models defined in Table 2

The considerations above motivate the following questions:

• 1. What are the relevant model comparisons for a main effect in a two-factorial design?

• 2. What are the relevant model comparisons for an interaction effect in a two-factorial design?

  • (a) Should the random main effects be included in all comparisons?

• (a) How can we explain the difference between the two versions of the RM ANOVA comparison?

• 3. For this example, is it theoretically meaningful to analyze random main effects when the data is aggregated?

Discussion

This manuscript illustrated the three main choices faced by researchers who apply mixed models: when and why to aggregate, which model comparisons to use when testing hypotheses about the presence or absence of an effect, and whether or not to collect more (albeit noisier) observations per participant. Testing for a fixed effect is not straightforward in the presence of random effects, and we presented three approaches to do so. First, the data can be aggregated, which minimizes the impact of the random effects in the inference for a fixed effect. Second, two models can be compared that both include the random effects, which controls for the random effects. Third, the fixed and random effect can be considered together, instead of trying to dissect the general effect into its constituent elements. Each of these three approaches has their own implications for the three main choices, and—especially in the case where more than one variable is considered—the consequences of these different choices can be profound.

Our aim is for this manuscript to initiate a discussion on best practices in Bayes factor model comparison in mixed models. Table 1 outlines the specific questions and their relevant examples. We note that this is not an exhaustive list of questions worth discussing in the context of mixed model comparison and we welcome contributors to go beyond. Mixed model comparisons are surprisingly intricate, and a systematic discussion of the most pressing topics is long overdue.

We hope that this discussion will result in broad consensus on best practices, even if this consensus is that those who apply mixed models should be aware what models are being compared and, consequently, what questions are being answered.