Effect of Fluid–Structure Interaction on Vibration and Deflection Analysis of Generally Orthotropic Submerged Micro-plate with Crack Under Thermal Environment: An Analytical Approach

Abstract

Purpose

To develop a new analytical model for vibration analysis of cracked-submerged orthotropic micro-plate affected by fibre orientation and thermal environment.

Methods

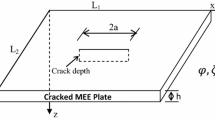
The proposed analytical model is based on Kirchhoff’s classical thin plate theory and the size effect is introduced using the modified couple stress theory. Effect of crack is deduced using appropriate crack compliance coefficients based on line spring model while the effect of thermal environment is introduced in terms of thermal in-plane moments and forces. The coupling of shear and normal stresses for fibre orientation is represented using the coefficient of mutual influence. The fluid forces associated with its inertial effects are added in the governing differential equation to incorporate the fluid–structure interaction effect.

Results

The results are presented for frequency response as affected by different fibre orientation, crack length, crack location, level of submergence, temperature variation and material length-scale parameter for simply supported boundary condition. Furthermore, to study the phenomenon of shifting of primary resonance in a cracked micro-plate, the classical relations for central deflection of plate is also proposed.

Conclusions

The results show that the fundamental frequency of micro-plate decreases by the presence of crack and thermal environment and this decrease in frequency is further intensified by the presence of surrounding fluid medium in present study. Another important conclusion is that with increase in temperature variation the reduction in frequency at 45° of fibre orientation is less when compared to 0 and 90° for both intact and cracked orthotropic plates.

Appendices

Appendix A

From the literature review, it is seen that many researchers used strain gradient (higher order) theories [38, 40, 46, 65,66,67] to consider the size effect of microstructure in form of length-scale parameter. Among them Tsiatas [43] and Yin et al. [46] proposed a new non-classical Kirchhoff’s plate model with a single internal material length-scale parameter for the analysis of isotropic micro-plates based on the simplified couple stress theory of Yang et al. [67].

In the simplified couple stress theory, the strain energy density (U) in three-dimensional body occupying a volume V bounded by the surface G is given by Yang et al. [67] as

$$U = \frac{1}{2}\int \left( {\sigma_{ij} \epsilon_{ij} + m_{ij} \aleph_{ij} } \right){\text{d}}V,$$

(46)

where

$$\epsilon_{ij} = \frac{1}{2}\left( {\frac{{\partial u_{i} }}{\partial j} + \frac{{\partial u_{j} }}{\partial i}} \right),$$

(47)

$$\aleph_{ij} = \frac{1}{2}\left( {\frac{{\partial \theta_{i} }}{\partial j} + \frac{{\partial \theta_{j} }}{\partial i}} \right),$$

(48)

are the strain tensor ($\epsilon_{ij}$) and the symmetric part of the curvature tensor ($\aleph_{ij}$), respectively, $u_{ij}$ is the displacement vector and $\theta_{ij}$ is the rotation vector which can defined as

$$\theta_{i} = \frac{1}{2}e_{ijk} \frac{{\partial u_{k} }}{\partial j},$$

(49)

where $e_{ijk}$ is the permutation symbol.

As per modified couple stress theory, the stress tensor ($\sigma_{ij}$) and the deviatoric part of the couple stress tensor ($m_{ij}$) can be expressed as (Ref. [43])

$$\sigma_{ij} = \lambda \epsilon_{kk} \delta_{ij} + 2\mu_{o} \epsilon_{ij} ,$$

(50)

$$m_{ij} = 2\mu_{o} l^{2} \aleph_{ij} ,$$

(51)

where $\lambda$ and $\mu_{o}$ are the Lamé constants, $\delta_{ij}$ is the Kronecker delta. Equations (50) and (51) described the two dimensional state of stress. From Eq. (51) it is observed that the couple stress tensor $m_{ij}$ is symmetric and from Eq. (48) the curvature tensor $\aleph_{ij}$ is also symmetric. That is, only the symmetric part of the rotation gradient and the symmetric part of displacement gradient contribute to the deformation energy (Ref. [67]) which is dissimilar from that in the classical couple stress theory.

In the work of Tsiatas [43], after the suitable replacement of the Lamé constants by the modulus of elasticity E and the Poisson’s ratio $\nu$, the stress tensor ($\sigma_{ij}$) and the couple stress tensor ($m_{ij}$) is expressed as

$$\sigma_{\alpha \beta } = \frac{E}{{1 - \nu^{2} }}\left[ { \nu \epsilon_{kk} \delta_{\alpha \beta } + \left( {1 - \nu } \right) \epsilon_{\alpha \beta } } \right],$$

(52)

$$m_{\alpha \beta } = 2Gl^{2} \aleph_{\alpha \beta } ,$$

(53)

where $G = E/2\left( {1 + \nu } \right)$ is the shear modulus, l is a material length-scale parameter and $\aleph_{ij}$ is the curvature tensor.

From Eqs. (52) and (53), the expression for the bending moment and couple moment tensors can be written as [43]

$$M_{\alpha \beta } = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\sigma_{\alpha \beta } } z{\text{d}}z,$$

(54)

$$Y_{\alpha \beta } = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {m_{\alpha \beta } } {\text{d}}z.$$

(55)

Expressing the curvature and strain tensors in form of lateral deflection of isotropic plate we have (Ref. [43])

$$M_{x} = M_{11} = - D\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)\quad Y_{x} = Y_{11} = 2D^{l} \frac{{\partial^{2} w}}{\partial x\partial y},$$

$$M_{y} = M_{22} = - D\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\quad Y_{y} = Y_{22} = - 2D^{l} \frac{{\partial^{2} w}}{\partial x\partial y},$$

$$M_{xy} = M_{11} = M_{yx} = M_{22} = D\left( {1 - \nu } \right)\frac{{\partial^{2} w}}{\partial x\partial y}\quad Y_{xy} = Y_{yx} = Y_{12} = Y_{21} = D^{l} \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right),$$

where $D = \frac{{Eh^{3} }}{{12\left( {1 - \nu ^{2} } \right)}}$ is the flexural rigidity of the isotropic plate and $D^{l} = \frac{{El^{2} h}}{{2\left( {1 + \nu } \right)}}$ shows the bending rigidity due to couple stress of micro-plate and l is a material length-scale parameter. This $D^{l}$ also shows the contribution of rotation gradients to the bending rigidity.

Tsiatas [43] employed the Gauss divergence theorem to the total potential energy of a deformable body and arrived at the expression of bending moment which shows two components of bending; (i) the bending due to microstructure and (ii) pure plate bending. This expression for moment can be written as

$$M_{ii}^{*} = M_{ii} + M_{ii}^{l} = - \left( {D + D^{l} } \right)\left( {\frac{{\partial^{2} w}}{{\partial i^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial j^{2} }}} \right)\;M_{ij}^{*} = M_{ij} + M_{ij}^{l} = \left( {D + D^{l} } \right)\left( {1 - \nu } \right)\frac{{\partial^{2} w}}{\partial i\partial j}.$$

From the above expression, it is seen that the effect of microstructure in the form of a single material length-scale parameter “l”, contributing to the bending moment and increasing the flexural rigidity by $D^{l} = \frac{{El^{2} h}}{{2\left( {1 + \nu } \right)}}$. The advantage of the modified couple stress theory developed by Tsiatas [43] is that a single parameter can capture the microstructure effect and its contribution to the flexural rigidity can be easily coupled with the rigidity used in classical plate theory. It is important here to note that Yin et al. [46] employed the additional rigidity ($D^{l}$) due to microstructure in their analysis of dynamics of micro-plate. The present work employs the additional flexural rigidity established by Tsiatas [43] for isotropic plate and applies it to the case of cracked orthotropic submerged plate in the presence of thermal environment.

Appendix B

Soni et al. [11] have formulated the fluid forces in form of virtual added mass using potential flow theory and presented the influence of fluid medium on vibration response of cracked isotropic plate. They used the velocity potential function along with Bernoulli’s equation to express the fluid dynamic pressures acting on the plate. Similar approach has been adopted here to find the fluid pressure for cracked orthotropic plate with the following assumptions:

• 1. The fluid flow is assumed to be small, incompressible, homogeneous and irrotational.

• 2. The dynamic fluid pressure is normal to the surface of the plate and shear forces are neglected as the fluid is inviscid.

• 3. Interaction between the cracked plate and fluid and influence of non-linearity at plate–fluid interface is neglected.

• 4. As the orthotropic plate is considered thin, the effect of fluid forces is ignored in the derivation of in-plane forces.

• 5. The fluid behaves like a thermal reservoir and the rise in temperature does not affect the fluid properties.

The velocity potential function $\phi$(x, y, z, t) satisfying the Laplace’s equation can be expressed in the Cartesian coordinate system as

$$\nabla^{2} \phi = \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi }}{{\partial y^{2} }} + \frac{{\partial^{2} \phi }}{{\partial z^{2} }} = 0.$$

(56)

Using Bernoulli’s equation, the fluid dynamic pressure at any point of plate–fluid boundary can be given by

$$P_{u} = P_{z = 0} = - \rho_{f} \left( {\frac{\partial \phi }{\partial t}} \right)_{z = 0} ,$$

(57)

$$P_{l} = P_{z = - h} = - \rho_{f} \left( {\frac{\partial \phi }{\partial t}} \right)_{z = - h} ,$$

(58)

where $\rho_{f}$ is fluid density per unit volume.

Assuming $\phi$ be the function of two discrete variables.

$$\phi \left( {x,y,z,t} \right) = F\left( z \right)S\left( {x,y,t} \right),$$

(59)

where $S\left( {x,y,t} \right)$ and $F\left( z \right)$ are the two discrete functions.

For the assumption of permanent contact between the surface of the plate and fluid layer, the kinematic boundary conditions at the fluid–plate interface can be written as (Ref. [11])

$$\left( {\frac{\partial \phi }{\partial z}} \right)_{z = 0} = \frac{\partial w}{\partial t},$$

(60)

$$\left( {\frac{\partial \phi }{\partial z}} \right)_{z = - h} = \frac{\partial w}{\partial t}.$$

(61)

By introducing Eq. (59) in Eqs. (60) and (61) we get

$$S\left( {x,y,t} \right) = \frac{1}{{\left( {{\raise0.7ex\hbox{${{\text{d}}F\left( z \right)}$} \!\mathord{\left/ {\vphantom {{{\text{d}}F\left( z \right)} {{\text{d}}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{d}}z}$}}} \right)_{z = 0} }}\frac{\partial w}{\partial t},$$

(62)

$$S\left( {x,y,t} \right) = \frac{1}{{\left( {{\raise0.7ex\hbox{${{\text{d}}F\left( z \right)}$} \!\mathord{\left/ {\vphantom {{{\text{d}}F\left( z \right)} {{\text{d}}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{d}}z}$}}} \right)_{z = - h} }}\frac{\partial w}{\partial t}.$$

(63)

By substituting Eqs. (62) and (63) in Eq. (59) the $\phi$ on fluid–plate interfaces (i.e. upper and lower surface of plate) can be stated as

$$\phi \left( {x,y,z,t} \right) = \frac{F\left( z \right)}{{\left( {{\raise0.7ex\hbox{${{\text{d}}F\left( z \right)}$} \!\mathord{\left/ {\vphantom {{{\text{d}}F\left( z \right)} {{\text{d}}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{d}}z}$}}} \right)_{z = 0} }}\frac{\partial w}{\partial t},$$

(64)

$$\phi \left( {x,y,z,t} \right) = \frac{F\left( z \right)}{{\left( {{\raise0.7ex\hbox{${dF\left( z \right)}$} \!\mathord{\left/ {\vphantom {{dF\left( z \right)} {dz}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${dz}$}}} \right)_{z = - h} }}\frac{\partial w}{\partial t}.$$

(65)

The following differential equation of second order can be obtained by putting Eq. (64) or (65) into Eq. (56).

$$\frac{{{\text{d}}^{2} F\left( z \right)}}{{{\text{d}}z^{2} }} - \mu^{2} F\left( z \right) = 0,$$

(66)

where $\mu$ represents wave number, which can be determined by $\mu = \pi \sqrt {\frac{1}{{l_{1}^{2} }} + \frac{1}{{l_{2}^{2} }}}$ (Ref. [19]).

The general solution for the differential equation (66) can be expressed as

$$F\left( z \right) = {\text{Ae}}^{\mu z} + {\text{Be}}^{ - \mu z} .$$

(67)

On substituting Eq. (67) into Eqs. (64) and (65) we get an expression for $\phi$ on plate–fluid interface as shown below:

$$\phi \left( {x,y,z,t} \right) = \frac{{{\text{Ae}}^{\mu z} + {\text{Be}}^{ - \mu z} }}{{\left( {{\raise0.7ex\hbox{${{\text{d}}F\left( z \right)}$} \!\mathord{\left/ {\vphantom {{{\text{d}}F\left( z \right)} {{\text{d}}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{d}}z}$}}} \right)_{z = 0} }}\frac{\partial w}{\partial t},$$

(68)

$$\phi \left( {x,y,z,t} \right) = \frac{{{\text{Ae}}^{\mu z} + {\text{Be}}^{ - \mu z} }}{{\left( {{\raise0.7ex\hbox{${{\text{d}}F\left( z \right)}$} \!\mathord{\left/ {\vphantom {{{\text{d}}F\left( z \right)} {{\text{d}}z}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{d}}z}$}}} \right)_{z = - h} }}\frac{\partial w}{\partial t},$$

(69)

where $A$ and $B$ denote the unknown constants which can be resolved utilizing two extreme limit conditions at plate–fluid interface and at fluid extremity surfaces z = h₁ and z = (h + h₂).

Assuming the disturbance because of free surface wave motion of liquid is irrelevant, the accompanying boundary condition can be applied for velocity potential at the free surface of liquid [19]

$$\left( {\frac{\partial \phi }{\partial z}} \right)_{{z = h_{1} }} = - \frac{1}{{g_{a} }}\left( {\frac{{\partial^{2} \phi }}{{\partial t^{2} }}} \right)_{{z = h_{1} }} ,$$

(70)

where ‘${\text{g}}_{a}$’ denotes the gravity acceleration. Substitution of Eq. (68) into Eqs. (70) and (60) gives the expression for velocity potential $\phi$ as

$$\phi \left( {x,y,z,t} \right) = \frac{1}{\mu }\left[ {\frac{{{\text{e}}^{\mu z} + {\text{Ce}}^{{ - \mu \left( {z - 2h_{1} } \right)}} }}{{1 - {\text{Ce}}^{{2\mu h_{1} }} }}} \right]\frac{\partial w}{\partial t},$$

(71)

where $C = \frac{{{\text{g}}_{a} \mu - \omega^{2} }}{{{\text{g}}_{a} \mu - \omega^{2} }}$ and $\omega$ represents wave motion frequency at free surface of fluid.

The fluid pressure acting on plate’s upper surface can be obtained by substituting Eq. (71) of velocity potential into Eq. (57) as

$$P_{u} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + {\text{Ce}}^{{2\mu h_{1} }} }}{{1 - {\text{Ce}}^{{2\mu h_{1} }} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }}.$$

(72)

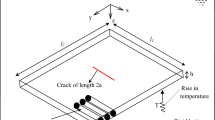
The boundary condition at the rigid base of the tank represented in Fig. 1 is referred to null-frequency condition and can be written as

$$\left( {\frac{\partial \phi }{\partial z}} \right)_{{z = - \left( {h + h_{2} } \right)}} = 0.$$

(73)

On substituting Eq. (69) into Eqs. (73) and (61), the expression for $\phi$ is obtained as

$$\phi \left( {x,y,z,t} \right) = \frac{1}{\mu }\left[ {\frac{{{\text{e}}^{\mu z} + {\text{e}}^{{ - 2\mu \left( {h + h_{2} } \right)}} {\text{e}}^{ - \mu z} }}{{{\text{e}}^{ - \mu h} - {\text{e}}^{{ - 2\mu \left( {h + h_{2} } \right)}} {\text{e}}^{\mu h} }}} \right]\frac{\partial w}{\partial t}.$$

(74)

From Eqs. (74) and (58), the fluid pressure at plate’s lower surface can be expressed as

$$P_{l} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + {\text{e}}^{{ - 2\mu h_{2} }} }}{{1 - {\text{e}}^{{ - 2\mu h_{2} }} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }}.$$

(75)

The resulting fluid dynamic pressure for the plate fully submerged in fluid is written as

$$\Delta P = P_{u} - P_{l} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + {\text{Ce}}^{{2\mu h_{1} }} }}{{1 - {\text{Ce}}^{{2\mu h_{1} }} }} - \frac{{1 + {\text{e}}^{{ - 2\mu h_{2} }} }}{{1 - {\text{e}}^{{ - 2\mu h_{2} }} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }},$$

(76)

$$\Delta P = m_{\text{add}} \frac{{\partial^{2} w}}{{\partial t^{2} }},$$

(77)

where $m_{\text{add}} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + {\text{Ce}}^{{2\mu h_{1} }} }}{{1 - {\text{Ce}}^{{2\mu h_{1} }} }} - \frac{{1 + {\text{e}}^{{ - 2\mu h_{2} }} }}{{1 - {\text{e}}^{{ - 2\mu h_{2} }} }}} \right]$ represents the virtual added mass of submerged plate.