Magnetohydrodynamic oscillatory flow of a physiological fluid in an irregular channel

Abstract

The impact of heat source on magnetohydrodynamic oscillatory flow of a chemically reacting viscoelastic fluid in an asymmetric wavy channel is analysed. The governing flow equations are transformed into ODEs by utilizing proper non-dimensional variables. The subsequent ordinary differential equations are solved analytically. The effects of different flow parameters on the fluid flow, thermal and species distributions as well as rate of heat and mass transfer coefficients are examined graphically. It is pointed out that the velocity of fluid is parabolic with extreme value along the channel centreline and minimum at the walls. The magnitude of fluid velocity increases with an increase in porous parameter and high heat transport of a system is due to the presence of oscillatory flow.

1 Introduction

Recently, many researchers [1,2,3,4,5,6,7,8,9,10] explored the MHD non-Newtonian fluid flows over various geometrical models in view of their significance in many engineering and industrial applications such as food processing, making a paper, slurry transporting etc.,. Physiological fluid is one of the non-Newtonian viscoelastic fluids which play an important role in many transport phenomenon’s (such as blood circulation, cancer treatment, transport of drugs, drug carriers). It is observed that the viscoelastic property of blood is less prominent with rising shear rate and gliding of cells (see Refs. [11, 12]). The blood flow properties are determined by the cell aggregation tendency, red cell concentration and mechanical relation between the particles (see Refs. [13,14,15,16,17,18,19]). The experimental studies reveal that, in case of cancer treatment by radiotherapy, chemotherapy or surgery, they destroy both malignant and normal cells. In view of these issues, Nikiforov [20] developed an electromagnetic hyperthermia technique where the dangerous cancer cells are exposed to a temperature field greater than 41 °C with the help of thermal radiation. In this method a magnetic liquid is injected to the malignant tissues and then exposing the framework to an alternative current. Due to this, the temperature is produced in the infused magnetic fluid and there by the cancer cells get destroyed (see Ref. [21]). Raftari and Vajravelu [22] studied the impact of magnetic field on a visco-elastic fluid flow through a channel by applying HAM analysis. Singh [23, 24] investigated the influence of slip and thermal radiation on visco-elastic fluid flow past a vertical channel. Abdalla and Abo Dahab [25] explored the rotating and non-Newtonian fluid effects in an asymmetric channel with peristaltic transport. Many researchers [26,27,28,29] considered the different mathematical models to study the impact of viscoelastic fluid flow through porous channels.

Now a days chemical reactions play a significant role in many science and engineering applications at different stages such as; chemical engineering processes, moisture over agricultural fields, energy transfer in a cooling tower power, cooling industry for drying, and the flow in desert cooler etc.,. In view of these, the visco-elastic fluid flow through a porous channel with chemical reaction was estimated analytically by Devika et al. [30]. Gireesha and Mahanthesh [31] explored the chemically reacting heat transfer flow of viscoelastic fluid through non uniform channels. Nayak et al. [32] analyzed the first order chemical reaction effects on viscoelastic fluid in the presence of porous medium. Venkateswarlu et al. [33] contemplated the chemically reacting viscoelastic fluid flow past a vertical channel.

It is also worth noting that most of afore mentioned studies have been considered in channels. Therefore, it would be interesting to explore the study of non-Newtonian fluid in an asymmetric wavy channel. In this way, the main aim of the present work is to investigate the visco-elastic fluid behavior of MHD oscillatory flow in an irregular channel. The governing equations are solved analytically. Impact of various flow parameters on the fluid flow characteristics are analyzed through graphs. Further, the comparison of the skin friction coefficient and Nusselt number for various values of magnetic field and heat source parameters are displayed in Table 1.

Table 1 Comparison of skin friction coefficient and Nusselt number for different values of M and Q respectively

2 Mathematical formulation

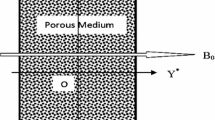
Unsteady incompressible, chemically reacting and thermally radiating non-Newtonian fluid is considered in an irregular channel with heat source. A constant magnetic field of strength B₀ is assumed normal to the flow. The fluid flow along x-direction is generated due to the oscillatory pressure gradient at the walls as shown in Fig. 1. T₁ and T₂ are respectively the temperatures of the fluid at walls of the channel. The magnetic Reynolds number is assumed to be very small compared to the external one and hence the induced magnetic field can be negligible. The inner and outer walls H₁ and H₂ are respectively given by [2, 34]

$$H_{1} = d_{1} + a_{1} \cos \frac{2\pi x}{\lambda }\quad {\text{and}}\quad H_{2} = - d_{2} - b_{1} \cos \left( {\frac{2\pi x}{\lambda } + \phi } \right),$$

(1)

where a₁, b₁, d₁, d₂ and ϕ satisfies the condition $a_{1}^{2} + b_{1}^{2} + 2a_{1} b_{1} \cos \phi \le \left( {d_{1} + d_{2} } \right)^{2} ,0 \le \varphi \le \pi$.

Fig. 1

Physical model of the problem

The governing flow, energy and concentration equations are given by [2, 26, 34]

$$\frac{{\partial U^{*} }}{\partial t} = - \frac{1}{\rho }\frac{\partial p}{\partial x} + \nu \frac{{\partial^{2} U^{*} }}{{\partial y^{2} }} + g\beta_{T} (T^{*} - T_{2} ) + g\beta_{C} (C^{*} - C_{2} ) - \frac{{\sigma B_{0}^{2} U^{*} }}{\rho } - \frac{\nu }{{k^{ * } }}U^{*} + \beta_{0} \frac{{\partial^{3} U^{*} }}{{\partial y^{2} \partial t}},$$

(2)

$$\frac{\partial T}{\partial t}^{*} = \frac{k}{{\rho c_{p} }}\frac{{\partial^{2} T^{*} }}{{\partial y^{2} }} - \frac{1}{{\rho c_{p} }}\frac{\partial q}{\partial y} + \frac{{Q_{H} }}{{\rho c_{p} }}\left( {T^{*} - T_{2} } \right),$$

(3)

$$\frac{{\partial C^{*} }}{\partial t} = D\frac{{\partial^{2} C^{*} }}{{\partial y^{2} }} - K_{r}^{ * } \left( {C^{*} - C_{2} } \right),$$

(4)

The boundary conditions are defined as [2, 34]

$$\begin{aligned} U^{*} & = 0,\quad T^{*} = T_{1} ,\quad C^{*} = C_{1} ,\quad on\quad y = H_{1} , \\ U^{*} & = 0,\quad T^{*} = T_{2} ,\quad C^{*} = C_{2} ,\quad on\quad y = H_{2} , \\ \end{aligned}$$

(5)

The thermal radiative is defined by Ogulu and Bestman [35] as

$$\frac{\partial q}{\partial y} = 4\alpha^{2} \left( {T_{2} - T^{*} } \right),$$

(6)

where $\alpha^{2} = \int\limits_{0}^{\infty } {K_{\lambda w} \frac{{\partial e_{b\lambda } }}{\partial T}} \,d\lambda$.The dimensionless variables are:

$$\begin{aligned} \bar{x} & = \frac{x}{\lambda },\quad \bar{y} = \frac{y}{{d_{1} }},\quad \bar{u} = \frac{{U^{*} }}{U},\quad \bar{t} = \frac{tU}{{d_{1} }},\quad h_{1} = \frac{{H_{1} }}{{d_{1} }},\quad h_{2} = \frac{{H_{2} }}{{d_{1} }},\quad d = \frac{{d_{2} }}{{d_{1} }}, \\ a & = \frac{{a_{1} }}{{d_{1} }},\quad b = \frac{{b_{1} }}{{d_{1} }},\quad D_{a} = \frac{{k^{ * } }}{{d_{1}^{2} }},\quad \text{Re} = \frac{{Ud_{1} }}{\nu },\quad Q = \frac{{Q_{H} d_{1}^{2} }}{k},\quad K = \frac{{d_{1}^{2} }}{{k^{ * } }},\quad Sc = \frac{D}{{Ud_{1} }}, \\ Kr & = \frac{{d_{1} K_{r}^{ * } }}{U},\quad \bar{p} = \frac{{d_{1}^{2} p}}{\rho \nu \lambda U},\quad Pe = \frac{{Ud_{1} \rho c_{p} }}{k},\quad R = \frac{{4\alpha^{2} d_{1}^{2} }}{k},\quad M = \frac{{\sigma B_{0}^{2} d_{1}^{2} }}{\rho \nu },\quad \beta = \frac{{B_{0} U}}{{\nu d_{1} }}, \\ Gr & = \frac{{g\beta_{T} \left( {T_{1} - T_{2} } \right)d_{1}^{2} }}{\nu U},\quad Gc = \frac{{g\beta_{C} \left( {C_{1} - C_{2} } \right)d_{1}^{2} }}{\nu U},\quad \theta = \frac{{T^{*} - T_{2} }}{{T_{1} - T_{2} }},\quad \phi = \frac{{C^{*} - C_{2} }}{{C_{1} - C_{2} }}, \\ \end{aligned}$$

(7)

The corresponding boundary conditions are

$$h_{1} = 1 + a\cos 2\pi x,\quad {\text{and}}\quad h_{2} = - d - b\cos \left( {2\pi x + \phi } \right),$$

(8)

where a, b, d and ϕ satisfies the form $a^{2} + b^{2} + 2ab\cos \phi \le \left( {1 + d} \right)^{2}$.

In view of non-dimensional quantities Eqs. (2)–(4) can be written as (neglecting bar symbols)

$$\text{Re} \frac{\partial u}{\partial t} = - \frac{\partial p}{\partial x} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + Gr\theta + Gc\phi - (M + 1/K)u + \beta \frac{{\partial^{3} u}}{{\partial y^{2} \partial t}},$$

(9)

$$Pe\frac{\partial \theta }{\partial t} = \frac{{\partial^{2} \theta }}{{\partial y^{2} }} + (R + Q)\theta$$

(10)

$$\frac{\partial \phi }{\partial t} = Sc\frac{{\partial^{2} \phi }}{{\partial y^{2} }} - Kr\phi ,$$

(11)

The corresponding non-dimensional boundary conditions are

$$\begin{aligned} u & = 0,\quad \theta = 1,\quad \phi = 1,\quad {\text{on}}\quad y = h_{1} , \\ u & = 0,\quad \theta = 0,\quad \phi = 0,\quad on\quad y = h_{2} , \\ \end{aligned}$$

(12)

3 Method of solution

In order to solve the system of PDEs (9)–(11) the following pressure gradient for purely oscillatory flow, velocity, thermal and concentrations fields are assumed as (see Refs. [34, 36,37,38,39])

$$- \frac{\partial p}{\partial x} = \lambda e^{i\omega t} ,\quad {\text{and}}\quad f(y,t) = f_{0} (y)e^{i\omega t} ,$$

(13)

where f is the u, θ and φ, f₀ is the u₀, θ₀ and φ₀.

In view of Eq. (13), the Eqs. (9)–(11), are reduced to

$$(1 + i\omega \beta )\frac{{d^{2} u_{0} }}{{dy^{2} }} - n^{2} u_{0} = - \lambda - Gr\theta_{0} - Gc\phi_{0} ,$$

(14)

$$\frac{{d^{2} \theta_{0} }}{{dy^{2} }} + m^{2} \theta_{0} = 0,$$

(15)

$$\frac{{d^{2} \phi_{0} }}{{dy^{2} }} - l^{2} \phi_{0} = 0,$$

(16)

The boundary conditions are

$$\begin{aligned} u_{0} & = 0,\quad \theta_{0} = 1,\quad \phi_{0} = 1,\quad {\text{on}}\quad y = h_{1,} \\ u_{0} & = 0,\quad \theta_{0} = 0,\quad \phi_{0} = 0,\quad {\text{on}}\quad y = h_{2} , \\ \end{aligned}$$

(17)

Solving the Eqs. (14)–(16) with the help of boundary conditions Eq. (17), we get the solutions for velocity, temperature and concentration are as follows

$$\begin{aligned} u\left( {y,t} \right) & = \frac{\lambda }{{n^{2} }}(1 + i\omega \beta )e^{i\omega t} + (1 + i\omega \beta )\left\{ {\frac{\lambda }{{n^{2} }} + \frac{Gr}{{m^{2} + n^{2} }} - \frac{Gc}{{l^{2} - n^{2} }}} \right\}\frac{{\sinh n(h_{2} - y)}}{{\sinh n(h_{1} - h_{2} )}}e^{i\omega t} \\ & \quad + (1 + i\omega \beta )\left\{ {\frac{\lambda }{{n^{2} }}\frac{{\sinh n\left( {y - h_{1} } \right)}}{{\sinh n(h_{1} - h_{2} )}} + \frac{Gr}{{m^{2} + n^{2} }}\frac{{\sin m(y - h_{2} )}}{{\sin m(h_{1} - h_{2} )}} - \frac{Gc}{{l^{2} - n^{2} }}\frac{{\sinh l\left( {y - h_{2} } \right)}}{{\sinh l\left( {h_{1} - h_{2} } \right)}}} \right\}e^{i\omega t} , \\ \end{aligned}$$

(18)

$$\,\,\theta \left( {y,t} \right) = \frac{{\sin m\left( {y - h_{2} } \right)}}{{\sin m(h_{1} - h_{2} )}}e^{i\omega t} ,$$

(19)

$$\phi (y,t) = \frac{{\sinh l\left( {y - h_{2} } \right)}}{{\sinh l\left( {h_{1} - h_{2} } \right)}}e^{i\omega t} ,$$

(20)

The skin friction coefficient, Nusselt and Sherwood number at the wall are define as follows

$$\begin{aligned} \tau & = \mu \left\{ {\frac{\partial u}{\partial y}} \right\}_{{y = h_{1} ,h_{2} }} = \mu (1 + i\omega \beta )\left\{ {\frac{nGc}{{l^{2} - n^{2} }} - \frac{nGr}{{m^{2} + n^{2} }} - \frac{\lambda }{n}} \right\}\frac{{\cosh n\left( {y - h_{2} } \right)}}{{\sinh n\left( {h_{1} - h_{2} } \right)}}e^{i\omega t} \\ & \quad + \mu (1 + i\omega \beta )\left\{ {\frac{{\lambda \cosh n\left( {y - h_{1} } \right)}}{{n\sinh n\left( {h_{1} - h_{2} } \right)}} - \frac{mGr}{{m^{2} + n^{2} }}\frac{{\cosh m\left( {y - h_{2} } \right)}}{{\sinh m\left( {h_{1} - h_{2} } \right)}} - \frac{lGc}{{l^{2} - n^{2} }}\frac{{\cosh l\left( {y - h_{2} } \right)}}{{\sinh l\left( {h_{1} - h_{2} } \right)}}} \right\}e^{i\omega t}, \\ \end{aligned}$$

(21)

$$Nu = - \left( {\frac{\partial \theta }{\partial y}} \right)_{{y = h_{1} ,h_{2} }} = - \frac{{m\cos m\left( {y - h_{2} } \right)}}{{\sin m\left( {h_{1} - h_{2} } \right)}}e^{i\omega t} = \left| J \right|\cos \left( {\omega t + \psi } \right),$$

(22)

$$Sh = - \left( {\frac{\partial \phi }{\partial y}} \right)_{{y = h_{1} ,h_{2} }} = - \frac{{l\cosh l(y - h_{2} )}}{{\sinh l(h_{1} - h_{2} )}}e^{i\omega t} = \left| F \right|\cos \left( {\omega t + \psi } \right),$$

(23)

The amplitude and phase angle of the rate of heat and mass transfer are respectively given by $J = J_{r} + iJ_{i} ,\quad \psi = \tan^{ - 1} (J_{i} /J_{r} ),\quad F = F_{r} + iF_{i} ,\quad \psi = \tan^{ - 1} (F_{i} /F_{r} )$where $l^{2} = Kr + i\omega /Sc,\quad m^{2} = Q + R - i\omega Pe,\quad n^{2} = M + 1/K + i\omega \text{Re}$.

4 Results and discussion

The aim of this paper is to analyze the non-Newtonian fluid behavior and oscillatory flow of visco-elastic fluid in an irregular channel. The solutions of the Eqs. (18)–(20) are obtained by using MATLAB code and the results are displayed through Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15 for various parameters entering into the problem. Table 1 displays the comparative study of skin friction and rate of heat transfer coefficients for Newtonian fluid with those of Ref. [2] by choosing ω = 0.1, λ = 0.1, t = 0.1, π = 3.14, a = 0.2, b = 1.2, d₁ = 2.0 and Re = 0.1. It is found to be good agreement between them.

Fig. 2

Influence of K on u

Fig. 3

Influence of M on u

Fig. 4

Influence of Gr and Gc on u

Fig. 5

Influence of Pe and Re on u

Fig. 6

Influence of Kr and Sc on u

Fig. 7

Influence of Kr and Sc on ϕ

Fig. 8

Influence of R on u

Fig. 9

Influence of Pe, Q and R on θ

Fig. 10

Influence of K on skin friction coefficient

Fig. 11

Influence of M on skin friction coefficient

Fig. 12

Influence of R on Nusselt number

Fig. 13

Influence of Kr on Sherwood number

Fig. 14

Influence of R on Nusselt number

Fig. 15

Influence of Sc on Sherwood number

Figure 2 displays the influence of porous parameter K on the velocity profile for both Newtonian (β = 0) and non-Newtonian (β ≠ 0) cases. It is noticed that the velocity profiles attains the maximum value with increase of K. Physically, rising estimations of K results the larger holes of porous medium and henceforth resistivity of the medium might be disregarded. Further, the velocity of Newtonian fluid is more than that of non-Newtonian fluid.

The impact of M on u is discussed in Fig. 3. It is noticed that the velocity along the boundary layer pulverizes with raising values of M. This is because of the way that the Lorentz force has the tendency to diminish the motion of the fluid and henceforth the fluid velocity diminishes.

The influence of Gr and Gc on u is displayed in Fig. 4. It is observed that the velocity mounting with rising values of Gr and decline with Gc values. Physically, Gr signifies the general impact of the thermal buoyancy force to the viscous hydrodynamic force in the boundary layer. Thus, as Gr increases the velocity of the fluid reaches maximum value in the middle region of the asymmetric channel and after that rots easily to the free stream velocity.

The influence of various values of Pe and Reynolds number Re on u across the boundary layer is shown in Fig. 5. The Peclet number is the ratio of thermal energy convected to the fluid to the thermal energy conducted within the fluid and the Reynolds number is the ratio of inertial forces to viscous forces. The results of velocity profile increase with increase in Pe and reverse effect with rise of Re. These parameters may play an important role in convective heat transfer processes.

Figures 6 and 7 display the consequences of velocity and concentration of dissimilar values of Kr and Sc respectively. It is noticed that the velocity of the fluid increases and concentration decreases with rising values of chemical reaction parameter. In addition, Schmidt number shows reverse effect on these two profiles. Physically, Schmidt number Sc is characterized as the ratio of momentum and mass diffusivity. Hence, as Sc increases the velocity and boundary layer thickness reduces and concentration of the fluid increases.

The influence of R on u is outlined in Fig. 8. It is seen that the velocity elevate with the ascent of R in the flow regime. This is due to the fact that the fluid particles get the heat energy from the electromagnetic waves and hence move very fast. Also the velocity of viscous fluid (β = 0) is more than that of non-Newtonian fluid (β ≠ 0).

Figure 9 represents the impact of R, Q and Pe respectively on θ. Plainly the temperature increment for every single developing value of R, Q and Pe in the stream locale. Physically, the thermal radiation is responsible for energy transfer by the emission of electro-magnetic waves which carry energy away as the fluid flows along asymmetric wavy channels and consequently the thermal boundary layer thickness winds up more slender. Experimentally, when blood flow in capillaries, there is a significant increase in the thickness of boundary layer due to rise in thermal radiation. Hence, the temperature of the boundary layer is raised by an appreciable extent.

Figures 10 and 11 display τ for diverse values of K and M respectively, for both Newtonian and non-Newtonian cases (β = 0 and β ≠ 0). It is clear that the skin friction coefficient vary periodically at asymmetric surface. The variations of heat and mass transfer rates against the time series for different values of R and Kr are respectively plotted in Figs. 12 and 13. From these graphs it is clear that Nu and Sh both vary periodically due to asymmetric surface motion.

Figure 14 illustrates the rate of heat transfer against H for dissimilar values of R at the walls y = h₁ and y = h₂. It is observed that the growth in R leads to a rise in the values of Nu at y = h₁ and opposite behaviour at y = h₂. Thus, the rate of heat transfer from the porous asymmetric channel decreases with the increase of R.

Figure 15 displays the variations of Sh against Kr for different values of Sc. It is clear that the rate of mass transfer decline with increase of Sc at the wall y = h₁ whereas the opposite effect at y = h₂.

5 Conclusion

The present study describes the effect of non-Newtonian visco-elastic fluid behaviour of MHD oscillatory flow in an irregular channel. The main conclusions of this study are:

• The temperature profiles increase for all increasing values of R, Q and Pe in the fluid flow along an asymmetric wavy channel.

• The velocity and skin friction coefficient in case of Newtonian fluid is more than that of non-Newtonian fluid. This is due to the presence of high viscosity.

• The skin friction coefficient, Nu and Sh are varying periodically due to surface motion.

• The heat transfer near the wall decrease with the rise of R.

• The Sherwood number reduces with rise of Sc at the walls y = h₁ and y = h₂.