1 Introduction

Nanomaterials have shown promising applications in different engineering sectors [1,2,3]. Adding nanoparticles (1–100 nm) into a base fluid in heating and cooling processes is one of the methods to increase the overall heat transfer coefficient between the fluid and the surrounding surfaces [4,5,6]. The main reason of this phenomenon is the significant increasing of the thermal conductivity of the nanofluid (with nanoparticles) compared with the base fluid (without nanoparticles) [7,8,9,10,11]. Effects of different parameters, such as temperature, volume fraction, particle shape and particle size) on the thermal conductivity ratio (TCR) of the nanofluid and that of its base fluid studied in many articles [12,13,14]. Thermophysical properties of different nanofluids types have been investigated including different nanoparticles types such as CuO [15], TiO2 [16], Fe3O4 [17], Al2O3 [18], and Ag [19] as well as different base fluid types such as water [20] and ethylene glycol [21].

Over the last three decades, nanofluids have attracted more and more attention. The main driving force for nanofluids research lies in a wide range of applications [22,23,24,25].

Various theoretical and experimental studies have been conducted on enhancement and prediction of the TCR of different types of nanofluids. The first theoretical investigation of the TCR can be traced back by Maxwell [26]. In this pioneering work, Maxwell presented a general equation to predict the thermal conductivity of dilute suspensions with micro particles. Then, several convenient and compact analytical and empirical equations for predicting TCR of nanofluids have been presented in the literature [27].

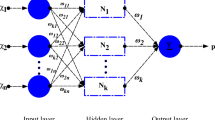
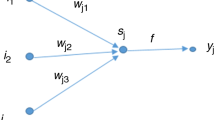
Available methods of measuring nanofluids thermal conductivity experimentally, is too costly and time-consuming task. Furthermore, the presented empirical and theoretical correlations in the literature are reliable for some operating parameters with limited ranges. Therefore, due to the nonlinear behavior the thermal conductivity, determining a practical correlation of it as a function of multiple operating parameters is often complicated and sometimes impossible. So, the application of intelligent systems based techniques such as ANNs was proposed by some researchers. ANNs show very important features such as generalization, mapping capabilities, fault tolerance, robustness, and high speed data processing. They also have the ability to learn by examples and detect complex inherent nonlinear relationships between the inputs and the outputs. ANN may be used as an excellent alternative to numerical and analytical based approaches without involving in solving complex mathematical models [28,29,30,31]. Hence, ANN is used as powerful tool to solve complex engineering problems in different real-world applications with a significant reduction in cost and time [32,33,34,35,36,37,38].

Ahmadloo et al. [39] presented a 5-input multi-layer perception (MLP) as an ANN model for the estimation of the TCR of various nanofluids. Fifteen nanofluids with different types of nanoparticles and base fluids were used to develop the MLP model using experimental data reported in the literature. Ariana et al. [40] presented a study to develop and validate MLP model to estimate the TCR of alumina/water nanofluids as a function of volume fraction, temperature and diameter of the nanoparticle. Papari et al. [41] employed MLP model to estimate TCR of nanofluids consisting of multi-walled carbon nanotubes suspended in different base fluids. Hemmat et al. [42] investigated the efficiency of MLP neural network in modeling TCR of water/EG (40–60%) nanofluid with Al2O3 nanoparticles. The measurement of nanofluid thermal conductivity at different volume fractions and temperatures was taken using KD2 Pro.. Longo et al. [43] presented a 3-input and a 4-input MLP ANN for predicting the TCR of oxide–water nanofluids. Both models employed for investigating the effect of nanoparticle thermal conductivity, nanoparticle volume fraction, and temperature, whereas the 4-input MLP model also considers the effect of the average size of nanoparticle cluster. Hemmat et al. [44] modeled the TCR of Al2O3–water nanofluid at different solid volume fractions and temperatures by ANN.

All the above-mentioned studies focused on prediction of the TCR of nanofluids using a limited number of input parameters and only one unknown target parameter (TCR). In this study, a general approach is proposed to predict multiple unknown parameters including TCR based on any number of known input parameters. To check the validity of the approach, it is applied to three different nanofluids using both theoretical and experimental data available in literature.

2 Self-organizing approach

In this article, self -organizing maps (SOM), as one an unsupervised ANN, is used to predict the TCR of nanofluids based on both theoretical and experimental literature data. As other ANNs approaches, SOM shows many important features such as generalization, data exploration, mapping capabilities, robustness, fault tolerance, and high speed data processing. Additionally, they have the ability to detect complex nonlinear relationships between the outputs and the inputs. Once the training process is accomplished, SOM can be utilized to predict the unknown outputs which are not used during training process. SOM is a powerful tool that used to convert the complex relationships into simple relationships. It is used in many engineering applications such as inverse dynamic control of industrial robots [45], unmanned aerial vehicle control [46], aircraft dynamics [47], and image processing [48].

SOM is formed by creating a two-dimensional network consists of many interconnected nodes Fig. 1; the two-dimensional network is the common used arrangement of the output neurons. First, the synaptic weight vector for each node (neuron) in the map is initialized by assigning them proper values selected randomly from the training data using the principal component initialization to achieve exact reproducibility of the obtained results [49]. Secondly, a random selected input vector from the input space is presented to the network and the response of each node is evaluated and the one which produces the maximum response, as well as those adjacent to it in the network, are adapted so as to produce a stronger response to that input. After a number of iterations of each input pattern the system should ideally reach a state where an ordered image of the inputs stored in the network. More details about the training process of the SOM as summarized here:

Fig. 1
figure 1

SOM network architecture

Full size image

2.1 Training algorithm

At each iteration, the value of a predefined discriminant function for each node is calculated using an input vector chosen randomly from the training dataset. The node that has the largest value of the discriminant function, at each iteration, is stated as the winner of the competition process [50, 51].

Let \(\bar{x}\) (with \(m\) space dimension) denotes input vector selected randomly from the input domain

$$\bar{x} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \ldots & {x_{m} } \\ \end{array} } \right]^{T}$$
(1)

The vector of synaptic weight (reference vector) of each node in the output layer has the same dimension of the input space (\(m\)). Let the synaptic weight vector of a node \(j\) be denoted by

$$\bar{w}_{j} = \left[ {\begin{array}{*{20}c} {w_{1} } & {w_{2} } & \ldots & {w_{m} } \\ \end{array} } \right]^{T} ,\quad j = 1,2, \ldots ,l$$
(2)

where \(l\) is the number of nodes in the map. To determine the best match node (BMN) of \(\bar{x}\) that has a synaptic weight of \(\bar{w}_{j}\), the algorithm computes the inner products \(\bar{w}_{j}^{T} \bar{x}\) for \(j = 1,2, \ldots ,l\), then the node with the leading inner product value is selected as BMN.

The best matching condition, \(\bar{w}_{j}^{T} \bar{x}\) is maximized, is expressed mathematically as Euclidean distance minimization between \(\bar{x}\) and \(\bar{w}_{j}\). If \(i(\bar{x})\) defines the BMN for \(\bar{x}\), \(i(\bar{x})\) could be computed by [50]

$$i(\bar{x}) = \arg \hbox{min} \left\| {\bar{x} - \bar{w}_{j} } \right\|,\quad j = 1,2, \ldots ,l$$
(3)

The BMN locates of a topological neighborhood of cooperating nodes on the map. Then, more nodes surrounding the BMN are adjusted. Mathematically, let \(h_{ki}\) denotes the topological neighborhood centered on the wining node \(i\), and \(k\) denotes a typical node of a set of excited (cooperating) nodes around wining node \(i\). The distance between wining node \(i\) and excited cooperating \(k\) is defined by \(d_{ik}\). Then, the topological neighborhood \(h_{ki}\) is defined as a function of the distance \(d_{ik}\), such that it satisfies two different conditions:

  1. 1.

    \(h_{ki}\) has a peak value at the BMN \(i\) for which the distance \(d_{ik}\) is diminished; in other words, it is symmetric about \(d_{ik} = 0\)

  2. 2.

    The topological neighborhood \(h_{ki}\) amplitude decreases monotonically with increasing lateral distance \(d_{ik}\), decaying to zero for \(d_{ik}\) approaches infinity; this is an important condition to obtain a better convergence.

A typical choice of \(h_{ki}\) that fulfills the aforementioned conditions is the well-known Gaussian function [50]

$$h_{ki} = \text{e}^{{\left( {\frac{{d_{ik}^{2} }}{{2\sigma^{2} }}} \right)}}$$
(4)

which is independent of the BMN location. Where \(\sigma\) is a parameter defines the effective width of the topological neighborhood. It measures the degree of participation in the learning process between the BMN and its excited neighbors.

The lateral distance \(d_{ik}\) between winning neuron \(i\) and excited neuron \(k\) is defined as [52]

$$d_{ik}^{2} = \left\| {\bar{r}_{k} - \bar{r}_{i} } \right\|^{2}$$
(5)

where the vector \(\bar{r}_{k}\) defines the position of excited node \(k\) and \(\bar{r}_{i}\) defines the position of winning node \(i\).

In addition, the topological neighborhood size shrinks with time based on the following exponential decay function [52]

$$\sigma = \sigma_{o} e^{{ - \frac{n}{\tau }}}$$
(6)

where \(\sigma_{o}\) is the initial value of \(\sigma\) and is equal to the lattice radius, \(n\) is the discrete time parameter and \(\tau\) is a time constant through the entire learning process which may be evaluated from [52]

$$\tau = {\raise0.7ex\hbox{${1000}$} \!\mathord{\left/ {\vphantom {{1000} {\log (\sigma_{o} )}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\log (\sigma_{o} )}$}}$$
(7)

By definition, for unsupervised and self-organizing ANN, \(\bar{w}_{j}\) of neuron \(j\) should be adjusted according to its relation to the input vector \(\bar{x}\); namely, \(\bar{w}_{j}\) is changed towards the input vector \(\bar{x}\). The synaptic weight vectors of all nodes are updated according to the following algorithm is [53]

$$\bar{w}_{j} (n + 1) = \bar{w}_{j} (n) + \alpha (n)h_{ki} (n)(\bar{x} - \bar{w}_{j} (n))$$
(8)

where \(\alpha (n)\) denotes the learning rate which decayed exponentially and evaluated by

$$\alpha (n) = \alpha_{o} {\text{e}}^{{\left( { - \frac{n}{\tau }} \right)}}$$
(9)

where \(\alpha_{o}\) is the initial learning rate and be chosen by experience to be less than 0.5 and \(\tau\) is a time constant.

These training procedures are repeated using a random selected input vector at each step to ensure that every input vector has been selected as an input pattern. It ensures the good formulation of feature areas on the lattice (map). Termination of the training process takes place after passing pre-specified number of training epochs.

2.2 SOM offline learning

Offline learning of SOM is accomplished using training data found in the literature according to the procedures described in the previous sections. The training vector is comprised of the nanofluid code (\(\chi_{ij}\)); where \(\chi\) is the code of the nanofluid number, \(i\), \(i = 1,2, \ldots ,m\), \(m\) is the number nanofluids, \(j = 1,2, \ldots ,n\), and \(n\) is the total number of the experimental data, \(\varphi_{ij}\) is the volume fraction of nanofluid \(i\) at instant \(j\), \(T_{ij}\) the accordance temperature at each experiment, \(d_{ij}\) is the nanoparticle diameter, and \(r_{ij}\) is the TCR between the nanofluid and base fluid, then the resultant vector will be

$$x_{ij} = \left[ {\begin{array}{*{20}c} {\chi_{ij} } & {\varphi_{ij} } & {T_{ij} } & {d_{ij} } & {r_{ij} } \\ \end{array} } \right]$$
(10)

2.3 SOM online testing

After the off-line learning of the SOM, the trained SOM is tested online. TCR, at least, is the unknown parameter, while nanofluid code, volume fraction, temperature and nanoparticles diameters are the known parameters. SOM is provided by a subspace of the input vector to compute the target output. This can be accomplished by using a projection matrix defined in Eq. (11) [54] that pre-multiplied by the input vector and defined as:

$$P = \left[ {\begin{array}{*{20}c} {I_{d} } & 0 & \ldots & 0 \\ 0 & 0 & \ldots & \ldots \\ \ldots & \ldots & \ldots & 0 \\ 0 & \ldots & 0 & 0 \\ \end{array} } \right]$$
(11)

where \(I_{d}\) denotes the identity matrix. Then the input vector \(x_{kj}\) is pre-multiplied by the projection matrix \(P\) to get the new input vector \(x_{kj}^{'}\)

$$\begin{aligned} x_{ij}^{'} & = P[x_{ij} ]^{T} \\ \, & = \left[ {\begin{array}{*{20}c} {\chi_{ij} } & {\varphi_{ij} } & {T_{ij} } & {d_{ij} } & 0 \\ \end{array} } \right]^{T} \\ \end{aligned}$$
(12)

It worthy mentioned that the minimization of the Euclidean distance will be calculated between the modified input vector \(x_{ij}^{'}\) and the modified weight vectors \(Pw_{j}\).

To get the TCR, the winning node output weight vector \(w_{j}\) is pre-multiplied the difference between the projection matrix and its corresponding identity matrix \((I - P)\). Then the required subspace of the weight vector \(w_{j}^{'}\) which represents the required heat fluxes and their position is calculated as follows

$$\begin{aligned} w_{j}^{'} & = \left( {I - P} \right)w_{j} \\ \, & = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {r_{ij} } \\ \end{array} } \right]^{T} \\ \end{aligned}$$
(13)

2.4 SOM quality estimation

Herein, the quantization error \(Q_{\text{e}}\) as a well-known criterion to investigate the map resolution of the SOM [55], is introduced to represent the SOM fitting to a given training data. The quantization error is evaluated by calculating the average distance between the input training vectors and the corresponding BMN’s. For any given training dataset, the quantization error can be simply reduced by increasing the number of map nodes, thus the training data are distributed more sparsely inside the map. The error of quantization is computed by:

$$Q_{e} = \frac{1}{N}\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left\| {x_{ij} - w_{{x_{ij} }} } \right\|} }$$
(14)

where \(N\), \(w_{{x_{ij} }}\), and \(x_{ij}\) denote the number of the training datasets, the BMN, the input vector, respectively. Our goal is to decrease the \(Q_{e}\) as much as possible (may be this is constrained by the available commercial computing hardware).

3 Results and discussions

In this section, two different examples will be illustrated to demonstrate the validity of the proposed method to predict the TCR for three types of water based nanofluids using three different nanoparticles, namely, aluminum oxide (Al2O3), copper oxide (CuO), and titanium oxide (TiO2). The goal is the prediction of the unknown TCR of the nanofluids based on measured data available in the literature. Both theoretical and experimental data are used as training data to the SOM. After SOM formation and training, unused data in the training process is used to test the validity of the approach.

SOM network with two-dimensional structure is used. The training process of the SOM is performed according to the procedures described in Sect. 2. The initial value of the learning rate \(\alpha_{o} = 0.3\) and decreases gradually up to \(\alpha_{f} \simeq 0.01\) with time constant \(\tau = 1000\);while the Gaussian function width parameter \(\sigma\) starts with \(\sigma_{o}\) equal to the lattice radius and decreases gradually with time constant calculated according to Eq. (7). The quantization error \(Q_{e}\) of different simulation results is ranged from 0.735 to 0.956 which is considered to be agreeable.

3.1 Example 1

In this illustrated example we will consider two types of nanofluids (Al2O3/water and CuO/water). The training data are generated from the theoretical model developed by [56] based on their experimental results. The main goal of this example, as the first step, is to investigate the validity of the proposed method to solve the problem understudy and avoiding the measuring errors which appeared during experiments and may affect the training process. According to their study, CuO and Al2O3 nanoparticles with average diameters of 29 and 36 nm, respectively, were mixed with water at volume fractions of 2%, 4%, 6%, and 10% and the experiments carried out at temperatures ranging from 27.5 to 34.7 °C. The empirical formulas of the TCR as a function in the volume fraction and the temperature for Al2O3/water and CuO/water nanofluids are given by:

$$r_{A} = 0. 5 3 7 8 5+ 0. 7 6 4 4 8\times \varphi_{A} + 0. 0 1 8 6 8\times T_{A}$$
(15)
$$r_{B} = 0. 6 9 2 6 6+ 3. 7 6 1 0 8 8\times \varphi_{B} + 0. 0 1 7 9 2 4\times T_{B}$$
(16)

where \(r\), \(\varphi\), and \(T\) denote the TCR, volume fraction and temperature in Celsius, respectively; and the subscripts \(A\) and \(B\) are used for Al2O3/water and CuO/water nanofluids, respectively.

For both nanofluids, the training data was taken at volume fraction ranged from 2 to 10% with step equal to 0.5% and temperature ranged from 27.5 to 32.5 °C with step equal to 0.5 °C with total number of data for each nanofluid equal to 255 as shown in Fig. 2. In this figure, CuO/water exhibits a better thermal conductivity ratio compared with Al2O3/water at all investigated conditions. However, it is worth to mention that CuO is unstable and is oxidized in water at T > 150 °C, so Al2O3/water nanofluid is a better choice for high temperature applications. All the training data elements, i.e., \(\chi_{ij}\), \(\varphi_{ij}\), \(T_{ij}\), \(d_{ij}\), and \(r_{ij}\), are normalized, before given to the SOM, to be ranged from − 1 to 1 with unitary variance and zero mean. So that the efficiency of the training process is enhanced by preventing the data dispersion to take place, as all input elements have the same importance regardless the magnitude of their values. After the learning process is finished, all data including the weights of SOM nodes are reverse-normalized.

Fig. 2
figure 2

Effect of the temperature and the volume fraction on the variation of TCR of: a Al2O3/water nanofluids, b CuO/water nanofluids

Full size image

To check the validity of the proposed method to solve the problem in hand, the network is tested using a new data which did not give to the network in the training process. Then, the SOM accuracy, as an estimation model, is evaluated by two different error related performance criteria, i.e., mean squared error (MSE) and mean absolute percent error (MAPE), between the exact (actual) and predicted values from the SOM which can be evaluated from the following relationships:

$$MSE = \frac{1}{t}\sum\limits_{i = 1}^{t} {\left( {x_{exact,i} - x_{pred,i} } \right)^{2} }$$
(17)
$$MAPE = \left( {\frac{1}{t}\sum\limits_{i = 1}^{t} {\left| {\frac{{x_{exact,i} - x_{pred,i} }}{{x_{exact,i} }}} \right|} } \right) \times 100$$
(18)

where \(t\) is the number of test points, \(x_{exact}\) are the exact values obtained from literature and \(x_{pred}\) are the predicted values obtained from the SOM model.

Smaller values of MSE and MAPE indicate better performance of the network.

Figure 3a, b shows the scatter plot of the predicted values obtained from the SOM model versus the exact values obtained from literature for Al2O3/water and CuO/water nanofluids, respectively. The known parameters fed to the network in the this test were \(\chi_{ij}\), \(\varphi_{ij}\), \(T_{ij}\), and \(d_{ij}\) which picked up randomly from the literature data to predict the corresponding unknown \(r_{ij}\) values. It is observed from this figure that the obtained results are acceptable. The MSE for Al2O3/water and CuO/water nanofluids are 9.4402e−06 and 8.2908e−05, respectively. While, the MAPE for Al2O3/water and CuO/water nanofluids are 0.2354% and 0.5358%, respectively.

Fig. 3
figure 3

Predicted versus exact values of TCR over the test datasets: a Al2O3/water nanofluids, b CuO/water nanofluids

Full size image

Figure 4a, b shows a comparative plot between the predicted values and the corresponding exact values of the TCR for Al2O3/water and CuO/water nanofluids, respectively, as a function of the temperature at different volume fractions (3.2, 5.8, and 8.4%). While, Fig. 5a, b shows a comparative plot between the predicted values and the corresponding exact values of the TCR for Al2O3/water and CuO/water nanofluids, respectively, as a function of the volume fraction at different temperature values (26.6, 30.2, and 33.8 °C). These two figures demonstrate the capability of the proposed method to predict the target values of the TCR regardless the nature of the input test datasets as long as the training process is achieved in a correct manner with sufficient and effective training datasets.

Fig. 4
figure 4

Effect of variations of the temperature on the TCR for three different volume fractions and the predicted values of the proposed ANN model. a Al2O3/water nanofluids, b CuO/water nanofluids

Full size image
Fig. 5
figure 5

Effect of variations of the volume fraction on the TCR for three different temperature values and the predicted values of the proposed ANN model. a Al2O3/water nanofluids, b CuO/water nanofluids

Full size image

3.2 Example 2

Herein, the proposed method will be applied to predict the TCR of TiO2/water nanofluid. The SOM performance will be investigated using training and test datasets from the available experimental results in the literature as reported in Table 1. This table shows the thermal conductivity of TiO2 reported in previous studies [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71]. Three different parameters have been included in this table: particle size, particle volume fraction, and temperature. The training data was taken at volume fraction ranged from 0.2 to 9.77%, temperature ranged from 1 to 70 °C, and particle diameters ranged from 5 to 100 nm with total number of 150 training vectors. After normalization of the training data components, i.e., \(\varphi_{ij}\), \(T_{ij}\), \(d_{ij}\), and \(r_{ij}\), the data are fed to the network. Finally, after finishing the learning process, all data including the weights of SOM nodes are reverse-normalized.

Table 1 Some previous studies on the thermal conductivity of TiO2/water nanofluid
Full size table

Figure 6 shows the scatter plot of the predicted values obtained from the SOM model versus the exact values found in literature TiO2/water nanofluid. The known parameters fed to the network in the this test were \(\varphi_{ij}\), \(T_{ij}\), and \(d_{ij}\) which picked up randomly from the literature data to predict the corresponding unknown \(r_{ij}\) values. The MSE and the MAPE for the resulted data were 5.5381e−05 and 0.5978%, respectively.

Fig. 6
figure 6

Predicted versus exact values of TCR over the test datasets for TiO2/water nanofluids

Full size image

The predicted results in this study imply that ANN may be used as a robust tool to predict the thermal conductivity of nanofluids. Moreover, it is recommended to apply different metaheurestic methods [72,73,74,75,76] to select the optimal nanofluids parameters that maximize their utilization as heat transfer fluid.

4 Conclusion

A general and accurate SOM model is used to predict TCR of oxide (Al2O3, CuO and TiO2)/water nanofluids under various operating conditions. The network was trained using both theoretical and experimental data available in literature. The model can not only learn multiple input parameters, such as nanofluid type, TCR, nanoparticle size, temperature, nanoparticle volume fraction, but also can be tested using multiple unknown parameters. The maximum mean squared error (MSE) of the SOM model is only 8.2908e−05; and the mean absolute percent error (MAPE) is 0.5978%. The proposed approach is accurate, fast, simple, robust, and applicable for any type of nanofluids. Furthermore, it can also be readily extended to predict any other thermo-physical properties of the nanofluids, which is our future work.