Mathematical modeling of micropolar fluid in blade coating using lubrication theory

Abstract

The blade coating process of a micropolar fluid using the plane and exponential coater has been studied. Equations are simplified utilizing lubrication approximation theory. The analytical expressions for flow rate, pressure gradient, and velocity are obtained, while load and coating thickness are computed numerically with the help of the shooting method. We show how the microrotation parameters $\epsilon$ and the coupling number $N$ influence the flow characteristics, such as pressure distribution, velocity, pressure gradient and related engineering quantities such as load and thickness in the blade coating process, and they are shown graphically as well as in tabular form. We find that, for coupling number $N$ and microrotation parameter $\epsilon$, the pressure increases when compared to the Newtonian fluid. Moreover, the coating thickness decreases for the Newtonian case when $N$ increases.

1 Introduction

Blade coating is a process in which a fluid layer is applied onto a moving substrate. The purpose of the coating is to protect or decorate an object as the coating improves the efficiency, quality, and life of the substrate. The coating is used widely at an industrial level due to its practical application and benefits. It is commonly used in paint industries, photographic films, magnetic storage devices, manufacturing of newspapers, metal coating, textile fibers, and electronic circuit boards, etc. Landau and Levich [1] have given the first coating technology description. They conducted a mathematical analysis of a liquid film in the dip-coating process. Booth [2] has given the example of coating of butter over toast described the relation between the angles of the blade with coating weight. Basically, in the blade coating process, the fluid flows in a gap between the blade and the moving substrate. The shear stress induced by the moving substrate is responsible for the flow. Naturally, coating films range from 10 to 50 μm. The article by Ruschak [3] and book by Middleman [4] are very helpful to understand the phenomenon of blade coating. Greener and Middleman [5] investigate coating theoretically and experimentally using viscous fluid on a two roll-coaters. The coating flows for Newtonian fluids were also presented by Kistler and Schweizer [6]. Ali et al. [7] studied the roll-over-web coating by using couple stress fluid. Atif et al. [8] used micropolar fluid in the study of the roll-over-web coating. Ross et al. [9] used power-law fluid in the blade coating process. He investigated the results using exponential and plane coater. Dien and Elrod [10] and Hwang [11] also studied the power-law fluid for a plane coater. Williamson fluid model was developed by Siddiqui et al. [12] to study the blade coating process. A mathematical model for a third-grade fluid in the process of blade coating was developed and analyzed by Sajid et al. [13]. Sajid et al. [14] used viscous fluid to investigate the magnetohydrodynamics and slip effects in the blade coating process. Shahzad et al. [15] studied blade coating analysis of an Oldroyd 4-constant fluid. They used LAT to simplify the equations of motions and obtained the numerical solution using stream functions.

Taylor and Zettlemoyer [16] used LAT to investigate the behavior of ink flow in printing. Hintermaier and White [17] also used LAT for the model of water flow between two rolls. Greener and Middleman [18] also used lubrication approximation theory for forward roll coating of viscous and viscoelastic fluids. Benkreira et al. [19] improved the Greener and Middleman model to a general case of two equal and nonequal rollers. Hsu et al. [20] used LAT and compared results theoretically and experimentally. Coyle et al. [21] used LAT to solve the Navier–Stokes equations and compared the results obtained by finite element techniques. The LAT model was accurate at high capillary numbers where the surface tension effect is weak. Carvalho and Scriven [22] found that LAT, at low capillary numbers (0 < Ca < 1), matches with finite element method results. LAT is used by Siddiqui et al. [23] for finding the effect of magnetohydrodynamics on Newtonian calendaring. Most recently Xu et al. [24] used LAT to analyze the sealing performance of VL seals.

Eringen [25] was the first who introduced the micropolar fluid theory in which he extended the Navier–Stokes theory to include the microrotation effects. Physically, fluids consisting of random particles suspended in the viscous medium are called micropolar fluids. These particles are confined in a little volume element and can rotate about its centroid. The motion of these particles results in internal fluid rotation in a volume element. To include these internal fluid particle rotations in volume element, additional laws of microinertia and balance of angular momentum are needed along with classical fluid dynamics. As a result, the field equations have two vector fields, called microrotation and velocity vector. A microrotation vector is used to represent the rotation. Lukaszewicz [26] discussed the mathematical model of micropolar fluid using LAT and porous media. Seddeek [27] investigated magnetic effects on micropolar fluid moving on a plate. Youn and Lee [28] studied two-dimensional micropolar fluid moving on a vertical porous plate in the presence of a magnetic field. Sherief et al. [29] studied the interaction between two rigid spheres moving in a micropolar fluid with slip surfaces. For further study on micropolar fluids and its importance in industry, readers are referred to [30,31,32,33,34].

The main contribution of this study is the investigation of the effects of microrotation and coupling number in the blade coating process using LAT. To determine the effects of microrotation and coupling number on flow characteristics, the mixture of the analytical and numerical solution are used. The paper is arranged as follows: The governing equations, mathematical formulation, and solution to the problem are discussed in the next section. In the result and discussion section, graphical results are discussed. In the final section, the conclusion is presented.

2 Governing equations and mathematical modeling

The governing equations for incompressible micropolar fluid are defined as [35]

$$\nabla .\varvec{V} = 0$$

(1)

$$\rho \left( {\varvec{V}.\nabla } \right) \varvec{V} = - \nabla p + k^{*} \nabla \times \varvec{q} + \left( {\mu + k^{*} } \right)\nabla^{2} \varvec{V}$$

(2)

$$\rho j\left( {\varvec{V}.\nabla } \right)\varvec{q} = - 2k\varvec{q} + k^{*} \nabla \times \varvec{V} - \gamma \left( {\nabla \times \nabla \times \varvec{q}} \right) + \left( {\alpha + \beta + \gamma } \right)\nabla \left( {\nabla .\varvec{q}} \right)$$

(3)

Notice that if $\alpha = \beta = \gamma = k^{*} = 0$, then $\varvec{q} = 0$ (microrotation) and Eq. (2) reduces to classical Navier–Stokes equations. Also, if $k^{*} = 0$, the $\varvec{q}$ and $\varvec{V}$ are uncoupled and consequently, microrotation has no effects on global motion. According to Eringen [35], it is essential that $\alpha ,$ $\beta$ and $\gamma$ satisfy the following

$$2\mu + k^{*} \ge 0, k^{*} \ge 0, 3\alpha + \beta + \gamma \ge 0, \gamma \ge \left| \beta \right|.$$

(4)

Consider the two-dimensional blade coating model in the Cartesian coordinate system (see Fig. 1). The substrate is placed at $y = 0$ and moving in the $x$-direction having constant velocity $U$. The blade (length of the blade is $L$) is fixed at an angle $\tan \theta = \frac{{H_{1} - H_{0} }}{L}$. The edges of the blade have heights $H_{0}$ and $H_{1}$ at $x = L$ and $x = 0$, respectively. We assume lubrication approximation theory is valid. An incompressible micropolar fluid dragged into the wedge formed between the blade and moving substrate, leaving a thin layer on a substrate having thickness $H$.

Fig. 1

Geometry of the blade coating process

Velocity and microrotation for two-dimensional flow are defined as

$$\varvec{V} = [u\left( {x,y} \right),v\left( {x,y} \right),0]$$

(5)

$$\varvec{q} = [0,0,q(x,y)]$$

(6)

Using Eqs. (5) and (6) into Eqs. (1)–(3), one gets

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(7)

$$\rho \left[ {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right] = - \frac{\partial p}{\partial x} + k^{*} \frac{\partial q}{\partial y} + \left( {\mu + k^{*} } \right)\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)$$

(8)

$$\rho \left[ {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right] = - \frac{\partial p}{\partial y} - k^{*} \frac{\partial q}{\partial x} + \left( {\mu + k^{*} } \right)\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)$$

(9)

$$\rho j\left[ {u\frac{\partial q}{\partial x} + v\frac{\partial q}{\partial y}} \right] = - 2kq + k^{*} \left( {\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}} \right) + \gamma \left( {\frac{{\partial^{2} q}}{{\partial x^{2} }} + \frac{{\partial^{2} q}}{{\partial y^{2} }}} \right)$$

(10)

The suitable boundary conditions are

$$u = U\;{\text{on}}\;y = 0$$

(11)

$$u = 0\;{\text{on}}\;y = h(x)$$

(12)

$$q = 0\;{\text{on}}\;y = 0$$

(13)

$$q = 0\;{\text{on}}\;y = h(x)$$

(14)

Equations (13) and (14) imply that the rotation of polymer molecules near the substrate and at the surface of the blade is zero.

To get the characteristic scales for the pressure and velocity, the order of magnitude analysis is conducted, where the scales $x$, $y$ and $u$ are defined in the following manner:

$$x \sim L_{\text{c}} , y \sim H_{0} , u \sim U$$

(15)

Using Eq. (15) in (7), we get

$$\frac{v}{U}\sim\frac{{H_{0} }}{{L_{\text{c}} }}$$

(16)

which shows $v \ll u$, and $H_{0} \ll L$.

From the above discussion, the dimensionless variables are defined as

$$\bar{u} = \frac{U}{u}, \bar{x} = \frac{x}{L}, \bar{y} = \frac{y}{{H_{0} }}, \bar{p} = \frac{{ H_{0}^{2} p}}{\mu U L}, \bar{h} = \frac{h}{{H_{0} }}, \bar{q} = \frac{{H_{0} q}}{U}, \bar{j} = \frac{j}{{H_{0}^{2} }} ,$$

(17)

Using Eq. (17) into Eqs. (7)–(10), (omitting the bar sign for simplicity), one gets

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(18)

$$\text{Re} \times Z\left[ {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right] = - \frac{\partial p}{\partial x} + N\frac{\partial q}{\partial y} + \left( {1 + N} \right)\left( {Z^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)$$

(19)

$$\text{Re} \times Z^{3} \left[ {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right] = - \frac{\partial p}{\partial y} + NZ^{2} \frac{\partial q}{\partial x} + \left( {1 + N} \right)Z^{2} \left( {Z^{2} \frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)$$

(20)

$$\text{Re} Z j\left[ {u\frac{\partial q}{\partial x} + v\frac{\partial q}{\partial y}} \right] = - 2Nq + N\left( {Z^{2} \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}} \right) + \epsilon \left( {Z^{2} \frac{{\partial^{2} q}}{{\partial x^{2} }} + \frac{{\partial^{2} q}}{{\partial y^{2} }}} \right)$$

(21)

where

• $N$ is coupling number and is defined as, $N = \frac{{k^{*} }}{\mu }$.

• $\text{Re} = \frac{{\rho UH_{0} }}{\mu }$ (the Reynolds number). For coating flows, it is less than one.

• $Z = \frac{{H_{0} }}{L}$ (the geometric parameter).

• $l = \sqrt {\frac{\gamma }{\mu }}$ (the characteristic material length). It is associated with the size of polymer molecules.

• $\epsilon = \frac{{l^{2} }}{{H_{0}^{2} }}$ is the micropolar parameter.

In the nip region, $H_{0} \ll L$, i.e., the gap between the blade edge and the substrate is very small, which gives $Z \ll 1$. Thus, the above system of equations is simplified as

$$\left( {1 + N} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + N\frac{\partial q}{\partial y} = \frac{\partial p}{\partial x}$$

(22)

$$\frac{\partial p}{\partial y} = 0$$

(23)

$$\epsilon \frac{{\partial^{2} q}}{{\partial y^{2} }} - 2Nq - N\frac{\partial u}{\partial y} = 0$$

(24)

The dimensionless form of the boundary conditions is

$$u = 1\;{\text{on}}\;y = 0$$

(25)

$$u = 0\;{\text{on}}\;y = h(x)$$

(26)

$$q = 0\;{\text{on}}\;y = 0$$

(27)

$$q = 0\;{\text{on}}\;y = h(x)$$

(28)

where $h\left( x \right)$ is defined as

$$h\left( x \right) = \left\{ {\begin{array}{*{20}l} {k - \left( {k - 1} \right)x,} \hfill & { {\text{for}}\;{\text{plane}}\; {\text{coater}}} \hfill \\ {k^{1 - x} } \hfill & { {\text{for}}\;{\text{exponential}}\; {\text{coater}}} \hfill \\ \end{array} } \right.$$

where $k = \frac{{H_{1} }}{{H_{0} }}$. Eliminating $u$ from Eqs. (22) and (24), we have

$$\frac{{\partial^{2} q}}{{\partial y^{2} }} - Aq = B\left( {\frac{\partial p}{\partial x}y + c_{1} } \right)$$

(29)

where $c_{1}$ is constant of integration, $A = \frac{{\left( {2 + N} \right)N}}{{\epsilon \left( {1 + N} \right)}}$ and $B = \frac{N}{{\epsilon \left( {1 + N} \right)}}$.

From Eqs. (29) and (22), we have

$$q\left( {x,y} \right) = c_{2} \cosh \sqrt A y + c_{3} \sinh \sqrt A y - \frac{{B\left( {\frac{{{\text{d}}p}}{{{\text{d}}x}}y + c_{1} } \right)}}{A}$$

(30)

$$u\left( {x,y} \right) = - a_{1} c_{2} \sinh \sqrt A y - a_{1} c_{3} \cosh \sqrt A y + \frac{{{\text{d}}p}}{{{\text{d}}x}}\frac{{y^{2} a_{2} }}{2} + c_{1} ya_{2} + c_{4}$$

(31)

where $c_{1} - c_{4}$ are constants of integration and can be found with the help of Eqs. (25)–(28).

$$c_{1} = \frac{{ - 2a_{1} \frac{{{\text{d}}p}}{{{\text{d}}x}}Bh\left[ { - 1 + \cosh \sqrt A h} \right] + A\left( {2 + a_{2} \frac{{{\text{d}}p}}{{{\text{d}}x}}h^{2} } \right)\sinh \left( {\sqrt A h} \right)}}{{4a_{1} B\left[ { - 1 + \cosh \left( {\sqrt A h} \right)} \right] - 2Aa_{2} h \sinh \left( {\sqrt A h} \right)}}$$

(32)

$$c_{2} = \frac{{B\left[ {2a_{1} \frac{{{\text{d}}p}}{{{\text{d}}x}}B h\left( { - 1 + \cosh \sqrt A h} \right)} \right] - A\left( {2 + a_{2} \frac{{{\text{d}}p}}{{{\text{d}}x}}h^{2} } \right)\sinh \left( {\sqrt A h} \right)}}{{2A\left[ { - 2a_{1} B\left( { - 1 + \cosh \left( {\sqrt A h} \right)} \right)} \right] + Aa_{2} h\sinh \left( {\sqrt A h} \right)}}$$

(33)

$$c_{3} = \frac{{\frac{{{\text{d}}p}}{{{\text{d}}x}}Bh\coth \left( {\frac{\sqrt A h}{2}} \right)}}{2A} + \frac{B}{{ - 2a_{1} B + Aa_{2} h\coth \left( {\frac{\sqrt A h}{2}} \right)}}$$

(34)

$$c_{4} = \frac{{1 + a_{1} \frac{{{\text{d}}p}}{{{\text{d}}x}}Bh\coth \left( {\frac{\sqrt A h}{2}} \right)}}{2A} + \frac{{a_{1} B}}{{ - 2a_{1} B + Aa_{2} h\coth \left( {\frac{\sqrt A h}{2}} \right)}}$$

(35)

where $a_{1} = \frac{N}{(1 + N)\sqrt A }$ and $a_{2} = \frac{A + BN}{A(1 + N)}$.

Volumetric flow rate $Q$, per unit width $W$, is defined as

$$\frac{Q}{W} = \mathop \int \limits_{0}^{h\left( x \right)} u{\text{d}}y$$

(36)

which is related to final coating thickness as

$$\frac{Q}{W} = UH$$

(37)

Using Eq. (31) into Eq. (36), the pressure gradient in dimensionless form is obtained.

$$\frac{{{\text{d}}p}}{{{\text{d}}x}} = \frac{{6A^{2} (h - 2\lambda )(1 + N)}}{{h\left( {12 N + A h^{2} (A + BN) - 6\sqrt A B h N\coth \left[ {\frac{\sqrt A h}{2}} \right]} \right)}}$$

(38)

where

$$\lambda = \frac{H}{{H_{0} }}.$$

The appropriate boundary conditions for pressure are

$$p\left( 0 \right) = 0 = p\left( 1 \right)$$

(39)

The analytical solution of Eq. (38) is not possible. So, it is solved numerically with the help of Eq. (39) to get the pressure and $\lambda$.

The load ${\mathcal{L}}$ on the blade surface is calculated as

$${\mathcal{L}} = \mathop \int \limits_{0}^{1} p{\text{d}}x$$

(40)

3 Results and discussion

The blade coating process has been studied using the plane, and exponential coater for micropolar fluid. The governing equations are simplified with the help of the lubrication approximation theory. To investigate the behavior of velocity, pressure gradient and pressure in the presence of coupling number $N$, microrotation parameter $\epsilon$, and normalized coating thickness $k$, graphs are drawn for variation of involved parameters that describe the flow. For this purpose, Figs. 2, 3, 4, 5, 6, 7 and 8 are presented. The results for plane coater are shown in panel (A), whereas panel (B) represents exponential coater. Physical parameters that are involved in the coating process are listed in Table 1 [8, 36, 37].

Fig. 2

Effects of $k$ on pressure distribution (A plane coater, B exponential coater)

Fig. 3

Effects of $N$ on pressure distribution (A plane coater, B exponential coater)

Fig. 4

Effects of $\epsilon$ on pressure distribution (A plane coater, B exponential coater)

Fig. 5

Plot for $p_{\hbox{max} }$ for different $N$ against $k$ (A plane coater, B exponential coater)

Fig. 6

Plot for $p_{\hbox{max} }$ for different $\epsilon$ against $k$ (A plane coater, B exponential coater)

Fig. 7

Effects of $N$ on pressure gradient (A plane coater, B exponential coater)

Fig. 8

Effects of $\epsilon$ on pressure gradient (A plane coater, B exponential coater)

Table 1 List of parameters used in coating process [8, 36, 37]

Figure 2 plots pressure against axial position $x$ for variation of normalized coating thickness $k$. A comparison is also made between the Newtonian fluid with the coupling number $N$. It is obvious from Fig. 2A that the magnitude of the pressure is greater than for the Newtonian fluid that the pressure is decreasing function of $k$ and that the maximum shifts toward the blade tip. It means that physically, the thickness increases with the increasement in the normalized coating parameter $k$ and that the maximum shifts toward the blade tip. Therefore, less pressure is required to maintain the flow. Also, near the tip of the blade, we have sharper pressure distribution. A similar trend can be seen for an exponential coater (Fig. 2B).

Figure 3A, B shows how the coupling number $N$ affects the pressure against axial position $x$. For $N = 0$, the results are matched with the results of Sajid et al. [14] results for the viscous case. For the viscous case, less pressure is required to maintain the flow. However, when the coupling number $N$ increases, the pressure also increases (see Fig. 3A, B).

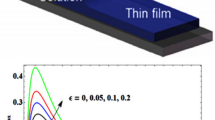
Figure 4 plots the pressure distribution for increasing values of microrotation parameter $\epsilon$. One sees that if the microrotation parameters increase, we need more pressure to maintain the flow.

In Figs. 5 and 6, $p_{\hbox{max} }$ is plotted against normalized coating thickness parameter $k$ to demonstrate the effects of coupling number $N$ and microrotation parameter $\epsilon$, respectively. For small values of $k$, maximum pressure increases and then starts decreasing with an increasing value of $k$. Also, for both cases (A and B) plot for $N = 0$ is similar to the Newtonian case. $p_{\hbox{max} }$ increases with increasing value of $N$ (coupling number) for both plane and exponential coater. Furthermore, for large values of normalized coating thickness parameter $k$, the influence of the coupling number reduces; see Fig. 5A, B.

In Fig. 6 a similar trend can be seen for microrotation parameter $\epsilon$, in both plane and exponential coater cases, $p_{\hbox{max} }$ increases. (see Fig. 6A, B)

Figures 7 and 8 show how coupling number $N$ and microrotation parameters $\epsilon$ effect on the pressure gradient. The pressure gradient increases with an increasing value of $N$ and $\epsilon$.

Table 2 gives numerical values of load and thickness for different coupling number $N$. For $N = 0$, the results are matched with the Newtonian fluid case, and for increasing $N$ the thickness reduces while loading increases.

Table 2 Numerical values of load and thickness for coupling number $\left( N \right)$

4 Conclusion

A blade coating analysis of a micropolar fluid using the plane and exponential coater has been presented. The equations of motions are simplified using LAT. The exact solution for pressure gradient, microrotation, velocity, and flow rate has been obtained. On the other hand, pressure, thickness, and load are computed numerically. Graphs display how the microrotation parameter and coupling number affect the pressure gradient, velocity, pressure, load, and thickness.

The main findings are listed below.

• Pressure and pressure gradient are decreasing functions of normalized coating thickness $k$. Physically it means that when $k$ increases, the coating thickness increases; hence, we need less pressure to maintain the flow.

• At the surface of the substrate, velocity decreases with a large microrotation parameter. However, moving away from the substrate, it is an increasing function of the microrotation parameter.

• The loading on the blade increases when the coupling number increases.

• The micropolar fluid reduces the coating thickness when compared to the Newtonian case.