Modeling and simulation of an integrated octagonal planar transformer for RF systems

Abstract

The work presented in this paper concerns the modeling of an integrated transformer in monolithic technology for high frequencies containing coils of planar type and magnetic circuit made of several layers of materials. Circular, square, and polygonal shapes of the planar coils are the important difference regarding transformer topologies. In this work, we have chosen the stacked octagonal form of coils. The transformer will be integrated into a converter of type flyback. We have opted for the Wheeler method and the S-parameters for determining the geometrical and the electrical parameters. The electrical π model presented summarizes perfectly the various parasitic effects generated by stacked layers of different materials constituting the transformer. The electromagnetic simulation, by using COMSOL Multiphysics 4.3 software, illustrates the current density and the distribution of magnetic field lines. We have also used software PSIM 6.0, to validate the equivalent electrical circuit of the transformer in flyback converter.

1 Introduction

Power electronics has never stopped to advance, since its appearance. Now, this discipline exists in the majority of electrical systems, ensuring control of energy supply and the integrity of the components. Passive components occupy 80% of electrical circuits’ surface as the low power converter. At present, the integration of active components has now become a classical thing; however, only the integration of passive components remains the obstacle of miniaturization [1, 2]. At the heart of isolated converters, there is an essential element, the transformer. To overcome the problem of integration and reducing the size of the transformer, the planar components were introduced [3,4,5]. The transformer is an inductive component formed by a thin magnetic circuit, usually made of ferrite, on which conductive coils are deposited. In these years, planar transformers are widely used in monolithic integrated circuits and are implemented in many systems for several applications [6, 7].

2 Presentation of the microtransformer

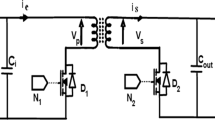
A transformer is an inductive component, it is considered as a device whose operation is based on mutual coupling between at least two inductors. Figure 1 shows a schematic diagram of an ideal transformer of two coils.

Fig. 1

Schematic diagram of transformer

In low frequencies, the behavior of the inductor is modeled by a pure inductance L in series with a resistance Rs, which characterizes the different losses (Fig. 2a). In high frequencies, the inductance L in series with resistance Rs are in parallel with capacitance Cs which characterizes the capacitive coupling between turns (Fig. 2b).

Fig. 2

Simplified model of inductor: a low frequency and b high frequency

The behavior of an integrated planar inductor on silicon was proposed in simple ‘‘π’’ model by Nguyen and Meyer and then was developed by Ashby and al (Fig. 3a). After, Yue and Yong presented a similar model with more appropriate parameters (Fig. 3b) [8, 9]. Later, Yamaguchi and al proposed the first equivalent circuit composed of magnetic material placed above or below the inductance (Fig. 3c), but the model became very complicated [10]; afterward, this work was simplified to show the different layers superimposed one on the other (Fig. 3d) [11].

Fig. 3

a Simple π model, b cross section of planar inductor, c ferromagnetic inductor, d cross section of planar inductor on ferrite

As a transformer is a coupling between two inductors, the integrated planar transformer composed of two integrated planar inductors was proposed by [12] (Fig. 4) which the coils are spiral with square form.

Fig. 4

a 3D cross section of an integrated planar transformer with square form of coils [12] and b equivalent electrical circuit

3 Presentation of octagonal planar transformer

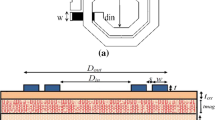
The coil’s shape is an important distinction regarding inductor and transformer topologies. Circular, square, and polygonal spirals have already mentioned to constitute their coils. In this study, we demonstrate another transformer model whose coils are of octagonal planar shape (Fig. 5).

Fig. 5

Octagonal topology of coils

3.1 Inductance value’s calculation

The calculation’s method developed by Wheeler [13] allows the inductance’s evaluation of hexagonal, octagonal or square form of coils, realized in a discrete way. This method is easy to implement, it has a low error compared with other methods, and it remains valid for reduced number of turns. The inductance L given by Wheeler method is represented by (expression 1):

$$ L = k_{1} \cdot \mu_{0} \cdot \frac{{n^{2} \cdot d_{\text{avg}} }}{{1 + k_{2} \cdot A_{\text{m}} }}, $$

(1)

d_avg is the average diameter, A_m is the form factor, n is the number of turns, and µ₀ is the vacuum permeability.

$$ d_{\text{avg}} = \frac{{d_{\text{out}} + d_{\text{in}} }}{2}, $$

(2)

$$ A_{\text{m}} = \frac{{d_{\text{out}} - d_{\text{in}} }}{{d_{\text{out}} + d_{\text{in}} }}. $$

(3)

The coefficients k₁ and k₂ depend on the different topologies of coils (Table 1).

Table 1 Values of coefficients k₁ and k₂ used in Wheeler method

Conferring to the form factor A_m, we can obtain the hollow or full inductors. Thus, a hollow inductor has a higher inductance than a full one because the turns located near the center of the spiral contribute to decrease the mutual positive inductances and increase the mutual negative inductances [13].

3.2 Feed lines position

As stacked topology is chosen in Fig. 5, the relative position between primary and secondary coils is considered in terms of the location of their feed lines. The proposition is to have the secondary completely rotated by 180-degree of the primary (Fig. 6). This configuration tends to weaken the coupling between coils because the feed lines are uncovered. The choice between these structures shows which one has better performance.

Fig. 6

Flipped transformer topologies

The inductance measurement results for transformers with flipped and non-flipped topologies are shown in Fig. 7. When the flipped topology is adopted, the curves illustrate a significant reduction in the resonant frequency. Self-inductances remain unchanged and magnetic coupling is weakened in low frequency. For frequencies greater than 100 MHz, flipped transformer demonstrates a lower minimum insertion loss, whereas, the non-flipped transformer presents a proper performance for a wider band.

Fig. 7

Flipped and non-flipped inductances

3.3 Geometrical parameters’ calculation

The octagonal planar coils are geometrically described by the outer and inner diameters, the number of turns, the width, the thickness, the spacing between turns, and the total length for each coil. We have opted for an outer diameter of 3000 µm and an inner diameter of 2000 µm; the angles are limited to multiples of 45°.

• Thickness of coil

The calculation of thickness depends on skin thickness δ (expression 4) which determines the zone where the current concentrates in a conductor (Fig. 8) [14].

$$ \delta = \sqrt {\frac{{\rho_{\text{Cu}} }}{{\pi \cdot \mu_{\text{Cu}} \cdot f}}} , $$

(4)

ρ_cu and µ_cu are, respectively, resistivity and permeability of copper, f is the operating frequency in high frequencies.

Fig. 8

Volume delimited by the skin effect δ in a conductor

To avoid the problem of the skin effect and make the current flowing in the entire conductor, it is necessary to fulfill the following condition:

$$ t \le 2 \cdot \delta . $$

(5)

The current density j(x) for x ranging from 0 to t/2 and its average value j_avg with J₀ = 10⁹ A/m² [15], are given by expressions 6 and 7:

$$ j\left( x \right) = j_{0} \cdot e^{{ - i\left( {\frac{x}{\delta }} \right)}} \cdot e^{{ - \left( {\frac{x}{\delta }} \right)}} , $$

(6)

$$ j_{\text{avg}} = j_{0} \cdot \frac{{\left[ {e^{{ - \left( {\frac{t}{2 \cdot \delta }} \right)}} + 1} \right]}}{2}. $$

(7)

The electric current i (expression 8) which passes through the conductor is a function of the current density and the conductor’s section. This is a function of the width w and the thickness t of the planar coil (expression 9).

$$ i = S_{\text{c}} \cdot j_{\text{avg}} , $$

(8)

$$ S_{\text{c}} = w \cdot t. $$

(9)

• Spacing between turns

  $$ s = \frac{{d_{\text{out}} - d_{\text{in}} - \left( {2 \cdot w \cdot n} \right)}}{{2 \cdot \left( {n - 1} \right)}} $$

  (10)

• Total length

  $$ l_{\text{t}} = \left( {4 \cdot n \cdot \left( {d_{\text{out}} - \left( {n - 1} \right) \cdot s - \left( {n \cdot w} \right)} \right)} \right) - s $$

  (11)

• Width

  $$ w = \frac{{\left[ {d_{\text{out}} - d_{\text{in}} - 2 \cdot s \cdot \left( {n - 1} \right)} \right]}}{2 \cdot n} $$

  (12)

4 Modeling of integrated planar octagonal transformer

In this work, the planar transformer is composed of two octagonal coils in copper, superimposed on a ferromagnetic layer of ferrite (NiZn), and isolated from there by a dioxide layer of silicon dioxide (SiO₂); all these layers of the different materials are superimposed on a layer of silicon (Si), which serves as a substrate. This transformer operates at a high frequency of the order of 100 MHz (Fig. 9).

Fig. 9

3D cross section of the integrated planar octagonal transformer

The magnetic core volume is calculated by (expression 13):

$$ V = \frac{W}{{W_{{{\text{v\;max}}}} }}, $$

(13)

W represents the total magnetic stored energy in the transformer’s coils (expression 14)

$$ w = \frac{1}{2} \cdot L \cdot i^{2} , $$

(14)

W_vmax represents maximum volume density of energy (expression 15)

$$ W_{{{\text{v\;max}} }} = \frac{{B_{\text{max} }^{2} }}{{2 \cdot \mu_{0} \cdot \mu_{\text{rNiZn}} }}, $$

(15)

B_max = 0.3T is the maximal saturation induction, and μ_rNiZn = 1400 is the relative permeability of NiZn ferrite.

Therefore, after calculation, the NiZn magnetic core’s volume equals 0.080 mm³, which is necessary to store 3.125 nJ of energy.

The core thickness is represented by the following expression.

$$ e_{\text{NiZn}} = \frac{V}{{d_{\text{out}}^{2} }}. $$

(16)

4.1 Technological parameters’ calculation

The equivalent electrical circuit (Fig. 10) extracted from (Fig. 9) demonstrates the electrical behavior of the integrated octagonal planar transformer.

Fig. 10

Equivalent electrical circuit of the integrated octagonal planar transformer

The equivalent circuit contains different electrical parameters, which are the inductances L and serial resistance R_s of the coils, oxide capacitance C_ox of the dielectric layer, magnetic resistance R_mag of the ferrite layer, resistances R_sub, capacitance C_sub associated with the silicon substrate, and coupling capacitance C_K between the two coils.

The analytical expressions of different elements constituting the electrical model (Fig. 10) of the octagonal transformer are represented by the following expressions:

$$ R_{\text{s}} = \rho_{\text{cu}} \cdot \frac{{l_{\text{t}} }}{{w \cdot t_{\text{eff}} }} , $$

(17)

ρ_Cu = 1.7 × 10⁻⁸ Ω m$t_{\text{eff}}$ is given by the expression below

$$ t_{\text{eff}} = \delta \cdot \left( {1 - e^{{ - \left( {\frac{t}{\delta }} \right)}} } \right), $$

(18)

$$ R_{\text{sub}} = 2 \cdot \rho_{\text{Si}} \cdot \frac{{e_{\text{Si}} }}{{w \cdot l_{\text{t}} }}, $$

(19)

ρ_Si = 18.5 Ω m

$$ R_{\text{mag}} = 2 \cdot \rho_{\text{NiZn}} \cdot \frac{{e_{{_{\text{NiZn}} }} }}{{w \cdot l_{\text{t}} }}, $$

(20)

ρ_NiZn = 10³ Ω m

$$ C_{\text{oxp}} = \frac{1}{2} \cdot \varepsilon_{0} \varepsilon_{\text{rox}} \cdot \frac{{w \cdot l_{\text{t}} }}{{t_{\text{ox}} }}, $$

(21)

ε_rox = 3.9

$$ C_{\text{sub}} = \frac{1}{2} \cdot \varepsilon_{0} \varepsilon_{\text{rSi}} \cdot \frac{{w \cdot l_{\text{t}} }}{{e_{\text{Si}} }}, $$

(22)

ε_rSi = 11.8

$$ C_{\text{kp}} = \frac{1}{2} \cdot \varepsilon_{\text{ox}} \cdot \frac{{t \cdot l_{\text{t}} }}{s}, $$

(23)

$$ C_{\text{k}} = \varepsilon_{0} \varepsilon_{{{\text{r}}\;{\text{air}}}} \cdot \frac{{d_{\text{out}}^{2} }}{{t_{\text{ox}} }}, $$

(24)

ε_{r air} = 1

4.2 Geometrical and electrical dimensioning results

The calculated geometric and electrical parameters of the octagonal planar transformer are shown in (Table 2).

Table 2 Results of calculated parameters

We notice that all the calculated values of different parameters are according with technical integration.

4.3 S-parameters concept

From the electrical model (Fig. 10), we can easily calculate the scattering parameters of the octagonal planar transformer [16]:First, we calculate the ABCD matrices for each block.

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\alpha } = \left[ {\begin{array}{*{20}c} 1 & 0 \\ {\frac{1}{{\frac{1}{{j \cdot \omega \cdot C_{\text{ox}} }} + R_{\text{mag}} + \frac{{R_{\text{sub}} }}{{1 + j \cdot \omega \cdot R_{\text{sub}} \cdot C_{\text{sub}} }}}}} & 1 \\ \end{array} } \right], $$

(25)

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\beta } = \left[ {\begin{array}{*{20}c} 1 & {R_{\text{s}} } \\ 0 & 1 \\ \end{array} } \right], $$

(26)

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\gamma } = - \left[ {\begin{array}{*{20}c} {\frac{L}{M}} & {j \cdot \omega \cdot \left( {\frac{{L^{2} }}{M} - M} \right)} \\ {\frac{1}{j \cdot \omega \cdot M}} & {\frac{L}{M}} \\ \end{array} } \right], $$

(27)

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\delta } = \left[ {\begin{array}{*{20}c} 1 & {R_{\text{s}} } \\ 0 & 1 \\ \end{array} } \right], $$

(28)

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\varepsilon } = \left[ {\begin{array}{*{20}c} 1 & 0 \\ {\frac{1}{{\frac{1}{{j \cdot \omega \cdot C_{\text{ox}} }} + R_{\text{mag}} + \frac{{R_{\text{sub}} }}{{1 + j \cdot \omega \cdot R_{\text{sub}} \cdot C_{\text{sub}} }}}}} & 1 \\ \end{array} } \right], $$

(29)

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\varphi } = \left[ {\begin{array}{*{20}c} 1 & {\frac{1}{{j \cdot \omega \cdot C_{k} }}} \\ 0 & 1 \\ \end{array} } \right]. $$

(30)

From this,

$$ M = k \cdot L. $$

(31)

Second, we can associate the blocks α, β, γ, δ, ε, φ in cascade:

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{I} = \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\alpha } .\left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\beta } .\left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\gamma } .\left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\delta } .\left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\varepsilon } .\left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\varphi } . $$

(32)

Third, we can associate the large intermediate block I with block φ in parallel to obtain he final ABCD matrix of the entire transformer F:

$$ \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]_{\text{F}} = \frac{1}{{B_{\text{I}} + B_{\varphi } }} \cdot \left[ {\begin{array}{*{20}c} {A_{\text{I}} \cdot B_{\varphi } + A_{\varphi } \cdot B_{\text{I}} } & {B_{\text{I}} \cdot B_{\varphi } } \\ {\left( {C_{\text{I}} + C_{\varphi } } \right) \cdot \left( {B_{\varphi } + B_{\text{I}} } \right) + \left( {D_{\text{I}} - D_{\varphi } } \right) \cdot \left( {A_{\varphi } - A_{\text{I}} } \right)} & {D_{\varphi } \cdot B_{\text{I}} + D_{\text{I}} \cdot B_{\varphi } } \\ \end{array} } \right]. $$

(33)

Finally, we convert the A, B, C, D parameters to S-parameters as follows:

$$ \left\{ {\begin{array}{*{20}l} {S_{11} = \frac{{A_{\text{F}} + \frac{{B_{\text{F}} }}{{Z_{0} }} - C_{\text{F}} \cdot Z_{0} - D_{\text{F}} }}{{A_{\text{F}} + \frac{{B_{\text{F}} }}{{Z_{0} }} + C_{\text{F}} \cdot Z_{0} + D_{\text{F}} }}} \hfill & {S_{12} = \frac{{2 \cdot \left( {A_{\text{F}} \cdot D_{\text{F}} - \left( {B_{\text{F}} \cdot C_{\text{F}} } \right)} \right)}}{{A_{\text{F}} + \frac{{B_{\text{F}} }}{{Z_{0} }} + C_{\text{F}} \cdot Z_{0} + D_{\text{F}} }}} \hfill \\ {S_{21} = \frac{2}{{A_{\text{F}} + \frac{{B_{\text{F}} }}{{Z_{0} }} + C_{\text{F}} \cdot Z_{0} + D_{\text{F}} }}} \hfill & {S_{22} = \frac{{ - A_{\text{F}} + \frac{{B_{\text{F}} }}{{Z_{0} }} - C_{\text{F}} \cdot Z_{0} + D_{\text{F}} }}{{A_{\text{F}} + \frac{{B_{\text{F}} }}{{Z_{0} }} + C_{\text{F}} \cdot Z_{0} + D_{\text{F}} }}} \hfill \\ \end{array} } \right\}. $$

(34)

Z₀ is the characteristic impedance of the line. Due to reciprocity, $A_{\text{F}} \cdot D_{\text{F}} - B_{\text{F}} \cdot C_{\text{F}} = 1$; therefore, S₁₂ = S₂₁.

From the S-parameters, we can obtain the Z-parameters such that:

$$ \left\{ {\begin{array}{*{20}c} {Z_{11} = Z_{0} \cdot \frac{{\left( {1 + S_{11} } \right) \cdot \left( {1 - S_{22} } \right) + S_{21} \cdot S_{12} }}{{\left( {1 - S_{11} } \right) \cdot \left( {1 - S_{22} } \right) - S_{21} \cdot S_{12} }}} & {Z_{12} = Z_{0} \cdot \frac{{2 \cdot S_{12} }}{{\left( {1 - S_{11} } \right) \cdot \left( {1 - S_{22} } \right) - S_{21} \cdot S_{12} }}} \\ {Z_{21} = Z_{0} \cdot \frac{{2 \cdot S_{21} }}{{\left( {1 - S_{11} } \right) \cdot \left( {1 - S_{22} } \right) - S_{21} \cdot S_{12} }}} & {Z_{22} = Z_{0} \cdot \frac{{\left( {1 - S_{11} } \right) \cdot \left( {1 + S_{22} } \right) + S_{21} \cdot S_{12} }}{{\left( {1 - S_{11} } \right) \cdot \left( {1 - S_{22} } \right) - S_{21} \cdot S_{12} }}} \\ \end{array} } \right\}. $$

(35)

From the Z-parameters, we can obtain the primary and secondary inductances (L_p and L_s) and series resistances (R_sp and R_ss) (expressions 36 and 37).

$$ L_{\text{p}} = \frac{{\text{Im} \left( {Z_{11} } \right)}}{\omega }\quad L_{\text{s}} = \frac{{\text{Im} \left( {Z_{22} } \right)}}{\omega }, $$

(36)

$$ R_{\text{sp}} = \text{Re} \left( {Z_{11} } \right)\quad R_{\text{ss}} = \text{Re} \left( {Z_{22} } \right). $$

(37)

Figure 11 shows the characteristics of inductance behavior. We observe that there are three distinct zones. The inductive behavior until 100 MHz, then the transition zone in which the value of the inductances becomes negative with a zero crossing corresponding to the resonant frequency of the inductance and the capacitive behavior beyond the operating frequency.

Fig. 11

Primary and secondary inductances versus frequency

Figure 12 demonstrates the influence of the frequency on series resistances of primary and secondary transformer coils. We notice that the inductances become purely resistive at 100 MHz operating frequency.

Fig. 12

Primary and secondary serial resistances versus frequency

The quality factor expresses losses in the transformer coils (expression 38).

$$ Q = 2\pi \cdot \frac{{{\text{stocked}}\;{\text{energy}}}}{{{\text{dissipate}}\;{\text{denergy}}}}. $$

(38)

It is also proportional to the difference between the maximum magnetic energy and the energy supply [17] (expression 39).

$$ Q = \frac{\omega \cdot L}{{R_{\text{s}} }} \cdot \frac{{R_{\text{p}} }}{{R_{\text{p}} + \left[ {\left( {\frac{\omega \cdot L}{{R_{\text{s}} }}} \right)^{2} + 1} \right] \cdot R_{\text{s}} }} \cdot \left[ {1 - \frac{{R_{\text{s}}^{2} \cdot \left( {C_{\text{s}} + C_{\text{p}} } \right)}}{L} - \omega^{2} \cdot L \cdot \left( {C_{\text{s}} + C_{\text{p}} } \right)} \right]. $$

(39)

In expression 39, the first term corresponds to the simplified quality factor, the second term expresses the losses substrate, and the third represents the self-resonance factor, L is the inductance, Rs is the serial resistance, C_s is the serial capacitance, ω is the pulsation. R_p and C_p are the coupling resistance and capacitance; they are related to the substrate resistance and capacitance R_Si and C_si and the oxide capacitance C_ox (expressions 40 and 41):

$$ R_{\text{p}} = \frac{1}{{\omega^{2} \cdot C_{\text{ox}}^{2} \cdot R_{\text{si}} }} + \frac{{R_{\text{si}} \cdot \left( {C_{\text{ox}} + C_{\text{p}} } \right)^{2} }}{{C_{\text{ox}}^{2} }}, $$

(40)

$$ C_{\text{p}} = C_{\text{ox}} \cdot \frac{{1 + \omega^{2} \cdot \left( {C_{\text{ox}} + C_{\text{si}} } \right) \cdot C_{\text{si}} \cdot R_{\text{si}}^{2} }}{{1 + \omega^{2} \cdot \left( {C_{\text{ox}} + C_{\text{si}} } \right)^{2} \cdot R_{\text{si}}^{2} }}. $$

(41)

From the Z-parameters, we can obtain the primary and secondary quality factors (Q_p, Q_s) (expressions 42).

$$ Q_{\text{p}} = \frac{{\text{Im} \left( {Z_{11} } \right)}}{{{\text{Re}}\left( {Z_{11} } \right)}}\quad Q_{\text{s}} \frac{{\text{Im} \left( {Z_{22} } \right)}}{{{\text{Re}}\left( {Z_{22} } \right)}}. $$

(42)

Figure 13 shows the evolution of the quality factor as a function of frequency for the primary and secondary coils. We notice that the first part of the curve corresponds to the zone where the coils have an inductive behavior. Then, the quality factor increases with the frequency until reaching a maximum value, which corresponds to the losses. Beyond the operating frequency, the quality factor decreases to zero at an operating point corresponding to the resonant frequency.

Fig. 13

Quality factor of the primary and secondary coils versus frequency

5 Electromagnetic behavior of transformer

Using COMSOL Multiphysics 4.3 software, which is based on finite elements method, we present 3D simulation of electromagnetic effects on the transformers at high frequency (100 MHz).

5.1 Mathematical model

The electromagnetic phenomenon is obtained by solving the Maxwell equations [12]. These allow us to visualize the distribution of the electric potential on the planar transformer coils and the density of electric current and as well as the magnetic field lines. The expressions are as follows:,

$$ \nabla \cdot \vec{H} = \vec{J}, $$

(43)

$$ \nabla \cdot \vec{A} = \vec{B}, $$

(44)

$$ \vec{E} = - \nabla V - j \cdot \omega \cdot \vec{A}, $$

(45)

$$ \vec{J} = \sigma \cdot \vec{E} + j \cdot \omega \cdot \vec{D}, $$

(46)

$$ \nabla \cdot \vec{J} = 0, $$

(45)

$$ \vec{B} = \mu_{0} \mu_{\text{r}} \cdot \vec{H}, $$

(46)

$$ \vec{D} = \varepsilon_{0} \cdot \varepsilon_{\text{r}} \cdot \vec{E}, $$

(47)

$\vec{H}$: magnetic field (A/m); $\vec{B}$: magnetic flux density (T); $\vec{J}$: electric current density (A/m²); $\vec{E}$: electric field (V/m); $\vec{A}$: magnetic vector potential (Wb/m); $\vec{D}$: electric displacement field standard (c/m²).

The boundary conditions on the study area boundaries are demonstrate by the following expressions:

$$ \vec{n} \cdot \vec{A} = 0, $$

(48)

$$ n_{x} \cdot A_{x} + n_{y} \cdot A_{y} + n_{z} \cdot A_{z} = 0, $$

(49)

$$ \vec{n} \cdot \vec{J} = 0, $$

(50)

the normal vector at the boundary (expression 51).

$$ \vec{n} = n_{x} \cdot \vec{i} + n_{y} \cdot \vec{j} + n_{z} \cdot \vec{k}. $$

(51)

Hence

$$ n_{x} \cdot J_{x} + n_{y} \cdot J_{y} + n_{z} \cdot J_{z} = 0. $$

(52)

To have a good precision, we proceed to an extremely fine mesh. Figure 14 illustrates the 3D fine mesh of the octagonal integrated transformer for only the two coils and for the global structure with the different layers.

Fig. 14

3D mesh transformer: a octagonal coils geometry and b global structure with different layers

Figure 15 illustrates the electric current density on the planar octagonal coils at 100 MHz, in which we notice that the current is mostly concentrated on the edges of the conductors for high frequency; this effect is due to the skin effect in the rectangular area of conductor.

Fig. 15

Current density distribution in the octagonal planar coils at 100 MHz

Figure 16 illustrates the electric potential distribution on planar coils of the octagonal transformer. The color of the flow current represents the magnitude of the electric potential. We notice that this last is maximum at the entry of current and decreases along the coil due to the conductor’s resistance.

Fig. 16

Electrical potential distribution in planar octagonal coils

Figure 17 illustrates the distribution of magnetic field lines in the octagonal planar transformer composed of copper coils deposited on ferrite NiZn magnetic layer and isolated by a dielectric layer, all these layers are deposited on a silicon substrate. We notice that the magnetic field lines are concentrated in the transformer and that is due to the ferrite layer.

Fig. 17

Distribution of magnetic field lines in the transformer: a 3D cross section, b above view, c lateral view, and d in front of view

6 Simulation of the operating converter

Using PSIM software 6.0, we perform in this section three simulations on flyback converter in order to test the operation of our integrated transformer. We have chosen a flyback converter because it is composed of one transformer and few passive components. The principle of operation of the flyback is based on the energy transfer from primary to secondary through a transformer.

To execute the simulations, we need to calculate the following parameters:

• Load resistance

The load resistance R of the flyback converter is given by:

$$ R = \frac{{V_{\text{out}} }}{{i_{\text{out}} }} = 5\;\varOmega . $$

(53)

Input voltage: V_in = 12 V; output voltage: V_out = 5 V.

• Capacitance

The capacitance of flyback converter is given by the following expression for an undulation voltage α of 0.25 V.

$$ C = \frac{{\alpha^{2} \cdot m \cdot V_{\text{in}} }}{{(1 - \alpha ) \cdot \Delta V_{\text{out}} \cdot R \cdot f}} = 20\;{\text{nF}} . $$

(54)

6.1 Simulation of the operating converter with the integrated transformer

In this simulation, the circuit of Fig. 18 contains an ideal transformer.

Fig. 18

Flyback with an ideal transformer

The figure below shows the converter’s output voltage and current waveform.

In Fig. 19, we notice two modes of the converter: the transient and steady state. The output voltage is 4.9 V instead of 5 V. This is due to voltage drops across the diode and transistor. In the steady state, the current is 0.98 A, which corresponds to an output power of 4.8 W instead of 5 W.

Fig. 19

Output voltage and current of flyback with an ideal transformer

The following figures show the waveform of the voltage and current across both transistor and diode of the flyback converter (Fig. 20).

Fig. 20

Voltage and current of both transistor and diode of the flyback with an ideal transformer

6.2 Simulation of the operating converter with the real transformer

In this simulation, the circuit of Fig. 21 contains a real transformer.

Fig. 21

Flyback with the real transformer

• Magnetizing inductance

The magnetizing inductance is defined by:

$$ L_{\text{m}} = n_{\text{p}}^{2} \cdot \frac{{\mu_{\text{NiZn}} \cdot d_{\text{out}}^{2} }}{{2 \cdot e_{\text{NiZn}} }} = 0.9\;{\text{mH}} . $$

(55)

The figure below shows the converter’s output voltage and current waveform.

In Fig. 22, we notice also two modes of the converter: the transient and steady state. The output voltage is 4.25 V instead of 5 V. This is due to voltage drops across the diode and transistor, the resistive losses in the conductor, and then the magnetic core losses. In the steady state, the current is 0.85 A, which corresponds to an output power of 3.6 W instead of 5 W. The following figures show the waveform of the voltage and current across both transistor and diode of the flyback converter (Fig. 23).

Fig. 22

Output voltage and current of flyback with the real transformer

Fig. 23

Voltage and current of both transistor and diode of the flyback with the real transformer

6.3 Simulation of the operating converter with the integrated transformer

In this simulation, the circuit of Fig. 24 contains an integrated octagonal planar transformer.

Fig. 24

Flyback with the integrated transformer

The figure below shows the converter’s output voltage and current waveform.

In Fig. 25, we notice again two modes of the converter: the transient and steady state. The output voltage is 4.24 V instead of 5 V. This is due to voltage drops across the diode and transistor, the resistive losses in the conductors, and then the magnetic core and the capacitive losses. In the steady state, the current is 0.84 A, which corresponds to an output power of 3.6 W instead of 5 W.

Fig. 25

Output voltage and current of flyback with the integrated transformer

The following figures show the waveform of the voltage and current across both transistor and diode of the flyback converter (Figs. 26, 27).

Fig. 26

Voltage and current of both transistor and diode of the flyback with the integrated transformer

Fig. 27

Evolution of the flyback converter efficiency versus frequency

After the simulation of the integrated transformer, we notice that the transformer delivers the same power as a real transformer because they give the same results.

6.4 Flyback converter efficiency

The converter efficiency (expression 56) represents its performance.

$$ \eta = \frac{{P_{\text{out}} - P_{\text{j}} - P_{\text{f}} }}{{P_{\text{out}} }}, $$

(56)

where

$$ P_{\text{out}} = V_{\text{out}} \cdot I_{\text{out}} , $$

(57)

$$ P_{\text{j}} = R_{\text{seq}} \cdot I_{\text{out}}^{2} , $$

(58)

$$ P_{\text{f}} = \frac{{V_{\text{in}}^{2} }}{{R_{\text{seq}} }}, $$

(59)

P_j: Joules losses in copper’s conductor; P_f: Ferromagnetic losses.

The efficiency found is around 82%, so near to the performance of an operating flyback converter which is 85%.

We conclude that this reduction corresponds to the joules losses generated by conducting coils and the iron losses in the ferromagnetic core of ferrite.

7 Conclusion

The aim of this work is the geometrical dimensioning of the transformer and its electromagnetic modeling to integrate it into a converter. This transformer is destined for the mobile and embedded electronic field requiring an energy conversion of low power and a very high frequency range. The integrated transformer is composed also of a stack of several layers of different materials, which are two copper coils, magnetic layers of ferrite material, insulating layers of dielectric material, and a substrate of semiconductor material. The geometry of the planar coils constituting the transformer is octagonal with 45° of angles to avoid the concentrated current in the corners. To determine the geometrical parameters, we have opted for the Wheeler method, which presents a low error compared with other methods. After, we have used the geometrical parameters to extract the electrical parameters, which present the parasitic effects in the different layers of transformer at the high frequency. In addition, we have used a finite elements simulator to visualize the distribution of magnetic field lines, electrical potential, and current density in the planar octagonal transformer. Besides, we have used another software simulator to validate our results; thus, we have compared the output voltage and current of the flyback in three cases of transformer. The waveforms of the converter’s currents and voltages containing the integrated transformer were in accordance with those of the literature and the measured values were very close to its ideal case.