Earthquake Forecasting Using Hidden Markov Models

Abstract

This paper develops a novel method, based on hidden Markov models, to forecast earthquakes and applies the method to mainshock seismic activity in southern California and western Nevada. The forecasts are of the probability of a mainshock within 1, 5, and 10 days in the entire study region or in specific subregions and are based on the observations available at the forecast time, namely the interevent times and locations of the previous mainshocks and the elapsed time since the most recent one. Hidden Markov models have been applied to many problems, including earthquake classification; this is the first application to earthquake forecasting.

Appendix

In this appendix, we present the well-known parameter estimation procedure for hidden Markov models, derive the post-event and scheduled forecast densities, and give a rigorous proof of the waiting time paradox result.

1.1 Estimating Parameters

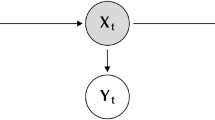
Recall the forward and backward variables $f_s(t)$ and $b_s(t)$ can be computed using (3) and (4) when the parameters of the HMM are known and the complete set of observations ${\mathcal{O}}$ is seen. These variables can then be used to find $\gamma_s(t) \equiv P(X_t=s |{\mathcal{O}}),$ the probability of being in state $s \in {\mathcal{S}}$ at time t, conditional on all the observations. By conditioning on the event $(X_t=s, y_1, \ldots, y_t)$ and using (2), it is easily seen that

$$ \gamma_s(t)=b_s(t)f_s(t)/P({\mathcal{O}}), \quad 1 \le t \le L. $$

(28)

Similarly, we can compute $\eta_{rs}(t) \equiv P(X_t=r, X_{t+1}=s | {\mathcal{O}}),$ the joint probability of being in state r at time t and in state s at time t + 1, conditional on the complete set of observations. By definition,

$$ \eta_{rs}(t)= P(X_t=r, X_{t+1}=s, y_1 \ldots, y_L)/P({\mathcal{O}}) $$

(29)

The denominator in (29) is given by (6). By a pair of conditioning arguments and simplification by the conditional independence in (2), we have:

$$\eta_{rs}(t) = P(X_t=r, X_{t+1}=s | {\mathcal{O}} )=f_r(t)a_{rs}b_s(t+1)p_s(y_{t+1})/P({\mathcal{O}}). $$

(30)

In summary, given the complete set of observations ${\mathcal{O}}$ and set of parameters $\Uptheta,$ we can compute $f_s(t), b_s(t),\gamma_s(t),$ and $\eta_{rs}(t),$ for all states $r, s \in S$ and times $t=1, {\ldots},L.$

To estimate the parameters of a HMM, we use the well-known Baum–Welch algorithm (Rabiner, 1989), described below. In the following, we replace P by $P_\Uptheta$ to emphasize the dependence on the parameter set.

The procedure begins with an initial guess for the parameters, say $\Uptheta^{(0)}.$ Then $f_s^{(0)}(t), b_s^{(0)}(t),\gamma_s^{(0)}(t),$ and $\eta_{rs}^{(0)}(t) (r, s \in S, t=1, \ldots, L)$, and $P_\Uptheta^{(0)}({\mathcal{O}})$ are computed using (3)–(6), (28), and (30). We then update the parameters as below to get a new estimate $\Uptheta^{(1)}.$ The key is that the likelihood of the observations increases under the new parameter set: $P_\Uptheta^{(1)}({\mathcal{O}}) \ge P_\Uptheta^{(0)}({\mathcal{O}})$ (Rabiner, 1989). The procedure is then iterated until the likelihoods converge to some desired precision or until successive parameter estimates differ by a predetermined small amount. The parameters are estimated by this final updating.

The parameter updates are:

$$ a_{rs}^{(n+1)}= \frac{\sum_{t=1}^{L-1} \eta_{rs}^{(n)}(t)}{\sum_{t=1}^{L-1}\gamma_r^{(n)}(t)} $$

(31)

$$ \pi^{(n+1)}_s= \gamma_s^{(n)}(1) $$

(32)

$$ \lambda_s^{(n+1)}= \frac{\sum_{t=1}^L \gamma_s^{(n)}(t)y_t}{\sum_{t=1}^L \gamma_s^{(n)}(t)} $$

(33)

$$ q_s^{(n+1)}(v)={\frac{\sum_{t=1, v_t=v}^L \gamma_s^{(n)}(t)}{\sum_{t=1}^L \gamma_s^{(n)}(t)} } $$

(34)

where $y_t$ is the tth observation.

The transition probability estimate in (31) is simply the ratio of the expected number of transitions from r to s to the expected number of transitions from r. The initial distribution in (32) is the probability of starting in state s under $\Uptheta^{(n)}.$ For a single exponential density, the maximum likelihood estimator of the mean is the sample mean; here, for state s, (33) weights each observation by the probability it came from state s. In (34), the probability the event occurs in region v given the state is s is estimated by the ratio of the expected number of times this occurs to the expected number of visits to the state.

Finally, note that estimation procedures exist for other state-specific distributions, including normal distributions (Rabiner, 1989). Obvious extensions to the forecast formulas in Sect. 3 are then possible.

1.2 Forecast Densities

We first derive the (post-event) density function for waiting time until the next earthquake, made immediately after an earthquake. We first derive this density in the framework of a general HMM. The problem is to find the probability density function of observation $Y_{t+1}$ conditional on the observation history up to time t, i.e., $P(Y_{t+1}=y |y_1, \ldots,y_t).$ By summing over all possible states at time t + 1, standard conditioning arguments, and (1),

$$ \begin{aligned}&P(Y_{ t+1}=y |y_1, \ldots ,y_ t)= \sum_{s \in {\mathcal{S}}} P(Y_{ t+1}=y |X_{ t+1}= s, y_1, \ldots , y_ t)P(X_{ t+1}= s |y_1, \ldots ,y_ t)\\ &\quad = \sum_{s \in {\mathcal{S}}} \sum_{r \in {\mathcal{S}}} P(Y_{ t+1}=y |X_{ t+1}= s)P(X_{ t+1}= s |X_ t=r, y_1, \ldots ,y_ t) \\&\qquad \times P( X_ t=r |y_1, \ldots ,y_ t)\\ &\quad = \sum_{s \in {\mathcal{S}}} \sum_{r \in {\mathcal{S}}} p_ s(y) P(X_{ t+1}= s|X_ t=r) P( X_ t=r , y_1, \ldots ,y_ t )/P(y_1, \ldots ,y_ t )\\& \quad=\sum_{s \in {\mathcal{S}}} \sum_{r \in {\mathcal{S}}} p_ s(y) a_{r s} f_r( t)/P(y_1, \ldots ,y_ t ).\end{aligned}$$

That is, at time t, the distribution of the next observation, given the observations available, is computable by

$$ P(Y_{t+1}=y | y_1, \ldots , y_t)= \sum_{s \in {\mathcal{S}}} c_{st}p_s(y) $$

(35)

where

$$ c_{st}=\sum_{r \in {\mathcal{S}}}a_{rs} f_r(t)/P(y_1, \ldots y_t). $$

(36)

Note that $\sum_{s \in \mathcal{S}}c_{st}=\sum_{r \in \mathcal{S}}f_r(t)(\sum_{s \in \mathcal{S}} a_{rs})/P(y_1, \ldots, y_t )=\sum_{r \in \mathcal{S}}f_r(t)/P(y_1, \ldots, y_t )=1$ by (5), hence

$$ \sum_{s \in {\mathcal{S}}}c_{st}=1 $$

(37)

Furthermore, an inspection of the above shows that

$$ c_{st}= P(X_{t+1}=s | y_1, \ldots , y_t). $$

(38)

Thus, (35)–(38) show that the forecast density of the next observation, conditional on the data available at that time is a mixture of the state-specific densities, in which the weight for $p_s(y)$ is (a) calculable and (b) interpretable as the conditional probability the system is in that state s given the data available at the forecast time.

Recall that in our application the observation $Y_t$ corresponding to earthquake t is the time in days since earthquake $t-1.$ Then, (7) and (35) give the density of the waiting time until the next earthquake, given the seismic history available just after an earthquake:

$$ P(Y_{t+1}=y |y_1, \ldots y_t)=\sum_{s \in {\mathcal{S}}}c_{st}(1/\lambda_s)\hbox{e}^{-y/\lambda_s}. $$

(39)

Next, we extend our method to scheduled forecasts, say weekly or daily, of the probability of an earthquake within a given time period in the region. Now what is known at the time of the forecast is the set of observed interevent times as well as the elapsed time since the previous earthquake. Here we derive the forecast density given in (13) and (14).

Suppose that t earthquakes have occurred at the forecast time and w days have elapsed since the most recent earthquake. The available data at forecast time is then $y_1, \ldots , y_t$ and the event $Y_{t+1} \ge w.$ The remaining waiting time until the next is $Y_{t+1}-w.$ We derive its density. Let $y>0.$ The forecast density of the remaining waiting time, given the available data, is

$$ \begin{aligned} &P(Y_{t+1}-w=y |y_1, \ldots, y_t, Y_{t+1} \ge w)= \frac{P(Y_{t+1}=y+w, Y_{t+1}\ge w |y_1, \ldots, y_t)}{P(Y_{t+1} \ge w | y_1, \ldots , y_t)}\\ &\quad =\frac{P(Y_{t+1}=y+w | y_1, \ldots, y_t)}{ P(Y_{t+1} \ge w | y_1, \ldots , y_t)}= \frac{P(Y_{t+1}=y+w | y_1, \ldots , y_t)}{\int_w^\infty P(Y_{t+1}=x | y_1, \ldots, y_t)\,\hbox{d}x}. \end{aligned} $$

The numerator and denominator in the final fraction, by (39), are

$$ \sum_{s \in {\mathcal{S}}} c_{st}\hbox{e}^{-w/\lambda_s} (1/\lambda_s)\hbox{e}^{-y/\lambda_s} \quad\hbox{and}\quad \int\limits_w^\infty \sum_{r \in {\mathcal{S}}} c_{rt} (1/\lambda_r)\hbox{e}^{-x/\lambda_r}\,\hbox{d}x, $$

respectively. The denominator simplifies to $\sum_{r \in {\mathcal{S}}} c_{rt}\hbox{e}^{-w/\lambda_r}.$

That is, at the time of the forecast, if t earthquakes have occurred and w days have elapsed since the previous earthquake, the density of the remaining waiting time $Y_{t+1}-w$ is

$$ P(Y_{t+1}-w=y |y_1, \ldots, y_t, Y_{t+1} \ge w) = \sum_{s \in {\mathcal{S}}}d_{st}(w) (1/\lambda_s)\hbox{e}^{-y/\lambda_s} $$

(40)

where

$$ d_{st}(w)=\frac{c_{st}\hbox{e}^{-w/\lambda_s}}{\sum_{r \in {\mathcal{S}}}c_{rt}\hbox{e}^{-w/\lambda_r}}. $$

(41)

It is easily shown that $d_{st}(w)=P(X_{t+1}=s |y_1, \ldots, y_t, Y_{t+1} \ge w),$ so that the forecast density is again a mixture of the densities $p_s(y)$ with the weight for $p_s(y)$ being the conditional probability of being in state s at the next earthquake, given all the information available at the forecast time.

The extension of the HMM and forecasts to include location as well as interevent time is straightforward. As mentioned in Sect. 5, the observation y is now a vector (u, v), where u > 0 is the interevent time in days and v is the region where the earthquake occurred. The observation variable $Y_t=(U_t,V_t).$ The state specific density in (7) is replaced by $p_s(y)=p_s(u,v)=(1/\lambda_s)\hbox{e}^{-u/\lambda_s} q_s(v).$ By (35), the post-event forecast density in (39) becomes

$$ P(U_{t+1}=u, V_{t+1}=v |y_1, \ldots, y_t)= \sum_{s \in {\mathcal{S}}}c_{st}(1/\lambda_s)\hbox{e}^{-u/\lambda_s}q_s(v) $$

(42)

and the scheduled forecast density in (40) becomes

$$ P(U_{t+1}-w=u, V_{t+1}=v |y_1, \ldots, y_t, U_{t+1} \ge w) = \sum_{s \in {\mathcal{S}}}d_{st}(w) (1/\lambda_s)\hbox{e}^{-u/\lambda_s}q_s(v). $$

(43)

1.3 Waiting Time Paradox

In Sect. 3.4, we gave a heuristic argument that an HMM model for seismicity with state-specific exponential distributions satisfies the waiting time paradox; here is a rigorous proof.

Denoting $E(Y_{t+1}-w | y_1, \ldots y_t, Y_{t+1} \ge w)$ by h(w), it follows from (16) and (14) that

$$ h'(w)= \sum_{s \in {\mathcal{S}}} \lambda_s \frac{d}{{d}w} \frac{c_{st}\hbox{e}^{-w/\lambda_s}}{\sum_{r \in {\mathcal{S}}}c_{rt}\hbox{e}^{-w/\lambda_r}} $$

(44)

After differentiating and simplifying, this gives

$$ {{h^{\prime}(w) = \sum\limits_{{s \in \mathcal{S}}} {\sum\limits_{{r \in \mathcal{S}}} {c_{{rt}} } } {\text{e}}^{{ - w/\lambda _{r} }} c_{{st}} {\text{e}}^{{ - w/\lambda _{s} }} \left( {\frac{{\lambda _{s} }}{{\lambda _{r} }} - 1} \right)} \mathord{\left/ {\vphantom {{h^{\prime}(w) = \sum\limits_{{s \in \mathcal{S}}} {\sum\limits_{{r \in \mathcal{S}}} {c_{{rt}} } } {\text{e}}^{{ - w/\lambda _{r} }} c_{{st}} {\text{e}}^{{ - w/\lambda _{s} }} \left( {\frac{{\lambda _{s} }}{{\lambda _{r} }} - 1} \right)} {\left( {\sum\limits_{{r \in \mathcal{S}}} {c_{{rt}} } {\text{e}}^{{ - w/\lambda _{r} }} } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( {\sum\limits_{{r \in \mathcal{S}}} {c_{{rt}} } {\text{e}}^{{ - w/\lambda _{r} }} } \right)^{2} }} $$

(45)

The denominator is positive, so the sign of h′(w) is determined by the numerator. Impose an order on the state space $\mathcal{S}$; since the terms vanish when r = s, the numerator in (45) can be rewritten as

$$\sum_{s \in{\mathcal{S}}}\sum_{r \le s}c_{rt}\hbox{e}^{-w/\lambda_r}c_{st}\hbox{e}^{-w/\lambda_s}\left(\frac{\lambda_s}{\lambda_r}-1\right)+ \sum_{s \in{\mathcal{S}}}\sum_{r \ge s}c_{rt}\hbox{e}^{-w/\lambda_r}c_{st}\hbox{e}^{-w/\lambda_s}\left(\frac{\lambda_s}{\lambda_r}-1\right) $$

(46)

In the second sum reverse the order of summation and then make a change of summation variables $(r \leftrightarrow s)$ to see that (47) equals

$$ \sum_{s \in{\mathcal{S}}}\sum_{r \le s}c_{rt}\hbox{e}^{-w/\lambda_r}c_{st}\hbox{e}^{-w/\lambda_s}\left(\frac{\lambda_s}{\lambda_r}-1+ \frac{\lambda_r}{\lambda_s}-1\right) $$

(47)

Since (λ _s /λ _r  − 1 + λ _r /λ _s  − 1) = (λ _s  − λ _r )²/(λ _r λ _s ) > 0, (45)–(47) show h′(w) > 0 for all w > 0 and thus $E(Y_{t+1}-w| y_1, \ldots y_t, Y_{t+1} > w)$ is an increasing function of w and our model satisfies the waiting time paradox.