Polygonal multiresolution topology optimization (PolyMTOP) for structural dynamics

Abstract

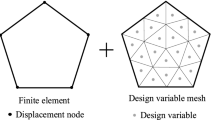
We use versatile polygonal elements along with a multiresolution scheme for topology optimization to achieve computationally efficient and high resolution designs for structural dynamics problems. The multiresolution scheme uses a coarse finite element mesh to perform the analysis, a fine design variable mesh for the optimization and a fine density variable mesh to represent the material distribution. The finite element discretization employs a conforming finite element mesh. The design variable and density discretizations employ either matching or non-matching grids to provide a finer discretization for the density and design variables. Examples are shown for the optimization of structural eigenfrequencies and forced vibration problems.

Appendices

Nomenclature

n :

number of density elements in the displacement element

K :

global stiffness matrix

K _e :

stiffness matrix of displacement element e

N _{e l} :

number of elements in mesh

D :

constitutive matrix

B :

strain-displacement matrix of shape function deriva tives

x :

position of a point in the domain, coordinate vector

E :

Young’s modulus

E ⁰ :

Young’s modulus of solid material

ρ :

density values determined based on position in domain (x)

p :

stiffness penalization parameter

M :

global mass matrix

M _e :

mass matrix of displacement element e

N ^e :

shape functions of element e

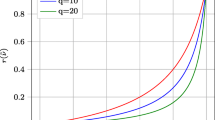
q :

mass penalization parameter

C :

static compliance

u :

global displacement vector

f :

global force vector

d :

vector of design variables

V _s :

prescribed volume

λ _j :

j _th eigenvalue of structure

ω _j :

j _th eigenfrequency of structure

ϕ _j :

j _th eigenvector of structure

d _n :

design variable n

β :

bound parameter for optimization

C :

global damping matrix

Φ:

dynamic compliance

ω _s :

initial angular frequency of external forces

ω _e :

final angular frequency of external forces

$r_{\min }$ :

minimum length scale parameter

w :

weight function for linear projection

M _S :

suspended mass

Appendix: Sensitivity analysis

To optimize for the objectives defined in Section 3, it is necessary that we calculate the sensitivity of the objective functions, and constraints with respect to the density variables. Since these are composed of the stiffness and mass terms, we calculate the derivatives of K _e and M _e as:

$$ \begin{aligned} &\frac{\partial \mathbf{K}_{e}}{\partial d_{n}}=\frac{\partial \mathbf{K}_{e}}{\partial \rho_{i}} \frac{\partial \rho_{i}}{\partial d_{n}}=\frac{\partial\left( {\sum}^{N_{n}}_{j=1}(\rho_{j})^{p}\mathbf{I}_{j}\right)}{\partial \rho_{i}}\frac{\partial \rho_{i}}{\partial d_{n}}\\ &=(\rho_{i})^{p-1}\mathbf{I}_{i}\frac{\partial \rho_{i}}{\partial d_{n}} \end{aligned} $$

(34)

and

$$ \begin{aligned} &\frac{\partial \mathbf{M}_{e}}{\partial d_{n}}=\frac{\partial \mathbf{M}_{e}}{\partial \rho_{i}} \frac{\partial \rho_{i}}{\partial d_{n}}=\frac{\partial\left( {\sum}^{N_{n}}_{j=1}(\rho_{j})^{q}\mathbf{H}_{j}\right)}{\partial \rho_{i}}\frac{\partial \rho_{i}}{\partial d_{n}}\\ &=(\rho_{i})^{p-1}\mathbf{H}_{i}\frac{\partial \rho_{i}}{\partial d_{n}} \end{aligned} $$

(35)

The sensitivity for the volume constraint can similarly be calculated as

$$ \frac{\partial V}{\partial d_{n}}=\frac{\partial V}{\partial \rho_{i}} \frac{\partial \rho_{i}}{\partial d_{n}} $$

(36)

Note that the calculation of the sensitivity of the density variables with respect to design variables (∂ ρ _i /∂ d _n ) is presented in Section 3.4. Subsequently, the sensitivity of static compliance can be calculated from the element displacement u _e as:

$$ \frac{\partial C}{\partial d_{n}}=-\mathbf{u}_{e}\frac{\partial \mathbf{K}_{e}}{\partial d_{n}}\mathbf{u}_{e} $$

(37)

1.1 A.1 Sensitivity analysis of eigenfrequencies

For free body vibrations the sensitivity of the fundamental eigenvalue λ for a specific element can be calculated as:

$$ \frac{\partial \lambda_{j}}{\partial d_{n}}=-\phi^{T}_{j e} \left( \frac{\partial \mathbf{K}_{e}}{\partial d_{n}} - \lambda_{j} \frac{\partial \mathbf{M}_{e}}{\partial d_{n}}\right)\phi_{j e} $$

(38)

where ϕ _{j e} is the eigenvector map for element e (Haftka and Adelman 1989). Furthermore the sensitivity of the first eigenvector for the entire structure can be re-written in vector form as:

$$ \begin{aligned} &\bigtriangledown \lambda_{j}=\left\{{\phi^{T}_{j}} \left( \frac{\partial \mathbf{K}}{\partial d_{1}} - \lambda_{j} \frac{\partial \mathbf{M}}{\partial d_{1}}\right)\phi_{j},\right.\\ &\left. ...,{\phi^{T}_{j}} \left( \frac{\partial \mathbf{K}}{\partial d_{N_{des}}} - \lambda_{j} \frac{\partial \mathbf{M}}{\partial d_{N_{des}}}\right)\phi_{j}\right\}\\ \end{aligned} $$

(39)

Alternatively, Pedersen and Pedersen (2013) have introduced eigenfrequency sensitivities based on local sub-domains. However, in the case where there are N multiple eigenfrequencies (Seyranian et al. 1994), the following generalized gradient can be used in the optimization:

$$ \begin{aligned} &\mathbf{f}_{sk}=\left\{{\phi^{T}_{s}} \left( \frac{\partial \mathbf{K}}{\partial d_{1}} - \lambda \frac{\partial \mathbf{M}}{\partial d_{1}}\right)\phi_{k},\right.\\ &\left. ...,{\phi^{T}_{s}} \left( \frac{\partial \mathbf{K}}{\partial d_{N_{des}}} - \lambda_{j} \frac{\partial \mathbf{M}}{\partial d_{N_{des}}}\right)\phi_{k}\right\}\\ & s,k=n,...,n+N-1. \end{aligned} $$

(40)

1.2 A.2 Sensitivity analysis of the dynamic compliance

Sensitivity analysis for the dynamic compliance in (24) with respect to a design variable d _n is derived by a chain rule for mathematical programming:

$$ \frac{\partial{\Phi}}{\partial d_{n}}=\sum\limits_{\rho_{i}}\frac{\partial{\Phi}}{\partial \rho_{i}} \frac{\partial \rho_{i}}{\partial d_{n}} $$

(41)

The derivatives of ∂Φ/∂ ρ _i can be obtained as follows

$$ \begin{aligned} \frac{\partial{\Phi}}{\partial \rho_{i}}=\left( \begin{array}{llll} \bigtriangledown \mathbf{U}_{\mathrm{R}}\mathrm{\Phi} \\ \bigtriangledown\mathbf{U}_{\mathrm{I}}{\Phi} \end{array}\right)^{\mathrm{T}} \left( \begin{array}{llll} \bigtriangledown\mathbf{\rho}_{i}\mathbf{U}_{\mathrm{R}}\\ \bigtriangledown\mathbf{\rho}_{i}\mathbf{U}_{\mathrm{I}} \end{array}\right)\end{aligned} $$

(42)

where

$$ \begin{aligned} \left( \begin{array}{llll} \bigtriangledown\mathbf{\rho}_{i}\mathbf{U_{R}} \\ \bigtriangledown\mathbf{\rho}_{i}\mathbf{U_{I}} \end{array}\right)=&-\left[\begin{array}{llll} \mathbf{K}-\omega^{2}\mathbf{M}&-\omega\mathbf{C} \\ \omega\mathbf{C} &\mathbf{K}-\omega^{2}\mathbf{M} \end{array}\right]^{-1}\\ &\times \frac{\partial}{\partial \mathbf{\rho}_{i}}\left[\begin{array}{llll} \mathbf{K}-\omega^{2}\mathbf{M} & -\omega{\mathbf{C}} \\ \omega{\mathbf{C}} & \mathbf{K}-\omega^{2}\mathbf{M} \end{array}\right]\left( \begin{array}{lllll} \mathbf{U}_{\mathrm{R}}\\ \mathbf{U}_{\mathrm{I}} \end{array}\right) \end{aligned} $$

(43)

Equation (43) is obtained from derivatives of (20). It is assumed that F _R and F _I are independent from the filtered density. The term in the first parentheses of (42) is used as

$$ \begin{aligned} \left( \begin{array}{lllll} \boldsymbol{\lambda}_{\mathrm{R}} \\ \boldsymbol{\lambda}_{\mathrm{I}} \end{array}\right)=\left[\begin{array}{cc} \mathbf{K}-\omega^{2}\mathbf{M}&-\omega\mathbf{C} \\ \omega\mathbf{C} &\mathbf{K}-\omega^{2}\mathbf{M} \end{array}\right]^{-\mathrm{T}}& \left( \begin{array}{lllll} \bigtriangledown\mathbf{U}_{\mathrm{R}}{\Phi}\\ \bigtriangledown\mathbf{U}_{\mathrm{I}}{\Phi}\end{array}\right)\end{aligned} $$

(44)

where ▽U _RΦ and ▽U _IΦ are the gradients of Φ with respect to U _R and U _I, respectively. Those gradients can be computed as

$$\begin{aligned} \bigtriangledown \mathbf{U}_{\mathrm{R}}{\Phi}=\frac{(\mathbf{F}_{\mathrm{R}}^{\mathrm{T}}\mathbf{U}_{\mathrm{R}}-\mathbf{F}_{\mathrm{I}}^{\mathrm{T}}\mathbf{U}_{\mathrm{I}})\mathbf{F}_{\mathrm{R}}}{\Phi}\\ +\frac{(\mathbf{F}_{\mathrm{R}}^{\mathrm{T}}\mathbf{U}_{\mathrm{I}}+\mathbf{F}_{\mathrm{I}}^{\mathrm{T}}\mathbf{U}_{\mathrm{R}})\mathbf{F}_{\mathrm{I}}}{\Phi}\\ \bigtriangledown \mathbf{U}_{\mathrm{I}}{\Phi}=\frac{(-\mathbf{F}_{\mathrm{R}}^{\mathrm{T}}\mathbf{U}_{\mathrm{R}}+\mathbf{F}_{\mathrm{I}}^{\mathrm{T}}\mathbf{U}_{\mathrm{I}})\mathbf{F}_{\mathrm{I}}}{\Phi}\\ +\frac{(\mathbf{F}_{\mathrm{R}}^{\mathrm{T}}\mathbf{U}_{\mathrm{I}}+\mathbf{F}_{\mathrm{I}}^{\mathrm{T}}\mathbf{U}_{\mathrm{R}})\mathbf{F}_{\mathrm{R}}}{\Phi} \end{aligned} $$

(45)

Similar to (19), let λ=λ _R+i λ _I, ▽UΦ=▽U _RΦ+i▽U _IΦ and assume M , C and K are symmetric. The complex vector form of (45) can be described as

$$\begin{aligned} \bigtriangledown\mathbf{U}{\Phi}=\frac{\mathbf{F^{\mathrm{T}}U}}{{\Phi}}\bar{\mathbf{F}} \end{aligned} $$

(46)

where F̄ denotes the complex conjugate of F. Then (44) can be expressed in complex form as:

$$ [\mathbf{K}+i\omega\mathbf{C}-\omega^{2}\mathbf{M}]\boldsymbol{\bar{\lambda}}=\overline{\bigtriangledown\mathbf{U}{\Phi}}= \frac{\bar{\mathbf{F}}^{T}\bar{\mathbf{U}}}{\Phi}\mathbf{F} $$

(47)

where λ̄ and ▽UΦ¯ denote the complex conjugate of λ and ▽UΦ, respectively. For the linear system, one can show that the solution of (47) in terms of λ̄ is proportional to one of (20) in terms of U. Therefore, the conjugate of λ̄ can be computed by a scalar factor, that is

$$ \boldsymbol{\bar{\lambda}}=\frac{\bar{\mathbf{F}}^{\mathrm{T}}\bar{\mathbf{U}}}{\Phi}\mathbf{U} $$

(48)

Finally, substitution of (44) and (48) into (42) yields the following

$$ \frac{\partial{\Phi}}{\partial \rho_{i}}=-\left( \begin{array}{c} \boldsymbol{\lambda}_{\mathrm{R}} \\ \boldsymbol{\lambda}_{\mathrm{I}} \end{array}\right)^{\mathrm{T}}\frac{\partial}{\partial \rho_{i}}\left[\begin{array}{cc} \mathbf{K}-\omega^{2}\mathbf{M} & -\omega{\mathbf{C}} \\ \omega{\mathbf{C}} & \mathbf{K}-\omega^{2}\mathbf{M} \end{array}\right]\left( \begin{array}{c}\mathbf{U}_{\mathrm{R}}\\\mathbf{U}_{\mathrm{I}}\end{array}\right) $$

(49)

$$\begin{aligned} \frac{\partial{\Phi}}{\partial \rho_{i}}&=-Re\left\{\frac{\bar{\mathbf{F}}^{\mathrm{T}}\bar{\mathbf{U}}}{\Phi}\mathbf{U}^{\mathrm{T}} \frac{\partial(\mathbf{K}+\mathit{i}\omega C-\omega^{2}M)}{\partial \rho_{i}}\mathbf{U} \right\} \\&=-Re\left\{\boldsymbol{\lambda}^{\ast}\frac{\partial(\mathbf{K}+\mathit{i}\omega C-\omega^{2}M)}{\partial \rho_{i}}\mathbf{U} \right\} \end{aligned} $$

(50)

where λ ^∗ is a Hermitian transpose of λ. That is $\boldsymbol {\lambda }^{*}:=\boldsymbol {\bar {\lambda }}^{\mathrm {T}}$