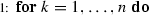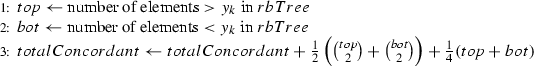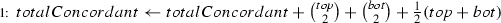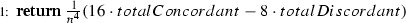Abstract
In an extension of Kendall’s \(\tau \), Bergsma and Dassios (Bernoulli 20(2):1006–1028, 2014) introduced a covariance measure \(\tau ^*\) for two ordinal random variables that vanishes if and only if the two variables are independent. For a sample of size n, a direct computation of \(t^*\), the empirical version of \(\tau ^*\), requires \(O(n^4)\) operations. We derive an algorithm that computes the statistic using only \(O \left( n^2\log (n)\right) \) operations.


Similar content being viewed by others
Notes
R code to reproduce the results of Tables 1, 2 and 3 can be found on the first author’s webpage: http://www.stat.washington.edu/~lucaw/public_resources/eff_comp_2015/tables.R.
References
Bergsma W, Dassios A (2014) A consistent test of independence based on a sign covariance related to Kendall’s tau. Bernoulli 20(2):1006–1028
Christensen D (2005) Fast algorithms for the calculation of Kendall’s \(\tau \). Comput Stat 20(1):51–62
Guibas LJ, Sedgewick R (1978) A dichromatic framework for balanced trees. In: 19th annual symposium on foundations of computer science, pp 8–21
Kendall MG (1938) A new measure of rank correlation. Biometrika 30(1/2):81–93
Martinian E (2005) Red-black tree C code. http://web.mit.edu/~emin/www.old/source_code/red_black_tree/index.html
R Core Team (2015) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, https://www.R-project.org/
Serfling RJ (1980) Approximation theorems of mathematical statistics, Wiley Series in Probability and Mathematical Statistics. Wiley, New York
Spearman C (1904) The proof and measurement of association between two things. Am J Psychol 15:72–101
Weihs L (2015) TauStar: efficient computation of the t* statistic of Bergsma and Dassios (2014). R package version 1.0.0, http://CRAN.R-project.org/package=TauStar
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Modifications for the V-statistic
This section provides an overview of necessary modifications to Algorithm 2 in order to compute the V-statistic version of \(t^*\). Suppose, as usual, that we have reordered the pairs \((x_1,y_1),\ldots ,(x_n,y_n)\) so that \(x_1\le x_2\le \cdots \le x_n\). Then the V-statistic for \(\tau ^*\) is
Here, the second equality holds since \(a(x_i,x_j,x_k,x_l)a(y_i,y_j,y_k,y_l)=0\) if any three of i, j, k, l are equal. The third equality holds because \(b_{ijjk}=0\) for all \(i< j< k\); indeed, \(x_i\le x_j \le x_k\) implies that \(b_{ijjk}\) corresponds to an inseparable collection of points. Note that, in the above equations, we have coefficients of \(\frac{1}{2}\) on \(b_{ijkk},b_{iijk}\) and \(\frac{1}{4}\) on \(b_{iikk}\), these are corrective factors to account for the fact that the number of permutations of four elements where exactly two are equal is \(|S_4|/2\) while the number of permutations where exactly two pairs of two are equal is \(|S_4|/4\). Now we may continue to rewrite \(t^*_V\) as
If \(k=n\) then \(\sum _{k<l\le n}\) is the empty sum which we define to equal 0. For a fixed \(k<l\) we know already, from Sect. 3, how to compute \(\sum _{1\le i < j<k} b_{ijkl}\) efficiently using a red–black tree and since \(b_{iikl},b_{ijkk}\), and \(b_{iikk}\) can only correspond to inseparable or concordant quadruples it is easy to see that
Thus we may compute \(t_V^*\) by running Algorithm 2 with the following modifications:
-
(i)
Change line 9 to
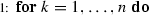
This corresponds to the outer sum of \(t^*_V\).
-
(ii)
After line 14 add the lines:
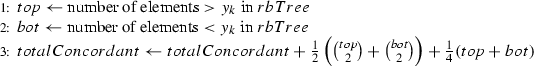
-
(iii)
Change line 23 to
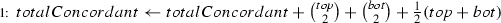
This corresponds to (15).
-
(iv)
Change line 42 to
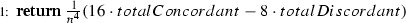
Finally, note that this Algorithm for computing \(t^*_V\) clearly remains \(O(n^2\log (n))\).
Appendix 2: Proof of Lemma 1
By permutation invariance, suppose we have relabeled so that \(x_1\le x_2\le x_3\le x_4\). We have 3 cases:
-
(i)
The points in A are inseparable. The fact that \(b_{1234}=0\) is an immediate consequence of Eq. (2).
-
(ii)
The points in A are concordant. In this case we must have that \(x_2<x_3\) and either \(\max (y_1,y_2) < \min (y_3,y_4)\) or \(\min (y_1,y_2) > \max (y_3,y_4)\). By symmetry we need only consider the case when \(\max (y_1,y_2) < \min (y_3,y_4)\). By Eq. (2) it follows, with some thought, that \(a(x_{\pi (1,2,3,4)}) = a(y_{\pi (1,2,3,4)})\) for all permutations \(\pi \in S_4\) and thus, for any \(\pi \in S_4\) we have \(a(x_{\pi (1,2,3,4)})a(y_{\pi (1,2,3,4)}) = a(x_{\pi (1,2,3,4)})^2\) with
$$\begin{aligned} a(x_{\pi (1,2,3,4)})^2&=\left\{ \begin{array}{lll} 1 &{} \quad \text{ if } \max (x_{\pi (1)}, x_{\pi (2)}) < \min (x_{\pi (3)}, x_{\pi (4)})\text { or} \\ &{} \min (x_{\pi (1)}, x_{\pi (2)}) > \max (x_{\pi (3)}, x_{\pi (4)})\text { or}\\ &{} \max (x_{\pi (1)}, x_{\pi (3)}) < \min (x_{\pi (2)}, x_{\pi (4)})\text { or}\\ &{} \min (x_{\pi (1)}, x_{\pi (3)}) > \max (x_{\pi (2)}, x_{\pi (4)}),\\ 0 &{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$But since \(x_1\le x_2 < x_3\le x_4\) we have that \(a(x_{\pi (1,2,3,4)})a(y_{\pi (1,2,3,4)})=1\) if and only if \(\{\pi (1),\pi (2)\} \in \{\{1,2\}, \{3,4\}\}\) or \(\{\pi (1),\pi (3)\} \in \{\{1,2\}, \{3,4\}\}\). There are exactly \(2^4=16\) such permutations and thus \(b_{1234}=16\).
-
(iii)
The points in A are discordant. Once again we must have that \(x_2<x_3\). It then follows, by the definition of discordant, that \(y_1\not =y_2\) and \(y_3\not =y_4\). We prove an intermediary lemma:
Lemma 2
Suppose that \((x_1,y_1),\ldots ,(x_4,y_4)\) are discordant and \(x_1\le x_2< x_3\le x_4\). Let
so that \((x_5,y_5),\ldots ,(x_8,y_8)\) are simply \((x_1,y_1),\ldots ,(x_4,y_4)\) with \(y_1,y_2\) switched. Then \(b_{1234} = b_{5678}\). Moreover, the same result is true if we flipped \(y_3,y_4\) instead of \(y_1,y_2\).
Proof
First note that, trivially, \(a(x_{\pi (1,2,3,4)}) = a(x_{\pi (5,6,7,8)})\) for any \(\pi \in S_4\). Let \(\pi \) be any permutation so that \(a(x_{\pi (1,2,3,4)})^2=1\). From case (ii) we know that we must have \(\{\pi (1),\pi (2)\} \in \{\{1,2\}, \{3,4\}\}\) or \(\{\pi (1),\pi (3)\} \in \{\{1,2\}, \{3,4\}\}\). Suppose that \(\{\pi (1),\pi (2)\}=\{1,2\}\), and let \(\pi '\in S_4\) be the permutation where
Then clearly \( a(x_{\pi (1,2,3,4)}) = a(x_{\pi '(1,2,3,4)}) = a(x_{\pi (5,6,7,8)}) = a(x_{\pi '(5,6,7,8)})\) but
and thus
As we may perform a similar procedure to all \(\pi \in S_4\) with \(a(x_{\pi (1,2,3,4)})^2=1\) (changing the choice of \(\pi '\)), we see that \(b_{1234} = b_{5678}\) as claimed.
Finally, pairing \(\pi \) with \(\pi '\) given by
shows that this result still holds if we had flipped \(y_3,y_4\) instead of \(y_1,y_2\). \(\square \)
By Lemma 2, we may assume that \(x_1\le x_2<x_3\le x_4\) and \(y_1<y_2\) and \(y_3<y_4\). Note that, by the definition of discordant, we must have that \(y_2 > y_3\) and \(y_1<y_4\). From case (ii) we know that there are only 16 permutations \(\pi \) for which \(a(x_{\pi (1,2,3,4)}) \not = 0\) and they satisfy
If \(\{\pi (1),\pi (2)\} \in \{\{1,2\}, \{3,4\}\}\) and \(\{\pi (1),\pi (3)\} \in \{\{1,4\},\{2,3\}\}\), then we have \(a(y_{\pi (1,2,3,4)}) = 0\). Similarly, \(a(y_{\pi (1,2,3,4)}) = 0\) if \(\{\pi (1),\pi (3)\} \in \{\{1,2\}, \{3,4\}\}\) and \(\{\pi (1),\pi (2)\} \in \{\{1,4\},\{2,3\}\}\). This leaves only 8 permutations \(\pi \in S_4\) for which \(a(x_{\pi (1,2,3,4)})a(y_{\pi (1,2,3,4)})\) may be non-zero, and we check these explicitly:
We conclude that \(b_{1234} = -8\) as claimed.
Rights and permissions
About this article
Cite this article
Weihs, L., Drton, M. & Leung, D. Efficient computation of the Bergsma–Dassios sign covariance. Comput Stat 31, 315–328 (2016). https://doi.org/10.1007/s00180-015-0639-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-015-0639-x