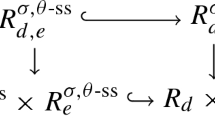Cohomological Hall Algebras, Vertex Algebras and Instantons

Abstract

We define an action of the (double of) Cohomological Hall algebra of Kontsevich and Soibelman on the cohomology of the moduli space of spiked instantons of Nekrasov. We identify this action with the one of the affine Yangian of $\mathfrak {gl}(1)$. Based on that we derive the vertex algebra at the corner ${\mathcal {W}}_{r_{1},r_{2},r_{3}}$ of Gaiotto and Rapčák. We conjecture that our approach works for a big class of Calabi–Yau categories, including those associated with toric Calabi–Yau 3-folds.

Appendices

A The Proof of Theorem 7.1.1

In this section, we prove Theorem 7.1.1 (1). Let $Y^+$ be the positive part of the affine Yangian $Y_{\hbar _1, \hbar _2, \hbar _3}(\widehat{\mathfrak {gl}(1)})$, and $\mathbf Sh$ be the shuffle algebra associated to the 2d COHA ${\mathcal {H}}^{(Q_3,W_3),\mathbf{T}_2}_{B_3=0}$ in Sect. 7.2. By Theorems 7.2.1 and 7.2.4, it suffices to show there is an algebra homomorphism from $Y^+$ to the shuffle algebra $\mathbf Sh$, the multiplication of which we denote by $\star$. We now check the assignment

$$\begin{aligned} \Psi : Y^+\rightarrow \mathbf Sh , \,\ \text {by }e_{r} \mapsto \lambda ^{r} \in \mathbf Sh (1)\cong \mathbf{C}[\hbar _1,\hbar _2,\lambda ] \end{aligned}$$

preserves the relations (Y1) and (Y6).

Let $\lambda _{12}=\lambda _1-\lambda _2$, and let

$$\begin{aligned}&{{\,\mathrm{fac}\,}}(\lambda _{12}):= \frac{(\lambda _{12}-\hbar _1)(\lambda _{12}-\hbar _2)(\lambda _{12}-\hbar _3)}{ \lambda _{12}}.\\ {}&{{\,\mathrm{fac}\,}}'(\lambda _{12}):={{\,\mathrm{fac}\,}}(\lambda _{21})= \frac{(\lambda _{12}+\hbar _1)(\lambda _{12}+\hbar _2)(\lambda _{12}+\hbar _3)}{ \lambda _{12}}. \end{aligned}$$

Let $\sigma _{2}:=\hbar _1\hbar _2+\hbar _2\hbar _3+\hbar _1\hbar _3$. Under the condition $\hbar _1+\hbar _2+\hbar _3=0$, we have the following identities.

$$\begin{aligned}&(X + \hbar _1) (X + \hbar _2) (X + \hbar _3) - (X - \hbar _1) (X - \hbar _2) (X - \hbar _3)= 2 \hbar _1 \hbar _2 \hbar _3. \end{aligned}$$

(27)

$$\begin{aligned}&(X + \hbar _1) (X + \hbar _2) (X + \hbar _3) + (X - \hbar _1) (X - \hbar _2) (X - \hbar _3)= 2 X^3+2\sigma _2X. \end{aligned}$$

(28)

Therefore,

$$\begin{aligned}&{{\,\mathrm{fac}\,}}(\lambda _{12})-{{\,\mathrm{fac}\,}}'(\lambda _{12})={{\,\mathrm{fac}\,}}(\lambda _{12})-{{\,\mathrm{fac}\,}}(\lambda _{21} )=-2\frac{\hbar _1\hbar _2\hbar _3}{\lambda _{12}}, \\&{{\,\mathrm{fac}\,}}(\lambda _{12})+{{\,\mathrm{fac}\,}}'(\lambda _{12})={{\,\mathrm{fac}\,}}(\lambda _{12})+{{\,\mathrm{fac}\,}}'(\lambda _{21} )=2\frac{ \lambda _{12}^3+\sigma _2\lambda _{12}}{\lambda _{12}}. \end{aligned}$$

Let $R=\mathbf{C}[\hbar _1, \hbar _2]$. By the shuffle formula (20), the multiplication of $\mathbf Sh$ is given by

$$\begin{aligned}&R[\lambda _1]\otimes R[\lambda _2] \rightarrow R[\lambda _1, \lambda _2]^{{\mathfrak {S}}_2}, \\&(f(\lambda _1), g(\lambda _2))\mapsto f(\lambda _1)g(\lambda _2) {{\,\mathrm{fac}\,}}(\lambda _{12}) +f(\lambda _2)g(\lambda _1) {{\,\mathrm{fac}\,}}'(\lambda _{12}). \end{aligned}$$

Therefore, for any $a, b\in \mathbf{N}$, $\lambda ^a\star \lambda ^b=\lambda _1^a\lambda _2^b {{\,\mathrm{fac}\,}}(\lambda _{12}) +\lambda _1^b\lambda _2^a {{\,\mathrm{fac}\,}}'(\lambda _{12})$. This gives that

$$\begin{aligned}&\lambda ^a\star \lambda ^b-\lambda ^b\star \lambda ^a=-2\frac{\hbar _1\hbar _2\hbar _3}{\lambda _{12}}\Big (\lambda ^a_1 \lambda ^b_2-\lambda ^b_1 \lambda ^a_2\Big ) \nonumber \\&\lambda ^a\star \lambda ^b+\lambda ^b\star \lambda ^a=\Big (\lambda _1^a\lambda _2^b +\lambda ^b_1\lambda ^a_2 \Big ) 2 \frac{\lambda _{12}^3+\sigma _2\lambda _{12}}{\lambda _{12}}. \end{aligned}$$

(29)

Using (27), we now compute

$$\begin{aligned}&\Psi ([e_{i+3}, e_j]-3[e_{i+2}, e_{j+1}]+3[e_{i+1}, e_{j+2}]-[e_i, e_{j+3}]+\sigma _2([e_{i+1}, e_j]-[e_i, e_{j+1}]))\\&\quad =-2\frac{\hbar _1\hbar _2\hbar _3}{\lambda _{12}} \Big (\lambda ^{i+3}_1 \lambda ^{j}_2-\lambda ^{j}_1 \lambda ^{i+3}_2 -3(\lambda ^{i+2}_1 \lambda ^{j+1}_2-\lambda ^{j+1}_1 \lambda ^{i+2}_2) +3(\lambda ^{i+1}_1 \lambda ^{j+2}_2-\lambda ^{j+2}_1 \lambda ^{i+1}_2)\\&\qquad -(\lambda ^{i}_1 \lambda ^{j+3}_2-\lambda ^{j+3}_1 \lambda ^{i}_2) +\sigma _2((\lambda ^{i+1}_1 \lambda ^{j}_2-\lambda ^{j}_1 \lambda ^{i+1}_2) -(\lambda ^{i}_1 \lambda ^{j+1}_2-\lambda ^{j+1}_1 \lambda ^{i}_2)) \Big )\\&\quad =-2\frac{\hbar _1\hbar _2\hbar _3}{\lambda _{12}} \Big (\lambda _1^{i}\lambda _2^j (\lambda _{12}^{3}+\sigma _2\lambda _{12})-\lambda _1^{j}\lambda ^i_2 (\lambda _{21}^{3}+\sigma _2\lambda _{21}) \Big )\\&\quad =-2\frac{\hbar _1\hbar _2\hbar _3}{\lambda _{12}} (\lambda _1^{i}\lambda _2^j+\lambda _1^{j}\lambda ^i_2) (\lambda _{12}^{3}+\sigma _2\lambda _{12}). \end{aligned}$$

By (29), the above is the same as

$$\begin{aligned} -\hbar _1\hbar _2\hbar _3 (\lambda ^i\star \lambda ^j+\lambda ^j\star \lambda ^i)=\Psi (-\sigma _3 \{e_i, e_j\}). \end{aligned}$$

Therefore, the assignment $\Psi$ preserves the relation (Y1).

By the shuffle formula (20), the multiplication of $\mathbf Sh$ is given by

$$\begin{aligned}&R[\lambda _1]\otimes R[\lambda _2, \lambda _3]^{{\mathfrak {S}}_2} \rightarrow R[\lambda _1, \lambda _2, \lambda _3]^{{\mathfrak {S}}_3}, \\&(f(\lambda _1), g(\lambda _2, \lambda _3)) \mapsto f(\lambda _1)g(\lambda _2, \lambda _3) {{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{13})\\&\quad +f(\lambda _2)g(\lambda _1, \lambda _3) {{\,\mathrm{fac}\,}}(\lambda _{21}) {{\,\mathrm{fac}\,}}(\lambda _{23}) +f(\lambda _3)g(\lambda _2, \lambda _1) {{\,\mathrm{fac}\,}}(\lambda _{32}) {{\,\mathrm{fac}\,}}(\lambda _{31}), \end{aligned}$$

and

$$\begin{aligned}&R[\lambda _1, \lambda _2]^{{\mathfrak {S}}_2}\otimes R[\lambda _3] \rightarrow R[\lambda _1, \lambda _2, \lambda _3]^{{\mathfrak {S}}_3}, \\&(f(\lambda _1, \lambda _2), g(\lambda _3)) \mapsto f(\lambda _1, \lambda _2)g(\lambda _3)) {{\,\mathrm{fac}\,}}(\lambda _{13}) {{\,\mathrm{fac}\,}}(\lambda _{23})\\&\quad + f(\lambda _3, \lambda _2)g(\lambda _1)) {{\,\mathrm{fac}\,}}(\lambda _{31}) {{\,\mathrm{fac}\,}}(\lambda _{21}) +f(\lambda _1, \lambda _3)g(\lambda _2)) {{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{32}). \end{aligned}$$

Therefore, we have

$$\begin{aligned}&e_{c}\star [e_{a}, e_{b}] = -2\sigma _3 \lambda _1^c\star \frac{\Big (\lambda ^a_2 \lambda ^b_3-\lambda ^b_2 \lambda ^a_3\Big )}{\lambda _{23}}\\&\quad =-2\sigma _3 \frac{(\lambda ^a_2 \lambda ^b_3-\lambda ^b_2 \lambda ^a_3)\lambda _1^c }{\lambda _{23}} {{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{13}) -2\sigma _3 \frac{(\lambda ^a_1 \lambda ^b_3-\lambda ^b_1 \lambda ^a_3)\lambda _2^c }{\lambda _{13}} {{\,\mathrm{fac}\,}}(\lambda _{21}) {{\,\mathrm{fac}\,}}(\lambda _{23})\\&\qquad -2\sigma _3 \frac{(\lambda ^a_2 \lambda ^b_1-\lambda ^b_2 \lambda ^a_1)\lambda _3^c }{\lambda _{21}} {{\,\mathrm{fac}\,}}(\lambda _{32}) {{\,\mathrm{fac}\,}}(\lambda _{31}), \end{aligned}$$

and

$$\begin{aligned}&[e_{a}, e_{b}] \star e_{c} =-2\sigma _3\frac{\Big (\lambda ^a_1 \lambda ^b_2-\lambda ^b_1 \lambda ^a_2\Big )}{\lambda _{12}}\star \lambda _3^c\\&\quad = -2\sigma _3\frac{(\lambda ^a_1 \lambda ^b_2-\lambda ^b_1 \lambda ^a_2)\lambda _3^c }{\lambda _{12}} {{\,\mathrm{fac}\,}}(\lambda _{13}) {{\,\mathrm{fac}\,}}(\lambda _{23}) -2\sigma _3\frac{(\lambda ^a_3 \lambda ^b_2-\lambda ^b_3 \lambda ^a_2)\lambda _1^c }{\lambda _{32}} {{\,\mathrm{fac}\,}}(\lambda _{31}) {{\,\mathrm{fac}\,}}(\lambda _{21})\\&\qquad -2\sigma _3\frac{(\lambda ^a_1 \lambda ^b_3-\lambda ^b_1 \lambda ^a_3)\lambda _2^c }{\lambda _{13}} {{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{32}). \end{aligned}$$

We compute

$$\begin{aligned}&[e_c, [e_a, e_b]] =e_c\star [e_a, e_b]-[e_a, e_b]\star e_c\\&\quad =-2\sigma _3 \frac{(\lambda ^a_2 \lambda ^b_3-\lambda ^b_2 \lambda ^a_3)\lambda _1^c }{\lambda _{23}} {{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{13}) -2\sigma _3 \frac{(\lambda ^a_1 \lambda ^b_3-\lambda ^b_1 \lambda ^a_3)\lambda _2^c }{\lambda _{13}} {{\,\mathrm{fac}\,}}(\lambda _{21}) {{\,\mathrm{fac}\,}}(\lambda _{23})\\ {}&\quad \quad -2\sigma _3 \frac{(\lambda ^a_2 \lambda ^b_1-\lambda ^b_2 \lambda ^a_1)\lambda _3^c }{\lambda _{21}} {{\,\mathrm{fac}\,}}(\lambda _{32}) {{\,\mathrm{fac}\,}}(\lambda _{31})\\ {}&\quad \quad +2\sigma _3\frac{(\lambda ^a_1 \lambda ^b_2-\lambda ^b_1 \lambda ^a_2)\lambda _3^c }{\lambda _{12}} {{\,\mathrm{fac}\,}}(\lambda _{13}) {{\,\mathrm{fac}\,}}(\lambda _{23}) +2\sigma _3\frac{(\lambda ^a_3 \lambda ^b_2-\lambda ^b_3 \lambda ^a_2)\lambda _1^c }{\lambda _{32}} {{\,\mathrm{fac}\,}}(\lambda _{31}) {{\,\mathrm{fac}\,}}(\lambda _{21})\\ {}&\quad \quad +2\sigma _3\frac{(\lambda ^a_1 \lambda ^b_3-\lambda ^b_1 \lambda ^a_3)\lambda _2^c }{\lambda _{13}} {{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{32})\\&\quad =-2\sigma _3 \lambda _1^c(\lambda ^a_2 \lambda ^b_3-\lambda ^b_2 \lambda ^a_3) \Big (\frac{ {{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{13})}{\lambda _{23}} +\frac{ {{\,\mathrm{fac}\,}}(\lambda _{21}) {{\,\mathrm{fac}\,}}(\lambda _{31})}{\lambda _{32}} \Big )\\&\quad \quad -2 \sigma _3 \lambda _2^c (\lambda ^a_1 \lambda ^b_3-\lambda ^b_1 \lambda ^a_3) \Big (\frac{{{\,\mathrm{fac}\,}}(\lambda _{21}) {{\,\mathrm{fac}\,}}(\lambda _{23})}{\lambda _{13} } +\frac{{{\,\mathrm{fac}\,}}(\lambda _{12}) {{\,\mathrm{fac}\,}}(\lambda _{32})}{\lambda _{31} } \Big ) \\&\quad \quad -2\sigma _3 \lambda _3^c (\lambda ^a_2 \lambda ^b_1-\lambda ^b_2 \lambda ^a_1) \Big (\frac{{{\,\mathrm{fac}\,}}(\lambda _{32}) {{\,\mathrm{fac}\,}}(\lambda _{31})}{\lambda _{21}} + \frac{{{\,\mathrm{fac}\,}}(\lambda _{23}) {{\,\mathrm{fac}\,}}(\lambda _{13})}{\lambda _{12}} \Big ). \end{aligned}$$

Plug the above formula into the following

$$\begin{aligned} {{\,\mathrm{Sym}\,}}_{{\mathfrak {S}}_3}[e_{i_1}, [e_{i_2}, e_{i_3+1}]]&=[e_{i_1}, [e_{i_2}, e_{i_3+1}]] +[e_{i_2}, [e_{i_1}, e_{i_3+1}]] + [e_{i_3}, [e_{i_2}, e_{i_1+1}]] \nonumber \\&\quad + [e_{i_1}, [e_{i_3}, e_{i_2+1}]] +[e_{i_2}, [e_{i_3}, e_{i_1+1}]] + [e_{i_3}, [e_{i_1}, e_{i_2+1}]]. \end{aligned}$$

(30)

The term in (30) involving $\lambda _1^{i_1}\lambda _2^{i_2}\lambda _3^{i_3}$ is

$$\begin{aligned}&-2\sigma _{3}\lambda _1^{i_1}\lambda _2^{i_2}\lambda _3^{i_3} \Big (-{{\,\mathrm{fac}\,}}(\lambda _{12}){{\,\mathrm{fac}\,}}(\lambda _{13}) +{{\,\mathrm{fac}\,}}(\lambda _{21}){{\,\mathrm{fac}\,}}(\lambda _{31}) -{{\,\mathrm{fac}\,}}(\lambda _{21}){{\,\mathrm{fac}\,}}(\lambda _{23})\\&\quad +{{\,\mathrm{fac}\,}}(\lambda _{12}){{\,\mathrm{fac}\,}}(\lambda _{32}) -{{\,\mathrm{fac}\,}}(\lambda _{32}){{\,\mathrm{fac}\,}}(\lambda _{31}) +{{\,\mathrm{fac}\,}}(\lambda _{23}){{\,\mathrm{fac}\,}}(\lambda _{13}) \Big )=0. \end{aligned}$$

By symmetry, all other terms involving $\lambda _1^{i_a}\lambda _2^{i_b}\lambda _3^{i_c}$, for $\{a, b, c\}=\{1, 2, 3\}$, in (30) are zero. Therefore, $\Psi ({{\,\mathrm{Sym}\,}}_{{\mathfrak {S}}_3}[e_{i_1}, [e_{i_2}, e_{i_3+1}]])=0$. This completes the proof. $\quad \square$

B The Proof of Proposition 6.4.1

In this section, we prove Proposition 6.4.1. We follow the notations from (11).

Definition B.0.1

Passing to the localization of $V_{\vec {r}}$ and $V_{\vec {r'}}\otimes V_{\vec {r''}}$, we define the map $l: V_{\vec {r}}\rightarrow V_{\vec {r'}}\otimes V_{\vec {r''}}$ in Proposition 6.4.1 as the inverse of the following morphism:

$$\begin{aligned} (-1)^{(r_1'+r_2'+r_3')n''} \eta ^{st}_{*} \circ (p^{st})^*: V_{\vec {r'}}(n')\otimes V_{\vec {r''}}(n'')\rightarrow V_{\vec {r}}(n). \end{aligned}$$

Lemma B.0.2

Notations as in Sect. 6.4, let ${\mathcal {V}}_n$ and ${\mathcal {E}}_{\vec {r}}$ be the tautological bundles on ${\mathcal {M}}_{\vec {r}}(n)$. We have

• 1. $p^*({\mathcal {V}}_{n'}\boxtimes {\mathcal {V}}_{n''})=\eta ^*{\mathcal {V}}_{n}$;

• 2. $p^*({\mathcal {E}}_{\vec {r'}}\boxtimes {\mathcal {E}}_{\vec {r''}})=\eta ^*{\mathcal {E}}_{\vec {r''}}$;

• 3. Consequently, for $\psi (z)\in {\mathcal {H}}^0$, and for all $x\in V_{r_1, r_2, r_3}$, we have

  $$\begin{aligned} \Delta ^{{{\,\mathrm{Dr}\,}}}(\psi (z))\bullet l(x)=l(\psi (z) \bullet x). \end{aligned}$$

Proof

The first two are clear by definition. Now we prove the last equation. By the definition of l, it suffices to show that

$$\begin{aligned} \eta ^{st}_{*} \circ (p^{st})^* (\Delta ^{{{\,\mathrm{Dr}\,}}}(\psi (z))\bullet {\tilde{l}} x)=\psi (z)\bullet x, \end{aligned}$$

where ${\tilde{l}}:=(-1)^{(r_1'+r_2'+r_3')n''} l$. By definition $\Delta ^{{{\,\mathrm{Dr}\,}}}(\psi (z))=\psi (z)\otimes \psi (z)$ and $\psi (z) \bullet x=\lambda _{-1/z}({\mathcal {F}}_{n,\vec {r}})\cdot x$. Therefore,

$$\begin{aligned} \eta ^{st}_{*} \circ (p^{st})^* (\Delta ^{{{\,\mathrm{Dr}\,}}}(\psi (z))\bullet {\tilde{l}} x)&=\eta ^{st}_{*} \circ (p^{st})^* (\psi (z)\otimes \psi (z)\bullet {\tilde{l}} x)\\&=\eta ^{st}_{*} \circ (p^{st})^* \Big (\lambda _{-1/z}({\mathcal {F}}_{n',\vec {r}'} \boxtimes {\mathcal {F}}_{n',\vec {r}'})\cdot {\tilde{l}} x\Big )\\&=\eta ^{st}_{*} \Big (\lambda _{-1/z}((\eta ^{st})^* {\mathcal {F}}_{n,\vec {r}}) \cdot (p^{st})^*({\tilde{l}} x)\Big )\\&=\lambda _{-1/z}({\mathcal {F}}_{n,\vec {r}}) \cdot \eta ^{st}_{*} (p^{st})^*({\tilde{l}} x) \\&= \psi (z)\bullet {\tilde{l}}^{-1} {\tilde{l}}(x) = \psi (z)\bullet x. \end{aligned}$$

This completes the proof. $\quad \square$

We now prove Proposition 6.4.1. Lemma B.0.2 implies Proposition 6.4.1 when $\alpha$ is an element in ${\mathcal {H}}^0$. We will now focus on the case when $\alpha \in \mathcal {SH}^{(Q_3, W_3)}$. The proof below is similar to the proof of associativity of the Hall multiplication.

The diagram (6) and correspondence (11) induce the following diagram

The disjoint union in the above breaks the diagram into two diagrams, one for each component of the disjiont union. The maps in the two diagrams are schematically represented as follows. Here the numbers $1, n', n''$ in the rectangle are the sizes of the corresponding matrices, which also schematically represents the subquotients in (6).

(31)

and

(32)

We have two ways from the lower left corner $(\mathfrak {gl}_1)^3 \times {\mathcal {M}}_{ \vec {r}}^{st}(n)$ to the upper right corner $({\mathcal {M}}_{\vec {r}'}^{st}(n'+1) \times {\mathcal {M}}_{\vec {r}''}^{st}(n'')) \sqcup ({\mathcal {M}}_{\vec {r}'}^{st}(n') \times {\mathcal {M}}_{\vec {r}''}^{st}(n''+1))$. The corresponding maps

$$\begin{aligned}&H^*_c((\mathfrak {gl}_1)^3 \times {\mathcal {M}}_{ \vec {r}}^{st}(n);\varphi _{{{\,\mathrm{tr}\,}}})^\vee \rightarrow \big (V_{\vec {r}'}(n'+1)\otimes V_{\vec {r}''}(n'')\big )\bigoplus \big (V_{\vec {r}'}(n')\otimes V_{\vec {r}''}(n''+1)\big ) \end{aligned}$$

will simply be referred to as Way 1 and Way 2.

Way 1: using the bottom horizontal and right vertical correspondences of (31) (32), and follow the standard procedure as in Sect. 5.

Way 2: using the left vertical and top horizontal correspondences of (31) (32), and follow the standard procedure as in Sect. 5.

For any $\alpha \in \mathcal {SH}^{(Q_3, W_3)}$, $x \in V_{\vec {r}}$, clearly Way 1 applied to $(\alpha \otimes x)$ gives $l (\alpha \bullet x)$. We claim that Way 2 applied to $(\alpha \otimes x)$ gives $\Delta ^{{{\,\mathrm{Dr}\,}}}(\alpha ) \bullet l(x)$. Then, convolutions on the level of critical cohomology of diagrams (31), (32) lead to $l (\alpha \bullet x)=\Delta ^{{{\,\mathrm{Dr}\,}}}(\alpha ) \bullet l(x)$. This in turn implies Proposition 6.4.1(1). As the maps l and $\Delta ^{{{\,\mathrm{Dr}\,}}}$ are co-associative in the natural sense, applying Proposition 6.4.1(1) iteratively gives Proposition 6.4.1(2).

In the rest of this section we present the proof in relative details.

The extension in (33) is

$$\begin{aligned} Z_{(0, \vec {r})}(1, n)^{st}=\{(B_i, I_{ab}, J_{ab})_{i\in {\underline{3}}, ab\in {\overline{3}}}\in {\mathcal {M}}_{ \vec {r}}(1+n)^{st}\mid B_i({\mathcal {V}}_1) \subset {\mathcal {V}}_1, J_{ab}({\mathcal {V}}_1)=0 \}. \end{aligned}$$

The extension consists of

$$\begin{aligned} Z_{(\vec {r}, 0)}(n,1)^{op}:=\{(B_i, I_{ab}, J_{ab})_{i\in {\underline{3}}, ab\in {\overline{3}}}\in {\mathcal {M}}_{ \vec {r}}(1+n)\mid B_i({\mathcal {V}}) \subset {\mathcal {V}}, I_{ab}({\mathcal {E}}_{r_c})\subset {\mathcal {V}}, a\ne b\ne c\}, \end{aligned}$$

where op means the opposite stability condition.

We consider

(33)

Lemma B.0.3

For $\alpha (\lambda )\in {\mathcal {H}}^{Q_3, W_3}(1)=\mathbf{C}[\lambda ]$, and $x\in V_{r_1, r_2, r_3}(n)$, we have the equality

$$\begin{aligned} (\eta _1)_*(p_1)^*(\alpha (\lambda ), x)=(-1)^{r_1+r_2+r_3}(\eta _2)_*\big (\psi (\lambda ) \cdot (p_2)^*(x, \alpha (\lambda ))\big ). \end{aligned}$$

Proof

Let us compute the difference between the two maps induced by the two diagrams above. Let ${\mathcal {V}}$ (resp. ${\mathcal {E}}_{r_i}, i=1, 2, 3$) be the tautological dimension n (resp. dimension $r_i, i=1, 2, 3$) bundle on ${\mathcal {M}}_{r_1, r_2, r_3}(n)$ and ${\mathcal {V}}_1$ is the tautological line bundle on ${\mathcal {M}}_{0, 0, 0}(1)$.

Let $\lambda$ be the Chern root of ${\mathcal {V}}_1$, $\lambda _1, \ldots , \lambda _n$ the Chern roots of ${\mathcal {V}}$, and $\mu _1, \ldots , \mu _{r_i}$ the Chern roots of ${\mathcal {E}}_{r_i}$, $i=1, 2, 3$. The difference of and is

$$\begin{aligned}&\Big ({{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {V}}) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {E}}_{r_1}) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {E}}_{r_2}) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {E}}_{r_3}) \Big )\\&-\Big ({{\,\mathrm{{Hom}}\,}}({\mathcal {V}}, {\mathcal {V}}_1) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_1}, {\mathcal {V}}_1) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_2}, {\mathcal {V}}_1)\oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_3}, {\mathcal {V}}_1) \Big ). \end{aligned}$$

Taking into account the torus action in Sect. 5.1, we have

$$\begin{aligned}&eu\Big (\oplus _{i=1}^3{{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, q_i{\mathcal {V}}) -\oplus _{i=1}^3{{\,\mathrm{{Hom}}\,}}({\mathcal {V}}, q_i{\mathcal {V}}_1) \Big )\\&\quad =\frac{eu({\mathcal {V}}_1^*\otimes q_1{\mathcal {V}})eu({\mathcal {V}}_1^*\otimes q_2{\mathcal {V}})eu({\mathcal {V}}_1^*\otimes q_3{\mathcal {V}}) }{eu({\mathcal {V}}^*\otimes q_1{\mathcal {V}}_1) eu({\mathcal {V}}^*\otimes q_2{\mathcal {V}}_1) eu({\mathcal {V}}^*\otimes q_3{\mathcal {V}}_1) } \\&\quad = \prod _{i=1}^n \frac{ \lambda _i -\lambda +\hbar _1}{ \lambda -\lambda _i +\hbar _1} \prod _{i=1}^n \frac{ \lambda _i -\lambda +\hbar _2}{ \lambda -\lambda _i +\hbar _2} \prod _{i=1}^n \frac{ \lambda _i -\lambda +\hbar _3}{ \lambda -\lambda _i +\hbar _3}\\&\quad = (-1)^{3n}\prod _{i=1}^n \frac{ \lambda -\lambda _i-\hbar _1}{ \lambda -\lambda _i +\hbar _1} \prod _{i=1}^n \frac{ \lambda -\lambda _i-\hbar _2}{ \lambda -\lambda _i +\hbar _2} \prod _{i=1}^n \frac{ \lambda -\lambda _i-\hbar _3}{ \lambda -\lambda _i +\hbar _3}. \end{aligned}$$

Similarly,

$$\begin{aligned}&eu\Big ({{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, q_2 q_3 {\mathcal {E}}_{r_1}) -{{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_1}, {\mathcal {V}}_1) \Big ) =eu\Big ({\mathcal {V}}_1^*\otimes q_2 q_3 {\mathcal {E}}_{r_1} -{\mathcal {E}}_{r_1}^*\otimes {\mathcal {V}}_1 \Big ) \\&\quad =\prod _{i=1}^{r_1}\frac{ \mu _i-\lambda -\hbar _1}{\lambda -\mu _i} =(-1)^{r_1} \prod _{i=1}^{r_1}\frac{\lambda - \mu _i+\hbar _1}{\lambda -\mu _i} \end{aligned}$$

and

$$\begin{aligned}&eu\Big ({{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, q_1 q_3 {\mathcal {E}}_{r_2}) -{{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_2}, {\mathcal {V}}_1) \Big ) =(-1)^{r_2} \prod _{i=1}^{r_2}\frac{\lambda - \mu _i+\hbar _2}{\lambda -\mu _i}, \\&eu\Big ({{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, q_1 q_2 {\mathcal {E}}_{r_3}) -{{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_3}, {\mathcal {V}}_1) \Big ) =(-1)^{r_3} \prod _{i=1}^{r_3}\frac{\lambda - \mu _i+\hbar _3}{\lambda -\mu _i}. \end{aligned}$$

Therefore,

$$\begin{aligned}&eu\Big (\big ({{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {V}}) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {E}}_{r_1}) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {E}}_{r_2}) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {V}}_1, {\mathcal {E}}_{r_3}) \big ) \nonumber \\&\qquad -\big ({{\,\mathrm{{Hom}}\,}}({\mathcal {V}}, {\mathcal {V}}_1) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_1}, {\mathcal {V}}_1) \oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_2}, {\mathcal {V}}_1)\oplus {{\,\mathrm{{Hom}}\,}}({\mathcal {E}}_{r_3}, {\mathcal {V}}_1) \big )\Big ) \nonumber \\&\quad = (-1)^{3n+r_1+r_2+r_3} \Big (\prod _{a=1}^{r_1}\frac{\lambda -\mu _a+\hbar _1}{\lambda -\mu _a} \prod _{b=1}^{r_2}\frac{\lambda -\mu _b+\hbar _2}{\lambda -\mu _b} \prod _{b=1}^{r_3}\frac{\lambda -\mu _c+\hbar _3}{\lambda -\mu _c} \nonumber \\&\phantom {123456789} \cdot \prod _{d=1}^{n}\frac{\lambda -\lambda _d-\hbar _1}{\lambda -\lambda _d+\hbar _1} \frac{\lambda -\lambda _d-\hbar _2}{\lambda -\lambda _d+\hbar _2} \frac{\lambda -\lambda _d-\hbar _3}{\lambda -\lambda _d+\hbar _3}\Big ). \end{aligned}$$

(34)

By the formula (16) of ${\mathcal {H}}^0$-action on $x\in V_{r_1, r_2, r_3}(n)$, (34) coincides with $(-1)^{3n+r_1+r_2+r_3}\psi (\lambda )\cdot x$. Recall that in the definition of $\eta _{i*}$ as in (13) Step 5, a change of group from a parabolic to ${{\,\mathrm{GL}\,}}_{n+1}$ appears, where the parabolics are opposite for $\eta _1$ and $\eta _2$, which results a sign $(-1)^n$ in the pushforwards, canceling the sign $(-1)^{3n}$ above. This completes the proof. $\quad \square$

Lemma B.0.4

Way 2 gives $\Delta ^{{{\,\mathrm{Dr}\,}}}(\alpha ) \bullet l(x)$.

Proof

Assume $\alpha =f(\lambda )$ is an element in ${\mathcal {H}}^{(Q_3, W_3)}(1) =\mathbf{C}[\lambda ]$, for some polynomial f. By definition of the Drinfeld coproduct, we have

$$\begin{aligned} \Delta ^{{{\,\mathrm{Dr}\,}}}(\alpha ) =&\psi (\lambda ) \otimes \alpha +\alpha \otimes 1\\ =&1\otimes \alpha -(\hbar _1\hbar _2\hbar _3) \sum _{j\ge 0} \psi _{j} \otimes \lambda ^{j+1} \alpha +\alpha \otimes 1 \in Y^{\ge 0}{\widehat{\otimes }} Y^{\ge 0}. \end{aligned}$$

For $\alpha \in {\mathcal {H}}^{(Q_3, W_3)}(1)$, and $x_1\in V_{\vec {r}'}, x_2\in V_{\vec {r}''}$, applying pullback and pushforward via the following correspondence,

we obtain $(\alpha \otimes 1)\bullet (x_1\otimes x_2)=(\alpha \bullet x_1) \otimes x_2$.

We now use the following correspondence

Notice that we need to switch $(\mathfrak {gl}_1)^3$ with ${\mathcal {M}}_{ \vec {r}'}^{st}(n')$ in order the apply pullback and pushforward to the above correspondence. By Lemma B.0.3, we obtain $(-1)^{r_1'+r_2'+r_3'}(\psi (\lambda ) \otimes \alpha ) \bullet (x_1\otimes x_2)$. Therefore, Way 2 gives $\Delta ^{{{\,\mathrm{Dr}\,}}}(\alpha ) \bullet l(x)$. This completes the proof. $\square$

C More on the Coproduct $\Delta ^{\vec {c}}$

In this section we prove Propositions 8.2.2 and 8.3.6. The outline of the proofs is as follows:

• 1. Prove the primitivity of the Heisenberg operator $B_1$ using the definition of the hyperbolic localization.

• 2. Take the opposite A-action on $\mathfrak {M}_{\vec {r}}$, and the comparison of these two A-actions defines an R-matrix. This R-matrix defines a subalgebra of $\mathrm{End}(\oplus _{\vec {r}}V_{\vec {r}})$ (a generalization of the Maulik–Okounkov Yangian in this 3d setting). Step 1, together with the geometric interpretations of the central and Cartan elements shows that $\mathbf SH ^{\vec {c}}$ has a natural map to this subalgebra.

• 3. When two of the three coordinates of $\vec {r}=(r_1,r_2,r_3)$ are zero, the hyperbolic localization $h:V_{\vec {r}}\rightarrow V_{\vec {r'}}\otimes V_{\vec {r''}}$, under the dimensional reduction, agrees with the one from Nakajima and hence the stable envelope of Maulik–Okounkov.

• 4. Observe that the map $\Delta ^{\vec {c}}:\mathbf SH ^{\vec {c}}\rightarrow (\mathbf SH ^{\vec {c}})^{\otimes 2}$ is uniquely determined by the fact that, when applied to modules $V_{\vec {r}}$ with two of the three coordinates of $\vec {r}=(r_1,r_2,r_3)$ being zero, it agrees with [67, 72, 93]. This in particular proves both Propositions 8.2.2 and 8.3.6. These will be done respectively in the rest of this section. Through out this section, for simplicity we ignore homological degree shiftings.

1.1 C.1 The primitivity of $B_1$

Consider the following commutative diagram

(35)

The right two squares in the diagram are not Cartesian. Nevertheless, the maps $p_2$ and $p_3$ factorize with $p_2''$ and $p_3''$ affine bundles, and the squares with $p_1,q_2, p_2',q_3'$ and $p_2,b_2,p_3',b_3'$ both Cartesian. For clarity, we remark that $p_2''$, defined as a map on the union of two varieties, is defined as the identity map when restricted to the component with $(n_2+1)$ in the index. Similarly, $p_3''$ is defined as the identity map on the component with $(n_1+1)$ in the index.

Remark C.1.1

It is tempting at this point to generalize $q_1^*:H^*_c(\mathfrak {M}_{\vec {r}}(n),\varphi )^\vee \rightarrow H^*_c(C_{\vec {r}}(n,n+1),\varphi )^\vee$ and similarly $q_3^*$ to the correspondence where dimensions differ by 1. However, it is crucial that the potential function on $C_{\vec {r}}(n, n+1)$ is the pullback of the potential function on $\mathfrak {M}_{\vec {r}}(n)$, a fact that does not generalize to higher correspondences.

For simplicity, for any variety X, the structure map $X\rightarrow \text {pt}$ is denoted by $t_X.$ Composing ${\mathbb {D}}t_{\mathfrak {M}_{\vec {r}}(n+1)!}$, $({{\,\mathrm{id}\,}}\rightarrow \eta _{3!}\eta _3^!)$, and $({{\,\mathrm{id}\,}}\rightarrow b_{1*}b_1^*)$, we get a commutative diagram

We have $t_{\mathfrak {M}_{\vec {r}}(n+1)!} \eta _{3!}=t_{\mathfrak {M}_{\vec {r}}(n+1)^A!} p_{3*}$. We compare $t_{\mathfrak {M}_{\vec {r}}(n+1)^A!} p_{3*}\eta _3^!({{\,\mathrm{id}\,}}\rightarrow b_{1*}b_1^*)$ and $t_{\mathfrak {M}_{\vec {r}}(n+1)^A!} ({{\,\mathrm{id}\,}}\rightarrow b_{3*}b_3^*)p_{3*}\eta _3^!$. By commutativity and Cartesian properties of (35), we have

$$\begin{aligned}&b_{3*}b_3^*p_{3*}\eta _3^!=b_{3*}b_3^{'*}p_3^{''*}p_{3*}''p_{3*}^{'}\eta _3^!\rightarrow b_{3*}b_3^{'*}p_{3*}'\eta _3^!=b_{3*}p_{2*}b_2^*\eta _3^!\\&=p_{3*}b_{2*}b_2^*\eta _3^!=p_{3*}b_{2*}\eta _2^!b_1^*=p_{3*}\eta _3^!b_{1*}b_1^*, \end{aligned}$$

we get a natural transform $(t_{\mathfrak {M}_{\vec {r}}(n+1)^A!} ({{\,\mathrm{id}\,}}\rightarrow b_{3*}b_3^*)p_{3*}\eta _3^!)\rightarrow (t_{\mathfrak {M}_{\vec {r}}(n+1)^A!} p_{3*}\eta _3^!({{\,\mathrm{id}\,}}\rightarrow b_{1*}b_1^*))$, which therefore gives a commutative diagram

This proves the commutativity of hyperbolic restrictions and pushforwards in the diagram (35).

Similarly, composing ${\mathbb {D}}t_{\mathfrak {M}_{\vec {r}}(n)!}$, ${{\,\mathrm{id}\,}}\rightarrow \eta _{1!}\eta _1^!$, and $(q_{1!}q_1^!\rightarrow {{\,\mathrm{id}\,}})$, we get a commutative square

We have $t_{\mathfrak {M}_{\vec {r}}(n)!}\eta _{1!}=t_{\mathfrak {M}_{\vec {r}}(n)^A!}p_{1*}$. Now we compare $p_{1*}\eta _1^!(q_{1!}q_1^!\rightarrow {{\,\mathrm{id}\,}})$ and $(q_{3!}q_3^!\rightarrow {{\,\mathrm{id}\,}})p_{1*}\eta _1^!$. As we have

$$\begin{aligned}&q_{3!}q_3^!p_{1*}\eta _1^!\rightarrow q_{3!}p_{2*}''p_2^{''!}q_3^!p_{1*}\eta _1^! =q_{3!}p_{2*}q_2^!\eta _1^!\\&=p_{1*}q_{2!}q_2^!\eta _1^! =p_{1*}q_{2!}\eta _2^!q_1^! =p_{1*}\eta _{1}^!q_{1!}q_1^!, \end{aligned}$$

we get a natural transform $(p_{1*}\eta _1^!(q_{1!}q_1^!\rightarrow {{\,\mathrm{id}\,}}))\rightarrow ((q_{3!}q_3^!\rightarrow {{\,\mathrm{id}\,}})p_{1*}\eta _1^!)$, which therefore gives a commutative diagram

This proves the commutativity of hyperbolic restrictions and pullbacks in the diagram (35).

1.2 C.2 The R-matrices

Using the correspondence

we have constructed the hyperbolic restriction map

$$\begin{aligned} h: V_{r_1, r_2, r_3} \rightarrow V_{r_1', r_2', r_3'} \otimes V_{r_1'', r_2'', r_3''}, \end{aligned}$$

where $(r_1, r_2, r_3)=(r_1', r_2', r_3')+(r_1'', r_2'', r_3'')$. Note that the map h depends on the torus A action $t \mapsto A(t)$, $t\in \mathbf{C}^*$. Consider the opposite action of A, that is, the action given by $t \mapsto A(t^{-1})$, $t\in \mathbf{C}^*$. This opposite action gives rise to another hyperbolic restriction map

$$\begin{aligned} h^{op}: V_{r_1, r_2, r_3} \rightarrow V_{r_1', r_2', r_3'} \otimes V_{r_1'', r_2'', r_3''}, \end{aligned}$$

which is an isomorphism after localization by the localization theorem in equivariant cohomology.

Similarly to [67], we define the R-matrix to be

$$\begin{aligned} h^{op}\circ h^{-1}: V_{r_1', r_2', r_3'} \otimes V_{r_1'', r_2'', r_3''} \rightarrow (V_{r_1', r_2', r_3'} \otimes V_{r_1'', r_2'', r_3''}). \end{aligned}$$

The geometrically defined R-matrix gives rise to a Yangian ${\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}$ in the 3d case using the $\hbox {RTT}=\hbox {TTR}$ formalism (see [67, Section 5.2] for details). In particular, ${\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}$ is a subalgebra

$$\begin{aligned} {\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}\subset \prod _{i_1,\ldots , i_n} \mathrm{End}(F_{i_1}(u_1)\otimes F_{i_2}(u_2)\cdots \otimes F_{i_n}(u_n)), \end{aligned}$$

where $F_{i}$’s form a family of representations, with each $V_{r_1,r_2,r_3}$ for $(r_1, r_2, r_3)\in \mathbf{Z}_{\ge 0}^{3}$ being so that $V_{r_1,r_2,r_3}\cong F_{i_1}(u_{i_1})\otimes \cdots \otimes F_{i_m}(u_{i_m})$ for some $i_1,\ldots ,i_m$ [67, Section 5.2.14]. Here the parameters $u_i$’s are identified with the T-equivariant parameters in the definition of $V_{r_1,r_2,r_3}$.

Lemma C.2.1

There is an algebra homomorphism $\mathbf SH ^{\vec {c}}\rightarrow {\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}$, such that the following diagram commutes.

Proof

The algebra $\mathbf SH ^{\vec {c}}$ is generated by $B_1, B_{-1}$ and $\mathbf SH ^{\vec {c}, 0}$. To show $\mathbf SH ^{\vec {c}}$ maps to ${\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}$, we only need to show the actions of $B_1, B_{-1}$ and $\mathbf SH ^{\vec {c}, 0}$ on $V_{\vec {r}}$ come from the Yangian, for any $\vec {r}\in \mathbf{Z}_{\ge 0}^{3}$. By Sect. 6, the action of $\mathbf SH ^{\vec {c}, 0}$ is given by the Chern classes of the tautological bundles, therefore, it lies in the Yangian. By step 1, the element $B_1$ is primitive. Thus, to show that it lies in the image of of the map ${\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}\rightarrow \mathrm{End}_{r\in \mathbf{Z}_{\ge 0}}(V_{\vec {r}})$, it suffices to prove this in the case when $\vec {r}$ has two components being zero. In this 2d case, it is known that $B_1$ is in the image of the map ${\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}\rightarrow \mathrm{End}_{r\in \mathbf{Z}_{\ge 0}}(V_{\vec {r}})$ [11, Section 5.2]. Similar argument holds for $B_{-1}$. $\quad \square$

Note that in particular, the generators of $\mathbf SH ^{\vec {c}}$ are closed under the comultiplication on ${\mathbb {Y}}_{(Q_3^{fr}, W_3^{fr})}$ which in turn is induced by h. Denote this comultiplication by $\Delta ^h$. In Section C.4 we will show $\Delta ^h$ agrees with $\varvec{\Delta }^{\vec {c}}$ from Proposition 8.2.2.

1.3 C.3 Dimensional reduction

Now we work with $\vec {r}=(r_1,r_2,r_3)$ such that two of the three coordinates are zero. Without loss of generality, assume $r_1=r\ne 0, r_2=r_3=0$. In this section, write $X=\{(B_2,B_3,I_{23},J_{23}) \in {\mathcal {M}}_{\vec {r}}(n) \mid \mathbf{C}\langle B_2,B_3\rangle I_{23}(\mathbf{C}^{r_{23}})=\mathbf{C}^n \}/{{\,\mathrm{GL}\,}}_n$, and hence by the definition of stability conditions we have $\mathfrak {M}_{\vec {r}}(n)=X\times \mathfrak {gl}_n$, endowed with a projection $\pi _X:X\times \mathfrak {gl}_n\rightarrow X$. Following the notations as in [19], here we write $Z\subset X$ be the locus consisting of orbits of $(B_2,B_3,I_{23},J_{23})$ where ${{\,\mathrm{tr}\,}}_W(B_k,I_{ij},J_{ij})_{k,i,j=1,2,3}=0$ for all $B_1\in \mathfrak {gl}_n$, with the natural embedding $i_Z:Z\rightarrow X$. Note that Z is isomorphic to the Nakajima quiver variety of dimension n and framing r.

Let $A\subseteq {{\,\mathrm{GL}\,}}_r$ be such that $\mathfrak {M}_{\vec {r}}(n)^A=\coprod _{n'+n''=n}\mathfrak {M}_{\vec {r'}}(n')\times \mathfrak {M}_{\vec {r''}}(n'')$. We focus on one component labeled by $n'+n''=n$, and denote the fixed points loci and the attracting loci by $(X\times \mathfrak {gl}_n)^A\cong X^A\times {\mathfrak {l}}$, $X^A$, $Z^A$, ${\mathcal {A}}_{X\times \mathfrak {gl}_n}\cong {\mathcal {A}}_X\times {\mathfrak {p}}$, ${\mathcal {A}}_X$, ${\mathcal {A}}_Z$ respectively. We have the following diagram.

Here we introduce the variety

$$\begin{aligned} Y=\{(c, x, x^*)\mid c\in {\mathfrak {p}}, x\in {\mathfrak {l}}, x^*\in {\mathfrak {l}}\mid c_{{\mathfrak {l}}}=[x, x^*]\}, \end{aligned}$$

where $c_{\mathfrak {l}}\in {\mathfrak {l}}$ is the projection of $c\in {\mathfrak {p}}$ under the natural map ${\mathfrak {p}}\twoheadrightarrow {\mathfrak {l}}$. Under ${\mathfrak {p}}\cong {\mathfrak {n}}\oplus {\mathfrak {l}}$, we decompose c as $c=c_{\mathfrak {l}}+c_{\mathfrak {n}}$, where $c_{\mathfrak {n}}$ is the corresponding element in ${\mathfrak {n}}$. Note that we have the isomorphism $Y\cong {\mathfrak {n}}\times {\mathfrak {l}}^2, (c, x, x^*)\mapsto (c_{\mathfrak {n}}, x, x^*)$. The maps are given by $q'_X: {\mathcal {A}}_X\rightarrow Y, (x, x^*)\mapsto ([x, x^*], x_{{\mathfrak {l}}}, x^*_{{\mathfrak {l}}})$, $d_Y: Y \rightarrow X^A, (c, x, x^*)\mapsto (x, x^*)$, and $i_Y: Z^A\rightarrow Y, (x, x^*)\mapsto (0, x, x^*)$. It is straightforward to check that the square with $i_Y$, $q'_X$, $q_Z$, and $i_{{\mathcal {A}}_Z}$ is Cartesian. The maps c, d are natural projections. Therefore, the square with c, $\pi '_{X^A}$, $q_X$, and $\pi _{{\mathcal {A}}_X}$ is Cartesian; The two left squares are both Cartesian.

The following identities are easy to prove, using the commutativity of the diagrams and the Cartesian properties liste above, as well as Lemma 8.3.1.

$$\begin{aligned} q_{Z!}j_Z^*i_Z^*= & {} i_Y^*q'_!j_X^* \end{aligned}$$

(36)

$$\begin{aligned} q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}\pi _X^*= & {} d_!d^*\pi ^*_{X^A}q_{X!}j_X^* \end{aligned}$$

(37)

$$\begin{aligned} i^*_{Z^A}q_{X!}= & {} i^*_{Z^A}d_{Y!}q'_!=i^{*}_Yd_Y^*d_{Y!}q'_! \end{aligned}$$

(38)

$$\begin{aligned} \pi _{X^A!}q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}= & {} q_{X!}j_X^*\pi _{X!} \end{aligned}$$

(39)

$$\begin{aligned} i_{Z^A*}q_{Z!}j_Z^*= & {} q_{X!}j_X^*i_{Z*} \end{aligned}$$

(40)

We have the dimensional reduction $\pi _{X!}\pi _X^!i_{Z*}i_Z^*=\pi _{X!}\varphi _{{{\,\mathrm{tr}\,}}W}\pi _X^*$ and $\pi _{X^A!}\pi _{X^A}^!i_{Z^A*}i_{Z^A}^*=\pi _{X^A!}\varphi _{{{\,\mathrm{tr}\,}}W}\pi _{X^A}^*$.

We write $\mathfrak {g}=\mathfrak {gl}_n$ for short. We have the natural isomorphisms of functors

$$\begin{aligned}&q_{X!}j_X^*\pi _{X!}\varphi \pi _X^*=\pi _{X^A!}q_{X\times \mathfrak {g}!}j_{X\times \mathfrak {g}}^*\varphi \pi _X^*=\pi _{X^A!}\varphi q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n} \pi _X^*\\&\quad =\pi _{X^A!}\varphi d_!d^*\pi ^*_{X^A}q_{X!}j_X^*\rightarrow \pi _{X^A!}\varphi \pi ^*_{X^A}q_{X!}j_X^*, \end{aligned}$$

with the equalities given by (39), Lemma 8.3.4, and (37) respectively. Here we apply Lemma 8.3.4 to the setting when A is the opposite 1-dimensional subgroup, and then use [10, Theorem 1] to identify the hyperbolic localization functors of Lemma 8.3.4 in that setting with the functors $q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}$ and $q_{X\times \mathfrak {g}!}j_{X\times \mathfrak {g}}^*$ used here. We also have

$$\begin{aligned}&q_{X!}j_X^*\pi _{X!}\pi _{X}^*i_{Z*}i_Z^*=\pi _{X^A!}q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}\pi _{X}^*i_{Z*}i_Z^*=\pi _{X^A!}d_!d^*\pi ^*_{X^A}q_{X!}j_X^*i_{Z*}i_Z^*\\ \rightarrow&\pi _{X^A!}\pi ^*_{X^A}q_{X!}j_X^*i_{Z*}i_Z^* =\pi _{X^A!}\pi ^*_{X^A}i_{Z^A*}q_{Z!}j_Z^*i_Z^*=\pi _{X^A!}\pi ^*_{X^A}i_{Z^A*}i_Y^*q'_!j_X^* \\ \rightarrow&\pi _{X^A!}\pi ^*_{X^A}i_{Z^A*}i_{Z^A}^*d_Y^*d_{Y!}q'_!j_X^*=\pi _{X^A!}\pi ^*_{X^A}i_{Z^A*}i^*_{Z^A}q_{X!}j_X^* \end{aligned}$$

with the equalities given by (39), (37), (40), (36), (38) respectively.

Lemma C.3.1

The following diagram is commutative.

(41)

with the vertical arrows the dimensional reductions, and horizontal arrows given as above.

Proof

We follow a similar strategy as in [19, Section A1], and by the same construction as in loc. cit. we have ${\tilde{i}}_{Z}$, ${\tilde{i}}_{{\mathcal {A}}_Z}$, and ${\tilde{i}}_{Z^A}$, with the natural transforms $\pi _{X!}{\tilde{i}}_{Z*}{\tilde{i}}_Z^*\varphi _{{{\,\mathrm{tr}\,}}W}\pi _X^*\rightarrow \pi _{X!}{\tilde{i}}_{Z*}{\tilde{i}}_Z^*\pi _X^*$, and $\pi _{X^A!}{\tilde{i}}_{Z^A*}{\tilde{i}}_{Z^A}^*\varphi _{{{\,\mathrm{tr}\,}}W}\pi _{X^A}^*\rightarrow \pi _{X^A!}{\tilde{i}}_{Z^A*}{\tilde{i}}_{Z^A}^*\pi _{X^A}^*$ being isomorphisms. Starting with $q_{X!}j_X^*$ composed with $\pi _{X!}{\tilde{i}}_{Z*}{\tilde{i}}_Z^*\varphi _{{{\,\mathrm{tr}\,}}W}\pi _X^*\rightarrow \pi _{X!}{\tilde{i}}_{Z*}{\tilde{i}}_Z^*\pi _X^*$, using (4) we get

which is a commutative square of natural isomorphisms. Then by [19, Lemma A.4] and Lemma 8.3.4, we get a natural isomorphism

$$\begin{aligned} \pi _{X^A!}\varphi _{{{\,\mathrm{tr}\,}}W}q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}\pi _X^*\rightarrow \pi _{X^A!}q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}{\tilde{i}}_{Z*}{\tilde{i}}_Z^*\varphi _{{{\,\mathrm{tr}\,}}W}\pi _X^*, \end{aligned}$$

(42)

which composes to

$$\begin{aligned} \pi _{X^A!}\varphi _{{{\,\mathrm{tr}\,}}W}q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}\pi _X^*\rightarrow \pi _{X^A!}q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}{\tilde{i}}_{Z*}{\tilde{i}}_Z^*\pi _X^.. \end{aligned}$$

(43)

Similarly, starting with $\pi _{X^A!}\varphi _{{{\,\mathrm{tr}\,}}W}\pi _{X^A}^*\rightarrow \pi _{X^A!}{\tilde{i}}_{Z^A*}{\tilde{i}}_{Z^A}^*\varphi _{{{\,\mathrm{tr}\,}}W}\pi _{X^A}^*\rightarrow \pi _{X^A!}{\tilde{i}}_{Z^A*}{\tilde{i}}_{Z^A}^*\pi _{X^A}^*$ composed with $q_{X!}j_X^!$, and use (2) we get a commutative diagram

(44)

Now using the analogues of (3), (1), and (5), we get a natural map

$$\begin{aligned} \pi _{X^A!}{\tilde{i}}_{Z^A*}{\tilde{i}}_{Z^A}^*q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}\pi _X^*\rightarrow \pi _{X^A!}q_{X\times \mathfrak {gl}_n!}j^*_{X\times \mathfrak {gl}_n}{\tilde{i}}_{Z*}{\tilde{i}}_Z^*\pi _X^*.\end{aligned}$$

Its composition with the right vertical map in (44) gives the same map as (43), due to the naturality of the transforms ${{\,\mathrm{id}\,}}\rightarrow {\tilde{i}}_{Z*}{\tilde{i}}_Z^*$ and $\varphi _{{{\,\mathrm{tr}\,}}_W}\rightarrow {{\,\mathrm{id}\,}}$. $\blacksquare$

Composing ${\mathbb {D}}t_{X!}$, ${{\,\mathrm{id}\,}}\rightarrow j_{X!}j_X^!$, and $\pi _{X!}\pi _X^!i_{Z*}i_Z^*=\pi _{X!}\varphi _{{{\,\mathrm{tr}\,}}W}\pi _X^*$, we get the commutative square

where the left vertical arrow gives the map of Braverman, Finkelberg, and Nakajima [11, (5.6.4)], and the right vertical arrow gives h. Applying the natural isomorphism of functors $t_{X!}j_{X!}j_X^!=t_{X^A!}q_{X!}j_X^*$, we get the commutative square

Combining this with Lemma C.3.1, this shows that the hyperbolic localization h defined here is compatible with th hyperbolic localization of Braverman, Finkelberg, and Nakajima [11, (5.6.4)] under the dimensional reduction. The later is in turn known [11, Theorem 1.6.1.(2) and Section 5.6] to be equal to the stable envelope of Maulik and Okounkov [67, 72, 93]. Therefore, in particular, $\Delta ^h$ agrees with $\varvec{\Delta }^{\vec {c}}$ when specialized to $\mathbf SH ^{\mathbf{c}^{k}}$, $k=1, 2, 3$. $\quad \square$

1.4 C.4 Concluding the proofs

By the definition of the central extended algebras, for each $k=1,2,3$, there is a specialization map $\mathbf SH ^{\vec {c}}\rightarrow \mathbf SH ^{\mathbf{c}^{(k)}}$, with $\mathbf SH ^{\mathbf{c}^{(k)}}$ isomorphic to the algebra $\mathbf SH ^{\mathbf{c}}$ defined in [93]. The direct sum of these three specialization maps embeds the algebra $\mathbf SH ^{\vec {c}}$ into $\bigoplus _{k=1, 2, 3}\mathbf SH ^{\mathbf{c}^{(k)}}$. Moreover, this embedding fits into the upper part of the following diagram.

In other words, $\mathbf SH ^{\vec {c}}$ is characterized as the universal central extension of $\mathbf SH$, which specializes into $\mathbf SH ^{\mathbf{c}^{(k)}}$ for each $k=1,2,3$.

From the formula of $\Delta ^{\vec {c}}$ on the generators of $\mathbf SH ^{\vec {c}}$ in Proposition 8.2.2 specializes to $\Delta ^{\mathbf{c}^{(k)}}: \mathbf SH ^{\mathbf{c}^{(k)}}\rightarrow (\mathbf SH ^{\mathbf{c}^{(k)}})^{\otimes 2}$ by specializing $\mathbf{c}^{(k')}\mapsto 0$, for $1\le k\ne k'\le 3$. These three maps $\Delta ^{\mathbf{c}^{(k)}}$ are well-defined algebra homomorphisms, which agree on the specialization $\mathbf SH$. Therefore, by the aforementioned universal property, $\Delta ^{\vec {c}}$ given in Proposition 8.2.2 is a well-defined algebra homomorphism. By the same universal property, $\Delta ^{\vec {c}}$ is coassociative. This in particular proves Proposition 8.2.2.

To prove Proposition 8.3.6, it suffices to prove the commutativity of the left part of the following diagram of the actions of $\mathbf SH ^{\vec {c}}$.

where $W: = (\oplus _{r_1} V_{r_1, 0, 0})\bigoplus (\oplus _{r_2} V_{0, r_2, 0})\bigoplus (\oplus _{r_3} V_{0, 0, r_3})$. By definition, $\Delta ^h$ from Section C.2 automatically makes the entire diagram commutative. Therefore we need to show that $\Delta ^h$ agrees with $\Delta ^{\vec {c}}$. By Section C.3, $\Delta ^{\vec {c}}$ makes the lower square (containing $\Delta ^{\vec {c}}$ and $h_W$) commutative. Thus, $\Delta ^{\vec {c}}$ and $\Delta ^h$ agree when restricting on $\mathbf SH ^{\mathbf{c}^{k}}$, $k=1, 2, 3$. By the same argument as above, $\Delta ^{\vec {c}}$ is determined by the three specializations $\Delta ^{\mathbf{c}^{(k)}}, k=1, 2, 3$. Therefore, $\Delta ^{\vec {c}}$ and $\Delta ^h$ agree.