Abstract
Chiral and non-chiral p-form gauge fields have gravitational anomalies and anomalies of Green-Schwarz type. This means that they are most naturally realized as the boundary modes of bulk topological phases in one higher dimensions. We give a systematic description of the total bulk-boundary system which is analogous to the realization of a chiral fermion on the boundary of a massive fermion. The anomaly of the boundary theory is given by the partition function of the bulk theory, which we explicitly compute in terms of the Atiyah–Patodi–Singer \(\eta \)-invariant. We use our formalism to determine the \(\mathrm {SL}(2,{\mathbb {Z}})\) anomaly of the 4d Maxwell theory. We also apply it to study the worldvolume theories of a single D-brane and an M5-brane in the presence of orientifolds, orbifolds, and S-folds in string, M, and F theories. In an appendix we also describe a simple class of non-unitary invertible topological theories whose partition function is not a bordism invariant, illustrating the necessity of the unitarity condition in the cobordism classification of the invertible phases.
Similar content being viewed by others
Notes
In this paper, d is the spacetime dimension on which an anomalous theory resides. The corresponding bulk topological phase correspondingly has the spacetime dimension \(d+1\).
Among the theories listed above, the Green-Schwarz mechanism in 10-dimensions is very subtle at the nonperturbative level. See [23] for the case of Type I superstring theory. We do not discuss this case in detail in this paper, but we will discuss an analog of it in Type IIB superstring theory.
Basically the same formula was found previously by S. Monnier and his collaborators in a series of papers where the spacetime was equipped with Wu structure. We will only use the spin structure in the following. More comments on this point will be given in the paragraph preceding Sect. 6.1.
Throughout the paper we assume that the normal bundle to the brane is trivial. The following discussion may require modifications or refinements in the presence of a nontrivial normal bundle, as already known in the case of M5-branes [63].
\(I_8\) of the 11-dimensional supergravity was determined in this way in an early paper on M-theory [64].
In more detail, a proof is as follows. Since \([{\mathsf {F}}] =0\), there exists a differential form \({\mathsf {A}}_0 \in \Omega ^p(X)\) such that \({\mathsf {F}}= \mathrm{d}{\mathsf {A}}_0\). By using (2.2) with \({\mathsf {N}}=0\), we get \(\delta ({\mathsf {A}}- {\mathsf {A}}_0) =0\) and hence \({\mathsf {A}}-{\mathsf {A}}_0 \in Z^p(X,{\mathbb {R}})\). By de Rham theorem, there exists a closed differential form \({\mathsf {A}}_1 \in \Omega _\mathrm{closed}^p(X)\) such that \({\mathsf {A}}-{\mathsf {A}}_0 = {\mathsf {A}}_1 + \delta {\mathsf {a}}\) for some \({\mathsf {a}}\in C^{p-1}(X,{\mathbb {R}})\). Thus, up to gauge transformations, we get \({\mathsf {A}}= {\mathsf {A}}_0 + {\mathsf {A}}_1 \in \Omega ^p(X)\).
\(P(x_1,x_2)\) in (2.14) is often denoted by \(x_1\cup _1 x_2\) and is called the cup-1 product, in the case of cellular cochains.
A cup product satisfying (2.13) is a chain map \(\cup : \bigoplus _{q} C^q \times C^{p-q} \rightarrow C^p\), where \(\delta \) on \(\bigoplus _{q} C^q \times C^{p-q}\) is defined by \( \delta ( x_1 , x_2)=( \delta x_1 , x_2) \oplus (-1)^{p_1}( x_1 , \delta x_2)\). We have \(\delta \cdot \cup = \cup \cdot \delta \). Then Q is a chain homotopy between two chain maps, \( \cup ' - \cup = Q \cdot \delta + \delta \cdot Q\).
Such a space can be obtained as follows. First let us discuss the case \(G = \mathrm {U}(n)\). In this case, let us show that we can take \(B\mathrm {U}(n) = G_{n}({\mathbb { C}}^N)\) with sufficiently large N, where \( G_{n}({\mathbb { C}}^N)\) is the Grassmannian manifold which is the set of complex n-dimensional planes inside \({\mathbb { C}}^N\). The reason is as follows. Suppose we have a \(\mathrm {U}(n)\) bundle on X. A \(\mathrm {U}(n)\) bundle is equivalent to an n-dimensional complex vector bundle E. It is not too hard to show (e.g. by using partition of unity argument associated to local patches of X) that E can be embedded into a trivial N-dimensional bundle \(\underline{{\mathbb { C}}}^N (= {\mathbb { C}}^N \times X)\) for some sufficiently large N, i.e. \(E \subset \underline{{\mathbb { C}}}^N\). Then, for each \(p \in X\), we get an n-dimensional subspace \(E_x \subset {\mathbb { C}}^N\). This defines a map \(f : X \rightarrow B\mathrm {U}(n) = G_{n}({\mathbb { C}}^N)\). From this construction, it is clear that E is a pullback of the tautological n-dimensional bundle of \(G_n({\mathbb { C}}^N)\) whose fiber is just the n-dimensional plane.
For an arbitrary compact Lie group G, we take a faithful unitary n-dimensional representation of G. This gives an embedding \(G \rightarrow \mathrm {U}(n)\). Let \(P_{\mathrm {U}(n)}\) be the universal \(\mathrm {U}(n)\) bundle on \(G_{n}({\mathbb { C}}^N)\). Then, we can consider the G-bundle \(P_{\mathrm {U}(n)} \times _{G} G\) whose base is \(BG = P_{\mathrm {U}(n)}/G\). This gives an example of a classifying space of G.
As we discuss later, the anomaly of the bosonic theory is \(\mathrm{d}C \wedge B\). On the other hand, the fermion side is as follows. Let us say that the left-movers couple to \(A_L\) and the right-movers couple to \(A_R\). Then their anomalies is given by \(\frac{1}{2} \int \mathrm{d}A_L \wedge A_L-\frac{1}{2} \int \mathrm{d}A_R \wedge A_R \). We note that the factors of \(\frac{1}{2}\) needs to be taken care of using quadratic refinements utilizing spin structures as we review in Sect. 4. B and C on the compact boson side is known to be given by \(B=A_L + A_R\) and \(2C=A_L - A_R\). The mechanism realizing it is a bit subtle. Let us start from the free fermion theory. We can obtain the boson theory by summing over spin structures, or in other words the \((-1)^F\) gauge field, of the fermion theory. Each of left and right \(\mathrm {U}(1)\) symmetries \(\mathrm {U}(1)_{L,R}\) has a mixed anomaly between the \((-1)^F\) symmetry, which can be seen by putting the fermion on a Riemann surface with unit flux of the \(\mathrm {U}(1)_L\) (or \(\mathrm {U}(1)_R\)) gauge field, and see that the path integral measure contains a single zero mode which is odd under \((-1)^F\). Since we are gauging \((-1)^F\) as a dynamical field, we want to avoid this anomaly. This can be done by taking the symmetry groups as vector and axial \(\mathrm {U}(1)\) symmetries, \(\mathrm {U}(1)_V\) and \(\mathrm {U}(1)_A\), whose gauge fields \(A_V\) and \(A_A\) are related to \(A_{L,R}\) as \(A_L=A_V+A_A\) and \(A_R = A_V- A_A\). Notice that \(\mathrm {U}(1)_L \times \mathrm {U}(1)_R = [ \mathrm {U}(1)_V \times \mathrm {U}(1)_A]/{\mathbb {Z}}_2\), so \( \mathrm {U}(1)_V \times \mathrm {U}(1)_A\) is a \({\mathbb {Z}}_2\) extension of \(\mathrm {U}(1)_L \times \mathrm {U}(1)_R\). Now there is no mixed anomaly between \((-1)^F\) and \(\mathrm {U}(1)_V \times \mathrm {U}(1)_A\), and we can sum over \((-1)^F\). The sum over \((-1)^F\) is equivalent to a sum over (say) \({\mathbb {Z}}_2 \subset \mathrm {U}(1)_V\), because \((-1)^F\) and \((-1) \in \mathrm {U}(1)_V\) has the same effect on the fermion. Therefore, the symmetry group after summing over \((-1)^F\) is \(\mathrm {U}(1)_V/{\mathbb {Z}}_2\) instead of \(\mathrm {U}(1)_V\), and the corresponding gauge field is \(B= 2A_V\). The \(\mathrm {U}(1)_A\) is unchanged and we rename the gauge field as \(C = A_A\). Thus we finally get \(B=A_L+A_R\) and \(2C = A_L - A_R\). For more discussions, see [2].
Beyond the perturbative level, the Green–Schwarz anomaly cancellation is very nontrivial and the formalism of quadratic refinement using the spin structure may be necessary. See [23] for the case of Type I superstring theory. To the best of the authors’ knowledge, the case of \(E_8 \times E_8\) has not been studied.
In this section, we are actually working not with differential cohomology elements, but with differential cocycles, meaning that we consider \(\check{A}, \check{B}, \check{C}\) before dividing by gauge transformations.
For more general theories which are not invertible, it is possible that the Hilbert space dimension becomes zero for certain backgrounds. For example, let us consider a 3-dimensional abelian Chern–Simons theory with level \(\kappa \), coupled to a background field B. (Here we use a sloppy description without using differential cohomology and precise quadratic refinement.) The action is \( \frac{2\pi {\mathsf i}\kappa }{2} \int A \wedge \mathrm{d}A + 2\pi {\mathsf i}\int B \wedge \mathrm{d}A \) where we normalized fields so that fluxes are integers. The equation of motion of A is \(\kappa \mathrm{d}A =- \mathrm{d}B\). Now consider the Hilbert space \(\mathcal{{H}}(\Sigma ) \) on a Riemann surface \(\Sigma \). If the flux \(\int _\Sigma \mathrm{d}B\) of the background is not a multiple of \(\kappa \), the above equation of motion implies that the Hilbert space is empty, \(\dim \mathcal{{H}}(\Sigma )=0\). The case \(\kappa =1\) is an invertible field theory, and in this case \(\int _\Sigma \mathrm{d}B\) is always a multiple of \(\kappa =1\) and \(\dim \mathcal{{H}}(\Sigma )=1\).
As an example which violates the axioms of quantum field theory, suppose that the partition function is zero on \(S^d\) with topologically trivial backgrounds. Moreover, for simplicity, we assume that the theory is a topological quantum field theory. In that case, it is possible to show by the axioms of topological quantum field theory that all partition functions are zero, and in particular, partition functions on \(S^1 \times X\) are zero for arbitrary X. (See e.g. Sect. 3 of [62] for how to prove this claim.) This is inconsistent if the theory has any Hilbert space of nonzero dimensions at all. More nontrivial versions of this kind of argument have been used to get useful constraints on the partition function of topological field theories [83, 84].
It can be shown by using part of the long exact sequence \(H^2(\mathbb {RP}^5, \widetilde{{\mathbb {Z}}}) \longrightarrow H^2(\mathbb {RP}^5, \widetilde{{\mathbb {Z}}}_2) \longrightarrow H^3(\mathbb {RP}^5, \widetilde{{\mathbb {Z}}}) \) and the fact that \(H^2(\mathbb {RP}^5, \widetilde{{\mathbb {Z}}}) =0\). These facts imply that \(H^2(\mathbb {RP}^5, \widetilde{{\mathbb {Z}}}_2) \longrightarrow H^3(\mathbb {RP}^5, \widetilde{{\mathbb {Z}}}) \) is injective, and this map is the Bockstein homomorphism \(\beta \). The second Stiefel–Whitney class \(w_2\) is nonzero in \(\mathbb {RP}^5\) and hence \(W_3 = \beta (w_2)\) is nonzero.
For ordinary differential cohomology, \(\int _{Y_\mathrm{closed}} {\mathsf {F}}\) is defined to be an integer. However, in the presence of O-planes, \(\int _{Y_\mathrm{closed}} F_5\) is not an integer. Therefore, \(C_4\) is not precisely a differential cohomology element.
More precisely, it is known that \(2{\mathsf {w}}\) is a differential form representative of an integral lift of the \(p+2\)-dimensional Wu class \(\nu _{p+2}\). On a manifold with dimension less than \(2(p+2)\), we automatically have \(\nu _{p+2}=0\) and hence \({\mathsf {w}}= (2{\mathsf {w}})/2\) becomes integral.
This follows from \(\Omega _3^\mathrm{spin}(B \mathrm {U}(1)) =0\). See e.g. [90] for a convenient collection of results for various bordism groups.
We can also use basic results in algebraic topology to show this. What needs to be shown is that \(\int _Z {\mathsf {F}}\wedge {\mathsf {F}}\) is even on a closed spin 4-manifold Z for \({\mathsf {F}}\in H^2(Z,{\mathbb {Z}})\). This follows if we can show \(\int _Z F\cup F=0\) mod 2 for \(F\in H^2(Z,{\mathbb {Z}}_2)\). This is indeed true since \(\int _Z F\cup F=\int _Z \mathrm {Sq}^2\, F =\int _Z \nu _2 \cup F = 0\). Here, we used a few facts in algebraic topology, namely that \(\mathrm {Sq}^n a=a\cup a\) for \(a\in H^n(M,{\mathbb {Z}}_2)\), that \(\int _M \mathrm {Sq}^m a=\int _M \nu _m \cup a\) for the Wu class \(\nu _m\), where \(\nu _1=w_1\), \(\nu _2=w_2+w_1^2\), \(\nu _3=w_1w_2\), \(\nu _4=w_4+w_1w_3 + w_2^2+w_1^4\), ..., and that \(w_1=w_2=0\) on spin manifolds. These facts can be found in the standard textbooks, e.g. [91].
Similarly to footnote 20, it can be shown also using basic results in algebraic topology. What needs to be shown is that \(\int _Z ({\mathsf {F}}\wedge {\mathsf {F}}+ (p_1/2) \wedge {\mathsf {F}})\) is even on any closed spin 8-manifold Z, for \({\mathsf {F}}\in H^4(Z,{\mathbb {Z}})\). First we use the result of [93] which says that \(p_1=\mathfrak {P}(w_2)+\iota _2 w_4\) mod 4, where \(\mathfrak {P}:H^2(X,{\mathbb {Z}}_2)\rightarrow H^4(X,{\mathbb {Z}}_4)\) is a certain cohomology operation known as the Pontrjagin square, and \(\iota _2\) is the homomorphism \({\mathbb {Z}}_2\rightarrow {\mathbb {Z}}_4\) sending 1 mod 2 to 2 mod 4. (This is a basic relation to analyze discrete theta angle in 4d SO gauge theory [94]). On a spin manifold \(w_2=0\), therefore \(p_1\) is divisible by 2, and \(p_1/2=w_4\) mod 2. Then all we have to show is that \(\int _Z (F\cup F+ w_4 \cup F)=0\) mod 2 for \(F\in H^4(Z,{\mathbb {Z}}_2) \). This follows since \(\int _Z F\cup F=\int _Z \mathrm {Sq}^4\, F = \int _Z \nu _4 \cup F= \int _Z w_4 \cup F\), where we used the fact \(\nu _4=w_4\) on a spin manifold.
The differential K-theory here is relevant to the dynamical field of the \(d+1 = 11\) dimensional bulk topological phase. From it, we will later construct a chiral 4-form field as part of the boundary mode in \(d=10\) dimensions. If the relevant generalized cohomology for the bulk dynamical field is \(K^0(Y)\), the generalized cohomology relevant for the boundary mode will be \(K^{-1}(X)\) as we will discuss at the end of Sect. 5.3. Conversely, if the \(d+1=11\) dimensional bulk dynamical field is described by \(K^1(Y)\), the boundary mode is described by \(K^0(X)\).
Equivalently, this reduction of the structure group of E also follows from the fact that the embedding \(\mathrm {U}(1) \rightarrow \mathrm {U}(N)\) gives the isomorphisms \(\pi _k(\mathrm {U}(1)) = \pi _k(\mathrm {U}(N)) \) for \(k=0,1,2\).
In \(d=10\), the cohomology should be changed to the appropriate K-theoretic cohomology group as discussed in Sect. 4.5. Then the following discussions are valid also in that case with minor modifications.
This quantization is done in the standard way, basically following [98]. By (4.7), and also by using the fact that \({\mathsf {w}}\) in that equation is zero on \(S^{p+1} \times S^{p+1}\), the equation of motion requires that the field is flat, \({\mathsf {F}}_A =0\). On \(S^{p+1} \times S^{p+1}\), the flatness also implies that \(\check{A}\) is topologically trivial, and hence it can be written by a flat differential form \(\check{A} = (0, {\mathsf {A}}_A, 0)\). The gauge invariant degrees of freedom are \(\phi _i = \int _{S^{p+1}_i} {\mathsf {A}}_A\), where the subscript \(i=1,2\) distinguishes the two spheres \(S^{p+1}\). These variables take values in \({\mathbb {R}}/{\mathbb {Z}}\). The Lagrangian (in Lorentz signature) is then given by \(\mathcal{{L}}= 2\pi \kappa \phi _1 \partial _t \phi _2\). The canonical quantization of this theory by regarding \(\phi :=\phi _2\) as the canonical position coordinate gives \(\varpi :=2\pi \kappa \phi _1\) as the canonical momentum coordinate. The wave functions are \(\Psi _m(\phi ) = e^{2\pi {\mathsf i}m \phi }\) for \(m \in {\mathbb {Z}}\), but \(\phi _1 \sim \phi _1 +1\) or in other words \(\varpi \sim \varpi + 2\varpi \kappa \) implies that the states \(\Psi _m\) and \(\Psi _{m+\kappa }\) should be identified. Thus we get \(|\kappa |\) states. The quantization here is rather ad hoc, but a more precise treatment by regarding wave functions as holomorphic sections of a line bundle on \(T^2=\{(\phi _1,\phi _2) \}\) would give the same result.
This is shown as follows. For simplicity we consider real coefficients \({\mathbb {R}}\) so that cohomology groups can be regarded as vector spaces. First, the exact sequence (5.14) implies that \(\ker \delta \) is the image of \(H^{p+1}(Y) \rightarrow H^{p+1}(X)\). So let us uplift \(a_1,a_2 \in {\mathbb {A}}\) to elements of \(H^{p+1}(Y)\). Then \(\int _X a_1 \cup a_2 = \int _Y \delta ( a_1 \cup a_2) =0\). Next, notice that \(\delta : {\mathbb {B}}\rightarrow H^{p+2}(Y,X)\) is injective since \({\mathbb {A}}\) is the kernel. Let \(\beta _i~(i=1,2,\cdots )\) be a basis of \({\mathbb {B}}\). The Poincaré duality between \(H^{p+2}(Y,X)\) and \(H^{p+1}(Y)\) implies that there are dual elements \(\alpha ^i \in H^{p+1}(Y)\) such that \(\int _Y \delta (\beta _j) \cup \alpha ^i = \delta ^i_j \). But \(\int _Y \delta (\beta _j) \cup \alpha ^i = \int _Y \delta (\beta _j \cup \alpha ^i ) = \int _X \beta _j \cup \alpha ^i\), so we get \( \int _X \beta _j \cup \alpha ^i = \delta ^i_j\). This in particular implies that \(\alpha ^i\) regarded as elements of \({\mathbb {A}}\subset H^{p+1}(X)\) are linearly independent, and hence \(\dim {\mathbb {A}}\ge \dim {\mathbb {B}}\). Because \(\int _X a_1 \cup a_2 =0\) for any \(a_1,a_2 \in {\mathbb {A}}\), the Poincaré duality in \(H^{p+1}(X)\) is possible only if \(\alpha ^i\) span the entire \({\mathbb {A}}\) and \(\dim {\mathbb {A}}= \dim {\mathbb {B}}\). We conclude that \(\alpha ^i\) and \(\beta _j\) are bases of \({\mathbb {A}}\) and \({\mathbb {B}}\) with \(\int _X \alpha ^i \cup \alpha ^j =0\) and \( \int _X \beta _j \cup \alpha ^i = \delta ^i_j\). By shifting \(\beta _j\) by linear combinations of \(\alpha ^i\) if necessary, we can also take \(\beta _j\) such that \(\int _X \beta _i \cup \beta _j=0\).
There is one difference between the cases of fermions and p-form gauge fields. In the case of fermions, chiral fermions are often realized in the literature as domain wall fermions in which we vary the mass parameter from positive to negative values as a function of space coordinates \(m(y), ~ y \in Y\). However, such a domain wall construction by a varying parameter is not possible in the case of p-form gauge fields. The parameter \(\kappa \) is quantized and cannot be changed as a function of the space coordinate. Also, the parameter \(e^2\) is positive and hence it does not make sense to change \(e^2\) from positive to negative values. In this case, what is physically sensible is the local boundary condition \({\mathsf {L}}\). Thus the strategy of [32] becomes especially important for the purposes of the present paper.
In the above discussion, we have considered the specific invertible field theory \(|\mathcal{{T}}|\). However, we can consider any invertible field theory \(\mathcal{{T}}_\mathrm{counterterm}\) whose Hilbert spaces are canonically isomorphic to \({\mathbb { C}}\), and modify \(\mathcal{{T}}\) as \(\mathcal{{T}}\otimes \mathcal{{T}}_\mathrm{counterterm}\). Anomalies are classified by invertible field theories \(\mathcal{{T}}\) up to such counterterms \(\mathcal{{T}}_\mathrm{counterterm}\).
For the computation of the absolute value of \({\det }' ( - {\mathsf i}\kappa *\mathrm{d})^{- \frac{1}{2}} \), it is necessary to perform gauge fixing and do the computation more carefully. However, for the phase contribution, we can just neglect these gauge fixings. The underlying reason is as follows. Introducing gauge fixings and ghosts would ultimately give an elliptic operator \(\mathcal{{D}}^\mathrm{sig}_Y\) acting on the space of all forms \(\Omega ^{p+1 +2\bullet }(Y)\). See [98] for the explicit construction of it in the case of \(p=0\). However, only the part (6.36) contributes to the \(\eta \)-invariant of \(\mathcal{{D}}^\mathrm{sig}\). This means that all the contributions cancels out except for \(\widetilde{\Omega }^{p+1}(Y)\).
The chirality of the 5-form field strength given by (5.12) is \(*{\mathsf {F}}= {\mathsf i}\kappa {\mathsf {F}}\). The \(\mathcal{{A}}_\mathrm{grav}\) is the gravitational anomaly in the case \(\kappa =+1\), so suppose that \(*{\mathsf {F}}= {\mathsf i}{\mathsf {F}}\). In that case, it can be shown (see e.g. [65]) that the chirality of the gravitino is negative, \(\overline{\Gamma }= -1\). Therefore, the anomaly of the gravitino is \(\eta (\mathcal{{D}}_Y^{\mathrm{Dirac}\otimes TY})-2\eta (\mathcal{{D}}_Y^\mathrm{Dirac})\) including the sign.
It is known that L/8 is given by an integer linear combination of the \(\hat{A}\) genus of the Dirac operator coupled to a tensor power of the tangent bundle in arbitrary dimensions of the form \(d+2=8\ell +4\), see [102]. In fact, the integrality of L/8 in dimensions \(d+2=8\ell +4\) would probably be required by the consistency of the differential K-theory in \(d+1 = 8\ell +3\) dimensions developed in Sect. 4.5. The reason is that the anomaly polynomial after taking the background \(\check{C}\) to be zero is given by L/8 since \({\mathsf {w}}=0\) in differential K-theory.
The spin bordism groups are given by
$$\begin{aligned} \begin{array}{c|ccccccccccccccccccccccccccc} d &{} 0&{} 1&{}2&{}3&{}4&{}5&{}6&{}7 \\ \hline \Omega _d^\text {spin} &{} {\mathbb {Z}}&{} {\mathbb {Z}}_2 &{}{\mathbb {Z}}_2 &{} 0&{} {\mathbb {Z}}&{} 0 &{}0 &{} 0\\ \hline \hline d &{}8&{}9&{}10&{}11&{}12&{}13&{}14 &{} 15 \\ \hline \Omega _d^\text {spin} &{} 2{\mathbb {Z}}&{} 2{\mathbb {Z}}_2 &{} 3{\mathbb {Z}}_2 &{} 0 &{} 3{\mathbb {Z}}&{} 0&{}0 &{}0 \\ \hline \hline d &{} 16 &{} 17 &{} 18 &{} 19 &{} 20 &{} 21 &{} 22 &{} 23 \\ \hline \Omega _d^\text {spin} &{} 5{\mathbb {Z}}&{} 5{\mathbb {Z}}_2 &{}6{\mathbb {Z}}_2 &{} 0 &{} 6{\mathbb {Z}}+{\mathbb {Z}}_2 &{}{\mathbb {Z}}_2 &{}2{\mathbb {Z}}_2 &{} 3{\mathbb {Z}}_2 \end{array} \end{aligned}$$More precisely it can be defined by using the obstruction theory argument as reviewed e.g. in [95], based on the fact that \(\pi _0(\mathrm {Spin})=\pi _1(\mathrm {Spin}) =\pi _2(\mathrm {Spin})=0\) and \(\pi _3(\mathrm {Spin})={\mathbb {Z}}\). We can also use \(\pi _{k}(B\mathrm {Spin}) = \pi _{k-1}(\mathrm {Spin}) \) and the Hurewicz theorem to find \(H^4(B\mathrm {Spin},{\mathbb {Z}}) = {\mathbb {Z}}\) and get the characteristic class \(c(\mathrm {Spin})\).
The \(c(\mathrm {Spin})_{{\mathbb {Z}}_2}\) is the generator of \(H^4(B\mathrm {Spin},{\mathbb {Z}}_2) = {\mathbb {Z}}_2\). So the only possibilities are \(w_4=0\) identically or \(w_4 = c(\mathrm {Spin})_{{\mathbb {Z}}_2}\). We can consider a vector bundle whose fiber is \({\mathbb { C}}^2\) and which has a minimal instanton number of \(\mathrm {SU}(2)\) acting on \({\mathbb { C}}^2\). By viewing \({\mathbb { C}}^2 \cong {\mathbb {R}}^4\), it gives an example for which \(w_4 =(e)_{{\mathbb {Z}}_2}=(c_2)_{{\mathbb {Z}}_2} \ne 0\), where \(c_2\) is the 2nd Chern class of the complex bundle \({\mathbb { C}}^2\), and e is the Euler characteristic class of \({\mathbb { C}}^2 \cong {\mathbb {R}}^4\). This bundle is also a \(\mathrm {Spin}(4)\) bundle. A minimal instanton of an \(\mathrm {Spin}(4)\) bundle gives an example that \(w_4\) is nontrivial, so \(w_4 = c(\mathrm {Spin})_{{\mathbb {Z}}_2}\).
On manifolds we have the Wu class \(\nu = 1+\nu _1+\nu _2+\cdots \nu _{[D/2]} \), where [D/2] is the largest integer which does not exceed D/2. It is known to satisfy \(\mathrm{Sq}(\nu ) = w\), where \(\mathrm{Sq}=1+\mathrm{Sq}^1+\mathrm{Sq}^2+\cdots \) is the total Steenrod square and \(w=w_1+w_2+\cdots \) is the total Stiefel–Whitney class of the manifold. See e.g. [107] for details. On spin manifolds, we have \(w_1=0, w_2=0,w_3=0\) corresponding to \(\pi _0(\mathrm {Spin})=0,\pi _1(\mathrm {Spin}) =0,\pi _2(\mathrm {Spin})=0\) respectively. Then we get \(\nu _1=0,\nu _2=0,\nu _3=0\). By dimensional reason, we conclude \(\nu =1\) if \(D \le 7\) and hence \(w=1\).
The study of the electromagnetic duality and its anomaly has a long history. The duality does not seem to be known to Maxwell himself, since he used the electric potential \(\phi \) and the vector potential \(\mathbf {A}\) in his original paper [117] from 1865; his notation was cumbersome to the extent that he used different alphabets for each component of \(\mathbf {A}\). It was Heaviside [118, 119] in 1885 who eliminated \(\phi \) and \(\mathbf {A}\) in favor of \(\mathbf {D}\), \(\mathbf {E}\), \(\mathbf {H}\) and \(\mathbf {B}\); it was also him who introduced both the vector calculus and the standard alphabetical symbols into electromagnetism. The duality should have been evident to Heaviside in his notation; he even introduced magnetic currents in addition to electric currents. We now note that when the quantization of electric and magnetic charges is ignored, the duality group is \(\mathrm {U}(1)_D\) under which \(\mathbf {E}\pm {\mathsf i}\mathbf {B}\) has charge \(\pm 1\). Equivalently, it assigns the charge \(\pm 1\) depending on the circular polarization of light, and a positive/negative helicity photon has charge \(\pm 1\). In other words, the total \(\mathrm {U}(1)_D\) charge is the total helicity of the photon. That this \(\mathrm {U}(1)_D\) can be implemented at the Lagrangian level was noted in [120, 121] in the late 70s and the early 80s. Then already in the late 80s, the mixed \(\mathrm {U}(1)_D\)-gravitational anomaly was derived perturbatively in [122,123,124,125,126]. This in particular means that there is an anomalous generation of the total helicity of light when the spacetime Pontryagin density \(\propto {{\,\mathrm{tr}\,}}R\wedge R\) is nonzero, with a very specific coefficient. This line of investigations was recently revisited in [127]. The \(\mathrm {U}(1)_D\) symmetry of the Maxwell equation is also being revisited in the field of atomic and molecular physics too, see e.g. a paper from 2013 [128] where mostly classical aspects were discussed.
For a general bundle E in five dimensions, the \(\eta \)-invariants of \(\mathcal{{S}}\otimes E\) and \(\mathcal{{S}}' \otimes E\) are negative of each other. Also, the \(\eta \)-invariants of \(\mathcal{{S}}\otimes E\) and \(\mathcal{{S}}\otimes E^*\) are negative of each other. Hence the \(\eta \)-invariants of \(\mathcal{{S}}\otimes E\) and \(\mathcal{{S}}' \otimes E^*\) are the same.
Elements of \(H^i(S^5/{\mathbb {Z}}_k, \widetilde{\mathbb {R}}^2)\) would be represented by harmonic differential forms annihilated by \(\mathrm{d}+ \mathrm{d}^\dagger \). By pulling back them to \(S^5\) under \(S^5 \rightarrow S^5/{\mathbb {Z}}_k\), we would get harmonic forms on \(S^5\), which is possible only if \(i=0,5\). The cases \(i=0,5\) are eliminated by the nontrivial twisting \(\widetilde{\mathbb {R}}^2\).
Elements of \(\Omega ^\text {spin}_k(B\mathrm {SL}(2, {\mathbb {Z}}), \xi ) \) may be constructed by Pontryagin-Thom construction as follows. The space \(B\mathrm {SL}(2, {\mathbb {Z}})\) has the bundle \(\xi \), and we consider the Thom space \(T(\xi )\) associated to \(\xi \) which is obtained by collapsing all points at infinity of \(\xi \) to a single point. Then, we consider a spin manifold \(Y_{k+2}\) with dimension \(k+2\), and a map \(F: Y_{k+2} \rightarrow T(\xi )\). By taking F sufficiently generic, we assume that the image of \(Y_{k+2}\) intersects transversally to the zero section of \(\xi \) in \(T(\xi )\). We take \(Y_k\) to be the inverse image of the zero section, which is a k-manifold. Its normal bundle inside \(Y_{k+2}\) is isomorphic to the pullback \(f^*(\xi )\), where f is the restriction of F to \(Y_{k} \subset Y_{k+2}\). Since \(Y_{k+2}\) is spin, the bundle \(TY_{k} \oplus f^*(\xi )\) has a spin structure. This construction, and its inverse, implies that the group \(\Omega ^\text {spin}_k(B\mathrm {SL}(2, {\mathbb {Z}}), \xi ) \) is equivalent to \(\widetilde{\Omega }^\text {spin}_{k+2}(T(\xi )) \), where \(\widetilde{\Omega }\) is the reduced group which, roughly speaking, does not care what happens away from the zero section of \(\xi \). The AHSS for generalized cohomology is applied to it with the \(E^2\) page given by \(\widetilde{H}_{p+2} (T(\xi ), \Omega ^\text {spin}_q(\mathrm{pt})) = H_{p} ( B\mathrm {SL}(2, {\mathbb {Z}}), \Omega ^\text {spin}_q(\mathrm {pt})) \) where we have used the Thom isomorphism theorem.
As in the case of \(\mathrm {SL}(2,{\mathbb {Z}})\), AHSS shows that \(|\Omega ^{\text {spin-}{\mathbb {Z}}_{8}}_5| \le 64\) and \(|\Omega ^\text {spin}_5(B{\mathbb {Z}}_3)| \le 9\). We will later present explicit generators which can be detected by \(\eta \)-invariants computed in Appendix D. Those generators saturate the above bounds.
For the \(\text {spin}-{\mathbb {Z}}_{8}\) structure to be well-defined, fermion charges under \({\mathbb {Z}}_8\) must be odd. For a charge q fermion, the value of s is effectively changed to \(s \rightarrow qs\). Let \(\eta (\mathcal{{D}}^{(q)})\) be the \(\eta \)-invariant of the Dirac operator of a fermion with \({\mathbb {Z}}_8\) charge q. By using the values of the \(\eta \)-invariants in Appendix D, one can check that \(\eta (\mathcal{{D}}^{(3)})\) and \(\eta (\mathcal{{D}}^{(1)}) + 9\eta (\mathcal{{D}}^{(3)})\) generate the dual of the bordism groups, \(\mathop {\mathrm {Hom}}({\mathbb {Z}}_{32} ,\mathrm {U}(1))\) and \(\mathop {\mathrm {Hom}}({\mathbb {Z}}_2,\mathrm {U}(1))\), where \({\mathbb {Z}}_{32}\) and \({\mathbb {Z}}_2\) are the ones appearing in \(\Omega ^{\text {spin-}{\mathbb {Z}}_{8}}_5 = {\mathbb {Z}}_{32} \oplus {\mathbb {Z}}_2\). A generator of \(\mathop {\mathrm {Hom}}({\mathbb {Z}}_{9} ,\mathrm {U}(1))\) (where \({\mathbb {Z}}_9=\Omega ^\text {spin}_5(B{\mathbb {Z}}_3)\)) is \(\eta (\mathcal{{D}}^{(1)})\) in a similar notation. They are precisely the dual basis of (8.64).
This line bundle \(\mathcal{{O}}(r)\) can also be represented as \([ ({\mathbb { C}}^{m} {\setminus }\{ 0 \}) \times {\mathbb { C}}]/{\mathbb { C}}^*\) which makes manifest the fact that it is a holomorphic line bundle over \(\mathbb {CP}^{m-1}\). The holomorphic sections of \(\mathcal{{O}}(r)\) are degree r polynomials of \(\mathbf {z}\) as can be seen from this definition of \(\mathcal{{O}}(r)\). This is a well-known fact in algebraic geometry.
The holonomy constrains \(\int _D {\mathsf {F}}_A \in \frac{1}{k} + {\mathbb {Z}}\). We can modify the connection if necessary by using the connection whose curvature is localized on \(\mathbb {CP}^{m-1} =\{[\mathbf {z},u=0] \}\subset Z\) to get (C.9).
In the terminology of algebraic geometry, M is a divisor class associated to the bundle \(\mathcal{{L}}_1^{\otimes k}\).
In fact, our manifold Z is a blowup of \({\mathbb { C}}^m/{\mathbb {Z}}_k\) at the singular point.
This intuition is not valid on the boundary Y, because the APS boundary condition is non-local. This is the reason that we have the contribution \( \eta (\mathcal{{D}}_Y, g) \) even if g acts freely on Y.
More precisely, we take Z to be a hemisphere which is extended by a cylinder so that the neighborhood of the boundary is of a product form \((-\epsilon , 0] \times S^{2m-1}\) with a product metric. The Riemann curvature is nonzero, but Pontryagin classes are zero. There are no zero modes, that is, not just the APS index is zero, but that each of the numbers of positive and negative chirality modes is zero. This fact follows from a vanishing theorem on manifolds with positive Ricci scalar curvature [49]. The vanishing theorem can be shown from the equation
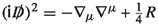 , where R is the Ricci scalar. This equation can be proved by a straightforward computation. The APS boundary condition is such that zero modes can be extended to an infinite cylinder region with square normalizable eigenfunctions. Then by using \(0 = \int \Psi ^\dagger (-\nabla _\mu \nabla ^\mu + \frac{1}{4}R)\Psi \) for a zero mode \(\Psi \), we get \(\Psi =0\), so there are no zero modes.
, where R is the Ricci scalar. This equation can be proved by a straightforward computation. The APS boundary condition is such that zero modes can be extended to an infinite cylinder region with square normalizable eigenfunctions. Then by using \(0 = \int \Psi ^\dagger (-\nabla _\mu \nabla ^\mu + \frac{1}{4}R)\Psi \) for a zero mode \(\Psi \), we get \(\Psi =0\), so there are no zero modes.On non-compact spaces, there are physical states which have more nontrivial statistics than signs \(\mathrm{deg}(a) =\pm 1\), such as anyon particles in 3-dimensions. However, on compact spaces, it seems that such generalized statistics do not arise and hence we assume that it is described just by signs.
We implicitly assume \(\langle a|a\rangle =1\) on the Hilbert space on the space which is a single point \(\mathrm{pt}\). For the case of the massive bc ghost system, this may be true since its quantization on \(\mathrm{pt}\) can be done in the same way as the massive fermion. However, the nontrivial \(S^1\) partition function implies that the Hilbert space on \(\mathrm{pt} \sqcup \mathrm{pt}\) may have a negative inner product.
Let \(\pm y_i~ (i=1,\cdots ,(D+1)/2)\) be the Chern roots of the bundle P in the vector representation of \(\mathrm {Spin}(D+1)_2\). This means that we regard the curvature 2-form (multiplied by \({\mathsf i}/2\pi \)), \(\frac{{\mathsf i}}{2\pi }F\), in the vector representation to have eigenvalues \(\pm y_i\). Then, the \(\frac{{\mathsf i}}{2\pi }F\) in the spinor representations \(\mathcal{{T}}^*_{\pm }\) have eigenvalues \( \frac{1}{2} (\pm y_1 \pm y_2 \cdots \pm y_{(D+1)/2} ), \) such that the product of the signs \((\pm )\) of the coefficients is equal to \(+1\) for \(\mathcal{{T}}^*_{+}\) and \(-1\) for \(\mathcal{{T}}^*_{-}\). From this fact, we see that the Chern characters of \(\mathcal{{T}}^*_{\pm }\) are given by \(({{\,\mathrm{tr}\,}}_{\mathcal{{T}}^*_{+}} + {{\,\mathrm{tr}\,}}_{\mathcal{{T}}^*_{-}}) \exp \left( \frac{{\mathsf i}}{2\pi }F \right) = \prod _{i} (e^{y_i/2}+ e^{-y_i/2})\) and \(({{\,\mathrm{tr}\,}}_{\mathcal{{T}}^*_{+}} - {{\,\mathrm{tr}\,}}_{\mathcal{{T}}^*_{-}}) \exp \left( \frac{{\mathsf i}}{2\pi }F \right) = \prod _{i} (e^{y_i/2}- e^{-y_i/2})\). In particular, taking the \((D+1)\)-form part, we get \(({{\,\mathrm{tr}\,}}_{\mathcal{{T}}^*_{+}} - {{\,\mathrm{tr}\,}}_{\mathcal{{T}}^*_{-}}) \exp \left( \frac{{\mathsf i}}{2\pi }F \right) |_{(D+1)\text {-form}} = \prod _i y_i :=E\) which is by definition the Euler characteristic class.
The relevant conditions are that (1) the image of \(G_k \rightarrow \mathrm {O}(k)\) includes \(\mathrm {SO}(k)\), and that (2) the commutative diagram \( \begin{array}{c@{}c@{}c} G_k &{}\rightarrow &{}\mathrm {O}(k) \\ \downarrow &{} &{} \downarrow \\ G_{k+1} &{} \rightarrow &{} \mathrm {O}(k+1) \end{array}\) is a pull-back diagram.
References
Álvarez-Gaumé, L., Bost, J.B., Moore, G.W., Nelson, P.C., Vafa, C.: Bosonization on higher genus Riemann surfaces. Commun. Math. Phys. 112, 503 (1987)
Thorngren, R.: Anomalies and Bosonization. Commun. Math. Phys. 378, 1775–1816 (2020). arXiv:1810.04414 [cond-mat.str-el]
Yao, Y., Fukusumi, Y.: Bosonization with a background \(U(1)\) gauge field. Phys. Rev. B 100, 075105 (2019). arXiv:1902.06584 [cond-mat.str-el]
Green, M.B., Schwarz, J.H.: Anomaly cancellation in supersymmetric \(D=10\) Gauge theory and superstring theory. Phys. Lett. 149B, 117–122 (1984)
Gaiotto, D., Kapustin, A., Seiberg, N., Willett, B.: Generalized global symmetries. JHEP 02, 172 (2015). arXiv:1412.5148 [hep-th]
Green, M.B., Schwarz, J.H., West, P.C.: Anomaly free chiral theories in six-dimensions. Nucl. Phys. B 254, 327–348 (1985)
Sagnotti, A.: A note on the Green–Schwarz mechanism in open string theories. Phys. Lett. B 294, 196–203 (1992). arXiv:hep-th/9210127
Álvarez-Gaumé, L., Witten, E.: Gravitational anomalies. Nucl. Phys. B 234, 269 (1984)
Monnier, S.: Geometric quantization and the metric dependence of the self-dual field theory. Commun. Math. Phys. 314, 305–328 (2012). arXiv:1011.5890 [hep-th]
Monnier, S.: The anomaly line bundle of the self-dual field theory. Commun. Math. Phys. 325, 41–72 (2014). arXiv:1109.2904 [hep-th]
Monnier, S.: The global gravitational anomaly of the self-dual field theory. Commun. Math. Phys. 325, 73–104 (2014). arXiv:1110.4639 [hep-th]
Monnier, S.: Canonical Quadratic Refinements of Cohomological Pairings from Functorial Lifts of the Wu Class. arXiv:1208.1540 [math.AT]
Monnier, S.: The global anomaly of the self-dual field in general backgrounds. Ann. Henri Poincare 17, 1003–1036 (2016). arXiv:1309.6642 [hep-th]
Monnier, S.: Global gravitational anomaly cancellation for five-branes. Adv. Theor. Math. Phys. 19, 701–724 (2015). arXiv:1310.2250 [hep-th]
Monnier, S.: The global anomalies of (2,0) superconformal field theories in six dimensions. JHEP 09, 088 (2014). arXiv:1406.4540 [hep-th]
Monnier, S.: Topological field theories on manifolds with Wu structures. Rev. Math. Phys. 29, 1750015 (2017). arXiv:1607.01396 [math-ph]
Monnier, S.: The anomaly field theories of six-dimensional (2,0) superconformal theories. Adv. Theor. Math. Phys. 22, 2035–2089 (2018). arXiv:1706.01903 [hep-th]
Monnier, S., Moore, G.W., Park, D.S.: Quantization of anomaly coefficients in 6D \(\cal{N}=(1,0)\) supergravity. JHEP 02, 020 (2018). arXiv:1711.04777 [hep-th]
Monnier, S., Moore, G.W.: Remarks on the Green–Schwarz terms of six-dimensional supergravity theories. Commun. Math. Phys. 372, 963–1025 (2019). arXiv:1808.01334 [hep-th]
Monnier, S., Moore, G.W.: A Brief Summary of Global Anomaly Cancellation in Six-Dimensional Supergravity. arXiv:1808.01335 [hep-th]
Seiberg, N., Tachikawa, Y., Yonekura, K.: Anomalies of duality groups and extended conformal manifolds. PTEP 2018, 073B04 (2018). arXiv:1803.07366 [hep-th]
Hsieh, C.-T., Tachikawa, Y., Yonekura, K.: Anomaly of the electromagnetic duality of Maxwell theory. Phys. Rev. Lett. 123, 161601 (2019). arXiv:1905.08943 [hep-th]
Freed, D.S.: Dirac charge quantization and generalized differential cohomology. In: Surveys in Differential Geometry, pp. 129–194. Cambridge (2000). arXiv:hep-th/0011220
Callan, C.G., Jr., Harvey, J.A.: Anomalies and fermion zero modes on strings and domain walls. Nucl. Phys. B 250, 427–436 (1985)
Faddeev, L.D., Shatashvili, S.L.: Algebraic and Hamiltonian methods in the theory of nonabelian anomalies. Theor. Math. Phys. 60, 770–778 (1985)
Faddeev, L.D., Shatashvili, S.L.: Algebraic and Hamiltonian methods in the theory of nonabelian anomalies. Teor. Mat. Fiz. 60, 206 (1984)
Freed, D.S.: Anomalies and invertible field theories. Proc. Symp. Pure Math. 88, 25–46 (2014). arXiv:1404.7224 [hep-th]
Monnier, S.: A modern point of view on anomalies. Fortsch. Phys. 67, 1910012 (2019). arXiv:1903.02828 [hep-th]
Freed, D.S., Moore, G.W.: Setting the quantum integrand of M-theory. Commun. Math. Phys. 263, 89–132 (2006). arXiv:hep-th/0409135
Deser, S., Jackiw, R., Templeton, S.: Topologically massive Gauge theories. Ann. Phys. 140, 372–411 (1982). [Erratum: Ann. Phys. 185, 406 (1988); Ann. Phys. 281, 409 (2000)]
Deser, S., Jackiw, R., Templeton, S.: Three-dimensional massive Gauge theories. Phys. Rev. Lett. 48, 975–978 (1982)
Witten, E., Yonekura, K.: Anomaly inflow and the \(\eta \)-invariant. In: The Shoucheng Zhang Memorial Workshop Stanford, CA, USA, May 2–4, 2019 (2019). arXiv:1909.08775 [hep-th]
Freed, D.S., Teleman, C.: Relative quantum field theory. Commun. Math. Phys. 326, 459–476 (2014). arXiv:1212.1692 [hep-th]
Dunne, G.V., Trugenberger, C.A.: Current algebra from Chern–Simons theories. Phys. Lett. B 248, 311–316 (1990)
Dunne, G.V., Trugenberger, C.A.: Odd dimensional gauge theories and current algebra. Ann. Phys. 204, 281–314 (1990)
Gukov, S., Martinec, E., Moore, G.W., Strominger, A.: Chern–Simons Gauge theory and the AdS\(_3\) / CFT\(_2\) correspondence. In: From Fields to Strings: Circumnavigating Theoretical Physics: A Conference in Tribute to Ian Kogan, pp. 1606–1647 (2004). arXiv:hep-th/0403225
Aharony, O., Witten, E.: Anti-de Sitter space and the center of the gauge group. JHEP 11, 018 (1998). arXiv:hep-th/9807205
Witten, E.: AdS/CFT correspondence and topological field theory. JHEP 12, 012 (1998). arXiv:hep-th/9812012
Belov, D., Moore, G.W.: Holographic Action for the Self-Dual Field. arXiv:hep-th/0605038
Belov, D., Moore, G.W.: Conformal Blocks for \(\text{AdS}_5\) Singletons. arXiv:hep-th/0412167
Pasti, P., Sorokin, D.P., Tonin, M.: On Lorentz invariant actions for chiral P-forms. Phys. Rev. D 55, 6292–6298 (1997). arXiv:hep-th/9611100
Sen, A.: Self-Dual Forms: Action, Hamiltonian and Compactification. J. Phys. A 53, 084002 (2020). arXiv:1903.12196 [hep-th]
Cheeger, J., Simons, J.: Differential characters and geometric invariants. In: Geometry and Topology, Volume1167 of Lecture Notes in Mathematics, pp. 50–80. Springer, Berlin (1985)
Hopkins, M.J., Singer, I.M.: Quadratic functions in geometry, topology, and M theory. J. Differ. Geom. 70, 329–452 (2005). arXiv:math/0211216 [math.AT]
Witten, E.: Five-brane effective action in M theory. J. Geom. Phys. 22, 103–133 (1997). arXiv:hep-th/9610234
Witten, E.: Duality relations among topological effects in string theory. JHEP 05, 031 (2000). arXiv:hep-th/9912086
Moore, G.W., Witten, E.: Selfduality, Ramond-Ramond fields, and K theory. JHEP 05, 032 (2000). arXiv:hep-th/9912279
Atiyah, M.F., Patodi, V.K., Singer, I.M.: Spectral asymmetry and Riemannian geometry. I. Math. Proc. Camb. Philos. Soc. 77, 43–69 (1975)
Atiyah, M.F., Patodi, V.K., Singer, I.M.: Spectral asymmetry and Riemannian geometry. II. Math. Proc. Camb. Philos. Soc. 78, 405–432 (1975)
Atiyah, M.F., Patodi, V.K., Singer, I.M.: Spectral asymmetry and Riemannian geometry. III. Math. Proc. Camb. Philos. Soc. 79, 71–99 (1976)
Hořava, P., Witten, E.: Eleven-dimensional supergravity on a manifold with boundary. Nucl. Phys. B 475, 94–114 (1996). arXiv:hep-th/9603142
Hořava, P., Witten, E.: Heterotic and type I string dynamics from eleven-dimensions. Nucl. Phys. B 460, 506–524 (1996). arXiv:hep-th/9510209
Ganor, O.J., Hanany, A.: Small \(E_8\) instantons and tensionless non-critical strings. Nucl. Phys. B 474, 122–140 (1996). arXiv:hep-th/9602120
Seiberg, N., Witten, E.: Comments on string dynamics in six-dimensions. Nucl. Phys. B 471, 121–134 (1996). arXiv:hep-th/9603003
Witten, E.: On flux quantization in M theory and the effective action. J. Geom. Phys. 22, 1–13 (1997). arXiv:hep-th/9609122
Diaconescu, E., Moore, G.W., Freed, D.S.: The M Theory Three Form and \(E_{8}\) Gauge Theory. arXiv:hep-th/0312069
Minasian, R., Moore, G.W.: K theory and Ramond-Ramond charge. JHEP 11, 002 (1997). arXiv:hep-th/9710230
Witten, E.: D-branes and K theory. JHEP 12, 019 (1998). arXiv:hep-th/9810188
Álvarez-Gaumé, L., DellaPietra, S., Moore, G.W.: Anomalies and odd dimensions. Ann. Phys. 163, 288 (1985)
Witten, E.: Fermion path integrals and topological phases. Rev. Mod. Phys. 88, 035001 (2016). arXiv:1508.04715 [cond-mat.mes-hall]
Freed, D.S., Hopkins, M.J.: Reflection positivity and invertible topological phases. Geom. Topol. 25, 1165–1330 (2021). arXiv:1604.06527 [hep-th]
Yonekura, K.: On the cobordism classification of symmetry protected topological phases. Commun. Math. Phys. 368, 1121–1173 (2019). arXiv:1803.10796 [hep-th]
Freed, D., Harvey, J.A., Minasian, R., Moore, G.W.: Gravitational anomaly cancellation for M theory five-branes. Adv. Theor. Math. Phys. 2, 601–618 (1998). arXiv:hep-th/9803205
Duff, M.J., Liu, J.T., Minasian, R.: Eleven-dimensional origin of string/string duality: a one-loop test. Nucl. Phys. B 452, 261–282 (1995). arXiv:hep-th/9506126
Tachikawa, Y., Yonekura, K.: Why are fractional charges of orientifolds compatible with Dirac quantization? SciPost Phys. 7, 058 (2019). arXiv:1805.02772 [hep-th]
Bergman, O., Hirano, S.: Anomalous radius shift in AdS\(_4\)/CFT\(_3\). JHEP 07, 016 (2009). arXiv:0902.1743 [hep-th]
Aharony, O., Hashimoto, A., Hirano, S., Ouyang, P.: D-brane charges in gravitational duals of 2+1 dimensional gauge theories and duality cascades. JHEP 01, 072 (2010). arXiv:0906.2390 [hep-th]
García-Etxebarria, I., Regalado, D.: \( \cal{N}=3 \) Four dimensional field theories. JHEP 03, 083 (2016). arXiv:1512.06434 [hep-th]
Aharony, O., Tachikawa, Y.: S-folds and 4D \({\cal{N}}=3\) superconformal field theories. JHEP 06, 044 (2016). arXiv:1602.08638 [hep-th]
Freed, D.S., Moore, G.W., Segal, G.: Heisenberg groups and noncommutative fluxes. Ann. Phys. 322, 236–285 (2007). arXiv:hep-th/0605200
Córdova, C., Freed, D.S., Lam, H.T., Seiberg, N.: Anomalies in the space of coupling constants and their dynamical applications I. SciPost Phys. 8, 001 (2020). arXiv:1905.09315 [hep-th]
Dijkgraaf, R., Witten, E.: Topological gauge theories and group cohomology. Commun. Math. Phys. 129, 393 (1990)
Freed, D.S., Witten, E.: Anomalies in string theory with D-branes. Asian J. Math. 3, 819 (1999). arXiv:hep-th/9907189
Witten, E.: Baryons and branes in Anti-de Sitter space. JHEP 07, 006 (1998). arXiv:hep-th/9805112
Witten, E.: The “parity” anomaly on an unorientable manifold. Phys. Rev. B 94, 195150 (2016). arXiv:1605.02391 [hep-th]
Wang, J., Wen, X.-G., Witten, E.: Symmetric gapped interfaces of SPT and set states: systematic constructions. Phys. Rev. X 8, 031048 (2018). arXiv:1705.06728 [cond-mat.str-el]
Tachikawa, Y.: On gauging finite subgroups. SciPost Phys. 8, 015 (2020). arXiv:1712.09542 [hep-th]
Kobayashi, R., Ohmori, K., Tachikawa, Y.: On gapped boundaries for SPT phases beyond group cohomology. JHEP 11, 131 (2019). arXiv:1905.05391 [cond-mat.str-el]
Witten, E.: On s duality in Abelian gauge theory. Sel. Math. 1, 383 (1995). arXiv:hep-th/9505186
Kapustin, A., Thorngren, R.: Anomalies of discrete symmetries in three dimensions and group cohomology. Phys. Rev. Lett. 112, 231602 (2014). arXiv:1403.0617 [hep-th]
Kapustin, A., Thorngren, R.: Anomalies of discrete symmetries in various dimensions and group cohomology. arXiv:1404.3230 [hep-th]
Yonekura, K.: Dai-Freed theorem and topological phases of matter. JHEP 09, 022 (2016). arXiv:1607.01873 [hep-th]
Córdova, C., Ohmori, K.: Anomaly Obstructions to Symmetry Preserving Gapped Phases. arXiv:1910.04962 [hep-th]
Córdova, C., Ohmori, K.: Anomaly Constraints on Gapped Phases with Discrete Chiral Symmetry. arXiv:1912.13069 [hep-th]
Fukaya, H., Onogi, T., Yamaguchi, S.: Atiyah-Patodi-Singer index from the domain-wall fermion Dirac operator. Phys. Rev. D 96, 125004 (2017). arXiv:1710.03379 [hep-th]
Dabholkar, A., Jain, D., Rudra, A.: APS \(\eta \)-invariant, path integrals, and mock modularity. JHEP 11, 080 (2019). arXiv:1905.05207 [hep-th]
Fukaya, H., Furuta, M., Matsuo, S., Onogi, T., Yamaguchi, S., Yamashita, M.: The Atiyah–Patodi–Singer index and domain-wall fermion Dirac operators. Commun. Math. Phys. 380, 1295–1311 (2020). arXiv:1910.01987 [math.DG]
Weinberg, S.: The Quantum Theory of Fields. Volume 3: Supersymmetry. Cambridge University Press, Cambridge (2013)
Belov, D., Moore, G.W.: Classification of Abelian Spin Chern-Simons Theories. arXiv:hep-th/0505235
García-Etxebarria, I., Montero, M.: Dai-Freed anomalies in particle physics. JHEP 08, 003 (2019). arXiv:1808.00009 [hep-th]
Milnor, J.W., Stasheff, J.D.: Characteristic Classes. Princeton University Press, Princeton, University of Tokyo Press, Tokyo (1974). Annals of Mathematics Studies, No. 76
Stong, R.E.: Calculation of \(\Omega _{11}^\text{ spin }(K (\mathbb{Z}, 4))\). In: Workshop on Unified String Theories Santa Barbara, California, July 29–August 16, pp. 430–437 (1985)
Thomas, E.: On the cohomology of the real grassmann complexes and the characteristic classes of \(n\)-plane bundles. Trans. Am. Math. Soc. 96, 67–89 (1960)
Aharony, O., Seiberg, N., Tachikawa, Y.: Reading between the lines of four-dimensional gauge theories. JHEP 08, 115 (2013). arXiv:1305.0318 [hep-th]
Witten, E.: Topological tools in ten-dimensional physics. Int. J. Mod. Phys. A 1, 39 (1986)
García-Etxebarria, I., Hayashi, H., Ohmori, K., Tachikawa, Y., Yonekura, K.: 8d gauge anomalies and the topological Green-Schwarz mechanism. JHEP 11, 177 (2017). arXiv:1710.04218 [hep-th]
Freed, D.S., Hopkins, M.J.: On Ramond-Ramond fields and K theory. JHEP 05, 044 (2000). arXiv:hep-th/0002027
Witten, E.: Quantum field theory and the Jones polynomial. Commun. Math. Phys. 121, 351–399 (1989)
Witten, E.: A note on boundary conditions in Euclidean gravity. Rev. Math. Phys. 33, 2140004 (2021). arXiv:1805.11559 [hep-th]
Manoliu, M.: Abelian Chern-Simons theory. J. Math. Phys. 39, 170–206 (1998). arXiv:dg-ga/9610001
Manoliu, M.: Abelian Chern-Simons theory. II: a functional integral approach. J. Math. Phys. 39, 207–217 (1998)
Liu, K.F.: Modular invariance and characteristic numbers. Commun. Math. Phys. 174, 29–42 (1995). arXiv:hep-th/9404053
Kapustin, A., Thorngren, R., Turzillo, A., Wang, Z.: Fermionic symmetry protected topological phases and cobordisms. JHEP 12, 052 (2015). arXiv:1406.7329 [cond-mat.str-el]
Anderson, D.W., Brown, E.H., Peterson, F.P.: Spin cobordism. Bull. Am. Math. Soc. 72, 256–260 (1966)
Anderson, D.W., Brown, E.H., Jr., Peterson, F.P.: The structure of the Spin cobordism ring. Ann. Math. (2) 86, 271–298 (1967)
Brumfiel, G.W., Morgan, J.W.: Quadratic functions, the index modulo \(8\), and a \(\mathbb{Z}/4\)-Hirzebruch formula. Topology 12, 105–122 (1973)
Milnor, J.W., Stasheff, J.D.: Characteristic Classes. Princeton University Press, Princeton (1974)
Redlich, A.N.: Gauge noninvariance and parity violation of three-dimensional fermions. Phys. Rev. Lett. 52, 18 (1984)
Redlich, A.N.: Parity violation and gauge noninvariance of the effective gauge field action in three-dimensions. Phys. Rev. D 29, 2366–2374 (1984)
Niemi, A.J., Semenoff, G.W.: Axial anomaly induced fermion fractionization and effective gauge theory actions in odd dimensional space-times. Phys. Rev. Lett. 51, 2077 (1983)
Witten, E.: World sheet corrections via D instantons. JHEP 02, 030 (2000). arXiv:hep-th/9907041
Sethi, S.: A relation between N=8 gauge theories in three-dimensions. JHEP 11, 003 (1998). arXiv:hep-th/9809162
Diaconescu, D.-E., Moore, G.W., Witten, E.: \(E_8\) gauge theory, and a derivation of K theory from M theory. Adv. Theor. Math. Phys. 6, 1031–1134 (2003). arXiv:hep-th/0005090
Bouwknegt, P., Mathai, V.: D-branes, B fields and twisted K theory. JHEP 03, 007 (2000). arXiv:hep-th/0002023
Bergman, O., Gimon, E.G., Sugimoto, S.: Orientifolds, RR torsion, and K theory. JHEP 05, 047 (2001). arXiv:hep-th/0103183
Garcia-Compean, H., Herrera-Suarez, W., Itza-Ortiz, B.A., Loaiza-Brito, O.: D-branes in orientifolds and orbifolds and Kasparov KK-theory. JHEP 12, 007 (2008). arXiv:0809.4238 [hep-th]
Maxwell, J.C.: Viii. A dynamical theory of the electromagnetic field. Philos. Trans. R. Soc. Lond. 155, 459–512 (1865)
Heaviside, O.: Electromagnetic induction and its propagation. In: Electrical Papers, vol. 1, pp. 429–560. MacMillan and Co., 1892. Reprints of articles in the journal The Electrician originally published in 1885–1886
Heaviside, O.: XIV. On the self-induction of wires. Lond. Edinb. Dublin Philos. Mag. J. Sci. 22, 118–138 (1886)
Deser, S., Teitelboim, C.: Duality transformations of abelian and nonabelian gauge fields. Phys. Rev. D 13, 1592–1597 (1976)
Deser, S.: Off-shell electromagnetic duality invariance. J. Phys. A 15, 1053 (1982)
Endo, R., Takao, M.: Chiral anomalies of antisymmetric tensor gauge fields in higher dimensions. Prog. Theor. Phys. 78, 440 (1987)
Reuter, M.: The chiral anomaly of antisymmetric tensor fields. Phys. Rev. D 37, 1456 (1988)
Vainshtein, A.I., Dolgov, A.D., Zakharov, V.I., Khriplovich, I.B.: Chiral photon current and its anomaly in a gravitational field. Sov. Phys. JETP 67, 1326–1332 (1988)
Vainshtein, A.I., Dolgov, A.D., Zakharov, V.I., Khriplovich, I.B.: Chiral photon current and its anomaly in a gravitational field. Zh. Eksp. Teor. Fiz. 94, 54 (1988)
Dolgov, A.D., Khriplovich, I.B., Vainshtein, A.I., Zakharov, V.I.: Photonic chiral current and its anomaly in a gravitational field. Nucl. Phys. B 315, 138–152 (1989)
Agullo, I., del Rio, A., Navarro-Salas, J.: Electromagnetic duality anomaly in curved spacetimes. Phys. Rev. Lett. 118, 111301 (2017). arXiv:1607.08879 [gr-qc]
Bliokh, K.Y., Bekshaev, A.Y., Nori, F.: Dual electromagnetism: helicity, spin, momentum and angular momentum. N. J. Phys. 15, 033026 (2013)
Borsten, L., Duff, M.J., Marrani, A.: Twin conformal field theories. JHEP 03, 112 (2019). arXiv:1812.11130 [hep-th]
Apruzzi, F., Giacomelli, S., Schäfer-Nameki, S.: 4d \(\cal{N}=2\) S-folds. Phys. Rev. D 101, 106008 (2020). arXiv:2001.00533 [hep-th]
Hsieh, C.-T.: Discrete Gauge Anomalies Revisited. arXiv:1808.02881 [hep-th]
Gilkey, P.B.: The Geometry of Spherical Space Form Groups, Volume 28 of Series in Pure Mathematics, 2nd edn. World Scientific, Singapore (2018)
Imamura, Y.: Notes on Supergravity (in Japanese). http://www2.yukawa.kyoto-u.ac.jp/~soken.editorial/sokendenshi/vol22/Imamura2016Jan_2_sugra.pdf
Gilkey, P.B.: The eta invariant and the \(K\)-theory of odd-dimensional spherical space forms. Invent. Math. 76, 421–453 (1984)
Donnelly, H.: Eta invariants for \(G\)-spaces. Indiana Univ. Math. J. 27, 889–918 (1978)
Álvarez-Gaumé, L.: Supersymmetry and the Atiyah-Singer Index Theorem. Commun. Math. Phys. 90, 161 (1983)
Kapustin, A.: Symmetry Protected Topological Phases, Anomalies, and Cobordisms: Beyond Group Cohomology. arXiv:1403.1467 [cond-mat.str-el]
Freed, D.S.: Lectures on Field theory and Topology, Volume 133 of CBMS Regional Conference Series in Mathematics. American Mathematical Society, Providence (2019). https://bookstore.ams.org/cbms-133/
Chang, C.-M., Lin, Y.-H.: On exotic consistent anomalies in (1+1)\(d\): A ghost story. SciPost Phys. 10, 119 (2021). arXiv:2009.07273 [hep-th]
Yamashita, M., Yonekura, K.: Differential models for the Anderson dual to Bordism theories and invertible QFT’s, I. arXiv:2106.09270 [math.AT]
Acknowledgements
CTH and YT are in part supported by WPI Initiative, MEXT, Japan at IPMU, the University of Tokyo. CTH is also supported in part by JSPS KAKENHI Grant-in-Aid (Early-Career Scientists), No.19K14608. YT is also supported in part by JSPS KAKENHI Grant-in-Aid (Wakate-A), No.17H04837 and JSPS KAKENHI Grant-in-Aid (Kiban-S), No.16H06335. KY is supported by JSPS KAKENHI Grant-in-Aid (Wakate-B), No.17K14265.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H-T.Yau
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Notations and Conventions
-
\({\mathsf i}= \sqrt{-1}\) : the imaginary unit.
-
\(\mathrm{d}\): the exterior differential.
-
X, Y, Z, M, N, ... : generic symbols for manifolds. (For general discussions, the dimensions are \(\dim X =d\), \(\dim Y = d+1\), \(\dim Z = d+2\).)
-
\(\overline{X}\) : the orientation reversal of a manifold X.
-
\( H^p(X,{\mathbb {A}})\) : the cohomology on X with coefficients \({\mathbb {A}}(={\mathbb {Z}}, {\mathbb {R}}, {\mathbb {R}}/{\mathbb {Z}})\). Coefficients with a tilde, such as \(\widetilde{{\mathbb {A}}}\), stand for twisted coefficient systems.
-
\(\Omega ^p(X)\) : differential forms of degree p, i.e. a p-form.
-
\(\Omega _\mathrm{closed}^p(X)\) : closed differential p-forms.
-
Square bracket \([x ]_{\mathbb {A}}\) : the cohomology element corresponding to a cocycle x with coefficients \({\mathbb {A}}\). (The subscript \({\mathbb {A}}\) may be omitted if it is clear from context.)
-
\( \check{H}^p(X)\) : the differential cohomology group on X.
-
A, B, C, a, b, c, ... : generic symbols for gauge fields as used usually by physicists.
-
\(\check{A}, \check{B},\check{C}, \check{a}, \check{b}, \check{c} ...\) : generic symbols for gauge fields as differential cohomology elements.
-
\(\check{A} = ({\mathsf {N}}_A, {\mathsf {A}}_A, {\mathsf {F}}_A)\) : the triplet representation of a differential cohomology element \(\check{A}\).
-
\(\mathcal{{Z}}\) : the partition function.
-
\(\mathcal{{A}}\in {\mathbb {R}}/{\mathbb {Z}}\) : the phase \(=\frac{1}{2\pi {\mathsf i}} \log \mathcal{{Z}}\) of the partition function \(\mathcal{{Z}}\) of the bulk anomaly theory on closed manifolds. We simply call this \(\mathcal{{A}}\) as the anomaly.
-
\(\mathcal{{Q}}\in {\mathbb {R}}/{\mathbb {Z}}\) : a quadratic refinement, possibly with \(\mathcal{{Q}}(0)\ne 0\). We also use
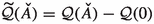 .
. -
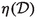 : the APS \(\eta \)-invariant for a Dirac operator
: the APS \(\eta \)-invariant for a Dirac operator 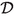 .
. -
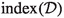 : the index of a Dirac operator \(\mathcal{{D}}\).
: the index of a Dirac operator \(\mathcal{{D}}\). -
\(\text {spin-}G\): a tangential structure on a manifold X such that the tangent frame bundle \(\mathrm {SO}(\dim X)\) is uplifted to \([\mathrm {Spin}(\dim X) \times G]/{\mathbb {Z}}_2 \), for a group G. A choice of an injection \({\mathbb {Z}}_2 \rightarrow G\) is assumed.
-
\(\Gamma ^I\): gamma matrices. \(\Gamma ^{I_1 I_2 \cdots I_m} = \frac{1}{m!} \sum _{\sigma } \mathop {\mathrm {sign}}(\sigma )\Gamma ^{I_{\sigma (1)}} \cdots \Gamma ^{I_{\sigma (m)}} \), where the sum is over all permutations \(\sigma \).
-
\(\overline{\Gamma }\): the chirality operator or the \({\mathbb {Z}}_2\) grading on spin bundles (or Clifford modules).
We also have some remarks related to index theorems:
-
In even spacetime dimensions 2m, the gamma matrices \(\Gamma ^1, \cdots , \Gamma ^{2m}\) and the chirality operator \(\overline{\Gamma }\) are related as \(\overline{\Gamma }= {\mathsf i}^{-m} \overline{\Gamma }^1 \cdots \overline{\Gamma }^{2m}\). In odd dimensions \(2m+1\), the gamma matrices are usually taken as \({\mathsf i}^{-m} \Gamma ^1 \cdots \Gamma ^{2m+1} = +1\). When the bundle with opposite representation \({\mathsf i}^{-m} \Gamma ^1 \cdots \Gamma ^{2m+1} = -1\) appears, we explicitly mention it.
-
\(\partial Y\), the boundary of a manifold Y, is taken with the orientation given by the following convention. If the neighborhood of the boundary has the form \((-\epsilon , 0] \times X \subset Y\) , then the oriented volume forms \(\omega _Y\) and \(\omega _X\) of Y and \(X = \partial Y\) are related as \(\omega _Y = \mathrm{d}\tau \wedge \omega _X\), where \(\tau \in (-\epsilon , 0]\) and \(\tau =0\) is the boundary. This is the standard orientation for Stokes’ theorem, but it is different from the usual convention for the APS index theorem in the literature. This leads to a sign change in the APS index theorem in front of the \(\eta \)-invariant. Namely, the APS index theorem on a manifold Z with boundary Y is of the form
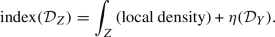 (A.1)
(A.1) -
In the conventions of the gamma matrices and the \(\eta \)-invariant used above, the anomaly of a chiral fermion with positive chirality \(\overline{\Gamma }=+1\) is given by \(\mathcal{{A}}= - \eta \) for a Dirac fermion (i.e. the bulk partition function is \(\mathcal{{Z}}= \exp (-2\pi {\mathsf i}\eta )\)), and \(\mathcal{{A}}= - \frac{1}{2}\eta \) for a Majorana fermion (i.e. the bulk partition function is \(\mathcal{{Z}}= \exp (-\pi {\mathsf i}\eta )\)). For negative chirality fermions, the sign is reversed.
Some Sign Factors in M-Theory
The purpose of this appendix is to fix various sign factors which appear in M-theory. In particular, let \(F^\mathrm{M}_4\) and \(F^\mathrm{M}_7\) be M-theory 4-form and 7-form field strength. We will determine the sign s in the duality equation
We want to determine whether it is \(s=1\) or \(-1\). After fixing some conventions of the Mp-branes and the fields \(F^\mathrm{M}_{p+2}\), the value of s is not a convention, but is fixed.
In this appendix, we are only concerned with sign factors, and hence we neglect topology of \(p+1\)-form fields \(C^\mathrm{M}_{p+1}\) and treat them as differential forms. In particular, \(F^\mathrm{M}_{p+2} = \mathrm{d}C^\mathrm{M}_{p+1}\).
1.1 Convention of Mp-branes and \((p+1)\)-form fields
We always use Euclidean signature for the metric unless otherwise stated. For gamma matrices, we take \(\Gamma ^0\) to be imaginary antisymmetric and other \(\Gamma ^I~(I=1,\cdots ,10)\) to be real symmetric. (In Lorentzian signature, all gamma matrices are real.) Then we see that the matrix
has the properties that
Moreover, we take them to satisfy
We use these conventions for the gamma matrices.
For M5 and M2 branes, we use the following conventions. Let \(Q^\mathrm{M}\) be the supercharge in 11-dimensions. An Mp-brane preserves the subgroups \(\mathrm {SO}(p+1) \times \mathrm {SO}(10-p) \subset \mathrm {SO}(11)\) of the Lorentz symmetry and half of the supersymmetry. Then, if we put it on \(x^{p+1}= \cdots x^{10}=0\) with the orientation determined by the volume form \(\omega _{p+1}=\mathrm{d}x^ 0 \wedge \cdots \wedge \mathrm{d}x^p\), it is clear that the supercharges preserved by the Mp-brane should be given by
Here the ambiguity is only sign factors ± and not a general complex phase, because \(Q^\mathrm{M}\) in Lorentz signature metric is real. The sign just specifies which we call as Mp-branes and which as anti-Mp-branes. We use the convention that Mp-branes (as opposed to anti-Mp-branes) with the worldvolume orientation
are specified by the unbroken supercharges
or more explicitly
These are just conventions.
Let us slightly rephrase the above conditions. The supersymmetry transformations are written as
where \(\epsilon \) is the supersymmetry parameter, and \(C (={\mathsf i}\Gamma _0)\) is the matrix defined above. The supersymmetry parameter for Mp-branes must satisfy,
or
This is the supersymmetry parameter relevant for Mp-branes.
The sign convention of \((p+1)\)-form fields \(C_{p+1}^\mathrm{M}\) coupled to Mp-branes is determined by the following requirement. Let us consider the above Mp-brane with the orientation of the worldvolume \(\omega _{p+1}\) given by (B.6). Let us also define
where
Then the coupling of \(C_{p+1}^\mathrm{M}\) to the Mp-brane is given by
The sign of \(C_{p+1}^\mathrm{M}\) is defined by this coupling.
Including the kinetic term, the action contains
where we are using the Planck unit \(2\pi \ell _\mathrm{M}=1\). The equation of motion is
Now suppose that we have the duality equation of field strength
where \(s_{p+2} = \pm 1\) are sign factors which we want to determine. Notice that we have already defined the sign convention for the fields \(C_{p+1}\) and hence there is no freedom to modify this self-dual condition.
Then we get
Because \(*^2=1\) in odd dimensional Riemann manifold, we have \(({\mathsf i}s_{p+2}) ( {\mathsf i}s_{9-p})=1\) or \( s_{p+2} s_{9-p} = -1\). Let us set \(s := s_4\). Then \(s_7=-s\) and
where \(S^{9-p}\) is the sphere surrounding the Mp-brane. We will see that the value of s is given by \(s=+1\).
Before computing s, let us explain more about the structure of various signs and why they are important for the anomaly of M5-branes. The signs of \(C_{p+1}\) are defined by (B.15), that is, \(C_{p+1}\) and \( - C_{p+1}\) are distinguished by the coupling to Mp-branes. The distinction between Mp-branes and anti-Mp-branes are defined by (B.8) and (B.9). They affect the computation of the anomaly in the following way.
First, the supercharge (B.8) determines the chirality of the worldvolume fields of the M5-brane. The chirality operator \(\overline{\Gamma }^{{\mathrm {M}}5}\) on the M5-brane with the orientation \(\omega _6= \mathrm{d}x^0 \wedge \mathrm{d}x^1 \wedge \mathrm{d}x^2 \wedge \mathrm{d}x^3 \wedge \mathrm{d}x^4 \wedge \mathrm{d}x^5\) is given as
By using (B.4), it can be written also as \(\overline{\Gamma }^{{\mathrm {M}}5} = - \Gamma ^6 \Gamma ^7 \Gamma ^8 \Gamma ^9 \Gamma ^{10}\). Under this chirality operator, \(Q^\mathrm{M5}\) has a definite chirality as
From this, the worldvolumes fermions \(\chi \sim [Q^\mathrm{M5} , \phi ]\) (where \(\phi \) represent worldvolume scalars) has negative chirality \(\overline{\Gamma }^{{\mathrm {M}}5} \chi = -\chi \) and so on. The chirality of the worldvolume fields affects the sign of the anomaly.
Next let us explain (B.9). We are interested in the M2-charge of the M-theory orbifold
Here the orbifold action on the coordinate
is given by
The question is how to define the uplift of this action to spinors. We define the action in such a way that the supercharges preserved by this orbifold action is a subset of the supercharges (B.9). In other words, adding M2-branes to the orbifold does not break supersymmetry, while adding anti-M2-branes breaks it. The uplift of (B.25) on spinors \(\Psi \) is either \(\Psi \rightarrow + {\mathsf {R}}(j/k) \Psi \) or \(\Psi \rightarrow -{\mathsf {R}}(j/k) \Psi \), where
In fact, one can check
which corresponds to (B.24). The sign ambiguity in \(\Psi \rightarrow \pm {\mathsf {R}}(j/m) \Psi \) is the standard one in going from \(\mathrm {SO}\) to \(\mathrm {Spin}\), and it determines the spin structure of \({\mathbb {R}}^8/{\mathbb {Z}}_k\). By requiring that \({\mathsf {R}}(j/k)\) preserves some of the charge \(Q^{{\mathrm {M}}2}\), we conclude that the sign must be such that
For example, \({\mathsf {R}}(1/2) = \Gamma ^3\Gamma ^4 \Gamma ^5\Gamma ^6 \Gamma ^7\Gamma ^8 \Gamma ^9\Gamma ^{10} \) and \({\mathsf {R}}(1/2)Q^{{\mathrm {M}}2} = Q^{{\mathrm {M}}2}\), and hence \(+{\mathsf {R}}(1/2)\) preserves the same supercharges as M2-branes, while \(-{\mathsf {R}}(1/2)\) preserves the same supercharges as anti-M2-branes. The choice (B.28) determines the spin structure of \({\mathbb {R}}^8/{\mathbb {Z}}_k\), and the spin structure affects the value of the \(\eta \)-invariant on \(S^7/{\mathbb {Z}}_k\). In this way the choice (B.9) affects the anomaly of the orbifold.
1.2 Supergravity background and supersymmetry
Mp-branes are realized as extremal black p-brane solutions in supergravity. As we will see, the remaining supersymmetries (i.e. Killing spinors in the extremal black brane solutions) depend on the sign of the flux \(F_{9-p}\). Our strategy is to relate the remaining supersymmetries (B.12) and the fluxes (B.20) and determine the sign factor s.
The Killing spinor equation has the following schematic form

where \(\epsilon \) is the Killing spinor, \(D_I\) is the covariant derivative, and

where \( \Gamma ^{JKLM} =\Gamma ^{[J}\Gamma ^K \Gamma ^L \Gamma ^{M]}\) is the product of gamma matrices with the indices J, K, L, M antisymmetrized. The above form of the Killing spinor equation may be inferred just by simple considerations of Lorentz structure and a counting of mass dimensions if we recover the Planck scale \(2\pi \ell _\mathrm{M}\). It is much more nontrivial to determine the coefficients \(c_{1,2}\). According to the equation (13.13) of [133] , they are given by \(|c_1| = 1/24\), \(|c_2| = 1/8\) and \(c_1c_2<0\). The overall sign of \(c_1,c_2\) depends on the convention of \(F^{{\mathrm {M}}}_4\).Footnote 44
Let us consider the Killing equation when the Lorentz index I is in the direction parallel to the Mp-brane, which we denote by the Greek letter \(\mu \). Then by translational invariance, we have \(\partial _\mu \epsilon = 0\). However, the covariant derivative \(D_\mu \) is still nonzero. The metric of the extremal black p-brane solution is of the form
where \(r=|\mathbf {z}|\). In this metric, we can take the orthonormal frame \(e_I^a\) as \(e_\mu ^a = E(r) \delta ^a_\mu \) as long as \(\mu \) is in the tangent direction. Then the spin connection \(\omega _{\mu IJ}\) is
where \(\Gamma ^{\hat{\mu }} \) and \( \Gamma ^{\hat{r}} \) are gamma matrices in the directions \(x^\mu \) and r normalized in such a way that \((\Gamma ^{\hat{\mu }} )^2 = (\Gamma ^{\hat{r}} )^2=1\), and \( \omega _{\hat{\mu }IJ} = E(r)^{-1} \omega _{ \mu IJ}\). Therefore, the Killing spinor equation is simplified to

In the M5 case (\(p=5\)), the \({F}^\mathrm{M}_4\) does not contain \(\mu \) components and hence  . On the other hand, in the M2 case (\(p=2\)), the term \(*{F}^\mathrm{M}_4 \propto {F}^\mathrm{M}_7\) does not contain \(\mu \) and r, and hence schematically \( {F}^\mathrm{M}_4 \sim \mathrm{d}x^{\mu _1} \wedge \mathrm{d}x^{\mu _2} \wedge \mathrm{d}x^{\mu _3} \wedge \mathrm{d}r\). Thus we get
. On the other hand, in the M2 case (\(p=2\)), the term \(*{F}^\mathrm{M}_4 \propto {F}^\mathrm{M}_7\) does not contain \(\mu \) and r, and hence schematically \( {F}^\mathrm{M}_4 \sim \mathrm{d}x^{\mu _1} \wedge \mathrm{d}x^{\mu _2} \wedge \mathrm{d}x^{\mu _3} \wedge \mathrm{d}r\). Thus we get  . Therefore, we get
. Therefore, we get

where \(Z(r) = \frac{1}{2} F(r)^{-1} \partial _r \log E(r) \), and the sign in \(\pm c_2\) depends on the sign in  .
.
It is possible to rewrite  in terms of
in terms of  which is defined in the similar way as in (B.30). Let us first notice that
which is defined in the similar way as in (B.30). Let us first notice that
which follows from (B.4). Also, we have \(F_4^\mathrm{M} = {\mathsf i}s *F_7^\mathrm{M}\) (because \(*F_4^\mathrm{M} = {\mathsf i}s F_7^\mathrm{M}\) and \(*^2=1\)) which is explicitly written as
Therefore,

For the Mp-brane solution, the flux \(F_{9-p}\) is such that
as we have seen in the previous subsection. Then we have

where the factor \( | {F}^\mathrm{M}_{9-p}| \sim 1/r^{9-p}\) is a positive function of r. Therefore (B.34) is written for the Mp-brane solution as
where \(K_p\) is defined by
Now let us notice that the sign of \(Z(r) = \frac{1}{2} F(r)^{-1} \partial _r \log E(r) \) is independent of whether we consider branes or anti-branes, or whether we consider M2 or M5, because gravity is always an attractive force. (Its absolute value depends on whether we consider M2 or M5.) More explicitly, \(\log E(r) \sim - 1 /r^{8-p}\) and hence \(Z(r)>0\). Therefore, the sign of the right-hand-side of (B.40) is determined simply by the sign of \( K_p\). By requiring that (B.40) coincides with (B.12), we get \(Z(r) = |K_p | | {F}^\mathrm{M}_{9-p}|\) and
The actual values of \(c_1\) and \(c_2\) are such that \(|c_2| > |c_1|\) and hence \(\mathop {\mathrm {sign}}(c_2 \pm c_1) = \mathop {\mathrm {sign}}(c_2)\). Then (B.41) and (B.42) give \(c_2>0\) and
which is what we wanted to show.
Cohomology Pairing and \(\eta \)-Invariant Modulo 1 on Lens Spaces
In this appendix we compute the differential cohomology pairing on \(S^7/{\mathbb {Z}}_k\) and the \(\eta \)-invariants mod 1 which are required in Sect. 7.2, and provide the values already quoted in (7.34). The strategy for the computation is to find a manifold Z whose boundary is \(Y = S^7/{\mathbb {Z}}_k\). For our purposes, Z does not have to be spin; a \(\text {spin}^c\) structure suffices. We also extend \(\mathcal{{L}}_1\) and \(\check{C}_1\) to Z, and use this Z to compute the quantities appearing in (7.34). Most of the discussions here can be generalized for \(S^{2m-1}/{\mathbb {Z}}_k\) without much difficulty, so we take m to be general. Then we obtain a formula for the \(\eta \)-invariant mod 1 for lens spaces of general dimensions when the Dirac operator is coupled to general flat line bundles. We note that we basically follow the discussion in [112]. We also emphasize that the computation in this section only gives the \(\eta \)-invariants mod 1, and not the \(\eta \)-invariants themselves. This is enough for the purposes of Sect. 7.2, but may not be enough for some other purposes, such as using the \(\eta \)-invariant of the signature operator \(\mathcal{{D}}^\mathrm{sig}\) which is multiplied by 1/8. A different computation of the \(\eta \)-invariants of lens spaces which gives their values as real numbers will be presented in Appendix D.
1.1 The geometry and the differential cohomology pairing
First, we consider \(\mathbb {CP}^{m-1}\) and define a line bundle \(\mathcal{{O}}(r)\) for an arbitrary integer \(r \in {\mathbb {Z}}\) as
where the \(\mathrm {U}(1)\) acts asFootnote 45
We denote the equivalence class of \((\mathbf {z},u)\) under the equivalence relation \((\mathbf {z}, u) \sim ( e^{{\mathsf i}\alpha } \mathbf {z}, e^{ {\mathsf i}r \alpha } u)\) as \([\mathbf {z}, u]\). Then \(\mathcal{{O}}(r) =\{ [\mathbf {z}, u] \}\).
Now we take the total space of \(\mathcal{{O}}( - k) \), and consider its subspace given by
On Y, we can fix “the gauge symmetry” \((\mathbf {z}, u) \sim ( e^{{\mathsf i}\alpha } \mathbf {z}, e^{ - {\mathsf i}k \alpha } u)\) by taking \(u=1\). Then the remaining gauge transformation is generated by \([\mathbf {z}, 1] = [e^{ 2\pi {\mathsf i}/k } \mathbf {z}, 1] \). Therefore, we conclude that \(Y = S^{2m-1}/{\mathbb {Z}}_k\). The manifold Z has this lens space as the boundary, \(Y =\partial Z\). One can also check that the orientation of Z as a complex manifold is compatible with the orientation of \(S^{2m-1}/{\mathbb {Z}}_k\) induced from the standard orientation of \(S^{2m-1}\).
On Z, we define a line bundle \(\mathcal{{L}}_{s}\) (\(s \in {\mathbb {Z}}\)) by
Notice that \(\mathcal{{L}}_s = \mathcal{{L}}_1^{\otimes s}\). The line bundle \(\mathcal{{L}}_1\) extends the one defined in (7.30) from \(Y =S^{2m-1}/{\mathbb {Z}}_k\) to Z. This is a pullback of \(\mathcal{{O}}(-1)\) from \(\mathbb {CP}^{m-1}\) to the total space of \(\mathcal{{O}}(-k)\).
Let us consider a connection on \(\mathcal{{L}}_1\) which becomes the flat connection in \(Y = S^{2m-1}/{\mathbb {Z}}_k\). We represent the connection by using a differential cohomology element \(\check{A} \in \check{H}^2(Z)\). Consider the holonomy \(\exp (2\pi {\mathsf i}\int {\mathsf {A}}_A)\) of this connection around a loop
in \(Y=S^{2m-1}/{\mathbb {Z}}_k\) for a fixed \((\mathbf {z}_0,u_0)\). The parallel transport of an element \([\mathbf {z}_0, u_0,v] \) of \(\mathcal{{L}}_1\) is given by \([e^{ 2\pi {\mathsf i}t/k }\mathbf {z}_0, u_0,v] \). From the fact that
we can see that the holonomy of the flat connection around the loop is \(e^{2\pi {\mathsf i}/k}\).
Next consider a two dimensional disk
Notice that the loop (C.6) is equal to \(\partial D\) because \([e^{ {\mathsf i}t/k }\mathbf {z}_0, u_0] =[\mathbf {z}_0, e^{ {\mathsf i}t }u_0 ]\). From the above holonomy, we see that its curvature integral on the disk is given byFootnote 46
In particular, \(\mathcal{{L}}_1^{\otimes k}\) has a connection \(k \check{A}\) which is trivial on Y and has the curvature integral given by \(\int _D k {\mathsf {F}}_{A} =1\). This implies that the connection \(k\check{A}\) can be continuously deformed (without changing the boundary values) to a connection which is trivial on Y and whose curvature is localized on
This M is isomorphic to \(\mathbb {CP}^{m-1}\). The localization of the curvature means \( k {\mathsf {F}}_{A} \sim \delta (M)\) where \(\delta (M)\) is the delta function localized on M.Footnote 47
We compute
where we have used the fact that \(\mathcal{{L}}_1\) restricted to \(M \cong \mathbb {CP}^{m-1}\) is \(\mathcal{{O}}(-1)\), and also used the standard fact that \(\int _{\mathbb {CP}^{m-1} } c_1(\mathcal{{O}}(t) )^{m-1} = t^{m-1}\) for any \(t \in {\mathbb {Z}}\).
Now we have done all the preparations to compute the pairing of \(\check{C}_1\) on \(Y = S^7/{\mathbb {Z}}_k\). In this paragraph we restrict our attention to the original case \(m=4\). We define \(\check{C}_1\) as \(\check{C}_1 = \check{A} \star \check{A}\) which indeed gives \([{\mathsf {N}}_{C_1}] = c_1(\mathcal{{L}}_1)^2\) on Y as we have defined in (7.31). Then the pairing on Y is given by
Thus we have obtained the first equation in (7.34). The pairing takes values in \({\mathbb {R}}/{\mathbb {Z}}\), so this equation is meaningful only mod 1.
1.2 The \(\eta \)-invariant
Next we want to go to the computation of the \(\eta \)-invariant. In this appendix we are interested not in \(\eta \) itself, but only \(\eta \mod 1\) for the purposes of computing anomalies. Thus we can use the APS index theorem to compute it by integrating the corresponding characteristic class on Z.
One point which we need to be careful is the following. We want to use the manifold (C.4). It is not always a spin manifold depending on the values of k (and m). However, the manifold Z (or any complex manifold) is a \(\text {spin}^c\) manifold. For the purpose of computing the \(\eta \)-invariant, it is enough to have a \(\text {spin}^c\) structure.
First let us discuss why Z is not necessarily \(\text {spin}\). If we restrict to the submanifold \(M \cong \mathbb {CP}^{m-1}\) defined in (C.10), the tangent bundle of Z splits as \(TZ = T \mathbb {CP}^{m-1} \oplus \mathcal{{O}}(-k)\). The reason is that the normal bundle to M in Z is \(\mathcal{{O}}(-k)\) which follows from the definition of Z as the total space of the \(\mathcal{{O}}(-k)\) bundle over \(\mathbb {CP}^{m-1}\). It is also well-known that if we add a trivial bundle \(\underline{{\mathbb { C}}} \) to \(T \mathbb {CP}^{m-1}\), we get a sum of m copies of \(\mathcal{{O}}(1)\),
The bundle \(m \mathcal{{O}}(1) \oplus \mathcal{{O}}(-k)\) has a spin lift only if \(m+k\) is even. This is the obstruction to the existence of a spin structure on Z.
Instead of spin structure, we consider the following bundle on a complex manifold Z. The following discussion is generally true for any complex manifold and is well-known in algebraic geometry. Let \({T}^*Z\) be the complex cotangent bundle of the complex manifold Z, and let \(\overline{T}^* Z\) be its complex conjugate bundle. (This \(\overline{T}^* Z\) is isomorphic to the complex tangent bundle TZ by introducing an explicit hermitian metric on TZ. Using the bundle \(\overline{T}^* Z\) may be more natural in the context of Dolbeault complex without an explicit hermitian metric.) We define
where \(\wedge ^\ell E\) of a vector space E means the \(\ell \)-th antisymmetric product of E. This is \(\text {spin}^c\) by the following reason. Let \(\Gamma _I ~(I=1,\ldots , 2\dim _{\mathbb { C}}W)\) be the gamma matrices of \(\dim _{\mathbb {R}}W = 2 \dim _{\mathbb { C}}W\) dimensional Clifford algebra. We take \(a_i = (\Gamma _{2i -1} + {\mathsf i}\Gamma _{2i})/2\) and \(a_i^\dagger = (\Gamma _{2i -1} - {\mathsf i}\Gamma _{2i})/2\). They may be regarded as creation and annihilation operators with \(\{a_i, a_j^\dagger \} = \delta _{ij}\). Then we can find a representation of the Clifford algebra by first taking \(|0\rangle \) such that \(a_i |0\rangle =0\), and then consider \(a_{i_1}^\dagger \ldots a_{i_\ell }^\dagger |0\rangle \). By this construction, we can see that \(\mathcal{{S}}_c\) defined above is a \(\text {spin}^c\) bundle (or more precisely an irreducible Clifford module) on which the Clifford algebra acts. More explicitly, on the bundle \(\mathcal{{S}}_c\), the actions of \(a_{i}\) and \(a_i^\dagger \) are given by \(a_{i}^\dagger = \mathrm{d}\bar{z}^i \wedge \) and \(a_i = \iota _{\bar{\partial }_i}\), respectively, where \(\mathrm{d}\bar{z}^i \wedge \) is an operator which acts on a differential form \(\omega \) as \(\omega \rightarrow \mathrm{d}\bar{z}^i \wedge \omega \), and \( \iota _{\bar{\partial }_i}\) is its adjoint. The ‘chirality’, or equivalently the \({\mathbb {Z}}_2\) grading of the bundle, is determined by the degree \(\ell \) of \( \wedge ^\ell (\overline{T}^* W)\) mod 2.
The canonical line bundle of a complex manifold W is defined by
Then, if there exists a square root \(\mathcal{{K}}^{1/2}\) of the canonical line bundle, we can define a spin bundle as
Therefore, \(\mathcal{{K}}^{1/2}\) measures the difference between \(\mathcal{{S}}\) and \(\mathcal{{S}}_c\).
Let us return to the case of our manifold (C.4). Near the boundary, the manifold \(Z = \{ [\mathbf {z},u] \}\) is embedded as a subspace of \({\mathbb { C}}^m/{\mathbb {Z}}_k \) by taking \(\mathbf {w}=u^{1/k}\mathbf {z}\) as the complex coordinates of \({\mathbb { C}}^4/{\mathbb {Z}}_k \) as far as \(\mathbf {w} \ne 0\). The equivalence relation is \(\mathbf {w} \sim e^{2\pi {\mathsf i}/k}\mathbf {w}\).Footnote 48 The tangent bundle TZ is described by tangent vectors \(\Delta \mathbf {w}\) with the equivalence relation \((\mathbf {w}, \Delta \mathbf {w}) \sim e^{2\pi i/k}(\mathbf {w}, \Delta \mathbf {w})\). From this, we see that TZ near the boundary is \(m \mathcal{{L}}_{-1} = (\mathcal{{L}}_{1})^{-1} \oplus \cdots \oplus (\mathcal{{L}}_{1})^{-1}\), i.e. the sum of m copies of \(\mathcal{{L}}_1^{-1}\). The canonical bundle near the boundary is \(\mathcal{{K}}= \mathcal{{L}}_1^{\otimes m} = \mathcal{{L}}_m\). A square root of \(\mathcal{{K}}\) exists near the boundary if m is even, and we take it to be \(\mathcal{{K}}^{1/2} =\mathcal{{L}}_1^{\otimes (m/2)} \). Now we define
on Z. We soon explain the case of odd m.
When restricted to the boundary \(Y = \partial Z\), the bundle \(\mathcal{{S}}'\) gives a spin structure of \(Y = S^{2m-1}/{\mathbb {Z}}_k\). The spin structure is not unique when k is even, because we can take a line bundle associated to a homomorphism \({\mathbb {Z}}_k \rightarrow {\mathbb {Z}}_2\) and modify the spin bundle by this line bundle. However, the spin structure of \(\mathcal{{S}}'\) coincides with the one which is realized in the M-theory orbifold (which is given in (B.28) of Appendix B) as one can check by representing all bundles as a sum of powers of \(\mathcal{{L}}_1\).
Inside Z, \(\mathcal{{S}}'\) is not spin, but \(\text {spin}^c\). However, that is not a problem in computing the \(\eta \)-invariant on \(Y = S^{2m-1}/{\mathbb {Z}}_k\). We multiply the bundle by \(\mathcal{{L}}_1^s\) to get
This is a \(\text {spin}^c\) bundle on Z. For the purpose of the computation of (7.34), we need to consider the \(\eta \)-invariant of the bundles with \(s=0\) and \(s=1\).
Although it is not directly relevant to (7.34), let us also comment on the case of odd m. In this case, \(\mathcal{{S}}'\) is not well-defined. In fact, for odd m and even k, \(S^{2m-1}/{\mathbb {Z}}_k\) is not a spin manifold as we explained before. However, the bundle \(\mathcal{{S}}_s\) is well-defined if we take \(s +m/2 \) to be integer. The following computation is valid also for these cases.
Recall that Z is described as the total space of the \(\mathcal{{O}}(-k)\) bundle on \(\mathbb {CP}^{m-1}\), and \(\mathcal{{L}}_1\) is the pullback of \(\mathcal{{O}}(-1)\) to this total space. In particular, the canonical bundle \(\mathcal{{K}}\) of Z is topologically given by \(\mathcal{{K}}= \mathcal{{K}}_{\mathbb {CP}^{m-1}} \otimes \mathcal{{O}}(k) = \mathcal{{O}}(k-m)\). Here we have used the fact that the canonical bundle of \(\mathbb {CP}^{m-1}\) is given by \( \mathcal{{K}}_{\mathbb {CP}^{m-1}} = \mathcal{{O}}(-m)\), which follows from (C.13). The bundles \(\mathcal{{O}}(s)\) here are understood as a pullback of \(\mathcal{{O}}(s)\) from \(\mathbb {CP}^{m-1}\) to Z. In fact, \(\mathcal{{O}}(k) =\mathcal{{L}}_1^{\otimes (-k)}\) is trivial near the boundary \(Y = S^{2m-1}/{\mathbb {Z}}_k\), so this canonical bundle reduces to what we have discussed above, that is, \(\mathcal{{K}}= \mathcal{{L}}_1^{\otimes m}\) near the boundary. The expression \(\mathcal{{K}}= \mathcal{{L}}_1^{\otimes (m -k)}\) is valid even inside Z.
Therefore, at the level of differential forms of the curvature (which is what is necessary for the computation of \(\eta \) by using the higher dimensional manifold), we can split the bundle as
where we have formally set \(\mathcal{{S}}= K^{1/2} \otimes \mathcal{{S}}_c\). Such a formal expression is valid when we consider the characteristic polynomial of the curvature in the index theorem. Let \(\hat{A}(R)\) be the A-roof genus of Z defined explicitly in terms of the Riemann curvature tensor R. Let \({\mathsf {F}}_A\) be the curvature of the connection \(\check{A}\) on \(\mathcal{{L}}_1\) which was considered in the computation of (C.11). We can now compute the \(\eta \)-invariant on \(Y = S^{2m-1}/{\mathbb {Z}}_k\) by using the APS index theorem. Let \(\mathcal{{D}}_s\) be the Dirac operator acting on to the (positive chirality part of) \(\mathcal{{S}}_s\) restricted to Y. From (C.19) we get
We can further simplify this expression as follows. The tangent bundle TZ is topologically the same as \(T\mathbb {CP}^{m-1} \oplus \mathcal{{O}}(-k)\). The characteristic class does not change even if we add a trivial bundle \(\underline{{\mathbb { C}}}\), and we have the splitting (C.13) Therefore, we get
where there are m copies of \(\mathcal{{L}}_1^{-1}\). Let \(\hat{A}( \mathcal{{L}}_1^{\oplus (k, -1,\cdots ,-1)} ) \) be the corresponding A-roof genus which is equal to \(\hat{A}(R)\) (up to the continuous deformation of the connection from the Levi-Civita connection on TZ to the connection on \( \mathcal{{L}}_1^{\oplus (k, -1,\cdots ,-1)}\) determined by the connection \(\check{A}\) on \(\mathcal{{L}}_1\)). This can be represented as a polynomial of \({\mathsf {F}}_A\). Explicitly, it is given by
The \(\eta \) is now given by
The integrand is just a polynomial of \({\mathsf {F}}_A \). Moreover, we know from (C.11) that
By using these results, we can compute the desired \(\eta \)-invariant.
The above result can be summarized as follows. Let us define power series of variables \(y,x_1,\cdots ,x_{m+1}\) which we denote (by abuse of notation) as \(\mathrm{ch}(y)\) and \(\hat{A}(x_1, \cdots , x_{m+1})\), and \(p(x_1,\cdots ,x_{m+1})\), by the following formulas:
where \(\mathrm{ch}_i\) is the degree i part of \(\mathrm{ch}\), and \(\hat{A}_i\) and \(p_i\) are the degree 2i parts of \(\hat{A}\) and p, respectively. \(\hat{A}\) can be expanded by p as
By using these notations, the \(\eta (\mathcal{{D}}_s)\) is obtained from (C.23) and (C.24) as
This result was obtained by Gilkey [134] by a different method.
Now let us restrict to the case \(m=4\). We get
Then we can compute the following, where all equalities are valid mod 1:
By putting \(s=1\), we get the second equation in (7.34). We can perform a consistency check of this result. For the background labeled by s, the gauge field \(s \check{A}\) gives a 3-form background \(\check{C} = (s \check{A}) \star (s \check{A}) = s^2 \check{C}_1\). Therefore, we have
By using \( - \widetilde{\mathcal{{Q}}}( \check{C}_1) = (k^2-1)/2k\) and \((\check{C}_1, \check{C}_1) = -1/k\), this equation gives the same result as (C.29) for general s.
We also compute
This is the last equation in (7.34).
Computation of the \(\eta \)-Invariant on Lens Spaces
In this appendix we present methods for computing the values of the \(\eta \)-invariant on lens spaces \(S^{2m-1}/{\mathbb {Z}}_k\) which are different from the method in Sect. C. We compute them as elements of \({\mathbb {R}}\) rather than \({\mathbb {R}}/{\mathbb {Z}}\).
The basic setup is as follows. Let
We consider the lens space defined by dividing the sphere \(S^{2m-1} = \{ | \mathbf {z} | =1 \} \) by the \({\mathbb {Z}}_k\) action
We denote this space as \(S^{2m-1}/{\mathbb {Z}}_k\).
On this space, we consider a \(\text {spin}^c\) connection as follows. Let \(\mathcal{{S}}_{{\mathbb { C}}^m} \) be the trivial \(\text {spin}^c\) bundle on \({\mathbb { C}}^m\). We denote the coordinate of the fiber \(\mathcal{{S}}_{{\mathbb { C}}^m} \) as \(\Psi \). Then we define the action of \({\mathbb {Z}}_k\) by
where \(s \in \frac{1}{2} {\mathbb {Z}}\) is a parameter which specifies the \(\text {spin}^c\) connection, and
Here \(\Gamma ^I ~(I=1,\cdots , 2m)\) are gamma matrices on \({\mathbb { C}}^m \cong {\mathbb {R}}^{2m}\). For this action to be a \({\mathbb {Z}}_k\) action, we must have
or equivalently
Then we define a bundle on \(S^{2m-1}/{\mathbb {Z}}_k\) as,
where \(\overline{\Gamma }\) is the chirality operator on \(\mathcal{{S}}_{{\mathbb { C}}^m} \). This is a \(\text {spin}^c\) bundle on \(S^{2m-1}/{\mathbb {Z}}_k\).
We may use the notation that \(\mathcal{{S}}_s = \mathcal{{S}}\otimes \mathcal{{L}}_s\), where \(\mathcal{{S}}= \mathcal{{S}}_{s=0}\) is the spin bundle defined by the above construction with \(s=0\), and \(\mathcal{{L}}_s\) is a line bundle. This splitting is possible only for even m, but we may also formally use such splitting for odd m. Such a formal splitting is possible if we are only concerned with curvatures of the bundles.
We also consider bundles associated to bi-spinor fields \(\Phi \). The relevant bundle on \({\mathbb { C}}^m\) for the bi-spinor is \(\mathcal{{S}}_{{\mathbb { C}}^m} \otimes \overline{\mathcal{{S}}_{{\mathbb { C}}^m}} \otimes \mathcal{{L}}_t\), which means that \(\Phi \) transforms as
Here \(t \in {\mathbb {Z}}\) is an integer parameter. We construct the corresponding bundle on \(S^{2m-1}/{\mathbb {Z}}_k\) by restricting the bi-spinor to \(\overline{\Gamma }\Phi = \Phi \). We denote the bundle as \(\mathcal{{S}}^\mathrm{sig}_t\); see Sect. 6.2 for the details of the signature index theorem.
Let \(\mathcal{{D}}_s\) and \(\mathcal{{D}}^\mathrm{sig}_t\) be the Dirac operator acting on sections of \(\mathcal{{S}}_s\) and \(\mathcal{{S}}^\mathrm{sig}_t\), respectively. We want to compute their \(\eta \)-invariant. We sometimes denote the \(\eta \)-invariant on a manifold Y as \(\eta (Y)\) if the operator \(\mathcal{{D}}\) is clear from the context, or if \(\mathcal{{D}}\) is a general operator.
We present two methods: In Sect. D.1, we use \({\mathbb {Z}}_k\) orbifolds of the torus \(T^{2m}\) to deduce the \(\eta \)-invariant. This method only uses the standard APS index theorem, but is only applicable to \(k=2,3,4,6\). In Sect. D.2, we introduce and utilize the equivariant APS index theorem. This requires the reader to learn an additional mathematical machinery, but it allows the computation for arbitrary k. These two subsections can be read mostly independently.
1.1 APS index theorem on \(T^{2m}/{\mathbb {Z}}_k\)
Here we describe a method which only uses the APS index theorem, but is restricted to the cases \(k=2,3,4,6\). It is done by computing the index on \(T^{2m}/{\mathbb {Z}}_k\). The method here was used e.g. in [60, 65].
The (singular) manifold \(T^{2m} /{\mathbb {Z}}_k\) is defined as follows. We first consider a torus \(T^{2m}\) whose complex coordinate is denoted as \(\mathbf {z} = (z^1, \cdots , z^m)\). It satisfies equivalence relations of the form \(\mathbf {z} \sim \mathbf {z} + \mathbf {p}+\tau \mathbf {q}\), where \(\mathbf {p}\) and \(\mathbf {q}\) are vectors whose components are integers, and \(\tau \) is the standard period matrix of the torus. For \(k=2,3,4,6\) with specific \(\tau \) for each k, we can act \({\mathbb {Z}}_k\) on the torus as in (D.2). Then we get \(T^{2m}/{\mathbb {Z}}_k\). We can define \(\text {spin}^c\) bundles in the same way as above.
The APS index theorem on \(T^{2m}/{\mathbb {Z}}_k\) can be applied as follows. First, notice that the manifold \(T^{2m}/{\mathbb {Z}}_k\) has orbifold singularities. Let \(B_i\) be a small ball which is centered around a orbifold singularity labelled by i. The boundary is \(\partial B_i = S^{2n-1}/{\mathbb {Z}}_{\ell _i}\) where \(\ell _i\) is a divisor of k and depends on i. The index is defined as the APS index on a manifold which is obtained by subtracting \(B_i\) from \(T^{2m}/{\mathbb {Z}}_k\),
This is nonsingular, and has as the boundary
where the overline means orientation reversal.
By the APS index theorem, we get

where we denote the \(\eta \)-invariant of the operator \(\mathcal{{D}}_s\) or \(\mathcal{{D}}^\mathrm{sig}_t\) on a manifold Y as \(\eta (Y)\), and also similarly for the index. The minus sign is due to the fact that \(\eta (\overline{Y}) = - \eta (Y)\).
More explicit form is determined by careful examination of the geometry. In the case \(m=1\), one can see directly the following. \(T^2/{\mathbb {Z}}_2\) has four orbifold points with \(\ell _i=2\). \(T^2/{\mathbb {Z}}_3\) has three orbifold points with \(\ell _i=3\). \(T^2/{\mathbb {Z}}_4\) has two orbifold points with \(\ell _i=4\), and one orbifold point with \(\ell _i=2\). \(T^2/{\mathbb {Z}}_6\) has one orbifold point with \(\ell _i=6\), one orbifold point with \(\ell _i=3\), and one orbifold point with \(\ell _i=2\).
Notice that if i is an orbifold point of \(T^2/{\mathbb {Z}}_k\) with \({\mathbb {Z}}_{\ell _i}\) orbifold singularity, its pre-image in \(T^2\) consists of \(k/\ell _i\) points. Notice also that if i and j are two points in \(T^2\) with orbifold singularity of type \({\mathbb {Z}}_{\ell _i}\) and \({\mathbb {Z}}_{\ell _j}\) respectively, then \(\{i\} \times \{j\} \in T^2 \times T^2 =T^4\) is a fixed point with \({\mathbb {Z}}_\ell \) orbifold singularity, where \(\ell \) is given by the greatest common divisor of \(\ell _i\) and \(\ell _j\). From these facts, one can determine the orbifold points of \(T^{2m}/{\mathbb {Z}}_k\) from the knowledge of \(T^2/{\mathbb {Z}}_k\).
The answer is given by

By solving these equations, we can determine the \(\eta \)-invariants as

The APS index theorem is valid under some boundary condition. In the present case of (D.9), the boundary condition is given by the following condition. We can shrink \(B_i\) to zero size, and we extend the zero modes to the entire \(T^{2m}/{\mathbb {Z}}_k\). The APS boundary condition is such that the extended zero modes remain finite at the orbifold points. This in turn implies that the zero modes come from the zero modes on \(T^{2m}\) which are invariant under the \({\mathbb {Z}}_k\) action.
Therefore the index on \(T^{2m}/{\mathbb {Z}}_k\) counts the net number of zero modes on \(T^{2m}\) which are invariant under \({\mathbb {Z}}_k\). The zero modes on \(T^{2m}\) are just constant modes \(\partial _I \Psi =0\). The reason is that the Dirac operator is given by \({\mathsf i}\Gamma ^I \partial _I\), and \(0=({\mathsf i}\Gamma ^I \partial _I)^2 \Psi = - \partial ^2\Psi \) which implies that \(0 = \int _{T^{2m}}\Psi ^\dagger (- \partial ^2\Psi ) = \int _{T^{2m}}\partial _I \Psi ^\dagger \partial _I\Psi \). Therefore, we just need to count the number of components of the spinor field \(\Psi \) which are invariant under \({\mathbb {Z}}_k\).
Let us consider the spinor field \(\Psi \) which transforms like (D.3). We consider operators \( {\mathsf i}^{-1} \Gamma ^{2i-1}\Gamma ^{2i}\) for \(i=1,\cdots ,m\). We denote the eigenvalues of \({\mathsf i}^{-1} \Gamma ^{2i-1}\Gamma ^{2i}\) as \(\sigma _i =\pm 1\). The chirality operator \(\overline{\Gamma }\) is given by
and hence its eigenvalues are \(\prod _{i=1}^m \sigma _i\). The condition that \(\Psi \) is invariant under (D.3) is given by
We need to count the number of components of \(\Psi \) satisfying this condition, and also determine the eigenvalues of \(\overline{\Gamma }\) of these components. For this purpose, we rewrite the equation as
Thus, the number of components which has \(\sigma _i = -1\) is of the form \(kj+s+\frac{m}{2}\) for \(j \in {\mathbb {Z}}\). The chirality of such components is \(\overline{\Gamma }= (-1)^{kj + s + \frac{m}{2}}\). Therefore, the index is given by using the binomial coefficient as

By putting this formula into (D.13), we get the values of the \(\eta \)-invariant.
The index of the operator acting on the bi-spinor field \(\Phi \) transforming as (D.8) is more complicated. But the basic idea is the same. We just count the number of components which are invariant under (D.8).
We list some examples. For the operator \(\mathcal{{D}}_s\), we get

For the operator \(\mathcal{{D}}^\mathrm{sig}_t\), we get

Some of the results here were announced and used in [22].
1.2 Equivariant index theorem
The equivariant index theorem states the following. Let Z be a manifold with boundary \(\partial Z = Y\). Suppose that a group G acts on the space Z (and any vector bundle on Z in which we are interested). We consider an element \(g \in G\) such that the fixed points of the g action on Z are isolated points \(p \in {\mathbb {Z}}\) which are not at the boundary, \(p \notin Y\). In particular, g acts freely on Y.
Let \(\mathcal{{D}}_Z\) be a Dirac operator which acts on sections of a bundle \(\mathcal{{S}}_Z\) on Z. Let \(\overline{\Gamma }\) be the chirality (or \({\mathbb {Z}}_2\) grading) operator \(\{ \mathcal{{D}}_Z, \overline{\Gamma }\} =0\). Then the index can be defined as  , where the trace is over the space spanned by the modes of \(\mathcal{{D}}_Z\), and \(\tau >0\) is an arbitrary positive constant. We can modify this definition by including \(g \in G\) as
, where the trace is over the space spanned by the modes of \(\mathcal{{D}}_Z\), and \(\tau >0\) is an arbitrary positive constant. We can modify this definition by including \(g \in G\) as

where on the right hand side g acts on the modes of \(\mathcal{{D}}_Z\).
We also define the \(\eta \)-invariant twisted by g as follows. Consider the Dirac operator \(\mathcal{{D}}_Y\) on Y which is constructed from \(\mathcal{{D}}_Z\) as described in Sect. 4.2. Let \(\psi _j\) be eigenmodes of \(\mathcal{{D}}_Y\) which is in an irreducible representation \(R_j(g)\) of G. Any mode in a single irreducible representation has the same eigenvalue \(\lambda _j\). Then we define
where the subscript \(\mathrm{reg}\) means an appropriate regularization.
If a point p is fixed by g, this element g acts on the fiber \((\mathcal{{S}}_Z)_{p}\) of the bundle \(\mathcal{{S}}_Z\) by some matrix. We denote this matrix as \(\rho _p(g)\). Also, g acts on the fiber \((TZ)_p\) of the tangent bundle TZ and we denote this matrix as \(\tau _p(g)\).
Now we can state the equivariant index theorem [135]. The index  for g satisfying the above conditions is given by
for g satisfying the above conditions is given by

The sum is over the fixed points of g on Z. The trace \( {{\,\mathrm{tr}\,}}(\overline{\Gamma }\rho _p(g) )\) may also be called the supertrace of \(\rho _p(g)\) under the \({\mathbb {Z}}_2\) grading \(\overline{\Gamma }\).
The above equivariant index theorem may be understood as follows. We may try to prove the index theorem by the heat kernel method, which means that we use the expression (D.20) and take the limit \(\tau \rightarrow +0\). Very roughly speaking, the boundary condition used in the APS index theorem is such that the boundary modes with \(\mathop {\mathrm {sign}}(\lambda _i) = +1\) contributes to (D.20) with \(\overline{\Gamma }=+1\), and the boundary modes with \(\mathop {\mathrm {sign}}(\lambda _i) = -1\) contributes to (D.20) with \(\overline{\Gamma }=-1\). This gives the boundary contribution \( \eta (\mathcal{{D}}_Y, g)\) to the index. The bulk contribution is understood as follows. We can regard \(H = \mathcal{{D}}_Z^2\) as a Hamiltonian of a quantum mechanical particle living on Z [136]. Then \(e^{ - \tau \mathcal{{D}}_Z^2}\) is the Euclidean time evolution operator. Within a very short time \(\tau \rightarrow +0\), it is very hard for a particle to go from a point \(p \in Z\) to another point \( g \cdot p \in Z\) unless these points are the same, \(p = g \cdot p\). This implies that only the fixed points \(p = g \cdot p\) contribute in the heat kernel method.Footnote 49 Near each fixed point p, we can approximate the manifold Z by a flat space \({\mathbb {R}}^D\) such that p corresponds to \( 0 \in {\mathbb {R}}^{D}\), where \(D = \dim Z\). Then the trace \( {{\,\mathrm{tr}\,}}( g \overline{\Gamma }e^{- \tau \mathcal{{D}}_Z^2})\) near the point p is given by
This is what appears in (D.22).
Now suppose that G is a finite group whose elements, except for the identity element \(1 \in G\), satisfy the above conditions. We can use the equivariant index theorem to compute the \(\eta \)-invariant on a manifold Y/G which is smooth because of the assumption that G acts freely on Y. The \(\eta \)-invariant on this manifold is given by
where |G| is the number of elements of the finite group G. The \( \eta (\mathcal{{D}}_Y, g) \) for \(g \ne 1\) is given by (D.22), while for \(g=1\) we simply use the ordinary APS index theorem

where F and R are gauge and Riemann curvatures on Z which are relevant to the index of the Dirac operator \(\mathcal{{D}}_Z\). Therefore, we get

This is the general expression.
In a special case that there are no zero modes of \(\mathcal{{D}}_Z\) and no curvature (\(F=0 \) and \(R=0\)), the formula becomes simple. This is the case for \(Z = B^{2m} = \{ \mathbf {z} \in {\mathbb { C}}^{m} ; |\mathbf {z}| \le 1 \} \), \(Y = S^{2m-1}\) and all the backgrounds are trivial.Footnote 50 We take \(G = {\mathbb {Z}}_k\) which acts as (D.2). There is only a single fixed point \(p =0 \in B^{2m}\). On this point we get
where \(j \in {\mathbb {Z}}_k\). The matrix \(\rho (g)\) is determined from (D.3) or (D.8). In each case the trace \( {{\,\mathrm{tr}\,}}(\overline{\Gamma }\rho _p(g) )\) is given by
where we have used the fact that the chirality is given by \( \overline{\Gamma }= \prod _{i=1}^m \left( {\mathsf i}^{-1} \Gamma ^{2i-1}\Gamma ^{2i} \right) . \) Therefore, the equivariant index theorem gives
As examples, we list the values for the case of \(m=4\), \(s=0\) and \(t=0\).
Notice the agreement with the results in Sect. D.1 for \(k=2,3,4,6\). The present method is valid for any k.
Non-unitary Counterexamples to Cobordism Classification
The recent understanding of the anomaly and the corresponding invertible phases states that unitary topological invertible phases are in bijection to the Pontryagin dual of the bordism classes [61, 62, 103, 137]. This statement is often called the cobordism classification of the invertible phases. In particular, the partition function of a unitary topological invertible phase is a bordism invariant.
Here we present a simple class of non-unitary invertible topological phases whose partition function is not a bordism invariant; in particular, its partition function on \(S^D\) is \(-1\).Footnote 51 These examples illustrate the necessity of the unitarity condition in the cobordism classification. In this Appendix, D is the spacetime dimensions of the bulk invertible phase, which was denoted by \(d+1\) in the main part of the text.
1.1 The simplest example
The simplest example is given by a “massive bc ghost system” in \(D=1\) dimensions,
where t is the time coordinate, and \(\tau = {\mathsf i}t\) is the Euclidean time coordinate. b and c obey Fermi-Dirac statistics, but they are not spinors; we will discuss their representations under Lorentz symmetry later for the case of general dimensions D, but for \(D=1\) one can think of them just as scalars. We regularize this theory by Pauli-Villars regularization with Pauli-Villars mass M, and we take \(m = - M \) and \(M \rightarrow \infty \). Because \(|m| \rightarrow \infty \), its Hilbert space is one-dimensional and spanned by the ground state. We need only \(\mathrm {SO}(D)\) symmetry to define this theory, and no spin structure is necessary.
When \(|M| = | m| \), the partition function on \(S^1\) is given by
It is \(\mathcal{{Z}}(S^1) = -1\) for \(m=-M\). Obviously \(S^1\) is trivial in the bordism group \(\Omega ^1_{\mathrm {SO}}(\text {pt})\). This gives a counterexample to the cobordism classification.
The point is that b and c obey the periodic boundary conditions and the zero mode contribute the above factor m/M. (Nonzero modes do not contribute to the phase of the partition function.) If we instead consider a massive fermion, the circle \(S^1_{\text {NS}}\) which is trivial in \(\Omega ^1_{\text {spin}}(\text {pt})\) has the anti-periodic boundary condition, and in that case we get \(\mathcal{{Z}}(S^1_{\text {NS}})=+1\). This is consistent with the cobordism classification. For the periodic boundary condition, we get \(\mathcal{{Z}}(S^1_{\text {R}})=-1\) which is of course consistent because \(S^1_{\text {R}}\) is the nontrivial element of \(\Omega ^1_{\text {spin}}(\text {pt}) = {\mathbb {Z}}_2\).
1.2 Abstract description
The abstract description of the system which is closely related to the above one was discussed in [61]. Here we reproduce a sketch of the argument; we refer the reader to [61, 62] for more details on the axioms used below.
First we give general discussions. If we have two Hilbert spaces \(\mathcal{{H}}_A\) and \(\mathcal{{H}}_B\), then \(\mathcal{{H}}_A \otimes \mathcal{{H}}_B\) and \(\mathcal{{H}}_B\otimes \mathcal{{H}}_A\) are isomorphic. We want a way to identify their elements, so we want to have a map
such that
where \(\epsilon _{a,b}\) is a sign factor. Mathematically, we need such \(\tau \) to define the symmetric monoidal category of super vector spaces.
Physically, we might expect the states \(|a\rangle \) and \(|b\rangle \) to have statistics \(\mathrm{deg} (a)\) and \(\mathrm{deg} (b)\).Footnote 52 Mathematically this is the \({\mathbb {Z}}_2\) grading in super vector spaces. \(\mathrm{deg}\) is even for Bose-Einstein statistics and odd for Fermi-Dirac statistics. Then we expect
Now we want to compute the partition function on \(S^1\). For this purpose, we first consider an interval \(I=[0,\beta ]\) and glue the two ends. The amplitude on the interval I is
in the obvious notation. To glue the two ends we need to exchange \( |a\rangle \otimes \langle a|\) to \(\langle a| \otimes |a\rangle \) and then use a natural map (gluing) \(\langle a| \otimes |b\rangle \rightarrow \langle a| b \rangle \). However, this exchange gives the sign
Let us also consider another quantity, which we denote as \(\mathrm{f}(a)\) and is defined by
Here \((-1)^F \in \mathrm {Spin}(D)\) is in the center. This quantity determines whether the state \(|a\rangle \) is a spinor or not.
Now the partition function on \(S^1\) is given byFootnote 53
where we have used the fact that \(S_\mathrm{{NS}}^1\) has an additional insertion of \((-1)^F \in \mathrm {Spin}(D)\). What makes the usual thermal partition function positive definite is the spin-statistics theorem \(\mathrm{deg}(a) + \mathrm{f}(a)=0 \mod 2\).
The massive bc system considered above has \(\mathrm{deg}(\Omega ) = 1\) but \(\mathrm{f}(\Omega )=0\), where \(|\Omega \rangle \) is the ground state, which is the only state in the limit of large mass gap. Therefore, we get \(\mathcal{{Z}}(S^1)=-1\).
1.3 Generalizations to odd dimensions
We generalize the above system to theories in dimension \(D=2n+1\). The following discussion is generally valid for \(D = 4\ell +1\), but for \(D=4\ell +3\) we will need to restrict to some specific dimensions as we discuss later.
Consider a manifold Y with \(\dim Y = D=2n+1\). We take c and b to be sections of \(\mathcal{{S}}\otimes \mathcal{{S}}^*\), where \(\mathcal{{S}}\) is the spin bundle on Y and \(\mathcal{{S}}^*\) is the dual to \(\mathcal{{S}}\). For this theory itself, we do not need spin structure because of the relation
Notice that only even degrees appear. There is an isomorphism \(\wedge ^{2i} T^* Y \cong \wedge ^{D-2i} T^* Y\), so we could have used odd degree instead. Sect. 6.2 for the details.
The Lagrangian of the theory is

Here gamma matrices \(\Gamma ^I\) of  only act on the first factor \(\mathcal{{S}}\) in \(\mathcal{{S}}\otimes \mathcal{{S}}^*\), while the covariant derivative \(D_I\) acts on both factors. Thus
only act on the first factor \(\mathcal{{S}}\) in \(\mathcal{{S}}\otimes \mathcal{{S}}^*\), while the covariant derivative \(D_I\) acts on both factors. Thus  is the Dirac operator relevant for the signature index theorem, which we discussed in detail in Sect. 6.2. However, we remark that \(\mathcal{{D}}^\mathrm{sig}_Y\) in Sect. 6.2 acts on \(\mathcal{{S}}\otimes (\mathcal{{S}}^* \oplus \mathcal{{S}}^*)\), so \(\eta (\mathcal{{D}}^\mathrm{sig}_Y)\) of that section is twice the \(\eta (\mathcal{{D}})\) of this appendix.
is the Dirac operator relevant for the signature index theorem, which we discussed in detail in Sect. 6.2. However, we remark that \(\mathcal{{D}}^\mathrm{sig}_Y\) in Sect. 6.2 acts on \(\mathcal{{S}}\otimes (\mathcal{{S}}^* \oplus \mathcal{{S}}^*)\), so \(\eta (\mathcal{{D}}^\mathrm{sig}_Y)\) of that section is twice the \(\eta (\mathcal{{D}})\) of this appendix.
As before, we take \(m = -M\) and \(M \rightarrow \infty \). Then the partition function is
The zero modes of the operator \(\mathcal{{D}}\) is given by the zero modes on \(\sum _{i=0}^n \wedge ^{2i} T^* Y\). Let us define
which is the sum of the Betti numbers of even dimensional cohomology. Then the number of zero modes is given by b, and
where the sum is over nonzero eigenvalues of \(\mathcal{{D}}\). By the discussion in Sect. 6.2, this sum over nonzero eigenvalues is the same as  of that section and hence we get
of that section and hence we get  .
.
Suppose that Y is a boundary of a \(D+1\)-manifold Z. By the signature index theorem (6.40) and the fact that  , we have
, we have
Here the signature is defined by the pairing on the relative cohomology \(H^\bullet ( Z, \partial Z, {\mathbb {R}})\).
Let us consider the partition function on \(Y = S^D\). It has \(b=1\) coming from \(H^0(S^D,{\mathbb {R}})\). We emphasize that \(H^D(S^D,{\mathbb {R}})\) does not contribute because we summed only over even-degree cohomology. We can take the \((D+1)\)-manifold as \(Z = B^{D+1}\), which is the \((D+1)\)-dimensional ball. The signature \(\sigma (Z)\) and the Hirzebruch polynomial L (for a round sphere metric) are zero on the ball \(B^{D+1}\). We conclude that
and hence
Notice that \(S^D = \partial B^{D+1}\) is trivial in the bordism groups of both \(\mathrm {SO}\) and \(\mathrm {Spin}\).
The above discussion was general for any \(D=2n+1\). For \(D=4\ell +1\), there is no perturbative gravitational anomaly in \(d=4\ell \) and hence the invertible theory on \(D=4\ell +1\) is topological. In fact, in these dimensions nonzero modes always cancel and we have
It is interesting that the partition function is determined by Betti numbers.
In dimensions \(D=7\) and \(D =8\ell +3\), we can combine the above theory with the anomaly theories relevant to fermions and self-dual 2-form fields to cancel the perturbative anomaly. Then we get a topological theory. The anomaly theories for fermions and 2-form fields are unitary, and hence they do not change the above conclusion \(\mathcal{{Z}}(S^D)=-1\).
1.4 Remark on the anomaly polynomial and the Euler characteristic class
Some theories we have discussed above, such as the ones in \(D=4\ell +1\)-dimensions, are topological theories in the sense that partition functions are topological invariants. But they can still be interpreted to have anomaly polynomials which are given by the Euler characteristic class. Let us explain this point.
To see the point clearly, and also to generalize the situation slightly, we consider a bundle P with the structure group \(\mathrm {Spin}(D+1)\) which is not necessarily associated to the tangent bundle. More precisely, we consider a \((D+1)\)-manifold Z with a bundle whose structure group is given by \([\mathrm {Spin}(D+1)_1 \times \mathrm {Spin}(D+1)_2]/{\mathbb {Z}}_2\), where the first \(\mathrm {Spin}(D+1)_1\) is the Lorentz group and the second \(\mathrm {Spin}(D+1)_2\) is the one we have introduced above. Below we consider as if the group is \(\mathrm {Spin}(D+1)_1 \times \mathrm {Spin}(D+1)_2\) just for notational simplicity, but the discussions below make sense even if we divide the group by \({\mathbb {Z}}_2\).
Let \(\mathcal{{T}}_{\pm }\) be the spin bundles with positive and negative chirality associated to P. We consider Dirac operators \({\mathcal {D}}_{Z,\mathcal{{T}}^*_{\pm }}\) coupled to \(\mathcal{{T}}^*_{\pm }\). Namely, it acts on sections of \(\mathcal{{S}}_{Z} \otimes \mathcal{{T}}^*_{\pm }\), where \( \mathcal{{S}}_{Z} = \mathcal{{S}}_+ \oplus \mathcal{{S}}_-\) is the spin bundle on the manifold Z associated to the tangent bundle TZ. Suppose that the manifold Z has a boundary \(\partial Z =Y\). We denote the relevant APS \(\eta \)-invariants as \(\eta ({\mathcal {D}}_{Y,\mathcal{{T}}^*_{\pm }} ) \). Here the Dirac operator \({\mathcal {D}}_{Y,\mathcal{{T}}^*_{\pm }}\) acts on sections of \(\mathcal{{S}}_Y \otimes \mathcal{{T}}^*_{\pm }\) where \(\mathcal{{S}}_Y := \mathcal{{S}}_+|_{Y} = \mathcal{{S}}_-|_{Y}\). By using the APS index theorem, one can see thatFootnote 54
where E is the Euler characteristic class of P, and \(I(p,p')\) is some polynomial of the Pontryagin classes of the tangent bundle (denoted as \(p=\{p_1,p_2,\cdots \}\)) and the Pontryagin classes of the bundle P (denoted as \(p'=\{p'_1,p'_2,\cdots \}\)). From the above formulas, we get
In particular, we see that \(\int _Z \left( E + I(p, p')\right) \) is divisible by 2 if the boundary is empty, \(\partial Z = \varnothing \).
Now let us consider the case that the bundle P is associated to the tangent bundle so that \(\mathcal{{T}}_{\pm } = \mathcal{{S}}_{\pm }\). In this case, \(\mathcal{{S}}:=\mathcal{{S}}_Y = \mathcal{{T}}_{+}|_{Y} = \mathcal{{T}}_{+}|_{Y} \). The above result implies that \(\frac{1}{2} \left( E + I(p, p)\right) \) (where we have set \(p'=p\)) is the anomaly polynomial for the theory (E.13). Notice that if \(D+1 = 4\ell +2\), the term \(\int I(p,p')\) is zero. Also, for a hemisphere which has the standard metric, we have
since the Euler number of the hemisphere is 1. More generally, the Euler number is a topological invariant even for manifolds with boundaries. (We usually need a term on the boundary related to extrinsic curvature, but the APS index theorem assumes that the region near the boundary is of cylindrical form, so the extrinsic curvature is zero.) Thus the theory (E.13) (for \(D=4\ell +1\)) is topological even though it has a nontrivial anomaly polynomial \(\frac{1}{2} E\).
Let us remark that the theories considered here can still be related to bordism theory in a certain generalization. As we have seen above, the polynomial \( \frac{1}{2} \left( E + I(p, p')\right) \) satisfies the integrality condition \( \frac{1}{2} \int \left( E + I(p, p')\right) \in {\mathbb {Z}}\) on closed manifolds. This is valid for any P not necessarily associated to the tangent bundle. In particular, it is valid in the special case that the bundle \(P \times _{\rho } {\mathbb {R}}^{D+1}\) (where \(\rho \) is the vector representation of \(\mathrm {Spin}(D+1)_2\)) is only stably isomorphic to the tangent bundle TZ, that is, \(P \times _{\rho } {\mathbb {R}}^{D+1} \oplus {\mathbb {R}}^K \simeq TZ \oplus {\mathbb {R}}^K\) for some K. By the result of [140], the theory in D-dimensions considered above give an element of the Anderson dual to a certain bordism theory, \((I\Omega ^G)^{D+1}(\text {pt})\). Here, we need to take the sequence of groups \(G=\{G_k\}\) in that paper to be \(G_k=\mathrm {SO}(k)\) for \(k \le D+1\), and \(G_k = \mathrm {SO}(D+1)\) for \(k >D+1\) so that we can allow the Euler density E as a possible characteristic class.
Finally, we note that the choice of \(G=\{G_k\}\) above does not satisfy the conditionsFootnote 55 discussed by Freed and Hopkins [61], which are required to formulate reflection positivity. Therefore, there is no contradiction with the results of [61, 62], which relates unitary invertible theories with Anderson/Pontryagin duals of bordism groups for \(G=\{G_k\}\) satisfying the conditions of Freed and Hopkins.
Rights and permissions
About this article
Cite this article
Hsieh, CT., Tachikawa, Y. & Yonekura, K. Anomaly Inflow and p-Form Gauge Theories. Commun. Math. Phys. 391, 495–608 (2022). https://doi.org/10.1007/s00220-022-04333-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-022-04333-w




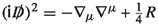 , where R is the Ricci scalar. This equation can be proved by a straightforward computation. The APS boundary condition is such that zero modes can be extended to an infinite cylinder region with square normalizable eigenfunctions. Then by using
, where R is the Ricci scalar. This equation can be proved by a straightforward computation. The APS boundary condition is such that zero modes can be extended to an infinite cylinder region with square normalizable eigenfunctions. Then by using 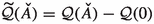 .
.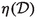 : the APS
: the APS  .
. : the index of a Dirac operator
: the index of a Dirac operator