1 Introduction

For low-Reynolds-number flyers (Re < 106), significant deterioration in aerodynamic performance due to flow separation has long challenges to the aerospace community (Mueller & DeLaurier 2003; Gursul 2004). The poor lift characteristics require such flyers to operate at high angle of attack and frequently enter post-stall regimes during maneuvers or gust encounters. Therefore, enhanced lift performance and delay of stall are crucial for a safe flight. Consequently, implementing flow control methods on stalled airfoils and wings, through both active and passive means, is necessary at low Reynolds numbers.

Post-stall flow control has received considerable attention over the past decades. The relevant work falls into active and passive methods depending on energy expenditure. For the active flow control applications, the main idea is to excite the flow instabilities (whether the separated shear layer or the wake instabilities) with external power. The external excitation may be by acoustic excitation (Zaman 1992), oscillating wires and flaps (Miranda et al. 2005), unsteady blowing (Wu et al. 1998), synthetic jets (Seifert et al. 1993, 1996), plasma actuators (Clifford et al. 2016), small-amplitude wing oscillations (Cleaver et al. 2011), etc. Previous studies suggest that the most effective excitation is found when the resonance with the wake instability occurs at the fundamental vortex shedding frequency and its subharmonic (Wu et al. 1998; Cleaver et al. 2011). The optimal frequency range found at active flow control studies (Greenblatt and Wygnanski 2000) agrees well with the wake resonance frequencies. Despite the promising progress on the above-mentioned active flow control methods, the practical implementation of active methods would lead to increased weight, power consumption and compromised structural integrity, thus may not be feasible or economical for small scales.

Passive flow control methods benefit from simplicity and require no external energy input. Flow instabilities may be excited by cavities on the suction surface of the airfoils (Di Luca et al. 2022), self-excited vibrations of flexible wings (Taylor et al. 2007; Gursul et al. 2014), and self-excited oscillations of flags attached to the airfoils (Tan et al. 2021). The latter has produced significant post-stall flow control, with about 8 deg delay in the stall angle and 34% increase in the maximum lift coefficient at a chord Reynolds number of \({Re}_{c}\) = 105.

The excitation of periodic leading-edge vortices, which produces post-stall lift enhancement, is also possible in the presence of periodic unsteady freestream (Gursul and Ho 1992; Gursul et al. 1994; Choi et al. 2015) and periodic upstream disturbances such as in the wakes of bluff bodies (Zhang et al. 2020; 2022). Recent investigations in turbulent wakes found that the mean lift becomes maximum at optimal locations which are located at the edge of the wakes where the velocity fluctuations are substantially smaller than at the centerline. Significant lift enhancement (~ 64%) and stall delay (~ 9°) have been reported (Zhang et al. 2020; 2022). The frequency of the Karman vortex street in the incident wake (excitation frequency) as well as the spanwise coherence of the flow interacting with the downstream wing play important roles.

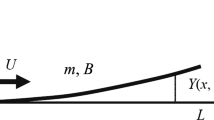
Motivated by the above-mentioned studies, in this paper, we investigate the effect of upstream flags (placed not too far away from the airfoil for practical reasons) on the post-stall performance of airfoils (see Fig. 1). By moving the flag upstream of the airfoil, rather than attaching it on the airfoil surface, we avoid any unwanted effects of the attached flags at pre-stall angles when they are not needed. The present flag configuration shown in Fig. 1 could be deployed only when needed (at post-stall angles of attack) to increase the lift. Compliant flags may be designed by choosing the length, thickness, and material properties in order to produce the optimal excitation frequencies.

Fig. 1
figure 1

Schematic of the airfoil in the wake of a flexible flag with a representative instantaneous vorticity field obtained from the measurements. The flag shapes are for illustrative purpose and not obtained from measurements

Full size image

The fluid–structure interaction of the flag oscillations is governed by the structure-to-fluid mass ratio μ, the bending rigidity KB, and the flag Reynolds number, which are defined as:

$$\mu =\frac{{\rho }_{s}t}{{\rho }_{f}L}$$
$${K}_{B}=\frac{\mathrm{EI}}{{\rho }_{f}{U}_{\infty }^{2}{L}^{3}}$$
$${Re}_{L}=\frac{{U}_{\infty }L}{\nu }$$

where \({\rho }_{s}\) is the density, \(t\) is the thickness, \(L\) is the length, \(\mathrm{EI}\) is the bending rigidity of the flag, \({\rho }_{f}\) is the density, \(\nu \) is the kinematic viscosity of the fluid, and \({U}_{\infty }\) is the freestream velocity. The use of compliant flags (low dimensionless rigidity) ensures the existence of flag oscillations for a wide range of mass ratio (see Fig. 3 in Shelley and Zhang 2011), although the nature of the oscillations may vary. With increasing mass ratio at low bending rigidity, periodic limit-cycle flag oscillations are predicted to become more irregular (Connell and Yue 2007) for low flag Reynolds numbers. The frequency spectra of the flag oscillations change from a single peak to multiple peaks and later more broadband. Similar broadening of the frequency spectra was predicted with decreasing rigidity (increasing freestream velocity) for inviscid flow (Alben and Shelley 2008). However, the hot-wire data of Taneda (1968) report dominant frequencies for up to \(\mu \) = 5.2 and \({Re}_{L}\) = 105. Taneda noted that with increasing freestream velocity, flag oscillations became irregular, but did not present any spectra. Eloy et al. (2008) suggested that three-dimensional effects appear in the deformation of high-aspect ratio flags. Tan et al. (2021) reported that for an oscillating flag with one end attached to an airfoil, the spanwise length scale of the flag oscillations (based on the two-point cross-correlations) was around 5 times the length of the flag at a flag Reynolds number of \({Re}_{L}\)= 20,000.

Previous experimental studies confirm that for our aim of passive flow control shown in Fig. 1, dominant flag frequencies may be found for up to \({Re}_{L}\) ≈ \({Re}_{c}\) (= 105). However, the degree of the periodicity may depend on the three flag parameters discussed above. The transition from a periodic flow with single frequency to a quasi-periodic flow with a broader dominant frequency is thought to be due to the nonlinear fluid–structure interactions and the three-dimensional deformation. This is not necessarily a disadvantage compared to the other methods of flow excitation. We note that a dominant frequency is observed in the turbulent wakes (with wake Reynolds numbers in the range of 10,000 to 50,000) but results in finite and small spanwise length scale in the incident vortices (Zhang et al. 2022). This implies that the excitation of the flow over the downstream wing will not be perfectly synchronized in the spanwise direction. There is an improvement of the two-dimensionality of the wake for oscillating bluff bodies (Bearman 1984) and plunging airfoils (Turhan et al. 2022). Thus, we may expect that the wakes of oscillating flags may have improved coherence. However, the inherent disadvantage of the three-dimensional deformation of the flag may reduce the two-dimensionality of the flow and thus will be examined in this paper.

The feasibility of using upstream flags for post-stall flow control was investigated in this paper using wind tunnel experiments that included force and velocity measurements. The experiments were carried out for a NACA0012 airfoil at a chord Reynolds number of \({Re}_{c}\) = 105. Compliant flags of varying thickness and length were used to produce wakes that interacted with the downstream airfoil placed at various cross-stream and streamwise locations. The unsteady characteristics of the flag wakes and their interaction with the airfoil placed at optimal locations in the wake were investigated. The strength and the dynamics of the leading-edge vortices as well as the spanwise coherence of the wakes were characterized. Optimal flag designs that provide the largest lift increase were identified.

2 Methodology

2.1 Experimental setup

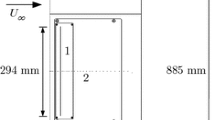
Experiments were conducted in the low-speed, closed-loop, open-jet wind tunnel with a circular working section of 0.76 m in diameter, located at the University of Bath. The wind tunnel has a maximum operating speed of 30 m/s and a freestream turbulence intensity of 0.1% at the maximum operational speed (Wang and Gursul 2012). The schematic of the experimental setup is shown in Fig. 2. The downstream airfoil has the NACA0012 profile, a chord length of c = 100 mm and span of b = 400 mm with two endplates. All tests were conducted at a constant freestream velocity of \({U}_{\infty }\)=15 m/s, which corresponds to a Reynolds number based on the chord length of \({Re}_{c}\)= 100,000.

Fig. 2
figure 2

Schematic of the experimental setup and PIV measurements

Full size image

The upstream flags of varying length L = 0.1c–0.5c and span of 4c are made of rubber sheets of thickness t = 0.2 and 0.5 mm. We note that the length and the thickness of the flag affect both the mass ratio and the bending rigidity. Therefore, it is not possible to tune mass ratio and bending stiffness separately in the experiments. However, we show later in the article that the mass ratio is the dominant parameter for the low stiffnesses considered in this paper. The measurements in our laboratory (Tan et al. 2021) have shown that the rubber sheet has a Young’s modulus E = 1.78 MPa and a density of \({\rho }_{m}\) = 940 kg/m3. The various combinations of flag length and thickness allow us to test a range of non-dimensional parameters: the structure-to-fluid mass ratio μ from 1.6 to 39.2, and the bending rigidity KB from 4.3 \(\times {10}^{-6}\) to 6.9 \(\times {10}^{-2}\). The Reynolds number based on flag length ReL is varied from 10,000 to 100,000. The flags are glued to a tensioned 1.5 mm diameter Bowden cable to minimize any vibration and are spanned between the two endplates for nominally two-dimensional wake. Although we have the experience of measuring high-speed large-deformation of flexible surfaces from our previous work and recently for an oscillating flag attached to an airfoil (Tan et al. 2021), we were not successful for the present flags as they exhibited very large tip displacements (on the order of flag length) with high structural modes. Nevertheless, some flag shapes were possible to extract from the instantaneous particle image velocimetry (PIV) images.

2.2 Force measurements

The force measurements were carried out over a range of angle of attack α of the downstream airfoil, from 0° to 35°. The lift force signal from a binocular load cell was amplified through an Analog Devices AD624 amplifier and logged to a personal computer via a National Instruments NI6009 DAQ at a sampling rate of 5 kHz. In each measurement, the force signal was recorded for 20 s which is sufficiently long for the mean and the RMS of the signal to reach a steady-state value. The uncertainty in the force measurement is estimated to be δCL = ± 0.03. Uncertainties were calculated based on the methods of Moffat (1985).

2.3 PIV measurements

Two-dimensional particle image velocimetry measurements were taken at the midspan plane and focused on the suction surface of the airfoil using a TSI 2D-PIV system. The flow was seeded with olive oil droplets of 1 μm in diameter produced by a TSI 9307-6 automizer and illuminated by NewWave Solo 120–15 Hz double-pulse laser system. The illuminated flow field was captured by an 8 MP Powerview Plus CCD camera with a Nikon AF Nikkor 50 mm f/1.8D lens. The laser pulse and the camera were synchronized via the LaserPulse 610036 synchronizer. The commercial software package Insight 4G and a Hart cross-correlation algorithm were used to analyze the images. In the image processing, an interrogation window size of 32 × 32 pixels was selected, resulting in an effective grid size of approximately 2 mm which corresponds to a spatial resolution of approximately 0.02c. For each run, 2000 instantaneous flow fields were captured at a rate of 1 Hz. The uncertainty for velocity measurements is within 2.2% of the freestream velocity U∞.

2.4 Phase-averaged flow

For the interaction of the quasi-periodic wake of the flag with the airfoil, a phase-averaging method based on the proper orthogonal decomposition (POD) method was used. The POD decomposes fluctuating flow fields as

$$ \mathop{u}\limits^{\rightharpoonup} \left( {\mathop{x}\limits^{\rightharpoonup} ,t} \right) = \mathop{U}\limits^{\rightharpoonup} \left( {\mathop{x}\limits^{\rightharpoonup} } \right) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{u^{\prime } }} \left( {\mathop{x}\limits^{\rightharpoonup} ,t} \right) = \mathop{U}\limits^{\rightharpoonup} \left( {\mathop{x}\limits^{\rightharpoonup} } \right) + \mathop \sum \limits_{1}^{N} a_{n} \left( t \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{\Phi_{n} }} \left( {\mathop{x}\limits^{\rightharpoonup} } \right) $$

where U and u′ denote the mean and fluctuating velocity components. In this equation, \({\mathop{\Phi }\limits^{\rightharpoonup}} _{n}\) and \({a}_{n}\) are the POD modes and corresponding mode coefficients. Van Oudheusden et al. (2005) provided a global and robust phase angle identification method using the first-order approximation of the POD decomposition using the first two POD modes:

$${\overrightarrow{u}}_{\mathrm{LOM}}=\overrightarrow{U}\left(\overrightarrow{x}\right)+{a}_{1}\left(\varphi \right){\overrightarrow{\Phi }}_{1}\left(x\right)+{a}_{2}\left(\varphi \right){\overrightarrow{\Phi }}_{2}\left(x\right)$$
$${a}_{1}=\sqrt{2{\lambda }_{1}}\mathrm{sin}\left(\varphi \right), \, {a}_{2}=\sqrt{2{\lambda }_{2}}\mathrm{cos}\left(\varphi \right)$$

where λ1 and λ2 are the eigenvalues of the two-point cross-correlation matrix. This low-order model is a good approximation if the first two eigenvalues are much larger than the remaining eigenvalues. In our case, \(\varphi \) is the phase angle of vortex shedding from the flag, assumed to increase linearly with time according to \(\frac{\mathrm{d}\varphi }{\mathrm{d}t}=2\mathrm{\pi} f\), and \(f\) is the fundamental frequency of vortex shedding in the flag wake.

For van Oudheusden’s method to work, the first two POD modes need to be dominant. Therefore, in the present study, a small field of view sufficiently upstream and away from the airfoil containing only the flag wake is selected to capture the quasi-periodic wake flow. For all measurements here, the energy captured by the first two modes are between 53 and 61%, slightly less than the 61–66% reported by van Oudheusden et al. (2005). Having determined the phase information for each instantaneous flow image using this method, the PIV data were then phase-sorted in a bin size of ± 10° and then averaged to obtain the phase-averaged flow fields. For each phase angle (e.g., φ = 0°), the selected bin size resulted in over 100 (5% of the total captured) instantaneous flow fields. The detailed description of the method can be found in Zhang et al. (2022).

3 Results and discussion

The variation of the time-averaged lift coefficient with angle of attack of the downstream airfoil for the baseline case (in freestream) is shown in Fig. 3. The stall angle of the present airfoil is around 10° at the test Reynolds number of Rec = 100,000. For the 2D airfoil tested in the present study, the experimental data are compared with others from literature at the same Reynolds number (Ohtake et al. 2007; Bull et al. 2021; Tan et al. 2021). There is reasonable agreement between the lift data and the stall angle obtained in different facilities and rigs, although there is a larger scatter of the post-stall lift coefficients. The nonlinear lift characteristics observed at small angles of attack are due to the laminar separation bubbles.

Fig. 3
figure 3

Time-averaged lift coefficient of 2D airfoil in freestream as a function of angle of attack at Re = 100,000

Full size image

3.1 Overview of airfoil aerodynamics in flag wakes

The time-averaged lift force on the downstream airfoil was measured for various flags placed upstream. We placed the flags at three selected streamwise locations, thus fixing the distance between the leading-edge of the flags (at the origin, see the coordinate system in Fig. 1) and the leading-edge of the airfoil \({x}_{\mathrm{LE}}\). These three stations are (i) \({x}_{\mathrm{LE}}/c\) = 1.1; (ii) \({x}_{\mathrm{LE}}/c\) = L/c + 0.1; and (iii) \({x}_{\mathrm{LE}}/c\) = 0. For each streamwise station, we fixed the flag and traversed the wing in the cross-stream direction. Figure 4 compares the variation of the time-averaged lift coefficient as a function of normalized offset distance \({y}_{LE}/c\) for the L/c = 0.25, t/c = 0.002 flag. The mean lift data of this flag are shown in Fig. 4 as it exhibited the best performance, although the other flags will also be presented later to discuss the effect of the flag frequency. The non-dimensional properties of this flag are the bending coefficient of \({K}_{B} = 2.8\times {10}^{-4}\), the mass ratio of μ = 6.27, and the Reynolds number based on the flag length of ReL = 25,000.

Fig. 4
figure 4

Time-averaged lift coefficient as a function of offset distance at various downstream locations for L/c = 0.25, t/c = 0.002, compared with H/c = 0.5 bluff body wake and freestream, \(\alpha ={20}^{\mathrm{o}}\). The bluff body is D-shaped cylinder which has a 5:1 elliptical leading-edge and square back, with a total length of 1.1c and a height of 0.5c in width

Full size image

We focused on the post-stall regime and fixed the angle of attack of the airfoil at 20°\(,\) because the lift enhancement became most significant at this post-stall angle of attack for these airfoil and Reynolds number (Zhang et al. 2020, 2022). It is shown in Fig. 4 that a significant lift enhancement compared with the freestream case is possible for all three streamwise locations. In addition, a local maximum in the time-averaged lift is observed at a cross-stream offset distance from the wake centerline for all three streamwise locations. We term these locations as “optimal locations”. Also, the time-averaged lift coefficient in the flag wake is compared with that in the bluff body wake reported by Zhang et al. (2022). The airfoil in the bluff body wake exhibits a similar level of lift enhancement (~ 50% compared to freestream) as in the flag wakes. The highest lift enhancement is seen when the airfoil is further downstream, located at \({x}_{\mathrm{LE}}/c=\) 1.1, where a time-averaged lift coefficient of 1.1 is observed, corresponding to 61% lift enhancement compared with the freestream case. We did not investigate flag locations further downstream. However, we note that there were gradual changes in the lift enhancement in the near-wake of the bluff bodies (Zhang et al. 2022).

For both the bluff body and flag wakes, the flow physics of finding the optimal locations away from the wake centerline is likely to be the same. The variation of the mean lift exhibits similar qualitative behavior, and the maximum mean lift occurs at the edge of the wake where the fluctuations of the velocity magnitude is much smaller than at the centerline. This was explained by the observation that leading-edge vortices do not continuously form at the wake centerline as the flow becomes attached partway through the cycle (Zhang et al. 2022). In contrast, at the optimal locations at the edge of the wake, small velocity fluctuations ensure that the flow is always separated at the leading-edge at the post-stall angle of attack and the leading-edge vortices continuously form, resulting in stronger vortices.

3.2 Characterization of incident flag wake

Figure 5 shows the POD analysis of the flow field downstream of the L/c = 0.25, t/c = 0.002 flag, in the absence of the downstream airfoil. This is the same flag used in the force measurements shown in Fig. 4. The domain for the POD analysis is selected slightly downstream of the flag to avoid the region adjacent to the flag where laser reflections cause deterioration of the data quality. The relative energy of the POD modes is shown in Fig. 5a as a function of the mode number. The first two modes have nearly half of the total energy, while the four most energetic modes add up to 64.5% of the total energy. Each mode pair (modes 1 and 2 and modes 3 and 4) consists of similar energy (25.9, 23.8, 7.5 and 7.4%, respectively). The first four mode shapes shown in Fig. 5b indicate that there exist two dominant frequencies of the flag wake shedding, with the second frequency being the second harmonic of the first one. The significantly less energy of the higher harmonic modes indicates that the higher harmonic wake shedding is less dominant than the first one. The wavelengths of the fundamental and the second harmonic shedding, determined from the POD mode shapes, are approximately 1.77c and 0.89c, respectively.

Fig. 5
figure 5

POD analysis of the wake of the flag, L/c = 0.25, t/c = 0.002, a relative energy as a function of mode number, b the first four dominant POD modes

Full size image

The phase-averaged flow field downstream of the flag is shown in Fig. 6. Comparing with the instantaneous flow field shown in Fig. 1, the phase-averaging provides essentially the same flow structure but has a smoothing effect similar to a spatial filter that weakens the small-scale vortices that link up the larger-scale vortices in the flag wake. Shedding of vortex pairs of opposite signs (with unequal strength) is more visible in the instantaneous flow. The phase-averaged large-scale vortex system downstream of the flag still suggests the existence of the vortex pairs of opposite signs, but one of the vortices appears very weak. The vortex shedding mode results in two separate branches of vortical structures staggered (shifted) about the wake centerline. The dimensionless properties of the flag (KB = 2.8 \(\times {10}^{-4}\) and μ = 6.27) on the map of flag modes (Yu et al. 2019) suggest that higher modes of flag oscillations are possible. Although we were not able to obtain direct deformation measurements, in some PIV images the instantaneous shapes could be identified. These (to be presented later) confirmed the existence of higher flag modes. It is not clear whether the particular wake is the consequence of higher modes. Nevertheless, Connell and Yue (2007) observed vortex pairs of opposite signs appearing away from the centerline for a large mass ratio in their simulations.

Fig. 6
figure 6

Phase-averaged vorticity contours superimposed with streamlines for L/c = 0.25, t/c = 0.002 flag wake

Full size image

The contours of the time-averaged streamwise velocity and the root-mean-square of the cross-stream velocity are shown in Fig. 7, which clearly reveal the two separate branches of the wake that are symmetrical about the wake centerline. Unlike the bluff body wake for which both the maximum velocity defect and the cross-stream velocity fluctuations are located at the wake centerline, in the present flag wake, the maximum velocity defect and the maximum rms cross-stream velocity are located away from the wake centerline. Also shown as black dots in Fig. 7a and b are the optimal locations at which the time-averaged lift becomes maximum when the airfoil is placed in the flow. It appears that at the optimal locations, there is not much correlation with the magnitude of the mean streamwise velocity. Also, the magnitude of the cross-stream velocity fluctuations does not need to be large. This is consistent with our finding for bluff body wakes (Zhang et al. 2020; 2022).

Fig. 7
figure 7

Contours of a time-averaged streamwise velocity, and b root-mean-square of cross-stream velocity; black dots correspond to the optimal locations where maximum lift is observed; c comparison of momentum thickness at various downstream locations in H/c = 0.5 bluff body wake and L/c = 0.25, t/c = 0.002 flag wake

Full size image

The two branches in Fig. 7 are related to the formation and shedding of the vortex pairs of opposite signs. We note the similarities with the wakes of oscillating airfoils (Lai and Platzer 1999; Cleaver et al. 2011) and low-aspect-ratio wings (Buchholz and Smits 2005; Dong et al. 2006). Lai and Platzer commented that “whereas the wake is indicative of drag, the mushroom-like-vortices are changing their orientation from pointing upstream to almost pointing vertically upward or downward”. It was suggested by Cleaver et al. (2011) that the dual-wake structure is caused by the interaction of the leading-edge and trailing-edge vortices. It appears that the dual-branch wake flows are possible for both drag and thrust producing cases.

For an indication of the drag of the flag, the momentum thickness calculated for various streamwise locations is compared with that of the H/c = 0.5 bluff body in Fig. 7c. It seems that the flag wake momentum thickness increases approximately linearly, at a shallow gradient, with streamwise location, but is lower in magnitude than that of the bluff body wake. The Strouhal number of the flag wake, calculated from the dominant frequency of the force balance signal, is approximately St = fc/U∞ = 0.27, which is almost identical to that of the H/c = 0.5 bluff body wake generator reported by Zhang et al. (2022).

3.3 Effect of airfoil location

To understand the effect of the airfoil location in the flag wake, the contours of the root-mean-square of the cross-stream velocity component are shown in Fig. 8. For the same angle of attack of α = 20°, the case of the airfoil in freestream in Fig. 8a together with the cases of the optimal airfoil locations (corresponding to the locations of maximum mean lift shown in Fig. 4) for the three streamwise locations are presented in Fig. 8b, c, and d. It is seen that at all three optimal locations there is some mutual interaction between the flag wake and the airfoil. Comparing with the flag wake in freestream shown in Fig. 7b, the presence of the airfoil causes some distortion of the wake structure. As the airfoil is moved closer to the flag in the streamwise direction, the lower branch of the wake is deflected toward the wake centerline and eventually merges with the upper branch. The effect of the airfoil on the flag wake is most significant when the airfoil is placed just below the flag. Although the distortion of the wake is minimal for the case of \({x}_{\mathrm{LE}}/c=\) 1.1 in Fig. 8, this case results in the largest lift increase among the three cases (see Fig. 4). However, for the three configurations, the changes in the flag wake shedding frequency are negligible (not shown here).

Fig. 8
figure 8

Contours of root-mean-square of the cross-stream velocity component for α = 20°, L/c = 0.25, t/c = 0.002, a in freestream, b \({x}_{\mathrm{LE}}/c=\) 1.1, \({y}_{\mathrm{LE}}/c=\)−0.32 c \({x}_{\mathrm{LE}}/c=\) \({L}_{\mathrm{flag}}/c\)+0.1, \({y}_{\mathrm{LE}}/c=\)−0.37, and d \({x}_{\mathrm{LE}}/c=\) 0, \({y}_{\mathrm{LE}}/c=\)−0.4

Full size image

Table 1 summarizes the momentum thickness θ calculated at 0.5c downstream of the trailing-edge of the airfoil, with the upstream flag. This represents the total drag of the combination of the airfoil and flag. We present the ratio of the momentum thickness to that of the airfoil in freestream (but no flag). It is seen that for all three configurations, the momentum thickness is larger than the momentum thickness of the airfoil alone (θ/θ0 > 1) due to the contribution of the flag. For the case of Configuration 1 (\({x}_{\mathrm{LE}}/c=\) 1.1), the momentum thickness is the smallest compared to the other configurations and the bluff body. The largest mean lift combined with smallest increase in drag due to the flag makes Configuration 1 optimal. We have not considered larger streamwise distances between the flag and the airfoil, since this distance should not be large for practical applications that implement this method for post-stall flow control.

Table 1 Ratio of momentum thickness measured at 0.5c downstream of the trailing edge of the airfoil with flag to that of the airfoil in freestream (θ0)
Full size table

Figures 9, 10, and 11 present the contours of the phase-averaged vorticity superimposed with streamlines for α = 20°, when the airfoil is located at the optimal locations in Configuration 1, 2 and 3, respectively, for the L/c = 0.25, t/c = 0.002 flag. The normalized time in the cycle is related to the phase angle defined in Sect. 2.4. For the airfoil located furthest downstream (Fig. 9), the separated shear layer from the upper surface starts to roll-up into the coherent LEV structure as the counter-clockwise vortex of the flag wake approaches the airfoil. The increased flow angle just upstream of the airfoil is noticeable between t/T = 0 and 0.25. Subsequently, at t/T = 0.375, as the counter-clockwise vortex of the flag wake impinges upon the leading-edge, the first sign of the LEV shedding appears. The LEV convects downstream in the remaining part of the cycle while weakening rapidly as the vortex becomes presumably more three-dimensional. For this configuration, the presence of the airfoil has little effect on the formation of the upper branch of the flag wake but weakens the vortices in the bottom branch.

Fig. 9
figure 9

Phase-averaged vorticity contours superimposed with streamlines for \({x}_{\mathrm{LE}}/c\) = 1.1, \({y}_{\mathrm{LE}}/c\) = −0.32, and α = 20°, L/c = 0.25, t/c = 0.002

Full size image
Fig. 10
figure 10

Phase-averaged vorticity contours superimposed with streamlines for \({x}_{\mathrm{LE}}/c\) =\({L}_{\mathrm{flag}}/c\)  + 0.1, \({y}_{\mathrm{LE}}/c\) = − 0.37, and α = 20°, L/c = 0.25, t/c = 0.002

Full size image
Fig. 11
figure 11

Phase-averaged vorticity contours superimposed with streamlines for \({x}_{\mathrm{LE}}/c\) = 0, \({y}_{\mathrm{LE}}/c\) = − 0.4, and α = 20°, L/c = 0.25, t/c = 0.002

Full size image

As the airfoil is moved upstream, in Fig. 10, there is no direct impingement of the incident vortex upon the airfoil. Instead, the lower branch of the flag wake is deflected up, resulting in the incident vortices passing over the airfoil leading-edge at close proximity. There are many similarities with the LEV formation and shedding observed for the bluff body wake (Zhang et al. 2022). Despite of the lack of direct impingement, the smaller velocity fluctuations induced by the incident vortex street at an offset distance ensures the formation and shedding of the LEVs at this post-stall angle of attack of α = 20°.

When the airfoil is located further upstream near the fixed end of the flag (Fig. 11), the vortex shedding from the flag is significantly affected by the presence of the airfoil. The roll-up of vorticity and strengthening of the LEV are still observed for up to t/T = 0.5. Soon after that shedding of the LEV occurs. Again, although there is no direct impingement of the incident vortices, their induced velocity can cause the formation of the LEVs. Overall, flag vortices have less coherence compared with both that in the freestream and in other configurations previously presented. Despite the very different interaction mechanisms, all three configurations clearly exhibit the roll-up of the leading-edge vortex, growth, and eventually shedding. We note that the process of the LEV roll-up and shedding process for all configurations are very similar to that of dynamic stall vortices on pitching and plunging wings (Ekaterinaris and Platzer 1998).

Noting the similarities of the LEVs in our experiments with the dynamic stall vortices, one would expect that the size and the circulation of the LEVs should be correlated with the time-averaged lift enhancement. In Fig. 12, the circulation of LEVs within the selected boundaries (shown with the dashed lines in Figs. 9, 10, 11) is computed and compared with that in the bluff body wake. It is seen that the maximum LEV circulation is similar for Configurations 2 and 3, but Configuration 1 results in the largest maximum LEV circulation. This agrees with the time-averaged lift coefficient present in Fig. 4. On the other hand, Fig. 12d reveals that the bluff body wake provides the highest LEV circulation, yet it results in a smaller maximum time-averaged lift than that of the flag in Configuration 1. This brings the question whether the degree of the two-dimensionality differs in the flag and bluff body wakes.

Fig. 12
figure 12

Time history of normalized LEV circulation for α = 20°, L/c = 0.25, t/c = 0.002, a \({x}_{\mathrm{LE}}/c\) = 1.1, \({y}_{\mathrm{LE}}/c\) =  − 0.32 b \({x}_{\mathrm{LE}}/c\) =\({L}_{\mathrm{flag}}/c\) + 0.1, \({y}_{\mathrm{LE}}/c\) =  − 0.37, c \({x}_{\mathrm{LE}}/c\) = 0, \({y}_{\mathrm{LE}}/c\) = − 0.4; and d \({x}_{\mathrm{LE}}/c\) =4.1, \({y}_{\mathrm{LE}}/c\) = − 0.6 for H/c = 0.5 bluff body

Full size image

To clarify the degree of the two-dimensionality, the cross-correlation coefficient of the cross-flow velocity component is studied in a cross-flow plane, and compared with that of the bluff body wake. Here, the two-point cross-correlation is defined (Bendat and Piersol 1986) for the cross-stream velocity component as:

$$ C_{{{\text{vv}}}} = \frac{{\overline{{v_{A}^{\prime } v_{B}^{\prime } }} }}{{\sqrt {\overline{{v_{A}^{\prime 2} }} } \sqrt {\overline{{v_{B}^{\prime 2} }} } }} $$

where \({v}_{A}^{^{\prime}}\) is the fluctuating cross-stream velocity component at the reference point A, and \({v}_{B}^{^{\prime}}\) is the fluctuating cross-stream velocity component at any arbitrary location B in the measured domain. In Fig. 13, the reference point A is the optimal offset location (y/c = − 0.32, − 0.37 and − 0.4 for configuration 1, 2 and 3, respectively) and midspan of the test section (z/c = 2). Figure 13a shows the cross-correlation contours at x/c = 2.1 for the L/c = 0.25, t/c = 0.002 flag. It is seen that the correlation decays much faster in the cross-stream direction than in the spanwise direction. Figure 13b compares the variation of the correlation coefficient as a function of spanwise distance at different downstream locations for the flag wake and the bluff body wake (Zhang et al. 2022). The cross-correlation barely changes with the streamwise distance for the flag. Compared with that of the bluff body wake at a similar downstream position, the cross-correlation for the flag wake initially decays faster but becomes larger with increasing spanwise distance. The spanwise-averaged cross-correlation coefficient over the measurement domain of 2c, defined as:

$${C}_{\mathrm{vv},\mathrm{avg}}=\frac{1}{2}{\int }_{\frac{z}{c}=1}^{\frac{z}{c}=3}{C}_{\mathrm{vv}}\left({\left(\frac{y}{c}\right)}_{\mathrm{opt}},\frac{z}{c}\right)\mathrm{d}\left(\frac{z}{c}\right)$$

is plotted as a function of the streamwise distance in Fig. 13c. The average cross-correlation varies little in the streamwise direction. The flag wake has a slightly larger cross-correlation in the spanwise direction, implying better two-dimensionality of the wake compared to the bluff body wake. Comparing the flag in Configuration 1 and the bluff body, the mean lift (see Fig. 4) increases by about 8%, while the maximum LEV circulation decreases by 33% and the spanwise-averaged cross-correlation increases by 10%. It appears that between the two key parameters discussed by Zhang et al. (2022), namely the LEV circulation and the coherence of the wake, the latter contributes more to the lift performance for the airfoil in the flag wake.

Fig. 13
figure 13

In the absence of airfoil, a contours of cross-correlation of cross-stream velocity at x/c = 2.1, b cross-correlation of cross-stream velocity as a function of spanwise distance, c spanwise-averaged cross-correlation as a function of streamwise distance, for L/c = 0.25, t/c = 0.002, and H/c = 0.5

Full size image

3.4 Effect of flag length and thickness

The length and thickness of the flag directly affect the wake frequency and the wavelength, therefore they are taken as the main variables in this section. For the airfoil positioned at a fixed downstream distance of \({x}_{\mathrm{LE}}/c=\) 1.1, Fig. 14 compares the variation of the time-averaged lift coefficient as a function of the cross-stream offset distance at α = 20° for varying flag length and thickness. Figure 14a for t/c = 0.002 and 14b for t/c = 0.005 reveal that optimal locations exist for all flags and the time-averaged lift across all offset locations is almost always larger than in freestream. For both flag thicknesses, increasing the flag length shifts the optimal location further away from the wake centerline, suggesting a wider wake for longer flags. Compared with the bluff body wake, apart from the longest flag (L/c = 1, t/c = 0.005), all flag wakes boost similar level of maximum lift enhancement at the optimal locations. The highest lift enhancement for each flag thickness is for L/c = 0.25, t/c = 0.002 and L/c = 0.5, t/c = 0.005, for which maximum lift coefficients of \({C}_{\mathrm{L},\mathrm{max}}\)= 1.1 and 1.07 are observed, respectively, corresponding to a lift enhancement of 61 and 58%, respectively.

Fig. 14
figure 14

Time-averaged lift coefficient as a function of offset distance for α = 20°, \({x}_{\mathrm{LE}}/c\) = 1.1, a t/c = 0.002 flag and b t/c = 0.005 flag

Full size image

Figure 15 summarizes the maximum lift coefficient enhancement (\(\Delta {C}_{L}\)=\({C}_{\mathrm{L},\mathrm{max}}-{C}_{L,\infty }\)) as a function of flag length L/c in part (a) and flag mass ratio µ in part (b) for α = 20°. It is seen that significant lift enhancement can be achieved regardless of the flag length and mass ratio. For the t/c = 0.002 flag, the \(\Delta {C}_{L}\) reaches a maximum of around 0.42 for the L/c = 0.25 flag (equivalently µ = 6.27). Further increase in flag length or equivalently decrease in mass ratio result in a decrease in the \(\Delta {C}_{\mathrm{L},\mathrm{max}}\). For a certain range of flag length, the lift enhancement is better than that of the bluff body wake reported previously. As for the thicker t/c = 0.005 flag, lift enhancement reaches a maximum at L/c = 0.5 (equivalently µ = 7.83). Any change in flag length results in a noticeable decrease in lift. Despite the difference in optimal flag length for the two thicknesses, the maximum lift is achieved for similar mass ratios. Therefore, we conclude that there exists an optimal mass ratio at around µ = 6–8 that produces the maximum lift enhancement. The collapse of the data for different thicknesses in Fig. 15b confirms that the mass ratio is the proper dimensionless number.

Fig. 15
figure 15

Change in the maximum lift coefficient with respect to freestream, for α = 20° and \({x}_{\mathrm{LE}}/c\) = 1.1, as a function of a normalized flag length, b mass ratio

Full size image

Figure 16 presents the variation of the time-averaged lift coefficient CL with angle of attack α for the two optimal flags when the wing is placed at the wake centerline, at the optimal offset location, and in the freestream. These are compared with the optimal case of bluff body wake (Zhang et al. 2022) shown in Fig. 16a. The lift curves for the bluff body and the flag wakes are very similar: when the airfoil is located at the wake centerline, the delay of the stall is clear whereas there is a decrease in the lift at pre-stall angles of attack, while the maximum lift coefficient changes slightly. In contrast, for the optimal locations, remarkable lift enhancement is observed at post-stall angles of attack, with significant delays in the stall angle. The maximum lift enhancement is observed when the airfoil is located downstream of the L/c = 0.5, t/c = 0.005 flag. The value CL,max ≈ 1.13 was measured at α = 25°, which is 4%, 12% and 66% higher compared with that in L/c = 0.25, t/c = 0.002 flag wake, bluff body wake and freestream, respectively. However, the longer flag length of L/c = 0.5 may produce larger drag than the L/c = 0.25 flag and may not be as practical to deploy as a passive flow control device as it will have to be placed further away from the airfoil.

Fig. 16
figure 16

Time-averaged lift coefficient as a function of angle of attack for a H/c = 0.5 wake generator, \({x}_{\mathrm{LE}}/c\) = 4.1; b L/c = 0.25, t/c = 0.002 flag, \({x}_{\mathrm{LE}}/c\) =1.1; and c L/c = 0.5, t/c = 0.005 flag, \({x}_{\mathrm{LE}}/c\) =1.1

Full size image

We summarize the present data by plotting the modified Strouhal number based on the projection of the airfoil chord length \({(\mathrm{St}}^{*}=fc \mathrm{sin}(\alpha )/{U}_{\infty })\) as well as the dimensionless frequency of the flag (\(fL/{U}_{\infty }\)) as a function of L/c (Fig. 17) and mass ratio (Fig. 18). The data were colored according to the magnitude of the lift increase. The dashed line in part (a) corresponds to the H/c = 0.5 bluff body wake. Figure 17 reveals that as flag length is increased, \({\mathrm{St}}^{*}\) decreases, whereas \(fL/{U}_{\infty }\) increases.

Fig. 17
figure 17

a Modified Strouhal number based on the projection of the airfoil chord length, and b dimensionless flag frequency as a function of flag length. The data were colored according to the magnitude of the lift increase. The dashed line corresponds to the H/c = 0.5 bluff body wake

Full size image
Fig. 18
figure 18

a Modified Strouhal number based on the projection of the airfoil chord length, and b dimensionless flag frequency as a function of flag mass ratio. The data were colored according to the magnitude of the lift increase. The dashed line in part a corresponds to the H/c = 0.5 bluff body wake

Full size image

Figure 18 shows that the modified Strouhal number (\({\mathrm{St}}^{*}\)) is a strong function of the flag thickness, whereas (\({fL}/{U}_{\infty }\)) exhibits very good collapse with the mass ratio of the flags. Since the data were colored according to the magnitude of the lift increase, we identify optimal Strouhal numbers for which lift enhancement is relatively larger. Both Figs. 17 and 18 suggest that the optimal values are about \({St}^{*}=\) 0.18 and 0.07 for the t/c = 0.002 and 0.005 flags, respectively. The dashed line in part (a) corresponds to the H/c = 0.5 bluff body wake (Zhang et al. 2022). Similar Strouhal numbers were identified for flags attached to the airfoil (Tan et al. 2021). All these results point out that the resonance with the wake vortex shedding instability at the fundamental and subharmonic frequencies play a major role for post-stall flow control as predicted by Wu et al. (1998). For the optimal flags, the dimensionless frequency falls into a band of \({fL}/{U}_{\infty }\)=0.10–0.14 regardless of the flag thickness.

In Fig. 18b, we also compare our data of \({fL}/{U}_{\infty }\) with others from the literature for flags in uniform freestream (Taneda 1968; Huang 1995; Goza and Colonius 2017; Akcabay and Young 2012; Alben 2022). The bending coefficients KB of the compliant flags tested or simulated in the previous studies have similar values to those in our study (4.3 \(\times {10}^{-6}\)–6.9 \(\times {10}^{-2}\)). However, the flag Reynolds numbers vary in a wide range. The slightly higher frequencies observed by Akcabay and Young (2012) and Goza and Colonius (2017) are likely to be due to the much lower flag Reynolds number (ReL = 840 and 500, respectively) compared with our testing conditions (ReL = 10,000 to 100,000). Nevertheless, relatively good agreement is found between the literature and the present results, which confirms that the dimensionless frequency \({fL}/{U}_{\infty }\) can be approximated as a function of the mass ratio only.

The collapse of the dimensionless frequency data is consistent with the prediction of Argentina & Mahadevana (2005). They suggested that in the limit of very large mass ratio, there is similarity to the oscillation of a rigid pivoted airfoil in a uniform flow and the flag oscillations frequency can be estimated as:

$$f\sim {\left(\frac{{\rho }_{f}{U}_{\infty }^{2}}{{\rho }_{s}tL}\right)}^{1/2}$$

which can be written as:

$$\frac{fL}{{U}_{\infty }}\sim {\left(\frac{{\rho }_{f}L}{{\rho }_{s}t}\right)}^{1/2}={\mu }^{-1/2}$$

Motivated by their suggestion for this scaling, we fit a curve into our data in Fig. 18b, by fixing the power of the mass ratio as (− 1/2). The curve fit is shown with a solid line in Fig. 18b and can be expressed as:

$${fL}/{U}_{\infty }=0.34/\sqrt{\mu }$$

We note that Argentina and Mahadevana (2005) made further predictions using the unsteady thin airfoil theory, which assumes that the flow remains attached to the flag throughout the flag oscillations. This is unlikely to occur for large flag displacements. Using the PIV images, we were able to find the flag shape in some instants for the L/c = 0.25, t/c = 0.002 flag whose wake was characterized in Figs. 5 and 6. The images were taken randomly; nevertheless, a set of the images shown in Fig. 19a reveals that the flag tip displacement is on the order of the flag length. We assume that at large flag displacements the flow on the suction surface will be fully separated. If one considers the limiting case of rigid flag as sketched in Fig. 19b, the fully separated flow can be modeled as the Kirchhoff (1869)-Rayleigh (1876) flow using the free-streamline theory.

Fig. 19
figure 19

a Instantaneous images of the flag shape for L/c = 0.25, t/c = 0.002; b schematic of the Kirchhoff-Rayleigh flow

Full size image

For the angular displacement θ of the rigid flat-plate sketched in Fig. 19b, the moment about the fixed leading-edge can be written as moment of inertia times angular acceleration:

$$\left(\frac{1}{3}{\rho }_{{\varvec{s}}}t{L}^{3}\right)\ddot{\theta }={C}_{M}\frac{1}{2}{\rho }_{f}{U}_{\boldsymbol{\infty }}^{2}{L}^{2}$$

where CM is the moment coefficient about the leading-edge of the flag. The equation of the motion can be rewritten as:

$$\ddot{\theta }=\frac{3}{2\mu }{\frac{{U}_{\boldsymbol{\infty }}^{2}}{{L}^{2}} C}_{M}$$

The Kirchhoff–Rayleigh free-streamline theory predicts the normal force coefficient as:

$${C}_{N}=\frac{2\mathrm{\pi sin} \theta }{4+\mathrm{\pi sin} \theta }$$

However, the free-streamline theory assumes that the wake pressure is equal to the freestream pressure, and underpredicts the normal force coefficient by a factor of roughly 2 compared to the experiments (Fage and Johansen 1927). The modified free-streamline theory of Wu (1962) defined a parameter called “wake under-pressure coefficient” σ, which allowed a better agreement with the experiments. Wu (1956) also provided approximate relations:

$${C}_{N}\cong \left(1+\sigma \right)\frac{2\mathrm{\pi sin} \theta }{4+\mathrm{\pi sin} \theta }$$

The center of pressure is approximately the mid-chord (Wu 1956), and the positive moment is in the clockwise direction in Fig. 19b. Hence,

$${C}_{M}\cong -\frac{{C}_{N}}{2} =-\frac{1}{2}\left(1+\sigma \right)\frac{2\mathrm{\pi sin} \theta }{4+\mathrm{\pi sin} \theta }$$

The experiments (Sefat 2011; Sefat and Fernandes 2012) suggest that σ ≅ 1.25. The equation of the motion is nonlinear. The linearized version is obtained for a small displacement θ as:

$$\mathrm{sin} \theta \approx \theta $$

and

$${C}_{M}=-1.77\theta $$

Hence, the equation of motion is obtained as:

$$\ddot{\theta }=\frac{3}{2\mu }\frac{{U}_{\boldsymbol{\infty }}^{2}}{{L}^{2}}(-1.77\theta )$$

which can be used to estimate the oscillation frequency as follows:

$${\omega }^{2}={(2\mathrm{\pi} f)}^{2}=\frac{2.66}{\mu }\frac{{U}_{\boldsymbol{\infty }}^{2}}{{L}^{2}}$$

and

$${fL}/{U}_{\infty }=0.26/\sqrt{\mu }$$

This prediction is shown with dashed lines in Fig. 18b and is in reasonable agreement with the curve fit to the experimental data presented previously.

4 Conclusions

The post-stall flow control using upstream flags was investigated on a NACA0012 airfoil at a chord Reynolds number of 100,000. The wind tunnel experiments included force and velocity measurements. Compliant flags of varying thickness and length were placed immediately upstream of the airfoil. The streamwise and cross-stream distances between the flag and the airfoil were varied.

The flag wakes produced comparable lift enhancement on the downstream airfoil and exhibited similar observations, including the existence of optimal locations away from the centerline and significant increase in the stall angle and the maximum lift coefficient, as for the case of bluff body wake previously reported. At the optimal location, the maximum time-averaged lift coefficients could reach levels up to 66% higher than that of the freestream case at an angle of attack of α = \({25}^{\mathrm{o}}\), corresponding to the increases of 38% in the maximum lift coefficient of the wing and 25° in the stall angle. In addition, the flag had smaller momentum thickness and possibly less drag compared to the bluff body wake. The best flag wake investigated had some differences from the traditional Karman vortex street, such as the shedding of the vortex pairs of opposite signs in half of the cycle and the resulting two branches of the wake. Nevertheless, there was comparable periodicity of the wake as measured by the POD mode energy and slightly better two-dimensionality (spanwise coherence). The flag oscillations were affected by the presence of the downstream airfoil, resulting in the distorted time-averaged wakes. This was noticed even for the most upstream location of the flag for which the largest lift enhancement was found. In all cases, flow separation, as well as formation and shedding of leading-edge vortices were the common feature. For the best streamwise (the most upstream) location of the flag, we found the largest maximum circulation of the leading-edge vortices, but the spanwise coherence was similar for all streamwise locations. In comparison with the case of the airfoil in the bluff body wake, the circulation of the leading-edge vortices was smaller, but the spanwise coherence of the wake was slightly better for the flag.

The flags with varying length and thickness all exhibited optimal locations in the wake at which the time-averaged lift became maximum. When plotted as a function of the flag mass ratio, an optimal range around µ = 6–8 was found to produce the maximum lift enhancement. The flags with the optimal mass ratios produce wakes with Strouhal numbers that cause resonance with the wake vortex shedding instability at the fundamental and subharmonic of the clean airfoil. The flag dimensionless frequency \(\mathrm{fL}/{U}_{\infty }\) exhibited very good collapse with the mass ratio of the flags, which could be predicted with a reduced order model. In the limit of very large mass ratio, the flag was approximated as a rigid pivoted flat-plate in a uniform flow. The separated flow around the flag was modeled as the Kirchhoff–Rayleigh flow using the modified free-streamline theory. For the optimal flags, the dimensionless frequency fell into a band \(\mathrm{fL}/{U}_{\infty }\)=0.10–0.14.