Accelerating the distance-minimizing method for data-driven elasticity with adaptive hyperparameters

Abstract

Data-driven constitutive modeling in continuum mechanics assumes that abundant material data are available and can effectively replace the constitutive law. To this end, Kirchdoerfer and Ortiz proposed an approach, which is often referred to as the distance-minimizing method. This method contains hyperparameters whose role remains poorly understood to date. Herein, we demonstrate that choosing these hyperparameters equal to the tangent of the constitutive manifold underlying the available material data can substantially reduce the computational cost and improve the accuracy of the distance-minimizing method. As the tangent of the constitutive manifold is typically not known in a data-driven setting, and as it can also change during an iterative solution process, we propose an adaptive strategy that continuously updates the hyperparameters on the basis of an approximate tangent of the hidden constitutive manifold. By several numerical examples we demonstrate that this strategy can substantially reduce the computational cost and at the same time also improve the accuracy of the distance-minimizing method.

1 Introduction

Data-driven methods have recently arisen as an alternative approach to conventional constitutive modeling. They generally seek to replace analytical constitutive equations by methods that do either not or only to a much smaller extent imply an a priori bias. One branch of data-driven constitutive modeling is relying on machine learning methods such as artificial neural networks [1,2,3,4,5,6,7]. For example, recently constitutive artificial neural networks (CANNs) were introduced [8] as a novel machine learning architecture that enables data-driven constitutive modeling on the basis of only a minimal amount of material data due to the incorporation of powerful (and general) a priori knowledge from continuum mechanics and materials theory.

An alternative to classical machine learning approaches in data-driven constitutive modeling is the local reconstruction of the constitutive manifold underlying the given material data [9,10,11,12]. Interestingly, this perspective opens up ways to interpret problems of data-driven constitutive modeling by way of mixed-integer programming [13].

Another branch of data-driven constitutive modeling that has attracted rapidly increasing attention over the last years are methods that interpret material data (i.e., strain–stress data) as a sort of discrete constitutive law. These methods seek to find a state that satisfies certain essential physical constraints of elasticity theory and yet falls (as closely as possible) into the set of given material data. This approach is often referred to as the distance-minimizing method and was introduced by Kirchdoerfer and Ortiz [14] and extended since then by numerous other works. The method was extended to solve problems of elasticity at finite strains [15], elastodyanmics [16, 17], fracture mechanics [18], and plasticity [19]. Besides, also aspects of the implementation have been addressed. For example, efficient data structures were proposed in [20] to reduce the computational cost of searching through a material database. Shannon’s information entropy and locally convex optimization techniques were applied to deal with noisy databases [11, 21]. Moreover, Leygue [22] proposed an algorithm to derive and to build a database of strain–stress pairs that sample mechanical responses of a material in in silico or in situ experiments. The mathematical background of the distance-minimizing method applied to small strain and finite strain elasticity problems has recently been examined in more detail by [23, 24]. Since in this data-driven framework there might exist no solution within the given material data set that satisfies at least the major physical constraints (the equilibrium equation and the compatibility condition on the strain field), a notion of relaxation must be introduced to define the data-driven solution of the distance-minimizing method. It is interesting to note that, according to [23], relaxation within the distance-minimizing framework is different from the classical relaxation of energy functions. For example, the relaxation of a bistable material would lead to material data sets that are no longer graphs. Such insights provide some first foundations for the application of the distance-minimizing framework also to non-convex stress–strain data sets. Moreover, a particularly interesting extension of the data-driven perspective towards the realm of stochastics has been proposed in [25].

Generally, in the distance-minimizing paradigm introduced by [14], a data-driven boundary value problem (BVP) is formulated as a double-minimization problem with an associated metric. Such a metric can be defined as a quadratic functional form on the strain–stress phase space [14, 17]. To weigh the contributions of the strain and the stress appropriately in the metric, a priori chosen tensor-valued hyperparameters are employed. These were considered to be of only numerical nature in the original work [14]. However, these hyperparameters affect the convergence rate of the distance-minimizing method formulated as a fixed-point iteration method. Moreover, for finite sets of material data, a poor choice of the hyperparameters can lead to low accuracy of data-driven solutions, even in case of noise-free material data. Despite several recent improvements and extensions of the distance-minimizing method, our understanding of the influence of its hyperparameters remains limited to date. In particular it remains poorly understood whether and how they could be chosen to optimize the numerical properties of the distance-minimizing method.

In this paper, we demonstrate that choosing these hyperparameters equal to the tangent of the constitutive manifold underlying the available material data can substantially reduce the computational cost and improve the accuracy of the distance-minimizing method. As the tangent of the constitutive manifold is typically not known in a data-driven setting, and the tangents evaluated at the strain solutions in each iteration change during an iterative solution process, we propose an adaptive strategy that is continuously updating the hyperparameters on the basis of an approximate tangent of the hidden constitutive manifold. We demonstrate the advantages of our novel adaptive strategy by several numerical examples.

2 Data-driven elasticity and distance-minimizing method

2.1 Terminology

To explain the distance-minimizing method for computational mechanics as well as its shortcomings, we revisit the classical BVP and then define a corresponding data-driven BVP.

• The primary field is the field on which we can impose the essential boundary conditions.

• The gradient field is defined as the gradient of the primary field.

• The energetically dual field is energetically conjugate to the gradient field.

The following discussion relies on the context of the small strain theory of continuum mechanics. Specifically, the primary field, the gradient field, and the dual field will be the displacements, the strains and the stresses stored at the material points. For stresses and strains we use Voigt’s notation herein, that is, they are not represented by second order tensors but rather by vectors (with 6 components for three-dimensional problems). Analogously, material stiffness and compliance are represented by matrices rather than fourth order tensors.

2.2 Classical versus data-driven boundary value problem

A standard boundary value problem consists of three ingredients besides boundary conditions: (A) Compatibility conditions, (B) conservation laws and (C) a constitutive law or a material law. In the following, we assume that the mechanical continuum on which the boundary value problem is defined has already been discretized, using, for example, the finite element method [26]. That is, we assume that the displacement field is represented by a displacement vector ${\mathbf {u}}= \{u_{i}\}_{i=1}^{N_\text {DOF}}$. Each of its components $u_{i}$ relates to a specific discrete point in the continuum (e.g., a node of a finite element discretization) and a certain coordinate direction. $N_\text {DOF}$ is the number of degrees of freedom of the discretization.

2.2.1 Compatibility conditions

Let the matrix ${\mathbf {B}}_{e}$ relate the displacement vector to the strain $\varvec{\epsilon }_{e}$ at a discrete material point e where the constitutive relation has to be evaluated (e.g., a Gauss point in a finite element discretization). If there are in total M such points, we have

$$\begin{aligned} \varvec{\epsilon }_{e} = {\mathbf {B}}_{e} {\mathbf {u}}, \quad e = 1, \ldots M. \end{aligned}$$

(1)

For example, if the continuum is discretized using $N_\text {elem}$ two-dimensional linear quadrilateral finite elements with four Gauss points each, $M = 4N_\text {elem}$ [17]. For a quadrature point e in a specific finite element, most components of ${\mathbf {B}}_{e}$ are zero and the non-zero components are computed from the gradient of the shape functions of the specific finite element (see also [26]). If the displacement field is sought as the solution and the strain is derived from this field, the compatibility conditions are automatically fulfilled in the discrete setting by applying (1).

2.2.2 Conservation laws

The conservation law for the deformation of a continuum body in quasi-static analysis is given in the strong form by

(2)

where $\Omega$ is the spatial domain the body occupies, $\varvec{\sigma }$ the Cauchy stress tensor, and ${\mathbf {f}}$ the external volume force exerted on the body. The continuum body has a prescribed displacement on the part $\Gamma _\mathrm {D}\subset \partial \Omega$ of the boundary and is subject to the external traction on the part $\Gamma _\mathrm {N}\subset \partial \Omega$ of the boundary, where ${\mathbf {n}}$ is the outer unit normal vector to the boundary $\partial \Omega$ and ${\mathbf {t}}$ is the prescribed traction. We assume that $\partial \Omega = \Gamma _\mathrm {D}\cup \Gamma _\mathrm {N}$ and $\Gamma _\mathrm {D}\cap \Gamma _\mathrm {N}= \emptyset$. This strong form together with the prescribed boundary conditions is first converted to a weak form, which is subsequently discretized by the standard finite element method yielding the discrete equilibrium equation

$$\begin{aligned} {\mathbf {F}}= \sum \limits _{e=1}^{M} w_{e} {\mathbf {B}}_{e}^{T} \varvec{\sigma }_{e}. \end{aligned}$$

(3)

Here, the external nodal force vector ${\mathbf {F}}$ captures the effect of external loading on each finite element node and is energetically conjugate to the nodal displacement vector ${\mathbf {u}}$. The right-hand side in (3) can be understood as an internal force vector that summarizes for each degree of freedom of the discretized continuum the overall effect of the elastic stresses in the continuum. The coefficients $\{w_{e}\}_{e=1}^{M}$ are weight factors of the different material points where the stress is evaluated (e.g., of the Gauss points in a finite element scheme), see also [17] for detail discussion of these coefficients. The matrix ${\mathbf {B}}_{e}^{T}$ captures numerical effects of the chosen discretization (e.g., of the chosen shape functions)

2.2.3 Material laws

To arrive at a closed system of equations, the strain and stress must be related to each other. In a classical boundary value problem, one defines to this end a function

$$\begin{aligned} \varvec{\sigma }= {\widehat{\varvec{\sigma }}}(\varvec{\epsilon }). \end{aligned}$$

(4)

that assigns to any strain $\varvec{\epsilon }$ a stress value. In the data-driven boundary value problem, a material law like (4) does not exist. Instead, there are abundant material data points collected in a material data set

$$\begin{aligned} \mathrm {D}= \big \{ (\varvec{\epsilon }_{j}, \varvec{\sigma }_{j}) \big \}_{j = 1}^{N_\text {data}}, \end{aligned}$$

(5)

which specifies for a number of $N_\text {data}$ discrete strain states $\varvec{\epsilon }_{j}$ the associated stress states $\varvec{\sigma }_{j}$. In a classical boundary value problem, we seek the solution to (3) that preserves both the compatibility condition (1) and a given material law (4). By contrast, in a data-driven framework for constitutive modeling, we seek the data points in $\mathrm {D}$ that minimize the violation of (1) and (3). In other words, we seek the solution to (3) that is closest to the data set $\mathrm {D}$. In the next section, these ideas will be formulated mathematically.

2.3 Distance-minimizing method

In this section, we introduce the data-driven boundary problem in the sense of the distance-minimizing method following the ideas and concepts of [14, 17].

2.3.1 Phase space

The phase space $\mathcal {Z}$ is defined as the set of all possible strain–stress states at all the material points of the system. Mathematically, the phase space $\mathcal {Z}$ and an element ${\mathbf {z}}\in \mathcal {Z}$ can be written as

$$\begin{aligned} \mathcal {Z}= \prod \limits _{e=1}^{M}(\mathbb {R}^{q} \times \mathbb {R}^{q}), {\mathbf {z}}= \prod \limits _{e=1}^{M} (\varvec{\epsilon }_e, \varvec{\sigma }_e), (\varvec{\epsilon }_e, \varvec{\sigma }_e) \in \mathbb {R}^{q}\times \mathbb {R}^{q}, \end{aligned}$$

where q is the dimension of $\varvec{\epsilon }$ and $\varvec{\sigma }$ and depends on the problem setting [17]. Each element ${\mathbf {z}}$ of the phase space consists of multiple strain–stress pairs, each of which corresponds to one material point. The addition of two elements and the multiplication of one element in $\mathcal {Z}$ by a real scalar are defined in a component-wise manner. The set of possible strain–stress states $(\varvec{\epsilon }_e, \varvec{\sigma }_e)$ specifically at the e-th material point is referred to in the following as local phase space $\mathcal {Z}_{e}$.

The strain–stress states at all the material points are collected in one global strain–stress state and denoted by $(\varvec{\epsilon }, \varvec{\sigma }) = \{(\varvec{\epsilon }_{e}, \varvec{\sigma }_{e})\}_{e=1}^{M}$. Therefore, the strain–stress pair without the subscript e will refer to the global state.

2.3.2 Material data space, constitutive manifold and physical-constraint space

The material data space $\mathcal {D}$

$$\begin{aligned} \mathcal {D}= \left\{ {\mathbf {d}}= \prod \limits _{e = 1}^{M} (\varvec{\epsilon }_{e}, \varvec{\sigma }_{e}), \quad \text {with } (\varvec{\epsilon }_e, \varvec{\sigma }_e) \in \mathrm {D}\right\} \end{aligned}$$

is the subset of $\mathcal {Z}$ that results if we admit only strain–stress pairs from the material data set $\mathrm {D}$.

Fig. 1

The material data $\mathrm {D}$ is typically located in the close neighborhood of some (in general unknown) constitutive manifold $\mathcal {M}$. The difference between the material data and the constitutive manifold is caused by the noise incorporated in the material data

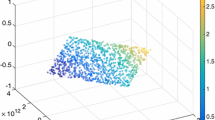
The material data $\mathrm {D}$ can be imagined to result from a combination of some hidden constitutive law $\varvec{\sigma }= {\widehat{\varvec{\sigma }}}(\varvec{\epsilon })$ following (4) and some additional noise. The hidden constitutive law can be represented in the local phase space $\mathcal {Z}_{e}$ by a so-called constitutive manifold

$$\begin{aligned} \mathcal {M}= \left\{ (\varvec{\epsilon }, \varvec{\sigma }), \quad \text {with } \varvec{\sigma }= {\widehat{\varvec{\sigma }}}(\varvec{\epsilon })\right\} , \end{aligned}$$

(6)

and the material data are located in a close corridor around $\mathcal {M}$, whose width is determined by the magnitude of the noise (Fig. 1).

The physical-constraint space $\mathcal {C}\subset \mathcal {Z}$ comprises of elements ${\mathbf {c}}= \{(\varvec{\epsilon }_e,\varvec{\sigma }_e)\}_{e = 1}^{M}$ satisfying both the compatibility conditions and the conservation law. $\mathcal {C}$ is also referred to as physical-constraint manifold.

2.3.3 Metric

With the above notions, we can equip the phase space $\mathcal {Z}$ with a metric [14, 17]

(7)

Herein, we use Voigt notation so that ${\mathbf {C}}_{e}$ and ${\mathbf {S}}_{e}$ are matrices and the central dot denotes a scalar product between two vectors. The matrices ${\mathbf {C}}_{e}$ and ${\mathbf {S}}_{e}$ are of numerical nature and must be defined a priori. They are the hyperparameters in the distance-minimizing method described below. $\Pi ^{\epsilon }$ and $\Pi ^{\sigma }$ denote energy-like terms whose definition will turn out convenient for the development below. The scalars $w_{e}$ are weights of the contribution of each material point.

Similarly to (7), also the local phase space $\mathcal {Z}_{e}$ can be equipped with a metric

$$\begin{aligned} \Vert (\varvec{\epsilon }_{e}, \varvec{\sigma }_{e}) \Vert _{e} = \Pi ^{\epsilon } (\varvec{\epsilon }_{e},{\mathbf {C}}_{e}) + \Pi ^{\sigma }(\varvec{\sigma }_{e},{\mathbf {S}}_{e}) \end{aligned}$$

(8)

so that the global metric (7) is determined as a weighted sum of the local metric (8), namely $\Vert (\varvec{\epsilon }, \varvec{\sigma }) \Vert \!=\! \sum \nolimits _{e=1}^{M} w_e \Vert (\varvec{\epsilon }_{e}, \varvec{\sigma }_{e}) \Vert _{e}$.

2.3.4 Distance-minimizing method

We define the data-driven boundary value problem in the sense of the distance-minimizing method as an optimization problem (see Fig. 2)

$$\begin{aligned} \{{\mathbf {c}}^{*}, {\mathbf {d}}^{*}\} = \arg \Big \{ \min \limits _{{\mathbf {c}}\in \mathcal {C}}\min \limits _{{\mathbf {d}}\in \mathcal {D}} \Vert {\mathbf {c}}- {\mathbf {d}} \Vert \Big \} = \arg \Big \{ \min \limits _{{\mathbf {d}}\in \mathcal {D}} \min \limits _{{\mathbf {c}}\in \mathcal {C}} \Vert {\mathbf {c}}- {\mathbf {d}} \Vert \Big \}.\nonumber \\ \end{aligned}$$

(9)

That is, we seek among all possible strain–stress states the state ${\mathbf {d}}^*$ in the material data space that is as close as possible to the physical-constraint space as well as the state ${\mathbf {c}}^*$ in the physical-constraint space that is as close as possible to the material data space. The actual data-driven solution can either be defined as ${\mathbf {z}}= {\mathbf {c}}^{*}$ or as ${\mathbf {z}}= {\mathbf {d}}^{*}$. In the first case, we strictly demand a strain–stress state of which it is sure that is possible (because it forms part of the given material data space $\mathcal {D}$) but allow an—as small as possible—violation of fundamental physical laws. By contrast, in the second case, we strictly demand that all fundamental physical laws are exactly satisfied and allow to this end also strain–stress states of which we do not know for sure that they are possible but which are at least as close as possible to strain–stress states of which we know that they are possible.

Both approaches are in principle possible and it is up to the user which of them to define as the solution to the data-driven BVP. It is worth mentioning that the minimization steps in (9) are interchangeable. The conceptualization of this minimization problem is visualized in Fig. 2.

At this point, it is instructive to distinguish between the setting of and the solution method for a boundary value problem (BVP). Whereas a classical BVP is associated with a constitutive law (4), a data-driven BVP comes along with a material data set replacing the constitutive law. The classical BVP can be solved both by a direct method or by the distance-minimizing method described in this section.

In the first case, we express the equilibrium equations in terms of the displacement field by eliminating the stress field from the system with the aid of the material law. Subsequently, we search a solution within the space of admissible displacement fields. By contrast, in the second case the solution to the classical BVP is simply found as the solution to (9). In this case ${\mathbf {c}}^* = {\mathbf {d}}^*$ because in a classical BVP there exists a state in the phase space that both satisfies all the physical constraints and the given constitutive equation (4) at the same time. While the classical BVP can be solved either by a classical, direct method or by the distance-minimizing method, the data-driven BVP cannot be solved by classical, direct methods but rather the distance-minimizing (or a similar) method is required.

2.3.5 Numerical implementation of the distance-minimizing method

In this section, we summarize the staggered scheme described in [14, 17] for solving the double-minimization problem (9). This problem is decomposed into a series of single minimization problems. We randomly pick an initial value ${\mathbf {d}}^{[0]} \in \mathcal {D}$ and then solve iteratively for $k=0,1,2,\dots$ the problems

$$\begin{aligned} \begin{aligned} {\mathbf {c}}^{(k)}&= \arg \Big \{ \min \limits _{{\mathbf {c}}\in \mathcal {C}} \big \Vert {\mathbf {c}}- {\mathbf {d}}^{[k]} \big \Vert \Big \}, \\ {\mathbf {d}}^{[k+1]}&= \arg \Big \{ \min \limits _{{\mathbf {d}}\in \mathcal {D}} \big \Vert {\mathbf {c}}^{(k)} - {\mathbf {d}} \big \Vert \Big \}, \end{aligned} \end{aligned}$$

(10)

until a converged solution is achieved. Here, both the superscripts (k) and [k] refer the iteration step k and ${\mathbf {c}}^{(k)}$ and ${\mathbf {d}}^{[k]}$ on the right-hand sides are known from the previous iteration step, respectively. Herein, the parentheses $(\diamond )$ imply that the associated quantities belong to the physical-constraint space $\mathcal {C}$ and the square brackets $[\,\diamond \,]$ that they belong to the material data space $\mathcal {D}$. Equivalently, we could also start with a random ${\mathbf {c}}^{(0)}\in \mathcal {C}$ for the initialization and then repeat the two steps in (10) in reversed order. The described solution scheme is demonstrated in Fig. 2.

Fig. 2

Algorithm for implementation of distance-minimizing computing method. The distance $\mathrm {dist}({\mathcal {D}},{\mathcal {C}})$ between two subsets $\mathcal {C}$ and $\mathcal {D}$ of the phase space $\mathcal {Z}$ can be computed by performing a sequence of projection operations defined by Eq. (10). The final solution can be chosen as either ${\mathbf {c}}^{*}$ or ${\mathbf {d}}^{*}$ depending on the user’s choice. Reprinted from Computer Methods in Applied Mechanics and Engineering, Volume 365, 112898, Lu Trong Khiem Nguyen, Matthias Rambausek, Marc-André Keip, Variational framework for distance-minimizing method in data-driven computational mechanics, with permission from Elsevier [17]

In general, we do not have a strain–stress pair $(\varvec{\epsilon }, \varvec{\sigma })$ satisfying the compatibility and equilibrium equations at initialization. Therefore, starting with a properly chosen ${\mathbf {c}}^{(0)}$ is typically not trivial. By contrast, it is easy to pick some ${\mathbf {d}}\in \mathcal {D}$. Hence, a numerical solution with the initialization in $\mathcal {D}$ is more favorable. Nevertheless, the final solution in $\mathcal {C}$ has the favorable property of respecting the physical laws.

The numerical scheme to solve (10) can be rewritten in a fixed-point formulation as

$$\begin{aligned} {\mathbf {d}}^{[k+1]} = \min \limits _{{\mathbf {d}}\in \mathcal {D}} \Big \Vert {\mathbf {d}}- \Big \{ \min \limits _{{\mathbf {c}}\in \mathcal {C}}\big \Vert {\mathbf {c}}- {\mathbf {d}}^{[k]} \big \Vert \Big \} \Big \Vert \quad \forall k \ge 0. \end{aligned}$$

(11)

The iteration scheme stops when there is no further effective change in the data selection process. The value of ${\mathbf {c}}$ from the last iteration with (10)$_1$ automatically yields ${\mathbf {c}}^*$ for (9). Section 2.5 discusses how to define stopping criteria for (11).

2.4 Data-driven solver for linear elasticity problem

In the following, we briefly summarize the single steps to the solution in the distance-minimizing method for linear elasticity problems, following [14, 17].

2.4.1 Projection on the physical-constraint space

The strain–stress state stored in the mechanical system in one particular step k ($k = 0$ for the initialization step) is given by ${\mathbf {d}}^{[k]} = (\varvec{\epsilon }^{[k]}, \varvec{\sigma }^{[k]})$. To solve (10)$_1$, we need to find ${\mathbf {c}}^{(k)} = (\varvec{\epsilon }^{(k)}, \varvec{\sigma }^{(k)})$ that minimizes the norm

$$\begin{aligned}&\big \Vert (\varvec{\epsilon }^{(k)} - \varvec{\epsilon }^{[k]}, \varvec{\sigma }^{(k)} - \varvec{\sigma }^{[k]}) \big \Vert \nonumber \\&\quad = \sum \limits _{e = 1}^{M} w_{e} \left[ \Pi ^\epsilon (\varvec{\epsilon }^{(k)} - \varvec{\epsilon }^{[k]},{\mathbf {C}}_{e}) + \Pi ^\sigma (\varvec{\sigma }^{(k)} - \varvec{\sigma }^{[k]},{\mathbf {S}}_{e}) \right] , \end{aligned}$$

(12)

and satisfies the physical constraints (1) and (3). The solution can be obtained by using the method of Lagrange multipliers with a Lagrangian function

(13)

Here we used (1) in the norm, which allows us to satisfy always the compatibility conditions. Then the only remaining constraint is the balance law, which is enforced by the (vectorial) Lagrange multiplier $\varvec{\eta }^{(k)}$. The stationary point of $\mathcal {L}$ is the solution to the following system

$$\begin{aligned} \begin{aligned} \bigg [ \sum \limits _{e=1}^{M} w_e {\mathbf {B}}_{e}^{T}{\mathbf {C}}_{e} {\mathbf {B}}_{e} \bigg ] {\mathbf {u}}^{(k)}&= \sum \limits _{e=1}^{M} w_e {\mathbf {B}}_{e}^{T} {\mathbf {C}}_{e} \varvec{\epsilon }_e^{[k]}, \\ \bigg [ \sum \limits _{e=1}^{M} w_e {\mathbf {B}}_{e}^{T}{\mathbf {S}}_{e}^{-1} {\mathbf {B}}_{e} \bigg ] \varvec{\eta }^{(k)}&= {\mathbf {f}}- \sum \limits _{e=1}^{M} w_e {\mathbf {B}}^{T}_{e} \varvec{\sigma }_e^{[k]}, \end{aligned} \end{aligned}$$

(14)

where the stress $\varvec{\sigma }_e^{(k)}$ has been resolved according to

$$\begin{aligned} \varvec{\sigma }_e^{(k)} = \sum \limits _{e=1}^{M} {\mathbf {S}}_{e}^{-1} {\mathbf {B}}_{e} \varvec{\eta }^{(k)} + \varvec{\sigma }_e^{[k]}. \end{aligned}$$

(15)

We will call the right-hand side of the second equation residual vector as the equilibrium state corresponds to this vector being close to zero. This result can be derived in a variational framework proposed in [17]. Finally, the solution $(\varvec{\epsilon }^{(k)}, \varvec{\sigma }^{(k)})$ is obtained by solving system (14) and computing the strains and stresses according to (1) and (15).

Following (14), it appears reasonable to choose ${\mathbf {S}}_{e} = {\mathbf {C}}_{e}^{-1}$ because this way the left-hand side of the two equations of (14) can be computed by one single assembly process. Thus, in the following we will strictly use ${\mathbf {S}}_{e} = {\mathbf {C}}_{e}^{-1}$ with ${\mathbf {C}}_{e}^{-1}$ being the inverse of ${\mathbf {S}}_{e}$ in the sense , where ${\mathbf {I}}$ is the identity matrix.

2.4.2 Projection on the material data space

Solving the minimization problem (10)$_2$ means pulling the solution ${\mathbf {c}}^{(k)} = (\varvec{\epsilon }^{(k)}, \varvec{\sigma }^{(k)})$ back to the material data space $\mathcal {D}$. For each material point in the continuum body, we seek

$$\begin{aligned}&(\varvec{\epsilon }_e^{[k+1]},\varvec{\sigma }_e^{[k+1]})\nonumber \\&\quad = \mathop {\text {argmin}} \limits _{(\varvec{\epsilon }_e,\varvec{\sigma }_e) \in \mathrm {D}} \left[ \Pi ^\epsilon (\varvec{\epsilon }_{e} - \varvec{\epsilon }_{e}^{(k)},{\mathbf {C}}_{e}) + \Pi ^\sigma (\varvec{\sigma }_{e} - \varvec{\sigma }_{e}^{(k)},{\mathbf {C}}_{e}^{-1}) \right] . \end{aligned}$$

(16)

This is simply a discrete optimization problem (without additional constraints). It can be solved by going through all the material data points in $\mathrm {D}$ and then selecting the one minimizing the above function. The combination of all the optimal local solutions of (16) at the individual material points constitutes the global solution ${\mathbf {d}}^{[k+1]} = (\varvec{\epsilon }^{[k+1]}, \varvec{\sigma }^{[k+1]})$ to the global problem as shown in [17].

2.5 Convergence criteria for the distance-minimizing method

The distance-minimizing method as expressed in (11) can be implemented by a fixed-point iteration scheme [14, 17] where

$$\begin{aligned} \big \Vert (\varvec{\epsilon }^{(k+1)} - \varvec{\epsilon }^{(k)}, \varvec{\sigma }^{(k+1)} - \varvec{\sigma }^{(k)}) \big \Vert \le \delta \end{aligned}$$

(17)

can be used as a stopping criterion. Note that the metric used in this condition depends on the hyperparameters ${\mathbf {C}}_{e}$ and ${\mathbf {S}}_{e}$. An alternative criterion is an inequality operating on the material data space in the form

$$\begin{aligned} \big \Vert (\varvec{\epsilon }^{[k+1]} - \varvec{\epsilon }^{[k]}, \varvec{\sigma }^{[k+1]} - \varvec{\sigma }^{[k]}) \big \Vert \le \delta . \end{aligned}$$

(18)

This criterion works equivalently to the criterion (17) as the projections of elements ${\mathbf {z}}\in \mathcal {Z}$ onto the data function space $\mathcal {D}$ and onto the physical-constraint space $\mathcal {C}$ are continuous and linear operators. Moreover, for this reason a sequence $\{{\mathbf {z}}^{(k)}\}_{k=0}^{\infty }$ obtained by applying consecutively the above projections between physical-constraint and material data space will finally converge to the classical solution for a classical BVP. A proof of this statement for a simple system will be presented in Sect. 5.1.2. All of the numerical examples shown below use (18) with $\delta = 10^{-10}$.

As mentioned above, the distance-minimizing method can be used to solve both classical and data-driven BVPs. In classical BVPs, the constitutive manifold $\mathcal {D}$ and the material data set are continuous domains so that one has to choose some small positive tolerance $\delta$. By contrast, since in data-driven BVPs the material data set is discrete with $|\mathcal {D}|< \infty$, also $\delta = 0$ can be used both in (17) and (18).

3 Role of hyperparameters in the distance-minimizing method

In this section, we consider the deformation of an in general multidimensional elastic continuum and examine how the choice of the hyperparameters affects the numerical iterations required for the distance-minimizing method. The goal is to find estimates for the hyperparameters of which one can hope that they accelerate the convergence of these iterations.

The distance-minimizing method consists of a series of projections of type (10)$_1$, where a projection from the material data space to the physical-constraint space is performed, and of type (10)$_2$, where a projection from the physical-constraint space to the material data space is performed. During both projections a step $\Delta {\mathbf {z}}_e = (\Delta \varvec{\epsilon }_e, \Delta \varvec{\sigma }_e)$ is performed at each material point in the local phase space $\mathcal {Z}_{e}$. To perform this step, for both projections a cost function has to be minimized. For projection steps of type (10)$_1$ the cost function is (16) and for projection steps of type (10)$_2$ the cost function is (12). Both cost functions consist of summands of the type

(19)

The magnitudes of the strain-related contributions $\Pi ^\epsilon (\Delta \varvec{\epsilon }_e,{\mathbf {C}}_{e})$ and the stress-related contributions $\Pi ^\sigma (\Delta \varvec{\sigma }_e,{\mathbf {C}}_{e}^{-1})$ depend on the hyperparameters ${\mathbf {C}}_{e}$, respectively. If both types of contributions are substantially different in magnitude, one will dominate the other during the solution of the minimization problem. In such cases, the iteration steps will be performed either in a way that focuses on strain and largely neglects the role of stress or vice versa. This implies little progress during the single iteration steps for the respectively neglected quantity. At the same time, however, the initial state at the beginning of the iterations differs from the sought solution typically both in stress and strain considerably. So, if the hyperparameters are chosen such that changes of one of these two quantities remain small during the single iteration steps, necessarily a large number of iteration steps will be required to obtain a solution that is optimal with respect to both. In other words, if the magnitudes of $\Pi ^\epsilon (\Delta \varvec{\epsilon }_e,{\mathbf {C}}_{e})$ and $\Pi ^\sigma (\Delta \varvec{\sigma }_e,{\mathbf {C}}_{e}^{-1})$ are substantially different, we have to expect in general slow convergence of the distance-minimizing method at least with respect to either stress or strain.

The key question is now under which conditions we can expect that $\Pi ^\epsilon (\Delta \varvec{\epsilon }_e,{\mathbf {C}}_{e})$ and $\Pi ^\sigma (\Delta \varvec{\sigma }_e,{\mathbf {C}}_{e}^{-1})$ are of comparable or, by contrast, starkly different order of magnitude. To understand this, we focus for simplicity on the later stage of the iterative solution procedure required by the distance-minimizing. Moreover, we assume a situation where abundant material data of high quality is available so that the strain–stress pairs computed by the projection steps (10)$_1$ the cost function is (16) and (10)$_2$ the cost function is (12) are—in the later stage of the iterative solution procedure—close to the (hidden) constitutive manifold $\varvec{\sigma }= {\widehat{\varvec{\sigma }}}(\varvec{\epsilon })$ of the material. It is important to note that this situation is indeed representative for many practically relevant application scenarios because there one will often seek to obtain a large amount of material data of good quality. Moreover, iterative solution procedures tend to spend most of their iterations in a relatively small neighborhood around the final solution to achieve the elevated accuracy that is numerically desired. As in that neighborhood strain–stress pairs are close to the (hidden) constitutive manifold, we can assume that stress increments between two subsequent steps in the iterative solution of the distance-minimizing problem are related to their associated strain increments by

$$\begin{aligned} \Delta \varvec{\sigma }_{e} = {\widehat{{\mathbf {C}}}}_e \Delta \varvec{\epsilon }_e + \mathcal {O}(\Vert \Delta \varvec{\epsilon }_{e}\Vert ^2) \end{aligned}$$

(20)

with the tangent of the hidden constitutive manifold $\widehat{{\mathbf {C}}}_e = \partial \widehat{\varvec{\sigma }} / \partial \varvec{\epsilon }(\varvec{\epsilon }_{e})$ computed at the strain–stress state (at the beginning or end) of the respective iteration step. Using this approximation,

(21)

and thus

(22)

Now we assume ${\mathbf {C}}_{e}= \gamma \widehat{{\mathbf {C}}}_{e}$, which allows us to discuss in a rule-of-thumb manner cases where the hyperparmaeters are either of comparable magnitude as the tangent stiffness of the hidden constitutive manifold ($\gamma = 1$) or much larger ($\gamma \gg 1$) or much smaller ($\gamma \ll 1$). From (22) we derive

$$\begin{aligned} \frac{\Pi ^\sigma (\Delta \varvec{\sigma }_e,{\mathbf {C}}_{e}^{-1})}{\Pi ^\epsilon (\Delta \varvec{\epsilon }_e,{\mathbf {C}}_{e})} \approx \frac{1}{\gamma ^2}. \end{aligned}$$

(23)

That is, we expect the strain-related contributions $\Pi ^\epsilon (\Delta \varvec{\epsilon }_e,{\mathbf {C}}_{e})$ and the stress-related contributions $\Pi ^\sigma (\Delta \varvec{\sigma }_e,{\mathbf {C}}_{e}^{-1})$ in the objective functions of the minimization problems solved in each step of the distance-minimizing method to be of similar order of magnitude if the hyperparameters are of similar magnitude as the tangent stiffness of the (hidden) constitutive manifold. By contrast, if this is not the case and the hyperparameters are chosen much larger or much smaller, we expect that in these minimization problems either the contributions of the type $\Pi ^\epsilon (\Delta \varvec{\epsilon }_e,{\mathbf {C}}_{e})$ or $\Pi ^\sigma (\Delta \varvec{\sigma }_e,{\mathbf {C}}_{e}^{-1})$ will dominate the respective other. And for the reasons above, we then expect slow convergence.

4 Distance-minimizing method with adaptive hyperparameters

4.1 Hyperparameters based on linear regressions

From the above sections it is clear that for an efficient and effective implementation of the distance-minimizing method it is essential to choose its hyperparameters comparable to the tangent of the hidden constitutive manifold. As the latter is not known, it is important to estimate it. Here we will discuss how this is possible on the basis of linear regression techniques, which are computationally cheap and simple.

To estimate the tangent of the hidden constitutive manifold in the neighborhood of a specific ${\mathbf {z}}_e = (\varvec{\epsilon }_e,\varvec{\sigma }_{e}) \in \mathcal {Z}_e$ at a material point e, we first have to identify the material data given in its neighborhood. We may do so by defining these data as

$$\begin{aligned} \mathcal {N}({\mathbf {z}}_e,r) = \mathcal {N}(\varvec{\epsilon }_e,r) = \{(\varvec{\epsilon },\varvec{\sigma }) \in D: \quad \Vert \varvec{\epsilon }- \varvec{\epsilon }_e \Vert _E < r \big \}.\nonumber \\ \end{aligned}$$

(24)

with the Euclidean norm $\Vert . \Vert _E$. Note that here we cannot use the above usually used phase space norm because its computation requires exactly the hyperparameters whose determination is the objective of the procedure described in this section. Therefore, we have to use a Euclidean (or alternatively other standard) norm here and can thus compare only either the stress or the strain components of a state in the local phase space to quantify proximity in some sense. Here we decide to focus on the strain components so that we can use $\mathcal {N}({\mathbf {z}}_e,r)$ and $\mathcal {N}(\varvec{\epsilon }_e,r)$ equivalently. By the denoting $k = |\mathcal {N}({\mathbf {z}}_e, r) |$, we can define $\mathcal {N}({\mathbf {z}}_e, k) := \mathcal {N}({\mathbf {z}}_e, r)$ as a set of k material data points in $\mathrm {D}$ that are closest to ${\mathbf {z}}_e$, that is, as the set of its k nearest neighbors. Based on the neighborhood data from (24) we can perform a linear regression [27]. To this end, we determine in

$$\begin{aligned} \varvec{\sigma }= {\widehat{{\mathbf {C}}}}^{a}({\mathbf {z}}_e) \varvec{\epsilon }+ \varvec{\sigma }_0({\mathbf {z}}_e), \quad (\varvec{\sigma },\varvec{\epsilon }) \in \mathcal {N}({\mathbf {z}}_e,r) \end{aligned}$$

(25)

the parameters ${\widehat{{\mathbf {C}}}}^{a}({\mathbf {z}}_e)$ and $\varvec{\sigma }_0({\mathbf {z}}_e)$ such that they best fit the material data in $\mathcal {N}({\mathbf {z}}_e,r)$. Then ${\widehat{{\mathbf {C}}}}^{a}({\mathbf {z}}_e)$ forms an estimate of the tangent ${\widehat{{\mathbf {C}}}}$ of the hidden constitutive law as introduced in (25). For practical purposes, r should be chosen small enough so that the hidden constitutive law can be approximated reasonably by a linear relation in its range. At the same time, r should be chosen large enough to suppress noise in the material data by averaging across a sufficient amount of data.

We make some minor remarks on a possibility of encountering the constitutive tangent tensor that can be not positive definite. Physically, such a tangent stiffness tensor is associated with an unstable material. As unstable materials have hardly had any applications in engineering (with possibly a few very special cases), we decided not to discuss such cases n depth in our paper. When focusing on practically relevant materials, we expect that issues with positive definiteness of the tangent stiffness could only arise as numerical artifacts of our regression techniques. Such problems could, however, be handled simply by eliminating any hyperparameters that are not positive definite in our set of pre-defined hyperparameters established by our divide and conquer strategy. This can be expected to affect the overall outcome in no significant way. Another way of ensuring positive definiteness of the hyperparameters, which we used in this work, is choosing the radii of neighborhoods appropriately.

4.2 Adaptive hyperparameters based on the constitutive manifold

The previous section discusses how to compute the hyperparameters so that they approximate the tangent of the hidden constitutive manifold. This tangent, however, may in general change from iteration step to iteration step and material point to material point in the general case of a nonlinear hidden constitutive law. Therefore, an adaptive procedure is required in practice. Such a procedure can be defined for the distance-minimizing method as follows: we start with some initial guess. Based on this initial guess we use at each material point linear regression to estimate the tangent of the hidden constitutive manifold, which yields us the hyperparameters for the next iteration step. With these hyperparameters, we can solve the minimization problem giving us the next intermediate configuration of our iterative solution process. From this intermediate configuration we again estimate the hyperparameters by linear regression, perform the next iteration step and so on. This adaptive hyperparameter strategy preserves the fixed-point property of the scheme (11) in the sense that still converges to a specific solution. As will be seen from the numerical examples in Sect. 5, the adaptive hyperparameter strategy described here indeed dramatically decreases the number of iteration steps required to this end. At the same time, however, also the computational cost per iteration step increases. The reason is that for constant hyperparameters the left-hand side of (14) has to be evaluated only once. By contrast, when using adaptive hyperparameters it has to be reevaluated in every iteration step, which means the computational cost of the assembly of an additional stiffness matrix in each iteration step. The computational effort is dominated by the process of recomputing hyperparameters at all the material points. Therefore, a simple adaptation of the hyperparameters in each iteration step does in practice often not lead to the desired substantial reduction of computational cost. In the next subsection we will discuss a strategy to overcome this caveat.

4.3 Divide and conquer technique for a finite set of representative hyperparameters

The key idea for a computationally efficient adaptation of the hyperparameters of the distance-minimizing method is to allow variations of the hyperparameters only within a finite set of predefined values. As will be seen below, this simple strategy can decrease the computational cost of hyperparameter adaptation substantially while still exploiting most of its benefits, noting that for a reduction of the number of iteration steps it is sufficient if the hyperparameters reasonably approximate the tangent of the hidden constitutive law whereas an accurate adjustment of them is not required. For an efficient adaptation of the hyperparameters, we proceed as follows: let $\Omega ^{\varvec{\epsilon }}$ be the domain of all possible strain states that are of interest. In practice, $\Omega ^{\varvec{\epsilon }}$ may often be chosen, for example, as the convex hull of the strain states in the material data set, potentially extended by some boundary layer to allow also a certain extrapolation beyond the available material data. We can divide $\Omega ^{\varvec{\epsilon }}$ into a set of non-overlapping subdomains $\Omega _i^{\varvec{\epsilon }}$. To each such strain subdomain, we assign an approximation ${\widehat{{\mathbf {C}}}}^{a}_i$ of the average tangent of the hidden constitutive manifold in this domain. This approximation may, for example, be computed as a weighted average of all the approximations gained from linear regression for all the states ${\mathbf {z}}_e \in D$ in the material data set whose strain components $\varvec{\epsilon }_e$ are located in $\Omega _i^{\varvec{\epsilon }}$ that is,

$$\begin{aligned} {\widehat{{\mathbf {C}}}}^{a}_i = \sum _{\varvec{\epsilon }_e \in \Omega _i^{\varvec{\epsilon }}} \alpha ({\mathbf {z}}_e){\widehat{{\mathbf {C}}}}^{a}({\mathbf {z}}_e), \quad \text {with} \quad {\mathbf {z}}_e = (\varvec{\epsilon }_e,\varvec{\sigma }_e)\in D. \end{aligned}$$

(26)

The weights $\alpha ({\mathbf {z}}_e)$ may be chosen equal to the (normalized) size of the part of $\Omega _i^{\varvec{\epsilon }}$ for which $\varvec{\epsilon }_e$ is representative. This size may, for example, be set equal to the size of an associated Voronoi cell if a Voronoi tesselation of $\Omega _i^{\varvec{\epsilon }}$ is performed based on the strain values in the material data set which fall into $\Omega _i^{\varvec{\epsilon }}$.

Having subdivided the strain space into $\Omega _i^{\varvec{\epsilon }}$ and computed the associated ${\widehat{{\mathbf {C}}}}^{a}_i$ once in the beginning, our strategy for hyperparameter adaptation is as follows: at a specific material point in a specific iteration step, one first determines the associated subdomain $\Omega _i^{\varvec{\epsilon }}$ and then uses for the next iteration step ${\widehat{{\mathbf {C}}}}^{a}_i$ as hyperparameter ${\mathbf {C}}_e$ at this material point.

5 Examples

The following examples not only demonstrate the advantages of the proposed strategy of adaptive hyperparameters but also support the underlying theoretical considerations, which is of particular importance since they could so far not yet be based on a rigorous mathematical proof. First, we present a set of examples where classical BVP is solved using the distance-minimizing method with various fixed hyperparameters. The effect of the choice of hyperparameters is discussed and numerically illustrated. Then, we show that the proposed method with adaptive hyperparameters outperforms the standard approach with constant hyperparameters especially when the noise in the material data increases. Finally, we show that the hyperparameter-adaptive solver leads to a better convergence rate with respect to the amount of available material data than that of the one with fixed hyperparameters.

5.1 Statically indeterminate three-member truss system

5.1.1 Problem setting

In Sect. 5.1 we study the three-member truss system illustrated in Fig. 3. As stresses and strains are constant within the three trusses, respectively, the state of the system is characterized by three strain–stress pairs $(\epsilon _e, \sigma _e), e = 1, 2, 3$ denoting strain and stress in the e-th truss respectively. We assume a linear constitutive law

$$\begin{aligned} \sigma _e = E \epsilon _e \end{aligned}$$

(27)

with $E = 1000$. For an external force $\{f_x, f_y\} = \{25, -25\}$ on the upper-right joint in Fig. 3, one can easily compute the analytical solution of the classical boundary value problem defined above as $\varvec{\epsilon }^{\mathrm {ref}} = [\epsilon _{1}^{\mathrm {ref}}, \epsilon _{2}^{\mathrm {ref}}, \epsilon _{3}^{\mathrm {ref}}]^T = \{0, -2.5\%, 2.5\%\}$.

Fig. 3

Three-truss system. The system consists of three trusses with unit cross section connected by a joint on the upper right. The respective other ends of the trusses are fixed with respect to their translational degrees of freedom but free to rotate. The joint on the upper right is subject to an external force ${\mathbf {f}}= (f_{x}, f_{y})$ (red arrows) and exhibits a displacement $(u_{x}, u_{y})$. (Color figure online)

5.1.2 Theoretical analysis

Now we discuss the solution of the classical BVP from Sect. 5.1.1 using the distance-minimizing method. For this specific problem, we can compute the sequence of iteration steps performed by the distance-minimizing method analytically because the underlying minimization problems can be solved analytically in each iteration step. Doing so allows us to study thoroughly the dependence of the convergence rate of the data-driven solver on the hyperpararmeters. If we solve (10) analytically and set all the three hyperparameters $C_e$ equal to a single constant C, we obtain

$$\begin{aligned} \varvec{\epsilon }^{[k+1]} = {\mathbf {M}}\varvec{\epsilon }^{[k]} + {\mathbf {R}}, \end{aligned}$$

(28)

with

$$\begin{aligned} {\mathbf {M}}= & {} \frac{1}{\kappa _1} \begin{bmatrix} 2(C^2 + \sqrt{2}E^2) &{} \sqrt{2}(C^2 - E^2) &{} \sqrt{2}(C^2 - E^2) \\ 2(C^2 - E^2) &{} (1+2\sqrt{2})C^2 + E^2 &{} -(C^2 - E^2) \\ 2(C^2 - E^2) &{} -(C^2 - E^2) &{} (1+2\sqrt{2})C^2 + E^2 \end{bmatrix}, \\ {\mathbf {R}}= & {} \frac{1}{\kappa _2} \begin{bmatrix} 2E(f_{x} + f_{y}) \\ E(-\sqrt{2}f_x + (4+\sqrt{2})f_y) \\ E((4+\sqrt{2})f_x - \sqrt{2}f_y \end{bmatrix}, \end{aligned}$$

$\kappa _1 = 2(1+\sqrt{2})(C^2 + E^2)$, and $\kappa _2 = 2(2+\sqrt{2})(C^2 + E^2)$ and the associated stresses $\sigma _{e}^{[k+1]} = E \epsilon _{e}^{[k+1]}$.

Now we recall the definition of the spectral radius of a matrix ${\mathbf {M}}\in \mathbb {R}^{n\times n}$ as

$$\begin{aligned} \rho ({\mathbf {M}}) = \max \big \{\, |\lambda _1 |, \ldots , |\lambda _n |\, \big \}. \end{aligned}$$

where $\lambda _1, \ldots , \lambda _n \in {\mathbb {C}}$ are the (in general complex) eigenvalues of ${\mathbf {M}}$. The theory of fixed-point schemes says [28] that the sequence $\{\varvec{\epsilon }^{[k]}\}_{k=0}^{\infty }$ generated by (28) converges if $\rho ({\mathbf {M}}) < 1$. Moreover, the smaller the spectral radius $\rho ({\mathbf {M}})$ is, the better the convergence rate. Using this theorem, we can prove that the iteration scheme (28) guarantees a convergent solution identical to the solution presented already at the end of Sect. 5.1.1. To this end, we first note that if there exists a fixed-point of (28), it must be the solution to the system $({\mathbf {M}}- {\mathbf {I}}) \varvec{\epsilon }+ {\mathbf {R}}= {\mathbf {0}}$. Solving this linear equation system immediately yields the solution presented above. Now there only remains the question whether there always exists a fixed point of (28). To examine this, we first compute the spectral radius $\rho ({\mathbf {M}})$ as

$$\begin{aligned} \rho ({\mathbf {M}}) = {\left\{ \begin{array}{ll} \displaystyle q_1(C):= \frac{E^2}{C^2 + E^2} \quad |C |< E,\\ \displaystyle q_2(C):= \frac{C^2}{C^2 + E^2} \quad |C |\ge E. \end{array}\right. } \end{aligned}$$

(29)

It is clear that $1/2\le \rho ({\mathbf {M}}) < 1$ for all $C \ne 0$ and thus a fixed-point is guaranteed. The scheme achieves the best convergence rate at $C = E$, where the spectral radius attains the smallest value $\rho ({\mathbf {M}}) = q_1 = q_2 = 1/2$. This is in excellent agreement with our above theoretical discussion where we argued that generally hyperparameters of the distance-minimizing method comparable to the tangent of the (in general hidden) constitutive manifold—which is here E—can be expected to yield the best convergence rate.

5.1.3 Numerical results

After having established by theoretical analysis that $C=E$ can be expected to be numerically optimal, we additionally tested different values for the hyperparameter C by solving the problem iteratively. As initial values, we used $\{\epsilon _{1}^{[0]}, \epsilon _{2}^{[0]}, \epsilon _{3}^{[0]}\} = \{-5\%, 5\%, 0\%\}$. The stopping criterion for the iterations was defined by (17) with $\delta = 10^{-10}$. The results are shown in Fig. 4.

Fig. 4

Convergence of the fixed-point scheme (28) for three values of the hyperparamter C. Note the different scale of the horizontal axis in the rightmost plot. For $C=E=1000$ the error decreases around 60 times faster compared to $C=0.1E = 100$ and $C=10E=10000$

Fig. 5

Convergence of the residual errors $R_{\sigma }^{[k]}$ and $R_{\epsilon }^{[k]}$ in the equilibrium equation and the compatibility condition. Fast convergence of both is observed only for $C=E=10^3$

In Fig. 4, we see that for $C = 10^3 = E$, the strains (and also the stresses) converge to the analytical solution solution around 60 times faster than for $C = 10^{2}$ or $C = 10^4$. These results strongly support our theoretical considerations and conclusions in Sect. 3. In particular, they illustrate the high importance of a proper choice of the hyperparameters in practical applications, where a difference in computation time by a factor of 60 is in many cases the difference between feasibility on the one hand and prohibitively high computational cost on the other hand.

To better understand the mechanism resulting in this substantial dependence of the number of iterations on the choice of the hyperparameters, it is instructive to examine the residual error $R_{\sigma }^{[k]}$ for the balance of linear momentum and the residual error $R_{\epsilon }^{[k]}$ for the compatibility condition. These are

$$\begin{aligned} R_{\sigma }^{[k]} = \sqrt{\big [R_{x}^{[k]} \big ]^2 + \big [R_{y}^{[k]}\big ]^2}, \quad R_{\epsilon }^{[k]} = \big |2\epsilon _1^{[k]} - \epsilon _{2}^{[k]} - \epsilon _{3}^{[k]} \big |,\nonumber \\ \end{aligned}$$

(30)

with

$$\begin{aligned} R_x^{[k]} = \frac{\sigma _1^{[k]}}{\sqrt{2}} + \sigma _{3}^{[k]} - f_x, \quad R_{y}^{[k]} = \frac{\sigma _1^{[k]}}{\sqrt{2}} + \sigma _2^{[k]} - f_y. \end{aligned}$$

In Sect. 3 we discussed that hyperparameter much larger or much smaller than the tangent stiffness would lead to a situation where either stress or strain is largely neglected during the minimization process so that it would take many iterations to reach a point where both is satisfactory. In (30) and Fig. 5 we see the underlying mechanism. If $C \ll E$, stress dominates the metric in (19). Therefore, the numerical scheme can quickly reduce error in stress, that is, the residual error $R_{\sigma }^{[k]}$ in the equilibrium equation. However, as strain is numerically neglected, our solution scheme is unsuccessful in reducing also the residual error $R_{\epsilon }^{[k]}$ of the compatibility equation, which does not depend on stress but only strain. By contrast, $C \gg E$ yields exactly the opposite situation.

5.1.4 Data-driven solution obtained by using various hyperparameters

We have proven that for the problem defined in Sect. 5.1.1 the distance-minimizing method converges to the correct solution. This is consistent with the theoretical analysis in [23] because a continuous constitutive law mimics the limit case where the number of material data points approaches infinity, thereby fully characterizing the constitutive law. However, it is important to note that convergence to the exact solution cannot necessarily be expected from the distance-minimizing method in case of a finite material data set. In this subsection we will demonstrate that if the hyperparameter C is chosen very different from the tangent of the (hidden) constitutive manifold, not only the convergence of the data-driven solution is slow (as shown in the previous sections) but that one requires also many more data to ensure that the limit of the convergence is close to the physically correct solution.

Assume that we have $N_\text {data}$ material data points such that $\mathrm {D}= \{(\epsilon _i,\sigma _i )\}_{i=1}^{N}$ samples the linear constitutive manifold (27) in the strain range $\Omega ^{\epsilon } = (-5\%, 5\%)$ with $N_\text {data} \in \{10^{j}+1, j = 2,3,4,5\}$ data points. The data points always included the point $(\epsilon , \sigma ) = (0, 0)$ to capture rigid body deformations, while the remaining data points uniformly sampled $\Omega ^{\epsilon }$. For these four different material data sets, we applied the data-driven solver with the three different hyperparameters $C \in \{20, 1000, 20000\}$. To measure convergence, we examined the error norm

$$\begin{aligned} \Vert \varvec{\epsilon }- \varvec{\epsilon }^{\text {ref}} \Vert = \Bigg [ \sum \limits _{i=1}^{3} ( \epsilon _{i} - \epsilon _{i}^\text {ref})^2\Bigg ]^{1/2} \end{aligned}$$

(31)

with the exact solution $\varvec{\epsilon }^{\text {ref}} = [\epsilon _{1}^{\text {ref}}, \epsilon _{2}^{\text {ref}}, \epsilon _{3}^{\text {ref}}]^{T}$.

In Fig. 6 we see that even with $10^{4}+1$ data points, the data-driven solutions obtained with $C \in \{20, 20000\}$ are still worse than the ones obtained with $C = 1000$ for $10^{2}+1$ data points. Additionally, for $C = 1000$ one can observe linear convergence with respect to the data size, while the convergence rate for $C \in \{20, 20000\}$ is clearly sub-linear. This demonstrates that a proper choice of the hyperparameters appears to accelerate—if the distance-minimizing method is applied—not only the numerical solution but to improve also its quality in case of a finite data set (which is in practice always the case).

Fig. 6

Convergence of data-driven solution with increasing number $N_{data}$ of material data points for three different hyperparameters C

Fig. 7

Convergence of the data-driven solution on noisy data with adaptive hyperparameters (circles) or constant hyperparameters (triangles). In the latter case, the hyperparameters were either fixed to $C = 1150$ (top) or $C = 100$ (bottom). In all cases the same set with $N_\text {data} = 1024$ material data points was used

5.1.5 Noisy data

In this subsection we test the effect of the hyperparameter adaptation introduced in Sect. 4. To this end, we slightly modify the three-truss problem introduced in Sect. 5.1.1 replacing the linear constitutive law (27) by a nonlinear constitutive law

$$\begin{aligned} \sigma = 50 \tanh (50 \epsilon ). \end{aligned}$$

(32)

The applied load is changed to $f_{x} = 45, f_{y} = -45$ and the exact solution can be shown to be $\epsilon _{1}^{\text {ref}} = 0$ and $\epsilon _{2,3}^{\text {ref}} = \pm \ln (19)/100$.

Fig. 8

Evolution of adaptive hyperparameters over the course of the iterations in the computations shown in Fig. 7 (bottom). The hyperparameters were always initialized as $C_j = 1150$ in the first step

Fig. 9

Planar system of trusses of unit length subject to vertical loading. The nodes at the left-most and right-most positions are fixed in both directions. Other bottom nodes are only vertically constrained. IDs of some trusses are shown in blue circles. (Color figure online)

Moreover, to mimic a more realistic situation, we generate material data with noise. To this end, we first generate a noise-free material data set $\widetilde{D} = \left\{ ({\widetilde{\epsilon }}_j, {\widetilde{\sigma }}_j)\right\} _{i=1}^N$ from the (hidden) constitutive law (32). Then we create from ${\widetilde{D}}$ a noisy material data set $D = \left\{ (\epsilon _j, \sigma _j)\right\} _{i=1}^N$, which we actually use for our computations and which is defined by

$$\begin{aligned} \sigma _j = (1 + r_j) {\widetilde{\sigma }}_j, \quad \epsilon _j = (1+r_j){\widetilde{\epsilon }}_j. \end{aligned}$$

with random numbers $r_j$ drawn from a uniform distribution in the interval $(-a, a)$. In Fig. 7 the results for three sets of material data with $a = 0, 2\%, 3\%$ are shown. To make a comparison with the original approach from [14], we first solved the problem with the same material data sets used there and with the fixed hyperparameter $C = 1150 = \frac{1}{3}\sum \nolimits _{j=1}^{3} C_{j}^{\text {ref}}$, where $C_{j}^{\text {ref}} = \{2500, 475, 475\}$. These $C_{j}^\text {ref}$ are the tangent stiffnesses of the truss elements at the state of the final solution, that is, $C_j^\text {ref} = 2500\,\mathrm {sech}^{2}(50 \epsilon _j^{\text {ref}})$. Therefore, the choice $C = 1150$ can be considered a particularly favorable choice in a situation where one generally relies on constant hyperparameters. Subsequently, we repeated the same computations with a less favorable choice of $C=100$. Finally, we repeated the computations again with adaptive hyperparameters, which we initialized one time as $C = 1150$ and another time as $C=100$. The adaptive hyperparameters were chosen among a finite set of 100 potential hyperparameters based on a division of the strain domain $(-5\%, 5\%)$ into 100 subdomains. The results of all these computations are illustrated in Figs. 7 and 8. Generally, the distance-minimizing method with adaptive hyperparameters performs never worse than with fixed hyperparameters. However, in case that the fixed hyperparameters are chosen close to the tangent of the hidden constitutive law in the state of the exact solution (top row in Fig. 7), the difference between adaptive hyperparameters and fixed hyperparameters is only small. Nevertheless, one has to keep in mind that in reality typically no such information about the tangent of the constitutive law is explicitly available. Therefore, in case of a nonlinear problem, fixed hyperparameters will typically be chosen far from the tangent of the constitutive law in the state of the final solution. This more realistic situation is illustrated in the second row of Fig. 7. There one indeed observes that the error obtained with our novel adaptive hyperparameter scheme is around one order of magnitude smaller than the one obtained with fixed hyperparameters. It is important to note that this holds even if we initialize the adaptive hyperparameter scheme with exactly the same value we use for the fixed hyperparameter scheme. The big advantage of the adaptive hyperparameter scheme is that an improper initialization is quickly resolved by the adaptation scheme as illustrated also in Fig. 8.

5.2 Multi-truss system

5.2.1 Problem setting

In this section, we deal with a planar multi-truss system consisting of $N_\text {elem} = 43$ truss elements and $N_\text {node} = 21$ nodes, as shown in Fig. 9. The trusses have unit length $L=1$. The top nodes are subject to a vertical load $F=40$ each. The constitutive law for all trusses is given by (32).

Fig. 10

a Data set $\mathrm {D}_{n+1}$ is generated from data set $\mathrm {D}_{n}$ by adding one additional data point in each strain interval; b Reference solution computed with nonlinear constitutive law and Newton-Raphson iterations (classical solution) versus data-driven solution with adaptive hyperparameters and 257 data points

Fig. 11

a Convergence of data-driven solution with adaptive (blue circles) and constant (orange triangles) hyperparameters as the material data set increases; b Number of iterations for the data-driven solution with constant and adaptive hyperparameters. (Color figure online)

5.2.2 Strategy of data enrichment and reference solution

Using this planar truss structure, we study the convergence of the data-driven solution as the amount of material data increases. To this end, we define a series of material data sets $\mathrm {D}_n$ such that $\mathrm {D}_{n} \subset \mathrm {D}_{n+1}$ and the material data are uniformly sampled in the strain domain $(-5\%, 5\%)$ by (32). A strategy of creating such data sets is illustrated in Fig. 10a and will be explained here. Assume that we currently have the data set $\mathrm {D}_n$ with the material data points given by

$$\begin{aligned} \sigma _{i}= & {} 50 \tanh \big [50 \big (-5/100\nonumber \\&+ i\cdot \Delta \epsilon ^{(n)}\big )\big ]\quad \forall i = 0, \ldots , N_n, \quad \text {where } \Delta \epsilon ^{(n)} = \frac{1}{10N_n},\nonumber \\ \end{aligned}$$

(33)

and $N_{n}$ is an even number. Then, the data set $\mathrm {D}_{n+1}$ is constructed by adding one additional strain in the center between each pair of neighboring strains in $\mathrm {D}_{n}$, see Fig. 10a. Subsequently, the corresponding stresses are computed using (32). Thus, $\Delta \epsilon ^{(n+1)} = \Delta \epsilon ^{(n)}/2$, and $N_{n+1} = 2 N_n$. No noise is considered in this section.

To obtain a reference solution for the distance-minimizing method, we first solved the above system in the classical fashion using the nonlinear finite element method where at each material point the nonlinear constitutive equation (32) was evaluated in an exact manner and the numerical solution was computed by Newton–Raphson iterations with a very low numerical tolerance to obtain a nearly exact solution.

The data-driven solution is obtained by the adaptive solver using a data set described as in (33). Figure 10b demonstrates that the data-driven solution agrees very well with the one obtained in the classical fashion already for a dataset of 257 data points.

5.2.3 Convergence of the data-driven solution with respect to the data size

In the following, the classically computed solution $\varvec{\epsilon }^{\text {C}} = \{\epsilon _{e}^\text {C}\}_{e=1}^{N_\text {elem}}$ is used as a reference solution in a convergence study of the data-driven solution $\varvec{\epsilon }^{\text {D}} = \{\epsilon _{e}^\text {D}\}_{e=1}^{N_\text {elem}}$. The distance between both is measured by the Euclidean norm

$$\begin{aligned} \big \Vert \varvec{\epsilon }^{\text {D}} - \varvec{\epsilon }^{\text {C}} \big \Vert = \bigg \{ \sum \limits _{e=1}^{N_\text {elem}} \big (\epsilon _{e}^{\text {D}} - \epsilon _{e}^{\text {C}} \big )^2 \bigg \}^{1/2}. \end{aligned}$$

(34)

The convergence of the data-driven solution with an increasing amount of material data is shown in Fig. 11a. We see that the adaptive hyperparameters give the linear convergence rate of the strain solution while the constant hyperparameters give sub-linear convergence rate. Figure 11b compares the performance of the distance-minimizing method with adaptive hyperparameters versus constant hyperparameters ($C = 2500$) in terms of the number of iterations. Apparently, the adaptive hyperparameters provide for the same amount of material data a much higher quality of the solution. Moreover, the number of iterations increases with an increasing number of material data points rapidly for constant hyperparameters but only very slowly for adaptive hyperparameters. This is a highly important feature for the practical application of the distance-minimizing method to ensure a feasible computational cost.

Fig. 12

Comparison of computation time for data-driven solver using constant hyperparameters (blue triangle), continuously updated hyperparameters (red circle), and hyperparameters computed with divide-and-conque strategy (black circle). (Color figure online)

5.2.4 Comparison of computational time

To demonstrate the benefits of the adaptive hyperparameter strategy, we measured the computation time of the data-driven solution with three different strategies: (i) constant hyperparameters, (ii) hyperparameters updated continuously with linear regression, (iii) hyperparameters computed using divide-and-conquer technique. The comparison of computational time is shown in Fig. 12. It is obvious that for all the three algorithms the computation time increases with the data size. However, the computation time for the solver using the strategy (i) is much lower than that of the strategy (ii). This is because the computational efforts for updating the hyperparameters by performing k-nearest-neighbor search and then linear regression are very large as compared to those for computing one entire iteration step in using the constant hyperparameters. By contrast, the computation time for strategy (iii) is much lower than for the other two strategies. The computational overhead for computing pre-defined hyperparameters is insignificant. This becomes especially clear when the number of finite elements, and hence the number of material points, increases as compared to the number of partitions of the strain domain $\Omega ^{\varvec{\epsilon }}$. In the divide-and-conquer strategy, the pre-defined hyperparameters are computed only once. Additionally, these hyperparameters are independent of the finite element mesh because it is only relevant how we partition the strain domain $\Omega ^{\varvec{\epsilon }}$. In contrast, if we do not apply the divide-and-conquer strategy, we must compute hyperparameters at every material point and in every fixed-point iteration. Henceforth, it is important to emphasize the necessity of the divide-and-conquer strategy as explained in Sect. 4.3.

5.3 Plane strain problem

In this section, we extend our scope from truss systems to problems of general continuum mechanics and demonstrate that the ideas and concepts introduced in this paper hold also there. To this end, we consider the two-dimensional continuum in plane strain condition that is illustrated together with its loading conditions in Fig. 13 (left). To solve this problem, the triangular mesh shown in Fig. 13 (right) was used with one quadrature point per element. It consists of $N_\text {element} = 1441$ triangular elements and 841 nodes. The mesh exhibits small elements around the circular holes to capture high stress concentration about the circular boundaries.

Fig. 13

Plane strain elasticity problem. The domain is composed of a unit square with three circular voids with the same radius $r = 0.12$. The two-dimensional solid is clamped at the left edge so that the displacement field ${\mathbf {u}} = (u_1, u_2)$ vanishes there and subject to the traction ${\mathbf {T}} = (3.0, 0)$ at the right edge. b Mesh with 1441 elements and 841 nodes will be used for all the subsequent simulations

Fig. 14

Number of iterations required to obtain the data-driven solution (left) and error convergence of the data-driven solution (right) for different ratios $\gamma$ between hyperparameters and tangent stiffness (in the load-free configuration) as well as adaptive hyperparameters. The legend for both subfigures is shown only on the right

To generate the material data for this example, we employed the constitutive law suggested by [17]. This law is constructed by combining a Neo-Hookean with a Saint-Venant material model [29], truncating strain terms of more than quadratic order. Its strain energy density is [17]

$$\begin{aligned} \psi (\varvec{\epsilon })= & {} \mu \big [ \mathrm {trace}(\varvec{\epsilon }) -\log \big [1 + \mathrm {trace}(\varvec{\epsilon })\big ] + \mathrm {trace}(\varvec{\epsilon }^2)\big ] \nonumber \\&+ \frac{\lambda }{2}\log ^2 \big [ 1 + \mathrm {trace}(\varvec{\epsilon }) \big ], \end{aligned}$$

(35)

where $\lambda = E\nu / [(1+\nu )(1-2\nu )]$ and $\mu = E/[2(1+\nu )]$ are the Lame parameters defined in terms of Young’s modulus E and Poisson’s ratio $\nu$. We assumed $E = 200$ and $\nu = 0.34$. We created four different data sets with increasing data size. To this end, the problem was first solved in a classical fashion with the analytical constitutive equation (35). Next, the maximum and minimum values of all the three strain components across all the quadrature points in the whole domain were identified. Finally, we generated a material data set sampling for each of these strain components the interval between the respective maximal and minimal strain value by $N_\text {data}^\text {1D} = 15 \times 2^{q}$ uniformly distributed data points, with $q = 0,1,2,3$. After that, also the reference solution $(\varvec{\epsilon }^\mathrm {ref}, \varvec{\sigma }^\mathrm {ref})$ at each quadrature point was added to the data set to enable the solver to find in principle at each point an exact solution. Altogether, this yielded a material data set of the size $N_\text {data}^{q} = (15 \times 2^{q})^{3} + N_\text {element}$. To examine role of the hyperparameters, we defined the hyperparameters for the data-driven solution as

$$\begin{aligned} {\mathbf {C}}_{e} = \gamma \frac{\partial ^2 \psi }{\partial \varvec{\epsilon }\partial \varvec{\epsilon }}(\varvec{\epsilon }= \mathbf {0}). \end{aligned}$$

(36)

That is, for $\gamma = 1$, the hyperparameters are equal to the tangent stiffness of the constitutive manifold in the stress-free condition. In addition to $\gamma =1$, we also tested $\gamma = 0.2$, $\gamma = 5$, and finally also the case where the hyperparameters were determined in each iteration step according to the adaptive scheme introduced in this paper. The results are shown in Fig. 14. Apparently, also in this two-dimensional problem the best numerical efficiency is reached for hyperparameters comparable to the tangent stiffness; see Fig. 14 (left). If the hyperparameters are much larger or much smaller, this increases the computational cost especially for a large material data set. As this example focuses on small strain elasticity, the tangent stiffness of the material in the unloaded configuration is a good approximation for the tangent stiffness in the loaded configuration. Therefore, it is not surprising that the number of iterations obtained with $\gamma = 1$ is similarly low as the one obtained with adaptive hyperparameters.

Figure 14 (right) shows the convergence of the strain vector error norm

$$\begin{aligned} \frac{\Vert \varvec{\epsilon }- \varvec{\epsilon }^\mathrm {ref} \Vert ^2}{\Vert \varvec{\epsilon }^\mathrm {{ref}} \Vert ^2 }= & {} \frac{\displaystyle \int _{\Omega } \left|\varvec{\epsilon }- \varvec{\epsilon }^\mathrm {ref} \right|^2 \,\mathrm {d}V}{ \displaystyle \int _{\Omega } \left|\varvec{\epsilon }^\mathrm {ref} \right|^2 \,\mathrm {d}V}\nonumber \\= & {} \frac{\displaystyle \int _{\Omega } \sum \nolimits _{i,j=1}^{2}( \epsilon _{ij} - \epsilon _{ij}^\mathrm {ref})^2 \,\mathrm {d}V}{\displaystyle \int _{\Omega } \sum \nolimits _{i,j=1}^{2} (\epsilon _{ij}^\mathrm {ref})^2 \,\mathrm {d}V}. \end{aligned}$$

(37)

where $\Omega$ is the domain of the two-dimensional continuum and |.| denotes a standard Euclidean vector norm. Interestingly, in terms of the strain error norm the solution obtained with adaptive hyperparameters does not only outperform the one obtained with poorly chosen hyperparameters ($\gamma = 0.2$ or $\gamma = 5$) but also—though to a much lesser extent—the one obtained with reasonably chosen ($\gamma =1$) but constant hyperparameters. As already seen from the comparison of computation time shown in Fig. 12 for the 2D truss system, it is reasonable to expect that the solver with adaptive hyperparameters (using the divide-and-conquer strategy) is more efficient than that with constant hyperparameters. However, the strategy of updating hyperparameters continuously with k-nearest-neighbor search and linear regressions should be avoided in general due to its excessive computational cost.

Fig. 15

Symmetric system of two trusses with equal cross section, which are aligned at an angle $\alpha$ relative to the horizontal direction

6 Conclusion

This work revisits the distance-minimizing method proposed by Kirchdoerfer and Ortiz [14] for data-driven boundary value problems in elasticity. Relying on the notion of the phase space of strain–stress states and its associated metric, the distance-minimizing method is formulated as a fixed-point iteration scheme. The distance-minimizing method was introduced in its original form with constant hyperparameters influencing the final data-driven solution. Herein, we demonstrated that setting these hyperparameters equal to the tangent of the hidden constitutive manifold can not only reduce the computational cost substantially but also improve the accuracy of the solution finally obtained. As the tangent of the hidden constitutive manifold is a priori not known in most cases, we proposed a computational approach in which the hyperparameters are updated after each iteration in the fixed-point scheme. To ensure computational efficiency, the hyperparameters are allowed to vary only within a finite set constructed by combining linear regressions and a divide-and-conquer strategy. In the process of adapting hyperparameters based on estimating the constitutive tangents of the hidden constitutive manifold, we have subtly based our data-driven framework on a sort of de-facto constitutive model, although one that is particularly robust against noise in the material data. Using several examples, we demonstrated the favorable numerical properties of this adaptive hyperparameter scheme, which can substantially reduce computational cost and improve accuracy compared to classical approaches with fixed hyperparameters. While we have presented above ample numerical evidence for our concept, we have not yet succeeded in supporting it by a rigorous mathematical proof for general cases. In Sect. 5.1.2 we presented such a proof for our ideas for a specific application example. This proof relied on the concept of the spectral radius. Unfortunately, we found in lengthy analyses that this type of proof can most likely not be extended in a way that captures also the most general case. Indeed, when working on such an extension, we found that there exist degenerate cases such as the one illustrated in Fig. 15 where the spectral radius does not become minimal if the hyperparameters are equal to the tangent of the hidden constitutive manifold but rather for zero hyperparameters. Interestingly, all such degenerate cases that we could construct also had the property that their special structure implied that the data-driven solution could be obtained in a single iteration step regardless of the hyperparameters. Therefore, although in these cases zero hyperparameters yielded the smallest spectral radius, they did in the end not lead to a faster convergence or more accurate solution than hyperparameters equal to the tangent of the constitutive manifold. Hence, these (rare and very special) cases are by no means in contradiction to the general ideas we presented in this paper. However, they yet reveal that developing a general mathematical proof for these ideas may require mathematically more advanced concepts than the one of the spectral radius. The identification and development of such concepts may form an interesting avenue of future research.