1 Introduction

Monitoring soil moisture in the vadose zone is crucial for weather forecasts (Ni-Meister et al. 2005), predicting natural disaster (Tohari et al. 2007), evaluating contaminant transport (Murdoch 2000), agriculture (Shaxson and Barber 2003), and many other societal needs.

The techniques of monitoring soil moisture can be divided into four main classes, and they are space-borne sensors, air-borne sensors, wireless sensor networks, and ground-based sensors (Vereecken et al. 2008). Tomographic ground penetrating radar (GPR) are superior to other approaches in the class of ground-based sensors, usually due to practical reasons. GPR does not provide the most accurate soil moisture measurement compared to some conventional sensors (e.g., gravimetric, frequency- and time-domain reflectometry (FDR and TDR), neutron probe and capacitance probe techniques), but in practice, it is very time-consuming to capture the spatial variability of soil moisture by using large numbers of closely spaced conventional sensors/probes. Moreover, conventional soil moisture measurement techniques at small scales are invasive and provide limited spatial coverage. GPR is a great practical choice given its spatial coverage, resolution, and efficiency. Based on the assumptions that GPR travel-times are closely related to dielectric permittivity distribution in the vadose zone, and that the dielectric permittivity is mainly determined by the soil moisture (Lunt et al. 2005), tomographic GPR data can be used to infer soil moisture (Moysey et al. 2003; Tsai et al. 2015). Tomographic GPR can provide centimeters to meters spatial resolution (Vereecken et al. 2008), sub-daily temporal resolution, and meanwhile is minimally invasive to the study site. In addition, through time-lapse and/or joint inversion, tomographic GPR has the capability for long-term monitoring of spatial distribution of soil moisture within the vadose zone (Binley et al. 2002; Hubbard et al. 1997), and for deriving other spatially heterogeneous soil physical properties (e.g., permeability and porosity) (Binley et al. 2002; Chen et al. 2001; Clement and Barrash 2006; Dubreuil-Boisclair et al. 2011; Hubbard et al. 1997, 2001; Kowalsky et al. 2004, 2005).

Interpreted tomographic GPR images of soil moisture from tomograms are subject to great uncertainty due to ill-conditioned nature of the inverse problem, non-uniqueness of solutions, variable spatial resolutions, and measurement errors. For example, variation in resolution within a tomogram makes pixel-specific inference of petrophysical properties uncertain. Regularization or smoothing among large number of possible solutions can stabilize solutions, but the inversion results usually overestimate the size but underestimate the magnitude of subsurface anomalies, and the true correlation structure is normally under represented (Day-Lewis 2004).

Inverting geophysical data can be done deterministically or stochastically. Deterministic approaches, such as least-square optimization, are computationally efficient, but are not able to accurately quantify uncertainties associated with the inversion, except under simplifying assumptions such as Gaussian likelihoods and linear models which have ellipsoid confidence intervals on the inferred parameters. Alternatively, data can be inverted within a stochastic framework wherein parameters are represented in a probabilistic manner. For example, Bayesian inference derives the posterior probability as a consequence of two antecedents, a prior probability and a “likelihood function” derived from a statistical model for the observed data, where parameters retain their probabilistic structure throughout inversion process and can be updated quantitatively when new data is available(Chen and Rubin 2003; Chen et al. 2008; Copty et al. 1993; Dubreuil-Boisclair et al. 2011; Hou and Rubin 2005; Hou et al. 2006; Hubbard et al. 2001; Kowalsky et al. 2004, 2005; Lehikoinen et al. 2010). The parameters are therefore estimated with uncertainty, which can be reduced continuously as more data/information are integrated or a more accurate inverse problem is formulated.

A Bayesian formulation of an inverse problem (as we adopted in this study) leads to an arbitrary expression for a probability density function (PDF), in terms of the parameters/quantities being estimated via the inverse problem. The PDF can be realized by sampling from it, using a method such as Markov chain Monte Carlo (MCMC). MCMC (Liang et al. 2010; Silva et al. 2017) methods describe a random walk in the parameter space, with each step in the walk being evaluated by a model (called the forward problem; in our case an GPR model) to gauge the quality of a new parameter proposal. Because most random steps are rejected, MCMC is computationally very expensive for finding sufficient number of samples to recover the PDF. The sufficiency of samples can be gauged by the Raftery–Lewis method (Raftery and Lewis 1996) or the Brooks–Gelman–Rubin method (Brooks and Gelman 1998). In order to improve the efficiency of sampling, adaptive MCMC methods e.g., Delayed Rejection Adaptive Metropolis (DRAM) (Haario et al. 2006) seeks to use previously accepted samples to identify an optimal subspace where proposals have a better chance of being accepted. As a further step to reduce computational time, multi-chain i.e., parallel MCMC methods have been developed, such as a parallel version of adaptive Metropolis (Solonen et al. 2012).

MCMC methods have been used to reconstruct soil-moisture content and/or other related soil physical properties using cross-hole GPR measurements. All such studies have two components in common that determine the quality of the reconstructions—the spatial parameterization for the spatially variable soil-moisture field (also called the random field model (RFM), whose parameters are the target of inference from GPR first-arrival-travel time measurements) and the MCMC algorithm that estimates the RFM’s parameters as a high-dimensional PDF. In Chen et al. (2004), the authors used GPR measurements and a Gibbs sampler to infer iron concentration at the South Oyster site, where soil is a mixture of sand and mud. The field was modeled as a grid where an indicator denoted whether a grid-cell was sand or mud (the lithofacies). Probabilistic linear models were used to relate the lithofacies to the electromagnetic (EM) attenuation; the attenuation and lithofacies were related to iron concentrations using yet another mixed linear model. A Gibbs sampler was used to sample the lithofacies field, attenuation, and iron concentration, conditional on cross-hole GPR data. In the work by Laloy et al. (2012), the authors developed a method for reducing the dimensionality of the random field model and inferred the water tracer distribution field using GPR data. A low dimensional parameterization for the moisture field was developed in terms of orthogonal (Legendre) moments of the water tracer field being estimated. Known constraints e.g., mass of water injected could be exactly satisfied in such a formulation. Linde and Vrugt (2013) developed three alternative formulations of a random field model to infer a field of EM transmission speeds using cross-hole GPR data. A water plume was the object of the imaging effort. They clearly distinguished between the mesh on which the EM ray-tracing eikonal equation was solved, i.e., where soil-moisture was described, and the far coarser mesh on which the quantity of interest (the EM velocity) was inferred. The best reconstructions were obtained using a relatively coarse 4 × 4 mesh field model that allowed an explicit retention of large length scales that could be informed by the GPR data and was also sufficiently low dimensional that the uncertainty bounds on the 16 parameters inferred were small. A 10 × 10 mesh, on the other hand, yielded the worst reconstruction since it had a high dimensionality, and had no way of disallowing very small length scales. More abstractly, this paper is about estimating a spatially variable field from indirect and limited observations. In geophysics, the field is often modeled by a multivariate Gaussian (mG) distribution, described by a covariance function. The true field is supposed to be a realization drawn from the distribution. Since the limited observations do not allow one to identify the correct realization, one reconstructs it approximately i.e., by drawing samples that explain the observations, given an error model. The sampling is often done using MCMC. Pioneering work has been done using MCMC for inversion of high dimensional problems (Hunziker et al. 2017; Jimenez et al. 2016; Laloy et al. 2015; Romary 2009; Rubin et al. 2010). These approaches have been successfully applied to solve various synthetic and real case inversion problems (Mara et al. 2016; Zanini and Kitanidis 2008). This study built upon these pioneering work and proposed an approach that is effective and efficient for real-time inverting and monitoring relative dielectric permittivity field.

In this paper, we study the inversion of a relative dielectric permittivity field using synthetic, first-arrival-travel time GPR data between multiple sources and receivers. We use a RFM based on the pilot point method, where relative dielectric permittivity is defined at a small set of points and a field in the domain of interest is created using a multi-variate Gaussian model. The correlation range of the variogram and the relative dielectric permittivity values at the pilot point are inferred using a parallel MCMC AM (Adaptive Metropolis). Our initial tests with DRAM revealed that Delayed Rejection did not contribute much to performance but slightly slowed down computational speed, leading us to turn it off in the DRAM algorithm (and thus retaining just AM).

Our paper introduces two novelties. The first is the use of the pilot point method as a RFM in an MCMC setting. Unlike (Laloy et al. 2012), we neither have a constraint to impose, nor do we require one to obtain a successful inversion. Unlike (Linde and Vrugt 2013), our method does not require the use of multiple meshes. However, it does face the issue of constructing a RFM of an appropriate sophistication/flexibility; this is equivalent to their search for the correct mesh resolution (4 × 4 versus 10 × 10). Laloy et al. (2015) and Hunziker et al. (2017) used geostatistical parameters, such as mean, variance, field smoothness, integral scale, and so on, to control the RFM, which significantly reduce the dimensions of the inversion problem. The method was successfully demonstrated for estimating the conductivity and permittivity fields. However, there are some cases where the stochastic field maybe hard to be described by the geostatistical parameters, such as layered structure. For example, the permittivity is mainly affected by soil moisture, which is usually dynamic rather than a “permanent” property of the subsurface domain. The permittivity field could be a layered structure or has gathered wet and dry zones, due to precipitation or other external forcing. Additionally, for a small area, it can be hard to get a reliable geostatistical parameter (Hunziker et al. 2017). Using pilot points to control RFM, as proposed in this study, is expected to help deal with the gathered zone or layered structure cases. Rubin et al. (2010) used the pilot point concept to control the stochastic field, but the approach requires direct measurements at the pilot points. Our proposed approach does not require direct permittivity measurements at the pilot points, and is integrated with multi-chain MCMC design, which is more feasible for efficient inversion and monitoring of changes of permittivity field. Jimenez et al. (2016) applied the pilot point concept as well, but the reference field was a deterministic field. Romary’s model (Romary 2009) used truncated Karhunen–Loeve expansion (Loeve 1955), which is effective for dimension reduction, but the approach usually leads to inverted fields smoother than the true case. Another novelty introduced in this paper is a procedure for configuring the RFM (i.e., devising its complexity) commensurate with observations, by exploiting the probabilistic inferences (obtained using MCMC) while varying the quality and quantity of observations and the dimensionality of the RFM. Thus our method requires an MCMC formulation that can accommodate the high dimensionality of the inverse problem (due to the number of parameters in the RFM) and a moderately expensive forward problem.

2 Methodology

2.1 Tomographic GPR and the forward model

Tomographic GPR transmits an EM pulse from a source in one borehole and recording the arrival of EM energy at a receiver position in a separate borehole. The source and receiver vertical locations are varied in the boreholes to collect a suite of data of signal arrival times and magnitude for various source-receiver pairs.

Inversion of the first-arrival-times of the EM signal is used to estimate the velocity, which is assumed to be closely related to the dielectric permittivity (\( \epsilon \)) distribution between the boreholes. For convenience, the dielectric permittivity is normalized by the speed of light in vacuum (\( c = 0.3 \) m/ns), and is called the relative dielectric permittivity (\( \epsilon_{r} \)). For high frequency GPR signals (~ 50–1000 MHz) and in low-loss environments (non-magnetic, low electrical conductivity), the relative dielectric permittivity (\( \epsilon_{r} \)) can be related to EM wave propagation velocity (\( v \)) by:

$$ \epsilon_{r} = \left( {\frac{c}{v}} \right)^{2} , $$
(1)

(Davis and Annan 1989). Since we are interested in the spatial variation of dielectric permittivity, which depends on the EM velocity spatial variation, the subsurface domain of interests is discretized into n grid blocks with velocities \( v_{1} , \ldots ,v_{n} \). The travel time data can be simulation with a forward model (\( \varvec{G} \)) that describes the propagation path (distance) travelled by the EM signal:

$$ \varvec{G}\left( \varvec{v} \right) = \varvec{t}\text{,} $$
(2)

where \( \varvec{v} \) is a vector of the velocities of the grid blocks, and \( \varvec{t} \) represents the vector of measured travel times. The relative dielectric permittivity (\( \epsilon_{r} \)) can be converted to the soil moisture according the the empirical relationship derived from the experiment measurements (Behari 2005; Mohan et al. 2015). Note that, the relationship between \( \epsilon_{r} \) and moisture is not identical, and may involve some uncertainties.

The GPR forward model (\( \varvec{G} \)) can be full-waveform methods, which directly solve Maxwell’s equations (Casper and Kung 1996; Kowalsky et al. 2001; Vasco et al. 1997) or ray-based methods (Cai and Mcmechan 1995; Peterson 2001; Zhang et al. 2005), which simplify and discretize the travel time between source and receiver as:

$$ t = \mathop \sum \limits_{i = 1}^{n} \frac{{d_{i} }}{{v_{i} }}, $$
(3)

where \( d_{i} \) is the distance travelled by the ray through the ith grid block. If the variation of EM signal velocity is small, such as smaller than 10% (Day-Lewis 2005), the straight-ray paths are assumed. Typically, solutions to model parameters (the grid blocks) are in terms of slowness, and can be approximated via iterative techniques like the algebraic reconstruction techniques (ART) (Peterson 2001; Peterson et al. 1985) or the simultaneous iterative reconstruction technique (SIRT) (Dines and Lytle 1979). However, when significant heterogeneity is expected, curved-ray methods that account for physically realistic ray trajectories including reflection and refraction phenomena should be used. The first-arrival-travel time through realistic bended path for 2-D or 3-D velocity problem is usually solved by finding the finite-difference (FD) approximation to the eikonal equation,

$$ \left( {\frac{\partial t}{\partial x}} \right)^{2} + \left( {\frac{\partial t}{\partial y}} \right)^{2} + \left( {\frac{\partial t}{\partial z}} \right)^{2} = S^{2} , $$
(4)

which was introduced by Reshef and Kosloff (1986) and Vidale (1988, 1990). \( t \) is the travel time from source to the spatial Cartesian coordinates \( x \), \( y \), and \( z \). \( S \) is the slowness at position \( x \), \( y \), and \( z \). The eikonal equation can be numerically solved by fast sweeping method (Tsai et al. 2003; Zhao 2005).

2.2 Pilot point concept

Considering the limited amount of observations and computational resources, it is very challenging to directly invert the dielectric permittivity and its probability distribution at every grid point, for a high resolution discretized 2-D or 3-D vadose zone. This is because the zone may be discretized by thousands of grid points. Pilot points and regularization can be used as an adjunct to geostatistics-based stochastic parameterization methods (Certes and Marsily 1991; Doherty 2003; Venue and Marsily 2001), which can significantly reduce the dimensionality of the inverse problem. With the assumption that a realistic dielectric permittivity field is not completely random and independent at every grid point, the field usually can be constrained by a few pilot points and spatial correlation range, and the permittivity at the grid points other than the pilot points can be estimated by sequential Gaussian simulation (SGSIM) algorithm (Deutsch and Journel 1998).

2.3 Multi-chain MCMC framework

A multi-chain MCMC framework (Solonen et al. 2012) is used to generate posterior distributions on model parameters, given experimental data and a prior distribution on model parameters. It also requires a presumed probabilistic relationship between experimental data and model output called the likelihood function. Then, by Bayes formula:

$$ \pi \left( {\theta |d} \right) \propto \pi \left( \theta \right)L\left( {d|\theta } \right) , $$
(5)

where \( \pi \left( {\theta |d} \right) \) is posterior parameter distribution, \( \pi \left( \theta \right) \) is prior parameter distribution, and \( L\left( {d|\theta } \right) \) is likelihood function. \( \theta \) represents model parameters, and \( d = \left\{ {d_{k} } \right\}, \quad k = 1, \ldots ,K, \) is the vector of observed data is the observed data. The observed data is assumed to be the summation of model output and an error, which is a composite of measurement errors and the forward model’s shortcomings:

$$ d = G\left( \theta \right) + \varepsilon , $$
(6)

where \( G\left( \theta \right) = \left\{ {G_{k} \left( \theta \right)} \right\},\quad k = 1 , \ldots ,K, \) are predictions from a forward model, and \( \varepsilon \) is error, which are assumed to be independent, zero mean Gaussian random variables with variance \( \sigma^{2} \). Hence, the likelihood is defined as:

$$ L\left( {d | \theta , \sigma^{2} } \right) = \mathop \prod \limits_{k = 1}^{K} \frac{1}{{\sigma \sqrt {2\pi } }}exp\left[ { - \frac{{\left\{ {\left( {d_{k} - G_{k} \left( \theta \right)} \right) / d_{k} } \right\}^{2} }}{{2\sigma^{2} }}} \right] $$
(7)

where the subscript \( k \) stands for the index of the observation, and runs from 1 to \( K \). Note that the likelihood function can base on either the absolute error (\( d_{k} - G_{k} \left( \theta \right) \)) or the relative error (\( \left( {d_{k} - G_{k} \left( \theta \right)} \right) / d_{k} \)). The absolute error may bias the likelihood towards larger values of \( d_{k} \), if the observations show a wide range of values. Therefore, the relative error is used, which provides more stable evaluation of the error for the likelihood function in this study. MCMC generates a chain of the parameters in sequence, whose probability density approximates the posterior distribution. Our method (Adaptive Metropolis) employs Metropolis–Hastings sampling. It first samples a candidate \( Y \) from the proposal density function \( q\left( {Y|\theta_{i} } \right) \), performs a model run to obtain the model prediction \( G\left( Y \right) \) and obtains the likelihood L(d|Y). It then calculates the acceptance ratio as

$$ \alpha \left( {\theta_{i} ,Y} \right) = min\left[ {1,\frac{{L\left( {d |Y} \right)\pi \left( Y \right)q\left( {Y|\theta_{i} } \right)}}{{L\left( {d |\theta_{i} } \right)\pi \left( {\theta_{i} } \right)q\left( {\theta_{i} |Y} \right)}}} \right]. $$
(8)

If \( \alpha \left( {\theta_{i} ,Y} \right) > z, z \sim{\text{U}}\left[ {0, 1} \right] \), then the new sample is \( \theta_{i + 1} = Y \), else the new sample is \( \theta_{i + 1} = \theta_{i} \). U[a, b] denotes a uniform distribution between a and b. MCMC usually requires more than 10,000 evaluations of the forward simulation model, which can be very expensive. With increase of the dimension of the parameter space, the requirement of number of the forward simulation evaluation may increase rapidly, which may reach 100,000 to 1,000,000. This cost is amortized over multiple chains as mentioned in the previous section. Note that the proposal density \( q (: | :) \) can be any distribution, including an asymmetric one (such as a log-normal). In such a case, to preserve detailed balance [see Chapter 1, (Gilks et al. 1996)], the proposal density appears in numerator and denominator of the expression for \( \alpha \). In our case, where we use a normal distribution (a symmetric distribution), the numerator and denominator cancel out and the expression for \( \alpha \) does not have \( q (: | :) \) in it actually.

In this study, MCMC proposes candidate input parameters such as dielectric permittivity at pilot point locations and spatial correlation range. The input parameters are then used to generate a candidate random dielectric permittivity (\( \epsilon_{r} \)) field by the SGSIM algorithm. The first-arrival-travel time between every source and receiver is computed by numerically solving the eikonal equation (Eq. 4), with slowness \( S = \frac{{\sqrt {\epsilon_{r} } }}{c} \). The estimated first-arrival-travel time for the candidate \( \epsilon_{r} \) field is compared to the observations, and the likelihood function is calculated using Eq. (7). Once the likelihood function is evaluated, the candidate input parameters are accepted or rejected via Eq. (8). This process is called the Metropolis–Hastings sampler.

The actual inference technique is slightly different as we infer \( \left\{ {\theta , \sigma^{2} } \right\} \) from the data. Thus Eq. (5) is restated as

$$ \pi \left( {\theta , \sigma^{2} |d} \right) \propto \pi \left( \theta \right)\pi \left( {\sigma^{ - 2} } \right)L\left( {d|\theta , \sigma^{2} } \right), $$
(9)

where we have included a prior for \( \sigma^{ - 2} \). The prior is an inverse Gamma prior i.e.

$$ \sigma^{ - 2} \sim \Gamma \left( {\alpha , \beta } \right) , $$
(10)

where \( \alpha = 1 \) and \( \beta = 10^{ - 6} \) are the shape and rate parameters of the Gamma distribution. This particular set of parameters makes our prior belief for \( \sigma^{ - 2} \) resemble \( {\text{U}}\left( {0, \infty } \right) \). The inverse Gamma prior is a conjugate prior, i.e., given a \( \theta \), a realization of \( \sigma^{ - 2} \) can be sampled as

$$ \sigma^{ - 2} \sim \Gamma \left( {\alpha + \frac{K}{2}, \beta + \frac{1}{2}\mathop \sum \limits_{k} \left\{ {\left( {d_{k} - G_{k} \left( \theta \right)} \right) / d_{k} } \right\}^{2} } \right). $$
(11)

This is called Gibbs sampling. Thus, in a given MCMC iteration, we obtain a realization of \( \theta \) first using Metropolis–Hastings, and then a sample of \( \sigma^{2} \), conditional on the previously selected \( \theta \), using Gibbs sampling. This yields a chain of \( \left\{ {\theta , \sigma^{2} } \right\} \) samples from which construct a joint probability density function (PDF) for the model parameters and the estimate for the model—data misfit. The entire construction is called a Metropolis-within-Gibbs sampling.

The sampling algorithm is described in Solonen et al. (2012). We start M MCMC chains which execute an adaptive Metropolis sampler, as described in Haario and Saksman (2001). Essentially, we describe a random walk that executes the Metropolis-within-Gibbs sampler described above. However, periodically, we use the samples collected by the chain to update the multivariate Gaussian proposal distribution \( q (: | :) \), so that the proposal distribution resembles the posterior distribution and thus provides good \( \theta \) candidates that have a higher chance of being accepted. This updating of \( q (: | :) \) can be done incrementally, using samples collected since the previous update.

In the multichain case, each chain collects samples from all the chains to perform the periodic update of its \( q (: | :) \). Thus each chain has the same proposal distribution, but informed by samples collected by all the chains. It provides a global view of the posterior distribution. Thereafter, the chains continue their independent exploration of the parameter space till the next update of \( q (: | :) \). At the end of the sampling run, each chain writes out the samples it collects to a file. The convergence of the MCMC was assessed by pooling the samples together and computing certain quantiles of the objects of interest. We performed this repeatedly by letting the chains proceed for increasingly more iterations and stopping when quantiles converge.

3 Synthetic experiment

Figure 1a shows the synthetic relative dielectric permittivity field between two boreholes generated using SGSIM, and is considered as the true field in this study. The study area is 4 m wide and 15 m deep. The true \( \epsilon_{r} \) field is created using a pilot point method using 8 pilot points and a variogram that has a range of 2 and 20 meters in the vertical and horizontal directions respectively. The base case considers 30 equally spaced source locations on the left side of the field (x = 0 m), and for each source location, GPR arrival time data is collected at 30 evenly spaced receiver locations on the right side of the field (x = 4 m) for a total of 900 observations. The forward GPR model computes the 900 first-arrival-travel times as shown in Fig. 1b, which are considered to be the observational data. The symbols “+” and numbers in Fig. 1a indicate the positions and indices of 24 pilot points. Pilot points 1–8 are the ones used to generate the true \( \epsilon_{r} \) field. Table 1 lists the position and true values of relative dielectric permittivity at the 24 pilot points. In Sect. 4, we examine the effects of the amount of noise in the observations, the number of sources and receivers, and the number of pilot points on the inversion results, with a view of identifying the most appropriate RFM.

Fig. 1
figure 1

Synthetic Data: a Relative dielectric permittivity of the synthetic field, where the symbols “+” and numbers indicate the positions and indices of the 24 pilot points; b Forward GPR simulated first-arrival travel times between the sources and receivers for the synthetic field

Full size image
Table 1 Position and relative dielectric permittivity for the 24 pilot points
Full size table

4 Results

Below we explore the usefulness of parallel MCMC in inverting the \( \epsilon_{r} \) field. We shall model the \( \epsilon_{r} \) field using multivariate Gaussians placed at the first 8 pilot points. The Gaussians are governed by the same variogram, whose range is also estimated from the \( \epsilon_{r} \) field data. Thus our RFM contains nine parameters including \( \epsilon_{r} \) at 8 pilot points and the variogram’s correlation range. They are treated as random variables in our statistical formulation of the inverse problem and their nine-dimensional joint PDF is inferred via MCMC. Although the same forward model is used for generation of the synthetic true field and MCMC inversion, there is still model-form error, as we use SGSIM, a stochastic generator of relative permittivity fields. It means that even if we use the same parameter values as the true case in the forward model, we will not reproduce the exact relative permittivity field or measurements as the true case. In other word, the MCMC inversion in this studied case is not an “inverse crime”. A more detailed explanation is in Sect. 4.1.

4.1 Inversions with observations with 2% noise (the base case)

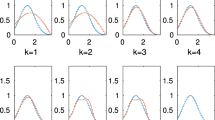
As a first step, we solve the inverse problem with 2% noise and limited observations. 30 sources and 30 receivers are used to calculate the first-arrival-travel time to compare against the 900 observations, as shown in Fig. 1b. In this study, we assume the horizontal correlation range of the variogram is 10 times larger than the vertical one. Prior distributions for relative dielectric permittivity at the pilot points is U[4, 18] and U[1, 3] for the correlation range. 20 MCMC chains were used, and Fig. 2 shows the posterior density distribution after 50,000 iterations per chain i.e., a total of 1 million parameters samples were explored for constructing the posterior density distribution. The red vertical lines are the true value. The density distributions show convergences to the true values for all the parameters except for the parameter spatial correlation range, although its distribution does encapsulate the true value. A possible reason is that the locations of the 8 pilot points already impose a length-scale for the \( \epsilon_{r} \) field, which may conflict with the 9th parameter (spatial correlation range). Further, there is no consistent over- or underestimation of \( \epsilon_{r} \) at the 8 pilot points. The MAP (maximum a posteriori) estimate for \( \epsilon_{r} \) i.e., the peak of the marginalized PDF, at pilot points 4 and 7 are overestimates, whereas \( \epsilon_{r} \) at pilot point 8 and the correlation range are underestimated. There is no substantial difference in the MAP estimates and true values for the rest of the parameters. Thus our formulation and implementation seem to be correct and do not introduce bias in the results. In this study, as mentioned in Sect. 3, the permittivity field covers 4 m by 15 m area, and is discretized into a 20 X 75 grid (1500 points total). The permittivity value on each point is calculated by sequential Gaussian simulation (SGSIM) algorithm (Deutsch and Journel 1998), which internally depends on a random number generator. SGSIM takes as its inputs the permittivity values at the pilot points, as well as the variogram for a multiGaussian distribution, and outputs a realization that serves as the permittivity field. For commonly used random number generator, an integer number is used as random seed (or seed state, or seed) for initializing a “pseudorandom” number generation. With a fixed random seed, the random number generator can always give the same random numbers series, which will provide the same permittivity field with given value at pilot points and correlation range. Figure 3 shows the results for an inversion test case with a fixed random seed, which is the same as the one used for the generation of the true field. The posterior distribution is very sharp and almost collapses to the true model parameters’ values (2% noise is added to the observations, which leads to a slightly imperfect collapse). The posterior distribution of the correlation range is wide, since the pilot points’ permittivity values partially constrain the correlation range.

Fig. 2
figure 2

Posterior density distributions for the base case (2% noise)

Full size image
Fig. 3
figure 3

Posterior density distributions for the base case (2% noise), and random seed same as the one used for generating the synthetic true case. This serves as a check for the MCMC method i.e., when we commit an inverse crime, our PDFs should be very sharp

Full size image

However, in this study, the random seed are deemed unknown, similar to a real inversion problem. The random seed cannot be calibrated as the relationship between random seed and generated random number series is chaotic. In summary, the generation of the true case/field is not repeatable if the random seed is unknown. Figure 4 shows an simple example to demonstrate how the random seed affects the posterior distribution. In this simple example, all the true values for the 8 pilot points and the parameter spatial correlation range are used to generate the stochastic field through SGSIM, but without knowing the random seed, there can be infinite number of the stochastic fields that look different from each other. All these stochastic fields can be used to calculate the travel time, and the travel times for the fields would be different from each other as well. The root-mean-square errors (RMSEs) between the computed travel times for the stochastic fields and the travel time calculated from the synthetic true field can be evaluated. The red line in Fig. 4 shows the distribution of the RMSEs for 1000 stochastic fields, which are all generated through SGSIM using true values of the pilot points and the parameter spatial correlation range. As a comparison, the blue line in Fig. 4 shows the distribution of the RMSEs of the 1000 fields where the pilot point 1 is 10% bigger than the true value (Keeping all other parameters the same as true case, only changing pilot point 1). Similar evaluations were done by increasing the pilot point 1 to be 25% and 50% bigger than the true value, shown as the green and black lines, respectively. There are obvious overlaps among these distributions, such as the pink shadow area indicating the overlap between the case with all true values (red line), and the case with the pilot point #1 to be 50% higher than the true value (black line). This represents the possibility that biased pilot points may yield a better-performing stochastic field than the stochastic field(s) generated with all the true values, although this possibility is only 5% (the pink shadow area in Fig. 4) in the example. Such possibilities are 42 and 23% respectively, when the pilot point 1 is 110 and 125% of the true value. This is the reason why the posterior does not perfectly collapse to the true value (the red line would stack at zero in that case). Please note that the values of the possibilities listed here are only for this simple example. Summarily, since we let the random seed to vary during MCMC iterations, it causes the posterior distribution to be wide, as shown in Fig. 2.

Fig. 4
figure 4

RMSE distribution for the simple example demonstrating the effects of random seed on the posterior distribution

Full size image

Figure 5 shows the convergence of the posteriors for the base case. Because there are one million data points for each parameter, it is difficult to check the convergence through the trajectories. Hence, the boxplot is used to show the convergence of the quantiles of the posteriors distributions. After about 20,000 iteration (totally 400,000 samples for 20 chains), the posteriors converged.

Fig. 5
figure 5

The convergence of the posterior distribution with number of MCMC iterations

Full size image

4.2 Inversions with different level of noise in observation

In practice, observations are noisy; they affect the quality of the inferences and the sophistication of the RFM that can be used with them. Here we investigate the impact of noisy observations on the inferred permittivity field. We do so by varying the noise added to observations. The noise is modeled as a normal distribution, with mean set to 0 and the standard deviation defined as a percentage of the average (true) observation. 4 cases were investigated with the noise standard deviation set to 2, 5, 10, and 15 percent of the mean of the synthetic true observation. The number of the sources and receivers is kept at 30. The results are based on 20 chains, each executing 50,000 iterations. The mean of the true, noiseless observations is 0.0765 (µs), and the standard deviation is 0.030025 (µs). Table 2 lists the standard deviation of the noise and the ratio of noise standard deviation over observation standard deviation.

Table 2 Standard deviation of the noise and the ratio of noise standard deviation over observation standard deviation
Full size table

Figure 6 shows the boxplots for the inferred permittivities and correlation range, as a function of the standard deviation of the noise added to observations. The horizontal red lines are the true value for the 8 pilot points and the correlation range. The horizontal axis of each plot shows the magnitude of the noise. When the noise’s standard deviation is smaller than 10% of the observations’ mean, the proposed approach captures the true values within the interquartile range (IQR) of the samples produced by MCMC. At noise levels of about 15%, the inversion is destabilized i.e., the information content in the observations is sufficiently masked that they can no longer constrain the nine-dimensional RFM with no model form error.

Fig. 6
figure 6

Boxplots for the noise magnitude study. The boxes show the IQRs of the MCMC posterior samples of the relative dielectric permittivity at the 8 pilot points and variogram range. The black horizontal line is the median of the MCMC samples and the red horizontal line represents the true value

Full size image

4.3 Data worth and redundancy

In this section, we investigate the effects of varying the number of sources and receivers to evaluate the data worth and redundancy issues. Equal numbers of sources and receivers are used. The sources and the receivers are uniformly distributed in their respective wells from 0 to -15 m at the left side (x = 0 m) and right side (x = 4 m) of the field. 12 cases were investigated with 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 75, and 100 sources and receivers. 2% noise is added to the true observations. The results are based on 20 chains, each executing 50,000 iterations. Figure 7 shows the boxplot of the 8 pilot points and the correlation range’s posterior density distribution. With the increase of sources and receivers, the posterior density distribution is seen to capture the true value better when the number of sources/receivers reach 30. The bound of the posterior cannot be improved when the number of sources/receivers exceeds 35. With the increase of number of sources/receivers, the distance between nearby receivers become smaller and smaller, which means that the measured travel time at nearby receivers are closer and closer. The small difference of the travel time between nearby receivers may be covered by the noise. The only exception is the 9th parameter, range, which is not affected much as the number of sources is varied. This is because the 8 pilot points already include the information on the field’s spatial correlation range.

Fig. 7
figure 7

Boxplots for inferred quantities with different number of sources and receivers

Full size image

4.4 Pilot points

In this section, we investigate the effects of changing the number of pilot points. The number of pilot points is increased from 4 to 24 incrementally, for a total of 6 test cases. The position and true value of the 24 pilot points are shown in Fig. 1a and Table 1. 2% noise is added to the true observations. The number of the sources and receivers is kept at 30 (900 observation data). The aim of this section is to show that with a given observational dataset, there is an optimal number of pilot-points. Commonly, when the number of pilot points increases, the variance of permittivity field in the domain should decrease. However, this assumes that the permittivity of the pilot points is known. In our case, the permittivity of the pilot points are unknown, and needs to be inferred from observations. As the number of pilot-points increases, and the number of indirect observations do not, it becomes progressively more difficult to infer them accurately. Figure 8 shows the boxplot of posterior density distribution for the pilot points in the 6 cases in the study. The horizontal red lines are the true value of the 24 pilot points. There are 24 boxplots in Fig. 8, representing the posterior density distribution of the 24 pilot points obtained for the 6 cases. For example, the first bar in the first plot (named “pilot point 1”) stands for the posterior distribution of the pilot point 1 in the case with a total of 4 pilot points modeling the field. For the plot named “pilot point 23”, there is one bar in the plot, because pilot point 23 can only be calibrated when the total numbers of pilot points is at least 23. With the increase in the total number of pilot points, the uncertainty ranges slightly increase, especially for the pilot points 1–8. Figure 9 (top) shows the mean dielectric permittivity field for the cases with 4, 8, 12, 16 and 24 pilot points controlling the field. The mean dielectric permittivity field is the average of 200,000 realizations of \( \epsilon_{r} \) fields generated using samples randomly picked from the MCMC chains. Compared to the true field (Fig. 1a), we see that the mean field computed with 4 and 8 pilot points can capture the main spatial variation of the field. The cases with 12 and 16 pilot points controlling the field capture more spatial details, though they might be spurious. In Fig. 9 (bottom) we plot the pointwise variance computed from the 200,000 realizations. One can see that as the number of pilot points in the RFM (i.e., its complexity, flexibility and consequently, dimensionality) increases, we see higher variance in \( \epsilon_{r} \). This is especially true for the most complex RFMs with 20 and 24 pilot points. Figure 10 shows the best dielectric permittivity field of the 200,000 realizations, i.e., the one whose simulations best match the observations. Note that the individual fields do not necessarily resemble Fig. 9 (top row). Figure 11 shows the root mean squared error (RMSE) between the 5 inverted fields and the true field. The black circles are for the RMSE between the mean field and the true field. The red circles are for the RMSE between the best inverted filed and the true field. The RFM with 8 pilot points, with limited observations (900 in this study), provides the best matches in terms of the estimated mean and best fields compared to other RFMs. However, a good agreement between observations and mean or best field does not automatically imply that the eight-pilot-point RFM is the one to use for the given observational dataset; rather the determination must be made based on all the realizations that may be obtained from a calibrated RFM.

Fig. 8
figure 8

Boxplots of posterior samples for the pilot points involved in the 6 case studies

Full size image
Fig. 9
figure 9

Top row: Mean of 200,000 realizations of \( \epsilon_{r} \) fields generated from posterior samples randomly picked from the MCMC chains. Results are generated for RFMs of increasing sophistication/flexibility/dimensionality. Bottom row: Pointwise (grid-cell-wise) standard deviations computed from the 200,000 realizations

Full size image
Fig. 10
figure 10

Best \( \epsilon_{r} \) field out of the 200,000 realizations, for which the simulated first-arrive traveltimes match the observations the most. Results are generated for RFMs of increasing sophistication/flexibility/dimensionality

Full size image
Fig. 11
figure 11

Root mean square errors between the true field and estimated fields for different numbers of pilot points

Full size image

This is accomplished using the cumulative rank probability score (CRPS); see Ray et al. (2015) for the definition of CRPS and how it can be used, along with an ensemble of predictions from a (Bayesian) calibrated model, to gauge the quality of the calibration. CRPS, loosely speaking, computes the discrepancy between an ensemble of predictions (by computing the empirical cumulative distribution function) and observations. It has units of the observed quantity (time, in our case) and smaller values of CRPS are preferred. In Fig. 12, we plot the CRPS of the ensemble predictions obtained from calibrated models that used RFMs of increasing complexity. We see that the 4-pilot-point RFM has the lowest CRPS, showing the difficulty of estimating permittivity accurately as the pilot points are increased.

Fig. 12
figure 12

DIC values computed using Bayesian estimations of \( \epsilon_{r} \) performed using RFMs with 1, 4, 8, 12, 16, 20 and 24 pilot points. The RFM with 4 pilot points is the most appropriate for the observations used in this study

Full size image

4.5 Discussion

The uncertainty in the inferred parameters—\( \epsilon_{r} \) at the pilot points and the correlation range of the variogram are caused by three factors: (1) the quality of the observational data, i.e., the magnitude of noise in it; (2) the quantity of observational data, and (3) the adequacy of the RFM in estimating a spatially complex \( \epsilon_{r} \) field. In Sect. 4.1–4.4 we performed a set of experiments, and we interpret the results to gauge the interplay of the three factors in deciding the quality of the inversion.

In Sect. 4.1, we check if the formulation of the likelihood and the MCMC implementation produces correct results i.e., if the inferences are bias-free when observations are noiseless. In Fig. 2 we find the inferences drawn with limited observations to be free of any systematic errors and we proceed to the problem of the information required to constrain a nine-dimensional RFM (Fig. 6). We find that for less than about 10% noise, the PDF for \( \epsilon_{r} \) get wider with the noise. For 15% noise, the median of the inferred PDFs shift away from the true value. Note that the observations may still be sufficiently informative to constrain a simpler RFM.

Having established an approximate lower bound on the amount of information required to constrain the RFM, we refine the analysis by removing the paucity of observational data/information. In Fig. 7 and Sect. 4.3 we perform inversions with the 8-pilot-point RFM while increasing the amount of observations. Figure 4 shows that the median \( \epsilon_{r} \), as inferred at the 8 pilot points, asymptote to position-specific constants by about 50 source-receiver pairs, while their uncertainty keeps shrinking as the number of source-receiver pairs increases. The parameters with the largest estimation errors are pilot point #4 and the correlation range. As seen in Fig. 1, pilot point #4 is near a sharp gradient in \( \epsilon_{r} \), and capturing it with a mixture of eight pilot points is difficult. The difficulty in estimating correlation range is explained by an ambiguity. There are two length scales in the inverse problem—the correlation range and the distance between the pilot points. The correlation range is therefore difficult to estimate and increasing the number of source-receiver pairs does not sharpen the PDF (see Fig. 7).

In reality, the appropriate RFM is not known a priori, and one typically has to investigate RFMs of increasing complexity to arrive at the best one. In our case, this implies performing the inversion using RFMs constructed with increasing numbers of pilot points. This is also investigated in Sect. 4.4, where we investigate RFMs constructed using 4–24 pilot points. As seen in Fig. 8, 9 and 11, a more sophisticated RFM does not necessarily lead to better reconstructions of \( \epsilon_{r} \) fields, if the quantity of observational data is held constant; instead it runs the danger of overfitting and providing poor predictions. In Fig. 8 (plots of \( \epsilon_{r} \) for pilot points #2, #4, #5 and #8), we see that the width of the uncertainty bounds seems to become constant after about 10 pilot points in the RFM. This is also reflected in Fig. 9. In the plots on top, where we plot the mean of 200,000 realizations of \( \epsilon_{r} \), increasing the complexity of the RFM seems to reconstruct more spatial details. However, the variance in the reconstructions [Fig. 9 (bottom row)] increases with the complexity of the RFM, and the details captured by the mean field are not necessarily more accurate, given the increasing uncertainty associated with them. Figures 9 and 10 reveal the danger of using a mean \( \epsilon_{r} \) field from the MCMC solution as a representative of the entire ensemble of \( \epsilon_{r} \) field realizations. As Fig. 9 (bottom) shows, the pointwise standard deviations are large, and consequently, the best field (Fig. 10) has little resemblance to the mean field (Fig. 9 (top row)).

Figure 11 also shows that the agreement between the true and estimated fields actually become worse as we add pilot points beyond 8 to the RFM. Figure 12, which plots the CRPS as the RFM complexity is increased, shows that the RMSE of the mean field is not a good guide for selecting RFMs, as it ignores the variability/uncertainty in the inferred field. The CRPS plot shows us that of the RFMs considered, the 4-pilot-point RFM is most appropriate for use with the dataset, even though the RMSE of the mean field it produces is not the most optimum. Thus while we may have 900 travel time observations, they may not be of much use in constraining a complex RFM. This may be due to the physics of the problem—EM waves can find alternative paths with much the same travel times as we place more pilot points—or it could be due to the variability of the multiGaussian permittivity fields generated by SGSIM.

In Fig. 13, we plot the estimate of the noise (\( \sigma \)) for the tests shown in Figs. 6, 7 and 8. In Fig. 13a, we see that when the observations are corrupted by 2, 5, 10 and 15% noise, we infer \( \sigma \) to be about 5, 8, 15 and 25%. This overestimate is due to the variability introduced by SGSIM and the limited nature of the observations. In Fig. 13b, we see that increasing the observations actually improves the estimate of \( \sigma \), drawing it closer to its true value of 2%; however, there is still some residual variability due to the stochastic nature of SGSIM. In Fig. 13c, we see that increasing the number of pilot points somewhat reduces \( \sigma \).

Fig. 13
figure 13

Boxplot for \( \sigma \) in Eq. (7); a different level of noise; b different number of sources and receivers (with 2% noise); c different number of pilot points (with 2% noise)

Full size image

5 Conclusion

We have developed a new inversion method to reconstruct relative dielectric permittivity fields from tomographic GPR arrival time data. It is based on a pilot-point modeling of relative dielectric permittivity field, so that the dimensionality of the inverse problem can be reduced. In order to capture the uncertainty in the quantities of interest inferred from GPR data, we use a multi-chain MCMC sampler. The solution is developed as a multi-dimensional PDF of the parameters of the pilot-point representation. For each set of pilot point parameters, we develop a relative dielectric permittivity field using SGSIM. In the absence of observational noises, we find that MCMC samples successfully capture true values of the relative permittivity field. The inversion test with noisy observational data shows that when the noise level is smaller than 10% of the mean observational magnitude, the proposed approach can well capture the true values within the IQR of the posterior samples. In some cases, e.g., in Fig. 6, the IQR contains most of the true values; in a well-calibrated inversion, only about half the true values would have lain within the IQR bounds. This indicates that in some low-noise inversions, the uncertainty in the inferred quantities is larger than in an ideal inversion. This could be due to the design of our spatial parameterization, since (1) we attempt to recreate the permittivity field using only 8 pilot points and (2) the correlation range and the distribution of pilot points impose two conflicting length scales in the problem.

We also see that when the amount of observation data increases, the posterior density distributions capture the true values better (i.e., more accurate and with narrower bounds). In our study case, the bounds of the posteriors narrow significantly when the number of sources/receivers exceeds 25 (625 observational GPR arrival times data). Increasing the number of pilot points while holding the amount of observational data constant is not always helpful: comparing the estimated dielectric permittivity field to the true one, the cases with 4 and 8 pilot points can capture the main spatial variation of the field, while the cases with more pilot points constraining the field can capture a little more spatial detail, but not necessarily lead to a more accurate inverted field due to increased number of unknowns. The RMSEs between the mean inverted fields and the true field indicates that the test cases with 8 pilot points, with limited observations (900 in this study); however, the use of RMSE of the mean field is misleading, as it ignores the effect of estimation uncertainty. This is rectified in Fig. 12, where we use CRPS to perform RFM selection. Note that a larger domain with the same length scale of spatial variation would likely require more pilot points, and consequently, more observations for inversion. Nevertheless, in practice, the use of CRPS to choose the most appropriate RFM for an observational dataset is the correct approach. It is a purely data-driven method for deciding on a suitable RFM, balances estimation accuracy and uncertainty and is a particular strength of MCMC solutions of inverse problems.