A multi-type branching process model for epidemics with application to COVID-19

Abstract

In this paper we model an infectious disease epidemic using Multi-type Branching Process where the number of offsprings of different types follow non-identical Poisson distributions whose parameters may vary over time. We allow for variation in parameters due to the behavior of citizens, government interventions in the form of lockdown, testing and contact tracing and the infectiousness of the variant of the virus in circulation at a time-point in a location. The model can be used to estimate several unknown quantities of interest in an epidemic such as the number of undetected cases and number of people quarantined following contact tracing. The model is fitted to the publicly available COVID-19 caseload data of India, South Korea, UK and US and is seen to provide good fit. It also provides good short-term forecast of the caseload for these countries. This model can be useful for health policy planners in assessing the impact of various intervention strategies such as testing, contact tracing, quarantine etc.

1 Introduction

In the ongoing COVID-19 pandemic several local and national governments across the globe have attempted to bring the pandemic under control through a variety of health policy measures such as lockdown, extensive testing, contact tracing of the infected individual, institutional or home quarantining of the infected individual etc. In contact tracing, all individuals who have been in physical proximity of the infected individual are sought to be found and they are tested and quarantined to prevent further transmission of the disease. Contact tracing is a challenging exercise with significant administrative costs. Ideally one would like that all contacts of the infected individual are traced, but this however may not actually be realized. Though health policy experts generally agree on the importance of contact tracing for containing an epidemic, the quantification of the impact is often difficult. This gives rise to adhoc claims made by the experts based on their own subjective assessment of the epidemic situation. An effective contact tracing program would be expected to lead to reduction in new cases, but the caseload data may not reflect accurately the number of infected persons if some infected individuals remain asymptomatic (as in COVID-19) or have mild disease that they do not report to health authorities. Also it may happen that there are infected individuals who have been detected but are not reported due to lack of administrative diligence. This has lead to interest in studying the effect of non-pharmaceutical interventions by various governments towards containing COVID-19 (Flaxman et al. 2020; Lavezzo et al. 2020; Faria et al. 2021; Parino et al. 2021). In the present article we propose a stochastic model based on Multi-type Branching Process to account for caseloads in the presence of these factors. We elaborate on the motivation of the paper in Sect. 2.

The standard model in epidemiology is the Susceptible-Infected-Removed (SIR) model, where the population is divided into these three compartments and an individual moves into and out of them with some rate. Several extensions of the SIR model have been considered. These are generally formulated under deterministic considerations. The reader may see Britton (2010) for advantages of stochastic models over deterministic models and a survey of stochastic epidemic models. In this article we consider time varying Multi-type Branching process (MBP) to model the transmission of infectious disease. Multi-type branching process is a generalisation of the simple branching process where each parent produces several types of offspring. Each individual may produce offsprings of different types. Further, the probability distribution of the offspring types may vary with the type of individual. Here additionally we consider multi-type branching process in a time varying environment. See Yadav (2019) and Athreya and Ney (2012) for a review of Branching processes. Refer to Jacob (2010) for a review of Branching processes in epidemiology.

Hellewell et al. (2020) consider a branching process model with the number of infected offspring following a negative binomial distribution to study the effect of contact tracing and quarantine on the spread of COVID-19. Their model follows static parameters. As the pandemic progressed, various kind of restrictions were imposed and subsequently relaxed by the governments. Also, as pandemic fatigue sets in, individuals tend to become lax in following appropriate social distancing behaviors. This results in variation of infection rate over time. Levesque et al. (2021) proposed a continuous time branching process model with the propagation following a negative binomial process which take into account contact tracing and quarantine. Both of these works do not take into account under-reporting of cases. Laha (2021) considered a time varying Multi-type branching process model for spread of infectious disease, which considered complete contact tracing. In this article we generalize this model further to account for time variation of infection rate, missed contact tracing and under-reporting of cases. This model fits the caseload data of each of the four countries US, UK, India and South Korea very well. Using the model we are able to estimate the number of undetected cases as well as the number of people quarantined through contact tracing at each time period. We are also able to estimate the number of spreaders and non-spreaders among the undetected cases at each time period. Since India and South Korea had contrasting approaches to control the COVID-19 epidemic as it evolved over time, we study these two countries in detail.

This paper is structured as follows. In Sect. 2 we elaborate on our motivation for proposing the model. In Sect. 3, we present the extended MBP model with Poisson offspring distribution. We present results about the expected number of cases under the model with partial contact tracing and underreporting of cases. In Sect. 4, we discuss fitting of the proposed model to COVID-19 data in India, South Korea, UK and US. We also discuss methods for forecasting future caseloads using this model and apply the same for the four countries mentioned above in Sect. 5. In Sect. 6 we discuss a metric analogous to widely used $R_0$ (reproduction number of SIR model) that emerges from the model and indicate some potential uses. In Sect. 7, we conclude the article.

2 Motivation

In the ongoing COVID-19 pandemic the difficulty of inference of epidemiological parameters has been acknowledged. Wood et al. (2021) argue that epidemiological parameters in case of COVID-19 pandemic would be country specific. This country-wise variation in parameters can be due to the behavior of her citizens, government interventions in the form of lockdown, testing and contact tracing and the infectiousness of the variant of the virus in circulation in that country, see Jalilian and Mateu (2021). Adin et al. (2022) find variability in excess mortality based on spatial factors which again indicates that disease propagation is not homogeneous. Additionally over the course of the pandemic these features can be expected to change. Accounting for this change is necessary to plan contact tracing measures, see Mahmood et al. (2021) where contact tracing is considered with varying levels of intensity of spread by individuals. In the case of COVID-19, several national and local governments imposed and relaxed lockdown restrictions several times. Similarly citizens have been known to experience “pandemic fatigue” that makes them less adherent to COVID-19 protocols, Haktanir et al. (2021). The socio-economic circumstances of each nation could be expected to uniquely affect both the government and citizen response.

In this paper we propose a new Multi-type Branching Process (MBP) based epidemic propagation model that can take into account the variation in the model parameters caused by the above mentioned factors. An interesting aspect of this model is that it can be used to study impact of health policy measures such as contact tracing and quarantining and can also be used to shed light on the number of undetected cases. In this context it may be noted that contact tracing in SIR model has been considered only recently (Okolie and Müller 2020; Zhang and Britton 2021). However partial contact tracing, i.e. some contacts but not all are traced, to the best of our knowledge has not been studied. We are able to obtain closed form expressions for the expected number of detected as well as undetected infections at each period using the model. This is again not possible in all epidemiological modelling frameworks since they are often intractable. In case of SIR model obtaining a closed form expression for the size of infectives has been difficult. Only recently Harko et al. (2014) presented a solution in parametric form which requires numerical integration to evaluate the expression. Modelling partially observed epidemic time series has been considered earlier in Cauchemez and Ferguson (2008) using a stochastic differential equation, we instead model it here using discrete time multi-type branching process. There has been interest in estimating the number of undetected COVID-19 cases (Langousis and Carsteanu 2020). Bhatia et al. (2020) estimate the number of undetected cases amongst travellers from China. Unwin et al. (2021) estimate the number of undetected COVID-19 cases in New Zealand using the method of next generation matrices.

The MBP model described in this paper can be estimated based on the publicly available caseload data which can be a major advantage. In this paper, we consider separate models for different countries and estimate different epidemiological parameters for them, see Sect. 4.1. The results (Sect. 4.1) indeed shows that there is significant variation in the parameter values during the course of the COVID-19 pandemic.

3 Model

In this section we briefly review and then extend the MBP model for modeling the number of confirmed cases of COVID-19 discussed in Laha (2021). The model discussed in Laha (2021) assumes that contact tracing of every individual who is detected with COVID-19 disease is exhaustive and all individuals found infected with COVID-19 during this process is quarantined and does not serve as originator of new COVID-19 cases. In this paper, we extend this model to reflect the following observations from developing countries such as India: (a) the contact tracing is not complete, which means that there are some infected individuals who are not found through the process of contact tracing and these individuals continue to spread the disease and (b) some infected individuals in the population who are not counted as confirmed cases quarantine themselves and help towards containing the spread of the disease. This may be due to several reasons such as they are not tested or they receive a false negative test report or their positive test result is not reported to the authorities. In addition there may be undetected infected individuals who do not spread the disease due to low viral load.

In the Laha (2021) model it is assumed that the infectious disease begins with a single undetected infected individual. This individual then infects $X_1$ individuals. Here it is assumed that $X_1\sim \text {Poi}(\lambda _1)$, where $\text {Poi}(\lambda _1)$ denotes the Poisson distribution with mean $\lambda _1$. It is assumed that each infected individual has a probability $p_1$ of being detected. Any infected individual who is detected is quarantined and then extensive contact tracing is initiated, wherein all individuals infected by the detected individual are identified and quarantined. It is assumed that quarantined individuals do not infect anyone else. The same process is then repeated in successive time periods with the possibility that the parameters $\lambda _n$ and $p_n$ may change with n. The variation in $\lambda _n$ reflects on the varying contagiousness of the disease, following (or lack thereof) disease appropriate behavior and protection granted by vaccination whereas the variation in $p_n$ reflects on the intensity of testing, disease awareness and the severity of the disease at that time. In keeping with the notation followed in Laha (2021), let $X_{n,ID}$ denote the number of infected individuals detected, $X_{n,IND}$ denote the number of undetected infected individuals and $X_{n,C}$ denote the total number of cases in the n-th generation. The total number of cases upto generation n is $S_{n,C}=\sum _{i=1}^nX_{i,C}$.

Theorem 3.1

(Laha 2021) For $n\ge 2$,

• 1. $E(X_{n,IND})=\prod _{k=1}^n\lambda _k(1-p_k)$

• 2. $E(X_{n,ID})=p_n\prod _{k=1}^{n-1}\lambda _k(1-p_k)$

• 3. $E(X_{n,C})=\lambda _{n-1}\lambda _n\{(1-p_{n-1})p_n+p_{n-1}\}\prod _{k=1}^{n-2}\lambda _k(1-p_k)$

As noted in Laha (2021), $\lim _{n \rightarrow \infty } E(S_{n,C})<\infty$ if,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{(1-p_{n})p_{n+1}+p_{n}}{(1-p_{n-1})p_{n}+p_{n-1}}\lambda _{n+1}(1-p_{n-1})<1 \end{aligned}$$

In what follows the model discussed in Laha (2021) has been extended to incorporate features that are often observed in real life epidemic situations including the ongoing COVID-19 pandemic. In the Laha (2021) model it is assumed that all detected individuals are contact traced. In the model proposed in this paper we relax this strong assumption to accommodate a more realistic situation where some individuals who are detected to have the disease are not contact traced for some reasons such as lack of adequate manpower or financial resources. Further in Laha (2021) it is assumed that all undetected cases can spread the virus. This assumption has also been relaxed in the model proposed in this paper. We now allow for the possibility that some infected but undetected individuals may not be spreaders. More details of the models can be found in Sect. 3.1 and 3.2. In Sect. 3.1 we consider the case where not all detected individuals are contact traced. In Sect. 3.2 we consider a further extension where not all undetected infected individuals are spreaders.

3.1 Partial contact tracing

In this sub-section we extend the above model to the case when contact tracing is partial i.e. contacts of some infected individuals are not traced. This may happen due to a variety of reasons like inability to identify all the contacts of the infected person, resource constraints hampering the work of departments carrying out contact tracing exercise etc. As in the earlier case, here also we assume that the infectious disease begins with a single undetected infected individual. Here also we assume that the number of individuals infected by a disease spreading individual follows a Poisson distribution. This individual then infects $X_1$ individuals where $X_1\sim \text {Poi}(\lambda _1)$ and $X_1=X_{1,ID}+X_{1,IND}$. The model can be applied assuming any parametric or non-parametric form of the probability mass function, but for ease of computation and assumption we choose the Poisson distribution as in Mode et al. (2011). Let $X_{1,T}$ be the number of detected infected individuals whose contacts were traced completely and $X_{1,UT}$ is the number of detected infected individuals whose contacts were not traced. Thus, $X_{1,ID}=X_{1,T}+X_{1,UT}$. Let $p_{1,1}$ be the probability of a detected infected individual to be contact traced in the first generation. We assume that when contact tracing is carried out, all infected contacts are identified and they are quarantined. Let ${p_{2,1}}$ be the probability that contact tracing is not carried out for a detected infected individual in the first generation. Then, $X_{1,T}\sim \text {Poi}(\lambda _1 p_{1,1})$, $X_{1,UT}\sim \text {Poi}(\lambda _1 p_{2,1})$ and $X_{1,IND}\sim \text {Poi}(\lambda _1(1-p_{1,1}-p_{2,1}))$. Further, $X_{1,T}, X_{1,UT} \text { and } X_{1,IND}$ are mutually independent. In real life situations it is often seen that the cases are detected by medical teams that operate separately from the administrative teams that carry out the contact tracing. Motivated by this we assume that detection of cases and contact tracing are independent procedures, and hence $X_{1,T}$ and $X_{1,UT}$ are assumed to be independent random variables. For similar reasons we also assume that non-detection of cases ($X_{1,IND}$) doesn’t depend on the number of cases being detected $(X_{1,UT})$ and/or contact traced $(X_{1,T})$. Since contact tracing is not carried out for these $X_{1,UT}$ detected infected individuals they can be treated akin to the $X_{1, IND}$ individuals. Now suppose that the i-th individual in the group of $X_{1,UT}$ detected infected individuals for whom contact tracing had not been carried out infects $\text {U}'_{2,i}$ individuals. We assume $\text {U}'_{2,i}=Y_{2,i}'+Z_{2,i}'$ where $Y_{2,i}'$ are the number of infected individuals who are detected in the second generation and $Z_{2,i}'$ are the number of infected individuals who are not detected in the second generation. Again, suppose that the i-th individual in the group of $X_{1,IND}$ undetected infected individual infects $U_{2,i}$ individuals. As before, assume $U_{2,i}=Y_{2,i}+Z_{2,i}$. As in the original model, we assume that the i-th individual in the group of $X_{1,T}$ detected infected individuals whose contacts are traced infects $W_{2,i}$ individuals prior to being detected where $W_{2,i}\sim \text {Poi}(\lambda _1)$. These $W_{2,i}$ individuals are all detected and quarantined so that they do not infect any more individuals.

Therefore,

$$\begin{aligned} X_{2,ID}=\sum _{i=1}^{X_{1,UT}}Y'_{2,i}+\sum _{i=1}^{X_{1,IND}}Y_{2,i} \end{aligned}$$

where $Y_{2,i}$ and $Y'_{2,i}\sim \text {Poi}(\lambda _2(p_{1,2}+p_{2,2}))$

$$\begin{aligned} X_{2,IND}=\sum _{i=1}^{X_{1,UT}}Z_{2,i}'+\sum _{i=1}^{X_{1,IND}}Z_{2,i} \end{aligned}$$

where $Z_{2,i}$ and $Z_{2,i}'\sim \text {Poi}(\lambda _2(1-p_{1,2}-p_{2,2}))$

$$\begin{aligned} X_{2,IQ}=\sum _{i=1}^{X_{1,T}}W_{2,i} \end{aligned}$$

where $W_{2,i}\sim \text {Poi}(\lambda _2)$. Here $\lambda _2$ is the average number of individuals infected by an infected individual in the second generation, $p_{1,2}$ is the probability of a detected infected individual to be contact traced and $p_{2,2}$ is the probability of a detected infected individual to not be contact traced in the second generation. The number of cases in the second generation is $X_{2,C}=X_{2,ID}+X_{2,IQ}$.

Continuing this process in the n-th generation, we have,

$$\begin{aligned} X_{n,ID}=\sum _{i=1}^{X_{n-1,UT}}Y'_{n,i}+\sum _{i=1}^{X_{n-1,IND}}Y_{n,i} \end{aligned}$$

where $Y_{n,i}$ and $Y'_{n,i}\sim \text {Poi}(\lambda _n(p_{1,n}+p_{2,n}))$

$$\begin{aligned} X_{n,IND}=\sum _{i=1}^{X_{n-1,UT}}Z_{n,i}'+\sum _{i=1}^{X_{n-1,IND}}Z_{n,i} \end{aligned}$$

where $Z_{n,i}$ and $Z_{n,i}'\sim \text {Poi}(\lambda _n(1-p_{1,n}-p_{2,n}))$

$$\begin{aligned} X_{n,IQ}=\sum _{i=1}^{X_{n-1,T}}W_{n,i} \end{aligned}$$

where $W_{n,i}\sim \text {Poi}(\lambda _n)$. Here $\lambda _n$ is the average number of individuals infected by an infected individual in the n-th generation, $p_{1,n}$ is the probability of a detected infected individual to be contact traced and $p_{2,n}$ is the probability of a detected infected individual to not be contact traced in the n-th generation. We note that the number of cases in the n-th generation is $X_{n,C}=X_{n,ID}+X_{n,IQ}$. The total number of cases upto the nth generation is, $S_{n,C}=\sum _{i=1}^nX_{i,C}$

Lemma 3.2

For all $n\ge 2$,

$$E(X_{{n,UT}} ) = E(X_{{n,ID}} )\frac{{p_{{2,n}} }}{{p_{{1,n}} + p_{{2,n}} }}{\text{ and }}E(X_{{n,T}} ) = E(X_{{n,ID}} )\frac{{p_{{1,n}} }}{{p_{{1,n}} + p_{{2,n}} }}$$

We prove Lemma 3.2 using induction and the details can be found in the Appendix.

Theorem 3.3

For $n \ge 2$,

• 1.

  • (a) $E(X_{n,IND})=\lambda _n(1-p_{1,n}-p_{2,n})\prod _{k=1}^{n-1}\lambda _k(1-p_{1,k})$

  • (b) $E(X_{n,ID})=\lambda _n(p_{1,n}+p_{2,n})\prod _{k=1}^{n-1}\lambda _k(1-p_{1,k})$

• 2. $E(X_{n,C})=\lambda _{n-1}\lambda _n((p_{1,n}+p_{2,n})(1-p_{1,n-1})+p_{1,n-1})\prod _{k=1}^{n-2}\lambda _k(1-p_{1,k})$

We prove Lemma 3.3 using induction and the details can be found in the Appendix.

Remark

Applying the D’Alembert’s ratio test it can be seen that $E(S_{n,C})<\infty$ if,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{(p_{1,n+1}+p_{2,n+1})(1-p_{1,n})+p_{1,n}}{(p_{1,n}+p_{2,n})(1-p_{1,n-1})+p_{1,n-1}}\lambda _{n+1}(1-p_{1,n-1})<1 \end{aligned}$$

3.2 Unreported cases

In this section we further extend the model discussed in Sect. 3.1 to incorporate the under-reporting of the number of infected individuals. While under-reporting can be due to several causes our model incorporates three specific types of under-reporting: (a) individuals who are asymptomatic or have very mild disease that did not require to seek medical consultation, (b) individuals who self-impose quarantine on own suspicion of being infected or on medical advice and (c) individuals who are diagnosed as infected and they are appropriately quarantined but their cases are not reported to the health authority due to lack of administrative diligence. We assume that these unreported infected individuals do not infect any other individual. We use a setup similar to that in Sect. 3.1, and based on the above discussion we additionally assume that at generation n, $X_{n,IND}=X_{n,IND}^U+X_{n,IND}'$ where $X_{n,IND}^U$ is the number of infected undetected individuals in generation n who do not infect any other individual (Undetected Non-spreaders) and $X_{n,IND}'$ are the remaining individuals in this group (Undetected-Spreaders). Further it is assumed that $X_{n,T},X_{n,UT},X_{n,IND}^U,X_{n,IND}'$ are mutually independent. We assume that detection of cases and contact tracing are separate procedures as was assumed in Sect. 3.1, therefore $X_{n,T}$ and $X_{n,UT}$ are assumed to be independent. In addition we assume that non-detection of cases also doesn’t depend on the number of cases being detected and/or contact traced. Hence we assume that $X_{n,IND}^U$, $X_{n,IND}'$, $X_{n,T}$ and $X_{n,UT}$ are mutually independent. We also assume that among the non-detected cases the number of spreaders $(X_{n,IND}')$ and non-spreaders $(X_{n,IND}^U)$ are independent of each other. Let $p_{3,n}$ be the probability that a randomly chosen infected undetected individual would not infect any other individual.

Therefore,

$$\begin{aligned} X_{n,ID}=\sum _{i=1}^{X_{n-1,UT}}Y_{n,i}'+\sum _{i=1}^{X_{n-1,IND}'}Y_{n,i} \end{aligned}$$

where $Y_{n,i}$ and $Y_{n,i}'\sim \text {Poi}(\lambda _n(p_{1,n}+p_{2,n}))$,

$$\begin{aligned} X_{n,IND}=\sum _{i=1}^{X_{n-1,UT}}Z_{n,i}'+\sum _{i=1}^{X_{n-1,IND}'}Z_{n,i} \end{aligned}$$

where $Z_{n,i}$ and $Z_{n,i}'\sim \text {Poi}(\lambda _n(1-p_{1,n}-p_{2,n}))$

$$\begin{aligned} X_{n,IQ}=\sum _{i=1}^{X_{n-1,T}}W_{n,i} \end{aligned}$$

where $W_{n,i}\sim \text {Poi}(\lambda _n)$

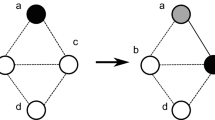
In Fig. 1 we show a possible sample path of the proposed model upto the third generation.

Lemma 3.4

For all $n\ge 2,$

• 1. $E(X_{n,IND}^U)=E(X_{n,IND})\frac{p_{3,n}}{1-p_{1,n}-p_{2,n}}$ and $E(X_{n,IND}')=E(X_{n,IND})\frac{1-p_{1,n}-p_{2,n}-p_{3,n}}{1-p_{1,n}-p_{2,n}}$

• 2. $E(X_{n,UT})=E(X_{n,ID})\frac{p_{2,n}}{p_{1,n}+p_{2,n}}$ and $E(X_{n,T})=E(X_{n,ID})\frac{p_{1,n}}{p_{1,n}+p_{2,n}}$

We prove Lemma 3.4 using induction and the details can be found in the Appendix.

Theorem 3.5

For $n\ge 2$,

• 1.

  • (a) $E(X_{n,IND})=\lambda _n(1-p_{1,n}-p_{2,n})\prod _{i=1}^{n-1}\lambda _i(1-p_{1,i}-p_{3,i})$

  • (b) $E(X_{n,ID})=\lambda _n(p_{1,n}+p_{2,n})\prod _{i=1}^{n-1}\lambda _i(1-p_{1,i}-p_{3,i})$

• 2. $E(X_{n,C})=\lambda _{n}\lambda _{n-1}((p_{1,n}+p_{2,n})(1-p_{1,n-1}-p_{3,n-1})+p_{1,n-1})\prod _{k=1}^{n-2}\lambda _k(1-p_{1,k}-p_{3,k})$

We prove Theorem 3.5 using induction and the details can be found in the Appendix.

Remark

Applying the D’Alembert’s ratio test it can be seen that $\lim _{n \rightarrow \infty } E(S_{n,C})<\infty$ if,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{(p_{1,n+1}+p_{2,n+1})(1-p_{1,n}-p_{3,n})+p_{1,n}}{(p_{1,n}+p_{2,n})(1-p_{1,n-1}-p_{3,n-1})+p_{1,n-1}}\lambda _{n+1}(1-p_{1,n-1}-p_{3,n-1})<1 \end{aligned}$$

(1)

Let $T_n=\frac{(p_{1,n+1}+p_{2,n+1})(1-p_{1,n}-p_{3,n})+p_{1,n}}{(p_{1,n}+p_{2,n})(1-p_{1,n-1}-p_{3,n-1})+p_{1,n-1}}\lambda _{n+1}(1-p_{1,n-1}-p_{3,n-1})$. We discuss the properties and application of $T_n$ further in Sect. 6.

4 Application to COVID-19 pandemic

In this section we discuss the application of the Multi-type Branching Process Epidemic (MBPE) model (described in Sect. 3.2) to COVID-19 pandemic in India, South Korea, United Kingdom(UK) and the United States of America(US). We study these countries because of their distinctive economic and demographic features. India and US are amongst the countries with high COVID-19 caseloads. India is a developing country whereas South Korea, US and UK are classified as developed economies. This has bearing on the resources governments in these countries can spend towards testing, contact tracing and reporting of cases. UK and South Korea are reported to have carried out much more extensive contact tracing than India. The average population density of India and South Korea are much more than that of US and UK. We seek to examine the empirical validity of the MBPE model by fitting it for caseload data from these four countries.

4.1 Estimation of the model parameters

We consider the MBPE model that takes into account partial contact tracing, quarantine and under-reporting of cases. In our model, all infections in the current generation are caused by infected individuals of the previous generation. For COVID-19 modelling, we consider each generation to be of 10 calendar days. This is motivated by the incubation period of COVID-19 (Lauer et al. 2020). For other infectious diseases one may adjust the generation length according to the characteristic of the disease transmission. In the rest of the paper we use the term “generation” and “period” interchangeably.

For fitting the MBPE model to the caseload data we need to estimate the parameters of the model. We adopt a regularized least-squares method for estimating the parameters as there are large number of parameters but only one observed caseload series for each country. Assuming constant parameters across generations is not realistic since the emergence of variants, changes in public policy intervention such as imposition or withdrawal of lockdown, mask mandates, etc. at various stages of the pandemic affects the disease transmission dynamics. On the other hand having too many parameters in the model significantly enhances the possibility of over-fitting. Through regularization we impose a penalty for abrupt changes in parameter estimates thus reducing the possibility of over-fitting. An alternative approach could have been to use Bayesian EM-MCMC but since there is only a single path realization for each country, we felt that it may not be able to provide ‘good’ estimates of the time varying parameters in the MBPE model.

Let $x_m$ be the reported number of new cases in the m-th period. For each country we have the sequence $\{x_1,\cdots ,x_m,\cdots ,x_n\}$ of the reported number of new cases in the n periods. Further let $\hat{X}_m=E(X_{m,C})$, then from Theorem 3.5, $\hat{X}_{m} = E(X_{{m,C}} ) = \lambda _{n} \lambda _{{m - 1}} ((p_{{1,m}} + p_{{2,m}} )(1 - p_{{1,m - 1}} - p_{{3,m - 1}} ) + p_{{1,m - 1}} )\prod\limits_{{k = 1}}^{{m - 2}} {\lambda _{k} } (1 - p_{{1,k}} - p_{{3,k}} )$. We consider the loss function is given by,

$$\begin{aligned} L(\lambda ,p) = & \sqrt {\sum\limits_{{i = 1}}^{n} {(x_{i} - \hat{X}_{i} )^{2} } } + k_{1} \lambda _{1} + k_{2} p_{{1,1}} + k_{3} p_{{1,2}} + k_{4} p_{{1,3}} \\ + & k_{5} \sum\limits_{{j = 2}}^{n} {(\lambda _{j} - \lambda _{{j - 1}} )^{2} } + k_{6} \sum\limits_{{j = 2}}^{n} {(p_{{j,1}} - p_{{j - 1,1}} )^{2} } \\ + & k_{7} \sum\limits_{{j = 2}}^{n} {(p_{{j,2}} - p_{{j - 1,2}} )^{2} } + k_{8} \sum\limits_{{j = 2}}^{n} {(p_{{j,3}} - p_{{j - 1,3}} )^{2} } \\ \end{aligned}$$

In the above we abbreviate $\lambda _{i}, i=1, \ldots , n$, and $p_{i,j}, i=1, 2, 3 \text { and } j=1, \ldots , n$ as $(\lambda ,p)$ in the argument of the loss function. We estimate $(\lambda ,p)$ by minimising $L(\lambda ,p)$. Since the loss function is non-convex and to the best of our knowledge there is no known exact optimization approach for such functions, hence we minimise this loss function using an evolutionary algorithm. We use the R-package DEoptim (Mullen et al. 2011) to minimize $L(\lambda ,p)$. We run the algorithm for 500000 iterations. We considered 500000 iterations since no further reduction in the value of L was observed after this stage.

In the loss function $L(\lambda ,p)$ the regularization parameters $k_1,k_2,k_3, \text { and } k_4$ impose a penalty for arbitrarily high values of the parameters of the first period since it may be expected that in the beginning of the pandemic these parameters would have low-to-moderate values as the number of cases at that stage is only a few. The parameters $k_5,k_6,k_7 \text { and }k_8$ imposes a penalty on jumps (or changes) in the parameter values across periods after the first period. As with most real-life physical phenomenon we expect that period to period changes in the parameter values would not be drastic.

From several initial experiments we found that the regularization parameters need to be chosen in a data adaptive manner. It was noted that for datasets with large number of cases higher value of regularization parameters produced estimates of $(\lambda ,p)$ that provided better model fit with observed data. A simple heuristic that was found quite useful is as follows, let $M=\max \{x_i:1\le i\le n\}$. We set $k_1=\frac{M}{20000}$, $k_6=k_7=k_8=\frac{M}{20}, k_2=k_3=k_4=k_5=\frac{M}{1000}$. We give these values of the regularization parameters for India, South Korea, US and UK in Table 1.

As discussed earlier (Sect. 3.2) one of the key features of the MBPE model is its ability to answer some key questions that may be of interest to the policy makers. One such quantity is the number of undetected cases. In Table 2 we report the model fitted cumulative number of detected cases along with actual cumulative number of reported cases for India, US, UK and South Korea. We find that the fitted values are within $1\%$ of the actual values for all the four countries under consideration. In Table 3 we report the model estimated number of undetected cases for India and South Korea. The model estimates that the number of undetected cases are more than 10 times higher than the reported cases for both India and South Korea upto 6 August 2021 and 11 July 2021 respectively.

Using the estimated parameters we are able to simulate the realizations of the MBPE model. This allows us to examine the variation in the estimated undetected case trajectory. For each country separately, we simulate from the model $k=10000$ times with the same estimated parameters and obtain the (detected) caseload trajectory for each realization. Let $\mathscr {A}=\{\{\alpha _1(t)\}_{t=1}^n,\{\alpha _2(t)\}_{t=1}^n,\cdots ,\{\alpha _{k'}(t)_{t=1}^n\}\}$, be the collection of all caseload trajectories that did not go extinct up to time n during the simulation. Note that $k'\le k$ as those paths which become extinct by time n are not included in $\mathscr {A}$. Now we consider those caseload trajectories which are “close” to the observed caseload trajectory for that country. By “close” we mean that these simulated caseload trajectories lie entirely in the 45-th to 55-th percentile interval band which is created by obtaining the 45-th and 55-th percentiles of the simulated caseload numbers from the $k'$ paths in $\mathscr {A}$ at each t, $1\le t \le n$. We denote the set of paths which are “close” to the observed caseload trajectory to be $\Gamma$. Now, for each trajectory $\gamma \in \Gamma$ we consider the undetected caseload trajectory. The collection of all these trajectories is denoted as $\mathscr {C}$. Now we create a “95% uncertainty band” for depicting the uncertainty in the estimated undetected cases as follows. We consider the trajectories in $\mathscr {C}$ and obtain the 2.5-th percentile and 97.5-th percentile of the undetected caseload numbers at each $t, 1\le t\le n$. The band so obtained is termed as the “95% uncertainty band”.

4.2 Data and model fit

All data has been obtained from public domain resources. We provide in-text citations to each resource with the url for accessing the data.

We obtain COVID-19 caseload data of India from covid19india (2021). We consider data from 15 March 2020 at 10 day intervals until 6 August 2021. Since our model assumes that the disease starts from a single individual and first case in India was detected on 30 January 2020, therefore the first observation considered in our model is assumed to be that of the sixth generation, i.e. ${t=6}$. We provide the fit of the model with the actual data in Fig. 2. In Fig. 3 we plot the estimated $\lambda$ for India. We find that the model fits the actual data very well across the entire duration of the study. India imposed a strict nationwide lockdown on 25 March 2020. The model shows a gradual reduction from the peak value of $\lambda$ in April 2020 to July 2020. Conditional relaxation of lockdown for certain regions and sectors began in June 2020 with a gradual relaxation for most of country in July 2020. The model fitted $\lambda$ shows a rise again from July 2020. In Fig. 4 we plot the estimated ${p_{1,t},p_{2,t},p_{3,t}}$ of the MBPE model for India. The model indicates a relatively higher percentage of contact tracing during the lockdown and it falls off later. In Fig. 5 we plot the estimated number of people who are quarantined through contact tracing, Infected-Undetected-Spreaders and Infected-Undetected-Non-spreaders for India. The model estimates a sharp increase in the number of undetected cases during April-May 2021 which coincided with the second wave of the pandemic in India. In Fig. 6 we provide the 95% uncertainty band of the undetected caseload trajectory. We find that the length between the upper and lower uncertainty band is maximum during the April-May 2021, yet the lower band is several times higher than the reported number of cases during the same period.

We obtain South Korea’s caseload data from WHO (2020). We consider data from 19 January 2020 to 11 July 2021. We assume the disease to have begun in the previous generation. We consider each generation to be of 10 days, where each generation counts the number of new cases in the last 10 days. We plot the fit of the model and of the actual South Korea data in Fig. 7. We find that the MBPE model fits the dataset well. In Fig. 8 we plot the estimated $\lambda$ for South Korea. South Korea implemented extensive contact tracing protocols with penalties for violation of COVID-19 protocols. By late February 2020, the government placed restrictions on movement. We observe a sharp fall in the estimated $\lambda$ from February 2020. By end of April 2020 the government had started to lift some of the restrictions and we see a jump in the estimated $\lambda$ in our model. In August 2020 and November 2020, South Korea increased the social distancing levels in some of her cities. We see a sharp reduction in $\lambda$ coinciding with it. In Fig. 9 we plot the estimated ${p_{1,t},p_{2,t},p_{3,t}}$ of the MBPE model for South Korea. The model estimates that the probability of contact tracing is highest during March 2020. In Fig. 10 we show the “95% uncertainty band” of the estimated Infected and undetected cases for South Korea. In contrast to India the upper and lower uncertainty bands for the undetected cases are narrower for South Korea. In Fig. 11 we plot the estimated number of people who are quarantined through contact tracing, Infected-Undetected-Spreaders and Infected-Undetected-Non-spreaders for South Korea. We estimate that the maximum number of people quarantined through contact tracing happened in June 2021. The MBPE model estimates three waves in terms of the rise in undetected cases in South Korea in May 2020, December 2020 and May 2021.

We also validate the fit of our model from the US and UK caseload data. We obtain COVID-19 case data of US from TheNewYorkTimes (2021). We consider data from 21 January 2020 to 24 July 2021. Since the first case in the US was recorded on 21 January 2020, we consider this as the starting generation. We plot the fit of the model and of the actual US data in Fig. 12. We obtain UK’s caseload data from WHO (2020). We consider data from 1 February 2020 to 25 July 2021. On 1 February 2020 the cumulative cases in the UK were 2, so we consider the disease to have begun in the previous generation, i.e. 22 January 2020. We plot the fit of the model and of the actual UK data in Fig. 13. We find that the MBPE model fits these datasets very well.

4.3 Counterfactual scenarios

From the estimated $\lambda _n, p_{1,n},p_{2,n},p_{3,n}$ we generate 6 counterfactual scenarios for different values of $p_{1,n},p_{2,n},p_{3,n}$. Through this we demonstrate the magnitude of the effect of these different probability parameters on the caseload trajectory. The findings of such study can be used for planning policy interventions during epidemics. We use the estimated value of $\lambda _n$ for each country and perturb $\{p_{1,n},p_{2,n},p_{3,n}\}$ in different ways (details are given below) for generating the caseload trajectory for each country. The six counterfactual scenarios considered in this paper are:

• 1. No contact tracing: In this scenario we assume that the probability of contact tracing, $p^{\text {scenario}}_{1,n}=0,\forall n$. We modify the other probabilities as follows,

  $$\begin{aligned} p^{\text {scenario}}_{2,n}&\rightarrow p_{2,n} + \frac{p_{1,n}}{3}\\ p^{\text {scenario}}_{3,n}&\rightarrow p_{3,n} + \frac{p_{1,n}}{3} \end{aligned}$$

  As one would expect, we see an exponential growth in caseloads for all the four countries in this scenario. This indicates the importance of contact tracing for containing the disease.

• 2. No partial contact tracing: In this scenario we assume that the probability of partial contact tracing, $p^{\text {scenario}}_{2,n}=0,\forall n$. We modify the other probabilities as follows,

  $$\begin{aligned} p^{\text {scenario}}_{1,n}&\rightarrow p_{1,n} + \frac{p_{2,n}}{3}\\ p^{\text {scenario}}_{3,n}&\rightarrow p_{3,n} + \frac{p_{2,n}}{3} \end{aligned}$$

  We find that in the absence of partial contact tracing, i.e. if all contacts of the detected cases are immaculately traced and the infected ones are quarantined then the growth of the caseload is slower than in Scenario 1. This further strengthens the observation from Scenario 1 that contact tracing is very important for rapid control of the epidemic.

• 3. All undetected cases are spreaders: In this scenario we assume that the probability of an undetected case not spreading the disease, $p^{\text {scenario}}_{3,n}=0,\forall n$. We modify the other probabilities as follows,

  $$\begin{aligned} p^{\text {scenario}}_{1,n}&\rightarrow p_{1,n} + \frac{p_{3,n}}{3}\\ p^{\text {scenario}}_{2,n}&\rightarrow p_{2,n} + \frac{p_{3,n}}{3} \end{aligned}$$

  In this scenario, we notice an exponential growth in the caseload for all the four countries. In fact the caseload growth is at a higher rate than in Scenario 1.

• 4. All undetected cases are non-spreaders: In this scenario we assume that the probability of an individual staying infected, undetected and being a spreader is $1-p^{\text {scenario}}_{1,n}-p^{\text {scenario}}_{2,n}-p^{\text {scenario}}_{3,n}=0,\forall n$. We modify the other probabilities as follows,

  $$\begin{aligned} p^{\text {scenario}}_{1,n}&\rightarrow p_{1,n} + \frac{1-p_{1,n}-p_{2,n}-p_{3,n}}{3}\\ p^{\text {scenario}}_{2,n}&\rightarrow p_{2,n} + \frac{1-p_{1,n}-p_{2,n}-p_{3,n}}{3} \end{aligned}$$

  In this scenario we assume that all the undetected infected individuals do not spread the disease. We find that the pandemic goes extinct in a few months.

• 5. No contact tracing and all undetected cases are spreaders: In this scenario we assume that $p^{\text {scenario}}_{1,n}+p^{\text {scenario}}_{3,n}=0,\forall n$. Thus, in this scenario there is no contact tracing and all undetected cases are spreaders. We modify the other probabilities as follows,

  $$\begin{aligned} p^{\text {scenario}}_{2,n}&\rightarrow p_{2,n} + \frac{p_{1,n}+p_{3,n}}{2} \end{aligned}$$

  We find that, as expected, the caseload is seen to grow at an exponential rate for all the four countries in this scenario.

• 6. Best case scenario: We assume that $p^{\text {scenario}}_{2,n}+(1-p^{\text {scenario}}_{1,n}-p^{\text {scenario}}_{2,n}-p^{\text {scenario}}_{3,n})=0,\forall n$. In this scenario all detected infected individuals are quarantined and all their contacts are traced meticulously. Further, all undetected cases are non-spreaders. We modify the other probabilities as follows,

  $$\begin{aligned} p^{\text {scenario}}_{1,n}&\rightarrow p_{1,n} + \frac{1-p_{1,n}-p_{3,n}}{2} \end{aligned}$$

  In this scenario we find that the pandemic extinguishes in the first few months in all the four countries considered. We note that in this Scenario the pandemic goes extinct much more quickly than in Scenario 4.

The caseload trajectory plots for all the six counterfactual scenarios for India and South Korea is shown in Fig. 14 and 15 respectively.

5 Forecasting

We consider the problem of forecasting future caseloads using the estimated model. The problem is challenging because for each period we need to forecast values of four new parameters $\lambda _j,p_{1,j},p_{2,j},p_{3,j}$. We use an adaptive approach in which we use the values of the estimated parameters to forecast. We apply the wavelet filtering based forecasting (WFF) method given in (Joo and Kim 2015; Conejo et al. 2005). Here each of the four time series of the estimated parameters are decomposed as trend plus variation, and then they are forecast using exponential smoothing (ETS). We use the function fittest.wavelet from the R-package TSPred, Salles and Ogasawara (2021) to implement this wavelet based forecasting method. After forecasting each parameter of the model we use Theorem 3.5 to obtain caseloads in the forecasting period. We present two slightly different methods to forecast the parameter values, named Method A and Method B, that are given below.

Let t be the last period for which actual caseload data is available. We would forecast the values of the caseload at periods $t+k, k=1,2,3$.

Method A:

Since $\lambda _j>0$ for all j, we forecast the transformed quantity $\log \lambda _j$. We forecast $\lambda _{t+k}$ as $\exp (f_k)$, where $f_k$ is the forecast of $\log \lambda _{t+k}$ using WFF method. Since, $0 \le p_{i,j}\le 1, i=1,2,3$, we forecast $\log (\frac{p_{i,j}}{1-p_{i,j}})$ using WFF method. We forecast $p_{i,t+k}$ as $\frac{\exp (f_{i,k})}{1+\exp (f_{i,k})}$, where $f_{i,k}$ is the forecast of $\log (\frac{p_{i,j}}{1-p_{i,j}})$ for period $t+k$.

Method B:

This approach is motivated by the fact that the changes in the parameter values are not likely to be drastic in successive time periods. Here, we forecast $\lambda _j$ using the series $\{\Delta _j=\log \lambda _j-\log \lambda _{j-1},j=2,\cdots ,t\}$. Suppose the forecast value of $\Delta _j$ at period $t+k$ is $f'_k$ using WFF method, then the forecast of $\lambda _{t+k}$ is $\lambda _{t+k-1}\exp (f'_k)$. Again, we forecast $p_{i,j}$ using the series of differences $\{\Psi _j=\log (\frac{p_{i,j}}{1-p_{i,j}})-\log (\frac{p_{i,{j-1}}}{1-p_{i,{j-1}}}),j=2,\cdots ,t\}$. Suppose the forecast value $\Psi _j$ for period $t+k$ is $f'_{i,k}$ using WFF method, then the forecast of $p_{i,t+k}$ is $p_{i,t+k-1}\frac{\exp (f'_{i,k})}{1-p_{i,t+k-1}+\exp (f'_{i,k})p_{i,t+k-1}}$.

We now apply both the methods A and B to predict for three periods for all the four countries. The results are given in Table 4. For India we have parameter estimates up to 6 August 2021. We forecast for the period from 7 August 2021 to 5 September 2021. We find that for method A, the forecast value is close in the first two periods. For method B, the forecast values are close in the last two periods. For US we obtained parameter estimates up to 24 July 2021. We forecast for the period from 25 July 2021 to 23 August 2021. For method A, the forecast values are lower in the first period, close to the actual in the second period and in the third period the forecast value is substantially higher than the actual number of cases. In method B, the forecast value is much closer in the first period than method A but doesn’t perform well in the second and third period. The model forecasts for UK for the period from 26 July 2021 to 24 August 2021. Method A forecast for the first period is close to that of the actually observed value. Both approaches under-forecast in the next two periods. For South Korea, we forecast the caseload from 12 July 2021 to 11 August 2021. Here approach A’s forecast value is closer to the actual in the first and third period. Thus it appears that both these forecasting methods are able to produce a reliable forecast of the caseload for the next period but the accuracy falls off for further periods. An ensemble approach with suitable weights given to each of the methods may be considered when predicting caseloads for periods beyond the next.

6 $T_n$: A time varying alternative to $R_0$

In this section we discuss an analogue from our model of the commonly studied reproduction number $R_0$ of an infectious disease epidemic. In the classical SIR model for epidemics, the reproduction number $R_0$ depends on the initial number of susceptible, the estimated recovery and transmission rate, Van den Driessche (2017). It may be noted that the recovery and transmission rate in the SIR model are assumed to be constant. This implies that the reproduction number under the SIR model is constant over time. However in real world scenarios the reproduction number of disease could vary over time due to mutations in the disease causing pathogen, change in behavior of the susceptible individuals and due to extraneous interventions. Therefore, one requires to estimate reproduction number that is varying over time. A time varying measure of reproductive number is a useful tool for the policymaker as it can indicate the effectiveness of a proposed or an ongoing intervention. There have been recent calls towards studying alternate measures of reproduction number (Hébert-Dufresne et al. 2020; Harvey and Kattuman 2021). Cori et al. (2013) proposed a statistical approach to estimate the reproduction number, that they refer to as $R_t$, from daily incidence data. They consider number of incidences at time t as a weighted sum of all past incidences multiplied by $R_t$, where recent incidences are more likely to cause a future incidence. One is required to specify a prior on the distribution for these weights, which is referred to as the serial interval distribution. They then estimate $R_t$ using Bayesian inference.

Definition 6.1

We define $T_n$, under the MBPE model as,

$$\begin{aligned} T_n&=\frac{E(X_{n+1,C})}{E(X_{n,C})}\\&=\frac{(p_{1,n+1}+p_{2,n+1})(1-p_{1,n}-p_{3,n})+p_{1,n}}{(p_{1,n}+p_{2,n})(1-p_{1,n-1}-p_{3,n-1})+p_{1,n-1}}\lambda _{n+1}(1-p_{1,n-1}-p_{3,n-1}) \end{aligned}$$

Thus $T_n$ is the ratio of the number of new cases expected under the model at generation $n+1$ to that in generation n. In our model the extinction is dependent on $T_n$ as noted in Equation 1 that $\lim _{n \rightarrow \infty } E(S_{n,C})<\infty$, i.e. $E(S_{n,C})$ converges if, $T_n<1$ as $n\rightarrow \infty$. Because of this property we propose to examine $T_n$ for understanding the behavior of the epidemic over a period of time. Similar to $R_0$ we note that the epidemic could be said to be declining if $T_n<1$ and enhancing if $T_n>1$ for successive generations. In computing $R_t$ as proposed in Cori et al. (2013) it is assumed that the serial interval distribution is not time varying. But in our model there is no such restriction and $T_n$ can accommodate changes in infectiousness rates brought about by measures such as lockdown and segregation by adjusting the values of $\lambda _n$. In fact at each generation n, we can attribute any variation in $T_n$ to one of the features such as change in infectiousness rate ($\lambda _{n+1}$) or change in the probabilities ($p_{1,n},p_{2,n}$ or $p_{3,n}$).

Now suppose that after a reasonably long duration of time the values of $\lambda _n, p_{1,n},p_{2,n},p_{3,n}$ have stabilised and don’t change significantly. In that case observe that $T_n \approx \lambda _{n+1}(1-p_{1,n}-p_{3,n})$. Thus, for $T_n<1$ for successive generations, we need to have either $\lambda _n$ to be low or $p_{1,n}+p_{3,n}$ to be close to 1 or both. Various health policy interventions can be designed to achieve these conditions. Policies such as lockdown can reduce the value of $\lambda _n$ while extensive testing and contact tracing along with good citizenship behaviour can enhance $p_{1,n}+p_{3,n}$. Since, in this situation the expression for $T_n$ does not depend on $p_{2,n}$, this indicates that mere detection of disease without meticulous contact tracing is not effective in controlling the epidemic.

We compute $R_t$ and $T_n$ for the caseload data of COVID-19 for India and South Korea. We assume the mean of the serial interval distribution to be 5 and the standard deviation to be 0.3 as in Rai et al. (2021). We use the R-package EpiEstim (Cori 2021) to compute $R_t$. To compute $R_t$ we used daily COVID-19 caseload data for each of these countries. We plot the results for India and South Korea in Fig. 16 and 17 respectively. $R_t$ and $T_n$ appear to move in tandem for both these countries.

In Table 5 we forecast the values of $T_n$ for the next 3 periods. We use the same forecasting method and periods as given in Sect. 5. The forecasted values of $T_n$ for India is around or less than one, which may indicate that cases do not rise in these periods.

7 Conclusion

In this article we propose a new Multi-type Branching process model for epidemic propagation that considers variation over time due to the behavior of citizens, government interventions in the form of lockdown, testing and contact tracing and the infectiousness of the variant of the virus in circulation in that country. In addition the model has tractability benefit as the key quantities can be obtained in a closed form. To the best of our knowledge this model is the first one that allows for theoretical examination of infectious disease transmission in the simultaneous presence of imperfection in containment strategies and under-reporting. We apply the model to the publicly available COVID-19 caseload data for four countries namely, India, South Korea, US and UK, and obtain good fit in each case. The short-term predictive performance of the model is seen to be good. The proposed model can be of use for health policymakers in formulating and evaluating interventions during a pandemic. An analogue of the widely used reproduction number ($R_0$) of the SIR model is given in Sect. 6 that can be of use for monitoring the progress of the epidemic.

It may be possible to adapt the MBPE model discussed in this paper to incorporate a spatial dependence structure that would allow estimation of unreported cases at a more granular level in the country. We intend to explore this problem in future. One of the major challenges we foresee in applying such a spatio-temporal model to real caseload data is to obtain reliable data at a suitably granular spatial scale. Another challenge that we anticipate is related to the specification of an appropriate spatial dependence structure. In developing countries migration for economic reasons is a very common occurrence. The disease may spread to geographically distant places through migration of diseased individuals. Thus along with information about geographical nearness we need to incorporate other information such as the extent of migration from one place to another while specifying the spatial dependence structure. Since, migration data at a granular scale is often not available the use of suitable proxies may need to be explored.

Fig. 1

A schematic of a possible path realization of the multi-type branching process described in Sect. 3.2 upto 3 generations

Table 1 The regularization parameter values used in the loss functions for fitting COVID-19 caseload data for the four countries

Table 2 Cumulative number of detected cases and cumulative number of model fitted detected cases in each country. The numbers are until 6 August 2021 for India, 24 July 2021 for US, 25 July 2021 for UK and 11 July 2021 for South Korea

Table 3 Cumulative number of detected cases and cumulative number of model fitted undetected cases in India and South Korea. The numbers are until 6 August 2021 for India and 11 July 2021 for South Korea

Fig. 2

Plot of model predicted detected cases in each period (blue) from 3 February 2020 to 6 August 2021 and observed cases in each period (red) from 24 March 2020 to 6 August 2021 in India

Fig. 3

Plot of estimated $\lambda _t$ in India from 3 February 2020 to 6 August 2021

Fig. 4

Plot of estimated $p_{1,t}$ (blue), $p_{2,t}$ (red) and $p_{3,t}$ (orange) in India from 13 February 2020 to 6 August 2021

Fig. 5

Plot of model predicted number of quarantining due to contact tracing, Infected-Undetected-Spreaders and Infected-Undetected-Non-Spreaders in India from 3 February 2020 to 6 August 2021

Fig. 6

Plot of Infected-Undetected cases with it’s 95% uncertainty band from 3 February 2020 to 6 August 2021 in India

Fig. 7

Plot of model predicted detected cases in each period (blue) from 9 January 2020 to 11 July 2021 and observed cases in each period (red) from 19 January 2020 to 11 July 2021 in South Korea

Fig. 8

Plot of estimated $\lambda _t$ in South Korea from 9 January 2020 to 11 July 2021

Fig. 9

Plot of estimated $p_{1,t}$ (blue), $p_{2,t}$ (red) and $p_{3,t}$ (orange) in South Korea from 9 January 2020 to 11 July 2021

Fig. 10

Plot of Infected-Undetected cases with it’s “95% uncertainty band” from 9 January 2020 to 11 July 2021 in South Korea

Fig. 11

Plot of model predicted number of quarantining due to contact tracing, Infected-Undetected-Spreaders and Infected-Undetected-Non-Spreaders in South Korea from 9 January 2020 to 11 July 2021

Fig. 12

Plot of model predicted detected cases in each period (blue) from 21 January 2020 to 24 July 2021 and observed cases in each period (red) from 21 January 2020 to 24 July 2021 in US

Fig. 13

Plot of model predicted detected cases in each period (blue) from 22 January 2020 to 4 August 2021 and observed cases in each period (red) from 1 February 2020 to 25 July 2021 in UK

Fig. 14

Plot of the caseload trajectory for counterfactual scenarios as described in Sect. 4.3 for India

Fig. 15

Plot of the caseload trajectory for counterfactual scenarios as described in Sect. 4.3 for South Korea

Table 4 Actual and forecasted values for the MBPE model in 3 successive forecasting periods for India, USA, UK and South Korea. The forecasting method is given in Sect. 5. The periods 1, 2, 3 for India end on 16 August 2021, 26 August 2021 and 5 September 2021 respectively. The periods 1, 2, 3 for USA end on 3 August 2021, 13 August 2021 and 23 August 2021 respectively. The periods 1, 2, 3 for UK end on 4 August 2021, 14 August 2021 and 24 August 2021 respectively. The periods 1, 2, 3 for South Korea end on 22 July 2021, 1 August 2021 and 11 August 2021 respectively

Fig. 16

Plot of $R_t$ and $T_n$ in India from 23 April 2020 to 6 August 2021

Fig. 17

Plot of $R_t$ and $T_n$ in South Korea from 28 April 2020 to 12 July 2021

Table 5 Forecasted values of $T_n$ in 3 successive forecasting periods for India and South Korea using the forecasting approaches discussed in Sect. 5. The periods 1, 2, 3 for India end on 16 August 2021, 26 August 2021 and 5 September 2021 respectively.  The periods 1, 2, 3 for South Korea end on 22 July 2021, 1 August 2021 and 11 August 2021 respectively

Appendices

Proof of theorem 3.3

In Sect. 3.1 we state Lemma 3.2 and we provide it’s proof here,

Proof of Lemma 3.2

Recall that $X_{2,ID}=X_{2,T}+X_{2,UT}$. Now, $X_{2,T}=\sum _{i=1}^{X_{2,ID}}U_i$, where $U_i$’s are i.i.d with $U_i\sim \text {Bernoulli}\left( \frac{p_{1,2}}{p_{1,2}+p_{2,2}}\right)$. Applying Wald’s lemma,

$$\begin{aligned} E(X_{2,T})=E(X_{2,ID})\frac{p_{1,2}}{p_{1,2}+p_{2,2}} \end{aligned}$$

and therefore, $E(X_{2,UT})=E(X_{2,ID})-E(X_{2,T})=E(X_{2,ID})\frac{p_{2,2}}{p_{1,2}+p_{2,2}}.$

Applying induction $\forall n>2$, it follows that,

$$\begin{aligned} E(X_{n,T})=E(X_{n,ID})\frac{p_{1,n}}{p_{1,n}+p_{2,n}} \end{aligned}$$

and therefore, $E(X_{n,UT})=E(X_{n,ID})-E(X_{n,T})=E(X_{n,ID})\frac{p_{2,n}}{p_{1,n}+p_{2,n}}.$

In Sect. 3.1 we state Theorem 3.3 and we provide it’s proof here,

Proof

• 1.

  • (a) Since $X_{1,T}\sim \text {Poi}(\lambda _1p_{1,1})$ and $X_{1,UT}\sim \text {Poi}(\lambda _1p_{2,1})$, $E(X_{1,ID})=E(X_{1,T})+E(X_{1,UT})=\lambda _1(p_{1,1}+p_{2,1})$ and $E(X_{1,IND})=\lambda _1(1-p_{1,1}-p_{2,1})$. We proceed with the proof using induction. Now for $n\ge 2$,

    $$\begin{aligned} E(X_{n,IND})&=E(X_{n-1,UT})E(Z'_{n,i})+E(X_{n-1,IND})E(Z_{n,i})\\&=E(X_{n-1,ID})\frac{p_{2,n-1}}{p_{1,n-1}+p_{2,n-1}}\lambda _n(1-p_{1,n}-p_{2,n})+E(X_{n-1,IND})\\ {}&\lambda _n(1-p_{1,n}-p_{2,n})\\&=\lambda _n(1-p_{1,n}-p_{2,n})\prod _{k=1}^{n-1}\lambda _k(1-p_{1,k}) \end{aligned}$$

  • (b) We prove using induction. For $n\ge 2$,

    $$\begin{aligned} E(X_{n,ID})&=E(X_{n-1,UT})E(Y_{n,i}')+E(X_{n-1,IND})E(Y_{n,i})\\&=E(X_{n-1,ID})\frac{p_{2,n}}{p_{1,n}+p_{2,n}}\lambda _n(p_{1,n}+p_{2,n})+E(X_{n-1,IND})\lambda _n(p_{1,n}+p_{2,n})\\&=\lambda _n(p_{1,n}+p_{2,n})\prod _{k=1}^{n-1}\lambda _k(1-p_{1,k}) \end{aligned}$$

• 2. $E(X_{n,IQ})=E(X_{n-1,T})E(W_{n,i})=\lambda _{n-1}\lambda _{n}p_{1,n-1}\prod _{k=1}^{n-2}\lambda _k(1-p_{1,k})$

  $$\begin{aligned} E(X_{n,C})&=E(X_{n,ID})+E(X_{n,IQ})\\&=\lambda _{n-1}\lambda _n((p_{1,n}+p_{2,n})(1-p_{1,n-1})+p_{1,n-1})\prod _{k=1}^{n-2}\lambda _k(1-p_{1,k}) \end{aligned}$$

Proof of theorem 3.5

In Sect. 3.2 we state Lemma 3.4 and we provide it’s proof here,

Proof of Lemma 3.4

• 1. Recall that $X_{2,IND}=X_{2,IND}^U+X_{2,IND}'$. Now $X_{2,IND}^U=\sum _{i=1}^{X_{2,IND}}U'_i$, where $U'_i$ is iid with $U'_i\sim \text {Bernoulli}\left( \frac{p_{3,2}}{1-p_{1,2}-p_{2,2}}\right)$. Applying Wald’s lemma,

  $$\begin{aligned} E(X_{2,IND}^U)=E(X_{2,IND})\frac{p_{3,2}}{1-p_{1,2}-p_{2,2}} \end{aligned}$$

  and therefore, $E(X_{2,IND}')=E(X_{2,IND})-E(X_{2,IND}^U)=E(X_{2,IND})\frac{1-p_{1,2}-p_{2,2}-p_{3,2}}{1-p_{1,2}-p_{2,2}}.$ Applying induction $\forall n>2$, it follows that,

  $$\begin{aligned} E(X_{n,IND}^U)=E(X_{n,IND})\frac{p_{3,n}}{1-p_{1,n}-p_{2,n}} \end{aligned}$$

  and therefore, $E(X_{n,IND}')=E(X_{n,IND})-E(X_{n,IND}^U)=E(X_{n,IND})\frac{1-p_{1,n}-p_{2,n}-p_{3,n}}{1-p_{1,n}-p_{2,n}}.$

• 2. Recall that $X_{2,ID}=X_{2,T}+X_{2,UT}$. Now $X_{2,T}=\sum _{i=1}^{X_{2,ID}}U_i$, where $U_i$ is iid with $U_i\sim \text {Bernoulli}\left( \frac{p_{1,2}}{p_{1,2}+p_{2,2}}\right)$. Applying Wald’s lemma,

  $$\begin{aligned} E(X_{2,T})=E(X_{2,ID})\frac{p_{1,2}}{p_{1,2}+p_{2,2}} \end{aligned}$$

  and therefore, $E(X_{2,UT})=E(X_{2,ID})-E(X_{2,T})=E(X_{2,ID})\frac{p_{2,2}}{p_{1,2}+p_{2,2}}.$ Applying induction $\forall n>2$, it follows that,

  $$\begin{aligned} E(X_{n,T})=E(X_{n,ID})\frac{p_{1,n}}{p_{1,n}+p_{2,n}} \end{aligned}$$

  and therefore, $E(X_{n,UT})=E(X_{n,ID})-E(X_{n,T})=E(X_{n,ID})\frac{p_{2,n}}{p_{1,n}+p_{2,n}}.$

In Sect. 3.2 we state Theorem 3.5 and we provide it’s proof here,

Proof of Theorem 3.5

• 1.

  • (a) The proof is similar to that of Theorem 3.3. We proceed with the proof using induction. For $n\ge 2$,

    $$\begin{aligned} E(X_{n,IND})&=E(X_{n-1,UT})E(Z'_{n,i})+E(X_{n-1,IND}')E(Z_{n,i})\\&=\lambda _n(1-p_{1,n}-p_{2,n})\prod _{i=1}^{n-1}\lambda _i(1-p_{1,i}-p_{3,i}) \end{aligned}$$

  • (b) We prove using induction, for $n\ge 2$,

    $$\begin{aligned} E(X_{n,ID})&=E(X_{n-1,UT})E(Y_{n,i}')+E(X_{n-1,IND}')E(Y_{n,i})\\&=\lambda _n(p_{1,n}+p_{2,n})\prod _{i=1}^{n-1}\lambda _i(1-p_{1,i}-p_{3,i}) \end{aligned}$$
• 2.
  $$\begin{aligned} E(X_{n,C})&=E(X_{n,ID})+E(X_{n,IQ})\\&=\lambda _{n}\lambda _{n-1}((p_{1,n}+p_{2,n})(1-p_{1,n-1}-p_{3,n-1})+p_{1,n-1})\prod _{k=1}^{n-2}\lambda _k(1-p_{1,k}-p_{3,k}) \end{aligned}$$