Single-image reconstruction using novel super-resolution technique for large-scaled images

Abstract

A fast and novel method for single-image reconstruction using the super-resolution (SR) technique has been proposed in this paper. The working principle of the proposed scheme has been divided into three components. A low-resolution image is divided into several homogeneous or non-homogeneous regions in the first component. This partition is based on the analysis of texture patterns within that region. Only the non-homogeneous regions undergo the sparse representation for SR image reconstruction in the second component. The obtained reconstructed region from the second component undergoes a statistical-based prediction model to generate its more enhanced version in the third component. The remaining homogeneous regions are bicubic interpolated and reflect the required high-resolution image. The proposed technique is applied to some Large-scale electrical, machine and civil architectural design images. The purpose of using these images is that these images are huge in size, and processing such large images for any application is time-consuming. The proposed SR technique results in a better reconstructed SR image from its lower version with low time complexity. The performance of the proposed system on the electrical, machine and civil architectural design images is compared with the state-of-the-art methods, and it is shown that the proposed scheme outperforms the other competing methods.

1 Introduction

A high-resolution image is always desirable in most digital image processing applications such as office automation, medical imaging, remote sensing, and video surveillance. A high-resolution image gives a better appearance and better classification of image regions. The image resolution means the scene area is represented by a single pixel, and higher resolution (HR) refers to a small area resulting in more spatial image details. This resolution of an image depends on the camera device used during image acquisition. There are various issues to obtaining a high-resolution image using hardware devices. However, algorithmic image reconstruction techniques are more promising for bringing HR images from low-resolution (LR) ones.

We may get the HR images from observed LR images by suppressing the degradation introduced during image acquisition and increasing the high-frequency components. The process is referred to as Super-Resolution (SR) technique. Moreover, during the SR process, the non-redundant information in LR images is combined with domain-specific knowledge to create an HR image. One commonly used approach to SR is single-image interpolation, which is used to increase the image size. In this case, no additional information is provided, and hence, the quality of the HR image is limited due to the nature of the problem. We adopt here the patch-based (or exemplar-based) method for SR, where an LR image $I_L$ is partitioned into several patches, and then each LR patch is replaced by its corresponding HR patch to reconstruct the HR image, say, $I_H$. Various methods differ mainly due to: (1) How to partition $I_L$ into LR patches; (2) How to generate or select HR patch corresponding to a given LR patch; (3) How to combine HR patches to reconstruct $I_H$.

The objective of this problem domain is to obtain the best possible SR image and accept the SR image as quickly as possible. The solution to this problem depends upon available single LR images or multiple LR images. So, the methods of SR technique are categorized into single-frame SR and multi-frame SR techniques. Moreover, the single-frame SR algorithm is also categorized into two approaches: (a) interpolation-based method and (b) patch-based method (Milanfa 2010).

Most of these methods use the single-frame and the patch-based super-resolution techniques to reconstruct HR images from LR images. These methods have achieved better performance in the research area of image super-resolution. From the great success of this single-frame and patch-based SR method (Yang et al. 2010), in this paper, patches are extracted from the input image I. Then, the implementation focuses on the recovering SR version of the given low-resolution version of I. To capture the significant co-occurrence prior and speed up the process, we obtain some representation from the image patch pairs extracted from HR and LR images. These representations are the first- and second-order gradients from each patch.

The contributions of the proposed work are as follows:

• To speed up the super-resolution (SR) image reconstruction, the LR patches are classified into homogeneous and non-homogeneous groups based on the features extracted from each patch. If an LR patch belongs to the non-homogeneous group, the proposed SR method is applied to obtain its HR patch; otherwise, the bi-cubic interpolation method is applied on the homogeneous patches.

• For the classification of homogeneous and non-homogeneous LR patches, an unsupervised clustering technique has been employed on the texture features computed from the grey-level co-occurrence matrices of the image patches.

• In the training phase, the features extracted from the LR and HR patch pair of $I_L$ and $I_H$ undergo a sparse representation to generate Dictionary. We have adopted this sparse representation using Dictionary, as a recent result suggests that HR signals’ linear relationships are well recovered from their lower-dimensional projection obtained from sparse representation. Moreover, image patch-based sparse representation plays an important role in regularizing SR ill-posed problems with effectiveness and robustness properties.

• The obtained HR image patches are fed to a prediction model to produce refined SR image patches.

The organization of this paper is as follows: Sect. 2 discusses some related works. Section 3 describes the proposed method with a detailed discussion of each component of the proposed system. The experimental results and discussions have been demonstrated in Sect. 4. Section 5 concludes this paper.

2 Related work

The interpolation-based methods such as Bilinear or Bicubic interpolation applied on smooth images with some jagged and ringing artefacts to exploit the natural image prior that results better results (Dai et al. 2007; Sun et al. 2008). The patch-based methods locally capture the prior co-occurrences between LR and HR image patch pairs. Then, it employs a large database of LR and HR patch pairs and uses a learning mechanism for the corresponding mapping between the LR and HR image patches that are applied to a new LR image to reconstruct its most likely HR version (Yang et al. 2010; Glasner et al. 2009). Generally, these methods are based on the image edge prior or image gradient prior (Sun et al. 2008). The objective of this kind of method is to magnify the image so that the edge sharpness and the texture details within the image are preserved. Natsui and Nagao (2016) proposed a single-frame SR technique using multiple graph-structured programs based on Cartesian Genetic Programming, which is one of the evolutionary methods like genetic algorithms. Lai et al. (2012) proposed a method for single-frame SR technique, where a total variation regularization was used to minimize the iterative back-projection-based SR reconstruction error by suppressing the chessboard and ringing artefacts at the time of acquiring the high-resolution image. Dang and Radha (2017) proposed a single-image SR technique using Tangent Space Learning of high-resolution patch manifold, which is based on the linear approximation of HR patch space using sparse subspace clustering algorithms. A method for compressed sensing reconstruction method with single plane wave transmission for super-resolution of ultrasound images had been proposed by Shu et al. (2018). A multi-frame SR technique based on the fusion of multiple low-resolution images captured at Visual Wavelength and Near-Infrared lighting conditions with different camera positions for synthesizing HR colour images had been proposed by Honda et al. (2018).

A well comprehensive survey for super-resolution of biometric images such as the face (2D+3D), iris, finger-print and gait based on operation domain (spatial and frequency), singe-frame, multi-frame, reconstruction, learning, feature domain and deep-learning-based SR techniques had been discussed by Nguyen et al. (2018). Akyol and GöKmen (2012) have proposed a method for face super-resolution by enhancing the shape and texture information of faces. A multi-channel constraint-based image super-resolution technique that has the capability for collaborative representations, clustering, multilayer mapping relationships to reconstruct HR images from LR images had been proposed by Cao and Li (2018). Zhao et al. (2017) proposed a method for SR technique where the adaptive sparse coding had been employed by establishing the regularization parameters with integrating correlation and sparsity terms in the regularization. Their SR method modulates the collaborative representation and the sparse representation. The CNN-based architectures with a subpixel network have been considered for the resolution enhancement of 2D cone-beam CT image slices of ex vivo teeth in Hatvani et al. (2018). A novel dehazing model for remote sensing images has been proposed by Singh and Kumar (2018a). Deep Learning and Transfer Learning-Based Super-Resolution Reconstruction from Single Medical Image has been proposed by Zhang and An (2017). A deep learning framework based on a generative adversarial network to perform super-resolution incoherent imaging systems has been proposed in  Liu et al. (2019). Metaheuristic-based deep COVID-19 screening model from chest X-ray has been proposed in images (Kaur et al. 2021). Further, a multi-objective differential evolution-based deep neural networks had been employed for multi-modality medical image fusion technique by Kaur and Singh (2021). Singh et al. had built a model for defogging of road images using gain coefficient-based trilateral filter (Singh and Kumar 2018b).

3 Proposed methodology

The proposed super-resolution (SR) technique is applied mainly to reconstruct the high-resolution (HR) image from the low-resolution (LR) image of electrical circuit drawings using the single-frame and patch-based super-resolution technique. The proposed method can also be applied to other drawings, such as mechanical drawing and architectural drawing. We have done some experiments in this direction to see the performance of the proposed method.

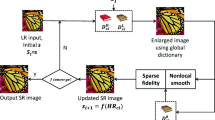
The proposed method has three main phases: (1) In the first phase, we partition m-training images $I_L$s into several patches. Then, the patches are divided into two clusters based on the homogeneous/non-homogeneous texture pattern using the k-means clustering algorithm. Then, classification of an LR patch of an individual LR image $I_L$ is done by comparing its GLCM texture features with that of the cluster centres; (2) In the second phase, the bicubic interpolation (Hwang and Lee 2004) (i.e. no super-resolution is applied on it) is applied on the homogeneous patches, while the non-homogeneous patches undergo for sparse representation based SR method followed by statistical prediction model based algorithms; (3) Here, the colour image I is transformed to its $(Y, C_b, C_r)$ colour channel and only luminance channel (Y) is used in the first and second phase. The remaining $C_b, ~C_r$ channels are interpolated using the bi-cubic interpolation technique and are combined with the obtained HR Y-channel in the third phase. A brief overview of the proposed system is shown in Fig. 1.

Fig. 1

Data flow diagram of the proposed system

3.1 Preprocessing

During preprocessing, (R, G, B) of each input low-resolution (LR) image $I_L$ is transformed to $(Y, C_b, C_r)$ colour channel, and super-resolution is performed only on Y-channel LR image to obtain the Y-channel HR (High Resolution) image. Here, we have employed the patch-based SR (Super-Resolution) technique. Hence, a patch $w_{n\times n}$ with overlapping of p pixels both the horizontal and vertical directions is considered from ${\mathcal {I}}_Y$. Then, Gray-level Co-occurrences Matrix (GLCM) texture features (Umer et al. 2016) ${\mathcal {F}}_{w_i}\in {\mathbb {R}}^{d\times 1}$ are computed from each $w_i$, i.e. ${\mathcal {I}}_Y$ gives $({\mathcal {F}}_{w_1},\cdots ,{\mathcal {F}}_{w_N}) \in {\mathbb {R}}^{d \times N}$, where N be the number of patches and d is the number of texture features from each patch. Now, k-means clustering algorithm is applied on GLCM texture features collected from m-training ${\mathcal {I}}_Y$ images to obtain a code-book $C\in {\mathbb {R}}^{d \times 2}$ considering two classes ($k=2$): homogeneous and non-homogeneous. Here, the usefulness of k-means clustering algorithm are: (1) It can well differentiate between the homogeneous and non-homogeneous patterns within the image based on GLCM texture features computed from patches; (2) It takes lesser time for finding the dictionary of discriminate patches; (3) The other clustering algorithm can take more time with better features. At the same time, the k-means provides an excellent pre-clustering technique and reduces the spaces between clusters into disjoint smaller sub-spaces better than the other clustering algorithms. For a given image ${\mathcal {I}}_Y$, the feature vector ${\mathcal {F}}_{w_i}\in {\mathbb {R}}^{d\times 1}$ corresponding to each $w_i$ is compared with $C\in {\mathbb {R}}^{d \times 2}$ using minimum distance classifier to predict whether $w_i$ has homogeneous or non-homogeneous region. The non-homogeneous $w_i$ is considered as LR ($y_i$) and undergoes for super-resolution technique. In the next section, we discuss the super-resolution technique using sparse representation.

3.2 SR using sparse representation (Case-1)

Sparse representation is a powerful technique for representing, compressing, and processing high dimensional signals in low dimensional space. The classes of signals such as images and audio can be modelled through sparse representation concerning their fixed bases. Effective and efficient convex optimization or greedy pursuit algorithms are available for computing those representations with high fidelity. These are the main reasons for a successful and wide use of sparse representation (Wright et al. 2010). So, the sparse representation has been extensively used in many computer vision tasks, such as super image resolution, image de-noising, image inpainting, motion and data segmentation, image classification, and face recognition. In most of these applications, using sparsity as prior, sparse representation outperforms the state-of-the-art results.

We have employed patch-based sparse representation for single-image super-resolution (SR) in this work. However, the non-overlapping patch-wise operation may cause block artefacts; hence, overlapping patches are employed to overcome this problem. The sparse representation provides high-quality image reconstruction for SR algorithms by using overlapping patches over the image (Toutounchi et al. 2017). On the other hand, overlapping patches leads to more time consumption. To overcome this, we have adopted only a tiny overlap between patches. To reduce the computational cost further, we have employed a technique for patch selection based on its homogeneous or non-homogeneous texture pattern (discussed above) and applied the sparse representation only on those patches that are non-homogeneous. During sparse representation, we consider LR patches ($y_i$) from Y-channel of LR image ${\mathcal {I}}_y$ and then extract features from each $y_i$.

In the training phase, more precisely during Dictionary learning, we take high-resolution (HR) image, say, ${\mathcal {I}}_x$ from the application domain and deliberately form its low-resolution (LR) version, say, ${\mathcal {I}}_y$ through the appropriate down-sampling method. If ${\mathcal {I}}_x$ is a gray-level image, so is ${\mathcal {I}}_y$. However, if we had to handle colour images, then consider that ${\mathcal {I}}_x$ and ${\mathcal {I}}_y$ are corresponding Y-channel images. Different features can be extracted from the LR patches which are mentioned in the existing literature. Freeman et al. (2000) extracted edge-based information from LR patches by using a high pass filter. Chang et al. (2004) and Yang et al. (2010) have extracted first- and second-order gradients from LR and HR patches. In this work, we also use first ($g_1 = [-1, 0, 1], g_1^T$) and second-order ($g_3 = [1, 0, -2, 0, 1], g_3^T$) gradients of patches. These filters are directly applied to the training images (LR ${\mathcal {I}}_y$ and HR ${\mathcal {I}}_x$), which yields four gradient maps at each location. Then, any patch is represented in terms of feature vector corresponding to its gradient map. To track the correspondence between HR (obtained original image) and LR patches (down-sampled image), feature vectors of $x_i$ and $y_i$ are concatenated to form $v_i$.

The above-mentioned feature vectors are used to create two dictionaries ${\mathcal {D}}_l$ and ${\mathcal {D}}_h$ corresponding to LR and HR patches, respectively, which will be subsequently exploited to obtain sparse representations of LR and HR patches, respectively.

Since sparse representation is an ill-posed problem, we take the help of constraints to solve this problem. First, the image observation model is considered where a low-resolution image ${\mathcal {I}}_y$ is obtained from the given high-resolution image ${\mathcal {I}}_x$, such that

$$\begin{aligned} {\mathcal {I}}_y =\mu {\mathcal {H}} {\mathcal {I}}_x \end{aligned}$$

(1)

where $\mu$ is the down-sampling factor and ${\mathcal {H}}$ is the blurring filter. Since Eq. (1) represents a many-to-one mapping, for a given low-resolution image ${\mathcal {I}}_y$ infinitely many solutions of ${\mathcal {I}}_x$ can be obtained by solving Eq. (1). To resolve this issue, we consider that each patch $x \in {\mathcal {I}}_x$ can be represented as a sparse linear combination of dictionary ${\mathcal {D}}_h$. Similar concept is true for $y \in {\mathcal {I}}_y$ also. Or, in general, the vector $v ~(= [x ~|~y])$ can be represented by a sparse combination of dictionary ${\mathcal {D}}$, which in turn would be concatenation of ${\mathcal {D}}_h$ and ${\mathcal {D}}_l$, i.e. ${\mathcal {D}} = {\mathcal {D}}_h ~|~ {\mathcal {D}}_h$. The vector v contains various features including pixel intensities of HR and LR patches concatenated together. Hence,

$$\begin{aligned} v={\mathcal {D}} \alpha \end{aligned}$$

(2)

for some coefficient vector $\alpha \in R^K$, where K is the number of words or elements in the Dictionary and $||\alpha ||_0 \le \le K$, which is a sparsity constraint. Note that both ${\mathcal {D}}$ and $\alpha$ are unknown and are learned simultaneously by optimizing the following equation.

$$\begin{aligned} \min ||\alpha ||_0~~\text {s.t.}~~||{\mathcal {D}} \alpha - v||^2_2\le \epsilon \end{aligned}$$

(3)

Thus, the above mentioned [Eq. (3)] sparse representation $\alpha$ corresponds to both HR and LR patches together, which have spatial compatibility between the neighbours. So using this $\alpha$ for x, the entire HR image ${\mathcal {I}}_x$ is regularized and refined using the reconstruction constant. For this purpose, local modelling for sparsity prior has been introduced for local patches to recover some HR patch x which may be lost during processing.

During local modelling, the HR patch $x_i$ is derived for the corresponding LR patch $y_i$. For these two dictionaries, ${\mathcal {D}}_l$ and ${\mathcal {D}}_h$ is needed separately. Recall that dictionary ${\mathcal {D}}$ is generated, through sparse model of the patches, from vector $v ~(= [x ~|~y])$. This suggests that dictionary ${\mathcal {D}}$ can straightaway be decomposed into ${\mathcal {D}}_l$ and ${\mathcal {D}}_h$. Also note that here both these dictionaries ${\mathcal {D}}_l$ and ${\mathcal {D}}_h$ have the same sparse representation $\alpha$ (i.e. $\alpha _l$ or $\alpha _h$ are same) for each $y_i$ and $x_i$ patch pairs. And this suggests the method for generating HR patch, given the test LR patch and two dictionaries. For each input LR patch $y_i$, the corresponding sparse representation $\alpha$ is obtained based on ${\mathcal {D}}_l$. Now, the patch bases of ${\mathcal {D}}_h$ are combined according to $\alpha$ to generate high-resolution patch $x_i$. This solution may be mathematically formulated as

$$\begin{aligned} \min ||\alpha ||_0~~\text {s.t.}~~||{\mathcal {D}}_l\alpha -{\mathfrak {F}} y||^2_2\le \epsilon \end{aligned}$$

(4)

where ${\mathfrak {F}}$ is the feature extraction operator that includes intensity mapping of the patch along with first- and second-order spatial derivatives of the patch. Solving Eq. (4), we obtain a $\alpha$ to represent y in terms of the dictionary ${\mathcal {D}}_l$. Now, same $\alpha$ is used to generate $x_i$ based on ${\mathcal {D}}_h$. So we have

$$\begin{aligned} x = {\mathcal {D}}_h \alpha \end{aligned}$$

(5)

The problem defined in Eq.(4) is NP-hard problem (Aharon et al. 2006), and it says that the obtained sparse representation $\alpha$ could be sufficiently sparse. This can be efficiently approximated by introducing $l_1$-norm in place of $l_0$ norm as follows:

$$\begin{aligned} \min ||\alpha ||_1~~\text {s.t.}~~||{\mathcal {D}}_l\alpha -{\mathfrak {F}} y||^2_2\le \epsilon \end{aligned}$$

(6)

Now, the regularization parameter is introduced in Eq. (6) to obtain following loss function

$$\begin{aligned} {\mathcal {J}}(\alpha ) = \min _{\alpha }||{\mathcal {D}}_l \alpha -{\mathfrak {F}} y||^2_2 + \lambda ||\alpha ||_1 \end{aligned}$$

(7)

Here, the term $\lambda$ balances the solution’s sparsity and the approximation’s fidelity to y. The formulation in Eq. (7) is Lasso (Yang et al. 2012) optimization problem, which is a linear regression regularization with $l_1$-norm on $\alpha$. In this work, we obtain corresponding HR patches for SR image to only those LR patches which are non-homogeneous regions. So, during processing, each non-homogeneous region is considered as $y_i$ image, and then, a patch slides in a raster scan, i.e. horizontally and then vertically. So, there may be the possibility of overlapping patches for the ambiguous region. So, to check closely the previously computed HR patch $x_i$ from the SR reconstruction ${\mathcal {D}}_h \alpha$ of y, we modify Eq.(7) as follows:

$$\begin{aligned} \min ||\alpha ||_1~~\text {s.t.}~~||{\mathcal {D}}_l \alpha - {\mathfrak {F}} y||^2_2 \le \epsilon ~ , ~||{\mathfrak {P}} {\mathcal {D}}_h \alpha -w||^2_2 \le \epsilon \nonumber \\ \end{aligned}$$

(8)

where w contains the value for the particular reconstructed HR image on overlap and ${\mathfrak {P}}$ is a matrix for overlap region between the target patch and the previously computed HR patch. The optimization in Eq.(8) is formulated as

$$\begin{aligned} \min _{\breve{\alpha }}||\hat{{\mathcal {D}}}\breve{\alpha } - {\hat{y}}||^2_2 + \lambda ||\breve{\alpha }||_1 \end{aligned}$$

(9)

where $\hat{{\mathcal {D}}}= [{\mathcal {D}}_l, \beta {\mathfrak {P}} {\mathcal {D}}_h]^T$ and ${\hat{y}}= [{\mathfrak {F}}y,\beta w]^T$. The parameter $\beta =1$ is the control of trade-off between the matching of LR input y and finding a HR patch x which is compatible with its neighbour. The final optimal solution of Eq.(9) is $\breve{\alpha }$, and the final HR patch $\breve{x}$ is computed as

$$\begin{aligned} \breve{x}=\hat{{\mathcal {D}}}\breve{\alpha } \end{aligned}$$

(10)

Fig. 2

Some generic HR images

Fig. 3

Result of the proposed SR technique using sparse representation

Fig. 4

Result of the proposed SR technique using sparse representation followed by prediction model

The HR patch $\breve{x}$ obtained from Eq. (10) has much more better resolution then the LR patch y.

3.3 SR using prediction model (Case-2)

Now, the obtained HR patch $\breve{x}$ undergoes a predicted model which generates much higher resolution HR patch ${\hat{x}}$ considering the previously obtained $\breve{x}$ as LR patch y. Here, also two dictionaries ${\mathcal {D}}_l$ and ${\mathcal {D}}_h$ have been used. The objective of this prediction model is to predict the missing HR details for each LR patch y (here $y=\breve{x}$) via ${\mathcal {D}}_l$ and ${\mathcal {D}}_h$, having different elements. Then, a statistical prediction model is being utilized for prediction the HR representation vector $\alpha _h$ of each patch from its corresponding $\alpha _l$. In above Case-1 technique, the sparse coefficient $\alpha$ is similar for $\alpha _l=\alpha _h$. To introduce more sparsity in $\alpha _l$, ${\mathfrak {z}}_l \in \{-1,1\}^{m_l}$ is computed from $\alpha _l$ which is as follows‘

$$\begin{aligned} {\mathfrak {z}}_{l,j}= \{ \begin{array}{ll} 1, &{} \alpha _{l,j}>\rho , \forall j=1,\cdots ,m_l \\ 0, &{} \text {otherwise} \end{array} \end{aligned}$$

(11)

where $\rho$ is a threshold which adaptively changes for each LR patch and is computed based on following criterion $\sum _{j=1}^{m_l} |\alpha _{l,j}|^2$ for $(|\alpha _{l,j} \le \rho |) \le n \lambda ^2$, where $\lambda$ is a pre-specified parameter. So, the sparsity patterns ${\mathfrak {z}}_l=\{-1,1\}^{m_l}$ for LR patch and ${\mathfrak {z}}_h=\{-1,1\}^{m_h}$ for the HR patch capture the relationships between these two patterns and for this a statistical prediction model is required which is described in the following section.

Table 1 Comparative performance for Case-1 and Case-2 SR techniques for generic images using PSNR and SSIM

Fig. 5

$Img_1$, $Img_2$, $Img_3$, $Img_4$, $Img_5$, $Img_6$, $Img_7$, $Img_8$ are large-scaled electrical circuit images, whereas $Img_9$, $Img_{10}$, $Img_{11}$, $Img_{12}$, $Img_{13}$, $Img_{14}$, $Img_{15}$, $Img_{16}$ are the large-scaled machine and civil layout design images

To capture the statistical dependencies within the sparsity pattern ${\mathfrak {z}}_l=\{-1,1\}^{m_l}$ and ${\mathfrak {z}}_h=\{-1,1\}^{m_h}$, the restricted Boltzmann machine (RBM) (Sutskever et al. 2009) technique is employed which may be described by the conditional probability (Peleg and Elad 2014) as follows:

$$\begin{aligned} p({\mathfrak {z}}_h/{\mathfrak {z}}_l)=\frac{1}{y}exp(b^T_h {\mathfrak {z}}_h+\mathsf {z}^T_h {\mathcal {W}}_{hl}{\mathfrak {z}}_h) \end{aligned}$$

(12)

where $b\in {\mathbb {R}}^m$ is the bias vector and ${\mathcal {W}}\in {\mathbb {R}}^{m_h \times m_l}$ is an interaction matrix between ${\mathfrak {z}}_l=\{-1,1\}^{m_l}$ and ${\mathfrak {z}}_h=\{-1,1\}^{m_h}$. Thus,

$$\begin{aligned} p({\mathfrak {z}}_h/{\mathfrak {z}}_l)=\prod _{j=1}^{m_h} \phi ((b_{h,j}+\mathbf {w}^T_{h_l}{\mathfrak {z}}_l){\mathfrak {z}}_{h,j}) \end{aligned}$$

(13)

where $\phi (s)=\frac{1}{(1+exp(-2s))}$ is the sigmoid function and is due to the elements of ${\mathfrak {z}}_h$ which are statistically independent of ${\mathfrak {z}}_l$. RBM is an exponential model that works with binary vectors, and it leads to the conditional marginal probability for each element of ${\mathfrak {z}}_h$ in ${\mathfrak {z}}_l$ such that

$$\begin{aligned} p({\mathfrak {z}}_{h,j}=1/{\mathfrak {z}}_l)=\phi (b_{h,j}+\mathbf {w}^T_{h_l}{\mathfrak {z}}_l),~~~\forall j=1,\cdots ,m_h \end{aligned}$$

(14)

The obtained ${\mathfrak {z}}_h$ is employed to compute the HR co-efficient $\alpha _h$ using $\alpha _l$ based on the below criterion:

$$\begin{aligned} \alpha _{h,j} = \{ \begin{array}{ll} {\mathcal {G}}_j, &{} ~~{\mathfrak {z}}_{h,j}=1 \\ 0, &{} ~~ {\mathfrak {z}}_{h,j}=-1 \end{array} \end{aligned}$$

(15)

where ${\mathcal {G}}\in {\mathbb {R}}^{m_h}$ is the Gaussian distribution, i.e. ${\mathcal {G}}\alpha _l \sim N({\mathscr {C}}_{hl}\alpha _l,\sum _{hl})$, where ${\mathscr {C}}_{hl}\in {\mathbb {R}}^{m_h \times m_l}$ and $\sum +{ml} \in {\mathbb {R}}^{m_h \times m_h}$. This leads to the following conditional expectation:

$$\begin{aligned} E[\alpha _{h,j}|{\mathfrak {z}}_{h,j}=1,\alpha _l]={\mathfrak {c}}^T_{hl}\alpha _{l}, \forall j=1,\cdots ,m_h \end{aligned}$$

(16)

The models defined in Eq.(15) and (16) show the linear mapping of $\alpha _l$ to $\alpha _h$ and it happens when ${\mathfrak {z}}_h$ is known. In the case where relation between $\alpha _l$ and ${\mathfrak {z}}_l$ is nonlinear, then the final estimate of $\alpha _h$ using $\alpha _l$, ${\mathfrak {z}}_h$, ${\mathfrak {z}}_l$ may be given by an MMSE estimator as follows:

$$\begin{aligned} \hat{\alpha }_{h,j}= & {} E[\alpha _{h,j}|{\mathfrak {z}}_l,\alpha _l] \nonumber \\= & {} \sum _{{\mathfrak {z}}_h\in \Gamma _j} E[\alpha _{h,j}|{\mathfrak {z}}_{h},{\mathfrak {z}}_{l},\alpha _l] P({\mathfrak {z}}_h|{\mathfrak {z}}_l,\alpha _l) \nonumber \\= & {} \sum _{{\mathfrak {z}}_h\in \Gamma _j}E[\alpha _{h,j}|{\mathfrak {z}}_{h,j}=1,\alpha _l] P({\mathfrak {z}}_h| {\mathfrak {z}}_l)) \nonumber \\= & {} E[\alpha _{h,j}|{\mathfrak {z}}_{h,j}=1,\alpha _l] P({\mathfrak {z}}_{h,j}=1|{\mathfrak {z}}_l)) \nonumber \\= & {} ({\mathfrak {c}}^T_{hl}\alpha _l) \phi (b_{h,j}+\mathbf {w}^T_{h,j}{\mathfrak {z}}_l) \end{aligned}$$

(17)

From the above MMSE estimator (Eq. (17)), the obtained $\alpha _h$ is not only sparse but also leads to better signal recovery (Peleg and Elad 2014). Moreover, MMSE estimator (Baum and Eagon 1967) can be represented as a product of linear terms with respect to $\alpha _l$ and a nonlinear term concerning ${\mathfrak {z}}_l$. The final predicted HR patch x is given by

$$\begin{aligned} x={\mathcal {D}}_h\hat{\alpha _h} \end{aligned}$$

(18)

3.4 Initial validation of proposed methods

Since we are more acquainted with natural images (or scenes), the above-discussed super-resolution (SR) techniques (both Case-1 and Case-2) are applied on generic images like Butterfly, Girl, Pepper, Starfish and Zebra as shown in Fig. 2. The effect of SR technique using sparse representation (Case-1) is shown in Fig. 3; whereas that of SR technique using sparse representation followed by prediction model (Case-2) is shown in Fig. 4. Moreover, the performance is also shown in Table 1 in terms of Peak Signal to Noise Ratio (PSNR) and Structural Similarity Index (SSIM) (Hore and Ziou 2010) indexes. The Table shows that the performance of Case-2 is much better than Case-1.

Note that the collection of HR and LR patch pairs, collected from natural image pairs, undergoes a dictionary learning process to obtain ${\mathcal {D}}_l$ and ${\mathcal {D}}_h$. For this learning, we have employed the parametric dictionary learning discussed in Yang et al. (2010) and Peleg and Elad (2014).

4 Experimental results

This section presents and evaluates the performance of proposed SR techniques when applied to engineering drawing (i.e. line drawing) images in general and electrical circuit drawings in particular.

Table 2 Description for employed Image names and their sizes

4.1 Data used

We demonstrate the results of the proposed single-image SR technique on electrical circuits, machine layout, and civil architectural design images originally captured in a high-resolution camera. These images are huge, and using these images for any application is computationally time-consuming on moderate capacity machines. We keep only its lower version (i.e. down-sampled version) and apply the proposed super-resolution (SR) techniques whenever required to speed up the process. Figure 5 shows the original version of the electrical circuit images ($Img_1$, $Img_2$, $Img_3$, $Img_4$, $Img_5$, $Img_6$, $Img_7$, $Img_8$), machine layout and civil architectural design images ($Img_9$, $Img_{10}$, $Img_{11}$, $Img_{12}$, $Img_{13}$, $Img_{14}$, $Img_{15}$, $Img_{16}$). Table 2 provides the size of these images in terms of (Rows) $\times$ (Columns) $\times$ (Channels). We have applied the proposed method to these images and have obtained the performance. These images are large-scaled images and huge. To make the system understandable, convenient and comparable with the other state-of-the-art methods, we have manually cropped a small region from these images (shown in Fig. 5) and considered them as original HR images and then down-sampled each cropped region to its lower resolution images (shown in Fig. 5).

Fig. 6

Performance of the proposed SR technique using the dictionary pair (${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times 512}$, ${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times 512}$), (${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times 1024}$,${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times 1024}$) and (${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times 2048}$, ${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times 2048}$, respectively

4.2 Results and discussion

During experimentation, each image I is converted to its (Y, $C_b$, $C_r$) colour channels. Then, only Y-channel of LR image (${\mathcal {I}}_y$) is considered to undergo to the proposed algorithm to reconstruct Y-Channel of HR image ${\mathcal {I}}_x$. Corresponding ${\mathcal {I}}_{C_b}$ and ${\mathcal {I}}_{C_r}$ are up-sampled and interpolated to be combined with ${\mathcal {I}}_x$ and then, converted to RGB image. Now, a window $w_i$ of size $50 \times 50$ slides over ${\mathcal {I}}_y$ with 50% overlapping of pixels in horizontal and vertical direction picks up the patches of same size. Then, GLCM (Umer et al. 2016) texture features ${\mathcal {F}}_{w_i}\in {\mathbb {R}}^{200\times 1}$ are extracted from each $w_i$. The collection of these texture features selected randomly from $m=5$ training images are used to obtain a code-book $CB\in {\mathbb {R}}^{200 \times 2}$ using k-means clustering algorithm for evaluating the homogeneous and non-homogeneous region for each $w_i \in {\mathcal {I}}_y$.

Table 3 Performance of the reconstructed SR image using the proposed system with respect to PSNR and SSIM indexes

Any homogeneous patch $w_i$ does not undergo the proposed SR technique. It is bicubic interpolated and converted to its RGB version. The up-sampled patches are used to form the high-resolution (HR) image. The non-homogeneous patches $w_i$ undergo the proposed SR technique. Here, during the super-resolution technique, we consider each non-homogeneous patch $w_i$ as an LR image ${\mathcal {Y}}$ and its reconstructed SR patch ${\mathcal {X}}'$ is utilized to form the final HR image. Note that for each non-homogeneous LR region ${\mathcal {Y}}$, we apply first-order gradient ($g_1$, $g_2$) and second-order gradient ($g_3$, $g_4$) features which yield four gradient maps at each location. Then, a window $w_{5 \times 5}$ with 50% overlapping is considered over each feature map of ${\mathcal {Y}}$. Now, feature vector with respect to each position of $w_{5 \times 5}$ is extracted from four feature map which are concatenated to obtain a feature vector for $w_{5 \times 5}$ to obtain its representation as $y_i \in {\mathbb {R}}^{100 \times 1}$. Then, the joint feature learning technique for the dictionary has been performed on the concatenated HR and LR patch pair features which derive ${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times K}$ and ${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times K}$, dictionary for the corresponding HR and LR patch pairs, respectively. Here, for each dictionary ${\mathcal {D}}_{h}$ or ${\mathcal {D}}_{l}$, $K=\{512,1024,2048\}$ items are considered. During dictionary learning, the colour images are transformed from the RGB to Y$C_bC_r$ channels and then, features are extracted from the corresponding Y-channel only.

The i-th LR patch ${\mathcal {Y}}_i$ corresponding to the non-homogeneous region is used to obtain it’s SR patch by employing the proposed SR technique via sparse representation technique described in Sect. 3.2. The obtained ${\mathcal {X}}_i$ undergoes to the statistical prediction model described in Sect. 3.3. The performance of the proposed SR technique for electrical circuit images $Img_1$, $Img_2$, $Img_3$, $Img_4$, $Img_5$, $Img_6$, $Img_7$, $Img_8$ and for machine and civil layout design images $Img_9$, $Img_{10}$, $Img_{11}$, $Img_{12}$, $Img_{13}$, $Img_{14}$, $Img_{15}$ and $Img_{16}$ using the dictionary pairs (${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times 512}$, ${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times 512}$), (${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times 1024}$, ${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times 1024}$) and (${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times 2048}$, ${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times 2048}$) are shown in Fig. 6, respectively.

Table 3 shows the performance of the proposed system in terms of PSNR (first row for each image) and SSIM (second row for each image) indexes for the images shown in Fig. 6 using the dictionary pairs (${\mathcal {D}}_{h} \in {\mathbb {R}}^{25 \times 512}$,${\mathcal {D}}_{l} \in {\mathbb {R}}^{100 \times 512}$), (${\mathcal {D}}_{h} \in {\mathbb {R}}^{25 \times 1024}$, ${\mathcal {D}}_{l} \in {\mathbb {R}}^{100 \times 1024}$) and (${\mathcal {D}}_{h} \in {\mathbb {R}}^{25 \times 2048}$, ${\mathcal {D}}_{l} \in {\mathbb {R}}^{100 \times 2048}$), respectively.

From the performance, as shown in Table 3 using different dictionary pairs in Fig. 6 for electrical circuit, mechanical, civil and architectural design images and also from Table. 3, it is observed that for dictionary pair (${\mathcal {D}}_{h} \in {\mathbb {R}}^{25 \times 2048}$, ${\mathcal {D}}_{l} \in {\mathbb {R}}^{100 \times 2048}$) produces slightly better reconstructed SR images. For further comparison of the proposed system with other competing methods such as Bicubic-Interpolation, Zhang et al. (2015), Marquina and Osher (2008), Purkait and Chanda (2012) and Yang et al. (2010), we have employed (${\mathcal {D}}_{l} \in {\mathbb {R}}^{25 \times 2048}$, ${\mathcal {D}}_{h} \in {\mathbb {R}}^{100 \times 2048}$) dictionary pair. Here, both visual perception analysis (Figs. 7 and 8) and the quantitative measures PSNR and SSIM (Table 4) have been employed with the reconstructed SR image obtained from the competing method and the proposed one. The performance of the proposed system with respect to visual information fidelity (VIF) evaluation index [?] is also reported in Table 4 (Third row) along with the PSNR and SSIM indexes. The performance comparison with respect to these indexes shows the superiority of the proposed system.

Fig. 7

Performance comparison of the proposed SR technique with the other existing state-of-the-art methods for $Img_1$, $Img_2$, $Img_3$, $Img_4$, $Img_5$, $Img_6$, $Img_7$ and $Img_8$, respectively

Fig. 8

Performance comparison of the proposed SR technique with the other existing state-of-the-art methods for $Img_9$, $Img_{10}$, $Img_{11}$, $Img_{12}$, $Img_{13}$, $Img_{14}$, $Img_{15}$ and $Img_{16}$, respectively

Table 4 Performance comparison of the proposed SR technique with the other existing techniques with respect to PSNR (first-rows), SSIM (second-rows), and VIF (third-rows) indexes

Bicubic-Interpolation is widely used for data interpolation on the two-dimensional regular grid. It is a relatively standard technique in image interpolation with good results and low complexity. Zhang et al. (2015) have given empirical studies on the sensitivity of different single-image super-resolution algorithms based on different blurring kernels. Marquina and Osher (2008) proposed a convolutional model that uses the total variation of the signal followed by the Bregman iterative refinement procedure for single-image super-resolution. Purkait and Chanda (2012) had modelled a nonlinear regularization method based on multiscale morphology for reserving the edges for super-resolution (SR) image reconstruction. Finally, Yang et al. (2010) had proposed an image super-resolution method using sparse representation technique only where the sparse representation for each low-resolution patch was used to get its coefficient as representation to obtain the corresponding high-resolution patch. From Figs. 7 and 8, it has been shown that the proposed system applied on images has better reconstructed.

Here, Table 5 shows the comparison performance with respect to time in Sec.. Since the proposed system and method in Purkait and Chanda (2012) outperforms other competing methods. Additionally, the performance of the proposed method and method in Purkait and Chanda (2012) is more or less the same even in some circumstances. It has been observed that for some images, the proposed system overcomes (Purkait and Chanda 2012). But due to some experimental setup and might be in some tuning of parameters, the proposed system will take lesser time than Purkait and Chanda (2012). Moreover, the performance reported in Table 4, it has been observed that the proposed system gives outstanding performance in terms of PSNR, SSIM, and VIF as compared to the methods reported in Table 5. Hence, the proposed system outperforms other competing methods.

5 Conclusions

This paper presents a novel method of single-image super-resolution technique. The proposed scheme has three components. In the first component, to speed up the process, the input image is divided into several regions analysed into homogeneous or non-homogeneous regions based on the texture pattern analysis in those regions. The non-homogeneous region undergoes a sparse representation technique to get a better-reconstructed HR region in the second component. In the third component, the reconstructed HR region from the second component undergoes a prediction model based on the statistical modelling of sparse representation using the Boltzmann machine technique to get a more enhanced reconstructed HR image. The homogeneous regions are bicubic interpolated and reflect the outcome image. Experimental results demonstrate that the proposed method better reconstructed SR images for electrical, machine, and civil design images. The comparison with the existing state-of-the-art methods shows that the proposed system outperforms other methods efficiently. The proposed approach might take some time to generate super-resolution images for the larger-scaled images. In the future, some deep learning models will be employed to solve super-resolution problems for the vastly scaled engineering design images.

Table 5 Average performance of the competing methods and the proposed system in terms of time (S)