A three-dimensional implicit constitutive relation for a body exhibiting stress softening: part I—theoretical underpinnings

Abstract

An implicit constitutive relation is proposed to describe stress softening exhibited by solids, using as a basis the second law of thermodynamics, and appropriate choices for the specific Helmholtz potential and the rate of entropy production function. The implicit constitutive relation that is developed is a generalization of the earlier one-dimensional model developed by Rajagopal and Srinivasa (Int J Plast 71:1–9, 2015). One subclass is studied, wherein the stress is the controlling variable, which permits the study of a body that softens with the stress.

Appendices

Appendix A: Reconsideration of the 1D model of Rajagopal and Srinivasa

In this Section we review the main features of the one-dimensional constitutive relation for the inelastic response for solids developed in [2]. Let $\sigma$, $\epsilon$ denote the one-dimensional stress and strain, and $\theta$ the temperature of a body, then the implicit model proposed by Rajagopal and Srinivasa [2] is of the form

$$\begin{aligned} {\mathsf {A}}\cdot \dot{{\mathsf {X}}}=\xi ({\mathsf {X}},\dot{{\mathsf {X}}}), \end{aligned}$$

(78)

where

$$\begin{aligned} {\mathsf {X}}=\left( \begin{array}{c}\epsilon \\ \sigma \\ \theta \end{array}\right) ,\quad {\mathsf {A}}=\left( \begin{array}{c}A_1\\ A_2\\ A_3\end{array}\right) , \end{aligned}$$

(79)

where $A_i=A_i({\mathsf {X}})$, $i=1,2,3$, and in [2] it is assumed that there exists a function ${\mathfrak {h}}={\mathfrak {h}}({\mathsf {X}})$ such that $A_1=\frac{\partial {\mathfrak {h}}}{\partial \epsilon }$, $A_2=\frac{\partial {\mathfrak {h}}}{\partial \sigma }$, and $A_3=\frac{\partial {\mathfrak {h}}}{\partial \theta }$. Furthermore, for the scalar function $\xi$ it is assumed the particular expression

$$\begin{aligned} \xi ({\mathsf {X}},\dot{{\mathsf {X}}})=\omega ({\mathsf {X}})H({\mathsf {U}}\cdot \dot{{\mathsf {X}}}){\mathsf {U}}\cdot \dot{{\mathsf {X}}}, \end{aligned}$$

(80)

where H(x) is the Heaviside step function and ${\mathsf {U}}={\mathsf {U}}({\mathsf {X}})$ is a vector function.

In the particular case of the model developed to describe loss of cohesion Rajagopal and Srinivasa [2] chose the strain $\epsilon$ as the controlling variable (they considered isothermal processes as well) and

$$\begin{aligned} {\mathsf {U}}=\left( \begin{array}{c}\sigma \\ 0\\ 0\end{array}\right) ,\quad \omega ({\mathsf {X}})=-\frac{1}{\sigma }H(\sigma +k\epsilon -\sigma _Y^*)(k\epsilon +\sigma ),\quad {\mathsf {A}}=\left( \begin{array}{c}-\sigma \\ \epsilon \\ 0\end{array}\right) \end{aligned}$$

(81)

where $\sigma _Y^*$ is connected with the ‘yield’ stress and k is a positive constant. Using (79)–(81) in (78) they obtained (see [2])

$$\begin{aligned} -\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=-H(\sigma +k\epsilon -\sigma _Y^*)(k\epsilon +\sigma ){\dot{\epsilon }}H(\sigma {\dot{\epsilon }}), \end{aligned}$$

(82)

from which we can see that it can be used to model the loss of cohesion in a rather simple manner. Let us study briefly the predictions of this model:

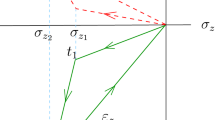
• 1. Let us assume that for the time interval $0\le t\le t_1$ we have that $\sigma >0$, $\epsilon >0$ and $\sigma {\dot{\epsilon }}\ge 0$ but that $\sigma +k\epsilon -\sigma _Y^*<0$. From (82) we obtain the differential equation $-\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=0$, whose solution is $\epsilon =C^{(0)}\sigma$, where $C^{(0)}$ is a constant. Choosing that constant to be $C^{(0)}=1/E$, where E is Young’s modulus of the body (before any deformation), for $0\le t\le t_1$ we have $\sigma =E\epsilon$.

• 2. At $t=t_1$ we assume we have yielding, therefore, $\sigma +k\epsilon -\sigma _Y^*=0$, and from $\sigma =E\epsilon$ that is valid at $t=t_1$ we obtain $\sigma \left( 1+\frac{k}{E}\right) =\sigma _Y^*$. At this point we can define $\sigma _Y$ as the yield stress for a one-dimensional body (in this case under tension), assuming that at the beginning of the process the body was undeformed and unstressed. Therefore, we obtain

  $$\begin{aligned} \sigma _Y^*=\sigma _Y\left( 1+\frac{k}{E}\right) . \end{aligned}$$

  (83)

• 3. Let us assume now that for $t_1\le t\le t_2$ we have that $\sigma +k\epsilon -\sigma _Y^*\ge 0$ and $\sigma {\dot{\epsilon }}>0$, then from (82) we obtain $\epsilon {\dot{\sigma }}=-k\epsilon {\dot{\epsilon }},$ and thus we have $\sigma =-k\epsilon +{\bar{C}}^{(1)}$, where ${\bar{C}}^{(1)}$ is a constant. That constant can be determined by assuming that the stress is continuous at $t=t_1$, which leads to $\sigma _Y=-\frac{k\sigma _Y}{E}+{\bar{C}}^{(1)}$, and as a result $\sigma =\sigma _Y^*-k\epsilon$.

• 4. Now, for $t\ge t_2$ we assume that $\sigma +k\epsilon -\sigma _Y^*>0$ but $\sigma {\dot{\epsilon }}<0$ (which means that $\epsilon$ decreases), therefore, from (82) we obtain the equation $-\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=0$, whose solution is $\sigma =C^{(2)}\epsilon$, where $C^{(2)}$ is a constant. Since the stress is continuous at $t=t_2$ we obtain $C^{(2)}\epsilon (t_2)=\sigma _Y^*-k\epsilon (t_2)$, and thus we obtain $C^{(2)}=\left( 1+\frac{k}{E}\right) \frac{\sigma _Y}{\epsilon (t_2)}-k$. It is possible to show that $C^{(2)}<E$.

In Fig. 1 we have a schematic view of how the body would behave for the above one-dimensional problem. We can observe that the body looses its cohesion since $C^{(2)}<E$.

Fig. 1

Stress versus strain for a one-dimensional problem for the 1D model for loss of cohesion of Rajagopal and Srinivasa

1.1 A model for softening and loss of cohesion considering the strain as the controlling variable

Let us study a modification of the above model (82) when we are interested in having different behaviour in compression and in tension, assuming that the strain is the controlling variable. In reality, strain is a consequence of applying a load which is its cause. However, let us suppose for the sake of discussion that we are able to supply the appropriate load to control the strain. Let us consider a generalization of (82) of the form

$$\begin{aligned} -\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=-[H(\sigma +k_T\epsilon -\sigma _{Y_T}^*)(k_T\epsilon +\sigma )H(\sigma )H(\epsilon )+H(-\sigma -k_C\epsilon -\sigma _{Y_C}^*)(k_C\epsilon \nonumber \\ +\sigma )H(-\sigma )H(-\epsilon )]{\dot{\epsilon }}H(\sigma {\dot{\epsilon }}), \end{aligned}$$

(84)

where in general we can assume that $k_T\ne k_C$ and $\sigma _{Y_T}^*\ne \sigma _{Y_C}^*$. Let us study again the behaviour of a body with the above model:

• 1. Let us assume that for the time interval $0\le t\le t_1$ we have that $\sigma >0$, $\epsilon >0$ and $\sigma {\dot{\epsilon }}\ge 0$ but that $\sigma +k\epsilon -\sigma _{Y_T}^*<0$. As in the previous case from (84) we obtain that $\epsilon =C^{(0)}\sigma$, where the constant can be assumed to be equal to Young’s modulus of the body⁹, i.e. $\sigma =E\epsilon$.

• 2. At $t=t_1$ we assume we have yielding, therefore, $\sigma +k_T\epsilon -\sigma _{Y_T}^*=0$, and from $\sigma =E\epsilon$ which is valid for $0\le t\le t_1$ we obtain that $\sigma \left( 1+\frac{k_T}{E}\right) =\sigma _{Y_T}^*$. At this point we can define $\sigma _{Y_T}$ as the yielding stress in tension for a one-dimensional body, assuming that at the beginning of the process the body was undeformed and unstressed. Therefore, we obtain (see (83)) $\sigma _{Y_T}^*=\sigma _{Y_T}\left( 1+\frac{k_T}{E}\right)$. If $k_T>0$ there is loss of cohesion, and if $k_T<0$ we can model softening.

• 3. Let us assume now that for $t_1\le t\le t_2$ we have that $\sigma +k_T\epsilon -\sigma _{Y_T}^*\ge 0$ and $\sigma {\dot{\epsilon }}>0$ , then from (84) we obtain that $\epsilon {\dot{\sigma }}=-k_T\epsilon {\dot{\epsilon }}$, and thus we have $\sigma =-k_T\epsilon +{\bar{C}}^{(1)}$, where ${\bar{C}}^{(1)}$ is a constant. That constant can be determined by assuming that the stress is continuous at $t=t_1$, therefore, $\sigma _{Y_T}=-\frac{k_T\sigma _Y}{E}+{\bar{C}}^{(1)}$, and as a result $\sigma =\sigma _{Y_T}^*-k_T\epsilon$.

• 4. Continuing, for $t\ge t_2$ we assume that $\sigma +k_T\epsilon -\sigma _{Y_T}^*\ge 0$ but $\sigma {\dot{\epsilon }}<0$ (which means now that $\epsilon$ decreases), therefore, from (84) we obtain the equation $-\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=0$, whose solution is $\sigma =C^{(2)}\epsilon$, where $C^{(2)}$ is a constant. Since the stress is continuous at $t=t_2$ we obtain that $C^{(2)}\epsilon (t_2)=\sigma _{Y_T}^*-k_T\epsilon (t_2)$, and hence we can conclude that

  $$\begin{aligned} C^{(2)}=\left( 1+\frac{k_T}{E}\right) \frac{\sigma _{Y_T}}{\epsilon (t_2)}-k_T. \end{aligned}$$

  (85)

  It is possible to see that $C^{(2)}<E$. Let us assume that the strain continues to decrease until it becomes negative, and in virtue of the relation $\sigma =C^{(2)}\epsilon$ the stress also decreases, and that for $t_2<t\le t_3$ since $-\sigma -k_C\epsilon -\sigma _{Y_C}^*<0$ we conclude that $\sigma =C^{(2)}\epsilon$ is still valid.

• 5. Let us assume that at some time $t=t_3$ we have that $-\sigma -k_C\epsilon -\sigma _{Y_C}^*=0$ (assuming that for $t=t_3$ we have $\epsilon <0$, $\sigma <0$ and $\sigma {\dot{\epsilon }}>0$). At this instant we have yielding in compression, and we obtain

  $$\begin{aligned} \sigma \left( -1-\frac{k_C}{C^{(2)}}\right) =\sigma _{Y_C}^*. \end{aligned}$$

  (86)

  The question is: Which value do we use for $\sigma _{Y_C}^*$? To answer the above question let us consider the body in compression starting from a situation where initially the body has not been deformed. In such a case, and in analogy to the case in tension presented before, for a time interval, $\epsilon$ will be proportional to the stress, and that constant of proportionality can be defined in terms of Young’s modulus. At some point, we will have yielding (now in compression), and now it is possible to define $\sigma _{Y_C}^*$ in terms of $\sigma _{Y_C}$ (the yielding stress in compression for a body that initially was unstrained and unstressed) as

  $$\begin{aligned} \sigma _{Y_C}^*=\sigma _{Y_C}\left( 1+\frac{k_C}{E}\right) . \end{aligned}$$

  (87)

  If we replace (87) in (86) we can obtain the stress at the moment of yielding (that is denoted as $\sigma _{Y_C}'$) as

  $$\begin{aligned} \sigma _{Y_C}'=-\sigma _{Y_C}\frac{\left( 1+\frac{k_C}{E}\right) }{\left( 1+\frac{k_C}{\breve{c}}\right) }. \end{aligned}$$

  (88)

  Since $C^{(2)}<E$ it is possible to show that $|\sigma _{Y_C}'|<\sigma _{Y_C}$, i.e. due to the previous deformation in tension the body yields at a lower stress (in absolute value), in comparison with the case the body did not suffer any deformation before being compressed.

In Fig. 2 we have a schematic plot of how the body would behave for the case studied above.

Fig. 2

On the left stress versus strain for a one-dimensional problem for a model with different yielding stress in compression and tension for loss of cohesion ($k_T>0$). On the right stress versus strain for a model showing stress softening ($k_T<0$)

1.2 A 1D model for softening considering the stress as the controlling variable

In this Section we present a 1D model based on the stress being the controlling variable, analogous to the model (82), that would be useful for studying softening of a solid. Let us consider the model

$$\begin{aligned} \epsilon {\dot{\sigma }}-\sigma {\dot{\epsilon }}=-H(q\sigma +\epsilon -{\bar{\sigma }}_Y^*)(\epsilon -q_T\sigma ){\dot{\sigma }}H(\epsilon {\dot{\sigma }}), \end{aligned}$$

(89)

and in the case that yielding is produced at a different level in compression and tension, a variation of the above model is

$$\begin{aligned} -\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=[H(q_T\sigma +\epsilon -{\bar{\sigma }}_{Y_T}^*)(\epsilon -q_T\sigma )H(\sigma )H(\epsilon )+H(-q_C\sigma -\epsilon -{\bar{\sigma }}_{Y_C}^*)(\epsilon \nonumber \\ -q_C\sigma )H(-\sigma )H(-\epsilon )]{\dot{\sigma }}H(\epsilon {\dot{\sigma }}), \end{aligned}$$

(90)

where $q_T$ and $q_C$ are positive constants, and ${\bar{\sigma }}_{Y_T}^*$, ${\bar{\sigma }}_{Y_C}^*$ are parameters related to the yielding of the solid. Let us analyse the above model in the same manner as in the previous Section:

• 1. Let us assume that for $0\le t\le t_1$ we have $\epsilon {\dot{\sigma }}\ge 0$ and $\sigma >0$, $\epsilon >0$, $q_T\sigma +\epsilon -{\bar{\sigma }}_{Y_T}^*<0$, then from (90) we obtain the ordinary differential equation $-\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=0$, which can be rewritten as $\dot{\overline{\ln \sigma }}=\dot{\overline{\ln \epsilon }}$, whose solution is $\epsilon =D^{(0)}\sigma$, where $D^{(0)}$ can be identified as 1/E, the reciprocal of Young’s modulus.

• 2. At $t=t_1$ we assume there is yielding, then $q_T\sigma (t_1)+\epsilon (t_1)={\bar{\sigma }}_{Y_T}^*$, assuming that for $0\le t\le t_1$ we have $\epsilon =D^{(0)}\sigma$, then $q_T\sigma (t_1)+\sigma (t_1)/E={\bar{\sigma }}_{Y_T}^*$ and we can determine $t_1$. The yielding stress is $\sigma (t_1)=\sigma _{Y_T}$, and from the above relation we find that ${\bar{\sigma }}_{Y_T}^*=\sigma _{Y_T}(q_T+1/E)$.

• 3. For $t_1\le t\le t_2$ we assume that $\epsilon {\dot{\sigma }}\ge 0$ and $\sigma >0$, $\epsilon >0$ but $q_T\sigma +\epsilon -{\bar{\sigma }}_{Y_T}^*\ge 0$, then from (90) we obtain the differential equation $-\sigma {\dot{\epsilon }}+\epsilon {\dot{\sigma }}=(\epsilon -q_T\sigma ){\dot{\sigma }}$, which becomes ${\dot{\epsilon }}=q_T{\dot{\sigma }}$, and thus we have $\epsilon =q_T\sigma +{\bar{D}}^{(1)}$. The constant ${\bar{D}}^{(1)}$ can be found by assuming that the strain is continuous at $t=t_1$, i.e. $\sigma (t_1)/E=q_T\sigma (t_1)+{\bar{D}}^{(1)}$. If $q_T$ is positive, from the above relation we find that if $\sigma$ increases then so does $\epsilon$, as shown in Fig. 3, where $q_T>1/E$. For the class of model (90), where the stress is the controlling variable we cannot model loss of cohesion, because this requires that for increasing $\epsilon$ we need $\sigma$ to decrease, i.e. the constant $q_T$ should be negative.

• 4. For $t_2\le t\le t_3$ we assume that $\epsilon >0$ but since ${\dot{\sigma }}<0$, i.e. $\epsilon {\dot{\sigma }}<0$, then it follows from (90) that $\epsilon =D^{(2)}\sigma$, where $D^{(2)}$ is a constant. We note that if $\sigma (t_3)=0$ then $\epsilon (t_3)=0$, i.e. there is no residual strain. If the strain is continuous at $t=t_2$ we have $q_T\sigma (t_2)+{\bar{D}}^{(1)}=D^{(2)}\sigma (t_2)$, and thereby $D^{(2)}$. In Fig. 3 we have a schematic representation of the behaviour for the body.

Fig. 3

Strain versus stress for a model showing stress softening

Parts of the above 1D model (89) are used as the basis of the three-dimensional model for stress softening in Sect. 4. In that Section we study a model where the stress is the control variable. In future work we will study a model for loss of cohesion, where the strain is the control variable, taking as starting point (89).

Appendix B: Determination of some derivatives concerning the natural logarithm of a second-order tensor

Here we present some expressions for the derivatives $\frac{\partial \gamma _i}{\partial {\mathbf {M}}}$ and $\frac{\partial {\mathbf {Q}}^{(i)}}{\partial {\mathbf {M}}}$ that appear in Sect. 4.1. From [18] we have

$$\begin{aligned} \frac{\partial \gamma _i}{\partial {\mathbf {M}}}= & {} {\mathbf {Q}}^{(i)},\end{aligned}$$

(91)

$$\begin{aligned} \frac{\partial {\mathbf {Q}}^{(i)}}{\partial {\mathbf {M}}}= & {} \left\{ \begin{array}{l} \prod _{\begin{array}{c} j=1\\ j\ne i \end{array}}^k({\mathbf {M}}-\gamma _i{\mathbf {I}})\otimes ({\mathbf {Q}}^{(i)}-{\mathbf {Q}}^{(j)})+\frac{1}{(\gamma _i-\gamma _j)}(\pmb {{\mathscr {I}}}-{\mathbf {I}}\otimes {\mathbf {Q}}^{(j)}),\quad \hbox {if}\quad k>1,\\ {\mathbf {0}}\quad \hbox {if}\quad k=1, \end{array}\right. \end{aligned}$$

(92)

where ${\mathscr {I}}_{abcd}=\frac{1}{2}(\delta _{ac}\delta _{bd}+\delta _{ad}\delta _{bc})$. Using these results for the derivative of ${\mathscr {F}}_{abcd}$ as described in Sect. 4.1 we obtain

$$\begin{aligned} \frac{\partial {\mathscr {F}}_{abcd}}{\partial M_{ef}}= & {} \sum _{i=1}^k\left\{ -\frac{1}{\gamma _i^2}Q^{(i)}_{ef}Q^{(i)}_{ac}Q^{(i)}_{bd}+\frac{1}{\gamma _i}\left[ \prod _{\begin{array}{c} j=1\\ j\ne i \end{array}}^k\frac{1}{(\gamma _i-\gamma _j)^2}(Q^{(i)}_{ef}-Q^{(j)}_{ef})(M_{ac}-\gamma _j\delta _{ac})\right. \right. \nonumber \\&+\frac{1}{(\gamma _i-\gamma _j)}({\mathscr {I}}_{acef}-Q^{(j)}_{ef}\delta _{ac})\Bigg ]Q^{(i)}_{bd}+\frac{1}{\gamma _i}Q^{(i)}_{ac}\left[ \prod _{\begin{array}{c} j=1\\ j\ne i \end{array}}^k\frac{(Q^{(i)}_{ef}-Q^{(j)}_{ef})}{(\gamma _i-\gamma _j)^2}(M_{bd}\right. \nonumber \\&-\gamma _j\delta _{bd})+\frac{1}{(\gamma _i-\gamma _j)}({\mathscr {I}}_{bdef}-Q^{(j)}_{ef}\delta _{bd})\Bigg ]\Bigg \}.\nonumber \\&+\sum _{i=1}^k\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^k\left\{ \left[ -\frac{1}{(\gamma _i-\gamma _j)^2}(Q^{(i)}_{ef}-Q^{(j)}_{ef})(\ln \gamma _i-\ln \gamma _j)\right. \right. \nonumber \\&+\frac{1}{(\gamma _i-\gamma _j)}\left( \frac{Q^{(i)}_{ef}}{\gamma _i}-\frac{Q^{(j)}_{ef}}{\gamma _j}\right) \Bigg ]Q^{(i)}_{ac}Q^{(j)}_{bd} +\frac{(\ln \gamma _i-\ln \gamma _j)}{(\gamma _i-\gamma _j)}\left[ \left( \prod _{\begin{array}{c} l=1\\ l\ne i \end{array}}^k\{M_{ac}\right. \right. \nonumber \\&-\gamma _i\delta _{ac}\}\{Q^{(i)}_{ef}-Q^{(l)}_{ef}\}+\frac{1}{(\gamma _i-\gamma _l)}\{{\mathscr {I}}_{acef}-\delta _{ac}Q^{(l)}_{ef}\}\Bigg )\Bigg ]Q^{(j)}_{bd}\nonumber \\&\left. \left. +Q^{(i)}_{ac}\left( \prod _{\begin{array}{c} l=1\\ l\ne j \end{array}}^k\{M_{bd}-\gamma _j\delta _{bd}\}\{Q^{(j)}_{ef}-Q^{(l)}_{ef}\}+\frac{1}{(\gamma _j-\gamma _l)}\{{\mathscr {I}}_{bdef}-\delta _{bd}Q^{(l)}_{ef}\}\right) \right] \right\} . \end{aligned}$$

(93)

Appendix C: On the scalar potentials

In this Section we obtain explicit expressions for $\phi ({\mathbf {E}})$ and $\varphi ({\mathbf {S}})$ described in (54.1,2). We have

$$\begin{aligned} \phi ({\mathbf {E}})= & {} \int _{\mathbf {0}}^{\mathbf {E}}\sum _{k=1}^K\frac{(-1)^{k+1}}{k}(\varvec{\iota }-{\mathbf {I}})^k:\mathrm{d}\varvec{\iota }+\phi _o=\sum _{k=1}^K\frac{(-1)^{k+1}}{k}\int _{\mathbf {0}}^{\mathbf {E}}(\varvec{\iota }-{\mathbf {I}})^k:\mathrm{d}\varvec{\iota }+\phi _o,\nonumber \\= & {} \int _{\mathbf {0}}^{\mathbf {E}}(\varvec{\iota }-{\mathbf {I}}):\mathrm{d}\varvec{\iota }-\frac{1}{2}\int _{\mathbf {0}}^{\mathbf {E}}(\varvec{\iota }-{\mathbf {I}})^2:\mathrm{d}\varvec{\iota }+\frac{1}{3}\int _{\mathbf {0}}^{\mathbf {E}}(\varvec{\iota }-{\mathbf {I}})^3:\mathrm{d}\varvec{\iota }\nonumber \\&-\frac{1}{4}\int _{\mathbf {0}}^{\mathbf {E}}(\varvec{\iota }-{\mathbf {I}})^4:\mathrm{d}\varvec{\iota }+\cdots ,\nonumber \\= & {} \frac{1}{2}\hbox {tr}({\mathbf {E}}^2)-\hbox {tr}({\mathbf {E}})-\frac{1}{2}\left[ \frac{1}{3}\hbox {tr}({\mathbf {E}}^3)-\hbox {tr}({\mathbf {E}}^2)+\hbox {tr}({\mathbf {E}})\right] +\frac{1}{3}\left[ \frac{1}{4}\hbox {tr}({\mathbf {E}}^4)-\hbox {tr}({\mathbf {E}}^3)\right. \nonumber \\&\left. +\frac{1}{2}\hbox {tr}({\mathbf {E}}^2)-\hbox {tr}({\mathbf {E}})\right] -\frac{1}{4}\left[ \frac{1}{5}\hbox {tr}({\mathbf {E}}^5)-\hbox {tr}({\mathbf {E}}^4)+2\hbox {tr}({\mathbf {E}}^3)-2\hbox {tr}({\mathbf {E}}^2)+\hbox {tr}({\mathbf {E}})\right] +\cdots .\qquad \end{aligned}$$

(94)

In the case of (54.2) we obtain

$$\begin{aligned} \varphi ({\mathbf {S}})= & {} \int _{\mathbf {0}}^{\mathbf {S}}\left[ K(\pmb {{\mathscr {A}}}:\varvec{\varsigma })-\left( \sum _{k=1}^K\frac{1}{k}\right) {\mathbf {I}}\right] :\mathrm{d}\varvec{\varsigma } =\int _{\mathbf {0}}^{\mathbf {S}}K(\pmb {{\mathscr {A}}}:\varvec{\varsigma }):\mathrm{d}\varvec{\varsigma }-\left( \sum _{k=1}^K\frac{1}{k}\right) \int _{\mathbf {0}}^{\mathbf {S}}{\mathbf {I}}:\mathrm{d}\varvec{\varsigma },\nonumber \\= & {} \frac{K}{2}(\pmb {{\mathscr {A}}}:{\mathbf {S}}):{\mathbf {S}}-\left( \sum _{k=1}^K\frac{1}{k}\right) \hbox {tr}({\mathbf {S}}). \end{aligned}$$

(95)

Appendix D: Alternative expression for the implicit relation

In this Section we present alternative expressions for $\dot{\overline{\ln (\pmb {{\mathscr {A}}}:{\mathbf {S}})}}$ and $\dot{\overline{\ln ({\mathbf {E}}_o+\pmb {{\mathscr {B}}}:{\mathbf {S}})}}$. From [18] we have that

$$\begin{aligned} \dot{\overline{\ln (\pmb {{\mathscr {A}}}:{\mathbf {S}})}}=\pmb {{\mathscr {G}}}_1:\dot{\hat{{\mathbf {S}}}},\quad \dot{\overline{\ln ({\mathbf {E}}_o+\pmb {{\mathscr {B}}}:{\mathbf {S}})}}=\pmb {{\mathscr {G}}}_2:\dot{\breve{{\mathbf {S}}}}, \end{aligned}$$

(96)

respectively, where $\pmb {{\mathscr {G}}}_1$ and $\pmb {{\mathscr {G}}}_2$ are fourth-order tensors, and where we have defined

$$\begin{aligned} \hat{{\mathbf {S}}}=\pmb {{\mathscr {A}}}:{\mathbf {S}},\quad \breve{{\mathbf {S}}}={\mathbf {E}}_o+\pmb {{\mathscr {B}}}:{\mathbf {S}},\quad \hat{{\mathbf {S}}}\tilde{{\mathbf {p}}}^{(i)}=s_i\tilde{{\mathbf {p}}}^{(i)},\quad \breve{{\mathbf {S}}}\bar{{\mathbf {p}}}^{(i)}=g_i\bar{{\mathbf {p}}}^{(i)}\quad \mathrm{no \,sum\, in}\ i, \end{aligned}$$

(97)

where $s_i$, $\tilde{{\mathbf {p}}}^{(i)}$ and $g_i$, $\bar{{\mathbf {p}}}^{(i)}$ are the eigenvalues and eigenvectors of $\hat{{\mathbf {S}}}$ and $\breve{{\mathbf {S}}}$, respectively. From [18] we have

$$\begin{aligned} \pmb {{\mathscr {G}}}_1= & {} \sum _{i=1}^{k_1}\frac{1}{s_i}\varvec{\Gamma }^{(i)}\boxtimes \varvec{\Gamma }^{(i)}+\sum _{i=1}^{k_1}\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{k_1}\frac{(\ln s_i-\ln s_j)}{(s_i-s_j)}\varvec{\Gamma }^{(i)}\boxtimes \varvec{\Gamma }^{(j)}, \end{aligned}$$

(98)

$$\begin{aligned} \pmb {{\mathscr {G}}}_2= & {} \sum _{i=1}^{k_2}\frac{1}{g_i}\varvec{\Lambda }^{(i)}\boxtimes \varvec{\Lambda }^{(i)}+\sum _{i=1}^{k_2}\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{k_2}\frac{(\ln g_i-\ln g_j)}{(g_i-g_j)}\varvec{\Lambda }^{(i)}\boxtimes \varvec{\Lambda }^{(j)}, \end{aligned}$$

(99)

where we have defined $\varvec{\Gamma }^{(i)}=\tilde{{\mathbf {p}}}^{(i)}\otimes \tilde{{\mathbf {p}}}^{(i)}$, $\varvec{\Lambda }^{(i)}=\bar{{\mathbf {p}}}^{(i)}\otimes \bar{{\mathbf {p}}}^{(i)}$ (there is no sum in i), and $k_1$ and $k_2$ are the independent eigenvalues $s_i$ and $g_i$, respectively.

From (38) we have

$$\begin{aligned} \frac{\partial \xi }{\partial {\mathbf {S}}}=\left\{ \begin{array}{ll}(\pmb {{\mathscr {G}}}_2:\dot{\breve{{\mathbf {S}}}}-\pmb {{\mathscr {G}}}_1:\dot{\hat{{\mathbf {S}}}})H(\hbox {tr}({\mathbf {E}}\dot{{\mathbf {S}}})),&{}\quad \hbox {if}\quad {\tilde{\sigma }}_1\ge \sigma ^*_{Y_T}\quad \hbox {or}\quad {\tilde{\sigma }}_3\le -\sigma ^*_{Y_C}\\ {\mathbf {0}}&{}\quad \hbox {otherwise}\end{array}\right. . \end{aligned}$$

(100)

In (98) and (99) we have $\ln s_i$ and $\ln g_i$ and in some cases $s_i$, $g_i$ could be negative, however, as explained in the footnote at the beginning of Sect. 4, when solving boundary value problems this is not an issue, as can be seen in Sect. 4 of Part II [16].