A three-dimensional implicit constitutive relation to describe stress softening: part II—analysis of some boundary value problems

Abstract

In Part I, an implicit constitutive relation was proposed to describe stress softening of solids. In this second part, we use the constitutive relation developed earlier to study different boundary value problems, namely the homogeneous compression of a cylinder without radial stresses, the homogeneous compression of a cylinder with radial stress (triaxial test), the simple shear of a slab, and the inflation of a cylindrical annulus, when the displacement gradients are small.

Appendices

Appendix A: Analysis of the implicit relation for 1D problems

In this Section, we study briefly a 1D counterpart of (12), (13) and compare that with the models presented in Appendix A of [12]. In that Appendix, we use the notation $\epsilon$, $\sigma$ for the 1D counterpart of the strain and stress tensors, ${\bar{D}}$ and D are the 1D counterpart of the tensors $\bar{{\mathbf {D}}}$ and ${\mathbf {D}}$, respectively, then (12) becomes:

$$\begin{aligned} \epsilon =\left\{ \begin{array}{ll}{\bar{D}}\left[ \epsilon _o+\frac{1}{3}(b_1+2b_2)\sigma \right] &{}\quad \text{ if }\quad \epsilon {\dot{\sigma }}\ge 0\quad \text{ and }\quad {\tilde{\sigma }}\ge \sigma ^*_{Y_T}\quad \text{ or }\quad {\tilde{\sigma }}\le -\sigma ^*_{Y_C}\\ \frac{D}{3}(a_1+2a_2)\sigma &{}\quad \text{ otherwise }\end{array}\right. \end{aligned}$$

(122)

where the counterpart of (13) is

$$\begin{aligned} {\tilde{\sigma }}=\frac{1}{3}(c_1+2c_2)\sigma +\frac{1}{3}(d_1+2d_2)\epsilon . \end{aligned}$$

(123)

The above equations can be compared with the results presented in Appendix A of [12].

Appendix B: A semi-analytical method to solve the boundary value problem for the annulus with radial traction on its inner surface

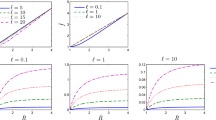
In this Appendix, we explore a numerical method to solve (121) for the case of the inflation of a cylindrical annulus, when there is stress-softening for a part of the annulus.

We assume that the functions ${\bar{D}}_r^{(1)}(r)$, ${\bar{D}}_\theta ^{(1)}(r)$, and ${\bar{D}}_z^{(1)}(r)$ in (121) are given by a Taylor series:

$$\begin{aligned} {\bar{D}}_r^{(1)}(r)\approx \sum _{n=0}^{N_r}\frac{\alpha _n}{n!}(r-r_\mathrm {i})^n,\quad {\bar{D}}_\theta ^{(1)}(r)\approx \sum _{n=0}^{N_\theta }\frac{\beta _n}{n!}(r-r_\mathrm {i})^n,\quad {\bar{D}}_z^{(1)}(r)\approx \sum _{n=0}^{N_z}\frac{\gamma _n}{n!}(r-r_\mathrm {i})^n, \end{aligned}$$

(124)

and we assume a similar approximate solution for ${^{\mathrm {(b)}}}{\sigma }_r$ as

$$\begin{aligned} {^{\mathrm {(b)}}}{\sigma }_r(r,t)\approx \sum _{n=0}^{N_\sigma }\frac{\phi _n(t)}{n!}(r-r_\mathrm {i})^n. \end{aligned}$$

(125)

In general, it is not necessary that $N_r$, $N_\theta$, $N_z$, and $N_\sigma$ are the same.

One way to solve the boundary value problem is described now:

• In the case of (115.1) from the boundary condition ${^{\mathrm {(a)}}}{\sigma }_r(r_\mathrm {o},t)=0$, we obtain

  $$\begin{aligned} {^{\mathrm {(a)}}}{C}_2(t)=\frac{{^{\mathrm {(a)}}}{C}_1(t)}{2r_\mathrm {o}^2}. \end{aligned}$$

  (126)

• From the boundary condition ${^{\mathrm {(b)}}}{\sigma }_r(r_\mathrm {i},t)=-P(t)$ and (125), we obtain

  $$\begin{aligned} \phi _0(t)=-P(t). \end{aligned}$$

  (127)

• Using (124) and (125) in (121) after some manipulations, which for brevity are not shown here, we obtain the polynomial equation

  $$\begin{aligned} \vartheta _0+\vartheta _1r+\vartheta _2r^2+\vartheta _3r^3+\cdots \vartheta _Mr^M=0, \end{aligned}$$

  (128)

  where $\vartheta _m$ are functions that depend on the constants $b_1$, $b_2$, $\alpha _n$, $\beta _n$, $\gamma _n$, $\epsilon _o$ and the functions $\lambda (t)$, P(t), and $\phi _1(t)$, $\phi _2(t)$,...,$\phi _{N_\sigma }(t)$. In particular, it is possible to see that $\vartheta _n$ depends linearly on the $\phi _n(t)$. If $N_\sigma -1\le M$, we demand that (128) is satisfied for any $r_\mathrm {i}\le r\le r_\mathrm {o}$ for the first $N_\sigma -1$ terms of the polynomial, i.e.

  $$\begin{aligned} \vartheta _0=0,\quad \vartheta _1=0,\quad \vartheta _2=0,\cdots \vartheta _{N_\sigma -1}=0. \end{aligned}$$

  (129)

  The above equations can be used to obtain $\phi _1(t)$, $\phi _2(t)$,...,$\phi _{N_\sigma -1}(t)$ in terms of $b_1$, $b_2$, $\alpha _n$, $\beta _n$, $\gamma _n$, $\epsilon _o$, and $\lambda (t)$, P(t). It is necessary to recognize that if $N_\sigma -1< M$, then (128) is only satisfied approximately.

• Using (115.1) and (125) in (108), we obtain

  $$\begin{aligned} -\frac{{^{\mathrm {(a)}}}{C}_1(t)}{2{r^*(t)}^2}+\frac{{^{\mathrm {(a)}}}{C}_1(t)}{2r_\mathrm {o}^2}=\sum _{n=0}^{N_\sigma }\frac{\phi _n(t)}{n!}(r^*(t)-r_\mathrm {i})^n, \end{aligned}$$

  (130)

  which can be used, for example, to find ${^{\mathrm {(a)}}}{C}_1(t)$ in terms of $r^*(t)$ ,and $\alpha _n$, $\beta _n$, $\gamma _n$, $\epsilon _o$, and $\lambda (t)$, P(t) (see the discussion above). In that case, we have

  $$\begin{aligned} {^{\mathrm {(a)}}}{C}_1(t)=\frac{2r_\mathrm {o}^2{r^*}^2}{\left( {r^*}^2-r_\mathrm {o}^2\right) }\sum _{n=0}^{N_\sigma }\frac{\phi _n(t)}{n!}(r^*(t)-r_\mathrm {i})^n. \end{aligned}$$

  (131)

A similar analysis can be carried out with the rest of the continuity conditions, which for brevity is not shown here.