GLONASS ambiguity resolution

Abstract

A new integer-estimable GLONASS FDMA model is studied and analysed. The model is generally applicable, and it shows a close resemblance with the well-known CDMA models. The analyses provide insights into the performance characteristics of the model and concern a variety of different ambiguity-resolution critical applications. This will be done for geometry-free, geometry-fixed and several geometry-based formulations. Next to the analyses of the model’s instantaneous ambiguity-resolved positioning and attitude determination capabilities, we show the ease with which the model can be combined with existing CDMA models. We thereby present the instantaneous ambiguity-resolution performances of integrated L1 GPS + GLONASS, both for high-grade geodetic and mass-market receivers. We also consider the potential of the single-frequency combined model for mixed-receiver processing, particularly for the case the between-receiver GLONASS pseudorange data are biased. In all cases, the speed of successful ambiguity resolution is studied as well as the precision with which positioning is determined. Software routines for constructing the model are also provided.

Introduction

In Teunissen (2019), a new formulation of the double-differenced (DD) GLONASS FDMA model was introduced. It closely resembles the CDMA-based systems, and it guarantees the estimability of the newly defined GLONASS ambiguities. This formulation was made possible because of a newly defined concept of integer-estimability, combined with an analytical construction of a special integer matrix canonical decomposition.

The close resemblance between the new GLONASS FDMA model and the standard CDMA models implies that available CDMA-based GNSS software is easily modified and that existing methods of integer ambiguity resolution can be directly applied. Due to its general applicability, we believe that the new model opens up a whole variety of carrier-phase-based GNSS applications that have hitherto been a challenge for GLONASS ambiguity resolution. We provide insight into the ambiguity resolution capabilities of the model and demonstrate for the first time its performance for a variety of different ambiguity-resolution critical applications.

After a brief review of the new integer-estimable GLONASS FDMA model, including the provision of the necessary software routines, we compare the strengths of the GLONASS geometry-free and geometry-fixed model and show how the geometry-fixed model provides a natural basis for undertaking data quality analyses. Then, the model’s performance for instantaneous ambiguity-resolved positioning and attitude determination is studied. It is thereby, for instance, shown that single-frequency GLONASS-only successful ambiguity-resolved direction finding is instantaneously possible. The ease with which the new GLONASS FDMA model can be integrated with CDMA models is then demonstrated afterwards. For three different data sets, collected with both high-grade and mass-market receivers at three different locations (Perth, Australia; Delft, Netherlands; Dunedin, New Zealand), the strength of the combined L1 GLONASS + GPS model is analysed. This is done for receiver combinations of the same make and type, as well as for mixed-receivers when between-receiver GLONASS code data may be biased. Two cases are hereby considered: L1 GLONASS phase with L1 GPS code + phase and L1 GLONASS phase with L1 GPS phase, the latter being an option when one wants to avoid the code data altogether, due to, for instance, the impact of heavy multipath. For all cases, the speed of ambiguity resolution performance is studied as well as the precision with which positioning is determined.

Integer-estimable GLONASS DD model

The new GLONASS FDMA DD model of (Teunissen 2019) is given as

$$\begin{aligned}{ \mathsf {E}}\left[ \begin{array}{c} p \\ \phi \end{array} \right] = \left[ \begin{array}{cc} e \otimes G &{} 0 \\ e \otimes G &{} \;\;\varLambda \otimes L \end{array} \right] \left[ \begin{array}{c} b \\ a \end{array} \right] \end{aligned}$$

(1)

in which $p \in {\mathbb {R}}^{2(m-1)}$ and $\phi \in {\mathbb {R}}^{2(m-1)}$ denote the DD pseudorange (code) and phase observables, m is the number of tracked satellites, $e=(1,1)^{T}$, $\otimes$ denotes the Kronecker product, $G \in {\mathbb {R}}^{(m-1) \times \nu }$ is the relative receiver-satellite geometry matrix, $\varLambda ={\mathrm{diag}}(\lambda _{1}, \lambda _{2})$ is the diagonal matrix of wavelengths; $L \in {\mathbb {R}}^{(m-1) \times (m-1)}$ is a full-rank, easy-to-compute lower-triangular matrix, $b \in {\mathbb {R}}^{\nu }$ is the baseline vector ($\nu =3$ in the absence of a Zenith Tropospheric Delay, otherwise $\nu =4$) and $a \in {\mathbb {Z}}^{2(m-1)}$ is the newly defined GLONASS integer ambiguity vector. For background information on GLONASS, we refer to ICD (2008), Leick et al. (2015) and Revnivykh et al. (2017).

Fig. 1

Pseudo-code for computing the lower-triangular L-matrix of the integer-estimable GLONASS FDMA model (1): (Left) The algorithm for computing the GLONASS L-matrix (2) for a given set of channel numbers; (Right) The Extended Euclidean algorithm, which is called by the L-algorithm to solve (3)

Note that the above model’s only difference with its CDMA counterpart is the presence of the lower-triangular matrix L (i.e. by setting $L=I_{m-1}$ one obtains the corresponding CDMA model). This close resemblance implies that available CDMA software is easily modified and that existing methods of integer ambiguity resolution can be directly applied. The entries of the lower-triangular matrix L are given as (Teunissen 2019)

$$\begin{aligned} L_{ii}= & {} 2848 \times \frac{g_{i+1}}{a_{i+1}g_{i}}\quad \;{\mathrm{for}}\; i=1, \ldots , m-1\nonumber \\ L_{ij}= & {} -2848 \times \frac{\alpha _{j}a_{1(i+1)}}{a_{i+1}g_{j}}\quad \;{\mathrm{for}}\; i=j+1, \ldots , m-1 \end{aligned}$$

(2)

where $a_{1(i+1)}=a_{i+1}-a_1$. The integers $\alpha _{i}$ and $\beta _{i}$ are given by

$$\begin{aligned} -\,\alpha _{i}a_{i+1}+\beta _{i}g_{i}=g_{i+1} \end{aligned}$$

(3)

in which $a_{i}=2848+\kappa ^{i}$, $\kappa ^{i} \in [-7, +6]$ are the channel numbers, $g_{1}=a_{1}$ and $g_{i} ={\mathrm{GCD}}(a_{1}, \ldots , a_{i})$ $(1<i \le m)$, with GCD denoting the Greatest Common Divisor. Software pseudo-code for computing the entries of matrix L is given in Fig. 1. We have also provided a MATLAB routine 'GLONASS_L.m' for the L-matrix computation. The routine can be accessed and downloaded via the GPS Toolbox website at http://www.ngs.noaa.gov/gps-toolbox.

We note that the double-differences in (1) have been defined by using the first satellite as reference satellite. However, if so desired one can choose any satellite as reference. In that case, one will have to pre-multiply the DD phase-equation of (1) with the $2(m-1) \times 2(m-1)$ matrix $I_{2} \otimes D_{\mathrm{new}}^{T}D_{1}(D_{1}^{T}D_{1})^{-1}$, in which $D_{1}^{T}=[-e_{m-1}, I_{m-1}] \in {\mathbb {R}}^{(m-1) \times m}$ is the between-satellite differencing matrix that takes the first satellite as reference, $D_{\mathrm{new}}^{T} \in {\mathbb {R}}^{(m-1) \times m}$ the user’s new choice of differencing matrix, and the needed inverse is simply given by $(D_{1}^{T}D_{1})^{-1}=I_{m-1}-\frac{1}{m}e_{m-1}e_{m-1}^{T}$, with $e_{m-1}$ being the $(m-1)$-vector of ones. In Teunissen (2019), it is shown that the performance of the model is invariant for the choice of differencing matrix.

Although the above model (1) is given for a single epoch and a short baseline, it is easily extended to multiple epochs and long baselines. In some of these extensions, for instance, in the long-baseline phase-only case, the integer-estimability of the ambiguities will change. In Teunissen (2019), it is shown how to recover in such cases the integer-estimability again. Also note that, although (1) is formulated for the dual-frequency case, its single-frequency variants are easily obtained by replacing $e=(1,1)^{T}$ by 1 and $\varLambda ={\mathrm{diag}}(\lambda _{1}, \lambda _{2})$ by $\lambda _{1}$ or $\lambda _{2}$, respectively.

As model (1) is generally applicable and guarantees, independent of the actual channel-number entries, the integer-estimability of the GLONASS ambiguities, we believe that the new model opens up a whole variety of carrier-phase-based GNSS applications that have hitherto been a challenge for GLONASS ambiguity resolution. We will demonstrate for the first time some of those applications.

GLONASS geometry-fixed model for data analysis

In this section, we determine the characteristics of the GLONASS geometry-free and geometry-fixed models and show how the latter can be used for GLONASS ambiguity resolution-based data analyses.

Geometry-free versus geometry-fixed model

The geometry-free and geometry-fixed models are known to be the weakest and strongest DD models, respectively. The geometry-free (GF) model is the weakest as it dispenses with the relative receiver-satellite geometry. It follows when matrix G in (1) is replaced by an identity matrix, $G=I_{m-1}$. As a result, the pseudorange and carrier-phase data become parametrized in the $m-1$ DD ranges instead of in the baseline vector. The geometry-fixed (GFi) model on the other hand is the strongest as it assumes the relative receiver-satellite geometry known. It follows from (1) by considering b known, thus leaving the integer ambiguity vector a as the only unknown in the model.

Fig. 2

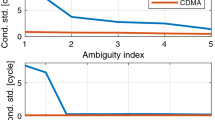
Single-epoch ($k=1$), geometry-free (GF) and geometry-fixed (GFi) spectra of the LAMBDA-transformed ambiguity conditional standard deviations $\sigma _{\hat{z}_{i|I}}$, $I=\{1, \ldots , (i-1)\}$ for $m=6$ and $\sigma _{p_{1}}=\sigma _{p_{2}}=30$ cm, $\sigma _{\phi _{1}}=\sigma _{\phi _{2}}=3$ mm: (Left) Single-frequency ($\lambda _{1}$) GF and GFi spectra ($i=1, \ldots , 5$); (Right) Dual-frequency GF and GFi spectra ($i=1, \ldots , 10$). The ADOP for each model are given for full and partial ambiguity resolution (between brackets)

To get insights into the relative strength of the two models for ambiguity resolution, we consider their spectrum of ambiguity conditional standard deviations for which the corresponding ambiguity variance matrices are needed. Due to the close resemblance of (1) with its CDMA counterpart, the GLONASS GF ambiguity variance matrix can be directly obtained from the CDMA-results (Teunissen 1997). To do so, we assume here and in the following that the stochastic model of (1) is given as

$$\begin{aligned} {\mathsf {D}}\left[ \begin{array}{c} p \\ \phi \end{array} \right] = \left[ \begin{array}{cc} Q_{pp} \otimes R &\quad{} 0 \\ 0 &\quad{} Q_{\phi \phi } \otimes R \end{array} \right] \end{aligned}$$

(4)

in which $Q_{pp}=2{\mathrm{diag}}(\sigma _{p_{1}}^{2}, \sigma _{p_{2}}^{2})$, $Q_{\phi \phi }=2{\mathrm{diag}}(\sigma _{\phi _{1}}^{2}, \sigma _{\phi _{2}}^{2})$, and $R=D_{1}^{T}W^{-1}D_{1}$, with the differencing matrix $D_{1}^{T}=[-e_{m-1}, I_{m-1}]$ and the diagonal satellite elevation weighting matrix W. The single-epoch GLONASS GF ambiguity variance matrix follows then as

$$\begin{aligned} Q_{\hat{a}\hat{a}}^{\tiny \text {GF}} = \varLambda ^{-1} \left( Q_{\phi \phi }+\frac{ee^{T}}{e^{T}Q_{pp}^{-1}e}\right) \varLambda ^{-1} \otimes L^{-1}RL^{-T} \end{aligned}$$

(5)

It is formed as a Kronecker product, with its first, $2 \times 2$, matrix driven by the measurement precision and wavelengths, and its second, $(m-1) \times (m-1)$, matrix driven by the GLONASS-specific lower-triangular L-matrix.

As the receiver-satellite geometry is assumed known under the geometry-fixed model, the GLONASS GFi ambiguity variance matrix follows then when the limit $Q_{pp} \rightarrow 0$ is taken of (5),

$$\begin{aligned} Q_{\hat{a}\hat{a}}^{\tiny \text {GFi}}=\lim _{Q_{pp} \rightarrow 0} Q_{\hat{a}\hat{a}}^{\tiny \text {GF}} = \varLambda ^{-1} Q_{\phi \phi } \varLambda ^{-1} \otimes L^{-1}RL^{-T} \end{aligned}$$

(6)

The single-frequency and dual-frequency spectra of the LAMBDA-transformed (Teunissen 1995) ambiguity conditional standard deviations of (5) and (6) are given in Fig. 2. There are two important aspects that we learn from the shown spectra. The first, which is GNSS-specific, concerns the difference in the level of the geometry-free and geometry-fixed conditional standard deviations. The second, which is GLONASS specific, concerns the signature of the spectra.

Fig. 3

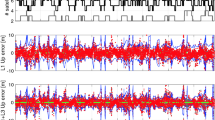
Samples of the zenith-referenced residuals (grey lines) given in (9), their 100-moving averages (blue lines), their 99.9%-confidence interval (black dashed lines) and their histograms (green bars) compared to their theoretical normal distribution (red line)

As to the first aspect, if we consider the values of the conditional standard deviations, we note that there is an approximate scale factor between those of the geometry-free model and those of the geometry-fixed model. In the single-frequency case (Fig. 2, left), this factor is about 100, while in the dual-frequency case (Fig. 2, right) it is about 10. This same scaling we also recognize in the ADOP (Ambiguity Dilution Of Precision), which equals the geometric mean of the conditional standard deviations. To understand this property, we recall that the ADOP is defined as

$$\begin{aligned} {\mathrm{ADOP} }= \sqrt{|Q_{\hat{a}\hat{a}}|}^{\frac{1}{f(m-1)}}\;\;{\mathrm{(cycles)}} \end{aligned}$$

(7)

with $Q_{\hat{a}\hat{a}}$ being the $f(m-1) \times f(m-1)$ ambiguity variance matrix and f the number of frequencies. If we now apply (7) to (5) and (6), we obtain the ratio

$$\begin{aligned} \frac{{\mathrm{ADOP}}^{\tiny \text {GF}}}{{\mathrm{ADOP}}^{\tiny \text {GFi}}}= \left( 1+ \frac{e^{T}Q_{\phi \phi }^{-1}e}{e^{T}Q_{pp}^{-1}e} \right) ^{\frac{1}{2f}} \approx (100)^{\frac{1}{f}} \end{aligned}$$

(8)

where use has been made of the phase-code variance ratio being $10^{-4}$. This result shows that a switch from the geometry-free model to the geometry-fixed model is driven by the very small phase-code variance ratio and that the factor between the conditional standard deviations of the two models must indeed be about 100 for $f=1$ and 10 for $f=2$.

The second aspect that we learn from the spectra of Fig. 2 concerns their signature. We note that all spectra are flat in the beginning and remain so except for their last value (in single-frequency case) or last two values (in dual-frequency case). This property is GLONASS specific and driven by the presence of the L-matrix in (5) and (6). A closer look at the entries of L (see 2) shows a large discontinuity in the greatest common divisors: $g_{1}=a_{1}>> g_{i}={\mathrm{GCD}}(a_{1}, \ldots , a_{i})$ for $i>1$, since the latter are never larger than the difference in channel numbers by virtue of the GCD-property ${\mathrm{GCD}}(a_{1}, a_{2})={\mathrm{GCD}}(a_{1}, a_{2}-a_{1})$. As the LAMBDA decorrelating transformation aims to flatten the spectrum thereby pushing the less precise ambiguity combinations towards the end, the persistence of the discontinuity results in large values of $\sigma _{\hat{z}_{i|I}}$ for $i=m-2$, in the single-frequency case, or for $i=2m-3$ and $i=2m-4$, in the dual-frequency case. These are, therefore, ambiguities that we rather like to avoid including in the ambiguity resolution process.

From the above, we draw the conclusion that although GF ambiguity resolution is not possible in a single epoch, instantaneous GFi ambiguity resolution is possible, in particular if we apply partial ambiguity resolution by keeping the least-precise transformed ambiguities float. This is therefore the approach that will be taken. Thus, if in the following we speak of the to-be-resolved ambiguities, we refer to the LAMBDA-decorrelated ambiguities without the least-precise ones, this being one in the case of single frequency and two in the case of dual-frequency ambiguity resolution. We also note that in the following sections, to show the truly bare experimental outcomes of the integer ambiguity estimations, we have explicitly refrained from including ambiguity validation (Verhagen and Teunissen 2013). With ambiguity validation included, the incorrectly fixed solutions would have been identified and discarded.

GLONASS data analysis

We make use of data sets acquired by receivers of different make and type at three different locations (Perth—AU, Dunedin—NZ and Delft—NL). In this section, we use the Perth data set to illustrate how the GFi model can be used for GLONASS data analysis. The goal is to form a maximum number of linearly independent functions of the observables p and $\phi$ which are (1) zero-mean and (2) their variances take one of the ‘zenith-referenced’ values $\sigma _{p_{j}}^{2}$ and $\sigma _{\phi _{j}}^{2}$ ($j=1,2$) given in (4). We refer to such functions as zenith-referenced residuals, since the solutions for $\sigma _{p_{j}}^{2}$ and $\sigma _{\phi _{j}}^{2}$—as the below will show—can be directly inferred from their samples.

In this respect, we put the known baseline vector b in the left-hand side of (1). For the code-equation, this yields the zero-mean functions $p-[e\otimes G]\, b$. For the phase-equation however, the expectation of the functions $\phi -[e\otimes G]\,b$ is still driven by the ambiguities of which $2(m-2)$ are successfully fixed to their integers (see Fig. 2). These resolved ambiguities, say $z_1$, can thus also be put in the left-hand side of (1). To see how the final structure of the ‘zenith-referenced’ residuals looks like, let the decorrelated ambiguity vector be partitioned as $z=[z_1^T,z_2^T]^T$ ($z_1\in {\mathbb {Z}}^{2(m-2)}$ and $z_1\in {\mathbb {Z}}^{2}$) with the corresponding design matrix $\varLambda \otimes [L_1,l_2]$ ($L_1\in {\mathbb {R}}^{(m-1)\times (m-2)}$ and $l_2\in {\mathbb {R}}^{(m-1)}$). Then, the ‘zenith-referenced’ residuals associated with model (1) can be shown to read

$$\begin{aligned} \tilde{p}= & {} [I_2\otimes R_p](p - [e\otimes G]\, b),\qquad \nonumber \\&{\mathsf {D}}(\tilde{p}) = Q_{pp} \otimes I_{m-1}\nonumber \\ \tilde{\phi }= & {} [I_2\otimes R_{\phi }\bar{L}_1^+](\phi - [e\otimes G]\, b-[\varLambda \otimes L_1]\, z_1),\; \nonumber \\&{\mathsf {D}}(\tilde{\phi }) = Q_{\phi \phi } \otimes I_{m-2} \end{aligned}$$

(9)

with the least-squares inverse $\bar{L}_1^+=(\bar{L}_1^TR^{-1}\bar{L}_1)^{-1}\bar{L}_1^TR^{-1}$, where $\bar{L}_1=L_1- l_2(l_2^TR^{-1}l_2)^{-1}l_2^TR^{-1}L_1$ (Teunissen 2000). Matrices $R_{p}$ and $R_{\phi }$ are the Cholesky factors of $R^{-1}$ and $(\bar{L}_1^+R\bar{L}_1^{+T})^{-1}$, respectively. Thus, $R_pRR_p^T=I_{m-1}$ and $R_{\phi }(\bar{L}_1^+R\bar{L}_1^{+T})R_{\phi }^T=I_{m-2}$.

Figure 3 shows samples of such zenith-referenced residuals on GLONASS code and phase L1 observables. As shown, they fluctuate randomly around zero (grey lines) and their histograms (green bars) are well approximated by a zero-centred normal distribution, showing that they are indeed zero-mean. Moreover, their empirical standard deviations represent solutions for $\sigma _{p_{1}}$ and $\sigma _{\phi _{1}}$. According to the results of Fig. 3, the code zenith-referenced standard-deviation on L1 is estimated as $\hat{\sigma }_{p_{1}} = 41$ cm, whereas its phase counterpart is estimated as $\hat{\sigma }_{\phi _{1}} = 1.5$ mm.

GLONASS-only positioning and attitude

In this section, we first show the model’s positioning capability and then its capability for instantaneous direction finding using a single frequency.

Fig. 4

GLONASS Positioning (single-epoch, dual-frequency): (left) Single-epoch ADOP time series with number of visible satellites in green and red (green for successful instantaneous ambiguity resolution); (right) Epoch-by-epoch, ambiguity-resolved horizontal scatterplot and vertical time series, with their $95\%$ confidence ellipse, for when ${\mathrm{ADOP}} \le 0.12$ cycle

Dual-frequency positioning

First, we will consider the epoch-by-epoch ambiguity-resolved positioning capability of model (1). As is well known, the success of GNSS ambiguity resolution depends on various factors of which the number of visible satellites is an important one (Leick et al. 2015; Teunissen and Montenbruck 2017). This dependence is also clearly visible in Fig. 4 (left). It shows periods for which instantaneous ambiguity resolution is successfully possible, but also periods for which it is impaired, i.e. when the ADOPs are too large due to a too-large drop in the number of visible satellites. For the periods with small-enough ADOPs, we computed the instantaneous ambiguity-resolved positions. Their horizontal scatterplot and vertical time series, together with their $95\%$ confidence ellipse, are shown in Fig. 4 (right). It demonstrates the epoch-by-epoch high-precision position capabilities of the GLONASS-only model (1). For the periods for which instantaneous ambiguity resolution is not possible, multiple epochs will be needed to compensate for the lack of satellites, which as a result may sometimes culminate into two minutes of time-to-first-fix.

Fig. 5

GLONASS Direction Finding (single-epoch, single-frequency): (Left) unit-sphere scatterplot of the length-constrained, ambiguity-float direction vector $\hat{b}_{\mathrm{BC}}/l$; (Middle) unit-sphere scatterplot of unconstrained ambiguity-fixed direction vector $\hat{b}(\check{z}_{\mathrm{UC}})/||\hat{b}(\check{z}_{\mathrm{UC}})||$, computed with LAMBDA; (Right) unit-sphere scatterplot of length-constrained, ambiguity-fixed direction vector $\check{b}(\check{z}_{\mathrm{BC}})/l$, computed with C-LAMBDA. The red/green dots indicate incorrectly/correctly fixed solutions. The instantaneous unconstrained/constrained success rates are $77.2\%/99.9\%$.The grey scatterplots on the latter two spheres are the direction vectors computed from the ambiguity-float estimators $\hat{b}$ and $\hat{b}_{\mathrm{BC}}$, respectively

Single-frequency direction finding

Once a baseline vector is determined, directional information can be derived from it. If the baseline vector $b=(b_{1}, b_{2}, b_{3})^{T}$ is parametrized in the local North-East-Up frame, heading H and elevation E can be computed as

$$\begin{aligned} H = \arctan \frac{b_{2}}{b_{1}}\;\;,\;\; E = \arctan \frac{b_{3}}{\sqrt{ b_{1}^{2}+b_{2}^{2}}} \end{aligned}$$

(10)

For a precise directional determination, we need integer ambiguity resolution so as to be able to exploit the very precise carrier-phase data. It is well known however that GNSS single-frequency ambiguity resolution is not instantaneous possible without an additional strengthening of the model. A customary strengthening for direction finding is to assume the baseline length between the two antennas known. This implies solving the single-frequency version of the GLONASS model (1) with the additional nonlinear constraint $||b||=l$, in which length l is known. Although different methods for dealing with this constraint have been proposed in the literature, see, e.g. Gong et al. (2015) and Giorgi (2017), the method that achieves the highest success rate is the one that incorporates the constraint integrally into the ambiguity objective function. As a result, the integer ambiguity solution is now not computed by minimizing a quadratic form over the space of integers, i.e. as the unconstrained (UC) integer estimator $\check{z}_{\mathrm{UC}} = \arg \min _{z \in {\mathbb {Z}}^{n}}\{ ||\hat{z}-z||_{Q_{\hat{z}\hat{z}}}^{2}\}$, but instead as the baseline-length-constrained (BC) integer estimator (Teunissen 2010),

$$\begin{aligned} \check{z}_{\mathrm{BC}} = \arg \min _{z \in {\mathbb {Z}}^{n}}\left\{ ||\hat{z}-z||_{Q_{\hat{z}\hat{z}}}^{2}+||\hat{b}(z)-\check{b}(z)||_{Q_{\hat{b}(z)\hat{b}(z)}}^{2} \right\} \end{aligned}$$

(11)

in which $\hat{b}(z)=\hat{b}-Q_{\hat{b}\hat{z}}Q_{\hat{z}\hat{z}}^{-1}(\hat{z}-z)$ is the conditional baseline estimator, $\check{b}(z) = \arg \min _{||b||=l} ||\hat{b}(z)-b||_{Q_{\hat{b}(z)\hat{b}(z)}}^{2}$ the corresponding length-constrained baseline solution, and $\hat{z}$ the decorrelated float solution of the GLONASS integer ambiguities. Note that with the objective function of (11), potential integer candidates $z \in {\mathbb {Z}}^{n}$ are now not only downweighted if they are further away from the float solution $\hat{z} \in {\mathbb {R}}^{n}$, but also if their corresponding conditional baseline $\hat{b}(z)$ is further apart from the origin-centred sphere of radius l. It is this additional penalty in the ambiguity objective function that allows for significantly higher success rates, see, e.g. Giorgi et al. (2010) and Teunissen et al. (2011). Once $\check{z}_{\mathrm{BC}}$ of (11) has been computed, the corresponding ambiguity-fixed, length-constrained baseline is computed as $\check{b}(\check{z}_{\mathrm{BC}})$. It is then from this solution that the precise directional information can be obtained.

To show the capabilities of GLONASS model (1) for single-epoch, single-frequency direction finding, as well as the importance of incorporating the baseline-length constraint, we compare the directional accuracy of four different single-frequency, instantaneous baseline estimators:

• 1. unconstrained, ambiguity-float baseline $\hat{b}$;

• 2. length-constrained, ambiguity-float baseline $\hat{b}_{\mathrm{BC}} = \arg \min _{||b||=l} ||\hat{b}-b||_{Q_{\hat{b}\hat{b}}}^{2}$;

• 3. unconstrained, ambiguity-fixed baseline $\hat{b}(\check{z}_{\mathrm{UC}})$;

• 4. length-constrained, ambiguity-fixed baseline $\check{b}(\check{z}_{\mathrm{BC}})$.

The unconstrained solution $\check{z}_{\mathrm{UC}}$ is computed with the LAMBDA method (Teunissen 1995), while the constrained ambiguity solution (11) is computed with the C-LAMBDA method, thereby using the numerically efficient bounding-function formulation of Lemma 3 in Teunissen (2010).

The results are shown in Fig. 5. The unit-sphere scatterplot of $\hat{b}_{\mathrm{BC}}/l$ is shown in Fig. 5 on the left, while those of $\hat{b}(\check{z}_{\mathrm{UC}})/||\hat{b}(\check{z}_{\mathrm{UC}})||$ and $\check{b}(\check{z}_{\mathrm{BC}})/l$ are shown on the middle and right, respectively. The ambiguity-float scatterplots are shown in grey, while the ambiguity-fixed scatterplots in green and red, depending on whether the fixing was done correctly or not. Note that elevation is less precise than heading (this is particularly pronounced in the ambiguity-float solutions), which is due to the height being poorer determined than the horizontal positions. Also note that the precision of the length-constrained ambiguity-float solution does not differ too much from that of the unconstrained ambiguity-float solution. Hence, the importance of the length constraint is not so much to improve the precision of the code-driven solution, but rather to improve the ambiguity resolution performance by means of which the solutions become driven by the very precise carrier-phase data.

From the above, we can now conclude the following with regard to the capability of GLONASS model (1) for direction finding: (a) without ambiguity resolution, the length-constrained baseline solutions $\hat{b}_{\mathrm{BC}}$ will not be precise enough for direction finding; (b) without the length constraint, the ambiguity-fixed baseline solutions $\hat{b}(\check{z}_{\mathrm{UC}})$ will not be reliable enough for direction finding; (c) precise and reliable GLONASS single-frequency direction finding is instantaneously possible with $\check{b}(\check{z}_{\mathrm{BC}})$, i.e. when model (1) is integer ambiguity resolved under the baseline constraint $||b||=l$ using (11).

Fig. 6

Single-frequency, single-epoch GLONASS+GPS (Perth, Australia, with pair of JAVAD TRE-G3T DELTA receivers and Trimble TRM59800.00 antennae on CUBB-CUCC baseline, 4 March 2019, with 30-s sampling rate): (Left) L1 GPS-only East-North scatterplots and Up-time series; (Right) Combined L1 GPS + L1 GLONASS East-North scatterplots and Up-time series; The ambiguity-float solutions are shown in grey, and the ambiguity-fixed solutions in green (correctly fixed) and red (incorrectly fixed). At the bottom are shown the two ADOP time series in cycles and colour magenta. The formal and empirical $95\%$ confidence ellipses are shown in black and blue, respectively. The instantaneous, empirical success rates of L1 GPS-only and L1 GLONASS + GPS are $92.6\%$ and $99.9\%$ , respectively

Fig. 7

Single-frequency, single-epoch GLONASS + GPS (Dunedin, New Zealand, with pair of U-blox ZED F9P receivers and Trimble Zephyr 2 antennae, 18 April 2019, with 1-second sampling rate): (Left) L1 GPS-only East-North scatterplots and Up-time series; (Right) Combined L1 GPS + L1 GLONASS East-North scatterplots and Up-time series; The ambiguity-float solutions are shown in grey, and the ambiguity-fixed solutions in green (correctly fixed) and red (incorrectly fixed). At the bottom are shown the two ADOP time series in cycles and colour magenta. The formal and empirical $95\%$ confidence ellipses are shown in black and blue, respectively. The instantaneous, empirical success rates of L1 GPS-only and L1 GLONASS + GPS are $96.0\%$ and $100\%$, respectively

Single-frequency GLONASS + GPS

In this section, we show the ease with which the new GLONASS FDMA model can be combined with existing CDMA models. We analyse and demonstrate the instantaneous ambiguity-resolved positioning capabilities of single-frequency GLONASS + GPS for both homogeneous-receiver and mixed-receiver processing.

Instantaneous positioning

We know that single-frequency, single-system, instantaneous CDMA-based integer ambiguity resolution is not reliably possible (Odolinski and Teunissen 2016, 2017). Since this is also true for GLONASS FDMA, we now investigate the instantaneous, single-frequency ambiguity resolution capability of combined GLONASS and GPS. With $m_{G}$ GPS satellites and $m_{R}$ GLONASS satellites, the combined, single-frequency, single-epoch model follows from (1) as

$$\begin{aligned} {\mathsf {E}}\left[ \begin{array}{c} y_{G}\\ y_{R} \end{array} \right] = \left[ \begin{array}{ll} e \otimes G_{G} &{} \;\;{\mathrm{diag}}(0, \lambda _{1, G}) \otimes I_{m_{G}-1} \\ e \otimes G_{R} &{} \;\;{\mathrm{diag}}(0, \lambda _{1, R})\otimes L \end{array} \right] \left[ \begin{array}{c} b \\ a \end{array} \right] \end{aligned}$$

(12)

with the single-frequency pseudorange and carrier-phase data of GPS (G) and GLONASS (R) contained in $y_{G}=(p_{G}^{T}, \phi _{G}^{T})^{T}$ and $y_{R}=(p_{R}^{T}, \phi _{R}^{T})^{T}$, respectively, matrices $G_{G} \in {\mathbb {R}}^{(m_{G}-1) \times 3}$ and $G_{R} \in {\mathbb {R}}^{(m_{R}-1) \times 3}$ capturing their relative receiver-satellite geometries, $\lambda _{1, G}$ and $\lambda _{1, R}$ being the used L1 wavelengths, and $a=(a_{G}^{T}, a_{R}^{T})^{T} \in {\mathbb {Z}}^{m_{G}+m_{R}-2}$ being the combined integer ambiguity vector.

To show the strength of model (12), we compare it with single-frequency GPS-only results. We do this for two locations (Perth, Australia, and Dunedin, New Zealand), with a high-grade geodetic receiver pair (JAVAD TRE-G3T DELTA) for Perth and a mass-market receiver pair (U-blox M8T) for Dunedin. The results, consisting of ambiguity-float and ambiguity-fixed horizontal scatterplots and Up-time series, are shown in Figs. 6 and 7, together with their ADOP time series and their formal and empirical $95\%$ confidence ellipses, depicted in black and blue, respectively.

We first discuss the results of Perth. The GPS-only results of Fig. 6 confirm that instantaneous, single-frequency single-system ambiguity resolution is not reliably possible. The empirical success rate, being $92.6\%$, is far too low. Note that the time series of the incorrectly fixed solutions show a clustering over time and that this is very well predicted by the ADOP time series in cycles, i.e. too-large ADOP-values correspond with epochs of the incorrect ambiguity resolution. These are therefore the periods when the GPS-only model is too weak to enable successful ambiguity resolution.

When we compare the results of the combined model (12) in Fig. 6 with those of GPS-only, we note an improvement in both the float solutions and fixed solutions. However, while the improvements in the float solutions are marginal, those for the fixed solutions are impressive. With the empirical success rate now being $99.9\%$, one can conclude that instantaneous single-frequency ambiguity resolution is indeed successfully possible with the GLONASS + GPS combined model (12).

These conclusions are confirmed by the results of Fig. 7. Remarkably, the mass-market receiver demonstrates a similar performance as that shown in Fig. 6. In fact, the empirical success rates are now even higher, namely $96\%$ for L1 GPS-only and $100\%$ for L1 GLONASS + L1 GPS. This is due to the fact that over Dunedin, more satellites were tracked than over Perth. Also note that the ADOPs again nicely reflect the ambiguity resolution behaviour, both for GPS-only and for GLONASS + GPS.

Mixed-receiver GLONASS phase-only positioning

So far, we have been working with baseline data sets of which both receivers were of the same make and type. We will now consider a data set with a mixed-receiver set-up, namely a Trimble NetR9 receiver and a single-frequency U-blox M8T receiver with patch antenna. First, as before, the data were analysed using the geometry-fixed model. From this, it followed that the between-receiver differential GLONASS code data were shown to be biased. An example time series of the L1 GLONASS DD code-residuals of 1-second sampling rate is shown in Fig. 8 (left). It clearly shows the bias as an almost constant, in this case negative, offset. The occurrence of such bias in mixed-receiver set-ups is consistent with previous GLONASS studies (Yamada et al. 2010; Chuang et al. 2013; Hakansson et al. 2017). Although these and other studies also concluded that these biases can be calibrated because of their stability over time, we were interested to find out whether that would be really needed in the single-frequency case when GLONASS is combined with GPS. We therefore consider the following two single-frequency cases:

• 1. L1 GLONASS phase with L1 GPS code + phase

• 2. L1 GLONASS phase with L1 GPS phase

Thus, in both cases the biased GLONASS code data were dispensed with. Data for the first case were processed on an epoch-by-epoch basis using the combined model (12). Data for the second case, however, cannot be processed on an epoch-by-epoch basis, because if only phase data are available, then instantaneous positioning becomes impossible. More than one epoch of phase data is namely needed to ensure that a sufficient change in receiver-satellite geometry is achieved. The L1 GLONASS + GPS phase-only data set was therefore processed with the multi-epoch model

$$\begin{aligned} {\mathsf {E}}\left[ \begin{array}{c} y(1)\\ \vdots \\ y(k) \end{array} \right] = \left[ \begin{array}{cc} G(1) &{} F\\ \vdots &{} \vdots \\ G(k) &{} F \end{array} \right] \left[ \begin{array}{c} b \\ a \end{array} \right] \end{aligned}$$

(13)

with $y(i)=[\phi _{R}(i)^{T}, \phi _{G}(i)^{T}]^{T}$, $G(i)=[G_{R}(i)^{T}, G_{G}(i)^{T}]^{T}$, and $F={\mathrm{blockdiag}}(\lambda _{1,R}L, \lambda _{1,G} I_{m_{G}-1})$ for $i=1, \ldots , k$, where k denotes the number of epochs.

Fig. 8

Mixed-receiver, single-frequency GLONASS phase-only positioning using a Trimble NetR9 (Leica antenna: LEIAR25.R3) and a single-frequency U-blox M8T (U-blox patch antenna). The 3-hour data set was collected in Delft, the Netherlands, at 1-second sampling rate on 12 August 2016, 14:00 - 17:00 GPS Time: (left) Sample of L1 GLONASS DD code zenith-referenced residuals with bias present; (middle) Instantaneous ambiguity-fixed positioning, combining L1 GLONASS phase-only with L1 GPS code + phase, having $99.9\%$ success rate; (right) 10-epoch ambiguity-fixed positioning, combining L1 GLONASS phase-only with L1 GPS phase-only, having $99.9\%$ success rate

The results for the two cases, as shown in Fig. 8 (middle and right), provide for some important conclusions. In the previous section, it was shown that ambiguity-resolved L1 positioning is instantaneously possible when the standard GPS DD model is combined with our GLONASS model (1). Such would then be the approach to follow when one is confident that the GLONASS DD code data are free from interchannel biases. However, as the above mixed-receiver results show, instantaneous ambiguity-resolved L1 positioning remains possible even if one dispenses with the GLONASS code data. That is, the underlying model is then still strong enough to resolve the GLONASS and GPS ambiguities successfully, while the reduction in positioning precision due to the absence of GLONASS code data is negligible in the final ambiguity-resolved solution.

The second important conclusion concerns the phase-only results. If one would be forced to also do away with the GPS code data, for instance, to avoid the impact of heavy code multipath, then the results show for the mixed-receiver case of Fig. 8-(right) that the single-frequency time-to-first-fix is only ten seconds. Thus, although instantaneous positioning is now not possible, fast L1 ambiguity-resolved phase-only positioning still is.

Summary and conclusions

We studied and numerically demonstrated for the first time the capabilities of the new GLONASS FDMA model (1). As the model guarantees, independent of the actual channel-number entries, the integer-estimability of its ambiguities, we studied the model’s performance for several different ambiguity-resolution critical applications.

We started of with the geometry-fixed formulation and showed that its excellent instantaneous ambiguity resolution capability provides a natural approach for testing and validating the stochastic model of the GLONASS carrier-phase data. We then studied the positioning and attitude determination capabilities of the model, first for GLONASS-only and then for single-frequency GLONASS + GPS. Instantaneous GLONASS-only ambiguity-resolved positioning was shown possible, but as expected becomes problematic if the ADOP is too large.

We also demonstrated that GLONASS-only single-frequency direction finding is instantaneously possible, provided model (1) is integer ambiguity resolved using the ambiguity objective function (11), in which the baseline-length constraint is integrally incorporated. This therefore also holds great potential for array-based attitude determination and array-based precise point positioning (Teunissen 2012).

The ease with which the GLONASS FDMA model (1) can be integrated with CDMA models was shown by analysing the potential of L1 GLONASS + GPS. The strength of the combined model (12) was analysed at two locations using a high-grade geodetic receiver pair as well as a mass-market receiver pair. For both cases, it was shown that instantaneous single-frequency ambiguity resolution is successfully possible with the combined model (12). We also considered the potential of the single-frequency combined model for mixed-receiver processing, particularly for the case the between-receiver GLONASS pseudorange data are biased. Two cases, which dispense with the biased GLONASS code data, were considered: L1 GLONASS phase with L1 GPS code + phase and L1 GLONASS phase with L1 GPS phase, the latter being an option when one wants to avoid the code data altogether, for instance, due to the impact of heavy multipath. For the first case, it was shown that despite the absence of the GLONASS code data, the underlying model is still strong enough to successfully resolve the GLONASS and GPS ambiguities instantaneously. For the second case, which requires changes in receiver-satellite geometry, it was shown that fast and precise L1 ambiguity-resolved positioning is still possible.

With the above performance studies, we have only presented a few of the many possible applications of the GLONASS FDMA model (1). Many more can be considered, such as those for long baselines, network-RTK, PPP-RTK and even for the direct combination of current GLONASS FDMA with its near-future GLONASS CDMA that is currently under development (Urlichich et al. 2011; Langley 2017). We therefore believe that the flexibility of the model and its close resemblance to CDMA models open up a whole variety of carrier-phase-based GNSS applications that have hitherto been a challenge for GLONASS ambiguity resolution.